
Найти медиану равнобедренного треугольника зная только периметр
Даю 30 баллов.

Светило науки — 5 ответов — 0 раз оказано помощи
Ответ:
Периметр равнобедренного треугольника — это сумма всех его трёх сторон. P (ABD) = AB + AD + BD = 24 (сантиметра). Так как данная медиана делит равнобедренный треугольник на два равных треугольника, то: АВ + AD = P (ABC): 2 = 32: 2 = 16 (сантиметров). И если мы из периметра треугольника ABD, суммы всех его трёх сторон, вычтем сумму двух из них, мы найдём третью сторону: BD = Р (ABD) — (AB + AD) = 24 — 16 = 8 (сантиметров). Ответ: 8 сантиметров.
Объяснение:
надеюсь поставишь❤ и 5 ⭐
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
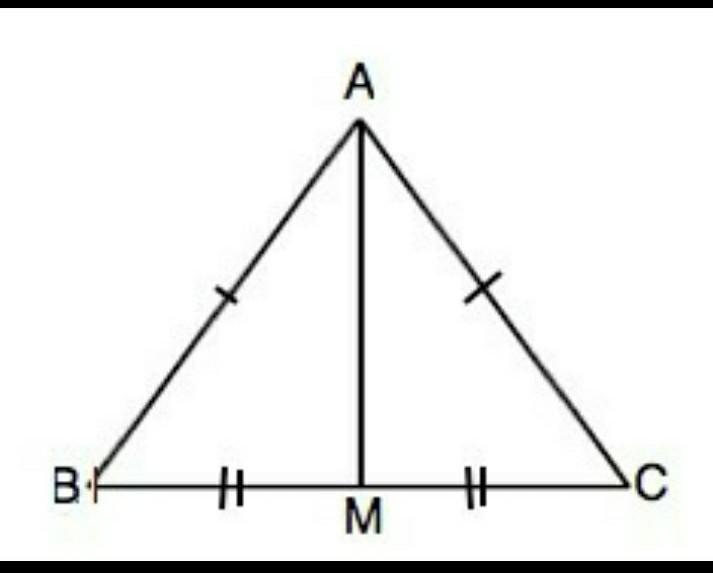
Треугольник АВС — равнобедренный , АМ — медина
АВ = АС; ВМ = МС
Р(АВМ) = АВ + ВМ + АМ = 62
АВ + ВМ = Р (АВС) : 2 = 80 : 2 = 40
(АВ + ВМ) + АМ — (АВ + ВМ) = 62 — 40 = 22
АМ=22 см
Приложения:
Задачи с подобным условием решаются однотипно.
Периметр треугольника АВМ=АВ+ВМ+АВ.
Медиана делит сторону, к которой проведена, пополам. ⇒
ВМ=МС.
Т.к. треугольник равнобедренный, его боковые стороны равны.
Следовательно, АС=АВ. и периметр треугольника АМС равен периметру АВМ.
Сложив периметры треугольников АВМ и АСМ, получим периметр треугольника АВС + 2 длины АМ.
24+24=32+2 АМ
2 АМ=16 см.
АМ=8 см
Пусть равнобедренный треугольник, данный по условию, треугольник АВС, АВ = ВС, АС — основание, ВМ — медиана.
Зная периметр, найдем основание треугольника АВС:
АВ + ВС + АС = 36;
13 + 13 + АС = 36;
АС = 36 — 26 = 10 (см).
Из свойств равнобедренного треугольника известно, что его биссектриса, медиана и высота равны между собой, поэтому можно сделать вывод, что ВМ не только медиана треугольника АВС, но и его высота, поэтому она перпендикулярна его основанию АС.
ВМ делит треугольник АВС на два равных прямоугольных треугольника. Рассмотрим один из них АВМ.
В треугольнике АВМ гипотенуза равна 13 см. Найдем катет АМ. Так как ВМ медиана, то она делит АС пополам на две части АМ и МС:
АМ = МС = АС / 2 = 10 / 2 = 5 (см).
Таким образом, в треугольнике АВМ нам известны гипотенуза и один из катетов, нам нужно найти второй катет ВМ, который является выстой и медианой треугольника АВС:
АВ^2 = АМ^2 + ВМ^2;
13^2 = 5^2 + ВМ^2;
ВМ^2 = 169 — 25;
ВМ^2 = 144;
ВМ = √144 = 12 (см)
Ответ: ВМ = 12 см

