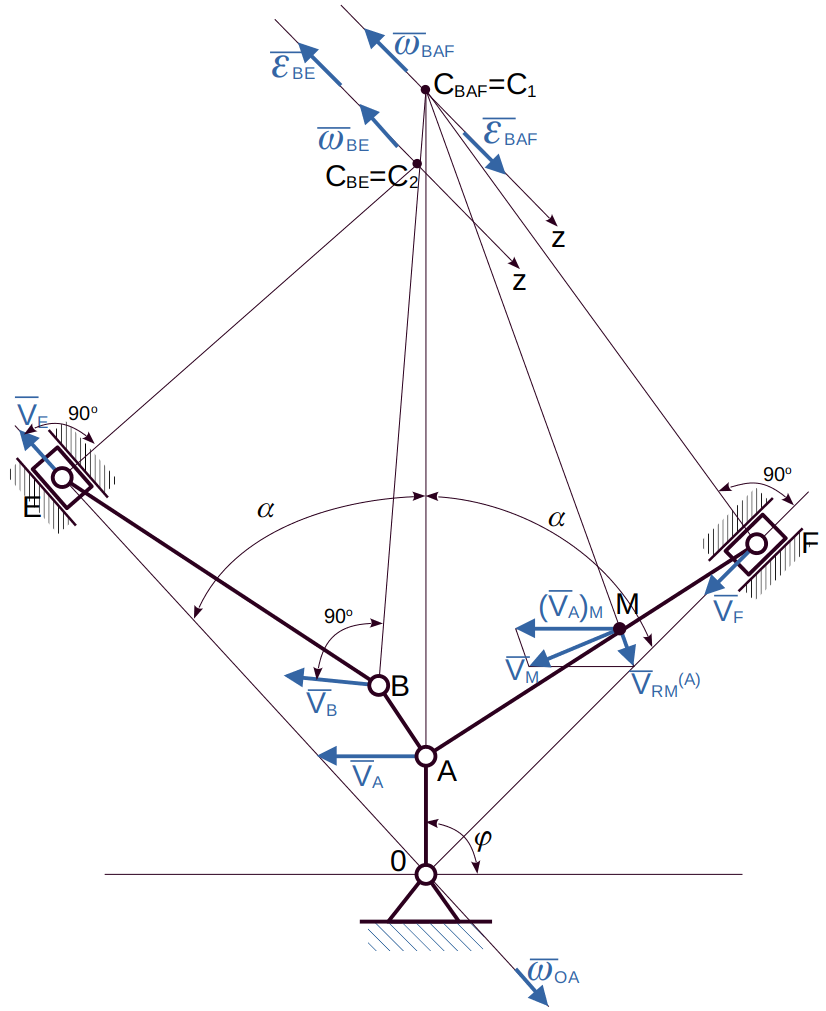
Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.
Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.
В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.
Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
Рисунок 2.16
При определении положения МЦС скорость любой точки может быть записана: VM = VCv + VMCv , где точка CV выбрана за полюс. Поскольку это МЦС и VCv=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:
VM=VCv+ VMCv=VMCv , VM=VMCv=ω∙CVM,
VN=VCv+ VNCv=VNCv , VN =VNCv=ω∙CVN,
VK=VCv+ VKCv=VKCv , VK=VKCv=ω∙CVK.
Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:
VM/CVM=VN/CVN=VK/CVK=ω
Рисунок 2.17
На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.
- CV совпадает с точкой B, VB=0. Шатун вращается вокруг точки B,
ωAB=VA/ACV=VA/AB; - VA/ACV=VB/BCV=ωAB;
- МЦС лежит в «бесконечности»:
VA/∞=VB/∞=ωAB=0, VB=VA; - VA/ACV=VB/BCV=ωAB.
На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.
VA/ACV=VB/BCV=ω
Рисунок 2.18
VB||VA
В этом случае МЦС находится в «бесконечности», т.е.
ω=VA/∞=VB/∞=ωAB=0, VB=VA
Рисунок 2.19
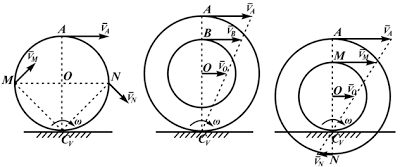
Рисунок 2.20
- VA/2R=V0/R=VM/(R√2)=ω,
- VA/2R=V0/R=VB/(R+r)=ω,
- VA/(R+r)=V0/r=VN/(R-r)=ω
Формулы справедливы при отсутствии проскальзывания в точке CV.
а б
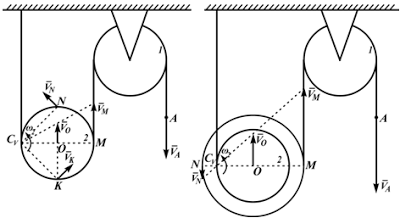
Рисунок 2.21
Для «а»:
VM=VA
VM/MCV=V0/OCV=VN/NCV=VK/KCV=ω2
Для «б»:
VA=VM
VM/MCV=V0/OCV=VN/NCV=ω2
Примеры решения задач >
Ускорение точки в плоскопараллельном движении >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
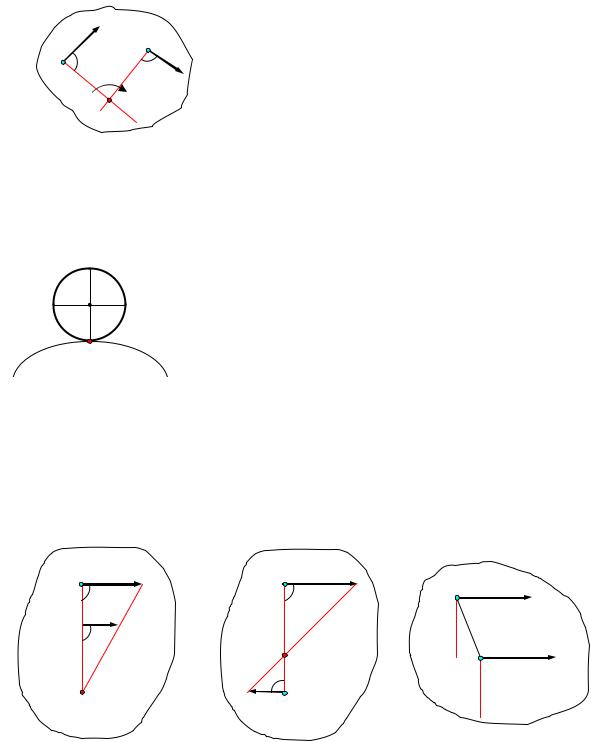
Рис.12
Способы нахождения мгновенного центра скоростей
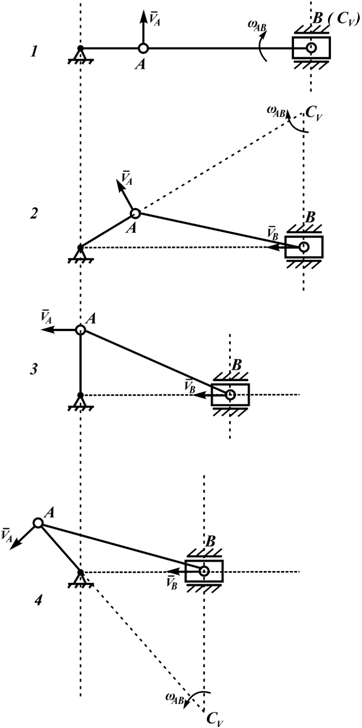
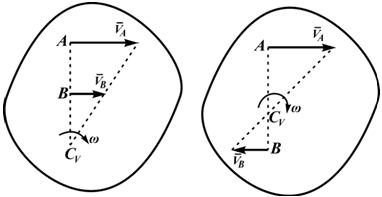
Для определения положения мгновенного центра скоростей плоской фигуры необходимо знать только направления скоростей двух ее точек.
Указанные свойства позволяют определить положение мгновенного центра скоростей плоской фигуры в различных случаях.
|
VA |
1. Если скорости двух точек не параллельны, |
||
|
А |
В |
VB |
то мгновенный центр скоростей лежит в точке |
|
900 |
пересечения перпендикуляров к ним, что следует из |
||
|
900 |
|||
|
теоремы о существовании мгновенного центра ско- |
Рростей (рис.12).
2. Если плоское движение осуществляется
качением без скольжения одного твердого тела по неподвижной поверхности другого, то точка их контакта Р имеет в данный момент скорость, равную нулю, и, следовательно, будет мгновен-
ным центром скоростей (рис.13).
3. Если скорости двух точек А и В плоской фигуры параллельны и с прямой, соединяющей эти точки, составляют прямые углы, то мгновенный центр скоростей Р находится как точка пересечения об-
Рщего перпендикуляра, восстановленного к скоро-
|
Рис.13 |
стям в данных точках, и прямой, проходящей через |
|
концы векторов скоростей (рис.14 и рис.15). |
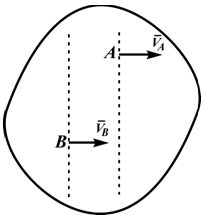
4. Если скорости двух точек параллельны и с прямой, соединяющей точки образуют острые углы, то мгновенный центр скоростей не суще-
ствует (находится в бесконечности). В этом случае скорости всех точек плоской фигуры равны, а угловая скорость равна нулю (рис. 16).
|
А |
VA |
А |
VA |
А |
VA |
||
|
90 |
0 |
90 |
0 |
||||
В
Р VB
В
|
Р |
900 |
|
|
В |
||
|
VB |
||
|
Рис. 14 |
Рис. 15 |
Рис. 16 |
10
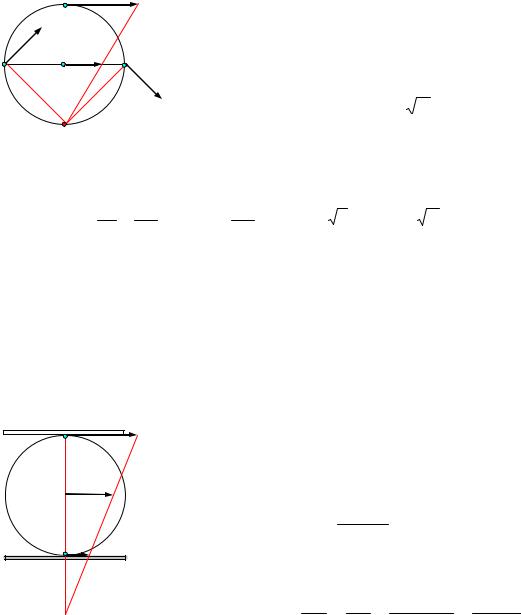
Решение задач с помощью мгновенного центра скоростей.
Задача 1. Найти скорости точек А, В и D обода колеса, катящегося по прямолинейному рельсу без скольжения, если скорость центра колеса С равна VC.
|
Определить скорости точек А, В, D и угловую скорость колеса. |
|||||||||||||||||
|
Решение. Мгновенный центр скоростей |
Р колеса находится (рис.177) в |
||||||||||||||||
|
точке контакта колеса с неподвижной плоскостью. Скорости точек А, В, D |
|||||||||||||||||
|
VD |
перпендикулярны к отрезкам, соединяющим эти |
||||||||||||||||
|
D |
точки с точкой Р, модули скоростей пропорцио- |
||||||||||||||||
|
VA |
нальны их длинам: |
||||||||||||||||
|
С |
VC |
В |
Расстояния точек А и В до мгновенного цен- |
||||||||||||||
|
А |
тра скоростей одинаковы, |
следовательно, скоро- |
|||||||||||||||
|
VB |
сти этих точек равны |
||||||||||||||||
|
VA =VB =VC |
2. |
||||||||||||||||
|
Скорость точки D равна 2VC , так как рас- |
|||||||||||||||||
|
P |
|||||||||||||||||
|
стояние точки D |
до мгновенного центра скоро- |
||||||||||||||||
|
Рис.17 |
|||||||||||||||||
|
VA = |
стей в два раза больше расстояния СР . |
||||||||||||||||
|
AP |
; V |
=V AP ; |
AP = R 2, V |
=V 2. |
|||||||||||||
|
V |
CP |
A |
C CP |
A |
C |
||||||||||||
|
C |
VC |
VC |
|||||||||||||||
|
Угловая скорость колеса равна |
ω = |
= |
. |
||||||||||||||
|
CP |
R |
Задача.2. Диск зажат между двумя рейками, (рис.18) которые движутся со скоростями V1 и V2 (V1 > V2).
Определить угловую скорость диска и скорость его центра, если его радиус равен R.
АVAa
С
ВVB
b
Р
Рис.18
Решение. Скорость точки А диска равна скорости верхней рейки, а скорость точки В – скорости нижней рейки. Мгновенный центр скоростей находится в точке Р (рис.16). Скорость точки С является средней линией трапеции ВАав:
VC = V1 +2V2 .
Угловая скорость
ω = VAPA = VBPB = APVA −−VBPB = V12−RV2 .
Задача 3. Кривошипно-шатунный механизм
11
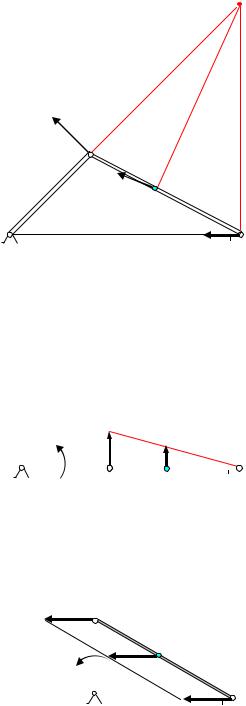
Угловая скорость кривошипа равна ωОА. Определить угловую скорость шатуна и скорости точек А,В, и С для трех положений механизма.
Кривошип ОА вращается вокруг точки О, шатун АВ совершает плоское движение в плоскости чертежа. Во всех случаях скорость точки А перпендикулярна кривошипу и равна VA =ωOA OA. , а скорость точки В направлена по
|
горизонтальной прямой. |
||||||||||||||||||||||||||||||||||||
|
1. Кривошип ОА образует острый угол с горизонтальной прямой |
||||||||||||||||||||||||||||||||||||
|
P |
(рис.19). В этом случае мгновенный |
|||||||||||||||||||||||||||||||||||
|
центр скоростей шатуна находится в |
||||||||||||||||||||||||||||||||||||
|
точке Р, где пересекаются восстановлен- |
||||||||||||||||||||||||||||||||||||
|
ные в точках А и В перпендикуляры к |
||||||||||||||||||||||||||||||||||||
|
скоростям в этих точках. |
||||||||||||||||||||||||||||||||||||
|
VA |
AP |
BP |
||||||||||||||||||||||||||||||||||
|
VA |
= BP |
VB =VA AP . |
||||||||||||||||||||||||||||||||||
|
VB |
||||||||||||||||||||||||||||||||||||
|
A |
Скорость точки С направлена перпенди- |
|||||||||||||||||||||||||||||||||||
|
VC |
C |
кулярно отрезку РС и находится из про- |
||||||||||||||||||||||||||||||||||
|
порции: |
||||||||||||||||||||||||||||||||||||
|
O |
VC |
= |
CP |
V |
=V |
CP . |
||||||||||||||||||||||||||||||
|
VB |
VA |
AP |
C |
A |
AP |
|||||||||||||||||||||||||||||||
|
B |
Угловая скорость шатуна равна |
|||||||||||||||||||||||||||||||||||
|
Pис.19 |
ωAB = |
VA |
||||||||||||||||||||||||||||||||||
|
AP |
||||||||||||||||||||||||||||||||||||
|
2. Кривошип и шатун расположены на одной прямой (рис.20). |
||||||||||||||||||||||||||||||||||||
|
В этом положении мгновенный центр скоростей находится в точке В, |
||||||||||||||||||||||||||||||||||||
|
VA |
поэтому скорость VB |
равна нулю. Ско- |
||||||||||||||||||||||||||||||||||
|
VC |
рость точки С находится из пропорции: |
|||||||||||||||||||||||||||||||||||
|
VC |
CB |
CB |
||||||||||||||||||||||||||||||||||
|
O |
= |
V =V |
. |
|||||||||||||||||||||||||||||||||
|
VA |
AB |
C |
A |
AB |
||||||||||||||||||||||||||||||||
|
A |
C |
|||||||||||||||||||||||||||||||||||
|
B |
Угловая скорость шатуна равна |
|||||||||||||||||||||||||||||||||||
|
Рис.20 |
ωAB = |
VA |
. |
|||||||||||||||||||||||||||||||||
|
AB |
||||||||||||||||||||||||||||||||||||
|
VA A |
3. |
Кривошип |
занимает |
|||||||||||||||||||||||||||||||||
|
вертикальное положение (рис.21). В |
||||||||||||||||||||||||||||||||||||
|
VC |
C |
этом случае мгновенный центр скоростей |
||||||||||||||||||||||||||||||||||
|
шатуна находится в бесконечности, скоро- |
||||||||||||||||||||||||||||||||||||
|
O |
VВ |
B |
сти всех его точек равны, угловая скорость |
|||||||||||||||||||||||||||||||||
|
шатуна равна нулю. |
||||||||||||||||||||||||||||||||||||
|
Рис. 21 |
||||||||||||||||||||||||||||||||||||
12
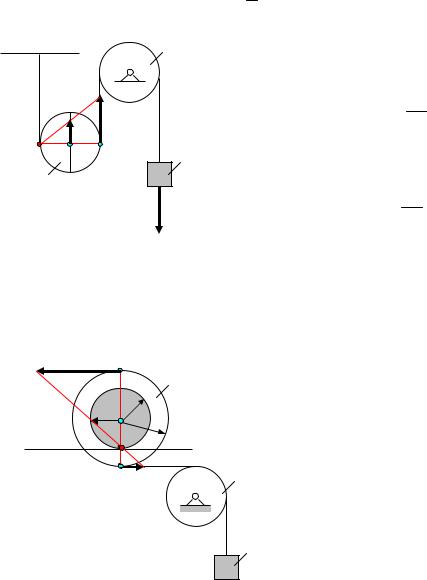
Задача 4. Определить скорости точек А, В, Р подвижного блока 3 (рис.22) и его угловую скорость, если скорость тела 1 равна V1
Решение. Подвижный блок совершает плоское движение. Скорость точки контакта Р подвижного блока с неподвижной нитью равна нулю: VР = 0, т.е. точка Р – мгновенный центр скоростей подвижного блока.
Скорость точки С перпендикулярна отрезку, соединяющему ее с мгновенный центром скоростей: VC CP .
|
2 |
|||
|
О |
|||
|
VС |
VА |
||
|
Р С |
А |
1 |
|
|
3 |
B |
||
|
Рис.22 |
V1 |
||
Скорости точек при плоском движении пропорциональны расстояниям до мгновенного центра скоростей
VC = CP .
VA AP
VA = V1, так как точка А и тело 1 связаны нерастяжимой нитью, тогда
VC = 0,5R .
V1 R
Следовательно, VC = 0,5 VA = 0,5 V1.
Задача 5. Определить угловую скорость и скорости точек А, В, С и Р катушки 3 (рис.23), если скорость груза 1 равна V1.
|
VA |
A |
3 |
|
|
VC |
С |
R |
|
|
r |
|||
|
P |
B VB |
2 |
|
|
O |
Рис.23

Решение. Скорость точки В катушки равна скорость груза 1, так как они связаны нерастяжимой нитью: VВ = V1.
При качении без скольжения в точке контакта катушки с рельсом находится мгновенный центр скоростей Р. Скорости точек А и С перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром скоростей и пропорциональны их расстояниям до мгновенного центра скоростей, поэтому
|
VC |
= |
CP |
; |
VC |
= |
r |
. |
|||
|
V |
BP |
V |
R −r |
|||||||
|
B |
B |
|
Отсюда |
VC |
= VB |
r |
= V1 |
r |
|||
|
R − r |
R |
|||||||
|
Аналогично определим скорость точки А. |
||||||||
|
VA = |
AP |
; |
VA = |
r +R |
. |
|||
|
BP |
||||||||
|
V |
V |
R −r |
||||||
|
B |
B |
Следовательно,
13
|
V |
=V |
r +R |
=V |
r +R |
. |
|||
|
B R −r |
||||||||
|
A |
B R −r |
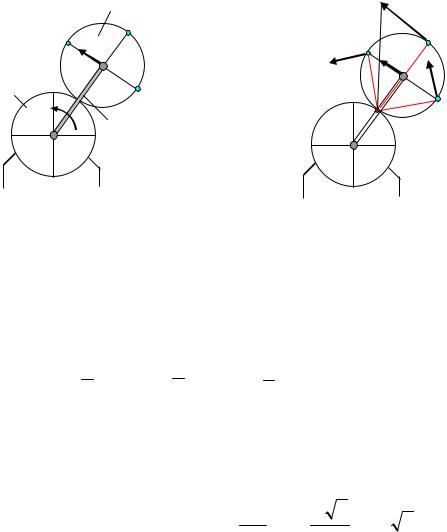
Задача 6. Определить угловую скорость и скорости точек А, В, D, E шестерни 3 (рис.24), которую приводит в движение кривошип ОА, вращающийся вокруг оси О неподвижной шестерни 1 с угловой скоростью ωОА.
|
3 |
VD |
|||||
|
D |
||||||
|
В VA |
В |
D |
||||
|
А |
VВ |
VA |
||||
|
VE |
||||||
|
1 |
Е |
|||||
|
А |
Е |
|||||
|
ωАВ |
P |
|||||
|
2 |
||||||
Решение. Скорость точки А, принадлежащей кривошипу ОА, перпендикулярна кривошипу и равна VA = ωAB AB.
Шестерня 3 совершает плоское движение, ее мгновенный центр скоростей находится в точке зацепления Р с неподвижной шестерней 1 (рис. 24а). Скорости точек В, Е и D перпендикулярны отрезкам, соединяющим их с мгновенным центром скоростей.
VB BP , VD DP , VE EP .
Скорости точек пропорциональны отрезкам, соединяющим эти точки с мгновенным центром скоростей Р.
VB =VE , так как расстояния этих точек до мгновенного центра скоростей равны: ВР = ЕР.
|
VA |
= AP ; откуда VB =VA BP |
=VA |
R |
2 |
=VA 2. |
||||
|
V |
R |
||||||||
|
BP |
AP |
||||||||
|
B |
|||||||||
|
Аналогично определяем скорость точки D. |
|||||||||
|
VA |
= |
AP ; |
откуда VD =VA DP =VA 2R |
= 2VA. |
|||||
|
V |
DP |
AP |
R |
||||||
|
D |
Задача 7. Определить скорости точек А, В, С, D и угловые скорости звеньев механизма, изображенного на рис. 25, если угловая скорость криво-
шипа ОА равна ωОА.
Решение. Во всех вариантах скорость точки А, являющейся концом кривошипа ОА, равна VA = ωОА OA и перпендикулярна кривошипу.
14

Звенья ОА и ОВ механизма (рис.25) совершают вращательное движение. Скорость точки А, являющейся концом кривошипа ОА, равна VA = ωОА OA и перпендикулярна кривошипу.
|
Скорость VB OB .Звенья АС и ВD совершают плоское движение. Звено |
||||||||||||||||||||||
|
Р2 |
СD движется |
поступательно, по- |
||||||||||||||||||||
|
этому скорости точек C и D равны: |
||||||||||||||||||||||
|
VB |
VC = VD . |
|||||||||||||||||||||
|
A |
Мгновенный |
центр |
скоростей |
|||||||||||||||||||
|
VA |
B |
звена АС лежит в точке Р1 пересе- |
||||||||||||||||||||
|
ωOA O |
чения перпендикуляров к скоростям |
|||||||||||||||||||||
|
в точках А и С. |
||||||||||||||||||||||
|
VC С |
D |
V |
= |
CP |
, |
CP |
||||||||||||||||
|
VD |
C |
1 |
V |
=V |
||||||||||||||||||
|
V |
AP |
1 . |
||||||||||||||||||||
|
A |
C |
A AP |
||||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||||
|
Угловая скорость звена АС равна |
||||||||||||||||||||||
|
ωAC = |
VA |
. |
||||||||||||||||||||
|
Рис.25 |
||||||||||||||||||||||
|
Р1 |
AP1 |
|||||||||||||||||||||
|
Проведем |
перпендикуляры к |
|||||||||||||||||||||
|
скоростям VВ |
и VD , точка их пересечения Р2 |
|||||||||||||||||||||
|
— мгновенный центр скоростей |
|
VB |
BP2 |
BP |
||
|
звена ВD. V |
= DP , откуда |
2 |
||
|
VB =VD DP . |
||||
|
D |
2 |
2 |
||
|
Угловая скорость звена ВD равна |
||||
|
ωBD = |
VB |
. |
||
|
BP2 |
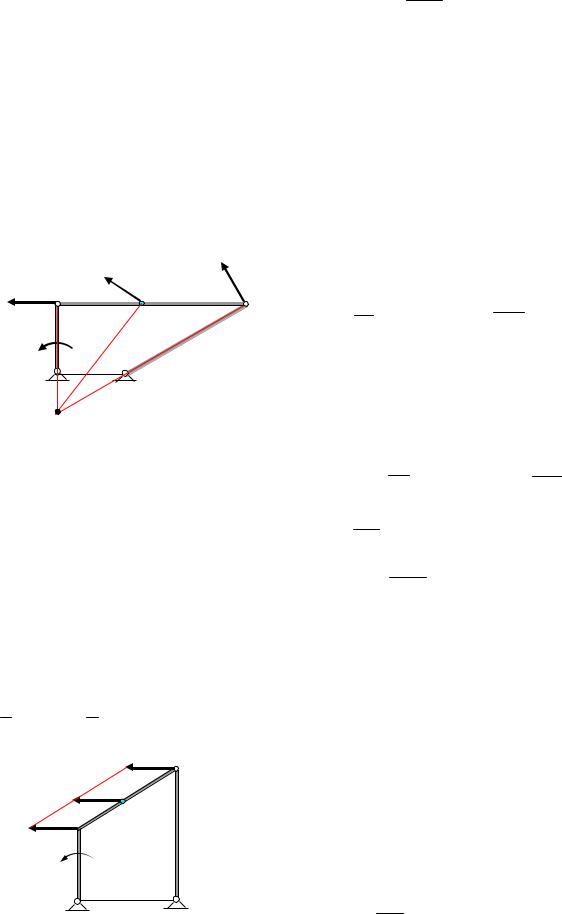
Задача 8. Определить скорости точек А, D и угловые скорости звеньев механизма, изображенного на рис. 26, если угловая скорость кривошипа ОА
равна ωОА.
Скорость точки А равна VA = ωОА OA и перпендикулярна кривошипу ОА. Звено АВ совершается плоское движение, скорость точки В направлена вертикально вниз. Мгновенный центр в данный момент находится в бесконечности, поэтому скорости всех его точек равны, а угловая скорость ωAB = 0 .
Скорость точки D перпендикулярна кривошипу О2D, следовательно, мгновенный центр скоростей звена ВD совпадает с точкой О2.
|
Тогда |
VD = |
DO2 ; |
откуда |
|||||||
|
О1 |
А |
D |
VB |
BO2 |
||||||
|
DO2 . |
||||||||||
|
ωОА |
VD |
90 |
0 |
V |
=V |
|||||
|
D |
B |
BO2 |
||||||||
|
VA |
В |
О2 |
BD |
|||||||
|
Угловая скорость |
звена |
|||||||||
|
равна ωBD = |
VB |
= VD . |
||||||||
|
VB |
BO2 |
DO2 |
||||||||
|
Угловая скорость кривошипа O2D равна ωBD |
= VD . |
||||||||||
|
DO2 |
|||||||||||
|
Задача 9. Определить скорости точек А, С, D и угловые скорости звень- |
|||||||||||
|
ев механизма, изображенного на рис. 25, |
если угловая скорость кривошипа |
||||||||||
|
ОА равна ωОА (рис.27). |
|||||||||||
|
Решение. Звенья О1А и О2В совершают вращательные движения, поэто- |
|||||||||||
|
му скорость точки А направлена перпендикулярно кривошипу О1А и равна |
|||||||||||
|
VA = ωОА· OA. |
|||||||||||
|
Скорость точки D перпендикулярна звену О2D. |
|||||||||||
|
Звено АD совершает плоское движение, мгновенный центр скоростей |
|||||||||||
|
этого звена лежит в точке Р пересечения перпендикуляров, проведенных в |
|||||||||||
|
VD |
точках А и D к скоростям VA и VD. |
||||||||||
|
VC |
Скорость точки D находим из про- |
||||||||||
|
VA |
А |
D |
|||||||||
|
С |
порции |
VD |
DP |
. VD |
=VA DP . |
||||||
|
= |
|||||||||||
|
ωОА |
VA |
AP |
AP |
||||||||
|
Соединим |
точек |
С с мгновенным |
|||||||||
|
О1 |
|||||||||||
|
О2 |
центром скоростей Р, скорость точки С |
||||||||||
|
будет направлена перпендикулярно от- |
|||||||||||
|
Р |
резку СР. |
||||||||||
|
Рис.27 |
Модуль этой скорости найдем из |
||||||||||
|
пропорции |
VC |
= CP |
, VC =VA CP . |
||||||||
|
VA |
AP |
AP |
|||||||||
|
Угловая скорость звена АD равна ωAD = |
VA . |
||||||||||
|
AP |
VD . |
||||||||||
|
Угловая скорость кривошипа равна |
ω |
= |
|||||||||
|
O2D |
O2 D |
||||||||||
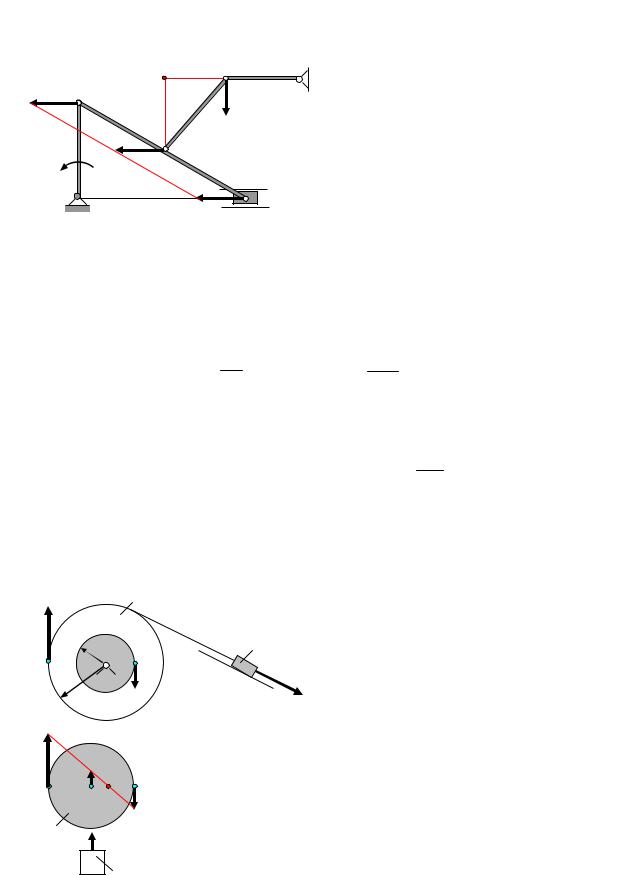
Задача 10. Определить скорости точек А, В, С, и угловые скорости звеньев механизма, изображенного на рис. 28, если угловая скорость криво-
шипа ОА равна ωОА.
Решение. Звенья ОА и DB совершают вращательные движения, поэтому
VA OA , VB
VC
VA
ωОА 
О
BD . Скорость точки А равна VA = ωОА· OA. Звено совершает
|
VВ |
плоское движение, так как скорости точек А и В |
||
|
В |
параллельны, то мгновенный центр скоростей |
||
|
С |
этого звена находится в бесконечности, поэтому |
||
|
скорости всех его точек геометрически равны |
|
VA = VB = VC. |
|
|
Угловая скорость звена AВ равна нулю. Уг- |
|
|
D |
ловая скорость кривошипа ВD равна |
|
ωBD = VB . |
|
|
BD |
Рис.28
16
|
Задача 11. Определить скорости точек А, В, С, D и угловые скорости |
|||||||||
|
звеньев механизма, изображенного на рис. 29, |
если угловая скорость криво- |
||||||||
|
Р |
D |
шипа ОА равна ωОА. |
|||||||
|
О2 |
Решение. |
Скорость точки А |
|||||||
|
VA |
А |
||||||||
|
VD |
перпендикулярна |
кривошипу |
и |
||||||
|
равна VA = ωОА· OA. Звено АВ со- |
|||||||||
|
VC |
С |
вершает |
плоское |
движение, |
ско- |
||||
|
ωОА |
рость VВ точки В направлена гори- |
||||||||
|
О1 |
VВ |
В |
зонтально влево. В данном положе- |
||||||
|
нии |
мгновенный |
центр скоростей |
|||||||
|
Рис.29 |
звена АВ находится в бесконечно- |
||||||||
|
сти, поэтому скоростей всех |
его |
||||||||
|
точек геометрически равны: VA = VB = VC. |
|||||||||
|
Звено CD совершает плоское движение, мгновенный центр скоростей |
|||||||||
|
этого звена лежит в точке Р пересечения перпендикуляров, проведенных к |
|||||||||
|
скоростям в точках С и D. Скорость точки D найдем из пропорции |
|||||||||
|
VC = |
CP |
, VD =VC |
DP . |
||||||
|
V |
DP |
CP |
|||||||
|
D |
|||||||||
|
Угловая скорость звена СD равна ωCD = VC . |
|||||||||
|
CP |
= VD . |
||||||||
|
Угловая скорость кривошипа О D равна |
ω |
||||||||
|
2 |
O2D |
DP |
|||||||
Задача 12. Определить скорость точки С и угловую скорость подвижного блока 3 (рис.30), если скорость тела 1 равна V1, r = 0,5R.
Решение. Блок 2 вращается вокруг точки О, скорость его точки В по ве-
|
VB |
2 |
личине равна скорости тела 1, так |
||||||||||||||||||
|
как они связаны нерастяжимой ни- |
||||||||||||||||||||
|
r O |
1 |
тью: VB = V1.Скорость |
точек |
при |
||||||||||||||||
|
B |
A |
вращательном |
движении пропор- |
|||||||||||||||||
|
R |
VA |
V1 |
циональны |
их |
радиусам |
вращения, |
||||||||||||||
|
поэтому |
VA |
= |
r |
= |
0,5R |
= 0,5 . |
Сле- |
|||||||||||||
|
VD |
VB |
R |
R |
|||||||||||||||||
|
VC |
довательно, VA = 0,5 VB. |
|||||||||||||||||||
|
D |
К |
Подвижный |
блок 3 совершает |
|||||||||||||||||
|
плоское движение, |
при этом |
VD = |
||||||||||||||||||
|
С |
P |
|||||||||||||||||||
|
VE |
VB, VК = VA, так как соответствую- |
|||||||||||||||||||
|
3 |
||||||||||||||||||||
|
V4 |
щие точки связаны нерастяжимыми |
|||||||||||||||||||
|
нитями. |
||||||||||||||||||||
|
4 |
||||||||||||||||||||
|
Рассмотрим движение блока 3. |
||||||||||||||||||||
|
Рис.30 |
Мгновенный центр скоростей нахо- |
|
|
дится в точке пересечения Р общего |
||
|
17 |
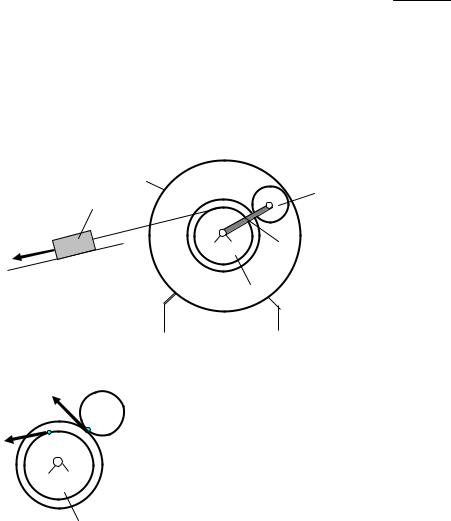
перпендикуляра, проведенного к скоростям VD и VК , и прямой, проходящей через концы этих векторов. Конец вектора скорости VС точки С лежит на прямой, соединяющей концы векторов скоростей VD и VК .
VК = VA = 0,5VB, VD = VB , тогда VК = 0,5VD.
Составим пропорцию:
VK = KP
VD DP .
Обозначив СР = х, тогда KP = R — x, DP = R + x. Подставив эти значения в пропорцию, получим
|
0,5 V |
R − x |
R |
|||||
|
V |
D = |
, |
откуда x = |
. |
|||
|
R + x |
|||||||
|
3 |
|||||||
|
D |
Тогда расстояние точки К до мгновенного центра скоростей Р равно KP = R – x = 2/3 R, т.е. расстояние точки С до мгновенного центра скоростей в два раза меньше, чем то же расстояние до точки К, поэтому скорость точки будет в два раза меньше скорости точки К. VC = 0,5· VK = 0,5 VA = 0,25 V1.
Угловая скорость блока 3 равна ω3 = CPVC = 0,25RV1 3 = 0,75VR1 .
Скорость груза 4, подвешенного на нити в точке С, равна скорости точки С.
V4 = VC = 0,25 V1.
Задача 13. Определить скорость точки С и угловую скорость кривошипа ОС указанного на рис.31 механизма, если скорость тела 1 равна V1 (радиусы тел 3 и 5 заданы).
|
2 |
5 |
Решение. Данный механизм со- |
||||||||||
|
C |
||||||||||||
|
1 |
стоит из пяти, соединенных между |
|||||||||||
|
V1 |
O |
4 |
собой тел. |
|||||||||
|
1. Тело 1, двигаясь вниз по на- |
||||||||||||
|
клонной плоскости, сообщает телу 3 |
||||||||||||
|
3 |
вращательное движение вокруг точ- |
|||||||||||
|
ки О. |
||||||||||||
|
Рис.31 |
В свою очередь тело 3, находясь |
|||||||||||
|
в зацеплении с телом 5, сообщает |
||||||||||||
|
VK |
ему плоское движение. |
|||||||||||
|
5 |
Точка С тела 5 приводит в движение кривошип ОС, кото- |
|||||||||||
|
VA |
K |
рый вращается вокруг точки О. |
||||||||||
|
A |
2. Рассмотрим движение тела 3 (рис.31а). Скорость |
|||||||||||
|
O |
точки А равна скорости груза 1, так как они связаны не- |
|||||||||||
|
растяжимой нитью. Определим скорость точки К. |
||||||||||||
|
3 |
Скорости точек вращающегося тела относятся как |
|||||||||||
|
их радиусы вращения: |
||||||||||||
|
Рис. 31 а |
VA |
= |
r |
. |
||||||||
|
VK |
||||||||||||
|
R |
18

Отсюда скорость
|
VC |
P |
VK =VA |
R |
=V1 |
R |
. |
|
|
r |
|||||||
|
5 |
r |
||||||
|
K |
C |
3. Рассмотрим движение тела 5 (рис.31 |
|||||
|
б). |
Точка Р является мгновенным центром |
||||||
скоростей, так как в этой точке тело 5 находится в зацеплении с неподвижной шестер-
3ней 2. Скорость точки находим из пропорции
|
VC |
= |
CP |
||||||||||||||||
|
, |
||||||||||||||||||
|
Рис. 31 б |
VK |
KP |
||||||||||||||||
|
CP |
r3 |
=VK |
=V1 R . |
|||||||||||||||
|
VC |
VC =VK |
= |
||||||||||||||||
|
KP |
||||||||||||||||||
|
C 5 |
2r3 |
2 |
2 r |
|||||||||||||||
|
4. Кривошип вращается (рис.31в) вокруг точки О |
||||||||||||||||||
|
определим по форму- |
||||||||||||||||||
|
O |
4 |
с угловой скоростью, которую |
||||||||||||||||
|
VC |
||||||||||||||||||
|
ле |
ωOC = |
. |
||||||||||||||||
|
OC |
3
Рис. 31 в
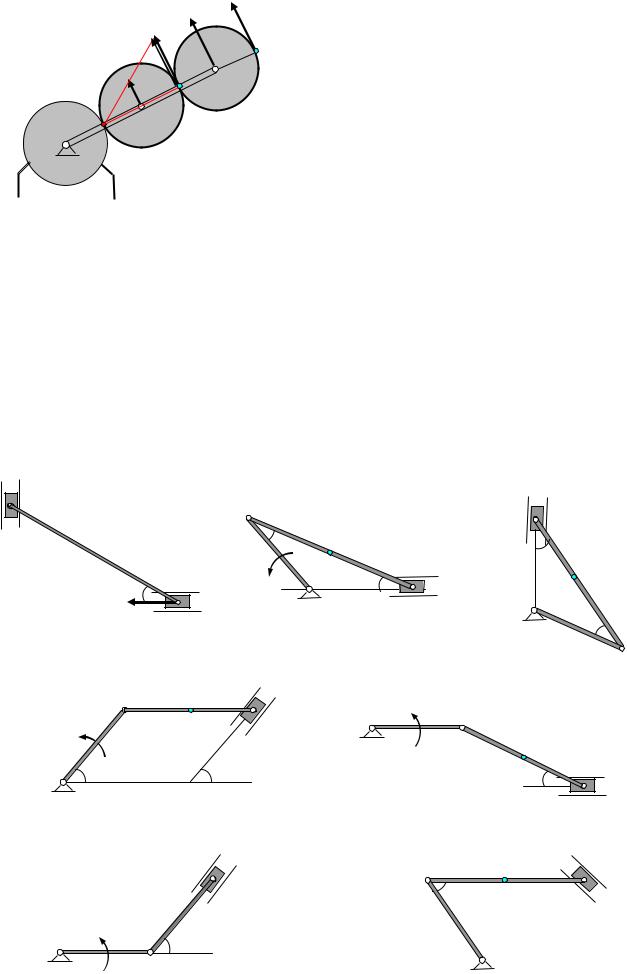
Задача 14. Кривошип ОС соединяющий центры трех шестерен одинакового радиуса R (рис.32), вращается вокруг точки О с угловой скоростью ω.
|
VС |
Шестерня |
1 закреплена |
неподвижно, |
|||
|
шестерни 2 и 3 приводятся в движение |
||||||
|
D |
||||||
|
кривошипом. Определить скорости точек |
||||||
|
VA |
С |
контакта |
между шестернями, скорость |
|||
|
точки D и угловые скорости подвижных |
||||||
|
ω |
||||||
|
А |
3 |
шестерен. |
||||
|
О |
2 |
Решение. |
||||
|
1. Рассмотрим движение кривошипа. |
||||||
|
1 |
||||||
|
Скорости точек А и С (рис.32) на- |
||||||
|
правлены |
перпендикулярно |
кривошипу |
||||
|
Рис.32 |
ОС и равны |
VA = ω·OA = 2 ω R, VC = ω·OC = 4 ω R.
2. Рассмотрим движение шестерни 2.
Шестерня 2 совершает плоское движение, (рис.32 а) скорость точки А известна. В точке контакта с неподвижной шестерней 1 находится мгновенный центр скоростей Р.
19
|
VD |
Скорость VK направлена перпендику- |
||||||||||||
|
лярно отрезку КР, |
модуль ее определяет- |
||||||||||||
|
VК |
VС |
||||||||||||
|
D |
ся из пропорции |
||||||||||||
|
VK |
= |
KP |
= |
2R |
= 2 , |
||||||||
|
VA |
С |
VA |
AP |
R |
|||||||||
|
А |
К |
откуда VK = 2 VA = 4ω R. |
|||||||||||
|
О Р |
Угловая скорость шестерни 2 равна |
||||||||||||
|
ω2 |
= |
VA |
= |
2ω R |
= 2ω . |
||||||||
|
R |
|||||||||||||
|
AP |
|||||||||||||
|
Рис.32 а |
3. Определим характер движения шес- |
терни 3.
Скорости точек С и D шестерни 3 равны по модулю и параллельны, следовательно, шестерня 3 совершает поступательное движение, угловая скорость такого движения равна нулю.
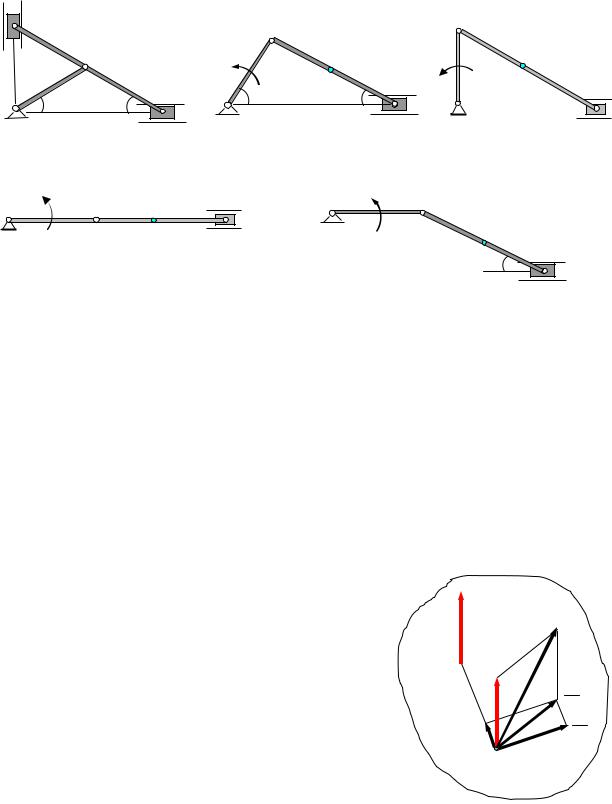
Упражнения.
Определить с помощью мгновенного центра скоростей скорости точек А, В и С в механизмах, представленных на чертежах
|
А |
В |
||||||||||
|
А |
|||||||||||
|
300 |
C |
300 |
|||||||||
|
30 |
0 |
В |
ωОА |
О |
300 |
В |
C |
||||
|
О |
|||||||||||
|
VВ |
|||||||||||
|
Рис.1 |
Рис.2 |
300 |
|||||||||
|
А |
|||||||||||
|
В |
Рис. 3 |
||||||||||
|
A |
C |
ωОА |
|||||||||
|
O |
A |
||||||||||
|
ωОА |
|||||||||||
|
C |
|||||||||||
|
O |
450 |
450 |
30 |
0 |
В |
||||||
|
Рис.5 |
|||||||||||
|
Рис.4 |
|||||||||||
|
B |
А |
C |
В |
||||||||
|
600 |
|||||||||||
|
O |
ωОА |
450 |
О |
||||||||
|
A |
20 |
||||||||||
Ускорения точек плоской фигуры.
Движение плоской фигуры в своей плоскости можно разложить на поступательное движение вместе с произвольно выбранной точкой, принимаемой за полюс, и вращательное движение вокруг этого полюса.
Следовательно, ускорение любой точки при плоском движении равно
геометрической сумме двух ускорений: ускорения выбранного полюса, и ускорения, полученного данной точкой при ее вращательном движении вокруг полюса.
Пусть известно ускорение точки А плоской фигуры, тогда ускорение другой точки этой фигуры будет равно (рис.33).
aB = aA + aBA ,
где ускорение вращательного движения точки А вокруг точки В раскладывается на нормальное и касательное ускорения:
aBA = aBAτ + aBAn .
aA
aB
A
aA
a BA a n a BAτ
BA B
Рис.33
Касательное ускорение вращательного движения точки вокруг полюса направлено перпендикулярно отрезку АВ, соединяющему точку В с полюсом А, и равно
21
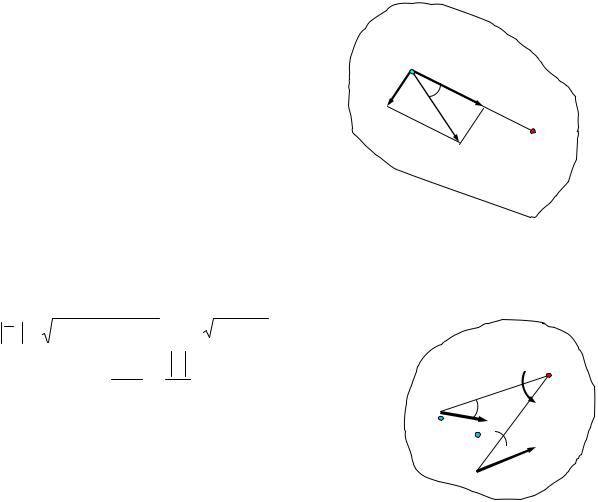
aτBA = ε BA.
Нормальное ускорение направлено по отрезку ВА к полюсу А и равно
aBAn =ω2 BA.
Окончательно, полное ускорение точки В равно геометрической сумме трех ускорений: ускорения выбранного полюса А, нормального и касательного ускорений вращательного движения точки В вокруг этого полюса:
aB = aA +aBAn +aBAτ .
Мгновенным центром ускорений называется точка, принадлежащая связанной с плоской фигурой плоскости, ускорение которой в данный момент равно нулю.
Если за полюс выбрать мгновенный центр ускорений, то ускорение произвольной точки плоской фигуры определяется как ускорение вращательного движения вокруг мгновенного центра ускорений (рис.34).
|
aA = aAL = aALn + aALτ , |
|||||
|
где L –мгновенный |
центр ускорений, aALn |
— |
|||
|
нормальное |
τ |
касательное ус- |
А |
||
|
ускорение, aAL — |
aALτ |
ε aALn |
|||
|
корение точки А вращательного движения пло- |
|||||
|
ской фигуры вокруг мгновенного центра уско- |
L |
||||
|
рений. |
aALn =ω2 AL, |
aτAL =ε AL. |
aA |
||
|
Ускорение aALn |
— направлено по AL , уско- |
||||
|
рение aALτ |
— перпендикулярно AL. Ускорение |
Рис.34 |
|||
|
aA точки А образует угол α с отрезком AL со- |
|||||
единяющим точку А с мгновенным центром ускорений и равно (рис.35)
|
aA = (aALn )2 +(aτAL )2 = AL ω4 +ε2 , |
||||
|
tgα = aτAL |
= |
ε |
. |
L |
|
aALn |
ω2 |
А |
ε |
|
Таким образом, если известно ускорение точки А плоской фигуры, то, чтобы найти положение мгновенного центра ускорений, следует это ускорение повернуть вокруг точки А на угол α в сторону вращения фигуры и на полученной прямой отложить расстояние
22
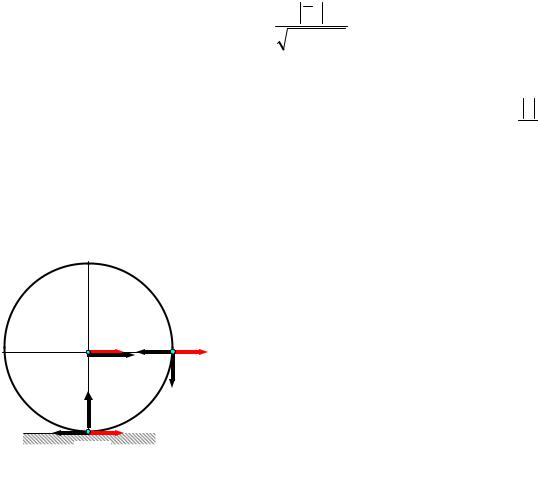
Если известны направления ускорений двух точек плоской фигуры, то мгновенный центр ускорений определяется как точка пересечения получен-
ных поворотом этих ускорений на один и тот же угол α = arctq ωε2 в сторону вращения.
Задача1. Центр колеса, катящегося без скольжения по горизонтальной плоскости, в данный момент имеет скорость VC = 2 м/c и ускорение аC = 1,6 м/c. Радиус колеса R = 0,4 м. Определить точек В и Р (рис. 36).
Решение. Так как скорость и ускорение точки С известны, то принимаем точку С за полюс.
|
С |
aC |
В |
aC |
Тогда aB = aC +aBCn +aBCτ |
|||
|
aP = aC +aPCn +aPCτ , |
|||||||
|
VC |
|||||||
|
aPCn |
a n |
где |
|||||
|
BC |
|||||||
|
τ |
aBCn = ω2 BC = ω2 R, |
aPCn = ω2 PC = ω2 R, |
|||||
|
aPC |
Р |
aC |
τ |
= ε BC = ε R, |
τ |
||
|
Рис. 36 |
aBC |
aPC = ε BC = ε R. |
Мгновенный центр скоростей колеса находится в точке Р – точке каса-
|
ния колеса с неподвижной плоскостью, поэтому |
||||||||||||||||||
|
VC = ωCP =ω R, откуда ω = |
VC |
, при t = 1c, ω =ω = |
2 |
=5 (1/ c). |
||||||||||||||
|
R |
0,4 |
|||||||||||||||||
|
Угловое ускорение колеса |
||||||||||||||||||
|
ε = |
dω |
= |
1 |
dVC |
= |
aC |
, при t =1 c, ε = |
1,6 |
= 4 (1/ c2 ) |
|||||||||
|
dt |
dt |
0,4 |
||||||||||||||||
|
R |
R |
|||||||||||||||||
|
Тогда |
aC |
aC |
||||||||||||||||
|
aτBC = ε R = |
R = aC , |
aτPC = ε R = |
R = aC . |
|||||||||||||||
|
R |
||||||||||||||||||
|
R |
Ускорение точки Р будет направлено к центру колеса точке С и равно
aP = aBCn =ω2 R = 52 0,4 =10 (м/ c2 ) .
Для определения ускорения в точке В спроектируем векторное равенство aB = aC +aBCn +aBCτ на горизонтальную ось x и вертикальную ось у:
23
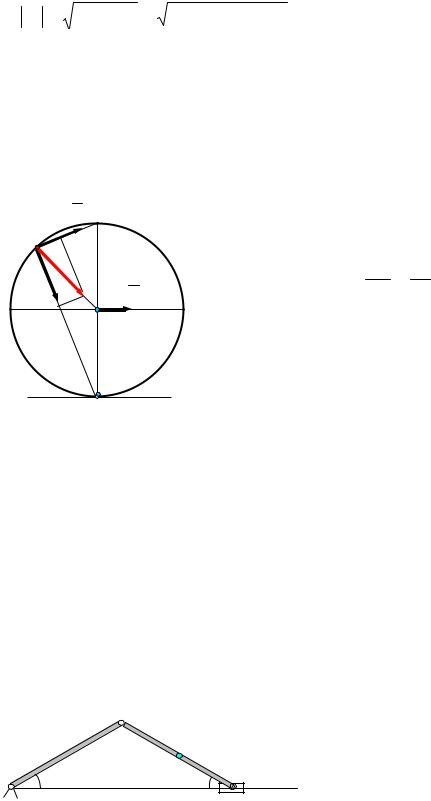
|
aBx |
= aC − aBCn = aC −ω2 R =1,6 −52 0,4 = −8,4 ( м/ с2 ) |
|
aBy |
= −aτDC = −aC = −1,6 ( м/ c2 ) |
|
aB = |
aBx2 + aBy2 = (−8,4)2 +(−1,6)2 ≈ 8,55 ( м/ c). |
Задача 2. Колесо радиуса R = 0,4 м катится без скольжения так, что центр колеса имеет постоянную скорость VC =2 м/c. Определить ускорения точек Р и М обода колеса(рис.37)
Решение. Так как скорость центра колеса является постоянной, то его
ускорение рений.
aMτ
M
aMn
aC = 0 , следовательно, точка С будет мгновенным центром уско-
VM
aMC VC

Мгновенный центр скоростей находится в точке Р – точке контакта с неподвижной плоскостью. Значит
ω = CPVC = VRC = const.
Отсюда следует,
|
& |
tgα = |
ε |
= 0, α = 0. |
|
|
чтоε =ω = 0, |
ω |
2 |
||
Следовательно, ускорения всех точек колеса будут направлены к центру колеса и равны
|
aM =ω2 |
2 |
|||
|
Рис.37 |
CM = ω2 R = VC . |
|||
|
R |
Ускорение точки М, находящейся на ободе колеса, являясь полным ускорением криволинейного движения, раскладывается на касательное, направленное по скорости в этой точке, и нормальное ускорение, направленное по перпендикуляру к скорости, т.е. по прямой, соединяющей точку М с мгновенным центром скоростей. (рис.37.).
aM = aMn + aMτ ; aMn = aM cosα, aτM = aM sin α.
Задача 3. Определить скорости точек А, В, С и ускорения точек А и В кри- вошипно-шатунного механизма (рис.38), если кривошип вращается с посто-
|
y |
янной угловой скоростью ωОА = 2 |
|||||||
|
А |
1/с, ОА = АВ = 0,6 м, МВ = 0,3 м, ϕ |
|||||||
|
C |
=300. |
|||||||
|
О |
ϕ |
ϕ |
В x |
Решение. Скорость точки А |
||||
|
(рис. 39) перпендикулярна криво- |
||||||||
|
Рис.38 |
шипу ОА и равна |
|||||||
|
VA =ωOA OA =1,2 м/c. |
24
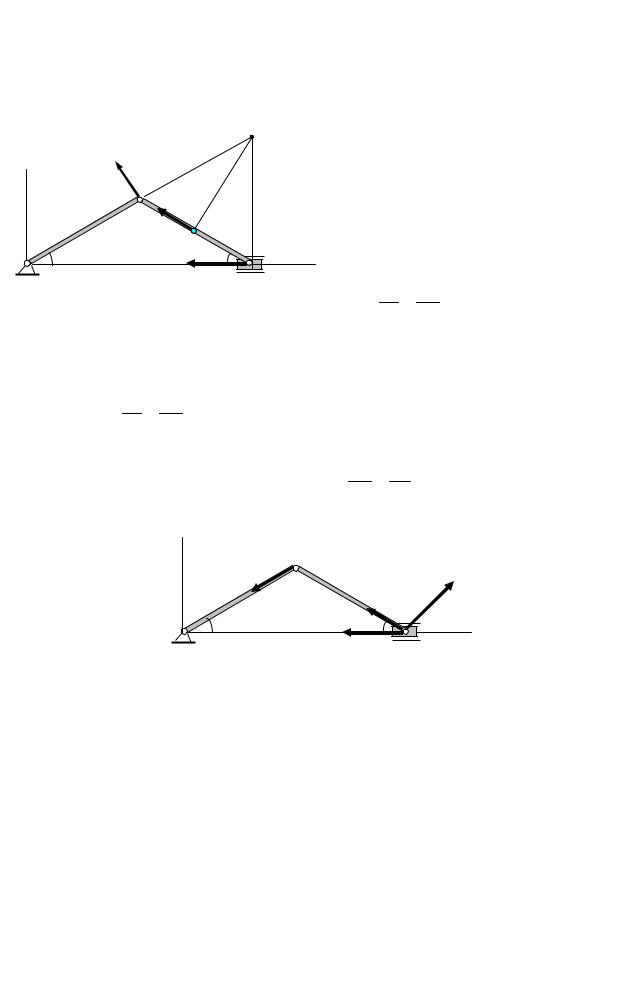
|
Звено АВ совершает плоское движение/ Скорость точки В направлена |
|||||||||||
|
горизонтально, что обусловлено направляющими, вдоль которых движется |
|||||||||||
|
ползун В. |
|||||||||||
|
Для определения скоростей точек А и В, принадлежащих шатуну АВ, оп- |
|||||||||||
|
ределим положение мгновенного центра скоростей этого звена. Проведем |
|||||||||||
|
P |
перпендикуляры |
к |
скоростям |
в |
|||||||
|
точках А и В, мгновенный центр |
|||||||||||
|
y |
VA |
скоростей Р находится в точке их |
|||||||||
|
A |
пересечения. |
||||||||||
|
VC |
Скорости точек при плоском |
||||||||||
|
C |
движении пропорциональны рас- |
||||||||||
|
О |
300 |
300 |
x |
стояниями до мгновенного центра |
|||||||
|
В |
скоростей. |
||||||||||
|
VB |
VB = |
AP |
|||||||||
|
Рис.39 |
. В треугольнике АВР: |
||||||||||
|
АР = ВР, следовательно, VB=VA=1,2 м/с. |
VA |
BP |
|||||||||
|
Скорость VC |
точки С направлена перпендикулярно отрезку СР, соеди- |
||||||||||
|
няющему точку С с мгновенным скоростей. Значение скорости VC находим |
|||||||||||
|
из пропорции: VC |
= CP . Из треугольника АСР: |
СР =AP sin 60. |
|||||||||
|
VA |
AP |
||||||||||
|
Следовательно, VC= VA sin 600 = 1,03 м/с. |
|||||||||||
|
Угловая скорость шатуна равна |
ωAB = VA |
= 1,2 |
= 2 |
м/c. |
|||||||
|
AP |
0,6 |
||||||||||
|
y |
А |
||||||||||
|
aAn |
|||||||||||
|
аВАn |
aBAτ |
||||||||||
|
О |
300 |
||||||||||
|
aB |
В |
x |
|||||||||
|
Рис.40 |
|||||||||||
|
Ускорение точки А представляет собой нормальное ускорение аАn , на- |
|||||||||||
|
правленное по кривошипу (рис. 40) |
|||||||||||
|
aAn =ωOA2 |
OA =2,4 м/c. |
||||||||||
|
Ускорение точки В направлено по оси х и определяется векторным равенст- |
|||||||||||
|
вом: |
aB = aAn +aBA = aAn +aBAn +aBAτ , |
||||||||||
|
(а) |
|||||||||||
|
где векторы aBAn |
и aBAτ |
представляют собой составляющие ускорения вра- |
|||||||||
|
щательного движения звена АВ вокруг точки А. Вектор |
aBAn |
направлен по |
|||||||||
|
радиусу вращения ВА , ускорение aBAτ |
— перпендикулярно АВ. |
||||||||||
|
25 |
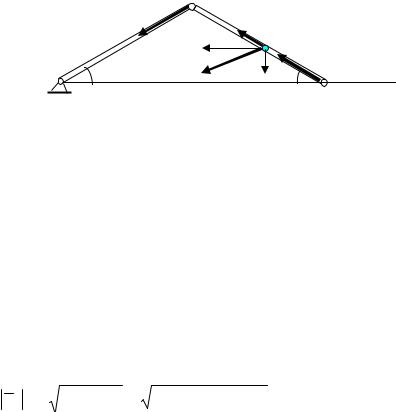
Нормальное ускорение
aBAn =ωAB2 AB =2,4 м/с.
Таким образом, в уравнении (а) неизвестными являются ускорения aB и aBAτ . Для их определения спроектируем равенство (а) на оси х и у.
|
На ось х: |
−aB |
= −aAn cos 300 |
−aBAn cos 300 |
+ aτBA sin 300 . |
(б) |
|||||||
|
На ось у: |
0 = −aAn sin 300 |
+aBAn |
sin 300 +aτBA cos300 . |
(в) |
||||||||
|
Из уравнения (в) находим aτBA = aAn tg300 −aBAn |
tg300 =0. |
|||||||||||
|
Угловое ускорение шатуна равно нулю. |
||||||||||||
|
Из уравнения (б) получаем aB =2,06 м/с. |
||||||||||||
|
Определим ускорение точки С (рис.41 ). |
||||||||||||
|
aC = aAn +aCA = aAn +aCAn +aCAτ |
(г) |
|||||||||||
|
аАn |
А |
|||||||||||
|
n |
||||||||||||
|
аCx |
аCА |
|||||||||||
|
аn |
||||||||||||
|
О |
300 |
аC |
аCy |
ВА В |
x |
|||||||
|
Рис.41 |
||||||||||||
|
Касательное ускорение |
aCAτ = 0 |
|||||||||||
|
Нормальное ускорение |
aCAn =ω2 AC = 22 0,6 =1,2 (м/ c2 ). |
Находим проекции уравнения (г)на оси Ох и Оу:
|
aCx = −aAn cos300 −aCAn cos300 |
= −1,82 (м/ c2 ). |
|
aC y = −aAn sin 302 +aCAn sin 300 = −2,4 0,5 +1,2 0,5 = −0,6( м/ c2 ). |
|
|
Ускорение точки С равно |
|
|
aC = aCx2 +aCy2 = (1,82)2 +(−0,6)2 |
=1,91 ( м/ c2 ) |
26
Контрольрые вопросы
1.Определение плоскопараллельного движения.
2.Уравнения движения плоской фигуры.
3.Определение скоростей точек плоской фигуры.
4.Теорема Жуковского.
5.Мгновенный центр скоростей. Свойства м.ц.с.
6.Способы нахождения мгновенного центра скоростей.
7.Решение задач с помощью мгновенного центра скоростей.
8.Ускорения точек плоской фигуры.
Библиографический список
1.Бутенин Н.В и др. Курс теоретической механики.
Лань, 2002.- 736 стр.
2.Тарг С.М. Краткий курс теоретической механики. Высшая школа, 2004. – 416 стр.
3.Яблонский А.А., Никифорова В.М. Курс теоретической механики. Интеграл-Пресс, 2004. – 608 стр.
4.Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике. Интеграл-Пресс, 2004. – 384 стр.
27
Соседние файлы в папке Термех
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Плоское движение тела:
При изучении темы ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА раздела КИНЕМАТИКА. вы научитесь применять аналитические и графические методы для определения скоростей и ускорений точек тел и механизмов. Хотя эти знания имеют самостоятельную ценность, особенно необходимы они будут для решения задач динамики тела и системы.
Приведены программы расчета кинематики плоского движения в математической системе Maple V. Анимационные возможности этой системы делают решение наглядным, позволяя глубже понять суть задачи.
Методы решения задачи кинематики плоского движения разнообразны. Выбрать оптимальный путь, который может существенно упростить решение, помогут примеры, приведенные в этой главе.
Скорости точек многозвенного механизма
Постановка задачи. Плоский многозвенный механизм с одной степенью свободы находится в движении. Известна угловая скорость какого-либо его звена или скорость одной из точек механизма. Найти скорости точек механизма и угловые скорости его звеньев.
План решения:
Рассмотрим два простых геометрических способа решения задачи, в которых, в отличие от аналитических методов, определяются модули скоростей и угловых скоростей. Не оговаривая отдельно, всякий раз под угловой скоростью
1-й способ. Мгновенные центры скоростей
1. Определяем положение мгновенного центра скоростей (МЦС) каждого звена. МЦС лежит на пересечении перпендикуляров, проведенных
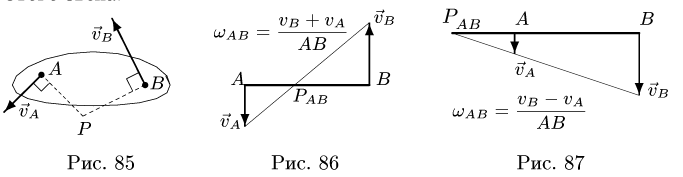
к скоростям точек, принадлежащих звену (рис. 85). У тех звеньев, у которых МЦС не существует (скорости двух точек параллельны и не перпендикулярны отрезку, их соединяющему), угловая скорость равна нулю, а скорости всех точек равны. Если векторы скоростей перпендикулярны отрезку их соединяющем}’, то имеют место два частных случая положения МЦС (рис. 86, 87).
Если тело (колесо, диск, цилиндр) катится по поверхности без проскальзывания, то МЦС этого тела находится в точке касания.
2. Для каждого звена определяем расстояния от его точек до МЦС этого звена.
3. Записываем систему уравнений для скоростей N точек звена 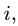
Здесь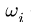
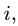
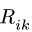
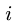
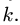
Этот пункт плана выполняем последовательно для всех звеньев механизма. Очередное звено должно иметь общую точку (шарнир) с предыдущим, для которого угловая скорость найдена или известна.
2-й способ. План скоростей
1. Как и в методе МЦС ведем расчет, переходя от одного звена к другому, шарнирно с ним соединенном}’.
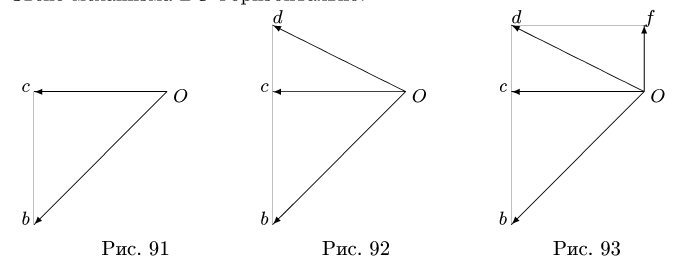
Построение начинаем с вектора, величина и направление которого известны или легко вычисляются. Этот вектор в заданном масштабе откладываем от некоторой произвольной точки О (рис. 91). Его конец определяет первую точку плана скоростей. Точку плана скоростей (конец вектора) отмечаем строчной буквой, соответствующей точке вектора скорости. Пусть первая точка плана скоростей обозначена как b.
2. Рассматриваем очередное звено, на котором имеется точка с уже известной скоростью. Необходимо, чтобы на этом звене была
еще одна точка с известным направлением вектора скорости (например, ползун или точка звена, совершающего вращательное движение). Пусть эта точка обозначена как С (рис. 88).
Справедливо правило, согласно которому неизменяемые отрезки механизма, обозначенные прописными буквами, перпендикулярны отрезкам плана скоростей, обозначенными теми же строчными буквами.
Следующая точка плана скоростей лежит на пересечении двух прямых. Одна прямая определяется направлением скорости точки С, вторая перпендикулярна ВС. Длина полученного отрезка Ос является модулем скорости 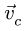
Скорости остальных точек этого звена (если таковые имеются) найдем по правилу подобия неизменяемых фигур механизма и фигур, обозначенных теми же строчными буквами плана скоростей.
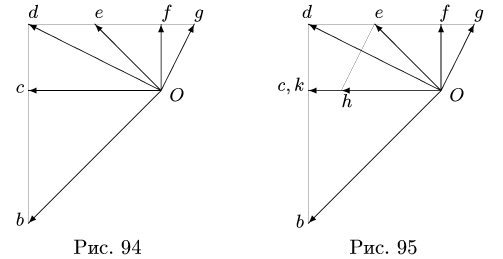
Пункт 2 плана выполняем для всех звеньев механизма (рис. 91-95).
3. После построения плана скоростей определяем угловую скорость каждого звена по простой формуле 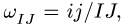
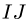
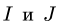
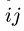
Задача №1
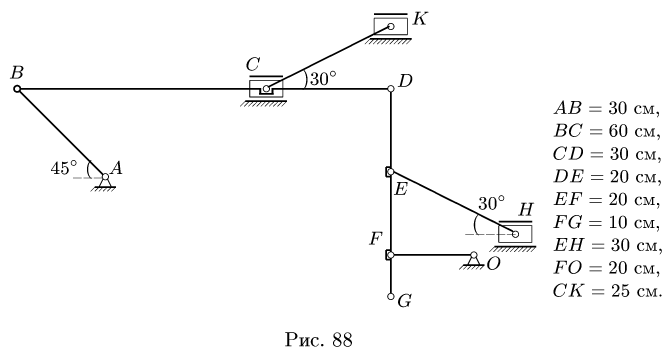
Плоский многозвенный механизм с одной степенью свободы приводится в движение кривошипом АВ, который вращается против часовой стрелки с угловой скоростью 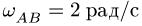
Ползуны С, К, Н движутся горизонтально, 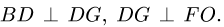
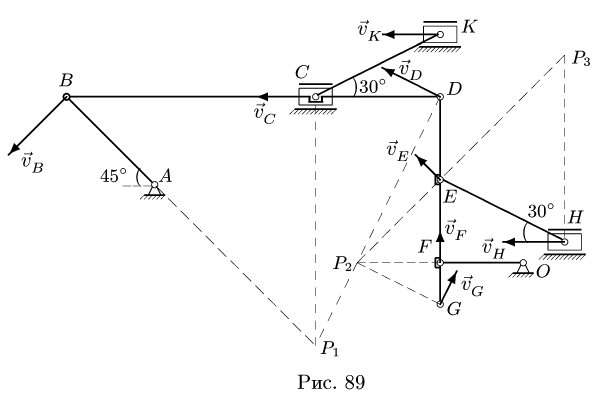
8.1.Скорости точек многозвенного механизма скорости его звеньев АВ, BD, DG, EH, FO, СК.
Решение
1-й способ. Мгновенные центры скоростей
1. Определяем положение мгновенного центра скоростей каждого звена АВ, BD, DG, СК, EH, FO.
МЦС звеньев АВ и FO искать не требуется. Они совершают вращательное движение вокруг шарниров А и О соответственно. Можно условно считать, что там находятся их МЦС.
Вектор 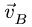
Остается точка С. Ползун С движется строго горизонтально. Вектор скорости 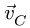
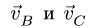
Со стержнем BCD имеют общие точки два стержня: СК и DG. Рассмотрим сначала стержень DG. Направление вектора скорости точки D уже известно. Чтобы определить положение МЦС, надо знать направление вектора еще одной точки на этом звене. Такой точкой является F. Вектор ее скорости перпендикулярен радиусу вращения FO и направлен вертикально. Перпендикуляры к векторам 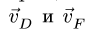
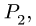
Перпендикулярно радиусам 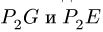
Переходим к звену ЕН, МЦС которого находим на пересечении перпендикуляров к 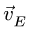
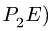
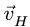
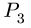
И, наконец, рассматриваем звено СК. Скорости 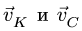
2. Определяем расстояния от МЦС звеньев до тех точек этих звеньев, скорости которых надо найти.
Звено BCD
Звено DEFG. Пользуясь подобием 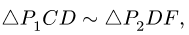
Звено ЕН (рис. 90). Находим расстояния до МЦС:
8.1.Скорости точек многозвенного механизма
3. Записываем систему уравнений для скоростей трех точек звена BCD, включая точку В с известной скоростью:
Решаем эту систему. Находим
Система уравнений для скоростей точек звена DEFG имеет вид
Из первого уравнения вычисляем угловую скорость:
Получаем скорости точек:
Система уравнений для скоростей точек звена ЕН имеет вид
Отсюда
Звено СК совершает мгновенно-поступательное движение. Следовательно, скорости точек С я К равны: 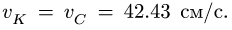
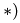
Частично проверить решение можно графически. Известно, что концы векторов скоростей точек неизменяемого отрезка лежат на одной прямой. Убеждаемся в этом, проводя прямую через концы векторов 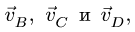
Аналогично, проверяем скорости 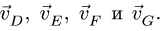
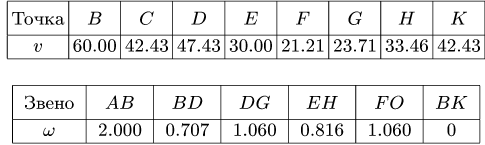
Результаты расчетов помещаем в таблицы. Скорости даны в см/с, угловые скорости — в рад/с.
2-й способ. План скоростей
1. Построение начинаем с вектора, величина и направление которого известны или легко вычисляются. В нашем случае это 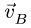
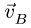
8.1.Скорости точек многозвенного механизма
Точки плана скоростей (концы векторов) отмечаем соответствующими строчными буквами. Таким образом, положение точки b на плане скоростей известно.
2. Рассматриваем звено BCD (рис. 90), на котором имеется точка В с известной скоростью. Неизменяемые отрезки механизма, обозначенные прописными буквами, перпендикулярны отрезкам плана скоростей, обозначенными теми же строчными буквами,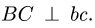
Следовательно, точка с плана скоростей лежит на одной вертикали с точкой b. Известно направление скорости ползуна С. Точку с находим на пересечении двух прямых. Вектор 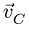
Так получаем точку d плана скоростей и, следовательно, величину и направление вектора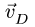
Определяем скорость 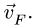
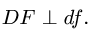
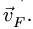
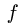
Из соотношения подобия 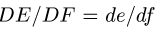
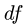
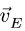
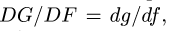
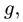
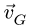
Аналогично, определяем скорость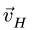
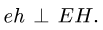
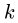
3. Угловые скорости звеньев определяем по простым формулам:
Ускорения точек многозвенного механизма
Постановка Задачи. Плоский шарнирно-стержневой механизм состоит из шарнирно соединенных стержней и ползунов. Механизм приводится в движение кривошипом, который вращается с заданной угловой скоростью. В указанном положении механизма найти ускорения всех его шарниров.
*) Существует еще несколько способов проверки вычисления скоростей точек многозвенного механизма.
8.2. Ускорения точек многозвенного механизма
План решения
1. Определяем угловые скорости звеньев и скорости точек механизма (см. § 8.1).
2. Определяем ускорение шарнира, принадлежащего звену с известным законом движения:
где R — длина звена. Если задан закон изменения утла поворота 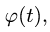
Если угловая скорость звена постоянна, 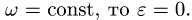
3. Для определения ускорения точки В тела, совершающего плоское движение, воспользуемся векторной формулой
Здесь 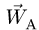
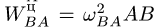
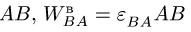
Возможны три случая определения ускорения по формуле (1). А. Точка В является ползуном, или направление ее вектора ускорения по каким-либо другим причинам известно. В этом случае формула (1) в проекциях на оси координат представляет собой систему двух линейных уравнений для неизвестного модуля ускорения ав и неизвестного углового ускорения звена
Б. В точке В шарнирно соединены звено АВ и звено ВС, где С — неподвижный шарнир. Таким образом, точка В движется по окружности с центром в С, и ее ускорение можно представить в виде векторной суммы нормального и тангенциального ускорения:
Величину нормального ускорения 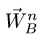
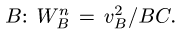
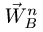
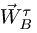
В результате, система уравнений (1-2), записанная в проекциях, дает четыре уравнения для четырех неизвестных 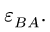
В. Точка В не удовлетворяет случаям А и Б. В этом случае либо она не является шарниром, либо к ней шарнирно присоединено тело, совершающее плоское (не вращательное и не поступательное) движение. Для решения задачи должны быть известны угловая скорость и угловое ускорение звена, на котором находится точка В. Они могут быть найдены при вычислении скорости и ускорения других точек этого звена. При этих условиях уравнение (1) является векторным уравнением для одной неизвестной 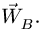
Этот пункт плана выполняем последовательно для всех звеньев механизма. Очередное звено должно иметь общую точку (шарнир) с предыдущим.
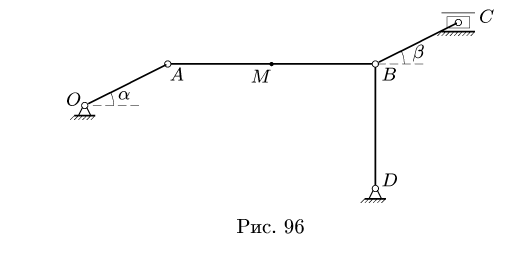
Задача №2
Плоский шарнирно-стержневой механизм состоит из четырех шарнирно соединенных стержней и горизонтально движущегося ползуна С (рис. 96). Механизм приводится в движение кривошипом OA, который вращается с постоянной угловой скоростью 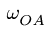
Решение
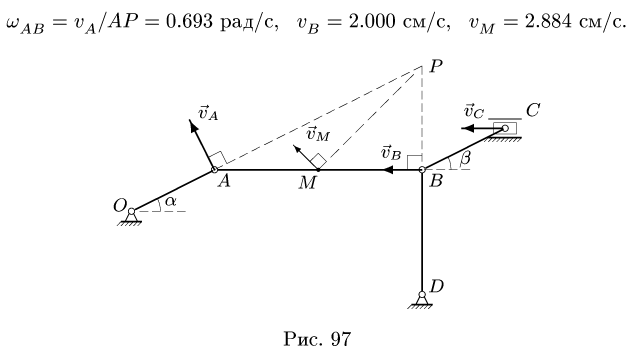
1. Определяем угловые скорости звеньев и скорости точек механизма. Находим величину скорости точки А:
Вектор 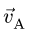
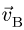
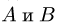
8.2. Ускорены точек многозвенного механизма
от точек А, В, М до МЦС:
Скорости точек находим из системы уравнений
В результате решения получаем
Найти скорость точки С не составит труда. Векторы 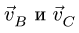
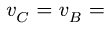
2. Определяем ускорение шарнира А, принадлежащего звену OA с известной постоянной угловой скоростью 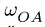
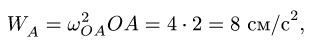
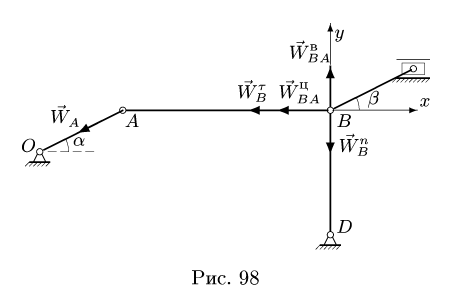
3. Находим ускорение точки В. Точка В движется по окружности с центром в неподвижном шарнире D, и ее ускорение можно представить в виде векторной суммы нормального и тангенциального ускорений:
С другой стороны, ускорение точки В выражается через ускорение точки А, лежащей на том же звене АВ. Рассматривая А в качестве полюса, имеем
Сравнивая (3) и (4), получаем, что
В проекциях на оси х, у (рис. 98) векторное уравнение (3) дает систем}’ двух уравнений относительно неизвестных
где
Решаем систему (5):
Окончательно, величина ускорения точки В
8.2. Ускорены точек многозвенного механизма
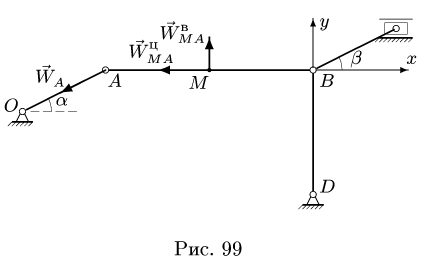
Вычисление ускорения точки М выполняем по п.ЗВ плана решения. Действительно, угловая скорость и угловое ускорение звена А В уже известны:
Рассматривая А в качестве полюса (рис. 99), записываем векторное уравнение
где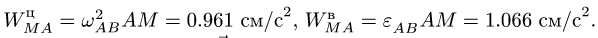
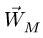
Величина ускорения точки M
Находим ускорение точки С. Скорости точек В я С звена ВС, совершающего мгновенно — поступательное движение, равны, однако, их ускорения различны.
Для определения 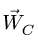
где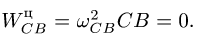
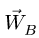
Векторное уравнение (7) содержит две неизвестных величины: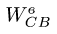
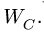
Спроецируем (7) на ось 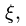
Находим
Результаты расчетов помещаем в таблицу (скорости в см/с, ускорения в см/
8.3. Уравнение трех угловых скоростей
Постановка задачи. Подобрать длины звеньев шарнирного четырехзвенника так, чтобы в некоторый момент движения угловые скорости его звеньев были бы равны заданным. Положение опорных шарниров четырехзвенника известно.
План решения:
Под угловыми скоростями будем понимать проекции соответствующих векторов на ось 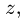
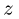
1. Последовательно нумеруем шарниры и звенья механизма. Выбираем систему координат, помещая ее начало в один из шарниров механизма. Определяем координаты шарниров.
2. Записываем уравнения трех угловых скоростей
где 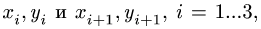
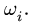
3. Решаем систему (1) относительно неизвестных координат. Определяем длины звеньев механизма (расстояния между шарнирами) по формулам
Задача №3
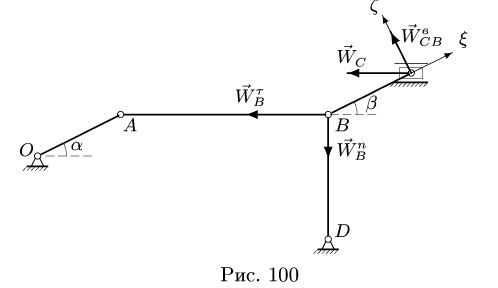
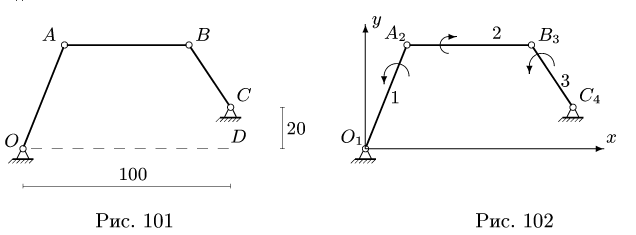
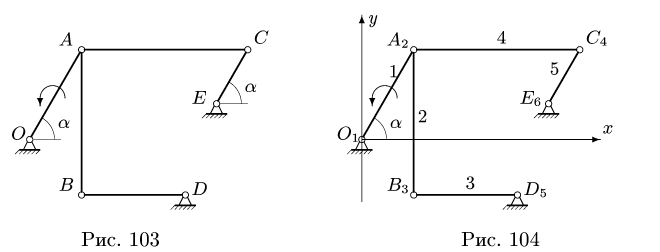
В положении, изображенном на рис. 101, известны угловые скорости шарнирного четырехзвенника О ABC: 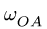
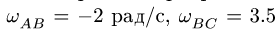
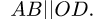
Решение
1. Последовательно нумеруем шарниры и звенья механизма. Номера шарниров указываем индексами у соответствующих букв. Выбираем систему координат, помещая ее начало в шарнир О. Определяем координаты шарниров (рис. 102):
2. Записываем уравнения трех угловых скоростей (1), где по условию
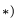
8.3. Уравнение трех угловых скоростей
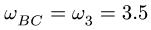
3. Решаем систему (2) относительно 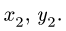
Кроме того, 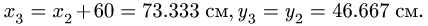
Уравнение трех угловых ускорений
Постановка задачи. Многозвенный механизм приводится в движение кривошипом, вращающимся с известной угловой скоростью и известным угловым ускорением. Найти угловые скорости и угловые ускорения звеньев механизма.
План решения:
Под угловыми скоростями и ускорениями будем понимать проекции соответствующих векторов на ось 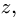
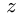
1. Нумеруем шарниры и звенья механизма. Выбираем систему координат, помещая ее начато в один из шарниров механизма. Определяем координаты шарниров.
2. Выделяем из механизма шарнирные четырехзвенники. Рассмотрим четырехзвенник, шарниры которого последовательно обозначены номерами 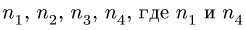
Гл. 8. Плоское движение тела
шарниров. Стержни четырехзвенника имеют номера 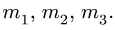
где 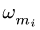
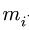
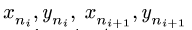
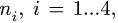
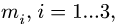
3. Из решения (1) получаем все угловые скорости механизма.
4. Записываем уравнения трех угловых ускорений для каждого четырехзвенника *) :
где 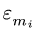
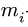
5. Решаем (2) относительно неизвестных угловых ускорений.
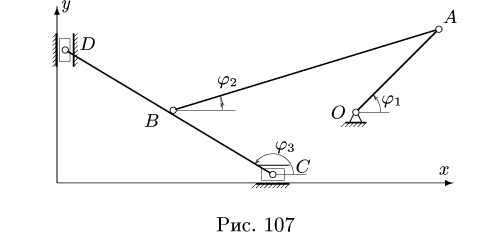
Задача №4
Многозвенный механизм приводится в движение кривошипом OA, вращающимся с угловой скоростью 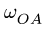
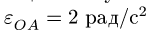
Дано: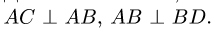
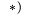
8.4. Уравнение трех угловых ускорений
Решение
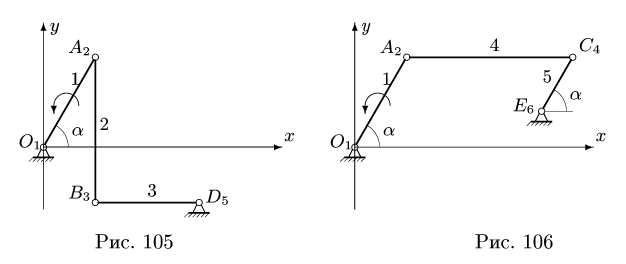
1. Нумеруем шарниры и звенья механизма (рис. 104). Выбираем систему координат, помещая ее начало в шарнир О. Определяем координаты шарниров:
2. Выделяем из механизма шарнирные четырехзвенники (рис. 105, 106). Записываем уравнения трех угловых скоростей для четырехзвенника OABD (рис. 105),
и для четырехзвенника О АСЕ (рис. 106),
(4)
3. Решаем систему четырех линейных уравнений (3), (4). Получаем угловые скорости звеньев: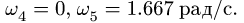
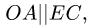
параллельны и но перпендикулярны АС. Мгновенного центра скоростей звена АС не существует (расположен в «бесконечности»), что соответствует
4. Записываем уравнения трех угловых ускорений для четырех-звенника OABD (рис. 105),
и для четырехзвенника ОАСЕ (рис. 106),
5. Из решения (5,6) получаем угловые ускорения:
Кинематические уравнения плоского движения
Постановка задачи. Составить кинематические уравнения плоского многозвенного механизма.
План решения:
1. Составляем кинематические графы механизма, выбирая наиболее короткие маршруты. Началом и концом графа должна быть точка с известной скоростью. Кинематические графы должны включать в себя все звенья механизма. Некоторые звенья могут входить в разные графы. Обозначения для графов приведены на с. 130.
8.5. Кинематические уравнения плоского движения
2. Записываем по два кинематических уравнения в проекциях на оси координат для каждого графа. Получаем систему дифференциальных уравнений.
3. Упрощаем систему уравнений, используя уравнения связей и тригонометрические формулы приведения.
Задача №5
Механизм состоит из стержней OA, АВ, CD и ползунов С и D. Ползун D движется вверх со скоростью 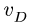
Решение
1. Составляем кинематические графы:
2. Записываем для каждого графа (1), (2) по два кинематических уравнения в проекциях на оси координат:
3. Упрощаем систему (3), используя уравнения связей,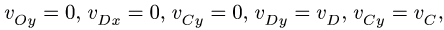
Гл. 8. Плоское движение тела
формулы приведения:
Задача №6
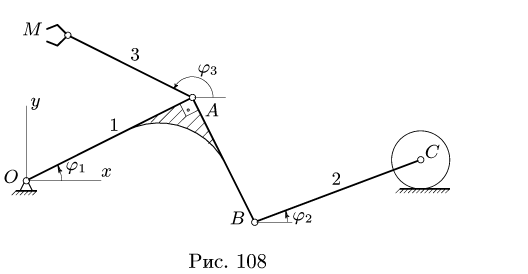
Плоский манипулятор состоит из жесткой детали ОАВ, стержней ВС, AM, колеса С и захвата М. Даны длины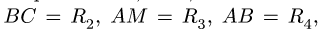
Составить кинематические уравнения манипулятора . Решение
1. Составляем кинематические графы:
2. Записываем по два кинематических уравнения в проекциях на оси координат для каждого графа (5):
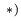
8.5. Кинематические уравнения плоского движения
3. Упрощаем систему (6), используя уравнения связей,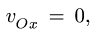
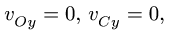
Замечание 1. В данной задаче скорости точек механизма можно найти для некоторого промежутка времени, а не для фиксированного момента времени, как в аналогичных задачах § 8.1, § 8.3. Решая нелинейную систему дифференциальных уравнений (4), получаем полную картину движения механизма . Для решения системы (4) необходимо дополнить ее начальными условиями:
где константы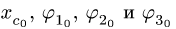
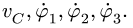
Замечание 2. В решении задачи следует использовать наиболее короткие графы. В данном случае вместо графа (2) можно было бы выбрать граф
Система дифференциальных уравнений изменится, однако в форме Коши ее вид останется прежним.
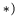
Замечание 3. Метод графов широко используется для решения задач кинематики и динамики. Примеры составления графов представлены также на с. 243, 244 310, 313, 316, 327, 329.
Замечание 4. Для того, чтобы проинтегрировать полученные кинематические уравнения, необходимо скорости ползунов выразить через соответствующие координаты, например, 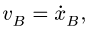
Предупреждение типичных ошибок:
- Кинематические графы являются ориентированными графами. Меняя направление маршрута, меняйте и угол. Следующие два графа
- эквивалентны:
- Угловая скорость звена, которому принадлежат точки А и В графа
, не обязательно равна
см., например, с. 243.
- Принцип виртуальных перемещений
- Аксиомы и теоремы статики
- Система сходящихся сил
- Моменты силы относительно точки и оси
- Равновесие вала
- Определение усилий в стержнях, поддерживающих плиту
- Тело на сферической и стержневых опорах
- Приведение системы сил к простейшему виду
Рис.1
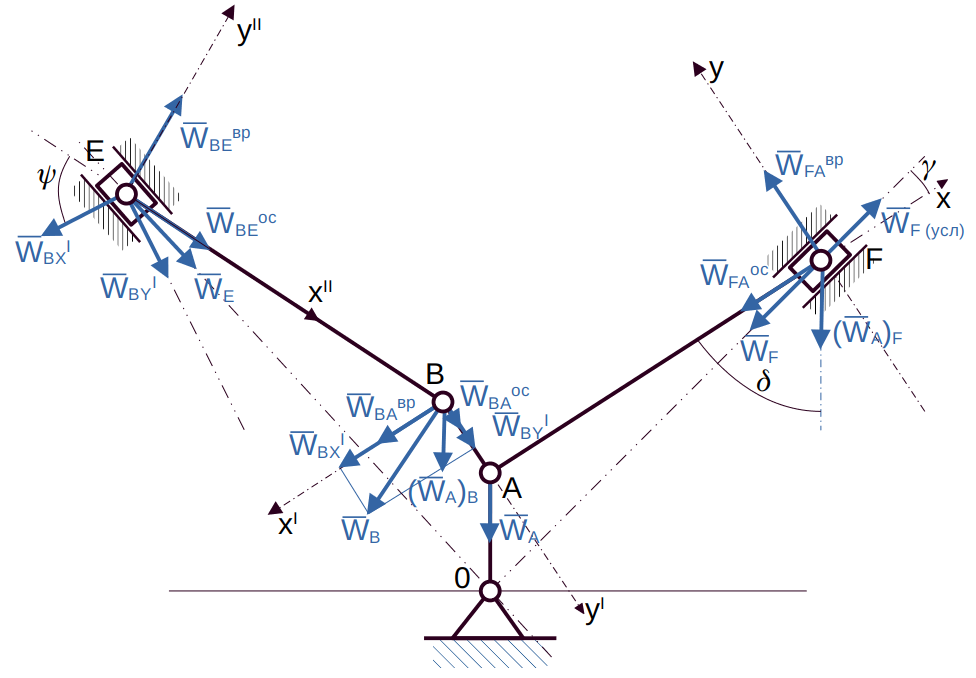
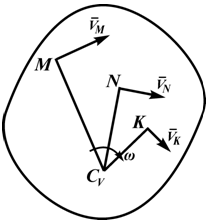
В положении механизма, указанном на рис.1, определить аналитически и построить на чертеже :
- положение мгновенных центров скоростей всех звеньев, совершающих плоское движение;
- скорости всех, точек механизма, расположенных в местах соединения звеньев (шарнирах);
- угловые скорости всех звеньев;
- ускорение точки А;
- ускорений других точек механизма методом полюса;
- угловые ускорения звеньев;
- касательное и нормальное ускорения точки В;
- установить характер движения точки В (ускоренное, замедленное, мгновенная остановка).
Дано:
= 30 об./мин.
Определить:
1) = ?
2) = ?
3) = ?
4) = ?
Решение:
I. Определим скорости точек и угловые скорости звеньев механизма (метод мгновенного центра скоростей, мцс)
1.1 Определим угловую скорость ведущего кривошипа OA:
C1: вектор оси
— оси вращения кривошипа OA (см. рис.1),
1.2 Рассмотрим кривошип OA:
C2: в сторону вращения кривошипа OA (см. рис.1)
1.3 рассмотрим уголковый шатун BAF
Точка — мгновенный центр скоростей шатуна BAF
ось — мгновенная ось вращения шатуна BAF.
(1)
Примечание: Так как на Рис.1 звенья механизма изображены в масштабе, то величины (размеры) мгновенных радиусов точек, а именно: и
берутся с рисунка.
C3: вектор скорости по направляющей в сторону поворота шатуна (вниз).
Определим скорость точки B
Угловая скорость шатуна BAF:
(2)
C4: Вектор , т.к. шатун относительно оси
поворачивается по часовой стрелке.
(3)
Примечание: Величина так-же берётся с Рис.1.
Из (3) получаем
C5: вектор и направлен в сторону вращения шатуна BAF.
1.4 Рассмотрим шатун «BE»
Точка — мгновенный центр скоростей шатуна «BE»
Ось — мгновенная ось вращения шатуна «BE»
(4)
Из (4) получаем:
C6: Вектор и направлен по направляющей вверх (см. Рис.1).
Угловая скорость шатуна BE:
(5)
Примечание: Величину берём из рис. 1 с учётом масштаба.
C7: вектор угловой скорости шатуна BE (от нас),
т.к. «отсюда» видим вращение по часовой стрелке относительно оси
1.5 Определим скорость точки M:
а) метод «мгновенного центра скоростей»:
Точка M шатуну BAF, точка
— мгновенный центр скоростей BAF,
— мгновенный радиус точки M.
(6)
Из (6) получаем:
C8: Вектор скорости и направлен в сторону вращения шатуна BAF
б) метод «полюса»: точка А — полюс
(7)
Где — вращательная скорость точки M относительно «полюса» A, вектор направлен перпендикулярно
= 0.342 (величина угла взята с рис.1)
Сравним = 0.68 m/c (мцс) и «метод полюса»
= 0.73 m/c : погрешность расчёта составляет
II. Определение ускорений точек и угловых ускорений звеньев механизма. (методом «полюса»)
2.1 Ускорение точки A, принадлежащей кривошипу OA, который вращается вокруг неподвижной оси 
(8)
(9)
где и
— вращательное и осестремительное ускорения точки A около оси
соответственно.
(10)
С учётом (9) и (10) из (8) получим:
(11)
(12)
тогда их (11) с учётом (12) получим
Рис.2
C9: направлен из точки A к оси
(см.рис.2).
2.2 Рассмотрим шатун BAF
а) определяем ускорение точки F
(13)
где и
— вращательное и осестремительное ускорения точки F вокруг «полюса» A, соответственно.
(14)
C10: Вектор осестремительного ускорения направлен от точки F к «полюсу» A (см.рис.2)
C11: Для вектора вращательного ускорения известна только линия действия (л.д.),
(направление также выбираем условно см.рис.2)
C12: Для вектора — (ускорения «ползуна» F) известна только линия действия (л.д.) — направляющая «OF» (направление также выберем условно)
(15)
Спроектируем векторное равенство (13) на оси координат «XFY»:
на ось :
(16)
на ось :
(17)
C13: (см.рис.2)
, где величину этих углов берём с чертежа (см.рис.2)
Далее перепишем (16) и (17), подставляя числовые значения:
(18)
(19)
Из уравнения (16) получим:
C14: Получили, что , следовательно, условное направление надо поменять на противоположное (см.рис.2)
Из уравнения (17) получим:
C15: Так как , то условное направление верно! (см.рис.2).
Определим угловое ускорение шатуна BAF:
(20)
Направление определяем из векторного произведения
(см.рис.2)
C16: Вектор и, так как
, то шатун «BAF» вращается замедленно ! (см.рис.1)
б) Определим ускорение точки  (метод «полюса»):
(метод «полюса»):
(21)
где (см. пункт I.)
C17: Вектор направлен по
от точки B к «полюсу» A (см.рис.2).
С учётом (20) получим, что:
(22)
C18: Вектор (см.рис.2).
Спроектируем векторное равенство (21) на оси :
на ось
(23)
на ось
(24)
угол берём с чертежа (см.рис.2).
Перепишем (23) и (24), подставляя числовые значения:
(25)
(26)
Далее находим абсолютную величину ускорения точки B:
(27)
Направление вектора определяется направляющими косинусами по отношению к осям BXY.
(28)
Соотношение (27) и (28) представляют вектор по величине (27) и направлению (28)
2.3 Рассмотрим шатун «BE»
Запишем для — вектора ускорения точки
шатуну «BE» (по методу «полюса») векторное равенство:
(29)
Спроецируем (29) на оси координат и
(см. рис.2)
(30)
(31)
Далее перепишем (30) и (31), подставляя числовые значения, получим
(32)
(33)
Здесь также значение угла берём с чертежа (см.рис.2)
Из (32) определим величину вектора ускорения точки E
Из (33) определим величину вектора вращательного ускорения точки «E» около «полюса» B:
(34)
Определим величину углового ускорения шатуна BE с учётом (34)
Направление вектора определим из векторного произведения:
(35)
C19: Так как получили (34), что , то следует условное направление вектора изменить на противоположное (рис.2), тогда чтобы удовлетворить векторное произведение (35), вектор
(см. рис.1), а поскольку получили, что
, то, значит, характер вращения шатуна «BE» — ускоренный.
Ответ:
Метод определения мгновенного центра скоростей
Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложное движение представляют в виде цепи вращений вокруг разных центров.
Задача сводится к определению положения мгновенного центра вращений (скоростей) (рис. 12.4).
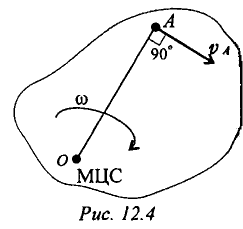
Мгновенным центром скоростей (МЦС) является точка на плоскости, абсолютная скорость которой в данный момент равна нулю.
Вокруг этой точки тело совершает поворот со скоростью 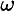
Скорость точки 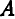
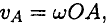
т. к. 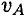
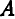
Существуют три способа определения положения мгновенного центра скоростей.
Первый способ. Известна скорость одной точки тела 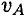
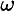
Точку 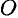
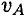
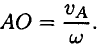
Соединяем точку 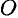
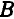
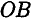
Второй способ. Известны скорости двух точек тела 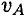
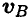
Проводим из точек 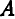
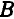
На пересечении перпендикуляров находим МЦС. Далее можно найти скорость любой точки 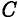
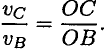
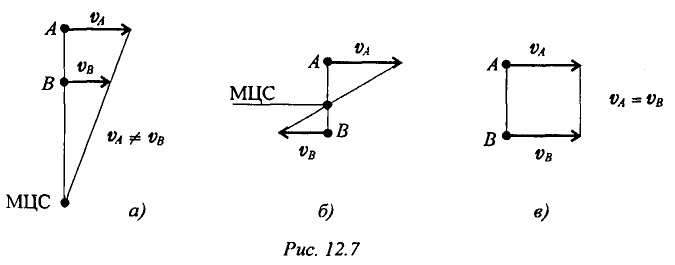
Соединяем концы векторов, МЦС находится на пересечении линии, соединяющей концы векторов с линией 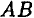
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:





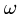
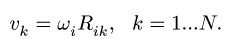
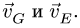
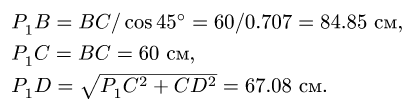
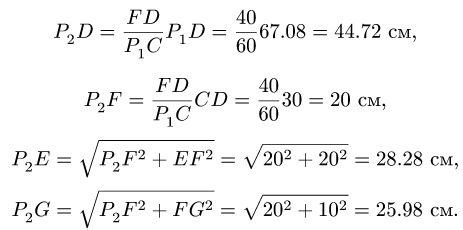
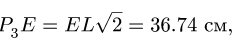
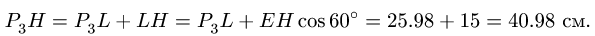
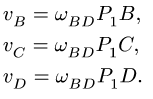
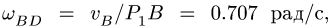
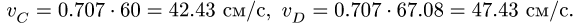
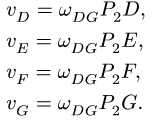
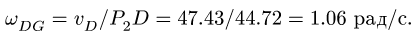
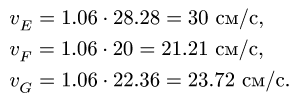

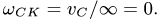
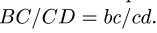
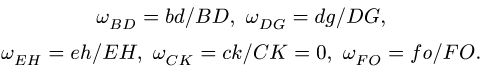
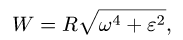
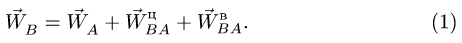
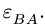

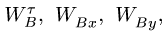
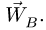
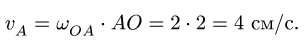
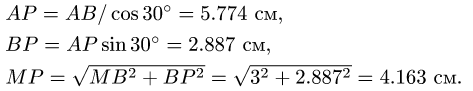
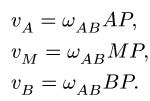

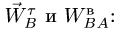
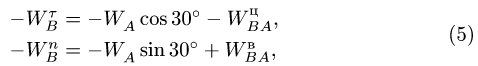
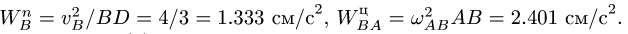
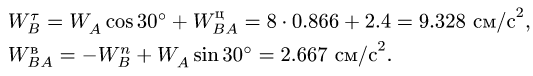
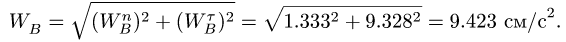
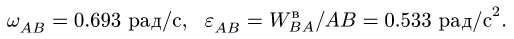
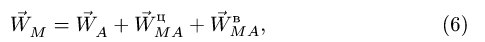
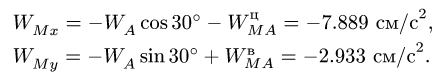
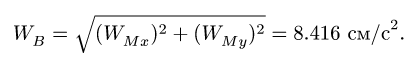
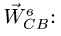
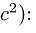

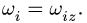
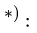
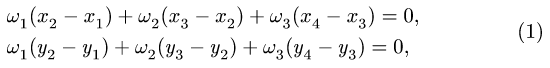
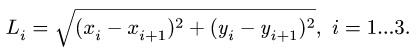
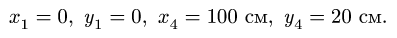
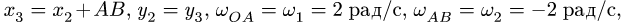

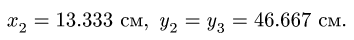
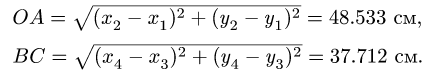
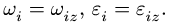
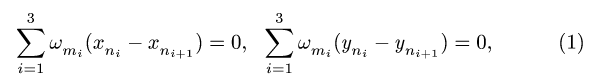
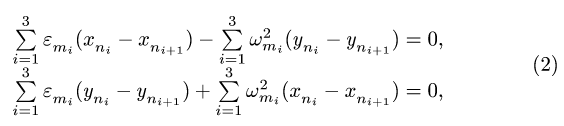
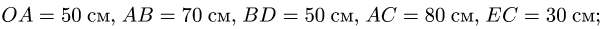
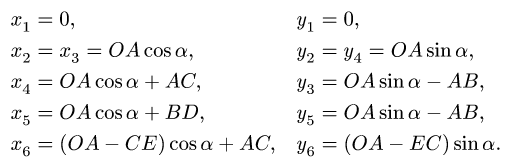
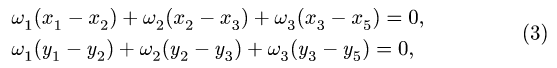
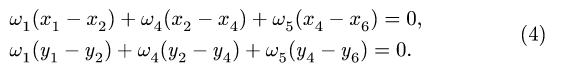
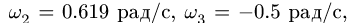
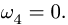
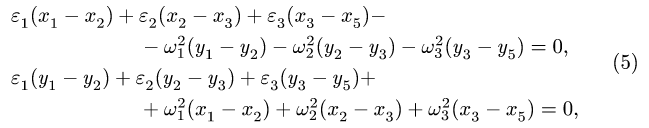
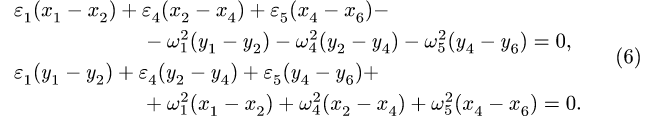
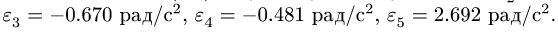
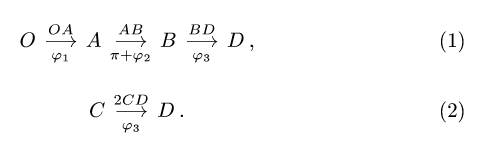
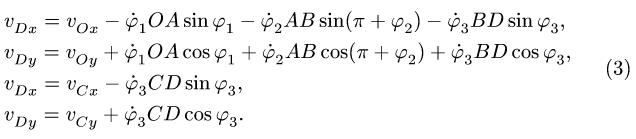
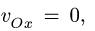
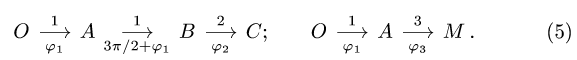
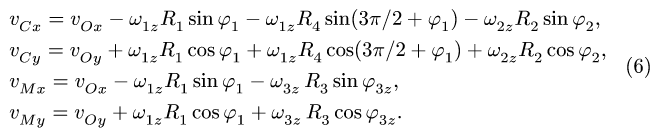
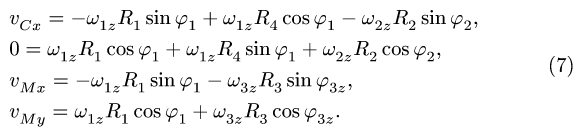
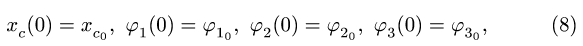
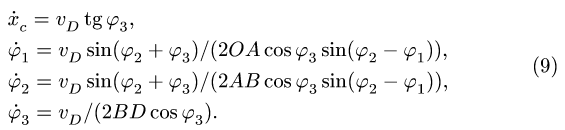
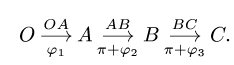
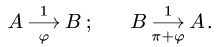
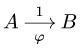 , не обязательно равна
, не обязательно равна 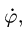 см., например, с. 243.
см., например, с. 243.