Действия с линейными преобразованиями. Произведение линейного преобразования на число.
Пусть
– линейное преобразование линейного
пространстваLнад
полемиk– любое число из
.
Линейное преобразованиепроизвольному вектору
ставит в соответствие единственный
вектор.
Векторk∙.
Если векторупоставить в соответствие векторk∙
,
то имеем преобразование пространства:
k∙
=
(
).
Это преобразование пространства
называютпроизведением преобразования
на число
и обозначают
:
()
=
(
)=
Теорема 1. Еслилинейное преобразование линейного
пространстванад полем
и
– любое число из
,
тоесть линейное преобразование линейного
пространства.
Теорема 2. Если– матрица линейного преобразования
линейного пространстваLв базисе
,
то матрица линейного преобразованияв базисе
естьkA.
Пример 1. Пустьматрица линейного преобразования
линейного пространства
над полем
в базисе
=(
,
).
Найти матрицу преобразования 2;
Решение. Матрица преобразования 2есть2A=
.
Сложение и вычитание линейных преобразований.
Пусть даны линейные преобразования
и
линейного пространства
.
Еслилюбой вектор из
,
то=
и
=
‑ векторы из
.
Если векторупоставим в соответствие единственный
векториз
,
то получим преобразование линейного
пространства.
Оно называетсясуммойлинейных
преобразованийи
и обозначается
+
.
Итак, по определению
(+
)
=
+
=
+
.
Аналогично определяется разность
линейных преобразований
(–
)
=
‑
=
‑
..
Теорема 3. Еслии
– линейные преобразования линейного
пространства,
то преобразования+
и
–
линейного пространства
являются линейными.
Теорема 4.Еслии
– матрицы, соответственно, линейных
преобразованийи
линейного пространстваLв базисе
,
то матрицы+
,
–
являются соответственно матрицами
линейных преобразований+
и
–
в том же базисе.
Пример 2.Пустьбазис линейного пространства
,
,
– его линейные преобразования и их
матрицы соответственно.
Найти матрицyлинейных
преобразований в базисе е:
-
2
+3
;
-
3
–
.
Решение.
1)2A+3B=;
2)3B–A=.
Умножение линейных преобразований.
В линейном пространстве
даны линейные преобразования
и
.
Результат последовательного выполнения
линейных преобразованийи
является преобразованием линейного
пространства.
Оно называетсяпроизведениемлинейных преобразованийи
и обозначается
Теорема 5.Произведение линейных
преобразованийи
линейного пространства
является линейным преобразованием
этого пространства.
Теорема 6.Еслии
,
соответственно, матрицы линейных
преобразованийи
линейного пространства
в базисе
,
то матрица линейного преобразованиялинейного пространства
в базисе
есть
.
Пример 3.Пусть,
матрицы линейных преобразований
соответственнои
линейного пространства
в базисе
.
Найти матрицы преобразований в базисе.
1)
;
2)
;
3) (+
)
;
Решение.
1)
.
2)
.
3)
.
Свойства
линейных операций над матрицами
Операции
сложения матриц и умножения матрицы на
число называются линейными
операциями над матрицами.
Непосредственно из определений вытекают
следующие свойства
линейных операций.
Для
любых матриц одинаковых
размеров и любых чисел справедливы
равенства:
1. (коммутативность
сложения);
2. (ассоциативность
сложения);
3. существует
нулевая матрица (тех
же размеров, что и ):
4. существует
матрица ,
противоположная матрице
5. ;
6. ;
7. ;
8. .
№28
Собственные
векторы и собственные значения линейного
оператора
Ненулевой
вектор называется
собственным вектором линейного
оператора ,
если (
для
комплексного ),
такое, что Число
называется
собственным числом (собственным
значением) оператора f,
соответствующим этому собственному
вектору.
Если
в некотором базисе оператор f имеет
матрицу А и
в том же базисе вектор имеет
координатный столбец X,
то или
Собственные
числа линейного
оператора —
корни характеристического уравнения ,
где —
матрица оператора f, —
символ Кронекера.
Для
каждого собственного значения соответствующие
собственные векторы могут быть найдены
из матричного уравнения или
соответствующей ему системы линейных
уравнений
Линейный
оператор называется оператором простой
структуры, если существует базис,
состоящий из собственных векторов этого
оператора. Матрица линейного оператора
в этом базисе имеет вид
где —
соответствующие собственные значения.
№29
Евкли́дово
простра́нство (также Эвкли́дово
простра́нство) —
в изначальном смысле, пространство,
свойства которого описываются аксиомами евклидовой
геометрии.
В этом случае предполагается, что
пространство имеет размерность 3.
Если
каждой паре векторов x, y линейного
пространства L поставлено
в соответствие действительное
число (x, y),
так, что для любых x, y и z из L и
любого действительного числа α справедливы
следующие аксиомы:
(x, y) = (y,
x),
(α·x, y) = α·(x, y),
(x + y, z) =(x, z) + (y, z),
(x, x)>
0 при x ≠
0, (0, 0) =
0,
то
в пространстве L определено скалярное
произведение (x, y).
Если
в линейном пространстве определено
скалярное произведение, то такое
пространство называется евклидовым
пространством.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
09.06.201514.68 Mб41P.N.Bibilo_Osnovy_yazika_VHDL(2007)1.djvu
- #
- #
- #
- #
Линейные операторы (преобразования)
Определение линейных операторов (преобразований)
Линейным преобразованием (линейным оператором) линейного пространства называется линейное отображение
пространства
в себя.
Поскольку линейное преобразование является частным случаем линейного отображения, к нему применимы все понятия и свойства, рассмотренные для отображений: инъективность, сюръективность, биективность, обратимость, ядро, образ, дефект, ранг и т.д.
Матрицей линейного оператора (преобразования) в базисе
пространства
называется квадратная матрица
, составленная из координатных столбцов образов базисных векторов
, найденных относительно базиса
.
Матрица биективного линейного оператора (преобразования) обратима, т.е. невырождена. Поэтому биективное (обратимое) преобразование называют также невырожденным.
Примеры линейных операторов (преобразований)
1. Обозначим — нулевое преобразование n-мерного пространства
, которое ставит в соответствие любому вектору
нулевой элемент
пространства
. Это преобразование не является инъективным, сюръективным, биективным, обратимым. Матрица нулевого преобразования (в любом базисе) нулевая, ядро преобразования
, образ преобразования
, дефект
, ранг
.
2. Обозначим — тождественное преобразование n-мерного пространства
, которое ставит в соответствие каждому вектору
этот же вектор
. Это преобразование является инъективным, сюръективным, биективным, обратимым. Матрица тождественного преобразования (в любом базисе) единичная n-го порядка, ядро преобразования
, образ преобразования
, дефект
, ранг
.
3. Обозначим — центральную симметрию n-мерного пространства
(относительно нулевого вектора
), т.е. преобразование, которое каждому вектору ставит в соответствие противоположный ему вектор:
. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Матрица преобразования противоположна единичной (в любом базисе):
; ядро преобразования
, образ преобразования
, дефект
, ранг
.
4. Обозначим — гомотетию n-мерного пространства
(с коэффициентом
), т.е. преобразование, которое каждому вектору ставит в соответствие коллинеарный ему вектор:
. Это преобразование линейное. При
оно инъективное, сюръективное, биективное, обратимое. Матрица преобразования пропорциональна единичной (в любом базисе):
, ядро преобразования
, образ преобразования
, дефект
, ранг
. При
(см. пункт 1); при
(см. пункт 2); при
(см. пункт 3).
5. Рассмотрим линейное пространство радиус-векторов (с общим началом в точке
), принадлежащих одной плоскости (рис. 9.1). Обозначим
— поворот вокруг точки
(на угол
в положительном направлении (против часовой стрелки)). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу поворота в стандартном ортонормированием базисе
. Раскладывая образы
базисных векторов по базису, получаем
Составляем матрицу (9.1) преобразования (оператора), записывая найденные координаты образов по столбцам:
Ядро оператора (преобразования) , образ преобразования
, дефект
, ранг
. При
(см. пункт 2); при
(см. пункт 3).
6. Обозначим — оператор дифференцирования, который каждому многочлену степени не выше и ставит в соответствие его производную, рассматриваемую как многочлен степени не выше
. Это преобразование линейное, неинъективное, несюръективное, небиективное, необратимое. Квадратная матрица ((n+l)-го порядка) преобразования в стандартном базисе имеет вид
Ядро преобразования — пространство многочленов нулевой степени, образ
— пространство многочленов степени не выше
, дефект
, ранг
.
Рассмотрим преобразование линейного пространства тригонометрических многочленов (частоты
) с действительными коэффициентами:
, т.е.
— множество функций вида
, где
. Заметим, что это множество является двумерным вещественным линейным пространством. Стандартный базис пространства
образуют функции
, поскольку они линейно независимы (тождественное равенство нулю
возможно только в тривиальном случае
). При дифференцировании функции
получаем функцию
того же вида. Следовательно, преобразование
определено. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу преобразования в стандартном базисе
. Раскладывая образы базисных векторов, получаем
Составляем матрицу (9.1) преобразования, записывая найденные координаты образов по столбцам: . Ядро преобразования
— нулевое подпространство, образ
, дефект
, ранг
,
.
Аналогичными свойствами обладает преобразование , где
— множество функций вида
с комплексными коэффициентами
и
. Множество
является двумерным комплексным линейным пространством.
7. Пусть линейное пространство разлагается в прямую сумму подпространств . Обозначим
— оператор проектирования на подпространство
параллельно подпространству
, который каждому вектору
, где
, ставит в соответствие его составляющую (проекцию)
, т.е.
(рис.9.2). Это преобразование линейное. При
оно неинъективное, несюръективное, небиективное, необратимое. Ядро преобразования
, образ преобразования
, дефект
, Ранг
,. При
; при
.
8. Пусть линейное пространство разлагается в прямую сумму подпространств . Обозначим
— оператор отражения в подпространстве
параллельно подпространству
(или преобразование симметрии относительно подпространства
параллельно подпространству
), который каждому вектору
, где
, ставит в соответствие вектор
, т.е.
(рис. 9.3). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Ядро преобразования
, образ преобразования
, дефект
, ранг
. При
.
Матрицы линейного оператора (преобразования) в разных базисах
Найдем связь матриц одного и того же линейного оператора (преобразования) в разных базисах.
Пусть в базисе преобразование
имеет матрицу
, а в базисе
— матрицу
. Если
— матрица перехода от базиса
к базису
, то
(9.4)
Докажем формулу (9.4). Пусть векторы и
в базисах
и
имеют координатные столбцы
и
соответственно. Если
, то по формуле (9.2) имеем
Подставляя в первое равенство связи координат векторов в разных базисах
получаем
или, учитывая обратимость матрицы
. Сравнивая последнее равенство с
, убеждаемся в справедливости (9.4).
Замечания 9.2
1. Матрицы линейного преобразования в разных базисах оказываются подобными. И наоборот, любые две подобные матрицы являются матрицами некоторого линейного преобразования, найденными относительно разных базисов.
2. Для матриц преобразований справедливы свойства, рассмотренные ранее. В частности, при фиксированном базисе матрица суммы преобразований равна сумме их матриц, матрица произведения преобразования на число равна произведению матрицы преобразования на это же число, матрица композиции преобразований равна произведению матриц преобразований, матрица обратного преобразования является обратной для матрицы обратимого преобразования.
Алгебра линейных операторов (преобразований)
Рассмотрим множество — линейных преобразований (операторов) n-мерного линейного пространства
. Напомним, что два преобразования
и
называются равными, если
.
На множестве определены две линейные операции: сложение преобразований и умножение преобразования на число, поскольку в результате этих операций получается линейное преобразование.
Нетрудно показать, что эти операции удовлетворяют условиям:
1. ;
2. ;
3. существует нулевое преобразование такое, что
;
4. для каждого преобразования существует противоположное преобразование
такое, что
;
5. и любого числа
;
6. и любых чисел
;
7. и любых чисел
;
8. .
В условиях 5-7 говорится о числах из того же числового поля, над которым определено линейное пространство .
Условия 1-8 повторяют аксиомы линейного пространства. Поэтому множество с линейными операциями является линейным пространством. Если пространство
вещественное (комплексное), то и пространство
вещественное (комплексное).
Найдем размерность пространства . При фиксированном базисе имеется взаимно однозначное соответствие между линейными преобразованиями и их матрицами, причем это соответствие сохраняет линейные операции. Следовательно, пространство
изоморфно пространству
— квадратных матриц n-го порядка. Размерность пространства
равна
. По теореме 8.3:
то есть
Кроме линейных операций в множестве определена операция умножения элементов. Произведением преобразований
и
назовем их композицию, т.е.
. В результате композиции линейных преобразований получается линейное преобразование. Операция умножения удовлетворяет следующим условиям:
1. ;
2. ;
3. ;
4. существует тождественное преобразование такое, что
.
Первое условие выражает ассоциативность операции умножения, условия 2 и 3 — законы дистрибутивности, условие 4 — существование нейтрального элемента. Множество с операциями сложения и умножения элементов является кольцом с единицей (вообще говоря, некоммутативное, так как в общем случае
).
Операции умножения операторов (преобразований) и произведения операторов на число (из заданного числового поля) удовлетворяют условию:
5.
Линейное пространство, которое является кольцом, удовлетворяющим условию 5, называется алгеброй. Поэтому множество называют алгеброй линейных операторов (преобразований).
Многочлены от линейного оператора (преобразования)
В алгебре можно определить целую неотрицательную степень оператора
, полагая по определению
Пусть — многочлен переменной
. Многочленом
от линейного преобразования
называется преобразование
.
Многочлен называется аннулирующим для линейного преобразования
, если
— нулевое преобразование. Заметим, что у каждого линейного преобразования
n-мерного линейного пространства
существует аннулирующий многочлен степени не выше
. Действительно, система из
элементов
линейного пространства
линейно зависима (так как
). Поэтому существуют такие числа
, не все равные нулю одновременно, что
. Следовательно, многочлен
— аннулирующий для преобразования
.
Замечания 9.3
1. При фиксированном базисе каждому преобразованию (оператору) можно сопоставить его матрицу. Свойства линейных операций 1-8, записанные для матриц преобразований, повторяют свойства линейных операций с матрицами, а свойствам 1-5 произведения операторов отвечают свойства операции умножения матриц.
2. При фиксированном базисе многочлен от линейного преобразования
имеет матрицу
, где
— матрица преобразования
в том же базисе. Поэтому свойства многочленов от матриц переносятся на многочлены от линейного преобразования. В частности, многочлены от одного преобразования перестановочны:
3. Функции от матриц определяются при помощи многочленов от матриц. Поэтому можно определить функции от линейных преобразований.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Действия над линейными преобразованиями
Сложение преобразований. Пусть в n -мерном пространстве R с базисом l1, l2, …, ln заданы два линейных преобразования А и В, определяемые как y = Ax и z = Bx.
Определение 28. Суммой линейных преобразований А и В называют преобразование С, обозначаемое С = А + В, если для каждого вектора x из пространства R справедливо Сх = (А + В)х = Ax + Вx. Тогда говорят, что преобразование С преобразует вектор х в вектор q равный сумме векторов у и z, т.е. q = y + z.
Из определения 28 очевидно, что матрица С, определяющая преобразование С, должна быть равна сумме матриц преобразований А и В: С = А + В.
Умножение преобразования на число. Пусть в n -мерном пространстве R с базисом l1, l2, …, ln задано линейное преобразование А, определяемом как y = Ax, и некоторое число 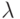
Определение 29. Произведением линейного преобразования А и числа 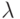
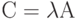

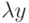
Произведение преобразований. Пусть в n -мерном пространстве R с базисом l1, l2, …, ln заданы два линейных преобразования А и В, определяемых как y = Ax и z = Bу, т.е. вектор x преобразуется преобразованием А в вектор y, который в свою очередь преобразуется в вектор z преобразованием В.
Определение 30. Произведением преобразований А и В называют преобразование С, обозначаемое С = ВА, если для каждого вектора 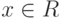
Заметим, что в этом случае матрица преобразования С, определяющая произведение преобразований А и В, будет выражаться произведением матриц соответствующих преобразований: С = ВА.
Обратное преобразование. Пусть в n -мерном пространстве R с базисом l1, l2, …, ln задано линейное преобразование А выражением y = Ax, где A — невырожденная квадратная матрица, для которой определена обратную матрицу A-1 как A-1A = AA-1 = Е, где Е — единичная матрица2Единичная матрица — это диагональная матрица, все элементы которой равны единице, или единичная матрица — это квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю..
Определение 31. Обратным преобразованием х = A-1у назовем такое, которое будет обратно прямому преобразованию y = Ax, причем произведение прямого и обратного преобразования будет переводить вектор в самого себя, т.е. х = A-1у = A-1Ax = Еx = х.
Очевидно, что матрица A-1 обратного преобразования А-1 будет являться обратной по отношению к матрице прямого преобразования А.
Содержание:
- Линейные преобразования. Собственные векторы и собственные числа линейного оператора
- Собственные векторы и собственные числа линейного оператора: определение, свойства
- Нахождение собственных чисел и собственных векторов
- Базис пространства из собственных векторов линейного оператора
- Линейная модель обмена (модель международной торговли)
Линейные преобразования. Собственные векторы и собственные числа линейного оператора
Линейные преобразования (линейные операторы). Матрица линейного преобразования
Пусть задано 


этого же пространства, говорится, что в векторном пространстве 


Вектор 



Преобразование 


То есть линейный оператор преобразует пространство 
Примерами простейших линейных преобразований являются:
тождественное преобразование: 

нулевой оператор 

Линейное преобразование 





Рассмотрим задачу об отыскании координат образа вектора 
Пусть в пространстве 







Но образы 

где 


С учетом (5.5) соотношение (5.4) принимает вид:
Группируя члены правой части относительно векторов базиса, имеем:
С другой стороны, если 


Сопоставляем (5.8) из (5.7) и получаем координаты вектора 
Следовательно, при линейном преобразовании:
координаты образа вектора являются линейными комбинациями координат прообраза, коэффициенты при которых составляют матрицу 

Матрица 




Каждый — 






Обратите внимание, что 

Каждому линейном оператору 



Например, с помощью оператора линейных преобразований можно описать поворот произвольного вектора с пространства 





где 


точки 

По соотношению (5.12) матрица линейного преобразования} 


а матрица обратного линейного преобразования 


Теорема 5.1 (о связи между матрицами оператора в различных базисах).
Матрицы 




где 
Доказательство. Пусть линейный оператор 








Умножим равенство (5.14) слева на матрицу 


Сравнив соотношение 

Две квадратные матрицы 




Соответствующие линейные операторы называются преобразованиями сходства.
Подобные матрицы описывают то же линейное преобразование, но в разных базисах, а матрица 
Подобные матрицы имеют те же ранги, суммы элементов главной диагонали и определители.
В базисе 


Определим матрицу 




Предоставим расписание векторов нового базиса по векторам исходного базиса: 
Ее определитель 

По теореме 5.1 определяем матрицу оператора 
Обратите внимание, что в новом базисе матрица оператора 
Собственные векторы и собственные числа линейного оператора: определение, свойства
Рассмотрим 



Ненулевой вектор 



Скаляр 


Согласно определениями собственного числа и собственного вектора имеем:
1) Если 




2) любой ненулевой 



Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы
Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы
Запишем матричное уравнение (5.17) в развернутом виде:
Таким образом, задача сводится к решению однородной системы 

Раскрытие определителя в соотношении (5.19) дает многочлен степени 




По основной теореме алгебры уравнения 





Множество всех собственных чисел матрицы называют спектром матрицы. Если в спектре матрицы то же собственное число повторяется 

Теорема 5.2 (о единственности собственного чucлa, что соответствует собственному вектору). Если 



Доказательство. Предположим, что кроме собственного числа 
скаляр 




Согласно теореме 5.2 говорят, что собственный вектор 


Теорема 5.3 (о множестве собственных векторов, принадлежащих собственному числу). Если матрица имеет собственный вектор, принадлежащий собственному числу 
Доказательство базируется на определении собственного вектора и свойствах ассоциативности и коммутативности операции умножения матрицы на скаляр.
Действительно, пусть 







Поскольку равенство (5.19) выполняется для произвольного 
Теорема 5.4 (критерий существования собственного вектора 






Доказательство сводится к тождественных преобразований матричных уравнений.
Необходимость уже доказано переходом от соотношения 

Достаточность. На основании свойств действий над матрицами с учетом условия 

Теорема 5.5 (пpo линейную независимость собственных векторов). Собственные векторы, принадлежащие различным собственным числам, является линейно независимыми.
Доказательство проведем методом от противного. Пусть 





Предположим обратное. Пусть (5.23) выполняется при условии, что одно из чисел 
Умножим левую и правую части (5.23) на собственное число 
Левую и правую части равенства (5.23) умножим на матрицу 
Сравним (5.25) и (5.24). Получаем:
По условию теоремы 




Если есть более двух собственных векторов, принадлежащих попарно различным собственным числам, доведение аналогичное (с использованием метода математической индукции).
Заметим, что собственные векторы, принадлежащих различным собственным числам, можно использовать как базисные векторы пространства 
Теорема 5.6 (пpo сумму и произведение собственных чисел). Если 

1) сумма собственных чисел равна сумме элементов главной диагонали матрицы 
2) произведение собственных чисел равна определителю матрицы 
Доказательство основывается на формулах Виета, которые описывают соотношение между корнями и коэффициентами многочлена 
Рассмотрим простейший случай 
С (5.29) по теореме Виета (для квадратного уравнения) имеем:
Сумму всех диагональных элементов матрицы называют следом (от нем. spur — след) этой матрицы и обозначают 
Для квадратной матрицы произвольного порядка 
при этом собственное число 
Нахождение собственных чисел и собственных векторов
Рассмотрим алгоритм нахождения собственных чисел матрицы 
Согласно соотношениями (5.18) и (5.19) имеем такой порядок отыскания собственных чисел и собственных векторов матрицы.
1. Составляем по исходной матрицей 
2. Подставляем поочередно каждое собственное число в систему (5.18) и находим все ее нетривиальные решения, что и дает множество собственных векторов, принадлежащих соответствующему собственному числу.
Замечания. Множество всех собственных векторов, принадлежащих определенному собственному числу, можно представить как линейную комбинацию фундаментальных решений однородной системы уравнений согласно (4.19), гл. 4.
Найдем собственные числа и собственные векторы матрицы
Характерным уравнением этой матрицы является квадратное уравнение:
Решив его, получим собственные числа 
Теперь описываем множества 

Для этого в матрицу 

Предоставляя параметру 

Теорема 5.7 (про собственные числа и собственные векторы симметричной матрицы).
Симметричная матрица 
Теорема приводим без доказательства.
Проиллюстрируем прав выводов данной теоремы на примере.
Пусть имеем симметричную матрицу
Найдем собственные числа и собственные векторы этой матрицы и докажем ортогональность собственных векторов, соответствующих различным собственным числам.
1. Составим характеристическое уравнение матрицы
2. Найдем корни полученного кубического уравнения относительно 

Нахождение других двух корней сводится к решению квадратного уравнения:
3. Опишем множества 

Для этого в матрицу 

Аналогично находим собственные векторы 
Система векторов 

Убеждаемся, что векторы 

Для этого определим их скалярные произведения:
Поскольку скалярные произведения векторов равны нулю, то векторы попарно ортогональны.
Если в выражениях (5.31-5.33) положить 
которая использовалась как базис пространства 





Теорема 5.8 (о преобразовании матрицы к диагональному виду). Матрица линейного оператора 


Теорему наводим без доказательств
Заметим, что при нахождении собственных чисел для заданной матрицы самой задачей является решение алгебраического уравнения 
Следующий пример был решен в пакете MatLab, в котором конечный результат вычислений предоставляется без промежуточных выкладок.
Найдем собственные числа и соответствующие им собственные векторы матрицы
Характерным уравнением для нахождения собственных чисел является уравнение
корнями которого будут числа 
Собственные числа и собственные векторы матриц имеют широкий спектр использования, в частности, в аналитической геометрии (Раздел 2), в задачах различных отраслей естественных наук и эконометрики.
Базис пространства из собственных векторов линейного оператора
По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Возникает вопрос, при каких условиях существует базис линейного пространства 
Лема. Если 





Доказательство. Согласно теореме 5.4 множество собственных векторов совпадает с множеством всех решений однородной системы линейных уравнений:
где 




Теорема 5.9 (о существовании базиса из собственных векторов матрицы). Пусть числа 





Доказательство. Согласно лемме каждое множество собственных векторов, соответствующих уравнению 


Поскольку собственные векторы матрицы 


Теорема 5.10 (о существовании базиса из собственных векторов симметричной матрицы). Если матрица 


Теорему принимаем без доказательств.
Построим ортонормированный базис пространства 
линейного преобразования 

Согласно теореме 5.9 такой базис существует, поскольку матрица 

и решим его: 

Для каждого из двух различных собственных чисел матрицы определим фундаментальную систему решений однородной системы уравнений: 

По последним шагом элементарных преобразований матрицы записываем общее решение системы:
Определяем фундаментальную систему решений однородной системы уравнений
Собственные векторы 

При 
По последнем шагом элементарных преобразований матрицы записываем общее решение системы:
Возлагаем 
Поскольку 



Это и есть ортогональный базис пространства 

По соотношению (5.13) определим матрицу 






По матричным уравнением (5.13) находим матрицу 

Следовательно, мы получили диагональную матрицу третьего порядка, элементами главной диагонали которой есть собственные числа матрицы 
Далее приведен пример применения собственных векторов и собственных чисел в одной из многих задач экономики.
Линейная модель обмена (модель международной торговли)
Практически все страны кроме внутреннего товарообмена осуществляют внешний товарообмен, то есть занимаются внешней торговлей. Торговля считается сбалансированной, или бездефицитной, если для каждой страны прибыль от торговли не меньше объем средств, которые она вкладывает в товарооборот (внутренний и внешний).
Постановка задачи. Несколько стран осуществляют взаимный товарообмен. Известную долю бюджетных средств, тратит каждая страна на закупку товаров у другой страны, учитывая и внутренний товарооборот. Определить, каким должно быть соотношение бюджетов партнеров для того, чтобы обеспечить бездефицитность торговли.
Построение математической модели. Введем обозначения количественных характеристик, описывающих торговлю между странами, и определим связь между этими характеристиками. Пусть 




Матрицу 

Эта матрица описывает взаимодействие стран в процессе международной торговли. Соотношение (5.34) означает, что сумма элементов каждого столбца матрицы равна
1. Если объем средств, которые тратит каждая страна на торговлю, обозначить через 


Чтобы торговля каждой страны была сбалансированной, по определению должно выполняться условие 



Группируя в левой части слагаемые, содержащие каждое из 
Учитывая соотношение (5.20), получим:
Отсюда следует, что сбалансированная торговля возможна только в случае знака равенства. Это, полагаем, понятно не только на основании аналитических выкладок, но и с экономической точки зрения (и даже просто с точки зрения здравого смысла): все страны в совокупности не могут получить прибыль. Более того, для одной из стран не может выполняться знак строгого неравенства 
Итак, условием сбалансированной торговли является равенства 

Введем в рассмотрение вектор (бюджетных) средств 
С (5.40) следует, что при условии сбалансированности торговли между странами вектор средств 



Рассмотрим товарообмен между тремя странами. Пусть структурная матрица торговли стран 
Найдем вектор средств, компонентами которого являются доли от общего объема торговли, должна вкладывать каждая из стран во внешней товарооборот для того, чтобы торговля была сбалансированной.
Искомый вектор средств является собственным вектором структурной матрицы, принадлежащий собственному значению 
Поскольку система является однородной, то расширенная матрица эквивалентна основной матрицы системы. Осуществим элементарные преобразования основной матрицы этой системы уравнений:
Находим общее решение системы, в котором 

Отсюда следует, что для сбалансированности торговли необходимо, чтобы средства, которые вкладывает в внешний товарооборот каждая страна, соотносились как
Лекции:
- Разложение в ряд Фурье четных и нечетных функций
- Функции многих переменных
- Наибольшее и наименьшее значение функции
- Уравнение плоскости
- Экстремум функции трёх переменных
- Как найти вероятность: пример решения
- Свойства определенного интеграла
- Комбинаторика
- Однородные дифференциальные уравнения
- Простейшие задачи аналитической геометрии































































































