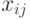Задача
Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках
и векторе объемов конечного использования
.
Требуется:
Указание:
При вычислениях производить округление с точностью до тысячных.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Матрица прямых затрат
Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора
:
Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:
Подставляя
числовые значения, получаем:
Матрица «Затраты — выпуск»
Найдем матрицу
«Затраты — выпуск»
Вектор конечного использования Y для валового объема выпуска X
Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения:
Для этого выполним умножение двух матриц
Матрица полных затрат
Найдем
матрицу коэффициентов полных материальных затрат
-она будет равна обратной матрице
:
Определитель матрицы
:
Алгебраические
дополнения:
Обратная матрица:
Вектор валового объема выпуска X для конечного использования Y
Вектор валового объема выпуска
для конечного продукта
определим формуле:
Приросты валовых объемов выпуска
Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на
по сравнению с
:
Матрица полных затрат ресурсов S
Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:
Суммарная потребность в ресурсах
Суммарная потребность в ресурсах для вектора Y0:
Суммарная потребность в ресурсах для вектора Yn:
Матрицы косвенных затрат и сумма затрат
Найдем
матрицы косвенных затрат первого, второго и третьего порядка
Сумма затрат:
Разность
матриц:
Вектор потребности в продукции
Найдем
вектор потребности в продукции всех отраслей материального производства bij
для получения единицы конечного продукта bj вида. Для этого
просуммируем столбцы матрицы полных затрат:
Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.
Лекция
Балансовые
модели
1.
Экономико-математическая модель МОБ
Основой
построения математической модели МОБ
является матрица коэффициентов
прямых материальных затрат:

Коэффициент
аij
показывает, какое количество i-го
продукта затрачивается на производство
единицы j-го
продукта.
Коэффициент
аij
является безразмерной величиной. Кроме
того, из (3) следует, что 0≤
аij<1.
С
учетом (3) запишем систему балансовых
уравнений (1) в виде:

Введем
в рассмотрение матрицу
коэффициентов прямых затрат
A=(aij),
вектор-столбец валовой продукции Х
и вектор-столбец конечной продукции Y:

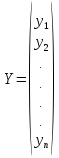
Тогда система (4) примет матричную форму:
X
=
AX
+
Y (5)
Система
уравнений (4) или в матричной форме (5)
называется ЭММ
МОБ (моделью Леонтьева)
или моделью «затраты-выпуск».
Модель
позволяет решить следующие задачи:
-
По
заданным объемам валовой продукции xi
определить объемы конечной продукции
отраслей yj:
Y
= X
—
AX
= (E
— A)
· X. (6)
E
– единичная матрица порядка n.
-
По
заданным объемам конечной продукции
yj
определить объемы валовой продукции
отраслей xi:
X
= (E
— A)-1
· Y
= B
Y. (7)
В
= (E
— A)-1
– матрица
коэффициентов полных материальных
затрат
(обратная матрица Леонтьева). Элемент
этой матрицы bij
показывает, каким должен быть валовой
выпуск i-й
отрасли xi
для того, чтобы с учетом прямых и косвенных
затрат обеспечить производство единицы
конечного продукта j-й
отрасли yj:

Коэффициенты
bij
могут использоваться для определения
влияния изменения объемов конечной
продукции отраслей на величину валового
выпуска некоторой отрасли:

где
Δxi
и Δyj
– изменения (приросты) величин валовой
и конечной продукции.
-
По
заданной матрице коэффициентов прямых
затрат А
определить матрицу коэффициентов
полных затрат В.
Обратную
матрицу В
= (E
— A)-1
можно вычислить, используя метод
обращения с применением формулы
разложения ее в матричный ряд:
В
= (E
— A)-1
= E
+ А
+ A2
+ A3
+ … + Ak
+ …
Матрицы
A2,
A3,
… , Ak,
… называются матрицами коэффициентов
косвенных затрат 1-го, 2-го и т.д. порядков.
Таким
образом, полные затраты bij
включают в себя прямые
(выражены коэффициентами аij)
и косвенные
(С
= B
— A
— E
= A2
+ A3
+ … + Ak
+ …) затраты.
Прямые
затраты
осуществляются непосредственно при
производстве данного продукта. Они не
отражают сложных взаимосвязей, в
частности, обратных связей.
Косвенные
затраты
относятся к предшествующим стадиям
производства и входят в производство
продукта не прямо, а через другие
(промежуточные) средства производства
(или другие ингредиенты, входящие в
данный продукт).
Например,
на изготовление трактора в виде прямых
затрат расходуется чугун, сталь и т.д.,
но для производства стали также нужен
чугун. Затраты этого чугуна являются
косвенными.
-
Задавая
для ряда отраслей объемы xi,
а для остальных отраслей величины yj,
можно найти величины yj
первых отраслей и объемы xi
вторых отраслей. В этом варианте расчета
удобнее пользоваться не матричной
формой модели, а системой линейных
уравнений (4).
2.
Решение типовой задачи МОБ
Рассмотрим
пример составления МОБ производства и
распределения продукции для 3-х отраслевой
ЭС, заданной матрицей коэффициентов
прямых затрат А
и вектором
конечной продукции Y:


Найти:
-
коэффициенты
полных затрат: В
= (bij); -
плановые
объемы валовой продукции: Х
= (xi)
= (x1,
x2,
x3); -
величину
межотраслевых потоков средств
производства, т.е. значения xij,
i=1,
2, 3; j
= 1, 2, 3; -
объемы
условно-чистой продукции zj; -
матрицу
косвенных затрат С
= (сij)
= B
— A
— E. -
По
заданному вектору увеличения выпуска
конечной продукции ΔY=(Δy1,Δy2,Δy3)=(20,
10, 5) определить изменение плана
производства валовой продукции ΔX.
Результаты
вычислений п.п. 1-4 представить в форме
МОБ.
Используем
уравнения МОБ
в
развернутом виде:
в
матричном виде: X
= (E
— A)-1
· Y
= B
Y.
-
Находим
матрицу полных затрат В
= (E
— A)-1:
E
— A
=

Обращаем
матрицу E
— A,
т.е. найдем В
= (E
— A)-1.
Вычисляем
определитель Δ=|E
— A|=
Так
как Δ≠0, то существует матрица В
= (E
— A)-1,
обратная заданной матрице E—A.
Находим
алгебраические дополнения для элементов
матрицы K
= E
— A:
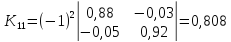








Составляем
матрицу из алгебраических дополнений:

Транспонируем
эту матрицу (получим приведенную матрицу)
и делим ее на определитель Δ=0,511; в
результате получаем обратную матрицу
В
= (E
— A)-1:
В
= (E
— A)-1
=

Рассмотрим
другой способ нахождения обратной
матрицы В
= (E
— A)-1,
присоединив к матрице E
— A
единичную матрицу и выполнив матричные
преобразования:
Таким
образом, матрица коэффициентов полных
затрат
В
= (E
— A)-1
=

-
Находим
объемы производства отраслей (валовая
продукция):
X
= B
Y
=

Следовательно,
плановые объемы валовой продукции трех
отраслей, необходимые для обеспечения
заданного уровня конечной продукции,
равны:
х1=102,197;
х2=41,047;
х3=26,383.
-
Рассчитываем
значения межотраслевых потоков xij=aij·
xj:
x11=0,3·102,2=30,7; x12=0,25·41,0=10,2; x13=0,2·26,4=5,3;
x21=0,15·102,2=15,3; x22=0,12·41,0=4,9; x23=0,03·26,4=0,8;
x31=0,1·102,2=10,2; x32=0,05·41,0=2,1; x33=0,08·26,4=2,1.
-
Результаты
вычислений представим в форме МОБ.
Величина условно-чистой продукции zj
определяется из формулы (2) как разница
между валовой продукцией отрасли xj
и суммой межотраслевых потоков в каждом
столбце:

|
Потребляющие
отрасли Производящие
отрасли |
1 |
2 |
3 |
Конечный yi |
Валовой xi |
|
1 |
30,7 |
10,2 |
5,3 |
56 |
102,2 |
|
2 |
15,3 |
4,9 |
0,8 |
20 |
41,0 |
|
3 |
10,2 |
2,1 |
2,1 |
12 |
26,4 |
|
Условно-чистый |
46,0 |
23,8 |
18,2 |
||
|
Валовой |
102,2 |
41,0 |
26,4 |
169,6 |
Таким
образом, на основе заданных матриц по
уровню конечного продукта Y
и коэффициентов прямых затрат A
получен полностью сбалансированный
план общего производства продукции и
ее распределения в качестве средств
производства между отраслями и в качестве
продукции для конечного использования.
-
Найдем
матрицу косвенных затрат по формуле:
С
= (сij)
= B
— A
— E
= =
-
Определяем
изменение плана ΔX,
которое потребуется при увеличении
выпуска конечной продукции 1-й отрасли
на 20 ед., 2-й – на 10 ед. и 3-й – на 5 ед.
ΔX
= B
ΔY
=
Следовательно,
потребуется увеличить выпуск валовой
продукции 1-й отрасли на Δx1=38,1
ед., 2-й отрасли – на Δx2=18,2
ед., 3-й отрасли – на 10,6 ед.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Перейдем к построению математической модели. Для этого введем понятие коэффициентов прямых материальных затрат:
(1)
Коэффициент aij показывает, какое количество i-го продукта затрачивается на производство единицы j-го продукта.
Поскольку продукция измеряется в стоимостных единицах, коэффициенты прямых затрат являются величинами безразмерными. Кроме того, из (1) следует, что
(2)
Считая коэффициенты прямых материальных затрат постоянными, запишем систему балансовых соотношений
следующим образом:
Перенося yi в правую часть, а xi в левую и меняя знаки на противоположные, получаем
В матричной форме эта система уравнений выглядит следующим образом:
X — AX = Y или (E — A) X = Y,
где Е — единичная матрица n-го порядка;
— матрица коэффициентов прямых материальных затрат.
Итак, мы получили систему уравнений межотраслевого баланса, которую называют моделью Леонтьева. Используя эту модель, можно ответить на основной вопрос межотраслевого анализа — каким должно быть валовое производство каждой отрасли для того, чтобы экономическая система в целом произвела заданное количество конечной продукции?
Следует отметить одно важное свойство А — сумма элементов любого ее столбца меньше единицы:
(3)
Для доказательства разделим обе части балансового соотношения
на хj и, выполнив простейшие преобразования, получим
где vj / xj= — доля условно-чистой продукции в единице валового выпуска.
Очевидно, что >0, так как в процессе производства не может не создаваться новой стоимости. Из этого следует справедливость соотношения (3).
Свойства (2) и (3) матрицы А играют ключевую роль в доказательстве ее продуктивности, т. е. в доказательстве того, что при любом неотрицательном Y система
X — AX = Y или (E — A) X = Y,
имеет единственное и неотрицательное решение Х=(Е-А)-1Y. Матрицу (Е-А)-1 обозначают через В и называют матрицей коэффициентов полных материальных затрат, или обратной матрицей Леонтьева. Коэффициент bij этой матрицы показывает, каким должен быть валовой выпуск i-й отрасли для того, чтобы обеспечить производство единицы конечного продукта j-й отрасли. Используя матрицу В, можем записать
Х = ВY
или в развернутом виде
Преимущество такой формы записи балансовой модели состоит в том, что, вычислив матрицу В лишь однажды, мы можем многократно использовать ее для вычисления Х прямым счетом, т.е. умножением В на Y. Это гораздо проще, чем каждый раз решать систему линейных уравнений.
Обратную матрицу В можно вычислить, используя метод обращения с применением формулы разложения ее в матричный ряд:
В=Е+А+А2+…+Аk+… (4)
Число членов ряда, необходимое для получения достаточно точного приближения, зависит от матрицы А, но в любом случае приемлемый результат достигается при k 30.
Формула (4) имеет строгое математическое доказательство. Но мы ограничимся тем, что попытаемся осмыслить ее, рассматривая Х как результат некоторого гипотетического процесса последовательного уточнения промежуточной продукции, необходимой для создания заданного конечного продукта.
Итак, вектор конечной продукции, которую должна произвести экономическая система, равен Y. Будем считать, что это и есть первоначальное задание отраслям, т. е. Х0 =Y. Для выполнения собственного задания каждая отрасль нуждается в продукции других отраслей. Если бы все отрасли подсчитали потребности и подали заявки в некоторый центр, то оказалось бы, что суммарная потребность составляет X1 =АХ0=АY. Вектор X1 можно рассматривать как промежуточную продукцию, необходимую для производства Х0. Но под обеспечение производства X1 тоже нужна промежуточная продукция: X2 =АХ1 =А2Y. Рассуждая так и далее, мы приходим к выводу, что
Х=Х0+Х1+Х2+…+Хk+… = Y+АY+А2Y+…+AkY+… =
= (Е+А+А2+…+Аk+…)Y.
Полные затраты можно разложить на прямую и косвенную составляющие. Прямые затраты осуществляются непосредственно при производстве данного продукта, а косвенные А2+А3+…+Аk+… относятся к предшествующим стадиям производства. Они осуществляются не прямо, а через посредство других ингредиентов, входящих в данный продукт. Элементы матрицы А2 представляют собой косвенные затраты первого порядка, элементы матрицы А3 — косвенные затраты второго порядка и т. д.
Пример 1. Рассматривается трехотраслевой МОБ. Известна матрица коэффициентов прямых материальных затрат и задан вектор конечного продукта:
.
Определить валовое производство X, обеспечивающее заданный конечный продукт.
Для ответа на поставленный вопрос необходимо составить и решить систему линейных уравнений (Е-А)Х = Y.
Получим соответствующую систему уравнений
Решим систему методом Крамера. Если определитель системы отличен от нуля, то система имеет единственное решение, которое находится по формулам
где — определитель, который получается из
заменой j-го столбца столбцом свободных членов.
Применяя формулы Крамера, получаем решение системы:
Пример 2. Вычислить изменение межотраслевых потоков, если известна матрица коэффициентов полных материальных затрат и задан вектор изменения конечного продукта:
Изменение межотраслевых потоков вычисляется по формулам
Вектор изменения валового производства определяется следующим образом:
Кроме того, нам необходимо знать матрицу А. Из формулы В=(Е-А)-1 следует, что
Теперь, отвечая на поставленный вопрос, получаем:
и т.д.
Источник: https://lms2.sseu.ru
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
3.4. Составление межотраслевого баланса затрат труда
Рассмотрим задачу межотраслевого баланса затрат труда и использования трудовых ресурсов. Предполагается, что труд выражается в единицах труда одинаковой степени сложности. Обозначим затраты живого труда в производстве 
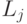


 |
( 3.9) |
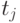

Полные затраты труда представляют сумму прямых затрат (живого труда) и затрат овеществленного труда, перенесенных на продукт через израсходованные средства производства. Пусть 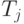




 |
( 3.10) |
Система (3.10) включает 
 |
( 3.11) |
отсюда, выполняя простые матричные преобразования, получим:
 |
( 3.12) |
Поскольку 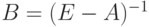
 |
( 3.13) |
где 

Умножим обе части уравнения (3.13) на 


 |
( 3.14) |
Уравнение (3.14) — баланс общих затрат труда: затраты в производстве 

Задача 3 .3.
Рассмотрим задачу с 3 секторами экономики (промышленность, сельское хозяйство и транспорт). В таблице приведены коэффициенты прямых затрат отчетного межотраслевого баланса, объемы конечной продукции в млн.руб. и затраты живого труда. Составить межотраслевой баланс затрат труда.
| Производящие отрасли | промышленность | Сельское хозяйство | Транспорт | Конечная продукция |
| Потребляющие отрасли | Коэффициенты прямых затрат | |||
| Промышленность | 0,2 | 0,3 | 0,2 | 160 |
| Сельское хозяйство | 0,4 | 0,1 | 0,3 | 443 |
| Транспорт | 0,3 | 0,5 | 0,1 | 466 |
| Затраты живого труда Lj | 910 | 719 | 637 |
Решение.
Для составления межотраслевого баланса затрат труда необходимо найти следующие показатели
- Матрицу коэффициентов полных затрат .
- Вектор валовой продукции
- Матрицу межотраслевых поставок
- Коэффициенты прямой трудоемкости
, Коэффициенты полной трудоемкости
- Межотраслевые затраты труда
- Затраты труда на конечную продукцию
- Заполнить матрицу МОБ. Выполнить проверку проведенных вычислений
- уравнения
Выполняем проверку проведенных вычислений. В таблице МОБ рассчитываем баланс:
Входные данные
Матрица прямых затрат:
Вектор конечной продукции:
Затраты живого труда: 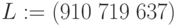
Решение:
Вводим единичную матрицу:
Матрица полных затрат: 
Вектор объемов валовой продукции: 
Матрица межотраслевых поставок:

Коэффициенты прямой трудоемкости: 

Затраты живого труда на конечную продукцию: 
Межотраслевые затраты труда: 
Рассчитываем баланс. Сумма межотраслевых затрат труда и затрат труда на конечную продукцию равна затратам живого труда




Основные итоги
Приведены основные параметры и уравнения МОБ. Показано, как построить модель задачи МОБ, как выделить блок данных и блок решения. Продемонстрированы методы работы с матрицами и матричными уравнениями.
Ключевые термины
Межотраслевой баланс — инструмент анализа и прогнозирования структурных взаимосвязей в экономике.
Валовый продукт отрасли — суммарный объем продукции, потребляемой n отраслями, и конечного продукта.
Конечный продукт — объем продукции отрасли, предназначенный к потреблению в непроизводственной сфере (объём конечного потребления).
Матрица межотраслевых поставок —


Коэффициент прямых затрат — количество продукции 

Коэффициент полных затрат — объем продукции 

Коэффициент полных затрат труда — затраты живого и овеществленного труда на производство единицы конечной продукции,
Коэффициент прямых затрат труда — затраты живого труда на производство единицы общего объема произведенной продукции.
Межотраслевой баланс
С помощью сервиса в онлайн режиме можно:
- найти коэффициенты полных материальных затрат, определить вектор валовой продукции;
- составить межотраслевой баланс, составить схему межотраслевого баланса труда;
- проверить продуктивность матрицы.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.
Система уравнений X = AX + Y называется экономико-математической моделью межотраслевого баланса (МОБ) или моделью «затраты — выпуск». C помощью нее можно выполнить следующие расчеты:
- подставив в модель объемы валовой продукции каждой отрасли Xi, можно определить объем конечной продукции отрасли Yj: Y = (E — A)X
- задав величины конечной продукции всех отраслей Yj, можно определить величины валовой продукции каждой отрасли Xi: X = (E — A) -1 Y
- установив для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти объемы конечной продукции первых отраслей и объемы валовой продукции вторых.
Здесь A – матрица прямых затрат, коэффициенты которой, aij показывают затраты i-й отрасли на производство единицы продукции j-й отрасли. Введем обозначение B = (E — A) -1 . Матрица B называется матрицей полных материальных затрат, коэффициенты которой, bij показывают полный объем продукции i-й отрасли, используемой для производства единицы продукции j-й отрасли. С учетом линейности соотношений эффект распространения спроса ΔX, вызванный изменением конечного спроса на величину ΔY рассчитывается как: ΔX = B·ΔY
Через C=A-B обозначают матрицу косвенных затрат.
Пример №1 . Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y .
Пример №2 . Дан межотраслевой баланс трехотраслевой модели хозяйства:
| № отрасли потребления | 1 | 2 | 3 | Конечный продукт | Валовый продукт | Y’ | |
| № отрасли | 1 | 20 | 20 | 60 | 100 | 200 | 150 |
| отрасли | 2 | 20 | 40 | 60 | 80 | 200 | 100 |
| производства | 3 | 20 | 0 | 10 | 70 | 100 | 100 |
Определить:
1) технологическую матрицу;
2) матрицу коэффициентов полных затрат;
3) дать экономический анализ каждого столбца матрицы коэффициентов полных затрат;
4) определить валовый выпуск X’ на новый ассортимент конечной продукции Y’;
Решение.
Находим валовой объем продукции xi;
x1 = 20 + 20 + 60 + 100 = 200
x2 = 20 + 40 + 60 + 80 = 200
x3 = 20 + 0 + 10 + 70 = 100
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | 20 | 20 | 60 | 100 | 200 |
| 20 | 40 | 60 | 80 | 200 | |
| 20 | 0 | 10 | 70 | 100 |
По формуле aij = xij / xj находим коэффициенты прямых затрат:
a11 = 20/200 = 0.1; a12 = 20/200 = 0.1; a13 = 60/100 = 0.6; a21 = 20/200 = 0.1; a22 = 40/200 = 0.2; a23 = 60/100 = 0.6; a31 = 20/200 = 0.1; a32 = 0/200 = 0; a33 = 10/100 = 0.1;
| 0.1 | 0.1 | 0.6 |
| 0.1 | 0.2 | 0.6 |
| 0.1 | 0 | 0.1 |
Определим матрицу коэффициентов полных затрат с помощью формул обращения невырожденных матриц.
а) Находим матрицу (E-A):
| (E-A) = |
|
б) Вычисляем обратную матрицу (E-A) -1 :
| 0,9 | -0,1 | -0,6 |
| -0,1 | 0,8 | -0,6 |
| -0,1 | 0 | 0,9 |
Найдем величины валовой продукции трех отраслей
| X’ = (B -1 *Y’) = |
|
* | = |
Пример №3 . В модели межотраслевого баланса
| Производство | Потребление | Конечная продукция | Валовая продукция | ||
| 1 | 2 | 3 | |||
| 1 | 10 | 5 | 15 | 70 | 100 |
| 2 | 20 | … | … | … | … |
| 3 | 30 | … | … | … | … |
| Оплата труда | 30 | … | … | … | … |
| Прибыль D | D | … | … | … | … |
прибыль D равна:
D = Валовая продукция – Затраты на производство – Оплата труда = 100 – (10+20+30) – 30 = 10.
Определение. Соотношение
называется уравнением линейного межотраслевого баланса. Вместе с описанием матричного представления это уравнение называется моделью Леонтьева.
Уравнение межотраслевого баланса позволяет решить следующие задачи:
- 1) найти вектор конечного продукта Y при известной матрице прямых затрат и заданном векторе валового продукта Х: ;
- 2) найти вектор валового выпуска Х при известной матрице прямых затрат, который обеспечивает заданный вектор конечного продукта Y: или , откуда .
Умножив обе части уравнения слева на , получим
Матрица
называется матрицей полных затрат.
Определение. Коэффициентами полных затрат называются величины sij валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли .
Заметим, что при известной матрице полных затрат А можно найти матрицу полных затрат
Определение. Матрица называется продуктивной, если для любого вектора существует решение уравнения . В этом случае модель Леонтьева называется продуктивной.
Заметим, что матрица А продуктивна, если для любых и
и существует номер j такой, что
Определение. Чистой продукцией отрасли называется разность между валовой продукцией этой отрасли и затратами продукции всех отраслей на производство данной отрасли.
Пример 1. Данные об исполнении баланса за отчетный период (усл. ден. ед.) приведены в таблице:
Матрица полных затрат и вектор валового выпуска
Модели данного класса регулярно строятся во многих странах мира. С их помощью решаются задачи анализа, планирования и прогнозирования развития экономических систем. Задачи, в решении которых могут быть применены матричные модели:
· регулирование экономического развития;
· расчеты по составлению долгосрочных планов;
· расчеты по оптимизации внешней торговли;
· составление межрегиональных балансов;
· расчеты по ценообразованию и т.д.
Типичным примером матричных моделей считается экономико-математическая модель межотраслевого баланса (модель В.В. Леонтьева). За разработку и применение этого метода к решению важных экономических проблем в 1973 году Василий Васильевич Леонтьев был удостоен Нобелевской премии в области экономики.
В западной литературе модели данного класса именуются как метод «затраты-выпуск».
ОБЩАЯ СТРУКТУРА МЕЖОТРАСЛЕВОГО БАЛАНСА
Центральным элементом матричных моделей является межотраслевой баланс. Он представляет собой таблицу, характеризующую связи между различными отраслями экономики страны.
Производственная сфера экономики представлена в балансе в виде совокупности n отраслей. Баланс состоит из четырех разделов (квадрантов).
Первый квадрант представляет собой матрицу, состоящую из (n+1) строки и (n+1) столбца. Этот раздел является важнейшей частью баланса, поскольку именно здесь содержится информация о межотраслевых связях.
Величина xij показывает, сколько продукции i-й отрасли было использовано в процессе материального производства j-й отрасли. Величины xij характеризуют межотраслевые поставки сырья, материалов, топлива и энергии, обусловленные производственной деятельностью. В i-й строке величины xi1, xi2, . xij, . xin описывают распределение продукции i-й отрасли как средства производства для других отраслей. Величины x1j, x2j, . xij, . xnj j-го столбца в этом случае будут описывать потребление j-й отраслью сырья, материалов, топлива и энергии на производственные нужды. Таким образом, первый раздел баланса дает общую картину распределения продукции на текущее производственное потребление всех n отраслей материального производства .
В зависимости от того, в каких единицах измеряются потоки продукции в балансе, существуют различные его варианты:
· в натуральном выражении;
· в денежном (стоимостном) выражении,
· в трудовых измерителях.
Рассмотрим баланс в стоимостном выражении, в котором потоки продукции измеряются на основе стоимости произведенной продукции в некоторых фиксированных ценах. Поскольку в этом случае величины xij отражают стоимость продукции, т.е. измеряются в одних и тех же единицах, их можно просуммировать.
Сумма по строке представляет собой сумму всех поставок i—й отрасли другим отраслям.
Сумма по столбцу характеризует производственные затраты j-й отрасли на приобретение продукции других отраслей.
На пересечении (n+1)-й строки и (n+1)-го столбца находится промежуточный продукт экономики
Второй раздел посвящен конечному продукту.
Столбец конечного продукта — (n+2)-й столбец. Величина yi — потребление продукции i-й отрасли, не идущее на текущие производственные нужды.
В конечную продукцию, как правило, включаются:
· возмещение выбытия основных средств;
· личное потребление населения;
· расходы на содержание государственного аппарата;
· а также сальдо экспорта и импорта.
Ко второму разделу относится также столбец валовых выпусков (Xi). В пределах первого и второго разделов справедливо соотношение:
Третий квадрант межотраслевого баланса отражает стоимостную структуру валового продукта отраслей. В (n+2)-й строке таблицы отражена условно чистая продукция (Vj), представляющая собой разницу между величиной валовой продукции отрасли и суммарными затратами отрасли:
Условно чистая продукция подразделяется на амортизационные отчисления и чистую продукцию отрасли .
Важнейшими составляющими чистой продукции отрасли являются заработная плата, прибыль и налоги. Можно показать, что суммарный конечный продукт равен суммарной условно чистой продукции
Таким образом, в третьем разделе также фигурирует конечный продукт, но если во втором разделе он разбивается на величины yi, характеризующие структуру потребления, то в третьем разделе величины Vj показывают, в каких отраслях произведена стоимость конечного продукта.
Четвертый раздел располагается под вторым.
Он характеризует перераспределения в экономике, осуществляемые через финансово-кредитную систему. В плановых расчетах четвертый раздел, как правило, не используется, и поэтому здесь рассматриваться не будет.
Итак, межотраслевой баланс — это способ представления статистической информации об экономике страны .
Он строится на основе агрегирования результатов деятельности отдельных предприятий. Такой баланс называют отчетным. Кроме этого строятся плановые балансы, предназначенные для разработки сбалансированных планов развития экономики.
n СТАТИЧЕСКАЯ МЕЖОТРАСЛЕВАЯ МОДЕЛЬ
Статические межотраслевые модели используются для разработки планов выпуска и потребления продукции и основываются на соотношениях межотраслевого баланса.
При построении модели делают следующие предположения:
1) все продукты, производимые одной отраслью, однородны и рассматриваются как единое целое, т.е. предполагается, что каждая отрасль производит один продукт ;
2) в каждой отрасли имеется единственная технология производства ;
3) нормы производственных затрат не зависят от объёма выпускаемой продукции ;
4) не допускается замещение одного сырья другим.
В действительности эти предположения не выполняются. Даже на отдельном предприятии обычно: выпускаются различные виды продукции, используются различные технологии, удельные затраты зависят от объема выпуска и допускается замена одного сырья другим. Следовательно, эти предположения тем более неверны для отрасли. Однако такие модели получили широкое распространение и, как показала практика, они вполне адекватны и применимы для составления планов выпуска продукции. При этих предположениях величина xij может быть представлена следующим образом:
Величина aij называется коэффициентом прямых материальных затрат . Она показывает, какое количество продукции i-й отрасли идет на производство единицы продукции j-й отрасли. Коэффициенты aij считаются в межотраслевой модели постоянными.
МАТРИЦА КОЭФФИЦИЕНТОВ ПРЯМЫХ МАТЕРИАЛЬНЫХ ЗАТРАТ
Подставляя выражение (3) в формулу (1), получим (4)
Можно записать в матричном виде
Коэффициенты прямых материальных затрат являются основными параметрами статической межотраслевой модели .
Их значения могут быть получены двумя путями:
1) статистически : коэффициенты определяются на основе анализа отчётных балансов за прошлые годы.
2) нормативно : предполагается, что отрасль состоит из отдельных производств, для которых уже разработаны нормативы затрат, на их основе рассчитываются среднеотраслевые коэффициенты. Выражение (4) принято называть балансом распределения продукции. Его можно использовать для анализа и планирования структуры экономики. Если известны коэффициенты прямых материальных затрат, то, задав конечный продукт по каждой отрасли, можно определить необходимые валовые выпуски отраслей. В этом заложена основная идея использования матричных моделей для планирования производства.
Преобразуем выражение (4):
где E — единичная матрица.
До начала планирования следует выяснить, существует ли матрица, обратная матрице (E-A), и не будут ли получены отрицательные значения выпуска по отраслям. Установим некоторые свойства коэффициентов прямых материальных затрат:
1. Неотрицательность , т.е. aij ≥ 0, это утверждение следует из неотрицательности величин xij и положительности валовых выпусков Xj
2. Сумма элементов матрицы A по любому из столбцов меньше единицы . Доказательство:
Для любой отрасли условно чистая продукция есть величина положительная, поскольку включает в себя заработную плату, амортизацию, прибыль и т.д., т.е. Vj>0. Поэтому, используя соотношение (2), можно записать:
При выполнении этих двух условий матрица B = (E — A) — 1 существует если ее элементы неотрицательны. Говорят, что в этом случае матрица прямых затрат А является продуктивной . Перепишем формулу
Матрица В носит название матрицы полных материальных затрат, а ее элементы bij называют коэффициентами полных материальных затрат . Коэффициент bij показывает, каков должен быть валовой выпуск i—й отрасли для того, чтобы обеспечить выпуск единицы конечного продукта j-й отрасли.
Можно показать, что
Умножим обе части на (E — A):
Из соотношения (7) следует bij ≥ aij, таким образом, коэффициент полных материальных затрат bij, описывающий потребность в выпуске продукции i-й отрасли в расчете на единицу конечного продукта j-й отрасли, не меньше коэффициента прямых материальных затрат aij, рассчитываемого на единицу валового выпуска. Кроме того, из соотношения (7) для диагональных элементов матрицы B следует: bii ≥ 1, взаимосвязь коэффициентов прямых и полных материальных затрат проследим на примере.
Пусть единицей выпуска хлебопекарной промышленности является хлеб. Взаимосвязь коэффициентов прямых и полных материальных затрат.
Полные затраты электроэнергии для нашего примера складываются из прямых затрат и косвенных затрат всех уровней. Косвенные затраты высоких уровней являются незначительными и при практических расчетах ими можно пренебречь.
Пример : Даны коэффициенты прямых затрат aij и конечный продукт Y для трехотраслевой экономики
a) коэффициенты полных затрат;
b) вектор валового продукта;
c) межотраслевые поставки продукции;
d) проверить продуктивность матрицы А;
e) заполнить схему межотраслевого баланса.
Для решения использовать функции Excel
Далее вычисляем матрицу коэффициентов полных затрат В-(Е-А).
Для вычисления матрицы В:
a. Выделить диапазон ячеек для размещения матрицы
b. Выбрать функцию МОБР в категории математические
c. Ввести диапазон ячеек, где содержится Е-А
d. Нажать клавиши CTRL+SHIFT+ENTER
Все элементы матрицы В неотрицательны, следовательно матрица А продуктивна. Вычислим вектор валового выпуска Х по формуле X = BY
Для умножения матриц необходимо:
a. Выделить диапазон ячеек для размещения результата умножения матриц
b. Выбрать функцию МУМНОЖ в категории математические
c. Ввести диапазоны ячеек, где содержатся матрицы B и Y .
Нажать клавиши CTRL+SHIFT+ENTER
1. Области применения матричных моделей?
2. Структура межотраслевого баланса?
3. Связь между конечной и условно чистой продукцией?
4. Экономический смысл, свойства и способы расчета коэффициентов прямых материальных затрат?
5. Коэффициенты полных материальных затрат?
6. Экономический смысл коэффициентов прямых затрат труда.?
http://vuzlit.ru/879453/opredelenie_sootnoshenie
http://www.sites.google.com/site/matematiceskaaekonomika/home/makroekonomiceskie-proizvodstvennye-funkcii