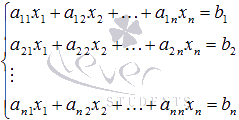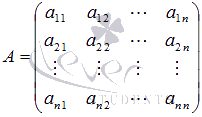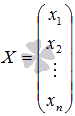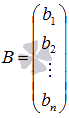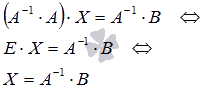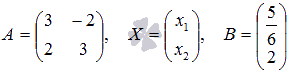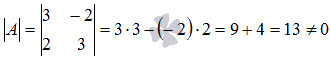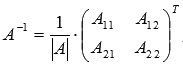Как найти матрицу исходов

Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.

Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.

Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.   

Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.

Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A^-1 · B, где A^-1 — обратная матрица.

Матричный метод решения состоит в следующем.

Пусть дана система линейных уравнений с nнеизвестными:

Её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A^-1 — матрицу, обратную к матрице A:  A^-1 (AX) = A^-1 B

Так как A^-1A = E, получаем X = A^-1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: detA≠ 0.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Пример решения неоднородной системы линейных алгебраических уравнений.

Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.

Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они  понадобятся для нахождения обратной матрицы.

Теперь найдём союзную матрицу и транспонируем  её, потом подставим в формулу для нахождения обратной матрицы.

Подставляя переменные в формулу, получаем:

Найдем неизвестные. Для этого перемножим обратную матрицу  и столбец свободных членов.

Итак, x=2; y=1; z=4.

Если у Вас есть вопросы или Вам нужна помощь в решении линейных уравнений или систем, записывайтесь на мои занятия. Буду рад Вам помочь.  

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Содержание:

• Матричный метод решения
• Примеры решения систем уравнений

Матричный метод решения

Запишем заданную систему в матричном виде:

$$AX=B$$

Если матрица $$A$$ невырождена, то тогда с помощью
операций над матрицами
выразим неизвестную матрицу $$X$$ . Операция деления на множестве
матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу $A^{-1}$ слева:

$$A^{-1} A X=A^{-1} B Rightarrow E X=A^{-1} B Rightarrow$$
$$X=A^{-1} B$$

Поэтому, чтобы найти неизвестную матрицу $$X$$ надо найти обратную матрицу
к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.

Примеры решения систем уравнений

Читать дальше: метод Крамера.

Матричный метод решения систем линейных уравнений

Матричный метод может применяться в решении систем линейных уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.

Другое условие применимости матричного метода — невырожденность матрицы коэффициентов при неизвестных, то есть неравенство нулю определителя этой матрицы.

Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в матричном виде, а затем решить её путём отыскания обратной матрицы к матрице системы.

Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .

Пусть нужно решить систему линейных уравнений:

Запишем эту систему уравнений в матричном виде:

Обозначим отдельно как A матрицу коэффициентов при неизвестных и как B матрицу неизвестных и матрицу свободных членов

.

То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц.

Алгоритм решения системы линейных уравнений матричным методом разберём на следующем примере системы линейных уравнений второго порядка.

Пример 1. Решить матричным методом систему линейных уравнений:

Решение состоит из следующих шагов.

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:

Матрица свободных членов:

Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:

По выведенному выше последнему равенству и будем вычислять решения данной системы.

Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть можем ли вообще применять матричный метод:

.

Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

.

Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

.

Следовательно, ответ правильный.

Для второго примера выберем систему линейных уравнений третьего порядка.

Пример 2. Решить матричным методом систему линейных уравнений:

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:

Матрица свободных членов:

Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:

.

Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

.

Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

.

Следовательно, ответ правильный.

Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение

Пример 3. Решить матричным методом систему линейных уравнений:

Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы

В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.

Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.

Найти решение системы n линейных уравнений с n неизвестными:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n

Матричный вид записи: А × X = B

где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.

X = x 1 x 2 ⋮ x n — столбец неизвестных,

B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.

Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :

A — 1 × A × X = A — 1 × B .

Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .

Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .

В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.

Пример решения системы линейных уравнений с помощью метода обратной матрицы

Решаем СЛАУ методом обратной матрицы:

2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2

• Записываем систему в виде матричного уравнения А X = B , где

А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .

• Выражаем из этого уравнения X :

• Находим определитель матрицы А :

d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25

d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.

• Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :

А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,

А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,

А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,

А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,

А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,

А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,

А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,

А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,

А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .

• Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :

А * = — 6 7 5 17 1 — 10 — 10 — 5 0

• Записываем обратную матрицу согласно формуле:

A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,

• Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:

X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1

Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1

Конспект на тему: «Решение системы линейных уравнений матричным методом»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Решение систем линейных уравнений матричным методом

Пусть дана система уравнений

Рассмотрим матрицу, составленную из коэффициентов при неизвестных .

Свободные члены и неизвестные можно записать в виде матриц-столбцов:

Тогда используя правило умножения матриц, эту систему уравнений можно записать так:

Это равенство называется простейшим матричным уравнением .

Чтобы решить матричное уравнение, нужно:

Найти обратную матрицу .

Найти произведение обратной матрицы на матрицу – столбец свободных членов В, т.е..

Пользуясь определением равных матриц, записать ответ.

Решить систему уравнений

Представим уравнение в виде матричного уравнения.

Решение . Перепишем систему в виде АХ=В, где

Решение матричного уравнения имеет вид .

Найдем обратную матрицу :

Следовательно, х=2, y =3, z =-2.

Решить систему уравнений матричным методом

Найдем обратную матрицу А -1 .

 = det A = 20 – 12 – 3 + 8 – 45+2= -30.

Находим матрицу Х.

Итого решения системы: x =1; y = 2; z = 3

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 932 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 575 831 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 10.06.2020
• 440
• 28

• 10.06.2020
• 433
• 16

• 10.06.2020
• 346
• 4

• 10.06.2020
• 113
• 1

• 10.06.2020
• 110
• 0

• 10.06.2020
• 380
• 8

• 10.06.2020
• 97
• 0

• 10.06.2020
• 291
• 8

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 10.06.2020 489
• DOCX 77.3 кбайт
• 24 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Ажулаева Патимат Магомедрасуловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет
• Подписчики: 0
• Всего просмотров: 134080
• Всего материалов: 69

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Минпросвещения подключит студотряды к обновлению школьной инфраструктуры

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Матричный метод решения систем линейных уравнений.

В
этой статье поговорим о матричном методе
решения систем линейных алгебраических
уравнений вида

,
которые в матричной форме записываются
как

,
где

—
основная матрица системы,

—
матрица-столбец неизвестных переменных,

—
матрица свободных членов.

Сначала
опишем суть матричного метода, остановимся
на условии применимости этого метода,
далее подробно разберем решения
нескольких примеров.

Сразу
оговоримся, что решение систем линейных
алгебраических уравнений матричным
методом и решение СЛАУ с помощью обратной
матрицы есть одно и то же. Поэтому
рекомендуем освежить в памяти теорию
раздела обратная
матрица: определение, свойства, методы
нахождения.

Приступим.

Пусть
для матрицы А
порядка n
на n
существует обратная матрица

.
Умножим обе части матричного уравнения

слева
на

(порядки
матриц A
⋅
X
и В
позволяют произвести такую операцию,
смотрите статью операции
над матрицами, свойства операций).
Имеем

.
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как

,
а по определению обратной матрицы

(E
– единичная матрица порядка n
на n),
поэтому

Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством

.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы

.

Мы
знаем, что квадратная матрица А
порядка n
на n
имеет обратную матрицу

только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n
НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ
МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ
ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ
НУЛЯ.

Рассмотрим матричный
метод на примерах. В некоторых примерах
мы не будем подробно описывать процесс
вычисления определителей матриц, при
необходимости обращайтесь к статье
вычисление
определителя матрицы.

Пример.

С
помощью обратной матрицы найдите решение
системы линейных уравнений

.

Решение.

В
матричной форме исходная система
запишется как

,
где

.
Вычислим определитель основной матрицы
и убедимся, что он отличен от нуля. В
противном случае мы не сможем решить
систему матричным методом. Имеем

,
следовательно, для матрицы А
может быть найдена обратная матрица

.
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как

.
Итак, задача свелась к построению
обратной матрицы

.
Найдем ее.

Мы знаем, что для матрицы

обратная
матрица может быть найдена как

,
где

—
алгебраические дополнения элементов

.

В
нашем случае

Тогда

Выполним
проверку полученного решения

,
подставив его в матричную форму исходной
системы уравнений

.
Это равенство должно обратиться в
тождество, в противном случае где-то
была допущена ошибка.

Следовательно,
решение найдено верно.

Ответ:

или
в другой записи

.

Системы линейных уравнений: основные понятия

24 Июня 2011

Определение.
Система линейных уравнений — это
объединение из n линейных уравнений,
каждое из которых содержит k переменных.
Записывается это так:

Многие,
впервые сталкиваясь с высшей алгеброй,
ошибочно полагают, что число уравнений
обязательно должно совпадать с числом
переменных. В школьной алгебре так
обычно и бывает, однако для высшей
алгебры это, вообще говоря, неверно.

Определение.
Решение системы уравнений — это
последовательность чисел (k₁,
k₂, …, k_n),
которая является решением каждого
уравнения системы, т.е. при подстановке
в это уравнение вместо переменных x₁,
x₂, …, x_n
дает верное числовое равенство.

Соответственно,
решить систему уравнений — значит найти
множество всех ее решений или доказать,
что это множество пусто. Поскольку число
уравнений и число неизвестных может не
совпадать, возможны три случая:

1. Система
   несовместна, т.е. множество всех решений
   пусто. Достаточно редкий случай, который
   легко обнаруживается независимо от
   того, каким методом решать систему.

2. Система
   совместна и определена, т.е. имеет ровно
   одно решение. Классический вариант,
   хорошо известный еще со школьной скамьи.

3. Система
   совместна и не определена, т.е. имеет
   бесконечно много решений. Это самый
   жесткий вариант. Недостаточно указать,
   что «система имеет бесконечное множество
   решений» — надо описать, как устроено
   это множество.

Определение.
Переменная x_i
называется разрешенной, если она
входит только в одно уравнение системы,
причем с коэффициентом 1. Другими словами,
в остальных уравнениях коэффициент при
переменной x_i
должен быть равен нулю.

Если
в каждом уравнении выбрать по одной
разрешенной переменной, получим набор
разрешенных переменных для всей системы
уравнений. Сама система, записанная в
таком виде, тоже будет называться
разрешенной. Вообще говоря, одну и ту
же исходную систему можно свести к
разным разрешенным, однако сейчас нас
это не волнует. Вот примеры разрешенных
систем:

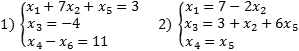
Обе
системы являются разрешенными относительно
переменных x₁,
x₃ и x₄.
Впрочем, с тем же успехом можно утверждать,
что вторая система — разрешенная
относительно x₁,
x₃ и x₅.
Достаточно переписать самое последнее
уравнение в виде x₅
= x₄.

Теперь
рассмотрим более общий случай. Пусть
всего у нас k переменных, из которых r
являются разрешенными. Тогда возможны
два случая:

1. Число
   разрешенных переменных r равно общему
   числу переменных k: r = k. Получаем систему
   из k уравнений, в которых r = k разрешенных
   переменных. Такая система является
   совместной и определенной, т.к. x₁
   = b₁, x₂
   = b₂, …,
   x_k = b_k;

2. Число
   разрешенных переменных r меньше общего
   числа переменных k: r < k. Остальные (k −
   r) переменных называются свободными —
   они могут принимать любые значения, из
   которых легко вычисляются разрешенные
   переменные.

Так,
в приведенных выше системах переменные
x₂, x₅,
x₆ (для
первой системы) и x₂,
x₅ (для
второй) являются свободными. Случай,
когда есть свободные переменные, лучше
сформулировать в виде теоремы:

Теорема.
Если в системе из n уравнений переменные
x₁, x₂,
…, x_r —
разрешенные, а x<sub>r
+ 1</sub>, x<sub>r
+ 2</sub>, …, x_k
— свободные, то:

1. Если
   задать значения свободным переменным
   (x<sub>r
   + 1</sub> = t<sub>r
   + 1</sub>, x<sub>r
   + 2</sub> = t<sub>r
   + 2</sub>, …, x_k
   = t_k), а
   затем найти значения x₁,
   x₂, …, x_r,
   получим одно из решений.

2. Если
   в двух решениях значения свободных
   переменных совпадают, то значения
   разрешенных переменных тоже совпадают,
   т.е. решения равны.

В
чем смысл этой теоремы? Чтобы получить
все решения разрешенной системы
уравнений, достаточно выделить свободные
переменные. Затем, присваивая свободным
переменным разные значения, будем
получать готовые решения. Вот и все —
таким образом можно получить все решения
системы. Других решений не существует.

Вывод:
разрешенная система уравнений всегда
совместна. Если число уравнений в
разрешенной системе равно числу
переменных, система будет определенной,
если меньше — неопределенной.

И
все бы хорошо, но возникает вопрос: как
из исходной системы уравнений получить
разрешенную? Для этого существует метод
Гаусса.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

Методы решения систем линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение

Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы

Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на для этого умножим все элементы первого столбца на эту неизвестную:

Второй столбец умножим на третий столбец — на -ый столбец — на и все эти произведения прибавим к первому столбцу, при этом произведение не изменится:

Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.

Определение: Определитель называется первым вспомогательным определителем СЛАУ.

Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:

31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.

Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы:

Пример:

Решить СЛАУ методом Крамера

Решение:

Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом

Найдем главный определитель СЛАУ (раскрываем по первой строке)

Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя

Воспользуемся формулами Крамера

Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.

Выполним проверку Отсюда видно, что СЛАУ решена верно.

• Заказать решение задач по высшей математике

Матричный способ решения СЛАУ

Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных матpицы-столбцы неизвестных и свободных коэффициентов

Тогда СЛАУ можно записать в матричном виде Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу к матрице А, получим в силу того, что произведение найдем Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

Пример:

Решить СЛАУ матричным способом

Решение:

Введем в рассмотрение следующие матрицы

Найдем матрицу (см. Лекцию № 2): найдем детерминант матрицы А.

Пример:

Решение:

Найдем алгебраические дополнения всех элементов Запишем обратную матрицу (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

Отсюда находим, что х = 1; y = l; z = l.

Метод Гаусса

Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:

Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.

Обменяем в расширенной матрице первую и вторую строки местами, получим Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки Разделим все элементы второй строки на (-5), получим эквивалентную матрицу

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки Разделим все элементы третьей строки на (-3), получим Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй — при неизвестной у, третий — при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):

Из первого уравнения находим, что х = 1.

Вывод: Из вышеизложенного материала следует, что вне зависимости от

способа решения СЛАУ всегда должен получаться один и тот же ответ.

Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.

Ранг матрицы. Теорема Кронекера-Капелли

Определение: Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Если то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.

При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.

Пример:

Найти ранг матрицы

Решение:

Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, среди миноров третьего порядка также есть миноры, которые не равны нулю, например, Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство для определителей). Следовательно, ранг матрицы А равен 3.

Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.

Следствия из теоремы Кронекера — Капелли

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.