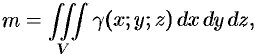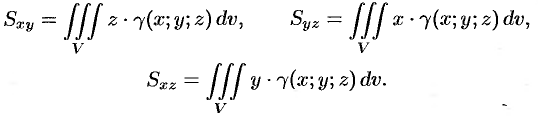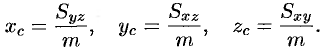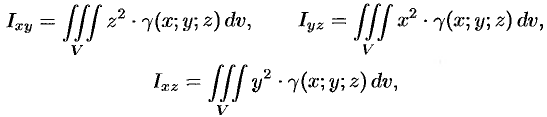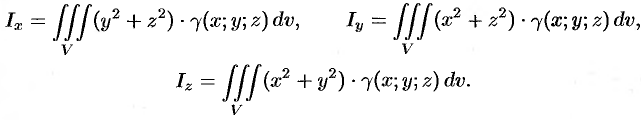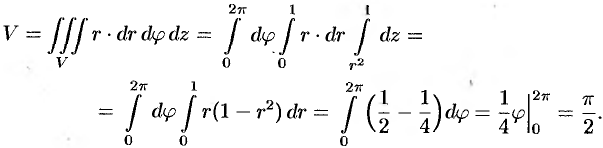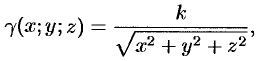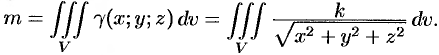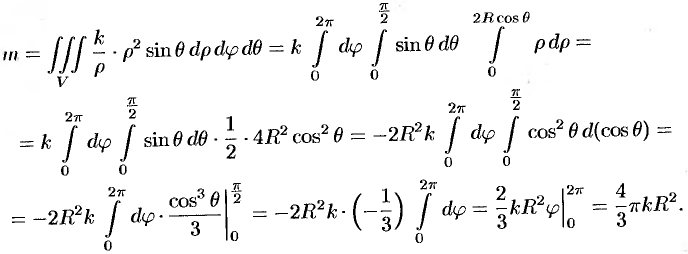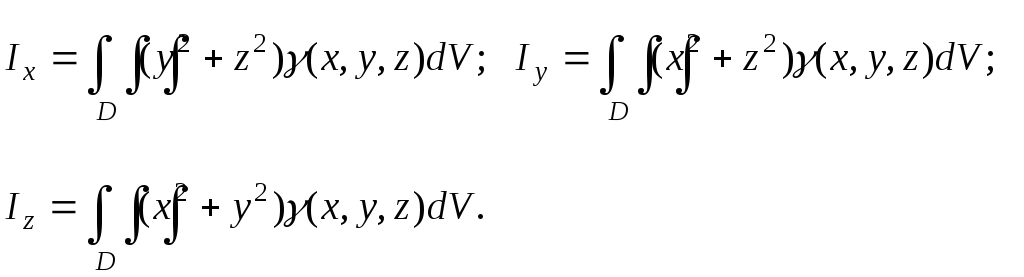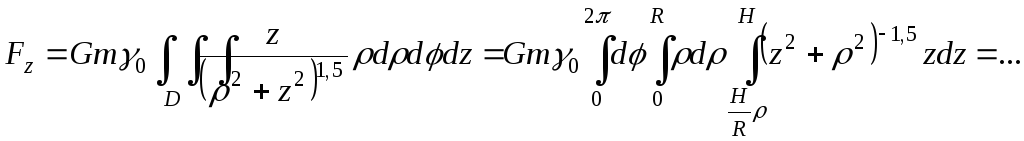Некоторые приложения тройного интеграла
Объем тела
Объем области 
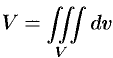
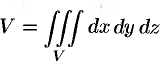
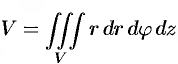
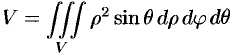
Масса тела
Масса тела 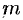
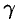
где 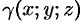
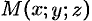
Статические моменты
Моменты 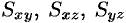
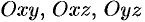
Центр тяжести тела
Координаты центра тяжести тела 
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
а моменты инерции относительно координатных осей:
Пример №54.4.
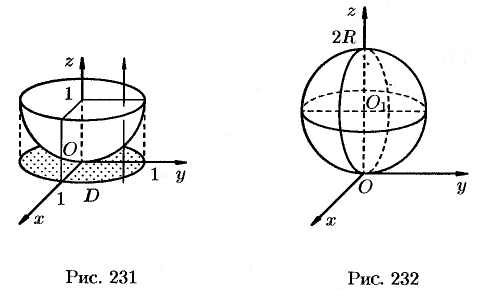
Найти объем тела, ограниченного поверхностями 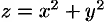
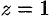
Решение:
Данное тело ограничено сверху плоскостью 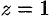
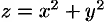
Пример №54.5.
Найти массу шара 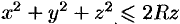
Решение:
Уравнение сферы 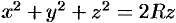
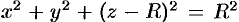
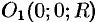
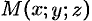
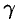
где 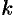
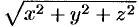

Итак,
Вычислять интеграл будем в сферических координатах. Уравнение сферы 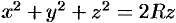

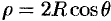
Поэтому сферические координаты будут изменяться в следующих пределах: 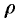
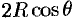
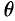
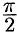
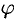
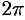
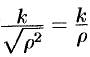
Из соображений симметрии следует, что 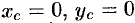
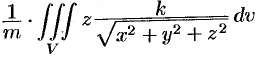
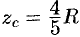
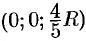
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
I Вычисление объёмов тел
.
Пример
1. Вычислить
объём тела, ограниченного поверхностями
,
,
.
Решение.
Тело, представляет собой полушар с
конической выемкой. Проекция на плоскость
– круг радиуса
с центром в начале координат, следовательно,
координатаССК изменяется от 0 до
.
Проекция на плоскость– полукруг с вырезанным сектором
(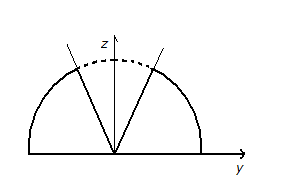
конусаэтой плоскостью – это
).
Координатаизменяется от
на образующих конуса до
на плоскости
.
И, наконец, координата.
Итак, объём тела
Здесь повторный
интеграл представляет собой произведение
трех интегралов, ибо внутренние интегралы
не зависят от внешних переменных.
II Вычисление масс тел
где
– плотность распределения массы.
Пример
2. Найти
массу шара
если плотность в каждой точке
пропорциональна расстоянию от
до некоторой фиксированной точки
поверхности шара.
Решение.
Поместим фиксированную точку в начало
координат, а центр шара на ось
.
Тогда уравнение сферы в сферических
координатах имеет вид (см. §6, замечание
3):,
.
Далее, плотность,.
Имеем для массы:
III Вычисление координат центра масс тела
Формулы для
координат центра масс тела выводятся
так же как аналогичные формулы для
плоской фигуры. Не будем выводить их, а
просто приведем:
П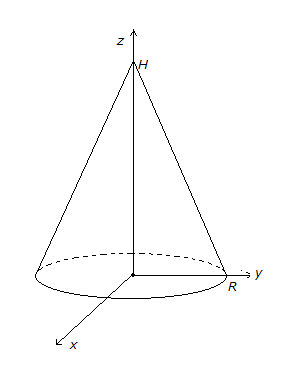
3. Найти
положение центра масс однородного
конуса с радиусом основания
и высотой
.
Решение.
Расположим конус обычным образом:
основание в плоскости
,
вершина на оси.
Выясним какие поверхности ограничивают
это тело. Одна из них – это плоскость,
а вторая – это нижняя часть конической
поверхности,
смещенная вверх наН.
Имеем:
Коэффициент
найдем из того усло-вия, что пересечение
этой поверхности с плоскостью– круг радиусаR:
.
Итак, задачу можно
сформулировать так: «Найти координаты
центра масс тела, ограниченного
поверхностями
и
,
если
».
Тело симметрично относительно оси
и в симметричных точках плотность
одинакова. Следовательно, центр масс
лежит на оси:
Итак, центр масс
однородного конуса расположен на его
оси на расстоянии четверти высоты от
основания.
IV Вычисление моментов инерции тела
Формулы для
всевозможных моментов инерции тела
аналогичны подобным формулам для плоской
фигуры.
Моменты инерции
относительно осей координат:
Моменты инерции
относительно координатных плоскостей:
Момент инерции
относительно начала координат:
Пример
4. Найти
момент инерции цилиндра
относительно фиксированной образующей,
если плотность в каждой его точке обратно
пропорциональна расстоянию от точки
до этой образующей.
Р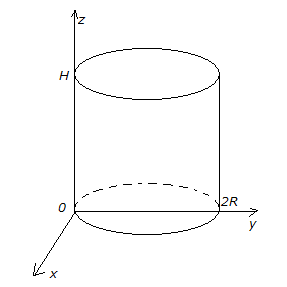
Пусть образующая, о которой говорится
в условии задачи, лежит на оси
,
а центр нижнего основания на оси.
Цилиндр ограничен поверхностями
Цилиндрическое
уравнение третьей поверхности:
.
Плотность
в силу условия
Итак, момент инерции:
V Вычисление силы притяжения точки телом
Пусть в точке А
находится
масса
,
а в точкеВ
– масса М.
Известно, что М
притягивает
(и наоборот) с силой
такой, что
,
где).
Пусть теперь эти
точки находятся в системе координат:
Проекции
силы
вычисляются по формулам
Но
поэтому, например,
где
Аналогичные формулы есть для
и
.
Итак, проекции силы:
Пусть теперь тело
имеет плотность
.
Как найти силу,
с которой телопритягивает массу
,
находящуюся в точке?
Можно поступить обычным, при построении
приложений интеграла, способом. Всю
областьразбиваем на части
,
выбираем точкии считаем, что вся масса
сосредоточена в
.
Получим системуматериальных точек:
с массой
.
(Подобным образом мы поступали при
вычислении координат центра масс и
моментов инерции плоской фигуры. Так
же можно поступить и при нахождении
этих характеристик пространственной
области.)
Точка
притягивает
с силой
,
где, например,
вычисляются
аналогично. Суммируя и переходя к
пределу, получим для проекций полной
силы
:
где
Пример 5.
Найти силу, с которой однородный конус
притягивает массу
,
находящегося в его вершине.
Решение.
Впишем данный конус в систему координат
так, как показано на рисунке. Такой конус
можно описать как тело, ограниченное
поверхностями
и
(смотри пример 3).
В силу симметрии
и однородности
сила притяжения направлена по оси
.
Имеем:
.
Переходим к
цилиндрическим координатам. Полярные
координаты проекции произвольной точки
тела на плоскость
изменяются в пределах
,
а координатаизменяется от конуса до плоскости, т.е.
отдо
.
Итак,
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
Объем


В сферических координатах этот интеграл имеет вид
(20.13)
А в цилиндрических координатах
Если тело занимает объем



Координаты центра тяжести тела вычисляются по формулам

Где
Моменты инерции тела относительно координатных плоскостей определяются интегралами
Момент инерции тела относительно оси Ои определяется интегралом
Где


Тела относительно координатных осей

Момент инерции тела относительно начала координат определяется формулой 
Ньютоновым потенциалом тела в точке

Где

Материальная точка массы


Пример 20.9. Найти объем тела, ограниченного поверхностями
Данное тело ограничено сферами радиусов




Для вычисления объема тела перейдем к сферическим координатам по формулам (20.9). Уравнение сферы






По формуле (20.13) находим
Пример 20.10. Вычислить объем тела, ограниченного поверхностями
Рис. 20.3 Рис. 20.4
Данное тело ограничено сферой



(уравнение параболоида). Отметим, что при постоянных значениях



До

При постоянном





(второй корень дает мнимые значения для р). Следовательно, для точек линии пересечения

Ф изменяется от 0 до 2тс, по формуле (20.14) получим
Пример 20.11. Вычислить объем тела, ограниченного эллипсоидом
При наличии выражения
Лезен переход к обобщенным сферическим координатам по формулам (20.11). Якобиан в этом случае равен
Уравнение данной поверхности в новых координатах примет вид

Для данного тела

Формуле (20.6) получим
Итак,

Ра
Замечание. Поскольку эллипсоидсимметричен относительно координатных плоскостей, то можно найти объем
От предыдущих.
Пример 20.12. Найти массу шара
Каждой точке обратно пропорциональна расстоянию ее до начала координат.
Пусть

Начала координат выражается формулой

Соответствиис условием задачи определяется формулой


Формуле (20.15) имеем
Где область

Интеграла перейдем к сферическим координатам по формулам (20.9). Подынтегральная функция

По формуле (20.10) находим
Пример 20.13. Найти центр тяжести шара
Воспользуемся формулами (20.16). Масса m была определена в предыдущей задаче (см. пример 20.12). Из соображений симметрии следует, что
Замечание. Координаты
Первых двух формул (20.16).
Следовательно,
Пример 20.14. Вычислить момент инерции однородного куба относительно одного из его ребер.
Начало прямоугольной декартовой системы координат поместим в одной из вершин куба, а оси направим вдоль трех взаимно перпендикулярных ребер. Обозначим через


Гпава 21
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
| < Предыдущая | Следующая > |
|---|
Механические и физические приложения поверхностного интеграла первого рода
Масса поверхности
Пусть на поверхности $sigma $ распределена масса с поверхностной плотностью $mu (mathbf { textit { x } } $,$mathbf { textit { y } } $,$mathbf { textit { z } } )$. Тогда масса $mathbf { textit { m } } $ поверхности равна
$mathbf { textit { m } } =iintlimits_sigma { mu (x,y,z)dsigma } $.
Статические моменты и центр масс
Статические моменты поверхности относительно координатных плоскостей $mathbf { textit { OYZ } } $, $mathbf { textit { OXZ } } $, $mathbf { textit { OXY } } $ равны соответственно $M_ { yz } =iintlimits_sigma { xmu dsigma } , M_ { xz } =iintlimits_sigma { ymu dsigma } , M_ { xy } =iintlimits_sigma { zmu dsigma } $
Координаты центра масс поверхности
$sigma $ равны $mathbf { textit { x } } _ { c } =frac { M_ { yz } } { m } $, $mathbf { textit { y } } _ { c } =frac { M_ { xz } } { m } $, $mathbf { textit { z } } _ { c } =frac { M_ { xy } } { m } $.
Моменты инерции
Момент инерции поверхности $sigma $ относительно прямой $mathbf { textit { L } } $ равен $mathbf { textit { I } } _ { L } =iintlimits_sigma { r_L^2 mu dsigma } $, где $r_L =mathbf { textit { r } } _ { L } (mathbf { textit { x } } ,mathbf { textit { y } } ,mathbf { textit { z } } )$ — расстояние от точки { $mathbf { textit { x } } ,mathbf { textit { y } } ,mathbf { textit { z } } $ } , лежащей на поверхности $sigma $, до прямой $mathbf { textit { L } } $. В частности, моменты инерции относительно координатных осей $mathbf { textit { OX } } ,mathbf { textit { OY } } $, $mathbf { textit { OZ } } $ равны
$I_x =iintlimits_sigma { (y^2+z^2)mu dsigma } $,
$I_y =iintlimits_sigma { (x^2+z^2)mu dsigma } $,
$I_z =iintlimits_sigma { (x^2+y^2)mu dsigma } $.
Момент инерции относительно точки $mathbf { textit { P } } (mathbf { textit { x } } _ { 0 } $,$mathbf { textit { y } } _ { 0 } $,$mathbf { textit { z } } _ { 0 } )$ равен $ I_p =iintlimits_sigma { ((x-x_0 )^2+(y-y_0 )^2+(z-z_0 )^2)mu (x,y,z)dsigma } $
Момент инерции относительно начала координат равен $ I_0 =iintlimits_sigma { (x^2+y^2+z^2)mu (x,y,z)dsigma =frac { 1 } { 2 } (I_x +I_y +I_z ). } $
Пример 1
Найти координаты центра масс полусферы $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { R } } ^ { 2 } ,mathbf { textit { z } } leqslant 0$, если поверхностная плотность в каждой точке сферы равна расстоянию от этой точки до оси $mathbf { textit { OZ } } $.
Решение
Масса полусферы $sigma $ равна
$ begin{array} { l } M=iintlimits_sigma { mu dsigma =iintlimits_sigma { sqrt { x^2+y^2 } dsigma = } } iintlimits_ { x^2+y^2leqslant R^2 } { sqrt { x^2+y^2 } cdot sqrt { 1+((sqrt { R^2-x^2-y^2 } { ) } ‘_x )^2+((sqrt { R^2-x^2-y^2 } { ) } ‘_y )^2 } } dxdy= \ =iintlimits_ { x^2+y^2leqslant R^2 } { sqrt { x^2+y^2 } cdot sqrt { 1+frac { x^2+y^2 } { R^2-x^2-y^2 } } dxdy= } iintlimits_ { x^2+y^2leqslant R^2 } { sqrt { x^2+y^2 } cdot frac { Rdxdy } { sqrt { R^2-x^2-y^2 } } =Rintlimits_0^ { 2pi } { dvarphi } intlimits_0^R { frac { r^2dr } { sqrt { R^2-r^2 } } = } } \ =2pi Rintlimits_0^R { frac { r^2-R^2+R^2 } { sqrt { R^2-r^2 } } dr=2pi Rleft( { R^2arcsin left. { frac { r } { R } }right|_0^R -intlimits_0^R { sqrt { R^2-r^2 } } dr }right)=frac { pi ^2R^3 } { 2 } . } \ end{array} $
{ Мы воспользовались тем, что интеграл $intlimits_0^R { sqrt { R^2-r^2 } dr } $ равен четверти площади круга радиуса $mathbf { textit { R } } $ , т.е. $frac { pi R^2 } { 4 } $ } .
Пример 2
Найти массу поверхности $G:left { { { begin{array} { * { 20 } c } { x^2+y^2+z^2=16 } hfill \ { ygeqslant 0 } hfill \ { 0leqslant zleqslant 3 } hfill \ end{array} } }right.$ с поверхностной плотностью $gamma = 2z^ { 2 } + 3$.
Решение
На рассматриваемой поверхности $z=sqrt { 16-x^2-y^2 } $,
$frac { partial z } { partial x } =-frac { x } { sqrt { 16-x^2-y^2 } } ,frac { partial z } { partial y } =-frac { y } { sqrt { 16-x^2-y^2 } } .$ Тогда
$ dS=sqrt { 1+frac { x^2 } { 16-x^2-y^2 } +frac { x^2 } { 16-x^2-y^2 } } dxdy=frac { 4 } { sqrt { 16-x^2-y^2 } } dxdy. $
Проекцией $D$ этой поверхности на координатную плоскость $Oxy$ является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.
Применяя формулу массы поверхности и перехода к полярным координатам, получим:
$ begin{array} { c } M=4iintlimits_D { frac { 2(16-x^2-y^2)+3 } { sqrt { 16-x^2-y^2 } } } dxdy=4intlimits_0^pi { dvarphi } intlimits_3^4 { frac { 2(16-rho ^2)+3 } { sqrt { 16-rho ^2 } } } rho drho = \ =4pi left( { -frac { 1 } { 2 } }right)intlimits_7^0 { frac { 2t+3 } { sqrt t } } dt=2pi intlimits_0^7 { left( { 2t^ { frac { 1 } { 2 } } +3t^ { -frac { 1 } { 2 } } }right) } dt=2pi left( { frac { 4 } { 3 } t^ { frac { 3 } { 2 } } +6t^ { frac { 1 } { 2 } } }right)left| { { begin{array} { * { 20 } c } { ^7 } hfill \ { _0 } hfill \ end{array} } }right.= \ =2pi left( { frac { 28 } { 3 } sqrt 7 +6sqrt 7 }right)=frac { 92sqrt 7 } { 3 } pi . \ end{array} $