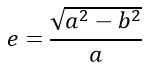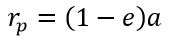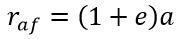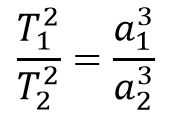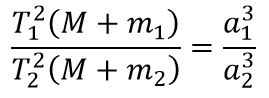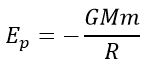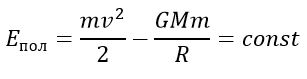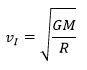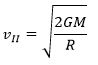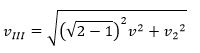Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
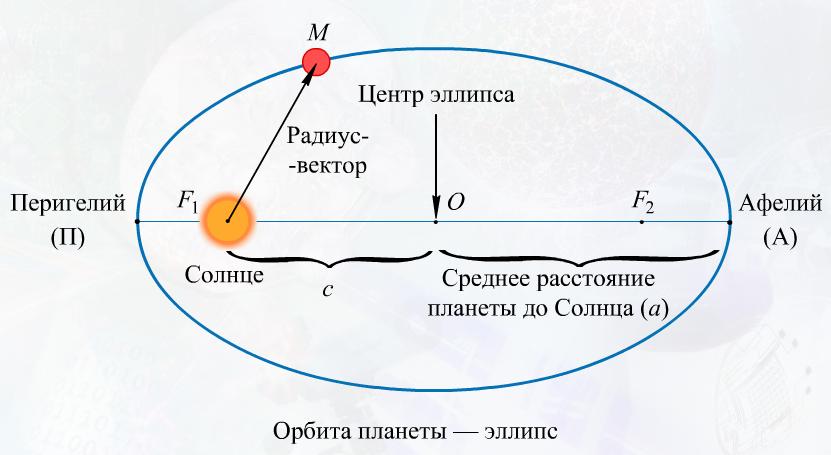
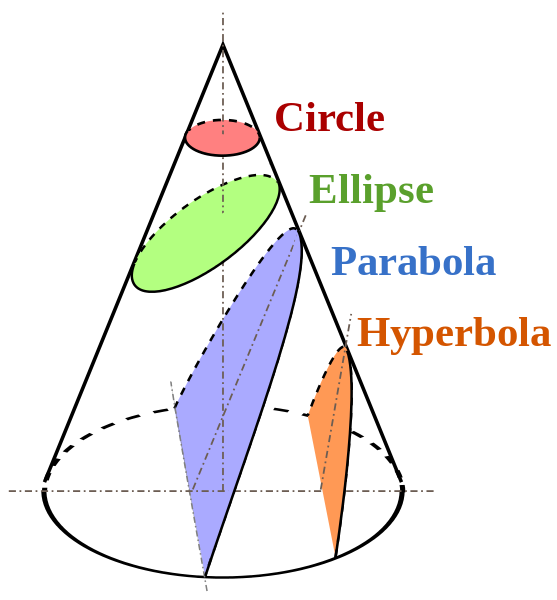
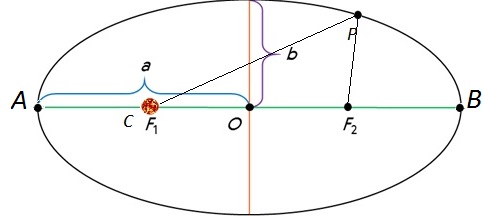
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
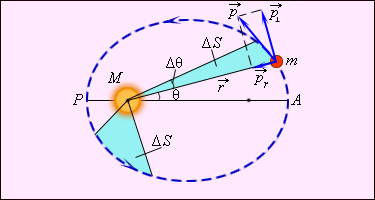
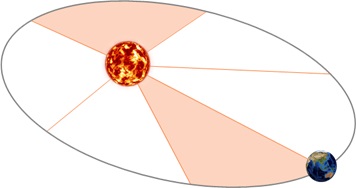
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
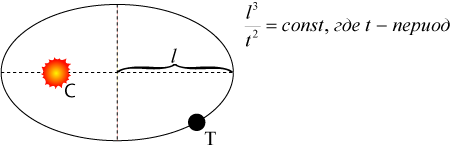
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
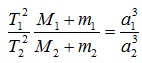
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
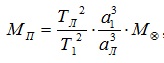
где Тл и αл— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.
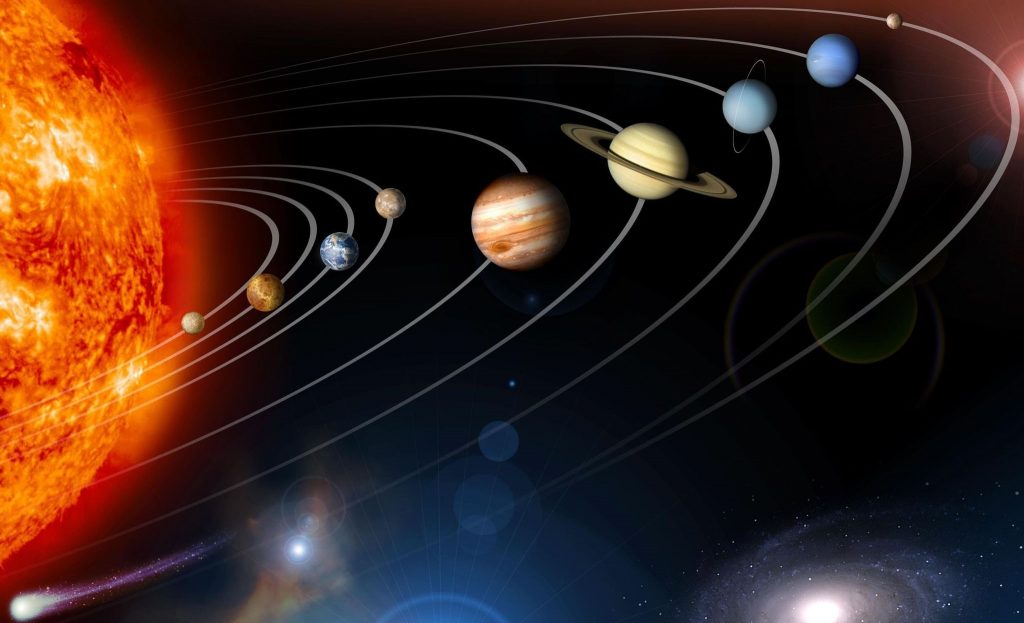
Планеты солнечной системы
Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).
Содержание:
- 1 Рассчитываем массу Земли и Луны
- 2 Общие методики определения масс планет
- 3 Значения масс планет Солнечной системы
- 4 Определение масс звезд и галактик
Рассчитываем массу Земли и Луны
Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.
Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:
Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.
Земля и луна
Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.
Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.
Общие методики определения масс планет
Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.
В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.
Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.
Значения масс планет Солнечной системы
Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.
Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.
Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.
Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.
Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Определение масс звезд и галактик
Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.
Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.
Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:
Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.
Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.
Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.
|
|
Качественная задача.
|
|
28/02/10 |
почему из наблюдений за движением планеты под действием силы притяжения к солнцу невозможно определить ее массу? Как найти массу планеты по наблюдениями за её спутниками. — Чт май 27, 2010 15:03:42 — Мои догадки:
|
|
|
|
|
ShMaxG |
Re: Качественная задача.
|
||
11/04/08 |
Масса обычно определяется по периоду обращения и значению большей полуоси. Вот коэффициент Масса солнца намного больше массы планеты, поэтому для вычисления массы планеты надо вычислять период с очень большой точностью. А масса спутников, как я понимаю, не на столько много меньше массы планеты, как масса планеты много меньше массы солнца.
|
||
|
|
|||
|
Feuer |
Re: Качественная задача.
|
|
28/02/10 |
|
|
|
|
|
ShMaxG |
Re: Качественная задача.
|
||
11/04/08 |
А что, формула в курсе не выводилась? Странно, довольно важная.
Ну а
|
||
|
|
|||
|
gris |
Re: Качественная задача.
|
||
13/08/08 |
Вот что-то я сомневаюсь в первом утверждении. Действительно, в третий закон Кеплера масса не входит, но в уточнённый Ньютоном закон входят массы планет и Солнца. Зная массу Солнца и Земли, можно определить и массу другой планеты, зная параметры её орбиты. — Чт май 27, 2010 16:16:26 — Пока мял клаву, всё уже сказали
|
||
|
|
|||
|
Feuer |
Re: Качественная задача.
|
|
28/02/10 |
Спасибо. Эти формула когда учатся?
|
|
|
|
|
ShMaxG |
Re: Качественная задача.
|
||
11/04/08 |
В общем действуйте так. 1) Выводите эту формулу для круговых орбит школьными методами.
|
||
|
|
|||
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Первый закон Кеплера (закон эллипсов)
Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.
Форма эллипса и степень его сходства с окружностью характеризуется отношением
или e = c/a,
где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось, b — малая полуось. Величина eназывается эксцентриситетом эллипса. При c = 0, и, следовательно, e = 0,эллипс превращается в окружность. В случае тонкого длинного эллипса е стремится к 1.
Перигелий — ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы.
Афелий — наиболее удаленная точка орбиты.
где a — большая полуось, е — эксцентриситет орбиты.
Современная формулировка распространяет действие закона на любые гравитационно-связанные системы тел:
В гравитационно-связанной системе тело B движется по эллипсу, в одном из фокусов которого находится тело A. Эксцентриситет эллипса определяется численным значением полной энергии системы. В гравитационно-несвязанной системе тело B движется по параболе (E= 0) или по гиперболе (E > 0), в фокусах которых находится тело A.
Доказательство связано с тем, что под действием гравитационной силы тела могут двигаться только по коническим сечениям – окружности, эллипсу, параболе или гиперболе.
Второй закон Кеплера (закон площадей)
Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
Из закона следует, что планета движется по орбите неравномерно, быстрее в перигелии (ближайшей к Солнцу точке) и медленнее в афелии (наиболее удаленной точке).
Доказательство закона связано с постоянством момента импульса планеты как материальной точки.
Третий закон Кеплера (гармонический закон)
Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет.
В формулировке Ньютона в закон входят и массы звезды и планеты:
Этот закон позволяет определить массы планет и спутников из известных орбит и периодов обращения.
Доказательство проводится на основе закона всемирного тяготения Ньютона.
Применение законов Кеплера
Потенциальная энергия взаимодействия двух тел
Пусть два тела с массами M и m находятся на расстоянии R друг от друга. Тогда энергия их взаимодействия равна
Полная энергия
Если тело находится в гравитационном поле и имеет некоторую скорость, то его полная энергия равна
Таким образом, в соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.
Теорема вириала
В случае кругового движения кинетическая энергия в 2 раза меньше по модулю потенциальной. Поэтому
2Eк+Eп= 0
Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела.
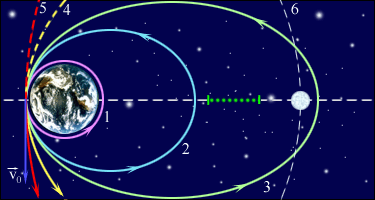
При Eпол < 0 тело не может удалиться от центра притяжения на расстояние r0 < rmax . В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы). Система с отрицательной полной энергией называется гравитационно связанной.
При Eпол = 0 тело движется по параболической траектории. Скорость тела на бесконечности равна нулю.
При Eпол > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.
Первая космическая скорость
Это скорость движения по круговой траектории вблизи поверхности Земли
Это минимальная скорость, которую нужно сообщить телу, чтобы оно преодолело притяжение Земли и стало спутником. Для Земли примерно 7,9 км/с.
Вторая космическая скорость
Это скорость движения по параболической траектории
Она равна минимальной скорости, которую нужно сообщить телу на поверхности Земли, чтобы оно, преодолев земное притяжение, стало искусственным спутником Солнца. Находится из условия равенства нулю полной энергии системы. Для Земли примерно 11,2 км/с.
Третья космическая скорость
Это скорость, при которой тело преодолевает притяжение Солнца
где v – орбитальная скорость планеты, v2 – вторая космическая скорость для планеты. Для Земли примерно 16,6 км/с.
Задачи:
Звезда и планета обращаются вокруг общего неподвижного центра масс по круговым орбитам. Найдите массу планеты m, если известно, что скорость движения планеты равна v1, а скорость движения и период обращения звезды равны v2 и T соответственно.
Если бы все линейные размеры Солнечной системы были пропорционально сокращены так, чтобы среднее расстояние между Солнцем и Землей стало 1 м, то какова была бы продолжительность одного года? Считайте, что плотность небесных тел при этом не меняется.
Автоматическая станция обращается вокруг планеты Марс с периодом T = 18 ч. Максимальное удаление от поверхности Марса (в апоцентре) a = 25000 км, минимальное (в перицентре) p = 1380 км. По указанным параметрам орбиты станции определите отношение массы Марса к массе Земли. Радиус Марса rм = 3400 км, радиус Земли rз = 6400 км.
Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты 422 тыс. км.
Вычислить параболическую скорость на поверхности Луны, RЛ = 0.27 радиуса Земли, MЛ = 1/81 массы Земли.
Источники:
http://wikiwhat.ru
https://ru.wikipedia.org/wiki/
http://ency.info/earth/etapi-astronomii/16-zakon
http://www.afportal.ru/taxonomy/term/128
Масса планеты
Найти массу Марса, по радиусу и периоду спутника на орбите
#16382
2013-09-27 20:52 GMT
Спутник планеты Марс Фобос обращается по приблизительно круговой орбите радиусом 9,4*106м с периодом 7ч 39мин. Определите массу планеты Марс.
Мое решение:
T = 2пR/v;
v = 2пR/T; v = 2*3,14*9,4*106/2754*10 = 2*103м/с
v2 = G*M/R;
M = v2*R/G;
M = 4*106*9,4*106/6,68*10-11 = 56,3кг.
Ответ не сошелся с учебником.
#16386
2013-09-28 19:34 GMT
(M=frac{4pi^2R^3}{GT^2})
#16390
2013-09-29 16:55 GMT
Спасибо. Правда когда выводил предложенную формулу, понял что это и есть то решение которое у меня написано. Пересчитал, оказывается ошибся в расчетах.

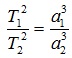
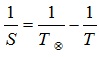
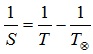






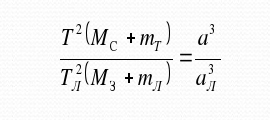
![$
[T = 2pi frac{{{a^{3/2}}}}
{{{mu ^{1/2}}}}]$ $
[T = 2pi frac{{{a^{3/2}}}}
{{{mu ^{1/2}}}}]$](https://dxdy-03.korotkov.co.uk/f/6/0/3/6035a88aba769e6dd36744202b53ac7782.png)
![$[mu = Gleft( {{M_c} + {M_{pl}}} right)]
$ $[mu = Gleft( {{M_c} + {M_{pl}}} right)]
$](https://dxdy-04.korotkov.co.uk/f/b/2/6/b26bd9eb0ebf0919bc757efd4a50f05d82.png) .
.![$ [T = 2pi frac{{{a^{3/2}}}} {{{mu ^{1/2}}}}]$ $ [T = 2pi frac{{{a^{3/2}}}} {{{mu ^{1/2}}}}]$](https://dxdy-01.korotkov.co.uk/f/8/f/a/8fa23bd6d81c7f8c0f8140ce17a63d0382.png) можно по подробней об этой формуле. Я её впервые вижу.
можно по подробней об этой формуле. Я её впервые вижу.![$[mu = Gleft( {{M_c} + {M_{pl}}} right)] $ $[mu = Gleft( {{M_c} + {M_{pl}}} right)] $](https://dxdy-02.korotkov.co.uk/f/5/c/8/5c8b2068633db8a79e84514ecdcf00a182.png) и это коэфициент чего?
и это коэфициент чего? — значение большей полуоси орбиты, по которой движется планета.
— значение большей полуоси орбиты, по которой движется планета. — просто число, равное произведению гравитационной постоянной на сумму масс планеты и солнца.
— просто число, равное произведению гравитационной постоянной на сумму масс планеты и солнца.