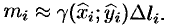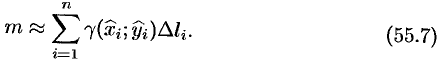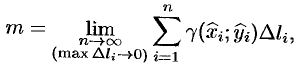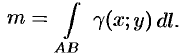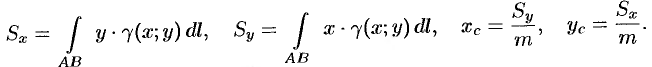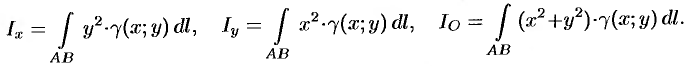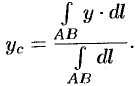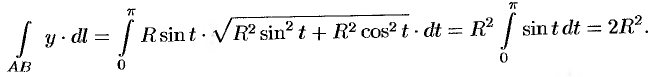Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
Сообщения без ответов | Активные темы | Избранное
|
|
Вычислить массу однородной дуги
|
|
27/09/17 |
|
|
|
|
|
svv |
Re: Вычислить массу однородной дуги
|
||
23/07/08 |
Проверьте внимательно
|
||
|
|
|||
|
Key27 |
Re: Вычислить массу однородной дуги
|
|
27/09/17 |
svv Ой, извиняюсь. Опечатка вышла.
|
|
|
|
|
Lia |
Re: Вычислить массу однородной дуги
|
|
20/03/14 |
Дуга однородная — это плотность постоянная. И меня бы смутила нулевая масса.
|
|
|
|
|
svv |
Re: Вычислить массу однородной дуги
|
||
23/07/08 |
И что, например, под корнем получается?
|
||
|
|
|||
|
Someone |
Re: Вычислить массу однородной дуги
|
||
23/07/05 |
Получается, что этот интеграл равен 0. Как получается-то? Напишите. Хотя у меня есть обоснованное предположение, что косяк связан с извлечением квадратного корня.
|
||
|
|
|||
|
ewert |
Re: Вычислить массу однородной дуги
|
||
11/05/08 |
у меня есть обоснованное предположение, что косяк связан с извлечением квадратного корня Нет, там ведь всего-навсего четверть периода.
|
||
|
|
|||
|
Key27 |
Re: Вычислить массу однородной дуги
|
|
27/09/17 |
|
|
|
|
|
Someone |
Re: Вычислить массу однородной дуги
|
||
23/07/05 |
Если сократить на
Нет, там ведь всего-навсего четверть периода. Правда. Я не обратил внимания. Тогда получение нуля выглядит совсем загадочно. И даже «сокращение» не помогает.
|
||
|
|
|||
|
Key27 |
Re: Вычислить массу однородной дуги
|
|
27/09/17 |
Согласен, ерунда. Но как это делать понятнее не стало.
|
|
|
|
|
svv |
Re: Вычислить массу однородной дуги
|
||
23/07/08 |
И, после этих преобразований, что получается под интегралом?
|
||
|
|
|||
|
Key27 |
Re: Вычислить массу однородной дуги
|
|
27/09/17 |
svv Уже не уверен в правильности, но у меня получилось
|
|
|
|
|
Someone |
Re: Вычислить массу однородной дуги
|
||
23/07/05 |
Уже не уверен в правильности, но у меня получилось А Вы формулу Ньютона—Лейбница видели? Если сократить на Собственно, как это Вы сократили? Вы считаете, что после «сокращения» получилось выражение, которое в точности равно исходному? Как, например, при сокращении дроби:
|
||
|
|
|||
|
svv |
Re: Вычислить массу однородной дуги
|
||
23/07/08 |
Сначала я подумал, что автор под сокращением понимает вынесение множителя из-под знака корня, оказалось, что он действительно на него сократил .
|
||
|
|
|||
|
Key27 |
Re: Вычислить массу однородной дуги
|
|
27/09/17 |
Уже не уверен в правильности, но у меня получилось А Вы формулу Ньютона—Лейбница видели? Если сократить на Собственно, как это Вы сократили? Вы считаете, что после «сокращения» получилось выражение, которое в точности равно исходному? Как, например, при сокращении дроби: Ну да, видел. Окей, возвращаюсь назад.
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Найти массу однородной дуги окружности
Центр масс и моменты инерции кривой;
Работа при перемещении тела в силовом поле;
Магнитное поле вокруг проводника с током (Закон Ампера);
Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея).
Рассмотрим эти приложения более подробно с примерами.
Пусть снова кусок проволоки описывается некоторой кривой (C,) а распределение массы вдоль кривой задано непрерывной функцией плотности (rho left( right).) Тогда координаты центра масс кривой определяются формулами [bar x = frac<<>>>,;;bar y = frac<<>>>,;;bar z = frac<<>>>,] где [ <> = intlimits_C right)ds> ,>;; <> = intlimits_C right)ds> ,>;; <> = intlimits_C right)ds> > ] − так называемые моменты первого порядка .
Моменты инерции относительно осей (Ox, Oy) и (Oz) определяются формулами [ <= intlimits_C <left( <+ > right)rho left( right)ds> ,>;; <= intlimits_C <left( <+ > right)rho left( right)ds> ,>;; <= intlimits_C <left( <+ > right)rho left( right)ds> .> ]
Работа при перемещении тела в силовом поле (mathbf) вдоль кривой (C) выражается через криволинейный интеграл второго рода [W = intlimits_C <mathbfcdot dmathbf> ,] где (mathbf) − сила, действующая на тело, (dmathbf) − единичный касательный вектор (рисунок (1)). Обозначение ( <mathbfcdot dmathbf>) означает скалярное произведение векторов (mathbf) и (dmathbf.)
Заметим, что силовое поле (mathbf) не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы (mathbf) иногда может оказаться отрицательной.
Если векторное поле задано в координатной форме в виде [mathbf = left( right),Qleft( right),Rleft( right)> right),] то работа поля вычисляется по формуле [W = intlimits_C <mathbfcdot dmathbf> = intlimits_C .] В частном случае, когда тело двигается вдоль плоской кривой (C) в плоскости (Oxy,) справедлива формула [W = intlimits_C <mathbfcdot dmathbf> = intlimits_C ,] где (mathbf = left( right),Qleft( right)> right).)
Если векторное поле (mathbf) потенциально , то работа по перемещению тела из точки (A) в точку (B) выражается формулой [W = uleft( B right) — uleft( A right),] где (uleft( right)) − потенциал поля.
Криволинейный интеграл от магнитного поля с индукцией (mathbf) вдоль замкнутого контура (C) пропорционален полному току, протекающему через область, ограниченную контуром (C) (рисунок (2)). Это выражается формулой [intlimits_C <mathbfcdot dmathbf> = <mu _0>I,] где (<mu _0>) − магнитная проницаемость ваккуума , равная (1,26 times <10^< — 6>>,text<Н/м>.)
Очевидно, в силу симметрии, (bar y = 0.) Чтобы найти координату центра масс (bar x,) достаточно рассмотреть верхнюю половину кардиоиды.
(C) − отрезок прямой (y = x;)
(C) − кривая (y = sqrt x.)
Согласно закону Фарадея [varepsilon = ointlimits_C = — frac<><
Предположим, что магнитное поле (mathbf) перпендикулярно плоскости кольца. Тогда за время (Delta t) изменение потока равно [Delta psi = 2rBx = 2rBvDelta t,] где (x = vDelta t,) (v) − скорость самолета, (B) − индукция магнитного поля Земли. Из последнего выражения получаем [varepsilon = — frac<><
Напряженность возникающего электрического поля найдем по формуле (varepsilon = intlimits_C <mathbfcdot dmathbf> .) В силу симметрии, наведенное электрическое поле будет иметь постоянную амплитуду в любой точке кольца. Оно будет направлено по касательной к кольцу в любой его точке. Это позволяет легко вычислить криволинейный интеграл. [varepsilon = ointlimits_C <mathbfcdot dmathbf> = ointlimits_C = Eointlimits_C = 2pi rE.] Следовательно, напряженность электрического поля равна [E = frac<varepsilon ><<2pi r>> = frac<<0,00025>><<2pi cdot 0,01>> = 0,004,text<В/м>.]
Электронная библиотека
Вычисление интеграла (1.4) и (1.5) сводится к определенному. Пусть, например, кривая К задана уравнениями: x = x(t), y = y(t), z = z(t), , тогда длина элементарной дуги , интеграл (1.4) выражается определенным интегралом:
Если, в частности, кривая К имеет явное задание y = y(x) , то
Из соотношения (1.7) и (1.8) следует, что криволинейный интеграл первого рода существует, если f – непрерывная функция на К.
Вычислить по длине плоской кривой y = ln x при .
Решение. Используем формулу (1.8), найдем, что и
Найти массу полуокружности x 2 + y 2 = 1, , если линейная плотность её в текущей точке M(x,y) пропорциональна ординате y.
Решение. За параметр возьмем величину угла t, тогда параметрическое уравнение линии К: x=cos t, y=sin t .
Элементарная масса dm = ky dl, т.е. тогда по формуле (1.7):
Решение. По формуле (1.7) имеем:
Задачи для упражнений
1) Найти , если К – дуга параболы , лежащая между и . Ответ: .
4) Определить массу окружности x 2 + y 2 = R 2 , если плотность её в точке М(х, у) равна: . Ответ: .
5) Определить координаты центра тяжести С(х0, у0) однородной полуокружности К: .
Указание. В механике доказано, что координаты центра тяжести однородной кривой К задаются формулами:
где L – длина дуги кривой К. Ответ: .
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Формула Грина. Площадь плоской области. Масса кривой
По этой ссылке вы найдёте полный курс лекций по математике:
Выведем формулу Грина, связывающую криволинейный интеграл по границе L некоторой плоской области D с двойным интегралом по этой области. Теорема 3. Если в замкнутой области D, ограниченной кусочно-гладким контуром L, функции Р(х, у) и Q(x, у) непрерывны и имеют непрерывные частные производные ^ и то справедливо равенство <формула Грина): есь символ § означает интегрирование по границе L области D, причем граница L проходится так, что область D остается слева (рис. 7).
Граница L плоской области D может состоять из одной или нескольких простых замкнутых кривых (компонент). В первом случае она называется односвязной, а во втором — многосвязной. Если граница L состоит из конечного числа кусочно-гладких замкнутых кривых L,-, то кривые Li называются связными компонентами границы. На рис. 8 изображена трехсвязная область.
Односвязная область D (область «без дырок») обладаеттем свойством, чтолюбая лежащая в ней замкнутая кривая может быть стянута в точку Р G D, оставаясь в процессе стягивания в области D. Доказательство теоремы проведем для односвязной области. М В силу свойства линейности достаточно доказать, что Формула Грина Площадь плоской области Масса кривой Площадь цилиндрической поверхности Площадь плоской фигуры Обобщение случай пространственной кривой Докажем первую из этих формул.
Предположим сначала, что кривая L пересекается каждой прямой, параллельной оси Оу, не более чем в двух точках или по целому отрезку (рис. 9). Если каждая такая прямая пересекает кривую L не более чем в двух точках, то кривую L можно разбить на две части L и Ь2 (верхнюю и нижнюю), каждая из которых проектируется взаимно однозначно на некоторый отрезок [а, Ь оси Ох.
Всилуаддитивности криволинейного интеграла имеем На каждой из кривых L и Li возьмем в качестве параметра абсциссу х и запишем уравнения этих кривых сояветстве нно в виде Тогда По предположению производная непрерывна в D, и значит, в силу известной формулы интегрального исчисления, приращение функции можно записать через интеграл от производной этой функции: Из формул получаем Повторный интеграл в правой части последнего соотношения равен двойному инте-фалу от функции ^ по области D, так что окончательно имеем Формула (2) доказана.
Соотношение (3) доказывается аналогично. Складывая почленно соотношения (2) и (3), получаем формулу Грина (1). Отметим, что формула Грина имеет место и для более сложных контуров L, и для неодносвязных областей D. Рассмотрим, например, случай двухсвязной области (рис. 10). Сделаем разрез А В этой области, превращающий ее в односвязную. Тогда Отсюда, учитывая, что получим где интегрирование по кривой L ведется в направлении против движения часовой стрелки, а по кривой Ь2 — в направлении движения часовой стрелки.
Отметим, что при этом кривые L и Ь2 проходятся так, что область D остается слева. Такое направление обхода контура принимается за положительное. Площадь плоской области Возьмем Тогда по формуле Грина (1) получаем где 5 — площадь области D. Отсюда получаем формулу для вычисления площади 5 плоской области D с помощью криволинейного интеграла по границе L этой области: (7) Прммр. Вычислить площадь области, ограниченной эллипсом L: Запишем уравнение эллипса в параметрической форме .
Искомая площадь находится по формуле (7), где криволинейный интеграл берется по эллипсу при обходе контура в положительном направлении, что соответствует изменен ик> параметра t от 0 до 2я. Так как то отсюда получаем, что Замечание. Пусть в пространстве задана ориентированная кусочно-гладкая кривая AD и пусть, кроме того, в некоторой области П, содержащей кривую AD, задана вектор-функция — непрерывные в О функции.
Аналогично плоскому случаю криволинейный интеграл от вектор-функции F по ориентированной кривой АВ определим выражением Масса кривой В примере 1 из § 1 было показано, что масса кривой L вычисляется с помощью интеграла 1-го рода где /(М) — переменная линейная плотность на кривой L. (Мы предполагаем, что f(M) — непрерывная фунмция на АВ.) 4.2. Площадь цилиндрической поверхности Пусть в плоскости хОу задана некоторая спрямляемая (т. е. имеющая длину) кривая АВ и на этой кривой определена непрерывная функция f(M) ^ 0.
Тогда совокупность точек (х, у, f(x, у)), или (М, /(М)), составит некоторую кривую, лежащую на цилиндрической поверхности, для которой кривая АВ является направляющей, а ее образующая параллельна оси Oz.
Требуется определить площадь цилиндрической поверхности ABDC, о»раниченной снизу кривой АВУ сверху — кривой z — f(M), где М € АВ, и вертикальными прямыми АС и BD (рис. 11). Для решения этой задачи поступим так: 1) разобьем кривую АВ на п частей точками так, как показано на рис. 11; 2) из каждой точки Мк проведем перпендикуляр к плоскости хОу высотой f(Mk) (при этом цилиндрическая поверхность А В DC разобьется на п полосок);
3) кажаую полоску заменим прямоугольником с основанием — длина дуги МкМк+, и высотой, равной значению функции /(М) в какой-нибудь точке этой дуги, например, в точке Мк. Тогда площадь fc-ой полоски будет приближенно равна. а площадь всей поверхности ABDC Это приближенное равенство будет тем точнее, чем мельче будут частичные дуги , на которые разбита кривая АВ. Пусть Д/ — наибольшая из длин А1к частичных .цт .
Возможно вам будут полезны данные страницы:
Тогда при 0 в пределе получим точное значение искомой площади Предел справа по определению есть криволинейный интеграл первого рода от функции /(Af) по кривой АВ. Итак, (2) Пример 1. Вычислить площадь части боковой поверхности цилиндра срезанного сверху поверхностью Сведем задачу к вычислению криволинейного интеграла t-ro рода от функции вдоль дуги окружности, расположенной в первой четверти. Будем иметь Параметрические уравнения линии Формула Грина Площадь плоской области Масса кривой.
Площадь цилиндрической поверхности Площадь плоской фигуры Обобщение случай пространственной кривой Площадь плоской фигуры Ранее мы установили, что площадь 5 плоской фигуры D, ограниченной линией L, вычисляется по формуле Правая часть есть криволинейный интеграл 2-го рода. 4.4. Работа силы Пусть в некоторой плоской области D, содержащей кривую АВУ задана сила где функции , а следовательно, и F(М) предполагаются непрерывными функциями точки ЛГ.
Требуется найти работу силы F, если под действием этой силы материальная точка М, имеющая единичную массу, переместилась из точки А в точку В по кривой АВ. Для решения этой задачи разделим кривую АВ на п частей точками (рис. 12), заменим каждую дугу хордой , предполагая для простоты , что на участке кривой (а значит, и на хорде сила Ffc имеет постоянное значение, например, равное ее значению в точке получим приближенное выражение работы силы на участке пути где — длина вектора — длина вектора.
Из формулы (4) с учетом (5) получим или Так как правая частьформулы (6) есть скалярное произведение векторов то, учитывая (7) и (8), будем иметь Суммируя по всем значениям , получим величину принимают за точное значение работы. Но с другой стороны, предел этой суммы есть криволинейный интеграл 2-го рода от вектор-функции F(M) по кривой АВ.
Итак, работа силы вычисляется по формуле Рис. 12 ( Пример 2. Найти работу силы при перемещении единичной массы по параболе 4 Применим формулу (9), положив в ней Так как то искомую работу можо вычислить так: Обобщение на случай пространственной кривой (рис. 14). Если в некоторой пространственной области П, содержащей пространственную кривую АВ, задана сила — непрерывные функции в области П, то рабога, совершаемая силой F(M) по перемещению материальной точки М с единичной массой из точки А в точку В по пространственной кривой АВ, равна Упражнения.
Вычислите криволинейные интегралы 1-го рода: 1. — четверть элл ипса ^ + = 1, л ежащая в первом квадранте. — окружность — отрезок прямой, соединяющий точки отреэо к прямой, соединяющий точки (— дуга параболы у2 = 2х от точки (0,0) до точки (I, первый виток винтовой линии Найдите длину дуги конической винтовой линии х — ас* cost, у = от точки .до точки 2?(а,0,а). Указание: точке А соответствует- значение параметра t( = -оо, а точке В — значение t2 = 0. 8. Найдите площадь боковой поверхности кругового цилиндра, находящейся под первым витком винтовой линии и выше плоскости z = 0. 9.
Найдите координаты центра тяисести
однородной полуарки циклоиды Вычислите криволинейные интегралы 2-го рода: дуга кривой у = х3 отточки (0,0) до точки верхняя половина эллипса , пробегаемая против хода часовой стрелки. где точки соединены кривой Ч2Г при . — дуга первой арки циклоиды пробегаемая в направлении возрастания параметра t. — окружность , пробегаемая против хода часовой стрелки. Указание . Используйте параметрические уравнения окружности. — виток винтовой линии — ломаная с вершинами 17.
Найдите массу дуги AB кривой у = lnz, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки, причем . 18. Найдите длину дуги кривой j между ее точками пересечения с осями координат. 19. Найдите площадь, ограниченную астроидой 20. Найдите работу силового поля j, когда точка массы m описывает окружность х = а соs t, у = a sin t, двигаясь по ходу часовой стрелки. 21. Поле образовано силой .
Вычислите работу при перемещении единицы массы по контуру квадрата со сторонами Применив формулу Пэина, вычислите интегралы в задачах 22-24: по контуру ЬАВС с вершинами по контуру фигуры, ограниченной линиями у вдоль единичной окружности в положительном направлении Формула Грина Площадь плоской области Масса кривой Площадь цилиндрической поверхности.
Площадь плоской фигуры Обобщение случай пространственной кривой — вдоль контура квадрата с вершинами в точках Л(1,0), при положительном направлении обхода. Ответы Указание. Перейдите к полярным координатам. Указание. Воспользуйтесь формулами (в зависимости от направления обхода).. Указание. Данный интеграл несобстве нный, так как в точках пересечения контура интегрирования с прямой х + у = 0 подынтегральн ос выражение принимает вид g. Формулу фина применять нельзя.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://libraryno.ru/1-1-2-vychislenie-krivolineynogo-integrala-pervogo-roda-spec_gl_vm/
http://natalibrilenova.ru/formula-grina-ploschad-ploskoj-oblasti-massa-krivoj-/
Некоторые приложения криволинейного интеграла I рода
Криволинейный интеграл I рода имеет разнообразные; приложения в математике и механике.
Длина кривой
Длина 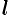

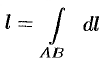
Площадь цилиндрической поверхности
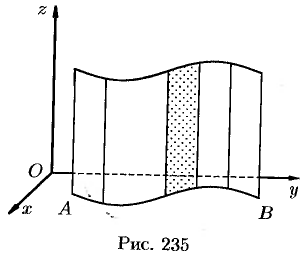
Если направляющей цилиндрической поверхности служит кривая 
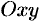
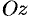
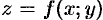
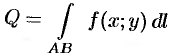
Масса кривой
Масса материальной кривой 
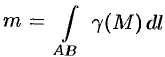
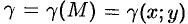

Разобьем кривую 

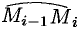
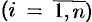
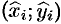
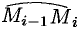
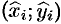
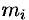
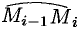
Суммируя, находим приближенное значение массы 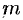
За массу кривой 
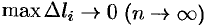
или, согласно формуле (55.2),
(Заметим, что предел существует, если кривая 

Статические моменты, центр тяжести
Статические моменты относительно осей 
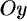

Моменты инерции
Для материальной кривой 
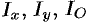

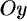
Пример №55.3.
Найти центр тяжести полуокружности 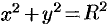
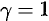
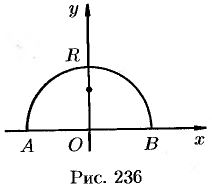
Решение:
Из соображений симметрии ясно, что центр тяжести находится на оси 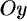
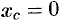
Знаменатель дроби — длина полуокружности. Поэтому 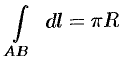
Для вычисления числителя воспользуемся параметрическими уравнениями окружности 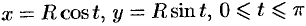
Следовательно, 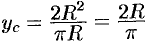
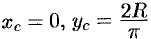
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Криволинейный
интеграл I
рода имеет разнообразные приложения
в математике и механике.
Длина
кривой
Д
кривой AB
плоской или пространственной линии
вычисляется по формуле
.
Площадь
цилиндрической поверхности
Если
направляющей цилиндрической поверхности
служит кривая AB,
лежащая в плоскости Oxy,
а образующая параллельна оси Oz
(см. рис.3), то площадь поверхности
задаваемой функцией z
= f(x;y),
находится по формуле
.
Масса
кривой
Рис.
3.
Масса
материальной кривой AB
(провод,
цепь, трос, …) определяется формулой
,
плоскость кривой в точкеM.
Разобьем
кривую AB
на n
элементарных дуг Mi-1Mi
(i
=
).
Пусть
– произвольная точка дуги Mi-1Mi.
Считая приближенно участок дуги
однородным, т.е. считая, что плотность
в каждой точке дуги такая же, как и в
точке,
найдем приближенное значение массы mi
дуги Mi-1Mi:
.
Суммируя,
находим приближенное значение массы
m:
,
(9.7)
За
массу кривой AB
примем предел суммы (9.7) при условии,
что
,
т.е.
или,
согласно формуле (9.2),
(Заметим,
что предел существует, если кривая AB
гладкая, а плотность задана непрерывной
в каждой точке AB
функцией).
Статические
моменты, цент тяжести
Статические
моменты относительно осей Ox
и Oy
и координаты центра тяжести материальной
кривой AB
определяются по формулам
.
Момент
инерции
Для
материальной кривой AB
моменты Ix,
Iy,
IO
инерции относительно осей Ox,
Oy
и начала координат соответственно
равны:
,
,
Пример
9.3. Найти
центр тяжести полуокружности x2
+ y2
= R2,
лежащей в верхней полуплоскости.
Плотность считать равной единице в
каждой точке кривой
.
Р
Из соображения симметрии ясно, что
центр тяжести находится на оси Oy
(см. рис. 4). Поэтому xc
= 0.
Ордината центра тяжести
Знаменатель
дроби – длинна полуокружности. Поэтому
Для
вычисления числителя воспользуемся
параметрическими уравнениями
Рис. 4.
окружности
Имеем:
.
Следовательно,
.
Итак,xc
= 0,
.
§10. Криволинейный интеграл II рода
10.1. Основные понятия
Решение
задач о вычислении работы переменной
силы при перемещении материальной
точки вдоль некоторой кривой (и других)
приводит к понятию криволинейного
интеграла II
рода.
Криволинейный
интеграл II
рода определяется почти также как и
интеграл I
рода.
Пусть
в плоскости Oxy
задана непрерывная кривая AB
(или L)
и функция P(x;y),
определенная в каждой точке кривой.
Разобьем кривую AB
точками M0
= A,
M1,
… Mn
= B
в направлении от точки A
к точке B
на n
дуг Mi-1Mi
с длинами Δli
(i
= 1,
2,
…, n).
На
каждой «элементарной дуге» Mi-1Mi
возьмем точку
и составим сумму вида

(10.1)
где
Δxi
= xi
– xi-1
– проекция дуги Mi-1Mi
на ось Ox.
(см. рис. 5).
Сумму
(9.1) называют интегральной
суммой для функции P(x;y)
по переменной x.Таких
сумм можно составить бесконечное
множество. (Отличие сумм (9.1) и (10.1)
очевидно).
Если
при
интегральная
сумма (10.1) имеет конечный предел, не
зависящий ни от способа разбиения
кривойAB,
ни от выбора точек ,
то его называют криволинейным
интегралом по координате x
(или
II
рода) от
функции P(x;y)
по кривой AB
и
обозначают
или
.
Рис. 5.
И

Аналогично
вводиться криволинейный интеграл от
функции Q(x;y)
по координате y:

где
Δyi
– проекция дуги Mi-1Mi
на
ось Oy.
Криволинейный
интеграл II
рода общего вида
определяется
равенством
.
Криволинейный
интеграл
по пространственной кривойL
определяется аналогично.
Терема 10.1.
Если кривая AB
гладкая, а функции P(x;y)
и
Q(x;y)
непрерывные на кривой
AB,
то криволинейный интеграл II
рода существует.
Отметим
лишь некоторые свойства криволинейного
интеграла II
рода.
1.
При изменении направления пути
интегрирования интеграл II
Рода изменяет свой знак на противоположный,
т.е.
(проекция
дуги Mi-1Mi
на оси Ox
и Oy
меняют знак с изменением направления).
2.
Если кривая АВ
с точкой С
разбита на две части АС
и СВ,
то интеграл по все кривой равен сумме
интегралов по частям, т.е.
.
3.
Если кривая АВ
лежит
в плоскости, перпендикулярной оси Ox,
то
(все
);
аналогично
для кривой, лежащей в плоскости,
перпендикулярной оси Oy:
(все
).
4.
Криволинейный интеграл по замкнутой
кривой (обозначается
)
не зависит от выбора начальной точки
(зависит только от направления обхода
кривой).
Д
(см.
рис. 6).
С
другой стороны,
.
Таким образом,
.
10.2.
Вычисление криволинейного интеграла
II
рода Рис.
6.
Вычисление
криволинейного интеграла II
рода, как и I
первого рода, может быть сведено к
вычислению определенного интеграла.
Параметрическое
представление кривой интегрирования
Пусть
кривая АВ
задана параметрическими уравнениями
x
= x(t)
и y
= y(t),
где функции x(t)
и y(t)
непрерывны вместе мо своими производными
x’(t)
и y’(t)
на отрезке [α;β],
причем начальной точке А
– кривой соответствует значение
параметра t
= α,
а конечной точке В
– значение t
= β.
И пусть функция P(x;y)
непрерывна на кривой АВ.
Тогда по определению,

Преобразуем
интегральную сумму к переменной t.
Так как
,
то по формуле Лангража имеем:,
где,
Выберем
точку
так,
чтобы
Тогда
преобразованная интегральная суммабудет
интегральной суммой для функции одной
переменнойна
промежутке [α;β].
Поэтому
(10.2)
Аналогично
получаем:
(10.3)
Складывая
почленно полученные равенства (10.2) и
(10.3), получаем
(10.4)
Явное
представление кривой интегрирования
Если
кривая АВ
задана уравнением y
= φ(x),
,
где функцияφ(x)
и ее производная φ’(x)
непрерывна на отрезке [a;b],
то из формулы (10.4), приняв x
за параметр, имеем параметрические
уравнения кривой АВ:
x
= x,
y
= φ(x),
,
откуда получим:
.
(10.5)
В
частности,
(10.6)
Если
АВ
– гладкая пространственная кривая,
которая описывается непрерывными на
отрезке [α;β]
функциями x
= x(t),
y
= y(t)
и z
= z(t),
то криволинейный интеграл
вычисляется
по формуле
(10.7)
З
интегралы I
и II
рода связаны соотношением
,
гдеα
и
β –
углы, образованные касательной к кривой
АВ
в точке M(x;y)
с осями Ox
и Oy
соответственно.
Пример
10.1.
Вычислить
—
ломанная криваяОАВ,
где О(0;0),
А(2;0),
В(4;2).
Решение:
Так как L
= OAB
= OA
+ AB
(см. рис. 7), то
Уравнение
отрезка ОА
есть y
= 0,
;
уравнение отрезкаАВ:
y
= x-2,
.
Согласно формуле (10.5), имеем:
Рис.7.
Пример10.2.
Вычислить
— отрезок прямой в пространстве от точкиА(1;0;2)
до точки В(3;1;4).
Решение:
Составим уравнение прямой проходящей
через точки А
и В:
или
в параметрической формеx
= 2t
+ 1, y
= t,
z
= 2t
+
2.
При перемещении от точки А
к точке В
параметр t
меняется от 0 до 1. По формуле (10.7) находим,
что
Соседние файлы в папке Матан_2
- #
- #
- #
- #
- #

 .
. .
.

 То есть опреденный интеграл будет равен
То есть опреденный интеграл будет равен 
 ?
? Надеюсь, что хоть это правильно. Тогда интеграл будет примерно таким
Надеюсь, что хоть это правильно. Тогда интеграл будет примерно таким