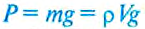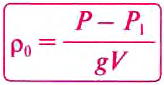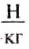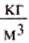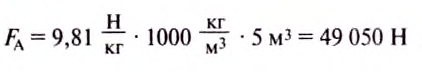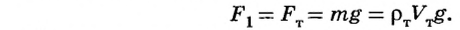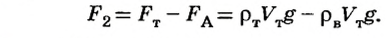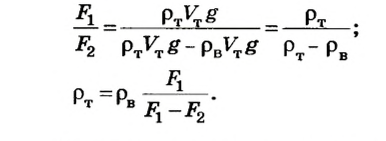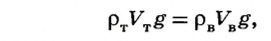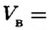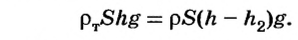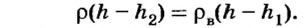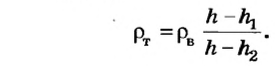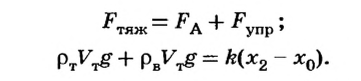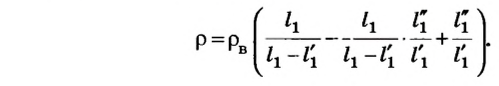Как найти массу бруска в воде

Условие задачи:

Брусок дерева плавает в воде. Объем погруженной части бруска 36 см³. Определить массу бруска.

Задача №3.3.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(V_{п}=36) см³, (m-?)

Решение задачи:

Если брусок плавает, значит сила Архимеда (F_{А}) равна по величине силе тяжести (mg).

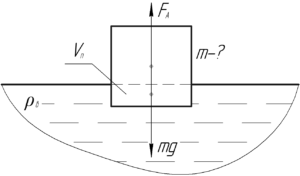
[{F_А} = mg;;;;(1)]

Силу Архимеда (F_{А}) определяют по следующей формуле, где (rho_{в}) – плотность воды (жидкости, в которую погружен брусок), (V_{п}) – объем погруженной части.

[{F_А} = {rho _в}g{V_п}]

Тогда равенство (1) станет таким:

[{rho _в}g{V_п} = mg]

Откуда искомую массу бруска (m) можно найти по формуле:

[m = {rho _в}{V_п}]

Плотность воды равна 1000 кг/м³ (это табличная величина). Переведем объем погруженной части в систему СИ и посчитаем ответ:

[36;см^3 = 36 cdot {10^{ – 6}};м^3]

[m = 1000 cdot 36 cdot {10^{ – 6}} = 0,036;кг = 36;г]

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.1 В воде плавает шар, погрузившись на 0,25 своего объема. Определить плотность
3.3.3 Льдина плавает на поверхности воды. Часть её объема, равная 150 м3, находится
3.3.4 На тело, находящееся в воде, действует выталкивающая сила 2 Н. С какой силой это тело

Содержание:

Гидростатическое взвешивание:

На этом принципе основан метод так называемого гидростатического взвешивания. Если в мензурку опустить деревянный брусок, то он будет плавать, но уровень воды поднимется. Объем этой воды равен объему погруженной части бруска, а ее вес — весу бруска. Зная объем и плотность воды, можно рассчитать вес воды и вес тела. Для случая, когда тело тяжелее воды, изготавливают специальный поплавок, дающий возможность телу плавать по поверхности воды.

Гидростатическое взвешивание

Гидростатическое взвешивание — это метод измерения плотности жидкости или твёрдого тела, основанный на законе Архимеда. Плотность твёрдых тел определяют методом двойного взвешивания тела: сначала в воздухе, а потом в жидкости, плотность которой известна. Если определяют плотность жидкости, то в ней взвешивают тело известной массы и объёма.

Если исследуемое сплошное твёрдое тело тонет в воде, то для выполнения задания нужен лишь лабораторный динамометр (или равноплечие весы) и сосуд с водой.

Сначала определяют вес Р исследуемого тела в воздухе:

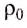
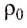
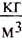
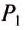
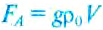
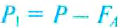
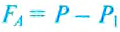
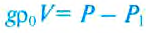
Потом твёрдое тело погружают в сосуд с жидкостью, плотность которой известна (в случае использования дистиллированной или чистой воды  = 1000 ), и определяют вес тела в жидкости, который по закону Архимеда меньше веса тела в воздухе на значение силы Архимеда       отсюда , или .

Из этой формулы можно определить плотность жидкости, если она неизвестна, а объём тела известен:

Объём жидкости, вытесненной телом, равен объёму тела, но

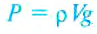
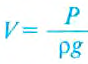
поскольку  то  . Подставим это в выражение

для архимедовой силы, получим 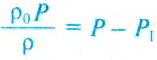  , отсюда и вытекает искомая формула для определения плотности вещества твёрдого тела: .

Пример №1

Купаясь в реке с илистым дном, можно заметить, что ноги больше вязнут на мелких местах, чем на глубоких. Объясните, почему.

Ответ: так как на глубоких местах действует большая выталкивающая сила.

Пример №2

Определите, какая архимедова сила действует на тело объёмом

5 м³ , погружённое полностью в воду?

Дано: 

V = 5м³

= 9,81 

= 1000 

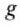
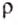
F_А = 49,05 кН

F_А = ?

Решение:

По формуле 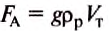определим архимедову силу:

Ответ: = 49,05 кН.

Пример №3

Нужно ли учитывать загрузку судна при переходе его из моря в реку? Догружать или разгружать нужно судно, чтобы его осадка была не глубже ватерлинии?

Ответ: при переходе судна из моря в реку нужно учитывать загрузку судна, так как плотность воды уменьшается. Судно нужно разгружать.

• Заказать решение задач по физике

Теоретические сведения

Гидростатическое взвешивание издавна применяется для определения плотности различных веществ. Для этого используют закон Архимеда. Плотность твердых тел определяют двойным взвешиванием: сначала тело взвешивают в воздухе (при этом в большинстве случаев выталкивающей силой воздуха пренебрегают), а потом — в жидкости, плотность которой известна (например, в воде). Рассмотрим методы определения плотности.

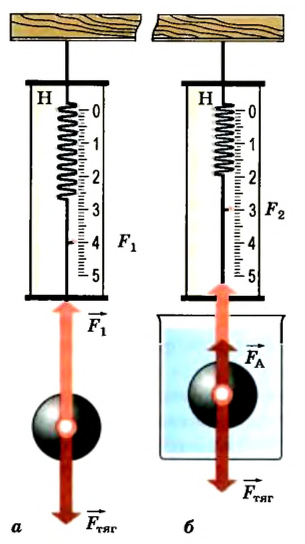
1. Если исследуемое тело тонет в воде (его плотность рт превышает плотность воды рв), то в таком случае используют динамометр и стакан с водой.

Сначала исследуемое тело взвешивают в воздухе (рис. 120, а):

В этом случае архимедовой силой, действующей на тело в воздухе, можно пренебречь, так как плотность воздуха намного меньше плотности тела и воды.

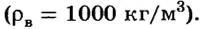
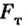
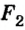
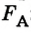
Потом тело опускают в стакан с водой (рис. 120, б), плотность воды известна В этом случае на тело, кроме сил тяжести и упругости пружины динамометра , действует сила Архимеда :

Таким образом, 

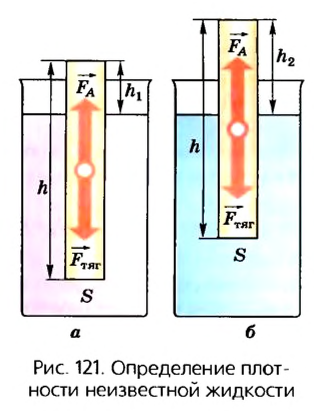
2. Для измерения плотности неизвестной жидкости можно воспользоваться также телом, которое не тонет в воде и исследуемой жидкости, например карандашом или другим телом правильной формы. Чтобы карандаш в жидкости занимал вертикальное положение, к его нижнему концу можно приколоть несколько кнопок или намотать несколько витков проволоки.

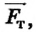
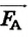
Если карандаш плавает в воде (рис. 121, а), то сила тяжести действующая на него, равна силе Архимеда . В этом случае

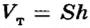
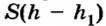
где  — объем тела, a — объем вытесненной телом воды (объем погруженной части тела).

Если тело опустить в неизвестную жидкость (рис. 121, б), плотность которой 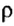, то

С этого уравнения имеем

Отсюда

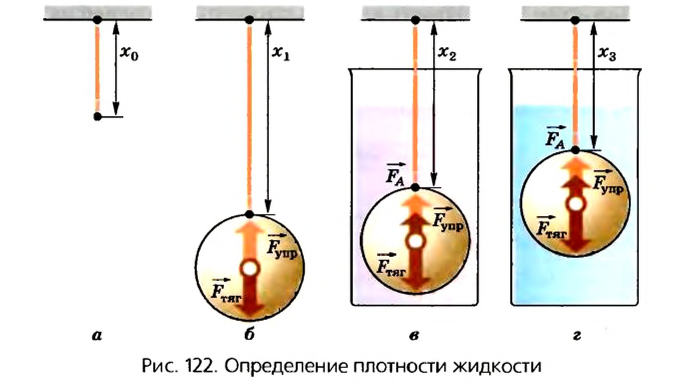
3.    Плотность неизвестной жидкости можно определить с помощью резиновой нити, тела, которое тонет в воде и неизвестной жидкости, и линейки. Последовательность действий при этом показана на рисунке 122.

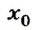
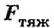
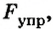
Длина резиновой нити (или пружины) без нагрузки (рис. 122, а). Если к ней прикрепить тело в воздухе (рис. 122, б), то сила тяжести будет равна по значению силе упругости возникшей в нити. Тело будет в состоянии равновесия.

Теперь, если тело опустить в воду (рис. 122, в), то на него будет действовать еще сила Архимеда:

Опустим тело в жидкость, плотность которой нужно определить (рис. 122, г).

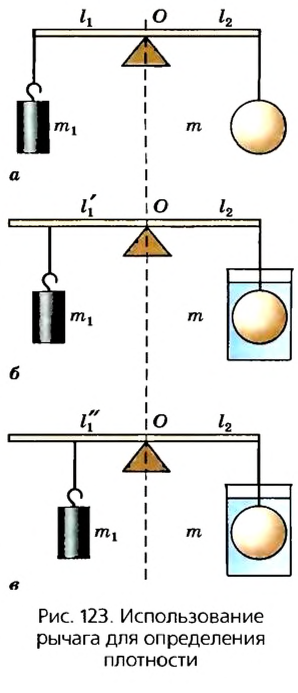
4.    Для определения плотности твердого тела или неизвестной жидкости можно использовать рычаг. Для этого нужно иметь две гирьки, плотность одной из них массой 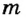необходимо определить, рычаг, линейку, стаканы с водой и неизвестной жидкостью. Последовательность действий показана на рисунке 123.

Для определения плотности тела используем формулу

Для определения плотности неизвестной жидкости можно использовать формулу