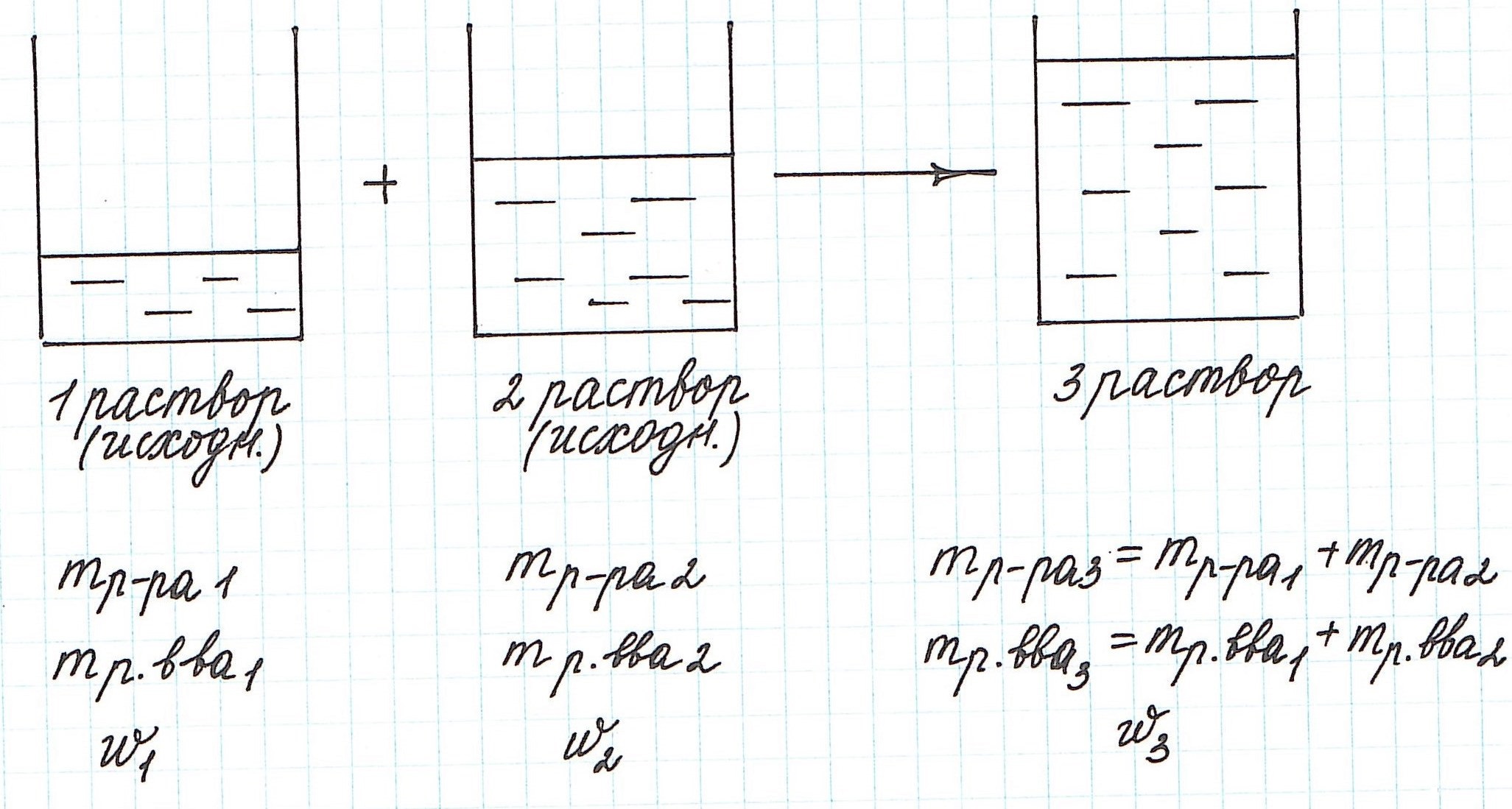
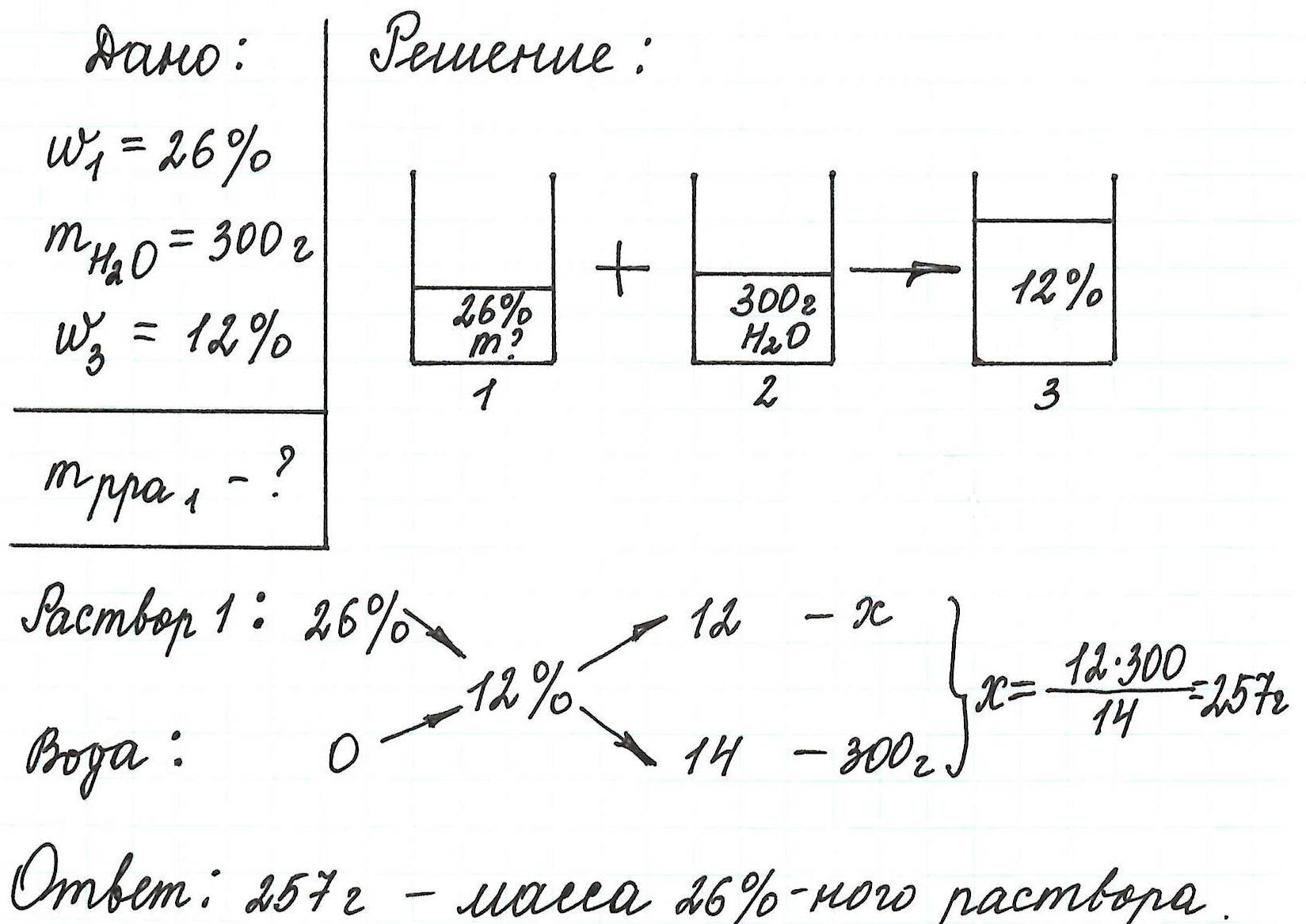
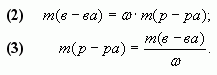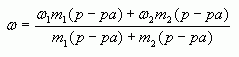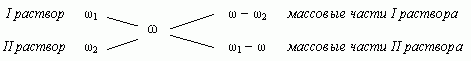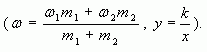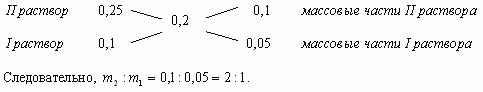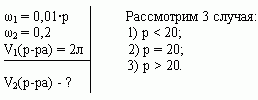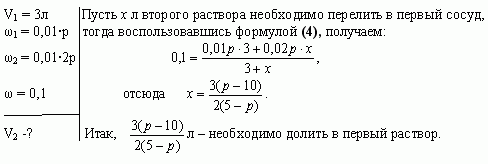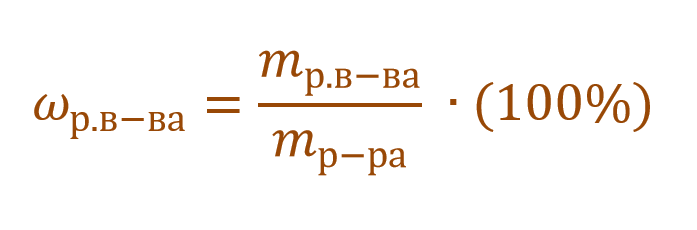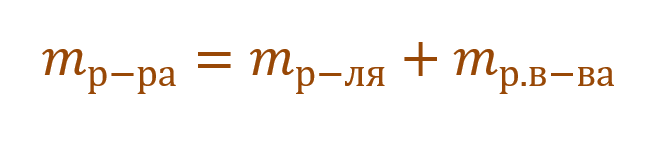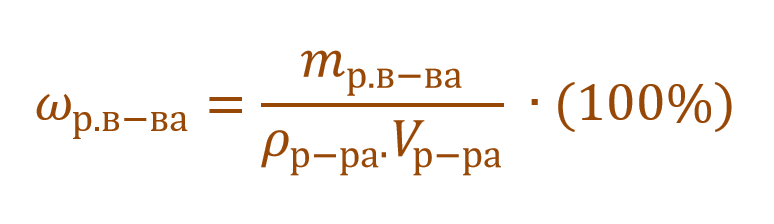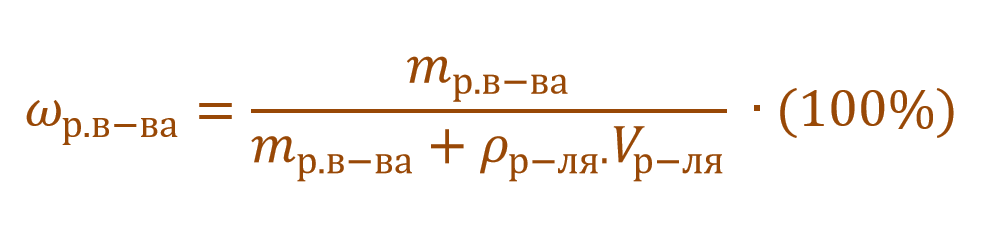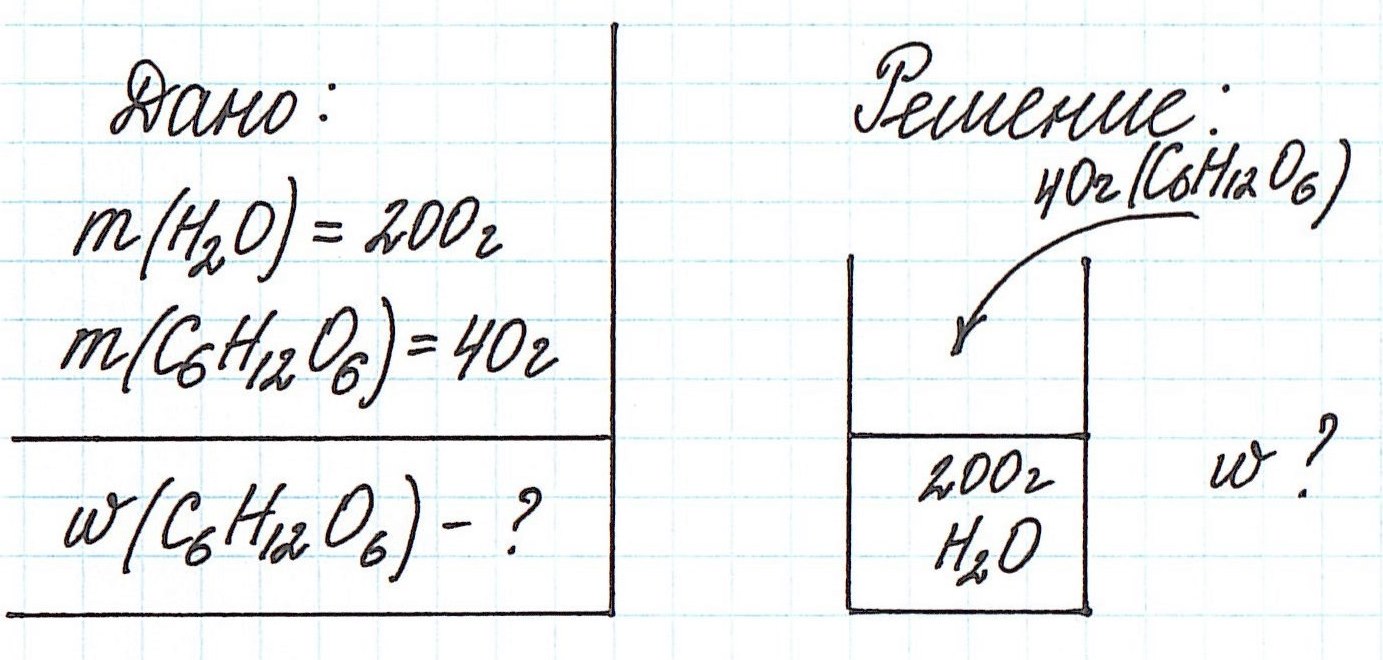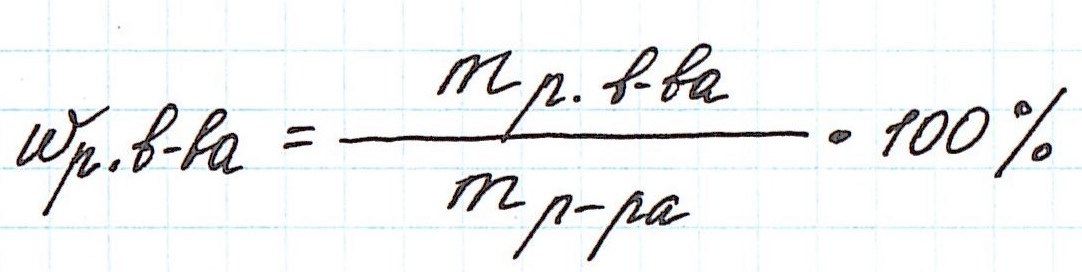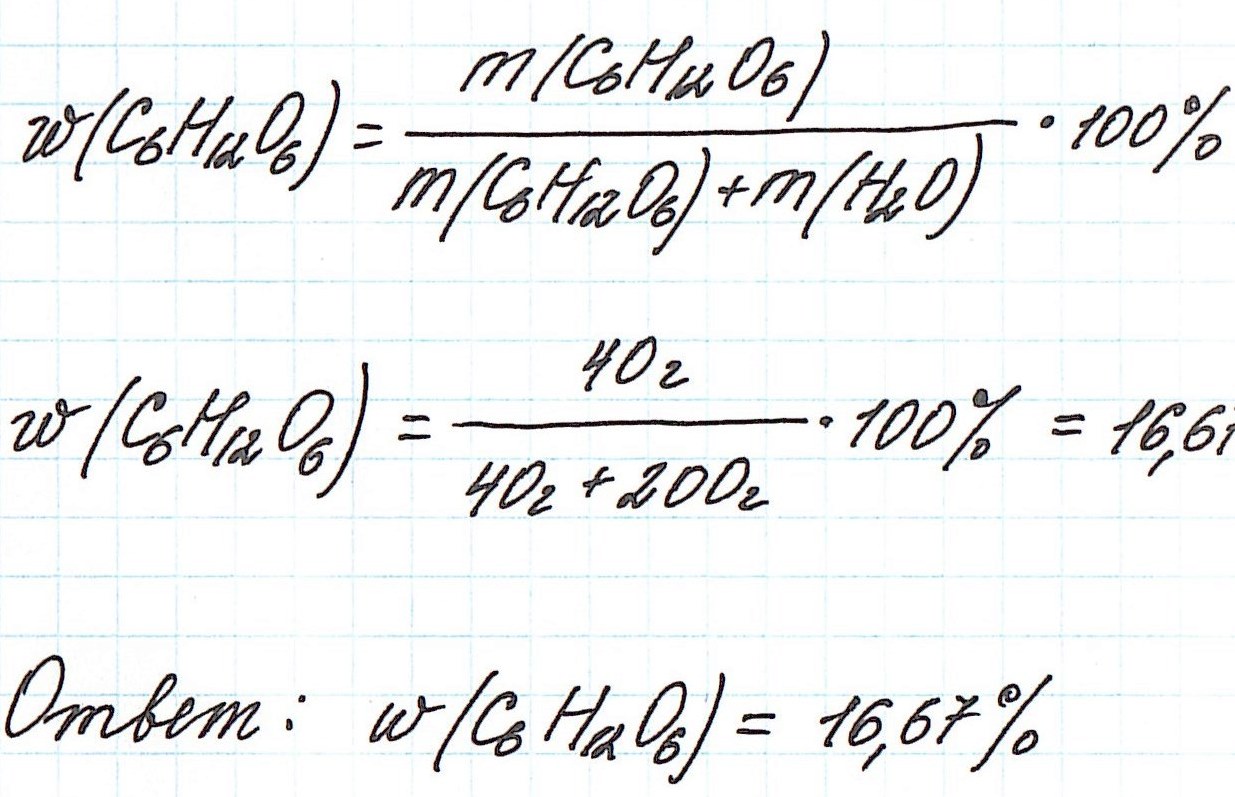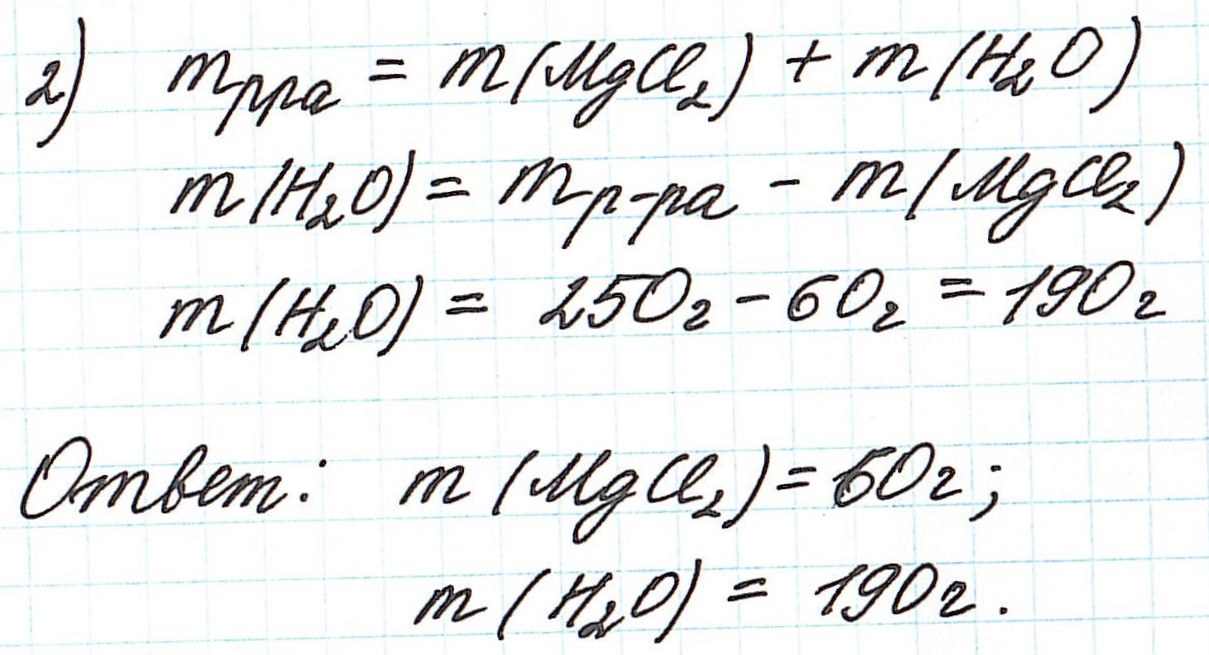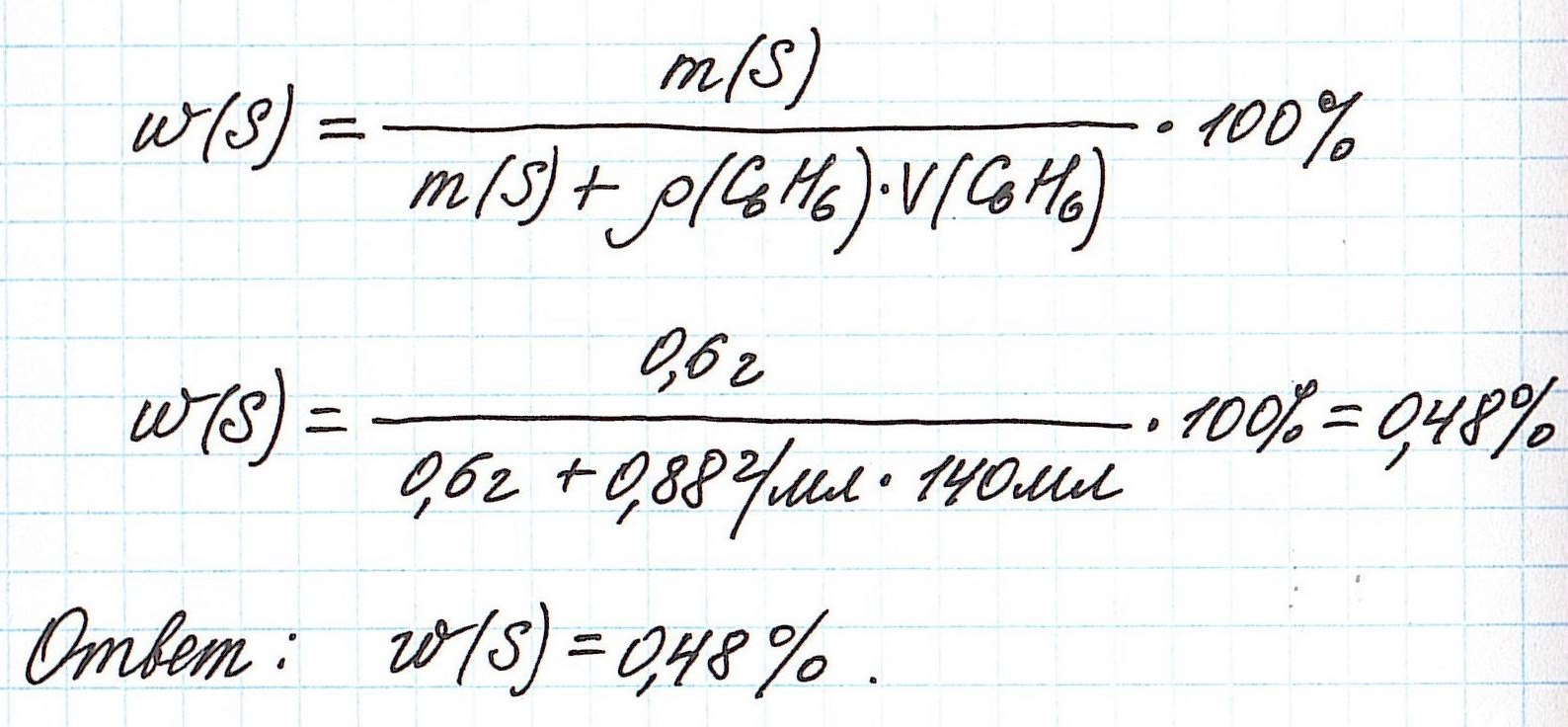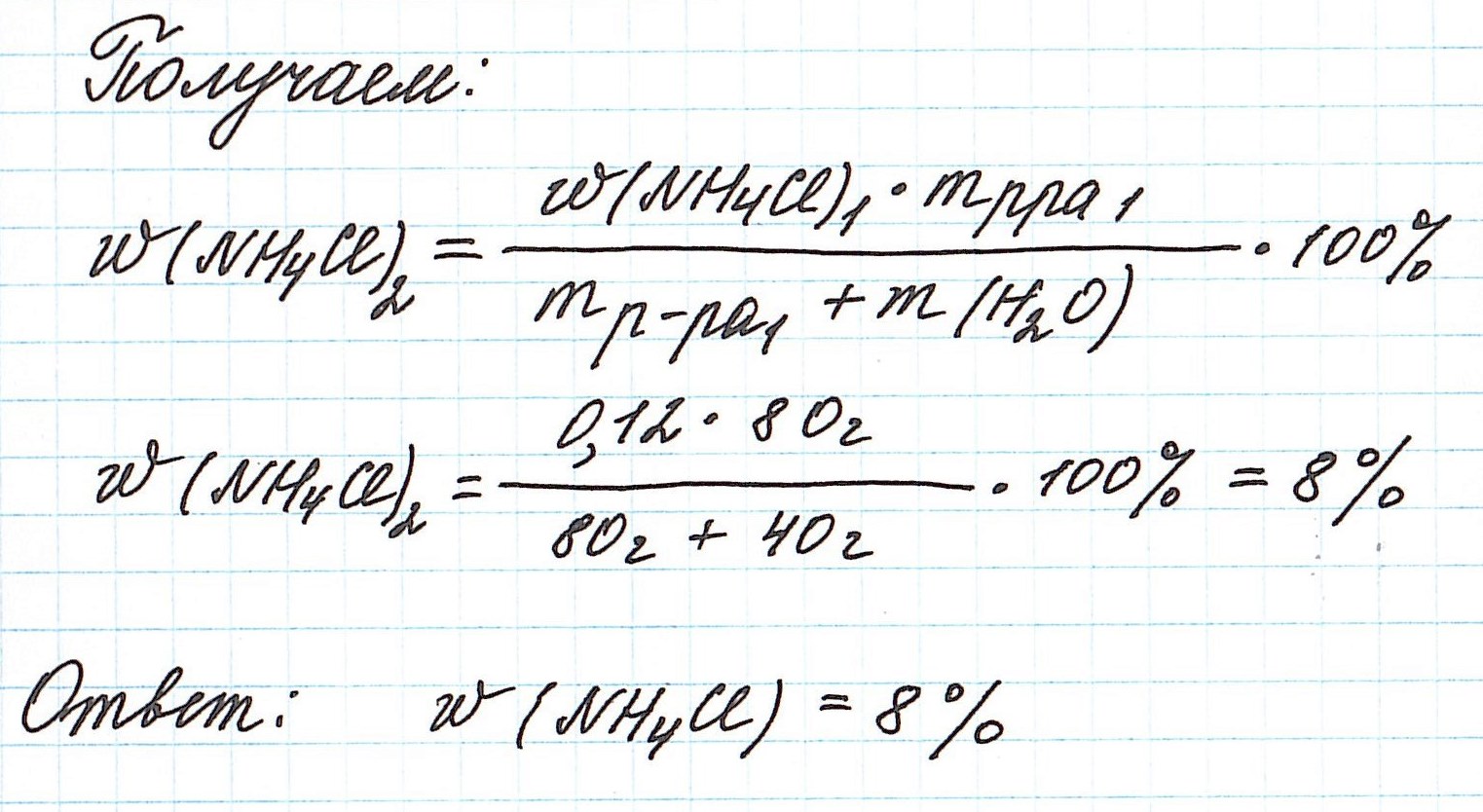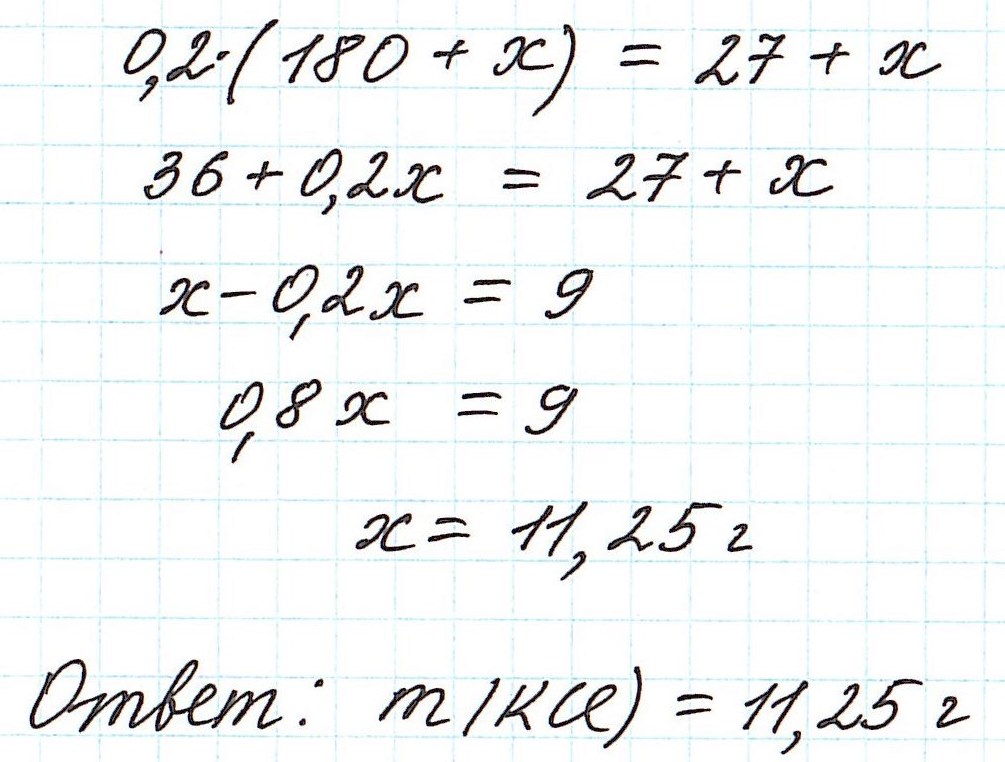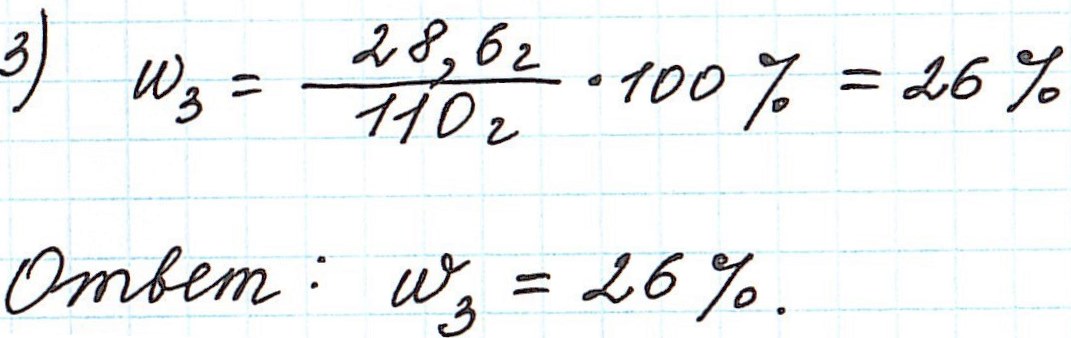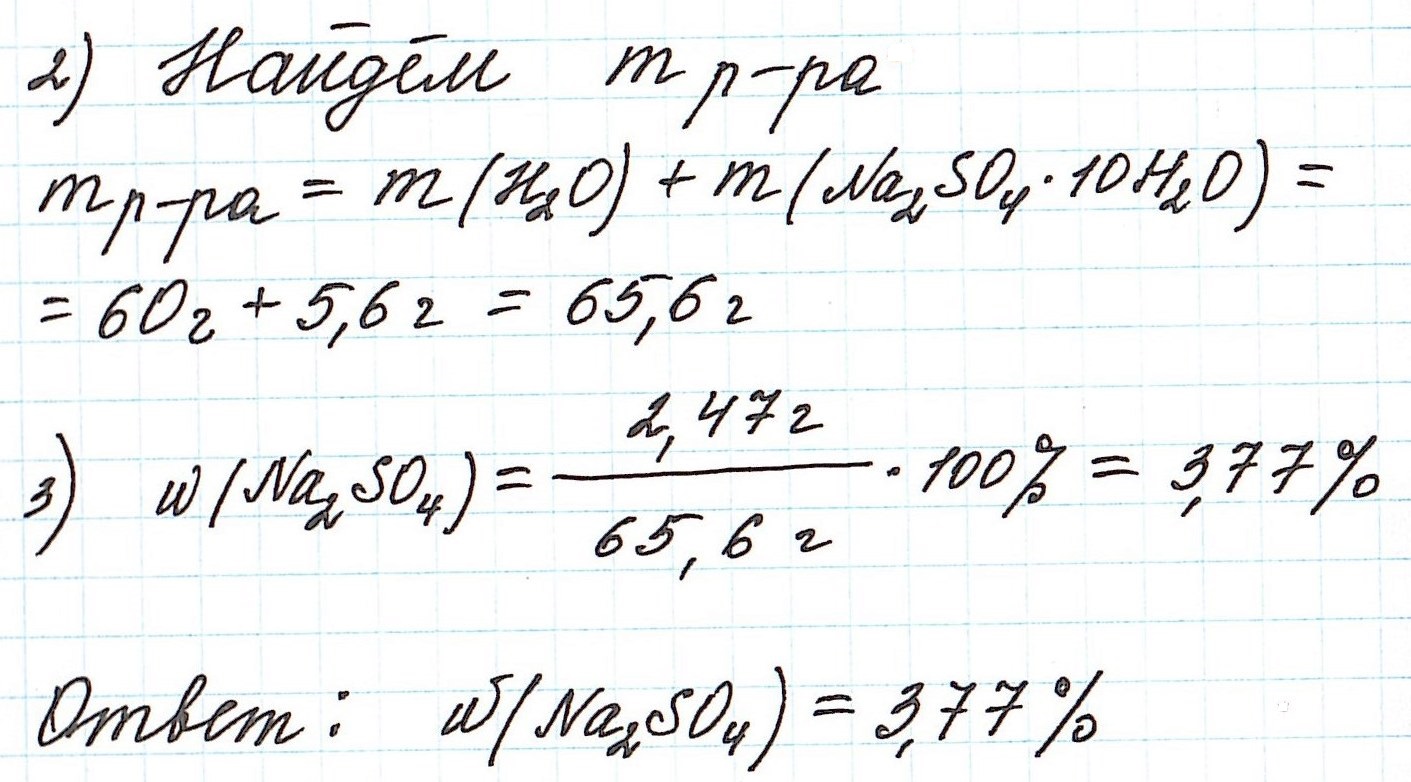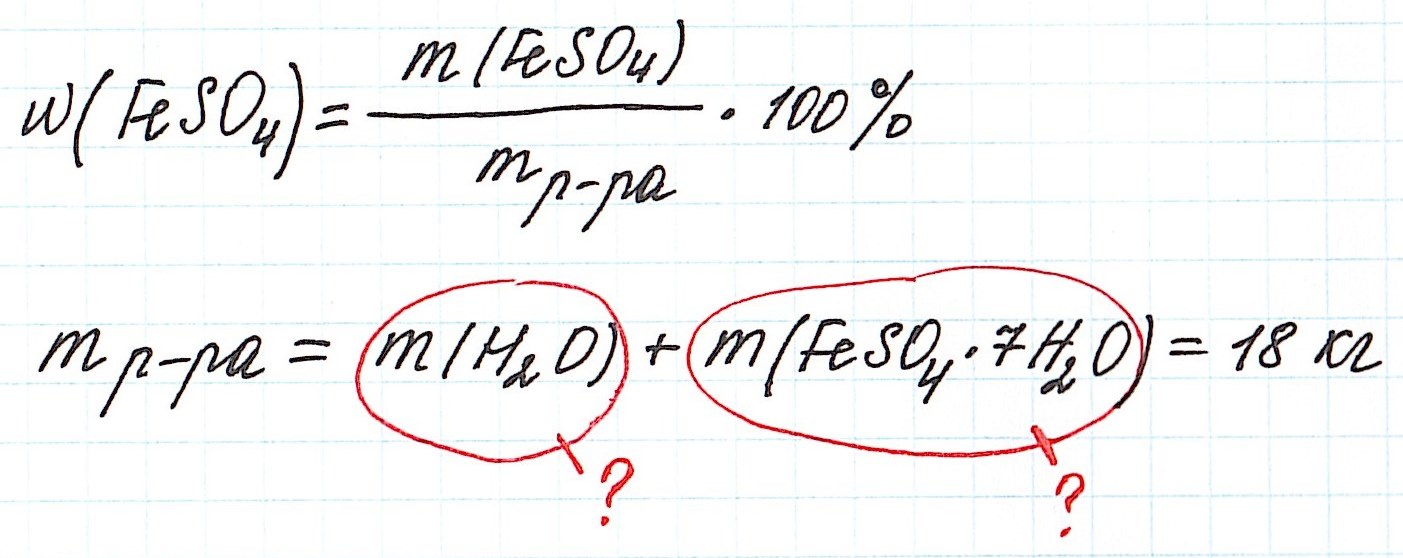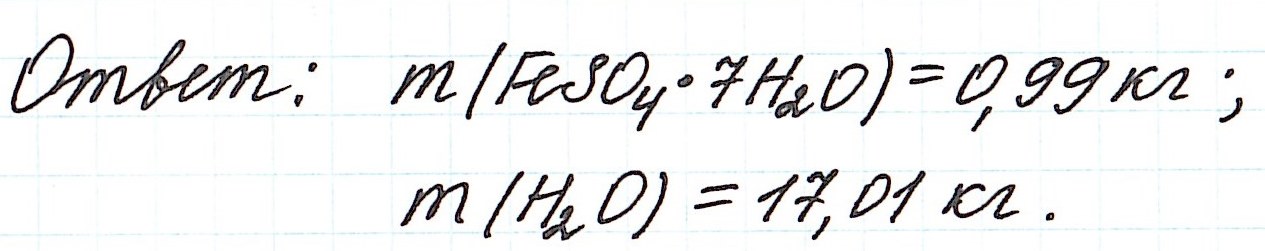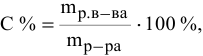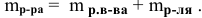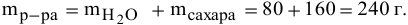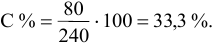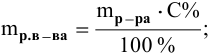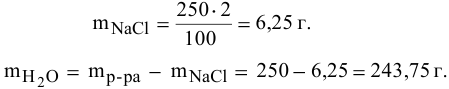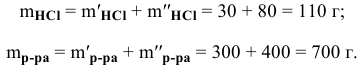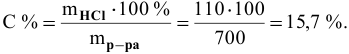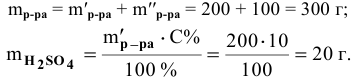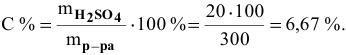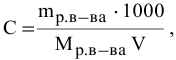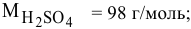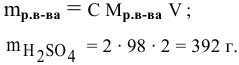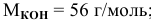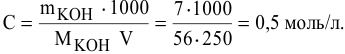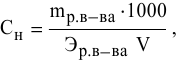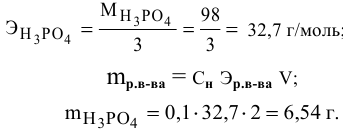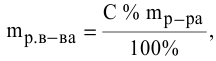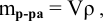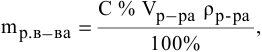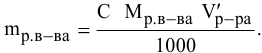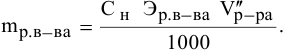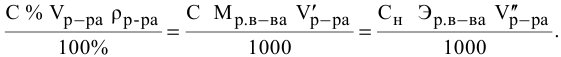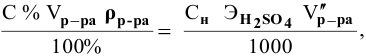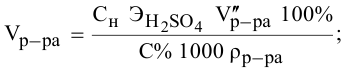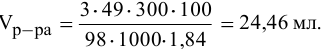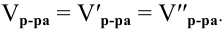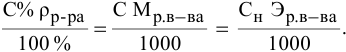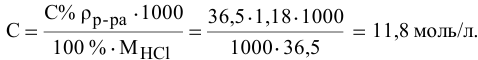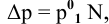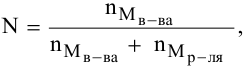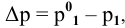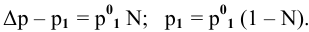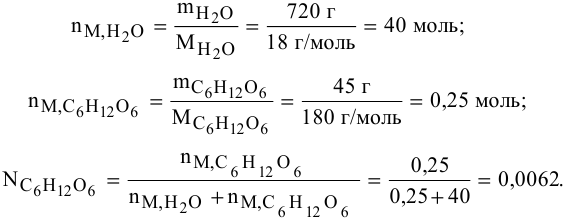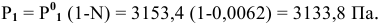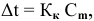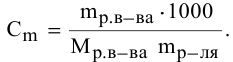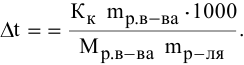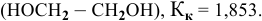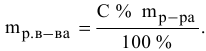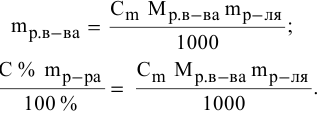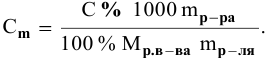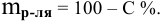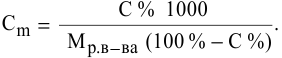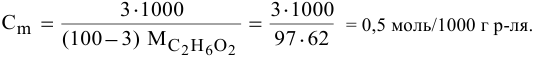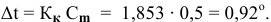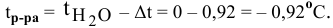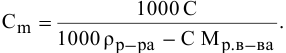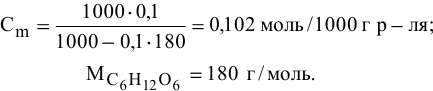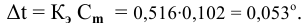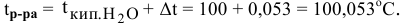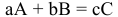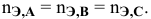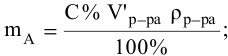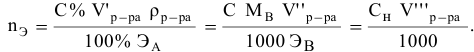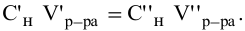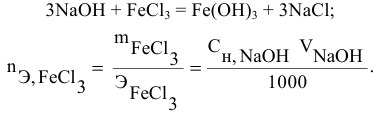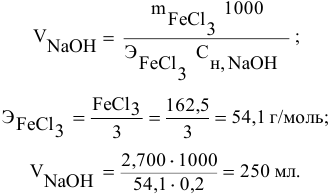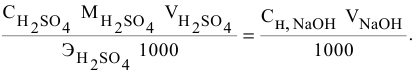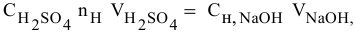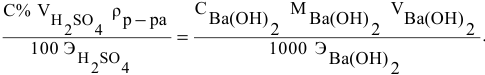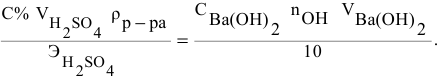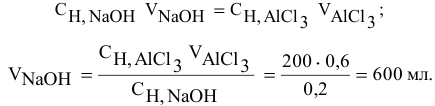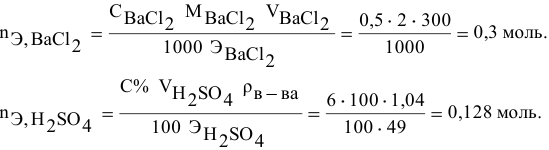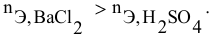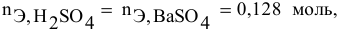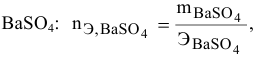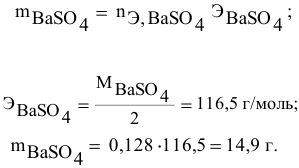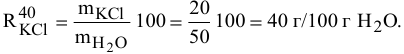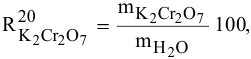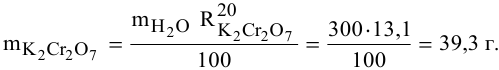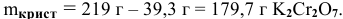“Только из союза двоих, работающих
вместе и при помощи друг друга, рождаются великие
вещи.”
Антуан Де Сент-Экзюпери
Математика многообразна и многогранна.
Существует ряд ситуаций в образовательном
процессе, когда при изучении какой-либо темы по
физике, химии, биологии и т.д. затрагиваются
понятия математики, например, существуют задачи,
которые решают как на уроках математики, так и на
уроках химии. Способы решения задач представляют
и учителя химии, и математики, но есть проблема:
математики знают математику, а химики — химию. И
не всегда способы совпадают.
В данной статье приводятся рекомендации по
решению химических задач на смешение растворов
разными способами: с помощью расчетной формулы,
“Правила смешения”, “Правила креста”,
графического метода, алгебраического метода.
Приведены примеры решения задач.
1. Основные химические понятия
Приведем некоторые указания к решению задач на
растворы.
Основными компонентами этого типа задач
являются:
а) массовая доля растворенного вещества в
растворе;
б) масса растворенного вещества в растворе;
в) масса раствора.
Предполагают, что:
а) все получившиеся смеси и сплавы являются
однородными;
б) смешивание различных растворов происходит
мгновенно;
в) объем смеси равен сумме объемов смешиваемых
растворов;
г) объемы растворов и массы сплавов не могут
быть отрицательными.
Определения и обозначения.
Массовая доля растворенного вещества в
растворе — это отношение массы этого вещества к
массе раствора.
где — массовая
доля растворенного вещества в растворе;
— масса
растворенного вещества в растворе;
— масса
раствора.
Следствия формулы (1):
Введем обозначения:
— массовая доля
растворенного вещества в первом растворе;
—
массовая доля растворенного вещества во втором
растворе;
—
массовая доля растворенного вещества в новом
растворе, полученном при смешивании первого и
второго растворов;
m1(в-ва), m2(в-ва), m(в-ва) — массы
растворенных веществ в соответствующих
растворах;
m1(р-ра), m2(р-ра), m(р-ра) — массы
соответствующих растворов.
Основными методами решения задач на смешивание
растворов являются: с помощью расчетной формулы,
“Правило смешения”, “Правило креста”,
графический метод, алгебраический метод.
Приведем описание указанных методов.
1.1. С помощью расчетной формулы
В наших обозначениях, получим формулу для
вычисления массовой доли вещества (?) в смеси.
1. Масса полученного при смешивании раствора
равна:
m(р-ра) = m1(р-ра) + m2(р-ра).
2. Определим массы растворенных веществ в
первом и втором растворах:
m1(в-ва)= •m1(р-ра), m2(в-ва)=
•m2(р-ра).
3. Следовательно, масса растворенного вещества
в полученном растворе вычисляется как сумма масс
веществ в исходных растворах:
m(в-ва) = m1(в-ва) + m2(в-ва) = •m1(р-ра) +
•m2(р-ра).
4. Таким образом, массовая доля растворенного
вещества в полученном растворе равна:
или
или
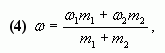
где — массы
соответствующих растворов.
Замечание: При решении задач удобно
составлять следующую таблицу.
|
1-й раствор |
2-й раствор |
Смесь двух растворов |
|
|
Масса растворов |
m1 |
m2 |
m1 + m2 |
|
Массовая доля |
|
|
|
|
Масса вещества в |
|
|
|
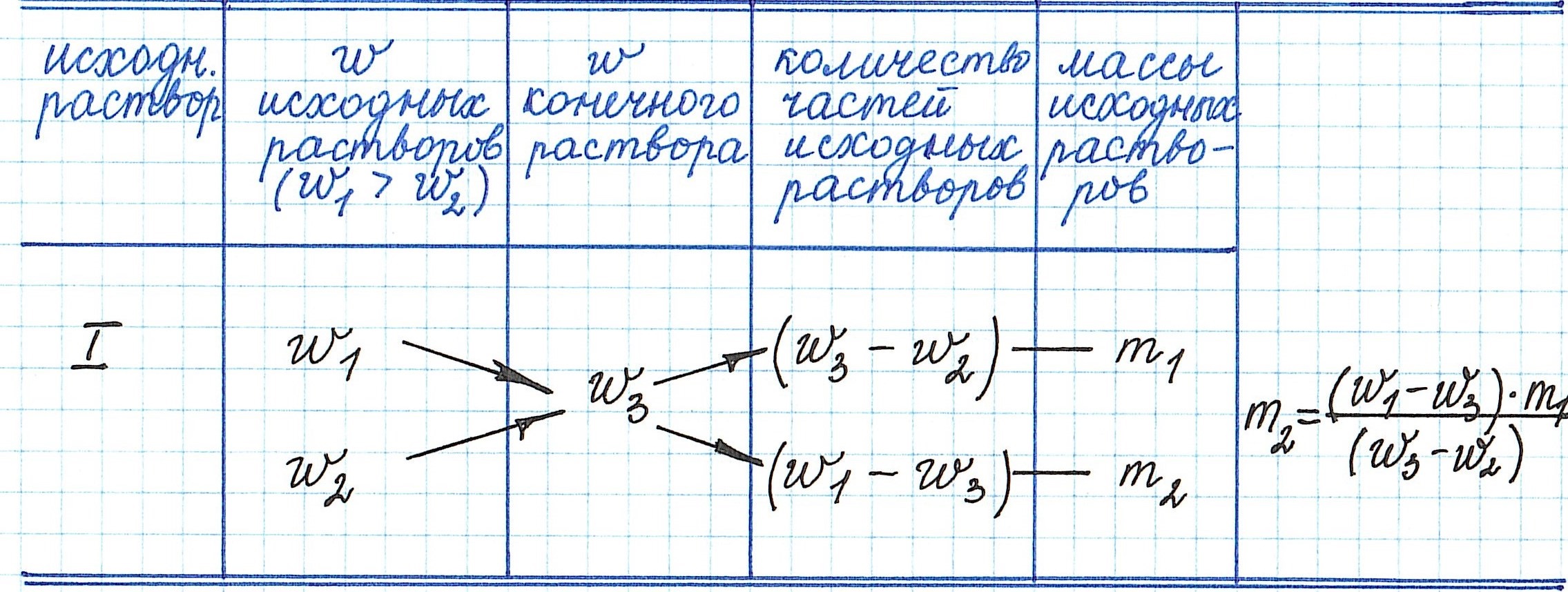
1.2. “Правило смешения”
Воспользуемся формулой (4):
тогда 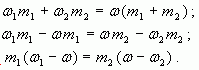
Отсюда
Таким образом, отношение массы первого
раствора к массе второго равно отношению
разности массовых долей смеси и второго раствора
к разности массовых долей первого раствора и
смеси.
Аналогично получаем, что при
Замечание: Формула (5) удобна тем, что на
практике, как правило, массы веществ не
отвешиваются, а берутся в определенном
отношении.
1.3. “Правило креста”
“Правилом креста” называют диагональную
схему правила смешения для случаев с двумя
растворами.
Слева на концах отрезков записывают исходные
массовые доли растворов (обычно слева
вверху-большая), на пересечении отрезков —
заданная, а справа на их концах записываются
разности между исходными и заданной массовыми
долями. Получаемые массовые части показывают в
каком отношении надо слить исходные растворы.
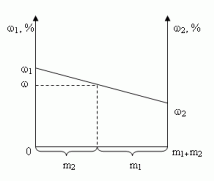
1.4. Графический метод
Отрезок прямой (основание графика)
представляет собой массу смеси, а на осях ординат
откладывают точки, соответствующие массовым
долям растворенного вещества в исходных
растворах. Соединив прямой точки на осях ординат,
получают прямую, которая отображает
функциональную зависимость массовой доли
растворенного вещества в смеси от массы
смешанных растворов в обратной пропорциональной
зависимости
Полученная функциональная прямая позволяет
решать задачи по определению массы смешанных
растворов и обратные, по массе смешанных
растворов находить массовую долю полученной
смеси.
Построим график зависимости массовой доли
растворенного вещества от массы смешанных
растворов. На одной из осей ординат откладывают
точку, соответствующую массовой доли , а на другой —
. Обозначим на оси абсцисс
точки А и В с координатами (0,0) и (m1 + m2,0),
соответственно. На графике точка А(0,0)
показывает, что массовая доля всего раствора
равна , а точка В(m1
+ m2,0) — массовая доля всего раствора равна . В направлении от
точки А к точке В возрастает содержание в
смеси 2-го раствора от 0 до m1+ m2 и
убывает содержание 1-го раствора от m1+ m2
до 0. Таким образом, любая точка на отрезке АВ будет
представлять собой смесь, имеющую одну и ту же
массу с определенным содержанием каждого
раствора, которое влияет на массовую долю
растворенного вещества в смеси.
Замечание: Данный способ является наглядным
и дает приближенное решение. При использовании
миллиметровой бумаги можно получить достаточно
точный ответ.
1.5. Алгебраический метод
Задачи на смешивание растворов решают с
помощью составления уравнения или системы
уравнений.
2. Примеры решения задач
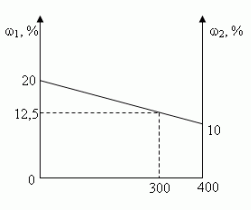
Задача 1. (№1.43, [1])
В 100 г 20%-ного раствора соли добавили 300 г её
10%-ного раствора. Определите процентную
концентрацию раствора.
Решение:
- C помощью расчетной формулы
- Графический
- Путем последовательных вычислений
- Сколько растворенного вещества содержится:
- Сколько вещества содержится в образовавшемся
растворе? - Чему равна масса образовавшегося раствора?
- Какова процентная концентрация полученного
раствора? - Алгебраический
Ответ: 12,5%
а) в 100 г 20%-ного раствора; [100•0,2 = 20(г)]
б) в 300 г 10%-ного раствора? [300•0,1 = 30(г)]
20 г + 30 г = 50 г
100 г + 300 г = 400 г
(50/400)100 = 12,5(%)
Ответ: 12,5%
Пусть х — процентная концентрация
полученного раствора. В первом растворе
содержится 0,2•100(г) соли, а во втором 0,1•300(г), а в
полученном растворе х•(100 + 300)(г) соли.
Составим уравнение:
0,2•100 + 0,1•300 = х•(100 + 300);
х = 0,125 (12,5%)
Ответ: 12,5%
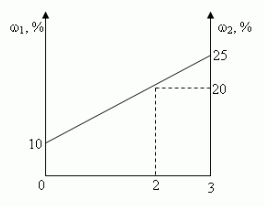
Задача 2. u(№10.26, [1])
Смешали 10%-ный и 25%-ный растворы соли и получили 3
кг 20%-ного раствора. Какое количество каждого
раствора в килограммах было использовано?
Решение:
- Алгебраический
- Графический.
- “Правило смешения”
- “Правило креста”
а) C помощью уравнения:
Пусть х (кг) — масса 1-го раствора, тогда 3-х (кг)
-масса 2-го раствора.
0,1•х (кг) содержится соли в 1-ом растворе,
0,25•(3-х) (кг) содержится соли в 2-ом растворе,
0,2•3 (кг) содержится соли в смеси.
Учитывая, что масса соли в 1-ом и 2-ом растворах
равна массе соли в смеси, составим и решим
уравнение:
0,1•х + 0,25•(3-х) = 0,2•3;
0,15х = 0,15;
х = 1, 1кг-масса 1-го раствора
3 — х = 3 — 1 =2 (кг) — масса 2-го раствора.
Ответ: 1 кг, 2 кг.
б) С помощью системы уравнений
Пусть х (кг) — количество первого раствора, у (кг)
— количество второго раствора. Система уравнений
имеет вид:
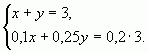
Ответ: 1 кг, 2 кг.
Ответ: 1кг, 2кг.

Составим диагональную схему
Ответ: 1кг, 2кг.
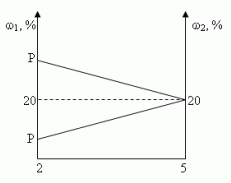
Задача 3 ([2])
Сосуд емкостью 5 л содержит 2 л р%-ного (по объёму)
раствора соли. Сколько литров 20%-ного раствора
такой же соли надо налить в сосуд, чтобы
процентное содержание соли в сосуде стало
наибольшим?
Решение (графический способ)
Заметим, что по условию, объём второго раствора
не превышает трёх литров.
- Ели р < 20, то для того, чтобы получить
максимальную массовую долю вещества в растворе,
необходимо добавить 3 л 20% — ного раствора соли; - Если р = 20, то при добавлении 2-го раствора,
процентное содержание соли в растворе не
изменится, следовательно, можно прилить от 0 л до 3
л 20% — ного раствора соли; - Если р > 20, то при добавлении 2-го раствора,
процентное содержание соли будет уменьшаться,
т.е. прилить нужно 0 л.
Ответ: 3 л, если 0 < р < 20, [0,3], если р = 20, 0л, если 20
< р 100.
Задача 4 (работа 5, №2, [1])
В двух сосудах по 5л каждый содержится раствор
соли. Первый сосуд содержит 3л р% — ного раствора, а
второй — 4л 2р% — ного раствора одной и той же соли.
Сколько литров надо перелить из второго сосуда в
первый, чтобы получить в нем 10% — ный раствор соли?
При каких значениях р задача имеет решение?
Решение
Найдем, при каких значениях р задача имеет
решение. По условию задачи 5-ти литровый сосуд
содержит 3л первого раствора, следовательно, к
нему можно прилить от 0 до 2л второго раствора.
Имеем, Решая
неравенство, получаем
Ответ:
3. Заключение
Данные рекомендации предназначены учителям
математики, желающим организовать элективные
курсы, как в девятых, так и в десятых и
одиннадцатых классах. Цель создаваемых курсов:
научить учащихся пользоваться математическим
аппаратом при решении химических задач.
Список литературы
- Галицкий и др. Сборник задач по алгебре для 8-9
классов: Учебное пособие для учащихся шк. и
классов с углубл. изуч. математики / М.Л. Галицкий,
А.М. Гольдман, Л.И. Звавич.-2-е изд. — М.:
Просвещение,1994. — 271с. - Сборник задач по математике для поступающих в
вузы: Учебное пособие/ П.Т.Дыбов, А.И.Забоев, А.С.
Иванов и др.; Под ред. А.И. Прилепко. — М.:Высш. школа,
1983. — 239 с. - Ерыгин Д.П., Шишкин Е.А. Методика решения задач по
химии: Учебное пособие для студентов пед. ин-тов
по биол. и хим. спец. — М.: Просвещение,1989. — 176с. - Хомченко Г.П., Хомченко И.Г. Задачи по химии для
поступающих в вузы: Учебное пособие. — 2-е изд..
исправ. и доп. — М.: Высш. школа, 1993. — 302 с.
Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.
Растворы. Способы выражения концентрации растворов
Способы выражения концентрации растворов
Существуют различные способы выражения концентрации растворов.
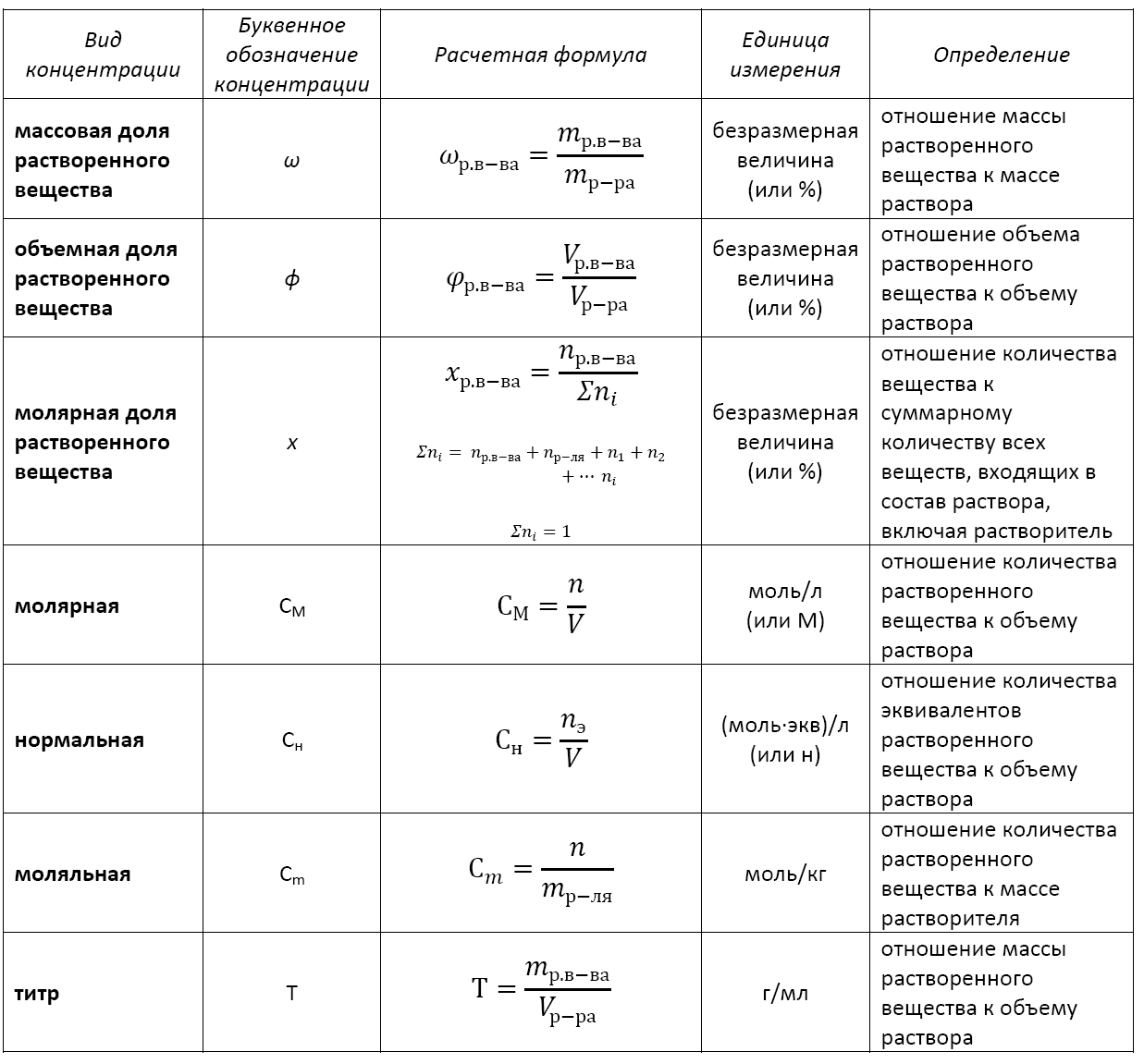
Массовая доля ω компонента раствора определяется как отношение массы данного компонента Х, содержащегося в данной массе раствора к массе всего раствора m. Массовая доля – безразмерная величина, её выражают в долях от единицы:
ωр.в. = mр.в./mр-ра (0 < ωр.в. < 1) (1)
Массовый процент представляет собой массовую долю, умноженную на 100:
ω(Х) = m(Х)/m · 100% (0% < ω(Х) < 100%) (2)
где ω(X) – массовая доля компонента раствора X; m(X) – масса компонента раствора X; m – общая масса раствора.
Мольная доля χ компонента раствора равна отношению количества вещества данного компонента X к суммарному количеству вещества всех компонентов в растворе.
Для бинарного раствора, состоящего из растворённого вещества Х и растворителя (например, Н2О), мольная доля растворённого вещества равна:
χ(X) = n(X)/(n(X) + n(H2O)) (3)
Мольный процент представляет мольную долю, умноженную на 100:
χ(X), % = (χ(X)·100)% (4)
Объёмная доля φ компонента раствора определяется как отношение объёма данного компонента Х к общему объёму раствора V. Объёмная доля – безразмерная величина, её выражают в долях от единицы:
φ(Х) = V(Х)/V (0 < φ(Х) < 1) (5)
Объёмный процент представляет собой объёмную долю, умноженную на 100.
φ(X), % = (φ(X)·100)%
Молярность (молярная концентрация) C или Cм определяется как отношение количества растворённого вещества X, моль к объёму раствора V, л:
Cм(Х) = n(Х)/V (6)
Основной единицей молярности является моль/л или М. Пример записи молярной концентрации: Cм(H2SO4) = 0,8 моль/л или 0,8М.
Нормальность Сн определяется как отношение количества эквивалентов растворённого вещества X к объёму раствора V:
Cн(Х) = nэкв.(Х)/V (7)
Основной единицей нормальности является моль-экв/л. Пример записи нормальной концентрации: Сн(H2SO4) = 0,8 моль-экв/л или 0,8н.
Титр Т показывает, сколько граммов растворённого вещества X содержится в 1 мл или в 1 см3 раствора:
T(Х) = m(Х)/V (8)
где m(X) – масса растворённого вещества X, V – объём раствора в мл.
Моляльность раствора μ показывает количество растворённого вещества X в 1 кг растворителя:
μ(Х) = n(Х)/mр-ля (9)
где n(X) – число моль растворённого вещества X, mр-ля – масса растворителя в кг.
Мольное (массовое и объёмное) отношение – это отношение количеств (масс и объёмов соответственно) компонентов в растворе.
Необходимо иметь ввиду, что нормальность Сн всегда больше или равна молярности См. Связь между ними описывается выражением:
См = Сн · f(Х) (10)
Для получения навыков пересчёта молярности в нормальность и наоборот рассмотрим табл. 1. В этой таблице приведены значения молярности См, которые необходимо пересчитать в нормальность Сн и величины нормальности Сн, которые следует пересчитать в молярность См.
Пересчёт осуществляем по уравнению (10). При этом нормальность раствора находим по уравнению:
Сн = См/f(Х) (11)
Результаты расчётов приведены в табл. 2.
Таблица 1. К определению молярности и нормальности растворов
| Тип химического превращения | См | Сн | Сн | См |
| Реакции обмена | 0,2 M Na2SO4 | ? | 6 н FeCl3 | ? |
| 1,5 M Fe2(SO4)3 | ? | 0,1 н Ва(ОН)2 | ? | |
| Реакции окисления-восстановления | 0,05 М KMnO4
в кислой среде |
? | 0,03 М KMnO4
в нейтральной среде |
? |
Таблица 2
Значения молярности и нормальности растворов
| Тип химического превращения | См | Сн | Сн | См |
| Реакции обмена | 0,2M Ma2SO4 | 0,4н | 6н FeCl3 | 2М |
| 1,5M Fe2(SO4)3 | 9н | 0,1н Ва(ОН)2 | 0,05М | |
| Реакции окисления-восстановления | 0,05М KMnO4 в кислой среде | 0,25н | 0,03М KMnO4
в нейтральной среде |
0,01М |
Между объёмами V и нормальностями Сн реагирующих веществ существует соотношение:
V1 Сн,1 =V2 Сн,2 (12)
Примеры решения задач
Задача 1. Рассчитайте молярность, нормальность, моляльность, титр, мольную долю и мольное отношение для 40 мас.% раствора серной кислоты, если плотность этого раствора равна 1,303 г/см3.
Решение.
Масса 1 литра раствора равна М = 1000·1,303 = 1303,0 г.
Масса серной кислоты в этом растворе: m = 1303·0,4 = 521,2 г.
Молярность раствора См = 521,2/98 = 5,32 М.
Нормальность раствора Сн = 5,32/(1/2) = 10,64 н.
Титр раствора Т = 521,2/1000 = 0,5212 г/см3.
Моляльность μ = 5,32/(1,303 – 0,5212) = 6,8 моль/кг воды.
Обратите внимание на то, что в концентрированных растворах моляльность (μ) всегда больше молярности (См). В разбавленных растворах наоборот.
Масса воды в растворе: m = 1303,0 – 521,2 = 781,8 г.
Количество вещества воды: n = 781,8/18 = 43,43 моль.
Мольная доля серной кислоты: χ = 5,32/(5,32+43,43) = 0,109. Мольная доля воды равна 1– 0,109 = 0,891.
Мольное отношение равно 5,32/43,43 = 0,1225.
Задача 2. Определите объём 70 мас.% раствора серной кислоты (r = 1,611 г/см3), который потребуется для приготовления 2 л 0,1 н раствора этой кислоты.
Решение.
2 л 0,1н раствора серной кислоты содержат 0,2 моль-экв, т.е. 0,1 моль или 9,8 г.
Масса 70%-го раствора кислоты m = 9,8/0,7 = 14 г.
Объём раствора кислоты V = 14/1,611 = 8,69 мл.
Задача 3. В 5 л воды растворили 100 л аммиака (н.у.). Рассчитать массовую долю и молярную концентрацию NH3 в полученном растворе, если его плотность равна 0,992 г/см3.
Решение.
Масса 100 л аммиака (н.у.) m = 17·100/22,4 = 75,9 г.
Масса раствора m = 5000 + 75,9 = 5075,9 г.
Массовая доля NH3 равна 75,9/5075,9 = 0,0149 или 1,49 %.
Количество вещества NH3 равно 100/22,4 = 4,46 моль.
Объём раствора V = 5,0759/0,992 = 5,12 л.
Молярность раствора См = 4,46/5,1168 = 0,872 моль/л.
Задача 4. Сколько мл 0,1М раствора ортофосфорной кислоты потребуется для нейтрализации 10 мл 0,3М раствора гидроксида бария?
Решение.
Переводим молярность в нормальность:
0,1 М Н3РО4 0,3 н; 0,3 М Ва(ОН)2 0,6 н.
Используя выражение (12), получаем: V(H3P04)=10·0,6/0,3 = 20 мл.
Задача 5. Какой объем, мл 2 и 14 мас.% растворов NaCl потребуется для приготовления 150 мл 6,2 мас.% раствора хлорида натрия?
Плотности растворов NaCl:
| С, мас.% | 2 | 6 | 7 | 14 |
| ρ, г/см3 | 2,012 | 1,041 | 1,049 | 1,101 |
Решение.
Методом интерполяции рассчитываем плотность 6,2 мас.% раствора NaCl:
6,2% =6% + 0,2(7% —6% )/(7 – 6) = 1,0410 + 0,0016 = 1,0426 г/см3.
Определяем массу раствора: m = 150·1,0426 = 156,39 г.
Находим массу NaCl в этом растворе: m = 156,39·0,062 = 9,70 г.
Для расчёта объёмов 2 мас.% раствора (V1) и 14 мас.% раствора (V2) составляем два уравнения с двумя неизвестными (баланс по массе раствора и по массе хлорида натрия):
156,39 = V1 1,012 + V2 1,101 ,
9,70 = V1·1,012·0,02 + V2·1,101·0,14 .
Решение системы этих двух уравнений дает V1 =100,45 мл и V2 = 49,71 мл.
Задачи для самостоятельного решения
3.1. Рассчитайте нормальность 2 М раствора сульфата железа (III), взаимодействующего со щёлочью в водном растворе.
12 н.
3.2. Определите молярность 0,2 н раствора сульфата магния, взаимодействующего с ортофосфатом натрия в водном растворе.
0,1 M.
3.3. Рассчитайте нормальность 0,02 М раствора KMnO4, взаимодействующего с восстановителем в нейтральной среде.
0,06 н.
3.4. Определите молярность 0,1 н раствора KMnO4, взаимодействующего с восстановителем в кислой среде.
0,02 M.
3.5. Рассчитать нормальность 0,2 М раствора K2Cr2O7, взаимодействующего с восстановителем в кислой среде.
1,2 M.
3.6. 15 г CuSO4·5H2O растворили в 200 г 6 мас.% раствора CuSO4. Чему равна массовая доля сульфата меди, а также молярность, моляльность и титр полученного раствора, если его плотность составляет 1,107 г/мл?
0,1; 0,695М; 0,698 моль/кг; 0,111 г/мл.
3.7. При выпаривании 400 мл 12 мас.% раствора KNO3 (плотность раствора 1,076 г/мл) получили 2М раствор нитрата калия. Определить объём полученного раствора, его нормальную концентрацию и титр.
255 мл; 2 н; 0,203 г/мл.
3.8. В 3 л воды растворили 67,2 л хлороводорода, измеренного при нормальных условиях. Плотность полученного раствора равна 1,016 г/мл. Вычислить массовую, мольную долю растворённого вещества и мольное отношение растворённого вещества и воды в приготовленном растворе.
0,035; 0,0177; 1:55,6.
3.9. Сколько граммов NaCl надо добавить к 250 г 6 мас.% раствору NaCl, чтобы приготовить 500 мл раствора хлорида натрия, содержащего 16 мас.% NaCl? Плотность полученного раствора составляет 1,116 г/мл. Определить молярную концентрацию и титр полученного раствора.
74,28 г; 3,05 М; 0,179 г/мл.
3.10. Определить массу воды, в которой следует растворить 26 г ВaCl2·2H2O для получения 0,55М раствора ВaCl2 (плотность раствора 1,092 г/мл). Вычислить титр и моляльность полученного раствора.
192,4 г; 0,111 г/мл; 0,56 моль/кг.
Формула концентрации раствора. Их множество. И каждая соответствует тому или иному способу выражения концентрации. А в химии их применяются достаточно: массовая доля растворенного вещества, молярная, нормальная, моляльная, титр и др.
Зачем так много? Ответ на этот вопрос очень прост. Каждый вид концентрации удобен в том или ином случае, когда применение другого вида концентрации неуместно.
Например, при исследовании содержания массы вещества в очень небольшом объеме раствора удобно пользоваться титром. А в каких-то технологиях вообще концентрация заменяется другими количественными характеристиками раствора. Так, в технологии посола рыбы для расчета необходимой концентрации тузлука (раствора поваренной соли) используют не его процентную концентрацию, а плотность.
Содержание:
1. Концентрация – что это такое
2. Формула концентрации раствора: основные виды
3. Массовая доля растворенного вещества и примеры ее вычисления
- разбавление раствора водой
- концентрирование раствора путем упаривания
- концентрирование раствора путем добавления растворенного вещества
- смешивание двух растворов
- применение кристаллогидратов для приготовления раствора (задачи на кристаллогидраты)
4. Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов
Концентрация – что это такое
Любой раствор имеет различные характеристики: качественные и количественные. Одной из важнейших количественных характеристик является концентрация раствора.
Концентрация раствора – это количество растворенного вещества, содержащееся в определенном количестве раствора.
Как видно из приведенного определения, основными компонентами раствора являются:
— растворитель;
— растворенное вещество.
Растворенного вещества в растворе всегда меньше, а растворителя больше.
И вот именно с вычислением количественного содержания растворенного вещества чаще всего и связаны все расчеты, основанные на применении формулы концентрации раствора.
Существует несколько видов концентрации раствора:
— массовая доля растворенного вещества;
— объемная доля растворенного вещества;
— молярная доля растворенного вещества;
— молярная (или молярность);
— моляльная (или моляльность);
— нормальная (или эквивалентная);
— титр.
Формула концентрации раствора: основные виды
Применение того или иного вида концентрации уместно в каждом конкретном случае. Не существует какой-то универсальной концентрации или универсальной формулы концентрации раствора.
Кстати, с помощью математических преобразований можно перейти от одной концентрации к другой или найти взаимосвязь между разными их видами.
Основные расчетные формулы концентрации раствора приведены в таблице:
Массовая доля растворенного вещества и примеры ее вычисления
Массовая доля растворенного вещества – это отношение массы растворенного вещества к массе раствора.
Ее расчетная формула выглядит так:
где ωр.в-ва – массовая доля растворенного вещества, mр.в-ва – масса растворенного вещества, mр-ра – масса раствора.
ωр.в-ва представляет собой долю или от единицы или от 100%. Так, например, имеется двухпроцентный раствор NaCl. Его концентрация будет записана в первом случае ω(NaCl) = 0,02, а во втором – ω(NaCl) = 2%. Форма записи основной сути не меняет. Можно записывать и так, и так.
Что же означает выражение ω(NaCl) = 0,02 или ω(NaCl) = 2%? Буквально следующее: в 100 г водного раствора поваренной соли содержится 2 г этой соли и 98 г воды.
Необходимо помнить, что раствор состоит из растворителя и растворенного вещества. Поэтому масса раствора будет состоять из массы растворителя и массы растворенного вещества:
Тогда основную расчетную формулу для массовой доли растворенного вещества можно преобразовать:
Очень часто в расчетах с процентной концентрацией используются плотность и объем раствора:
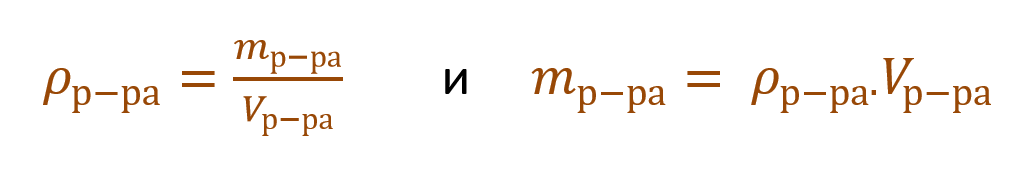
В других ситуациях могут использоваться объем и плотность не раствора, а растворителя. Тогда основная формула для расчета концентрации будет выглядеть так:
На практике бывает необходимо не только приготовить раствор с какой-либо определенной концентрацией, но и увеличить, либо уменьшить ее значение. Это достигается различными приемами:
— упариванием раствора;
— добавлением растворенного вещества;
— добавлением к раствору растворителя (например, воды).
Кроме того, приходится часто смешивать друг с другом растворы разных концентраций.
Разберем все возможные случаи.
Мы рекомендуем задачи, в которых речь идет о растворах, решать с использованием схематических рисунков. Это очень наглядно, особенно, когда речь идет о смешивании растворов.
Начнем с самого простого: вычислим концентрацию раствора.
Пример 1. В 200 г воды растворили 40 г глюкозы. Вычислите массовую долю глюкозы в полученном растворе.
Обратите внимание, что речи о каком-либо химическом взаимодействии не идет! Поэтому записывать уравнения реакций не требуется!
Запишем общую формулу для расчета массовой доли растворенного вещества:
В данной задаче глюкоза (C6H12O6) – растворенное вещество, а вода (H2O) – растворитель. Масса раствора будет складываться из массы глюкозы и массы воды:
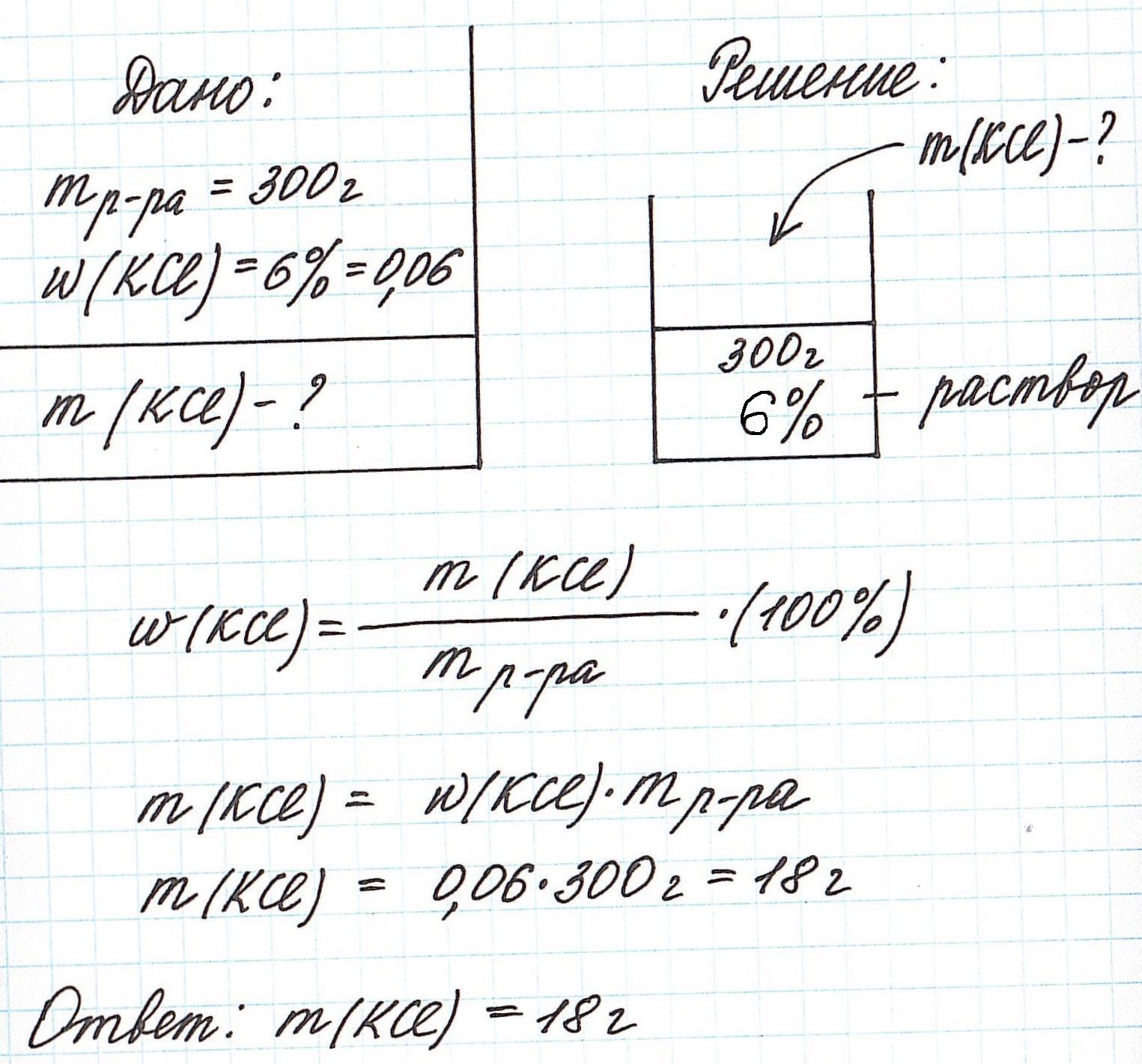
Пример 2. Рассчитайте, сколько потребуется хлорида калия, чтобы приготовить 300 г раствора с массовой долей соли 6%.
Обратите внимание, для того, чтобы расчеты были менее громоздкими, будем использовать выражение концентрации не в %, а в долях от единицы.
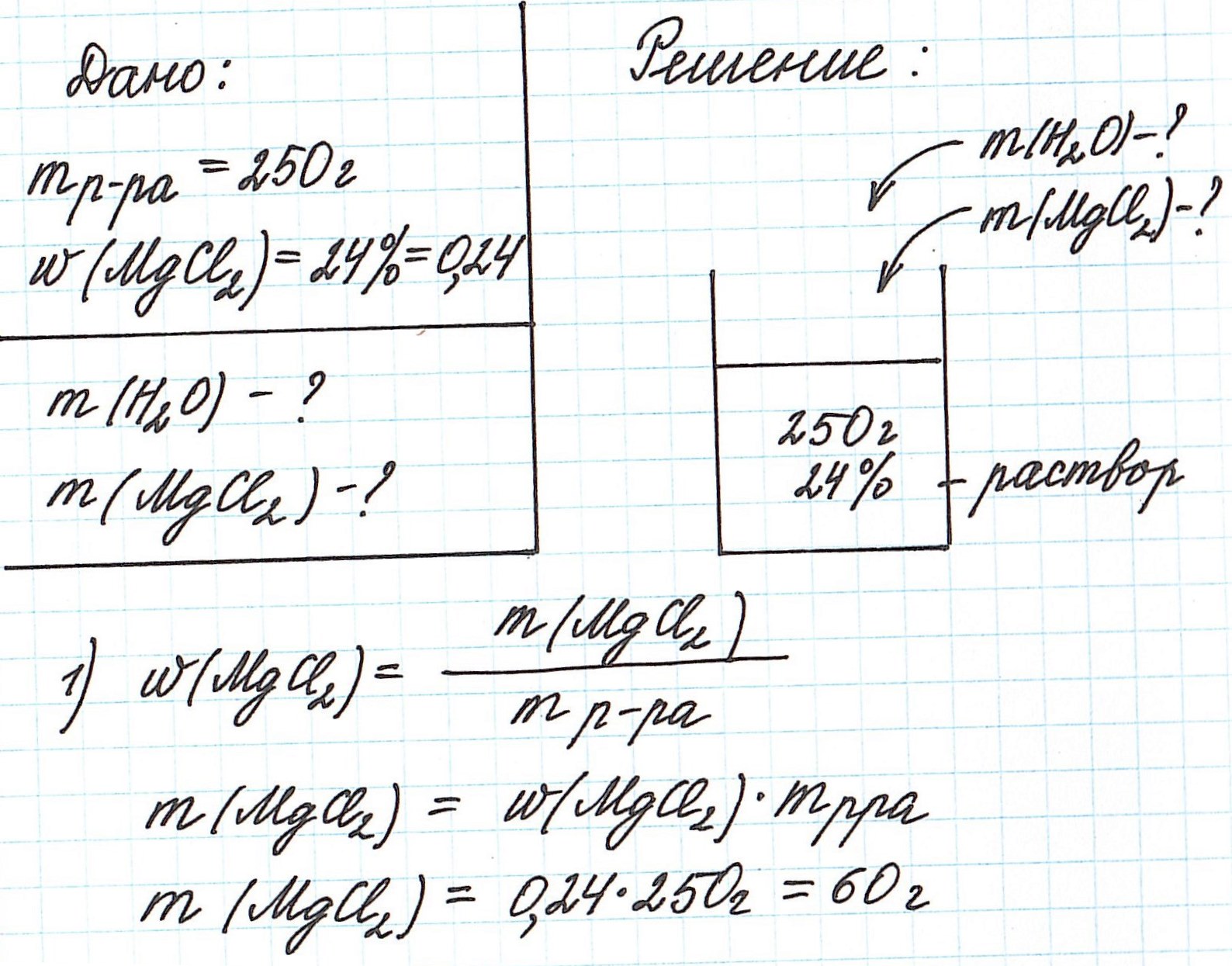
Пример 3. Необходимо приготовить 250 г раствора с массовой долей хлорида магния 24%. Рассчитайте массу требуемых воды и соли.
Так как раствор готовится из хлорида магния и воды, то и масса раствора равна сумме масс хлорида магния и воды:
Рассмотрим задачу, в которой в качестве растворителя выступает не вода, а другое вещество.
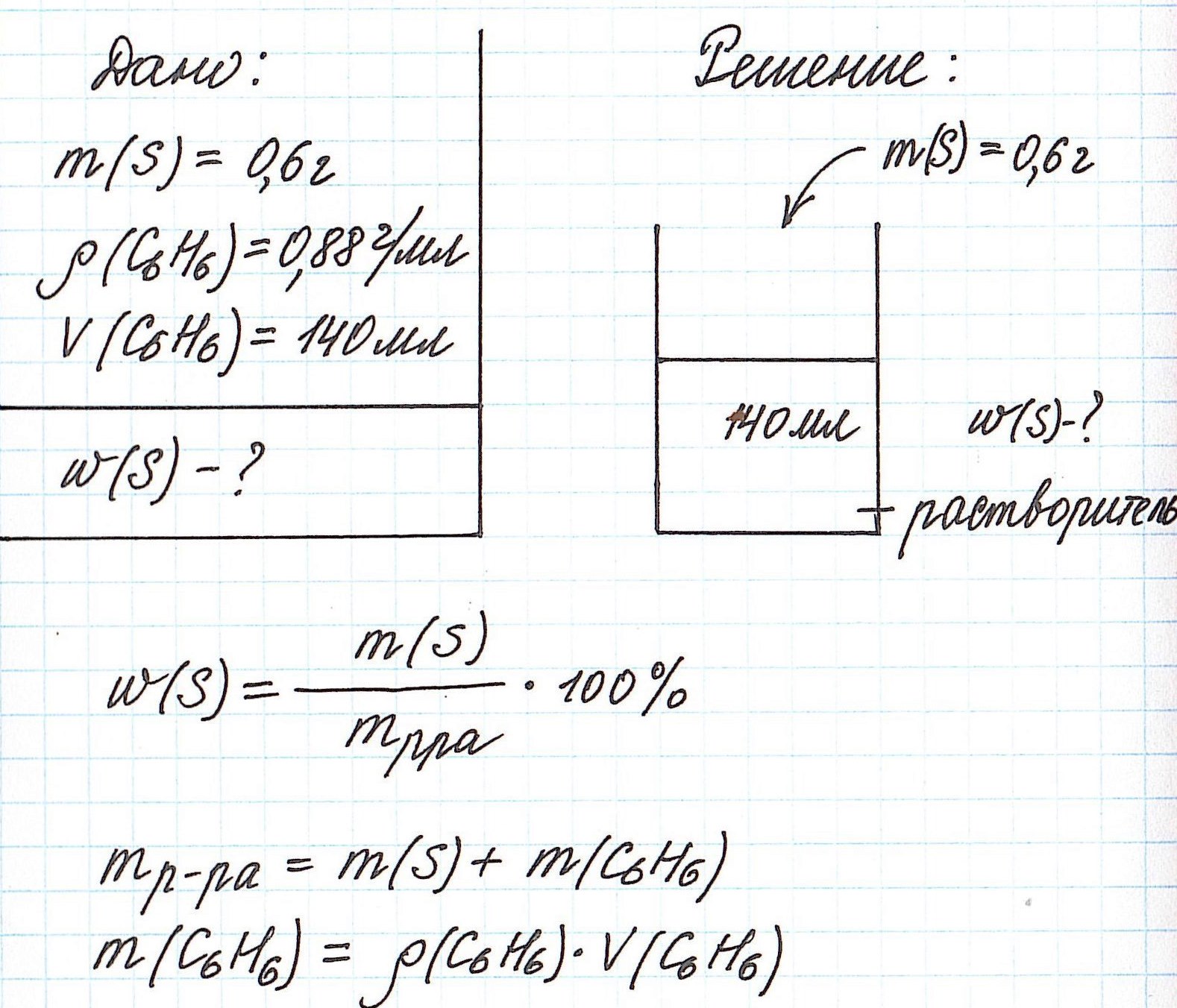
Пример 4. В органическом растворителе бензоле объемом 140 мл растворили серу массой 0,6 г. Вычислите массовую долю серы в полученном растворе, если плотность бензола составляет 0,88 г/мл.
Обратите внимание, что здесь:
— масса раствора не известна;
— масса растворителя (бензола) не известна;
— известны объем и плотность растворителя (бензола), что позволяет нам найти его массу;
— масса раствора состоит из массы растворителя (бензол) и массы растворенного вещества (сера).
Объединим все расчетные формулы в одну и подставим в нее имеющиеся численные значения:
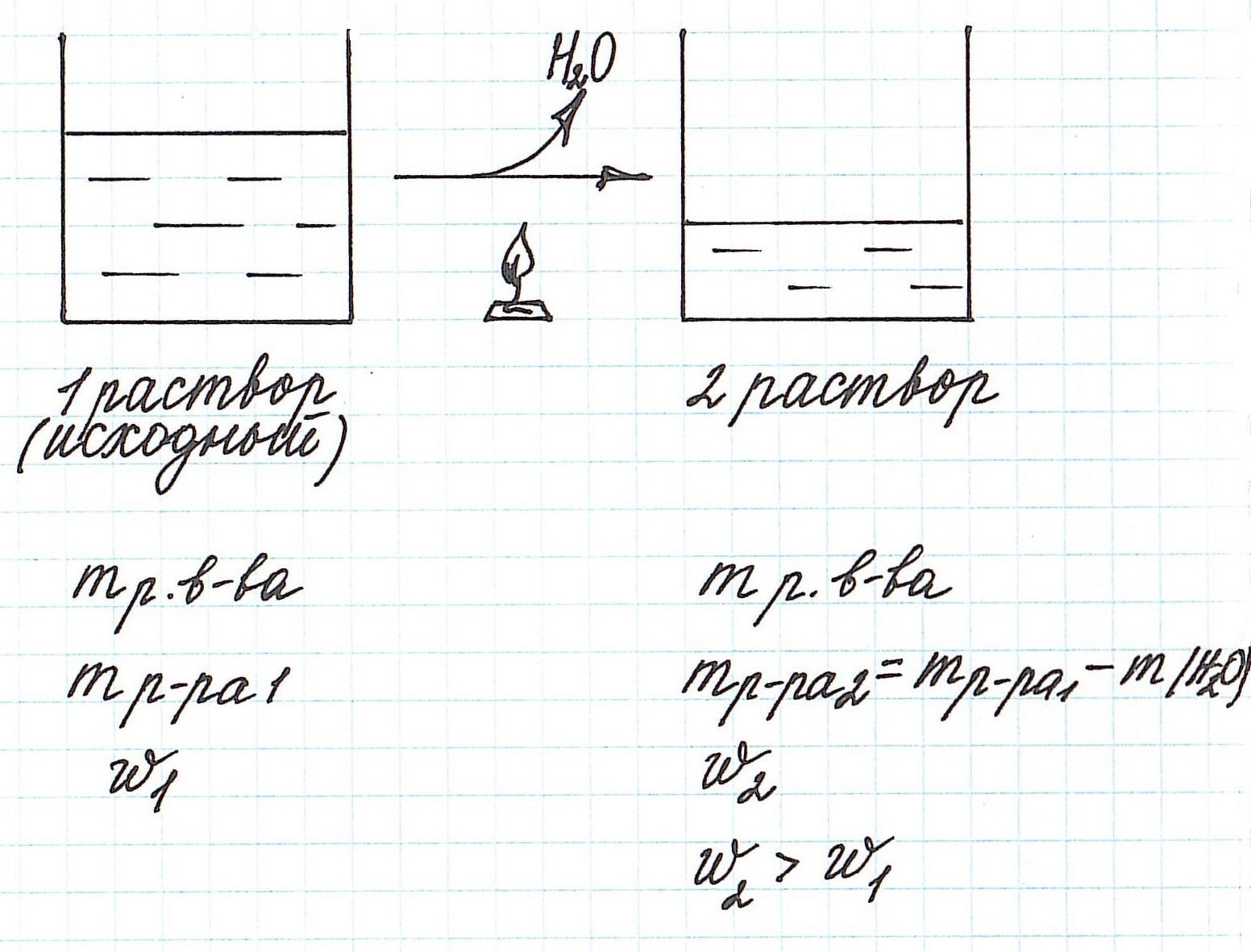
Вычисление массовой доли растворенного вещества при разбавлении раствора водой
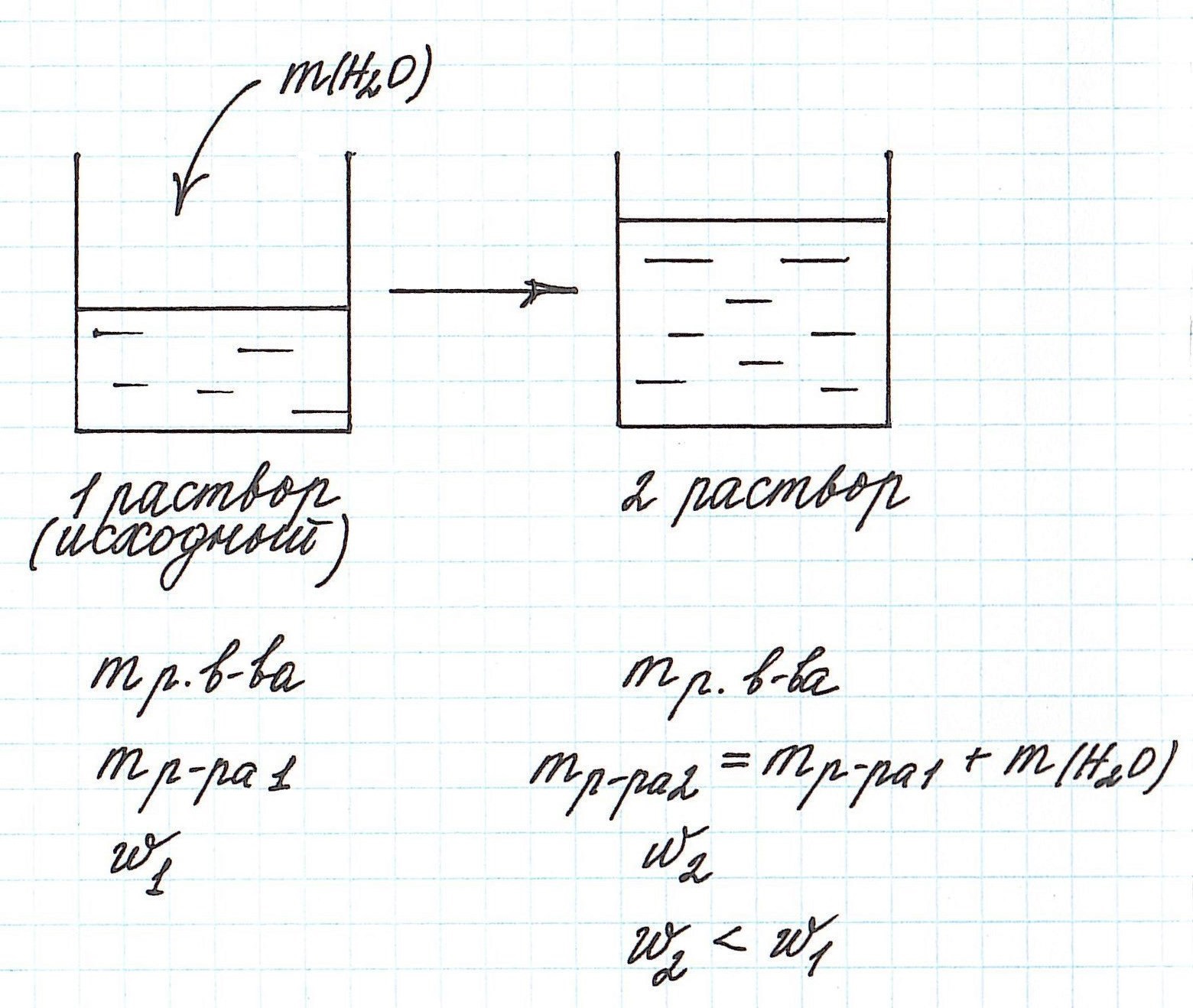
Разбавление раствора водой приводит к уменьшению его концентрации.
Запомним, что в таких случаях:
— увеличивается масса раствора;
— увеличивается масса растворителя;
— масса растворенного вещества остается постоянной.
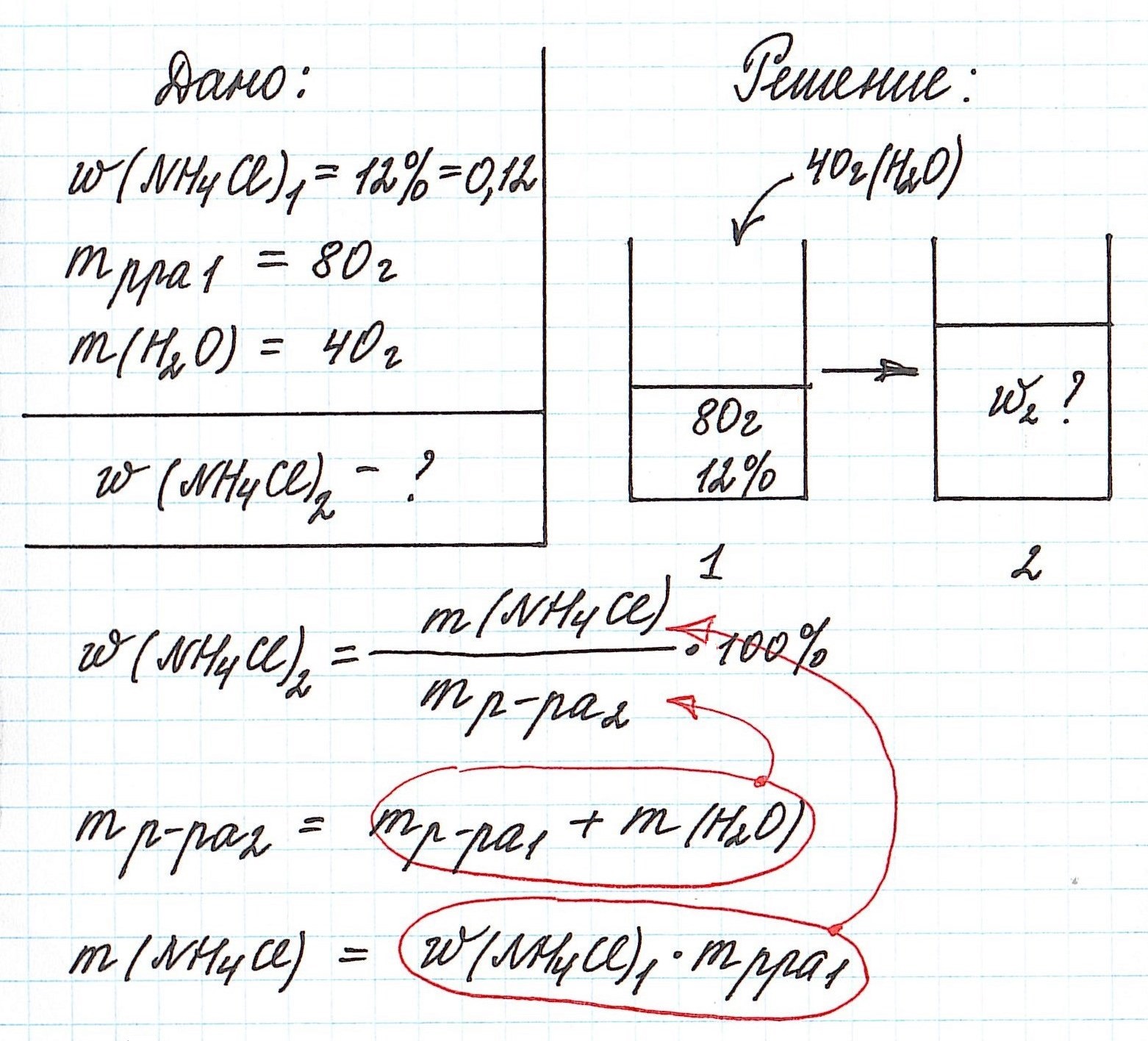
Пример 5. К 80 г раствора с массовой долей NH4Cl 12% добавили 40 г воды. Вычислите массовую долю хлорида аммония в полученном растворе.
Объединим все полученные формулы в одну и подставим имеющиеся данные:
Пример 6. Рассчитайте объем раствора фосфорной кислоты (массовая доля кислоты 12%, плотность 1,065 г/мл), который потребуется для приготовления раствора с массовой долей H3РO4 4% объемом 250 мл (плотность 1,02 г/мл).
В данной задаче речь напрямую о разбавлении раствора не идет. Но судя по тому, что исходный раствор имел концентрацию 12%, а конечный – 4%, становится ясно: последний раствор можно получить путем разбавления первого водой.
Вычисление массовой доли растворенного вещества при концентрировании раствора путем упаривания
Упаривание раствора, т.е. его нагревание, при котором происходит испарение воды, приводит к увеличению концентрации.
Учтите, что при этом:
— уменьшается масса раствора;
— уменьшается масса растворителя;
— масса растворенного вещества остается постоянной (при условии, что растворенное вещество не разлагается при данной температуре).
Пример 7. Из 200 г 27%-ного раствора глюкозы выпарили 20 г воды. Определите массовую долю глюкозы в полученном растворе.
Вычисление массовой доли растворенного вещества при концентрировании раствора путем добавления растворенного вещества
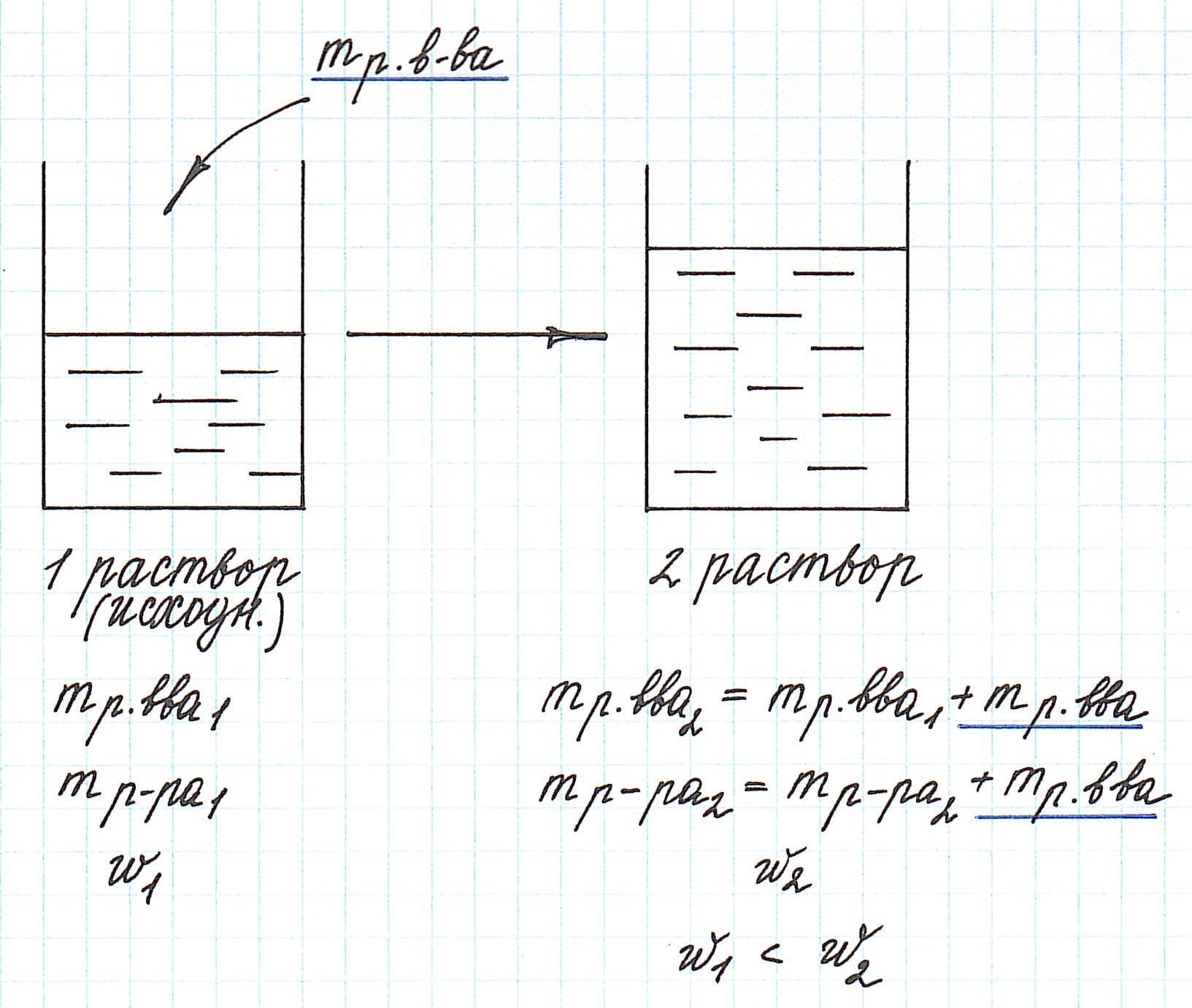
Добавление к уже существующему раствору новой порции растворенного вещества приводит к увеличению концентрации раствора.
Помните, что в таких случаях:
— увеличивается масса раствора;
— увеличивается масса растворенного вещества.
Пример 8. Определите массу хлорида калия, который надо добавить к 180 г 15%-ного раствора этой соли, чтобы получить 20%-ный раствор.
Вычисление массовой доли растворенного вещества при смешивании двух растворов
При смешивании двух растворов (речь о растворах одного и того же вещества конечно же) изменяются все количественные характеристики:
— увеличивается масса раствора;
— увеличивается масса растворенного вещества;
— изменяется массовая доля растворенного вещества.
Пример 9. Смешали 80 г 32%-ного раствора и 30 г 10%-ного раствора нитрата меди (II). Какова концентрация соли в полученном растворе?
Вычисление массовой доли растворенного вещества с применением кристаллогидратов для приготовления раствора
Кристаллогидраты используются для приготовления растворов довольно часто. Кристаллогидраты представляют собой вещества, в состав которых помимо основного вещества входят молекулы воды. Например:
CuSO4·5H2O – кристаллогидрат сульфата меди (II) (или медный купорос);
Na2SO4·10H2O – кристаллогидрат сульфата натрия (или глауберова соль).
Больше примеров здесь.
Вода, входящая в состав кристаллогидрата, называется кристаллизационной.
Кристаллогидраты различаются прочностью связи между основным веществом и кристаллизационной водой. Одни из них теряют воду при комнатной температуре с течением времени и перестают быть кристаллогидратами (например, Na2СO3·10H2O). Другие – обезвоживаются только при сильном нагревании (например, CuSO4·5H2O).
При расчете концентрации с использованием кристаллогидратов для получения растворов часто приходится учитывать и кристаллизационную воду.
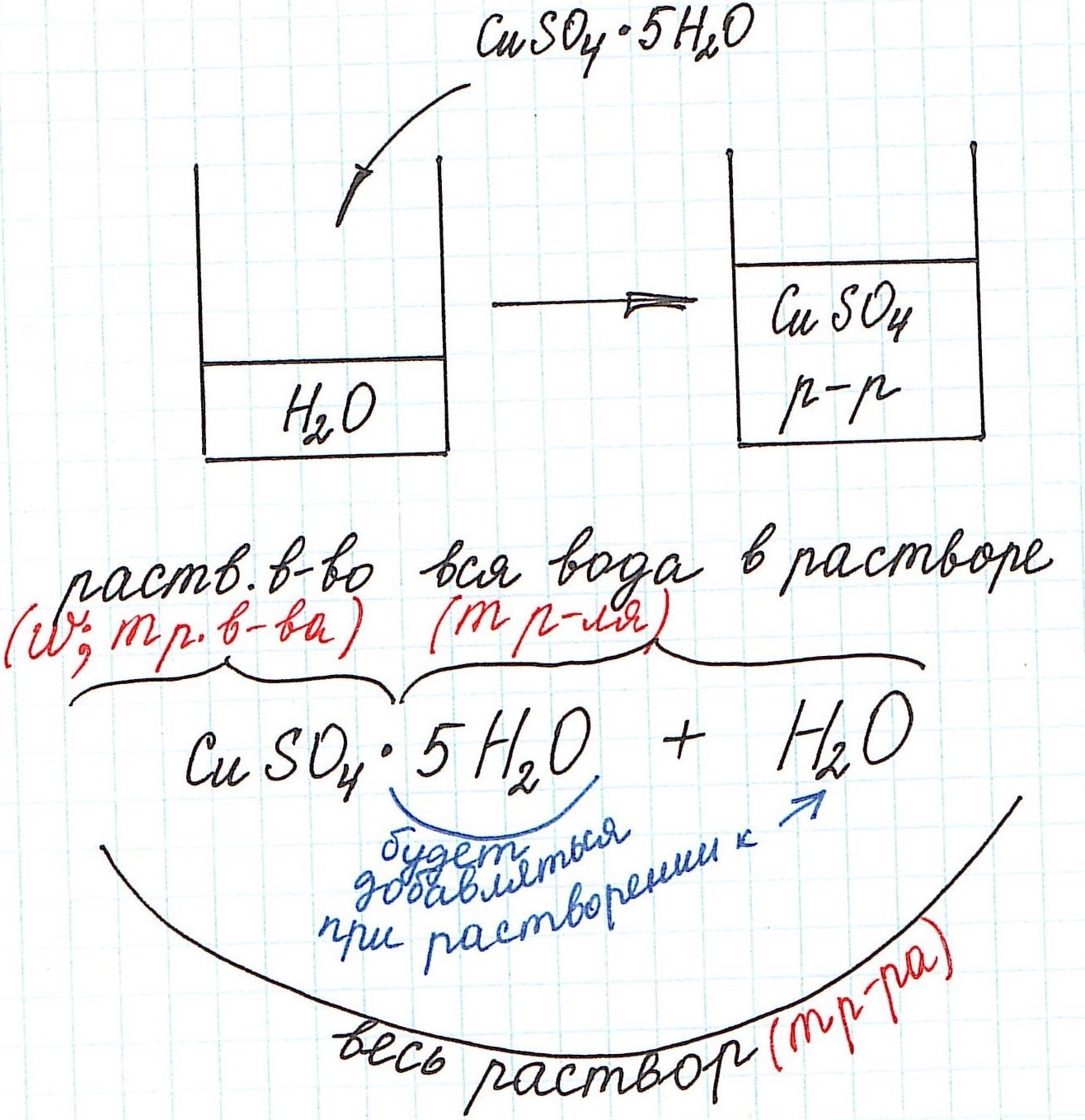
Но сначала поясним некоторые нюансы на конкретном примере:
1) Формула CuSO4·5H2O означает, что 1 моль CuSO4·5H2O содержит 1 моль CuSO4 и 5 моль H2O. Это можно было бы записать так:
n(CuSO4) = n(CuSO4·5H2O); n(H2O) = 5n(CuSO4·5H2O)
2) Относительная молекулярная (и численно молярная) масса будет складываться из относительной молекулярной массы вещества и относительной молекулярной массы воды. Например:
Mr(CuSO4·5H2O) = Mr(CuSO4) + 5·Mr(H2O) = 160 + 5·18 = 250 и, соответственно,
M(CuSO4·5H2O) = M(CuSO4) + 5·M(H2O) = 160 + 5·18 = 250 г/моль.
3) Еще одну особенность поясним с помощью рисунка:
Итак, разберем несколько типичных задач.
Пример 10. В 60 г воды растворили глауберову соль Na2SO4·10H2O массой 5,6 г. Какова массовая доля сульфата натрия в полученном растворе?
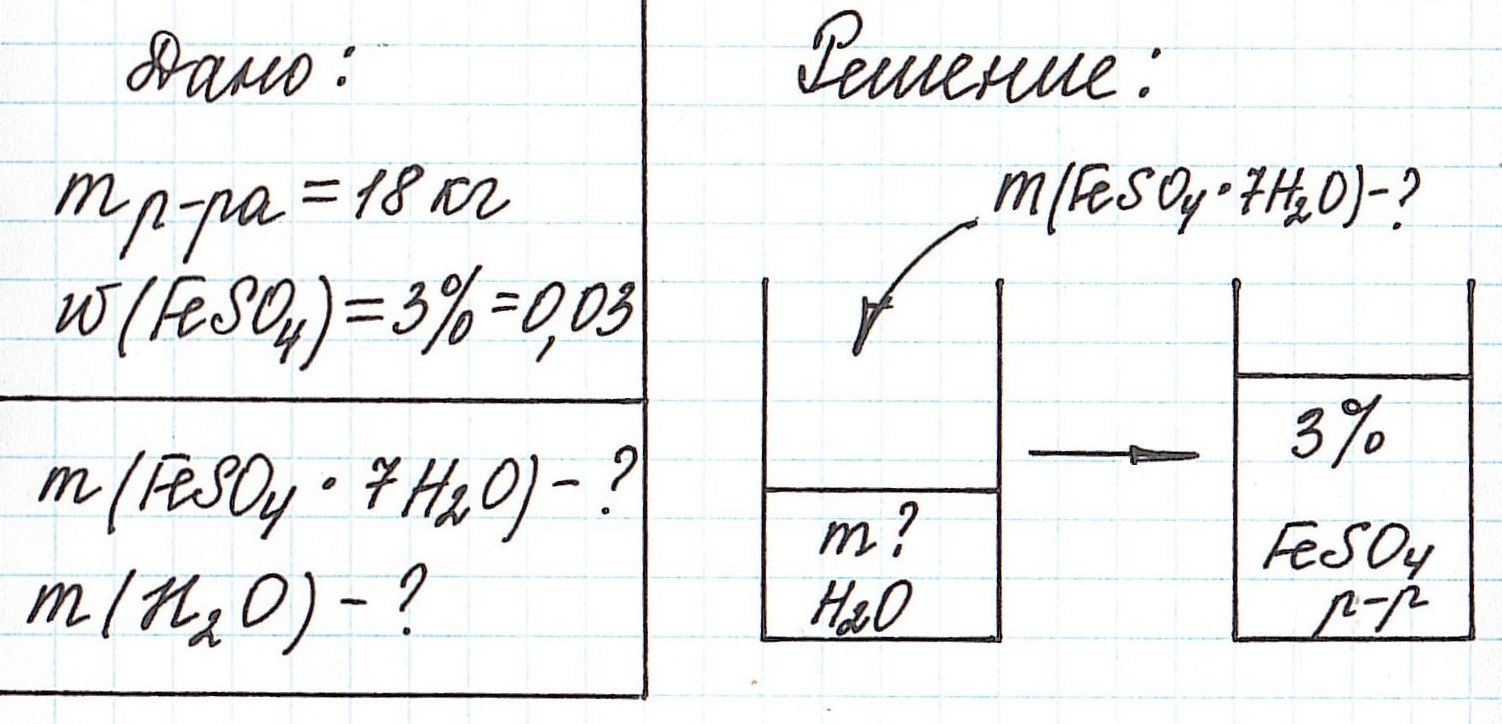
Пример 11. Какая масса железного купороса FeSO4·7H2O и воды потребуется для приготовления 18 кг раствора сульфата железа (II) с массовой долей FeSO4 3%?
Обратите внимание, что масса раствора дана не в граммах (г), а в килограммах (кг). Для того, чтобы привести в ходе расчетов все единицы измерения к единой системе, можно перевести килограммы в граммы и вычислять как обычно.
Но есть более простой способ. Можно считать количество вещества не в моль, а в киломоль (кмоль). Молярную массу вычислять не в г/моль, а в кг/кмоль. В этом случае ответ в задаче мы сразу получим в килограммах.
Пример 12. Вычислите массу кристаллогидрата сульфата никеля NiSO4·7H2O, который надо добавить к 180 г раствора с массовой долей сульфата никеля 1,5%, чтобы получить раствор с массовой долей соли 6%?
Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов
Правилом «креста» (или «квадратом Пирсона») очень удобно пользоваться в расчетах, связанных с разбавлением или смешиванием растворов.
Общая схема вычислений выглядит так:
Пример 13. Какую массу 5%-ного раствора глюкозы надо добавить к 70 г 21%-ного раствора этого же вещества, чтобы получить 12%-ный раствор?
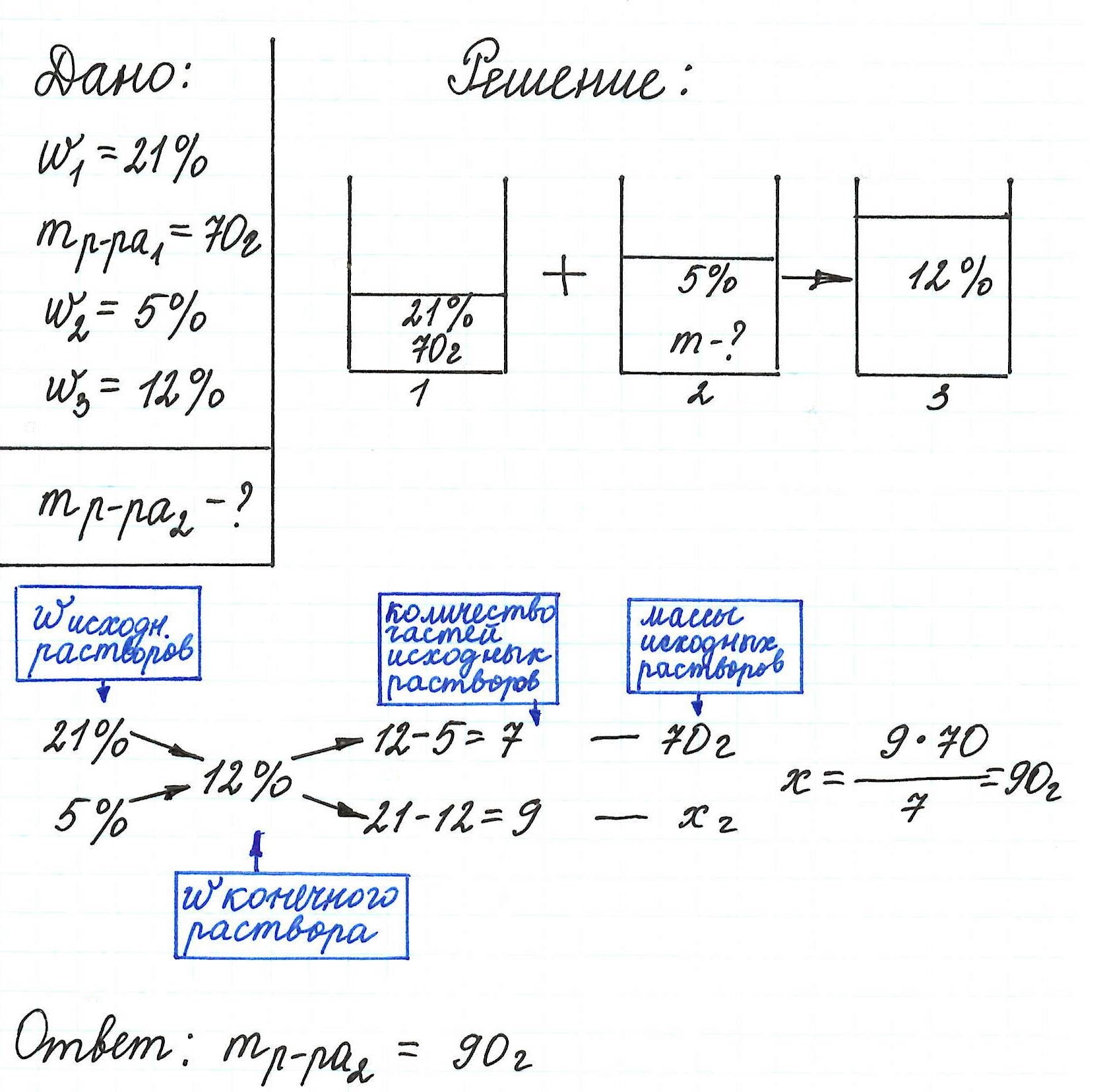
Еще примеры с применением правила «креста» можно посмотреть здесь.
Мы рассмотрели достаточно примеров расчетов, где используется формула такой концентрации раствора как массовая доля растворенного вещества. Как видим, ситуаций, в которых требуется ее применение, множество. Однако, есть достаточно случаев, когда более приемлемыми являются формулы других концентраций (молярной, нормальной, титра и т.д.). Об этом читайте в других статьях.
Чтобы самыми первыми узнавать о новых публикациях на сайте, присоединяйтесь к нашей группе ВКонтакте.
или на Одноклассниках
Пожалуйста, оцените публикацию. Большая просьба, если вы оцениваете публикацию от 1 до 3 звезд, обязательно оставьте свой комментарий с указанием того, что не так с этой публикацией. Мы постараемся устранить недостатки.
Ваше мнение для нас важно!
Отношение количества
или массы вещества, содержащегося в
системе, к объему или массе этой системы
называется концентрацией.
Рассмотрим несколько
способов выражения концентрации.
Процентная
концентрация
(массовая доля растворенного вещества)
(ω) показывает, сколько единиц массы
растворенного вещества содержится в
100 единицах массы раствора. Массовая
доля – безразмерная величина, ее выражают
в долях единицы или процентах:
,
где ω – массовая
доля (%) растворенного вещества; m1
– масса растворенного вещества, г; m
– масса раствора, г.
Масса раствора
равна произведению объема раствора V
(мл) на его плотность r
(г/см3):
,
тогда
.
Молярная
концентрация (молярность)
раствора – показывает, сколько молей
растворенного вещества содержится в
1л раствора.
Молярную концентрацию
(моль на литр) выражают формулой
,
где m1
– масса растворенного вещества, г; М –
молярная масса растворенного вещества,
г/моль; V
– объем раствора, л.
Количество вещества
в молях определяется по формуле:
n
= m1
/М, тогда
Нормальная
концентрация (нормальность раствора)
показывает, сколько грамм-эквивалентов
растворенного вещества содержится в 1
л раствора (моль на литр):
,
где m1
– масса растворенного вещества, г; V
– объем раствора, л.
Э – эквивалентная
масса растворенного вещества (г/моль),
которую рассчитывают по формуле:
Э=(г/моль),
где М – мольная
масса вещества, n
– количество катионов (анионов), В
– валентность. Валентность – это
способность атомов элемента присоединять
определенное число атомов другого
элемента. Эквивалент кислоты можно
определить по формуле: Э = М (кислоты)
/ основность (число атомов водорода).
Например: Э
Н2SO4==49г/моль;
эквивалент основания по формуле: Э = М
(основания) / кислотность (число ОН—
групп), так Э
Fe(OH)3==35,6г/моль;
эквивалент соли по формуле: Э = М(соли)
/ число атомов металла * валентность
металла,
Э Al2(SO4)3==114г/моль.
Моляльность
раствора Сm
показывает
количество растворенного вещества,
находящееся в 1 кг растворителя:
,
где m2
– масса растворителя, кг; n
– количество растворенного вещества,
моль.
Пример
1.
Вычислить молярность и нормальность
40 %-го раствора фосфорной кислоты,
плотность которого 1,25 г/см3.
Объем раствора 1л.
Решение.
Для расчета молярности и нормальности
раствора найдем массу фосфорной кислоты
в 1 л (1000 мл) 40 %-го раствора:
w
= m1
· 100/V
∙ r;
.Молярная
масса Н3РO4
равна 98 г/моль, следовательно,
=
500/98 = 5,1 моль/л.
Молярная
масса эквивалента Н3РO4
равна 98/3 = 32,7 г/моль.
Тогда
СН
= 500/32,7 =
1,53 моль/л.
Пример
2.
Вычислить
массовую долю КОН в 2н. растворе, плотность
которого 1,08 г/см3.
Решение.
Поскольку
нормальность рассчитывается на 1 л
раствора, найдем массу растворенного
вещества в 1 л:
СН=
m1/Э∙V;
ЭKOH
= 56 г/моль;
mКОН=2∙56∙1=112
г.
Теперь
вычислим массовую доли КОН в растворе,
содержащем 112
г
гидроксида калия:
w=
m1∙100/V∙r=112∙100/1000∙1,08=10,4
%.
Пример 3.
На нейтрализацию 50 см3
раствора кислоты израсходовано 25 см3
0,5 н. раствора щелочи. Чему равна молярная
концентрация эквивалентов кислоты?
Решение.
Так как вещества взаимодействуют между
собой в эквивалентных соотношениях, то
растворы равной молярной концентрации
эквивалентов реагируют в равных объемах.
При разных молярных концентрациях
эквивалентов объемы растворов реагирующих
веществ обратно пропорциональны их
нормальностям, т.е.
V1:
V2
= С2
: С1
или V1∙
С1
= V2
∙
С2
50С1
= 25 • 0,5; откуда С1
= 25 • 0,5 / 50 = 0,25н.
Задание:
решить следующие задачи, принимая объем
раствора равным
1 л:
|
Вариант |
Вещество |
Концентрация |
Плотность |
Вычислить |
|
121 |
Na2CO3 |
0,30 |
1,030 |
Процентную |
|
122 |
HNO3 |
9,0 |
1,275 |
Процентную |
|
123 |
NH4Cl |
10 |
1,028 |
Молярную |
|
124 |
Al2(SO4)3 |
0,55 |
1,176 |
Процентную |
|
125 |
HNO3 |
2 |
— |
Нормальную |
|
126 |
HCl |
15,0 |
1,073 |
Нормальную |
|
127 |
H2SO4 |
13,0 |
1,680 |
Процентную |
|
128 |
H3PO4 |
44,0 |
1,285 |
Нормальную |
|
129 |
HClO4 |
9,0 |
1,150 |
Процентную |
|
130 |
H2SO4 |
2 |
— |
Нормальную |
|
131 |
CH3COOH |
34,0 |
1,043 |
Молярную |
|
132 |
BaCl2 |
2,30 |
1,203 |
Процентную |
|
133 |
K2CO3 |
4 |
— |
Нормальную |
|
134 |
CuSO4 |
14,0 |
1,155 |
Нормальную |
|
135 |
FeCl3 |
1,90 |
— |
Нормальную |
|
136 |
K2CO3 |
6,0 |
1,567 |
Процентную |
|
137 |
NaCl |
3 |
— |
Молярную |
|
138 |
NaCl |
20 |
1,148 |
Молярную |
|
139 |
HClO4 |
4,0 |
1,230 |
Процентную |
|
140 |
K2CO3 |
3 |
— |
Нормальную |
Задание: решить
следующие задачи
|
№ задачи |
|
|
141 |
На |
|
142 |
Смешали |
|
143 |
Определить |
|
144 |
Смешали |
|
145 |
Для |
|
146 |
Смешали |
|
147 |
На |
|
148 |
Смешали |
|
149 |
На |
|
150 |
Вычислить |
|
151 |
Определить |
|
152 |
Вычислить |
|
153 |
Определить |
|
154 |
Определить |
|
155 |
Вычислить |
|
156 |
Вычислить |
|
157 |
Определить |
|
158 |
Смешали |
|
159 |
Определить |
|
160 |
Вычислить |
Соседние файлы в папке му по химии
- #
- #
- #
- #
- #
- #
- #
Концентрация растворов. Растворы неэлектролитов. Растворимость
Задача:
Расчеты по процентной концентрации растворов. Формула, выражающая процентную концентрацию раствора —
где 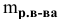
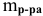
Задача:
Рассчитать процентную концентрацию раствора, полученного растворением 80 г сахара в 160 г воды.
Решение:
Задача:
Рассчитать массы поваренной соли и воды, необходимые для приготовления 250 г 2,5%-ного раствора.
Решение:
Задача:
Рассчитать концентрацию раствора, полученного смешением З00 г 10%-ного раствора хлороводорода и 400г 20%-ного раствора хлороводорода.
Решение:
Определяем массы растворенной 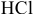
После смешивания
Определяем концентрацию полученного раствора:
Задача:
Какова концентрация серной кислоты в растворе, полученном смешиванием 200г 10%-ного раствора серной кислоты и 100г 5%-ного раствора сульфата натрия?
Решение:
Масса полученного раствора определяется как сумма масс смешанных растворов:
Далее определим концентрацию серной кислоты в полученном растворе:
Задача:
Расчеты по молярной концентрации (молярности) раствора.
Формула для расчета молярности раствора —
где С — молярность раствора, моль/л;
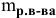
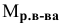
V — объем раствора, мл; если объем выражается в литрах, тогда в формуле исчезает коэффициент 1000.
Задача:
Какая масса серной кислоты необходима для приготовления 2 л 2-молярного раствора?
Решение:
Задача:
250 мл раствора содержат 7г КОН. Какова молярность этого раствора?
Решение:
Задача:
Расчеты по нормальной концентрации (нормальности) раствора.
Для расчета нормальности пользуемся следующей формулой:
где 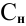
Задача:
Какая масса фосфорной кислоты необходима для приготовления 2 л 0,1 н раствора?
Решение:
Задача:
Расчеты по разбавлению растворов.
Выведем формулу для расчетов при разбавлении растворов, учитывая, что концентрация как исходного, так и приготовленного растворов может быть выражена любым способом 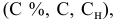
Для раствора, концентрация которого выражена в процентах,
а так как
то
где 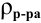
Для молярной концентрации
Для нормальной концентрации
Приравниваем правые части уравнений:
Задача:
Сколько миллилитров 98%-ного раствора серной кислоты
(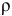
Решение:
Воспользуемся первым членом приведенного выше уравнения для концентрированного исходного раствора кислоты и третьим членом — для приготовления разбавленного раствора серной кислоты:
где С% = 98 %;
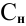
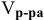
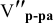
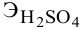
Отсюда
Задача:
Расчеты по переходу от одного способа выражения концентрации данного раствора к другому.
При переходе от одной концентрации данного раствора к другой остаются постоянными не только масса растворенного вещества, но и объем раствора, т.е.
Предыдущая формула принимает следующий вид:
Задача:
Определить молярность 36,5%-ного раствора соляной кислоты (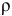
Решение:
Воспользуется первым и вторым членами последнего уравнения и выведем выражение для определения молярности:
Задача:
Расчеты по законам Рауля. Давление паров разбавленного раствора.
По закону Рауля, понижение давления пара 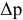
где 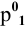
N — мольная доля растворенного вещества,
где 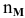
где 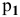
Отсюда
Задача:
Определить давление насыщенных паров раствора, содержащего 45 г глюкозы 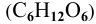
Решение:
Рассчитываем мольную долю растворенного вещества:
Определяем давление паров воды над раствором:
Задача:
Расчеты по понижению температуры замерзания растворов.
По закону Рауля понижение температуры замерзания прямо пропорционально моляльной концентрации раствора:
где 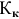
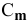
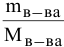
Отсюда
Задача:
Рассчитать температуру замерзания 3%-ного водного раствора этиленгликоля
Решение:
Выведем формулу для перехода от процентной концентрации к моляльности раствора.
Для процентной концентрации
Для моляльности
Отсюда
Если принять 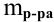
Находим моляльность рассматриваемого раствора:
Рассчитаем понижение температуры замерзания раствора:
Температура замерзания водного раствора
Задача:
Рассчитать температуру кипения 0,1 молярного водного раствора глюкозы (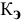
Решение:
Формула для перехода от молярной концентрации к моляльной —
Так как раствор разбавленный, то принимаем 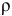
Определяем повышение температуры кипения раствора:
Температура кипения этого раствора
Задача:
Расчеты по уравнению химической реакции, протекающей в растворе.
Для химического уравнения общего вида
верно следующее соотношение числа эквивалентов:
Если участвующие в реакции вещества взяты в виде растворов и если их концентрации выражены:
а) для вещества А — С %;
б) для вещества В — С (молярность);
в) для вещества С — 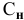
тогда массы и число эквивалентов каждого из веществ, находящихся в определенных объемах растворов этих веществ, определяются по формулам:
Так как числа эквивалентов, участвующих в реакции веществ, равны между собой, то можно записать:
Если концентрации участвующих в реакции веществ выражены в нормальности, то формула для расчетов приобретает вид:
Задача:
Какой объем 0,2 н раствора щелочи необходим для осаждения 2,708 г хлорида трехвалентного железа в виде гидроксида железа?
Решение:
Предложенный метод не требует обязательного написания уравнения реакции для осуществления таких расчетов.
Отсюда
Задача:
Для нейтрализации 20 мл 2-молярного раствора 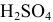
Решение:
Формула для расчета —
Так как 
откуда
Задача:
Какой объем 80 %-ного раствора 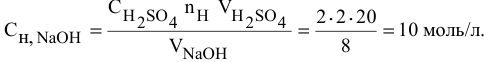
Решение:
Формула для расчета —
Так как 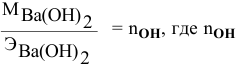
Отсюда
Задача:
Какой объем 0,2 н раствора щелочи необходим для реакции осаждения 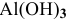
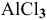
Решение:
Формула для расчета —
Задача:
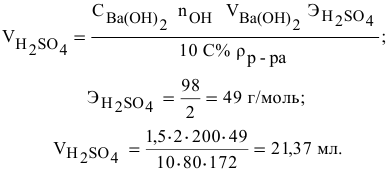
Смешивается 300 мл 0,5 М раствора хлорида бария со 100 мл 6 %-ного раствора серной кислоты (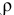
Решение:
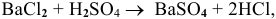
Так как указаны количества обоих реагирующих веществ, то необходимо определить вещество, взятое в избытке.
Таким образом, 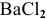
Дальнейший расчет производим по веществу, взятому в недостатке, т.е. по серной кислоте.
Так как
находим массу
откуда
Задача:
Для приготовления насыщенного раствора К.С1 при 40°С взято 50г воды и 20г КС1. Какова растворимость К.С1 в воде при данной температуре?
Решение:
Задача:
В 300г горячей воды растворено 219г 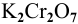
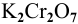
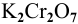
Решение:
Определяем, сколько может быть растворено 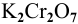
Откуда
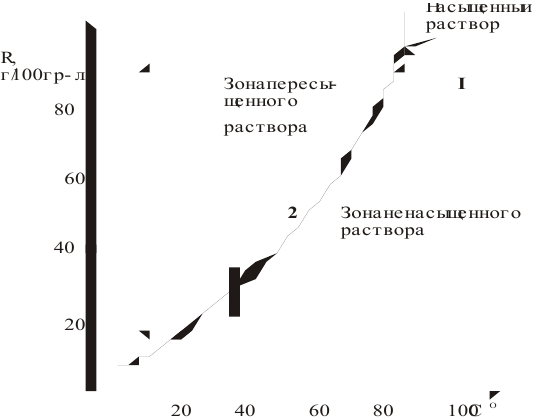
Масса кристаллов — это разность массы растворенного вещества в горячем растворе и массы растворенного вещества в охлажденном растворе (рис.З):
Рис. 3 — Графическое изображение процесса выпадения кристаллов при охлаждении раствора:
1 — участок охлаждения ненасыщенного раствора от заданной температуры до температуры образования насыщенного раствора;
2 — участок охлаждения насыщенного раствора до заданной температуры с уменьшением растворимости вещества, что приводит к его кристаллизации (в данном случае мы предполагаем, что пересыщенный раствор не образуется).
Эти задачи взяты со страницы решения задач по неорганической химии:
Задачи с решением по неорганической химии
Возможно эти страницы вам будут полезны: