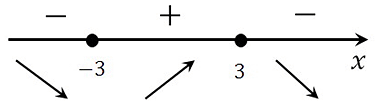
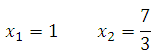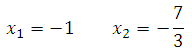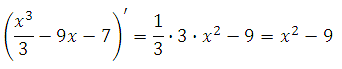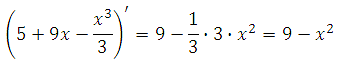Пришло время в данном разделе рассмотреть степенные функции. На блоге уже представлены задания на нахождение точек максимума и минимума различных функций, а именно: функций с числом е, с логарифмами, тригонометрические, рациональные.
Алгоритм нахождения данных точек оговаривался уже неоднократно, кратко повторюсь:
1. Находим производную функции.
2. Находим нули производной (приравниваем производную к нулю и решаем уравнение).
3. Далее строим числовую ось, на ней отмечаем найденные точки и определяем знаки производной на полученных интервалах. *Это делается путём подстановки произвольных значений из интервалов в производную.
4. Далее делаем вывод.
Если вы совсем не знакомы со свойствами производной для исследования функций, то обязательно изучите статью «Исследование функций. Это нужно знать!».Также повторите таблицу производных и правила дифференцирования (имеются в этой же статье). Рассмотрим задачи:
77431. Найдите точку максимума функции у = х3–5х2+7х–5.
Найдём производную функции:
Найдем нули производной:
3х2 – 10х + 7 = 0
Решая квадратное уравнение получим:
*Это точки возможного максимума (минимума) функции.
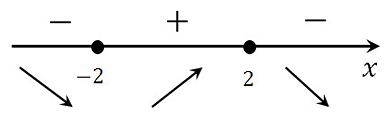
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(0)‘ = 3∙02 – 10∙0 + 7 = 7 > 0
у(2)‘ = 3∙22 – 10∙2 + 7 = – 1< 0
у(3)‘ = 3∙32 – 10∙3 + 7 = 4 > 0
В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 1
77432. Найдите точку минимума функции у = х3+5х2+7х–5.
Найдём производную функции:
Найдем нули производной:
3х2 + 10х + 7 = 0
Решая квадратное уравнение получим:
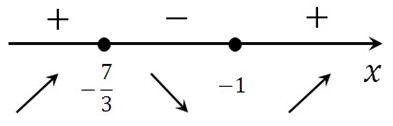
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)‘ = 3∙(–3)2 + 10∙(–3) + 7 = 4 > 0
у(–2)‘= 3∙(–2)2 + 10∙(–2) + 7 = –1 < 0
у(0)‘= 3∙02 – 10∙0 + 7 = 7 > 0
В точке х = –1 производная меняет свой знак с отрицательного на положительный, значит это есть искомая точка минимума.
Ответ: –1
77435. Найдите точку максимума функции у = 7+12х–х3
Найдём производную функции:
Найдем нули производной:
12 – 3х2 = 0
х2 = 4
Решая уравнение получим:
*Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)‘=12 – 3∙(–3)2 = –15 < 0
у(0)‘=12 – 3∙02 = 12 > 0
у(3)‘=12 – 3∙32 = –15 < 0
В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 2
*Для этой же функции точкой минимума является точка х = – 2.
77439. Найдите точку максимума функции у = 9х2– х3.
Найдём производную функции:
Найдем нули производной:
18х –3х2 = 0
3х(6 – х) = 0
Решая уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–1)‘=18 (–1) –3 (–1)2 = –21< 0
у(1)‘=18∙1 –3∙12 = 15 > 0
у(7)‘=18∙7 –3∙72 = –1< 0
В точке х = 6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 6
*Для этой же функции точкой минимума является точка х = 0.
77443. Найдите точку максимума функции у = (х3/3)–9х–7.
Найдём производную функции:
Найдем нули производной:
х2 – 9 = 0
х2 = 9
Решая уравнение получим:
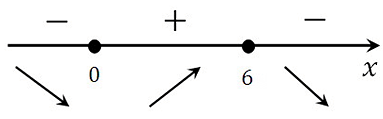
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)‘= (–4)2 – 9 > 0
у(0)‘= 02 – 9 < 0
у(4)‘= 42 – 9 > 0
В точке х = – 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: – 3
*Для этой же функции точкой минимума является точка х = 3.
77443. Найдите точку максимума функции у = 5+9х– (х3/3).
Найдём производную функции:
Найдем нули производной:
9 – х2 = 0
х2 = 9
Решая уравнение получим:
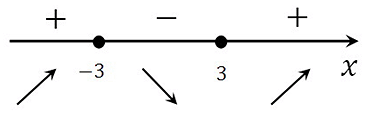
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)‘= 9 – (–4)2 < 0
у(0)‘= 9 – 02 > 0
у(4)‘= 9 – 42 < 0
В точке х = 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 3
*Для этой же функции точкой минимума является точка х = – 3.
77419. Найдите точку максимума функции у = х3– 48х+17. Решение.
77423. Найдите точку максимума функции у = х3–3х2+2. Решение.
77427. Найдите точку максимума функции у = х3+2х2+х+3. Решение.
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
I’m looking to program a Python function that takes in 6 variables, a, b, c, d, e, f, where a, b is the interval to compute on (e.g. [1, 3], all real numbers), and c, d, e, f are the coefficients of the cubic polynomial, i.e. f(x) = cx^3 + dx^2 + ex + f, and returns the local min/max on the interval [a, b].
I have a rough idea (although the computing time would be bad) of how to program this, where I create a new list of steps 0.01 or something similarly small from a to b, evaluate f at each value, then simply return the min/max of the list. This would take very long for a, b values that are very far apart.
What is the best way to go about making this? Are there any outside libraries for scientific/mathematical computing? Thank you.
Кубическая парабола задается функцией y=x3
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции 
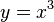
Перечислим основные свойства функции
1.Область определения – любое действительное число:.
2.Область значений – любое действительное число:.
3.Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием .
Производная кубической функции 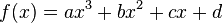
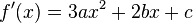





Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Загрузить PDF
Загрузить PDF
Во многих задачах требуется вычислить максимальное или минимальное значение квадратичной функции. Максимум или минимум можно найти, если исходная функция записана в стандартном виде: 

-
1
Запишите функцию в стандартном виде. Квадратичная функция — это функция, уравнение которой включает переменную
. Уравнение может включать или не включать переменную
. Если уравнение включает переменную с показателем степени больше 2, оно не описывает квадратичную функцию. Если нужно, приведите подобные члены и переставьте их, чтобы записать функцию в стандартном виде.[1]
-
2
-
3
-
4
Найдите соответствующее значение f(x). Подставьте найденное значение «x» в исходную функцию, чтобы найти соответствующее значение f(x). Так вы найдете минимум или максимум функции.
-
5
Реклама
-
1
Запишите квадратичную функцию через координаты вершины параболы. Такое уравнение имеет следующий вид:[3]
-
2
-
3
Найдите минимальное или максимальное значение функции. Если функция записана через координаты вершины параболы, минимум или максимум равен значению коэффициента
. В приведенных выше примерах:
-
4
Реклама
-
1
Сначала рассмотрим стандартный вид уравнения. Запишите квадратичную функцию в стандартном виде:
. Если нужно, приведите подобные члены и переставьте их, чтобы получить стандартное уравнение.[5]
- Например:
.
- Например:
-
2
Найдите первую производную. Первая производная квадратичной функции, которая записана в стандартном виде, равна
.[6]
-
3
Производную приравняйте к нулю. Напомним, что производная функции равна угловому коэффициенту функции в определенной точке. В минимуме или максимуме угловой коэффициент равен нулю. Поэтому, чтобы найти минимальное или максимальное значение функции, производную нужно приравнять к нулю. В нашем примере:[7]
-
4
Найдите «x». С помощью математических операций изолируйте «x», чтобы найти значение этой переменной, когда производная равна нулю. Так вы вычислите координату «x» вершины параболы, в которой находится ее максимум или минимум.[8]
-
5
-
6
Запишите ответ. Вы вычислили максимум или минимум функции. В нашем примере
координаты вершины равны
. Коэффициент
положительный, поэтому парабола направлена вверх. Следовательно, минимальное значение функции – это координата «у» вершины, которая равна
.[10]
Реклама
Советы
- Ось симметрии параболы описывается уравнением x=h.
Реклама
Об этой статье
Эту страницу просматривали 96 245 раз.