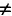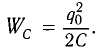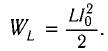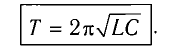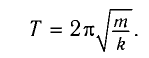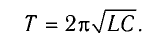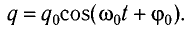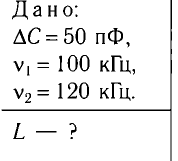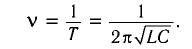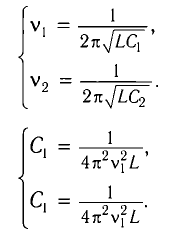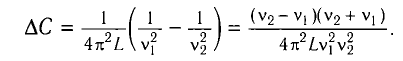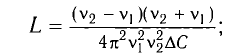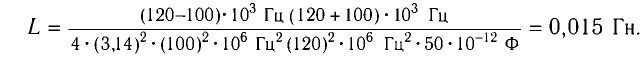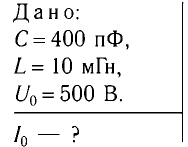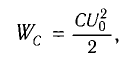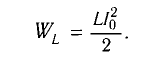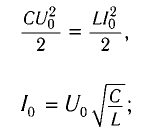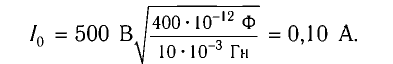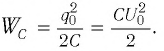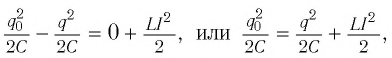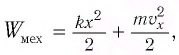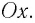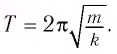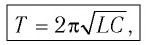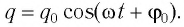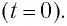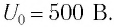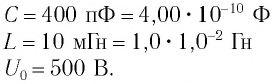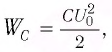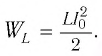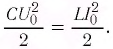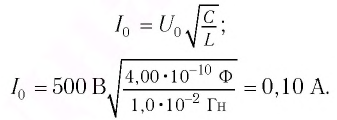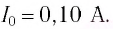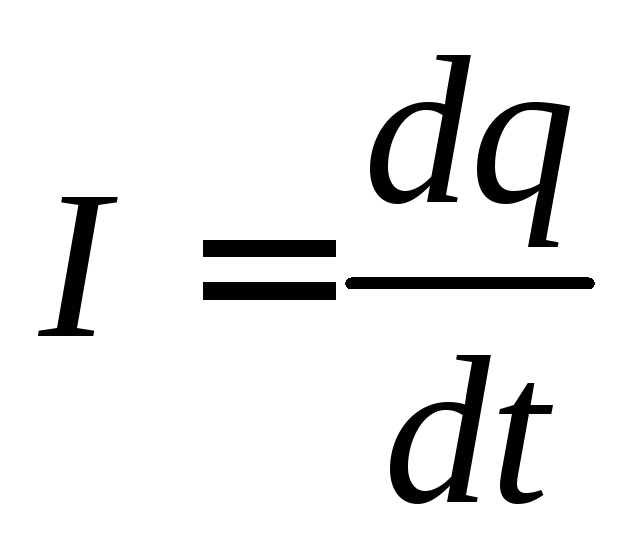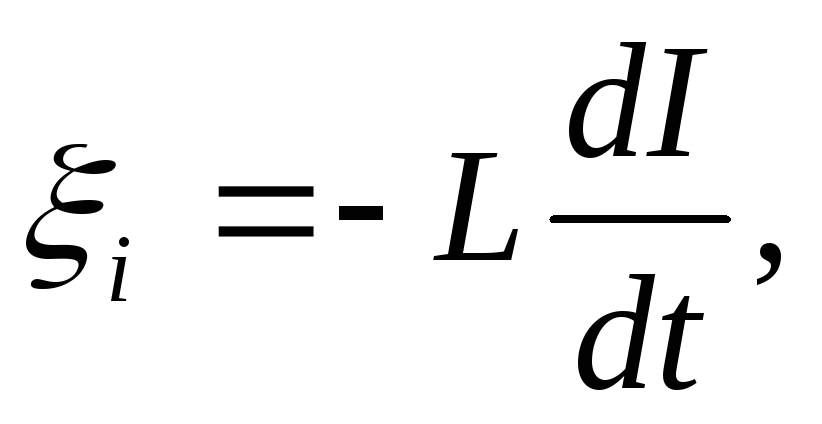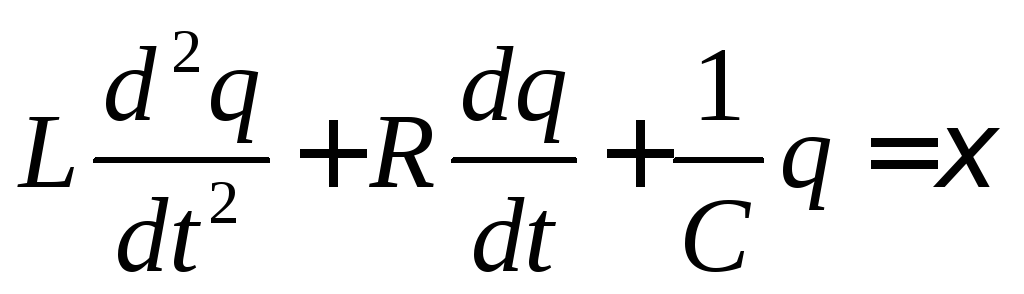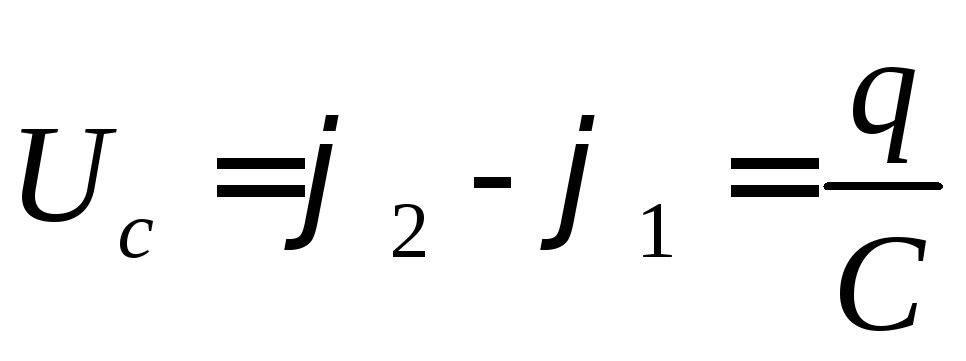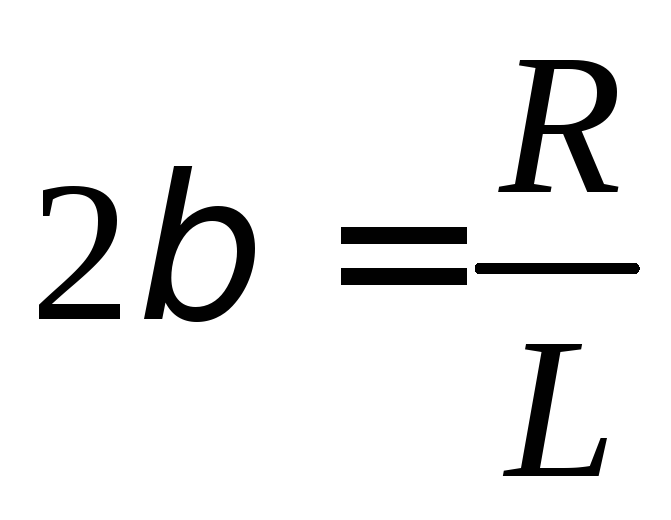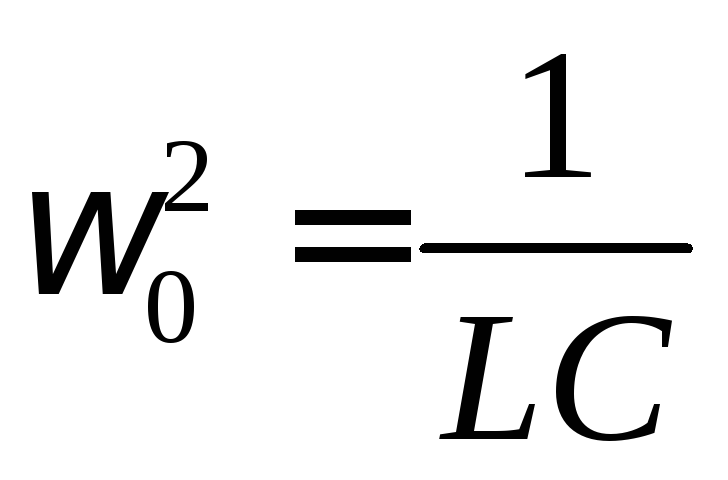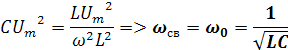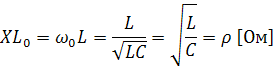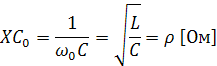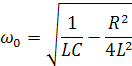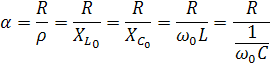Условие задачи:
Определите максимальный ток в контуре, если длина электромагнитной волны в вакууме, на которую настроен колебательный контур – 75,36 м, а максимальный заряд конденсатора равен 10 нКл.
Задача №9.13.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(lambda=75,36) м, (q_m=10) нКл, (I_m-?)
Решение задачи:
Известно, что максимальная энергия магнитного поля тока катушки колебательного контура равна максимальной энергии электрического поля конденсатора этого же контура, поэтому из закона сохранения энергии следует, что:
[frac{{LI_m^2}}{2} = frac{{q_m^2}}{{2C}}]
Откуда максимальный ток в контуре (I_m) равен:
[{I_m} = frac{{{q_m}}}{{sqrt {LC} }};;;;(1)]
Частоту электромагнитных волн, излучаемых колебательным контуром, можно определить по формуле:
[nu = frac{1}{{2pi sqrt {LC} }};;;;(2)]
В этой формуле (L) – индуктивность катушки, (C) – электроемкость конденсатора.
Известно, что электромагнитные волны распространяются со скоростью света (c) (в вакууме она равна 3·108 м/с). Между скоростью распространения электромагнитных волн (скоростью света (c)), их частотой колебаний (nu) и длиной волны (lambda) существует следующее соотношение:
[c = lambda nu ]
Откуда длина волны (lambda) равна:
[lambda = frac{c}{nu }]
В эту формулу поставим выражение (2):
[lambda = 2pi csqrt {LC} ]
Отсюда следует, что:
[sqrt {LC} = frac{lambda }{{2pi c}}]
Учитывая последнее полученное равенство, формула (1) примет вид:
[{I_m} = frac{{2pi c{q_m}}}{lambda }]
Посчитаем численный ответ задачи:
[{I_m} = frac{{2 cdot 3,14 cdot 3 cdot {{10}^8} cdot 10 cdot {{10}^{ – 9}}}}{{75,36}} = 0,25;А]
Ответ: 0,25 А.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.13.3 При изменении тока в катушке индуктивности на 1 А за 0,6 с в ней индуцируется ЭДС
9.13.5 В каком диапазоне длин волн можно улавливать радиопередачи приемником
9.13.6 Радиопередатчик искусственного спутника Земли работает на частоте 20 МГц
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
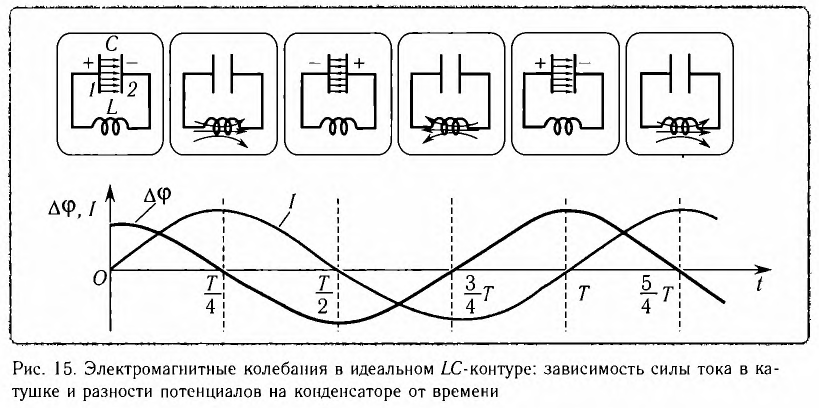
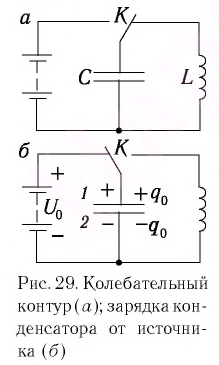
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +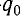

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения 
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 
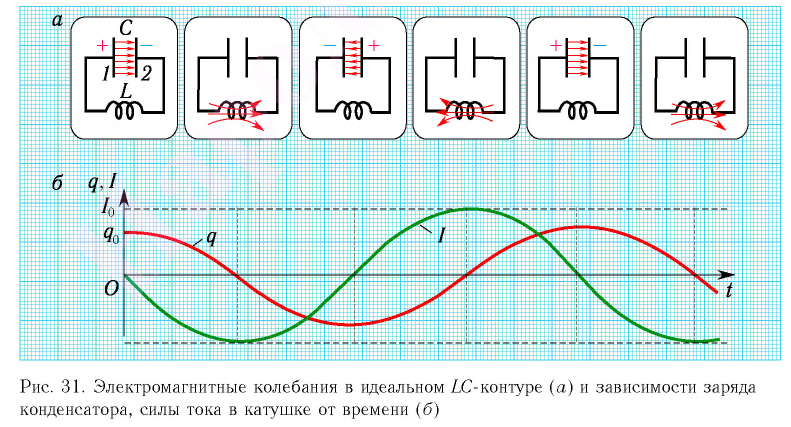
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений 

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
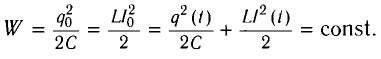
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
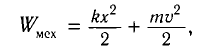
и период его колебаний
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора 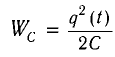
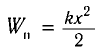
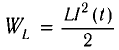
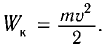
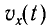
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на 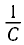
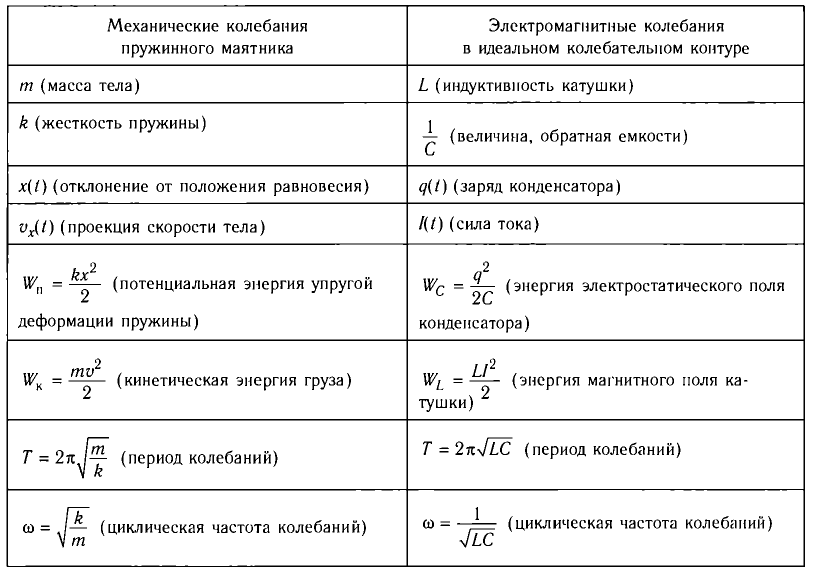
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы 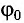
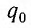
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на 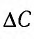
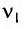
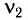
Решение
Частота колебаний в контуре
Поскольку частота колебаний в контуре увеличилась (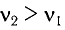
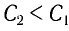
Из условия задачи получаем систему уравнений
Откуда
Вычитая из первого уравнения второе, получаем
Откуда находим
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока 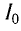
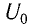
Решение
Максимальная энергия электростатического поля конденсатора
а максимальная энергия магнитного поля катушки
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 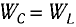
откуда
Ответ: 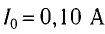
Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 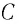
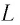
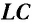
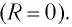
Подключив (при помощи ключа 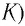
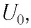
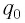
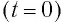
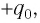
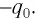
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 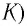
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 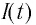
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 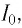
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где 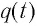
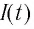
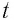
В момент полной разрядки конденсатора 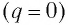
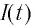
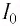
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения 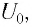
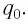
Таким образом, в идеальном 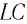
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 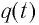
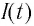
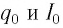
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 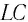
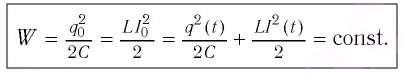
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где 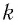
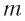
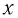
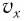
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 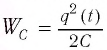
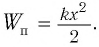
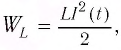
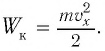
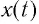
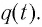
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 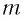
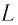
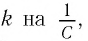
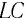
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 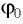
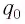
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 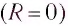
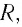
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью 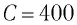
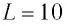
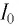
Дано:
Решение
Максимальная энергия электростатического поля конденсатора:
а максимальная энергия магнитного поля катушки:
Так как контур идеальный 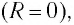
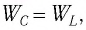
Отсюда
Ответ:
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Распространение механических волн в средах
- Электромагнитное поле
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
Колебательный контур состоит из катушки индуктивностью 1 мГн к конденсатора емкостью 10 мкФ. Определить максимальную силу тока в контуре, если конденсатор заряжен до максимального напряжения 100 В
Закон сохранения энергии для колебательного контура:
$frac{CU^2}{2}=frac{LI^2}{2}$
$I=U*sqrt{frac{C}{L}}=100*sqrt{frac{10*10^{-6}}{1*10^{-3}}}=10;A$
«Гармонические колебания» — Называются. 1. Разность фаз равна нулю или четному числу?, то есть. Рисунок 4. Тема 2 СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ. 2.3 Сложение взаимно перпендикулярных колебаний. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д. Рисунок 5. Тогда. ?1 – фаза 1-го колебания. — Результирующее колебание, тоже гармоническое, с частотой?:
«Частота колебаний» — Инфразвук. Какими общими свойствами обладают все источники звука? От чего зависит высота звука? Вспомнить все, что знаем о звуке. Каждый из нас знаком с таким звуковым явлением, как эхо. Что называется чистым тоном? Содержание проекта: Звук камертона является чистым тоном. Подготовила ученица 9 класса: Смольянинова Екатерина.
«Физика Колебания и волны» — Уметь: Рассчитывать период и частоту колебаний маятника, ускорение свободного падения с помощью математического маятника, длину волны. Обобщение темы Литература для работы: 1.Физика-9 – учебник 2.Физика -8 .автор Громов 3. Физика, человек, окружающая среда. (приложение к учебнику). Изучив тему.Колевания и волны, ты должен…
«Свободные колебания» — Формула Томпсона. Если Um = const , то амплитуда вынужденных колебаний силы тока зависит от? : Магнитный поток Ф сквозь плоскость рамки: Где i и q – сила тока и электрический заряд в любой момент времени. Рис.1. Циклическая частота свободных электромагнитных колебаний в контуре: Из закона Ома для участка цепи переменного тока:
«Механические колебания» — Вынужденные. Вынужденные колебания. Волны. Выполнила: ученица 11 класса «А» Олейникова Юлия. Поперечные. Гармонические колебания. Свободные. Упругие волны – механические возмущения, распространяющиеся в упругой среде. Механические колебания и волны. Колебания — движения или процессы, которые характеризуются определенной повторяемостью во времени.
«Резонанс» — Из-за огромной массы и инерционности жидкость реагирует на сотрясения с запозданием. Акустический резонанс — трубка с водой и камертон без резонатора. Очень важно грамотно установить и настроить все компоненты системы. Биение сердца, сокращение желудка, деятельность кишечника имеют колебательный характер.
Всего в теме
10 презентаций
1.Колебательный
контур.
2 Уравнение
колебательного контура
3.
Свободные колебания в контуре
4.Свободные
затухающие колебания в контуре
5.
Вынужденные электрические колебания.
6.
Резонанс в последовательном контуре
7.
Резонанс в параллельном контуре
8.
Переменный ток
1. 5.1. Колебательный контур.
Выясним,
каким образом в колебательном контуре
возникают и поддерживаются электрические
колебания.
Пусть вначале
верхняя обкладка конденсатора
заряжена положительно
,а нижняя
отрицательно
(рис. 11.1,а).
При
этом вся энергия колебательного контура
сосредоточена в конденсаторе.
Замкнем ключ К..
Конденсатор начнет разряжаться, и
через катушкуL
потечет ток. Электрическая энергия
конденсатора начнет превращаться в
магнитную энергию катушки. Этот процесс
закончится, когда конденсатор полностью
разрядится, а ток в цепи достигнет
максимума (рис. 11.1,б).
С этого момента
ток, не меняя направления, начнет
убывать. Однако он прекратится не сразу
— его будет поддерживать э. д. с.
самоиндукции. Ток будет перезаряжать
конденсатор, возникнет электрическое
поле, стремящееся ослабить ток. Наконец,
ток прекратится, а заряд на конденсаторе
достигнет максимума.
С этого момента
конденсатор начнет разряжаться опять
ток потечет в обратном направлении и
т. д. — процесс будет повторяться
В контуре при
отсутствии сопротивления
проводников
будут совершатьсястрого периодические
колебания
. В ходе процесса периодически
изменяются: заряд на обкладках
конденсатора, напряжение на нем и ток
через катушку.
Колебания
сопровождаются взаимными превращениями
энергии электрического и магнитного
полей.
Если же сопротивление
проводников
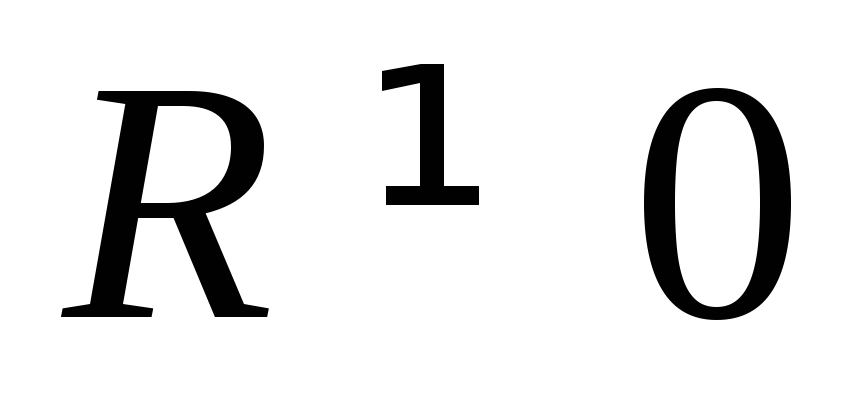
то помимо описанного процесса будет
происходить преобразование электромагнитной
энергии в джоулеву теплоту.
Сопротивление
проводников цепи
R
принято называть
активным
сопротивлением.
1.5.2. Уравнение колебательного контура
Найдем уравнение
колебаний в контуре, содержащем
последовательно соединенные конденсатор
С,
катушку индуктивностиL
,
активное сопротивлениеR
и внешнюю переменную э. д. с.(рис. 1.5.1).
Выберем
положительное направление обхода
контура, например по часовой стрелке.
Обозначим
черезq
заряд той
обкладки конденсатора, направление от
которой к другой обкладке совпадает с
выбранным положительным направлением
обхода контура.
Тогда ток в контуре
определяется как
(1)
Следовательно,
если I
>
О, то иdq
>
0, и наоборот
(знак
I
совпадает
со знакомdq
).
Согласно закону
Ома для участка цепи 1
RL
2
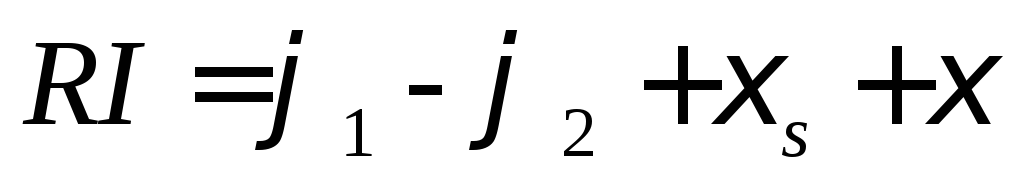
(2),
где
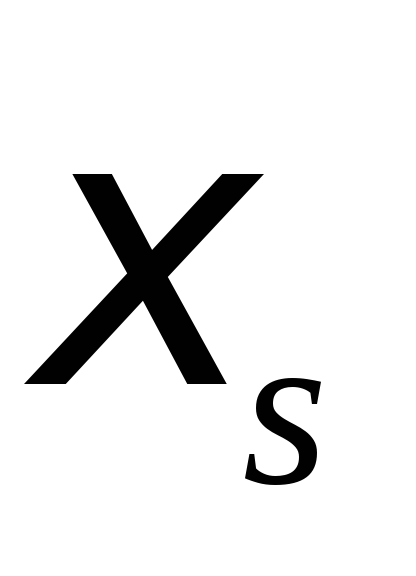
э. д. с. самоиндукции.
В нашем случае
(знак q
должен совпадать со знаком разности
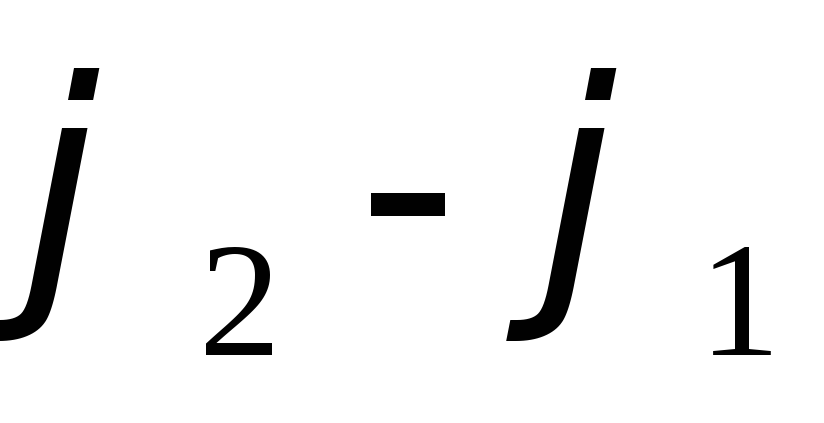
ибоС >
0).
Поэтому уравнение
(2) можно переписать в виде
или с учетом (1)
как
Это и есть уравнение
колебательного контура
—
линейное дифференциальное неоднородное
уравнение второго порядка с постоянными
коэффициентами. Найдя с помощью этого
уравненияq
(t
),
мы можем легко вычислить- напряжение
на конденсаторе
и силу токаI- по
формуле (1).
Уравнению
колебательного контура можно придать
иной вид:
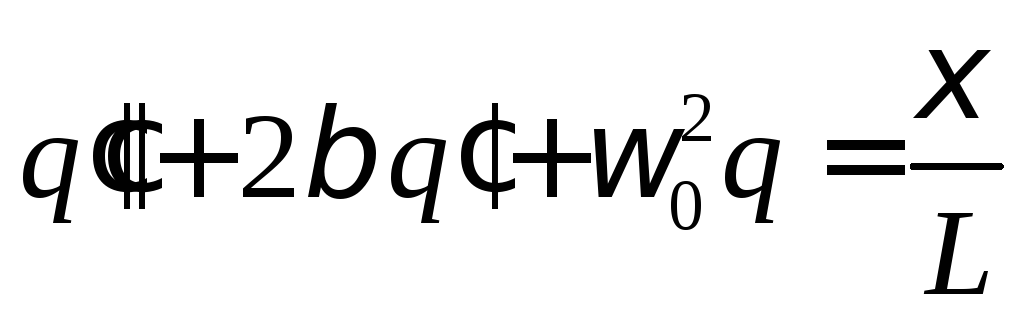
где
введены обозначения
.
(6)
Величину
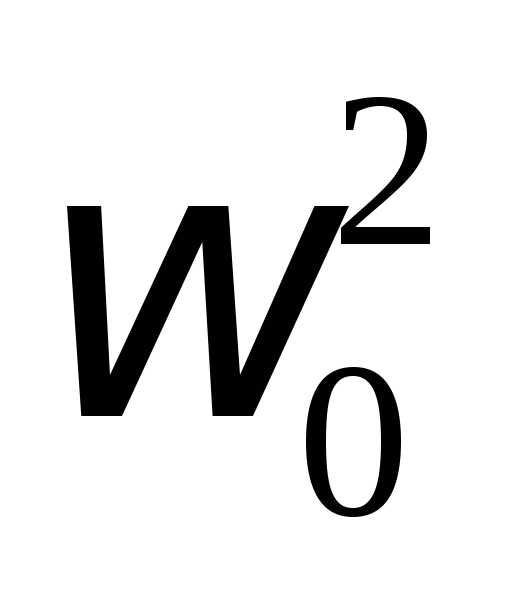
называютсобственной
частотой
контура,
β
—
коэффициентом
затухания.
Если
ξ = 0, то колебания принято называть
свободными.
—
При R
= О они будут
незатухающими,
—
при
R
≠0 —
затухающими.
Колебательный контур
называется
идеальным, если он состоит из катушки
и емкости и в нем нет сопротивления
потерь.
Рассмотрим
физические процессы в следующей цепи:
1 Ключ стоит в положении 1. Конденсатор
начинает заряжаться, от источника
напряжения и в нем накапливается энергия
электрического поля,
т.е.конденсатор становится источником
электрической энергии.
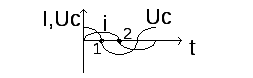
2. Ключ в положении 2. Конденсатор начнет
разряжаться. Электрическая энергия,
запасенная в конденсаторе переходит в
энергию магнитного поля катушки.
Ток в цепи достигает максимального
значения(точка 1). Напряжение на обкладках
конденсатора уменьшается до нуля.
В период от точки 1 до точки 2 ток в контуре
уменьшается до нуля, но как только он
начинает уменьшатся, то уменьшается
магнитное поле катушки и в катушке
индуцируется ЭДС самоиндукции, который
противодействует уменьшению тока,
поэтому он уменьшается до нуля не
скачкообразно, а плавно. Так как возникает
ЭДС самоиндукции, то катушка становится
источником энергии. От этой ЭДС конденсатор
начинает заряжаться, но с обратной
полярностью (напряжение конденсатора
отрицательное) (в точке 2 конденсатор
вновь заряжается).
Вывод:
в цепи LC происходит
непрерывное колебание энергии между
электрическим и магнитным полями,
поэтому такая цепь называется колебательным
контуром.
Получившиеся колебания называются
свободными
илисобственными
,
поскольку они происходят без помощи
постороннего источника электрической
энергии, внесенной ранее в контур (в
электрическое поле конденсатора). Так
как емкость и индуктивность идеальны
(нет сопротивления потерь) и энергия из
цепи не уходит, амплитуда колебаний с
течением времени не меняется и колебания
будут незатухающими
.
Определим угловую частоту свободных
колебаний:
Используем равенство энергий электрического
и магнитного полей
Где ώ угловая частота свободных
колебаний.
[
ώ
]=1/с
f
0=
ώ
/2π
[Гц].
Период свободных колебаний Т0=1/f
.
Частоту свободных колебаний называют
частотой собственных колебаний контура.
Из выражения: ώ²LC=1
получимώL=1/Cώ
, следовательно, при токе в контуре с
частотой свободных колебаний индуктивное
сопротивление равно емкостному
сопротивлению.
Характеристические сопротивления.
Индуктивное или емкостное сопротивление
в колебательном контуре при частоте
свободных колебаний называется
характеристическим сопротивлением.
Характеристическое сопротивление
вычисляется по формулам:
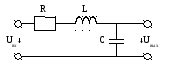
5.2 Реальный колебательный контур
Реальный колебательный контур обладает
активным сопротивлением, поэтому при
воздействии в контуре свободных колебаний
энергия предварительно заряженного
конденсатора постепенно тратится,
преобразуясь в тепловую.
Свободные колебания в контуре являются
затухающими, так как в каждый период
энергия уменьшается и амплитуда колебаний
в каждый период будет уменьшаться.
Рисунок — реальный колебательный контур.
Угловая частота свободных колебаний в
реальном колебательном контуре:
Если R=2… , то угловая частота равна нулю,
следовательно свободные колебания в
контуре не возникнут.
Таким образом колебательным контуром
называется электрическая цепь состоящая
из индуктивности и емкости и обладающая
малым активным сопротивлением, меньшим
удвоенного характеристического
сопротивления, что обеспечивает обмен
энергией между индуктивностью и емкостью.
В реальном колебательном контуре
свободные колебания затухают тем
быстрее, чем больше активное сопротивление.
Для характеристики интенсивности
затухания свободных колебаний используется
понятие «затухание контура» — отношение
активного сопротивления к характеристическому.
На практике используют величину, обратную
затуханию – добротность контура.
Для получения незатухающих колебаний
в реальном колебательном контуре
необходимо в течение каждого периода
колебаний пополнять электрическую
энергию на активном сопротивлении
контура в такт с частотой собственных
колебаний. Это осуществляется с помощью
генератора.
Если подключить колебательный контур
к генератору переменного тока, частота
которого отличается от частоты свободных
колебаний контура, то в цепи протекает
ток с частотой равной частоте напряжения
генератора. Эти колебания называют
вынужденным.
Если частота генератора отличается от
собственной частоты контура, то такой
колебательный контур является
ненастроенным относительно частоты
внешнего воздействия, если же частоты
совпадают, то настроенным.
Задача:
Определить индуктивность, угловую частоту контура, характеристическое
сопротивление, если емкость колебательного
контура 100 пФ, частота свободных колебаний
1,59 МГц.
Решение:
Тестовые задания:
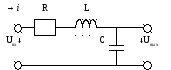
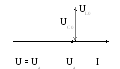
Тема занятия 8: РЕЗОНАНС НАПРЯЖЕНИЙ
Резонанс напряжений – явление возрастания
напряжений на реактивных элементах,
превышающих напряжение на зажимах цепи
при максимальном токе в цепи, которое
совпадает по фазе с входным напряжением.
Условия возникновения резонанса:
Последовательное соединение LиCс генератором переменного
тока;
Частота генератора должна быть равна
частоте собственных колебаний контура, при этом характеристические сопротивления
равны;
Сопротивление должно быть меньше, чем
2ρ, так как только в этом случае в цепи
возникнут свободные колебания,
поддерживаемые внешним источником.
Полное сопротивление цепи:
так как равны характеристические
сопротивления. Следовательно, при
резонансе цепь носит чисто активный
характер, значит, входное напряжение,
и ток в момент резонанса совпадают по
фазе. Ток принимает максимальное
значение.
При максимальном значении тока напряжение
на участках L и C будут большими и равными
между собой.
Напряжение на зажимах цепи:
Рассмотрим следующие соотношения:
,
следовательно
Q
–
добротность
контура –при резонансе напряжения
показывает, во сколько раз напряжение
на реактивных элементах больше входного
напряжения генератора, питающего цепь.
При резонансе коэффициент передачи
последовательного колебательного
контура
резонанса.
Пример:
Uc=Ul=QU
=100В,
то есть напряжение на зажимах меньше
напряжений на емкости и индуктивности.
Это явление называется резонансом
напряжений
При резонансе, коэффициент передачи
равен добротности.
Построим векторную диаграмму напряжения
Напряжение на емкости равно напряжению
на индуктивности, следовательно
напряжение на сопротивлении равно
напряжению на зажимах и совпадает по
фазе с током.
Рассмотрим энергетический процесс в
колебательном контуре:
В цепи имеется обмен энергии между
электрическим полем конденсатора и
магнитным полем катушки. К генератору
энергия катушки не возвращается. От
генератора в цепь поступает такое
количество энергии, которое тратится
на резисторе. Это необходимо для того,
чтобы в контуре наблюдались незатухающие
колебания. Мощность в цепи только
активная.
Докажем это математически:
,
полная мощность цепи, которая равна
активной мощности.
Реактивная мощность.
8.1 Резонансная частота. Расстройка.
Lώ=l/ώC
, следовательно
,
угловая резонансная частота.
Из формулы видно, что резонанс наступает,
если частота питающего генератора равна
собственным колебаниям контура.
При работе с колебательным контуром
необходимо знать, совпадает ли частота
генератора и частота собственных
колебаний контура. Если частоты совпадают,
то контур остается
настроенным в резонанс, если не совпадает
– то в контуреприсутствует
расстройка.
Настроить колебательный контур в
резонанс можно тремя способами:
1 Изменять частоту генератора, при
значениях емкости и индуктивности
const, то есть изменяя частоту генератора
мы подстраиваем эту частоту под частоту
колебательного контура
2 Изменять индуктивность катушки, при
частоте питания и емкости const;
3 Изменять емкость конденсатора, при
частоте питания и индуктивности const.
Во втором и третьем способе изменяя
частоту собственных колебаний контура,
подстраиваем ее под частоту генератора.
При ненастроенном контуре частота
генератора и контура не равны, то есть
присутствует расстройка.
Расстройка – отклонение частоты от
резонансной частоты.
Существует три вида расстройки
:
Абсолютная – разность между данной
частотой и резонансной
Обобщенная – отношение реактивного
сопротивления к активному:
Относительная – отношение абсолютной
расстройки к резонансной частоте:
При резонансе все расстройки равны
нулю
, если частота генератора меньше
частоты контура, то расстройка считается
отрицательной,
Если больше – положительной.
Таким образом добротность характеризует
качество контура, а обобщенная расстройка-
удаленность от резонансной частоты.
8.2 Построение зависимостейX
,
X
L
,
X
C
отf
.
Задачи:
Сопротивление контура 15 Ом, индуктивность
636 мкГн, Емкость 600 пФ, напряжение питающей
сети 1,8 В. Найти собственную частоту
контура, затухание контура,
характеристическое сопротивление,
ток, активную мощность, добротность,
напряжение на зажимах контура.
Решение:
Напряжение на зажимах генератора 1 В,
частота питающей сети 1 МГц, добротность
100, емкость 100 пФ. Найти: затухание,
характеристическое сопротивление,
активное сопротивление, индуктивность,
частоту контура, ток, мощность, напряжения
на емкости и индуктивности.
Решение:
Тестовые задания:
Тема занятия 9 :
Входные и передаточные
АЧХ и ФЧХ последовательного колебательного
контура.
9.1 Входные АЧХ и ФЧХ.
В последовательном колебательном
контуре:
R – активное сопротивление;
X – реактивное сопротивление.
Электрическим колебательным контуром
называют замкнутую цепь, состоящую из конденсатора С
и катушки индуктивности L
(рис. 9.8). Периодически повторяющиеся изменения силы тока в катушке и напряжения на конденсаторе при отсутствии внешних воздействий называются свободными колебаниями.
При подключении к обкладкам заряженного конденсатора (рис. 9.8а
) катушки индуктивности в ней возникает ток. Если электрическое сопротивление катушки пренебрежимо мало, то энергия электрического поля W е
заряженного конденсатора начинает превращаеться в энергию магнитного поля W м
. Мгновенной раз-рядке конденсатора препятствует ЭДС самоиндукции, сдер-живающая процесс возрастания силы тока в катушке.
В тот мо-мент, когда конденсатор полностью разрядится, сила тока в катушке и энергия магнитного поля достигнут максимальных (амплитудных) значений (рис. 9.8б
). После разрядки конденсатора ток в катушке убывает, но это приводит к уменьшению магнитного потока, что вызывает появ-ление в катушке ЭДС самоиндукции и индукционного тока. Сейчас на-правление индукционного тока таково, что он препятствует умень-шению магнитного потока.
Конденсатор заряжается индукционным током катушки. Когда ток исчезнет, конденсатор окажется заряженным до первоначального значения заряда, но противоположного знака (рис. 9.8в
). После этого происходит следующий процесс перезарядки конденсатора током, протекающим в противоположном направлении (рис. 9.8г
), и возврат в исходное состояние после совершения одного полного колебания (рис. 9.8д
). В верхней части рисунка показаны значения времени соответ-ству-ющих состояний, выраженные в долях периода
Где w 0
— круговая (циклическая) частота колебаний в контуре.
Из закона сохранения энергии следует, что при отсутствии в контуре сопротивления максимальное значение энергии W e
электрического поля заряжен-ного конденсатора равно максимальному значению энергии магнитного поля W м
катушки: , откуда можно получить связь амплитудных значений тока в катушке и напряжения на конденсаторе: . Это отношение имеет размерность сопротивления, поэтому величину называют волновым,
или характеристическим
сопротивлением контура.
В реальном электрическом контуре из-за потерь энергии на нагревание проводников и диэлектриков энергия магнитного и электрического полей по-степенно превращается во внутреннюю энергию. Свободные электромагнитные колебания в контуре оказываются затухающими
.
Потери энергии в контуре можно учесть путем введения активного сопротивления (рис. 9.9). Поскольку потери в диэлектрике конденсатора малы, это сопротивление практически равно активному сопротивлению катушки индуктивности. Считая направление тока, заряжающего конденсатор, положительным, запишем закон Ома для участка цепи от отрицательно заряженной обкладки конденсатора 1
до положительно заряженной 2
. В соответствии с (2.13) получаем: .
Направление обхода контура от точки 1
к точке 2
совпадает с направлением тока, поэтому произведение iR
положительно. ЭДС самоиндукции по правилу Ленца отрицательна. Так как потенциал отрицательно заряженной пластины меньше, чем потенциал положительной, разность потенциалов (j 1 — j 2)
отрицательна: , где q
— заряд на конденсаторе. Изменение заряда конденсатора вызывается током, поэтому . С учетом вышеизложенного на основании закона Ома можно записать:
, или
, (9.8)
где b = R/2L
— коэффициент затухания, — собственная частота.
Дифференциальное уравнение (9.8) подобно уравнению, полученному для механического пружинного маятника (см. раздел «Механика»). Решение данного уравнения имеет вид: , (9.9)
где q 0
— амплитуда тока в начальный момент времени,
Частота затухающих колебаний. Из (9.9) следует, что уменьшение амплитуды со временем происходит по экспоненциальному закону (рис. 9.10). Частота затухающих колебаний меньше частоты собственных колебаний w 0
. Из (9.10) следует, что при большом затухании (b ³ w 0
) частота становится мнимой величиной. Это означает, что колебательного процесса не происходит и заряд конденсатора уменьшается до нуля без перезарядки. Такой процесс называется апериодическим
.
Выразим условие перехода от колебательного процесса к апериодическому через параметры цепи. Имеем: (R/2L) 2 ³ 1/LC
или .
Степень затухания колебаний принято характеризовать логариф-мичес-ким декрементом затуханияl
. Он равен логарифму натуральному двух амплитуд через период Т
:
или (9.11)
Еще одной характеристикой контура является добротность.
Она связана с логарифмическим декрементом затухания соотношением . Нетрудно показать, что при малом затухании, когда b << w 0
и w»
» w 0 ,
добротность выражается через параметры колебательного контура следующим образом: , (9.12)
то есть равна отношению характеристического сопротивления контура к активному сопротивлению потерь.