Как найти максимальный элемент каждой строки матрицы - AvtoShod.ru

Given a matrix, the task is to find the maximum element of each row.
Examples:

Input :  [1, 2, 3]
         [1, 4, 9]
         [76, 34, 21]

Output :
3
9
76

Input : [1, 2, 3, 21]
        [12, 1, 65, 9]
        [1, 56, 34, 2]
Output :
21
65
56

Method 1: The idea is to run the loop for no_of_rows. Check each element inside the row and find for the maximum element. Finally, print the element.
Below is the implementation :

Python

import numpy

def maxelement(arr):

no_of_rows = len(arr)

no_of_column = len(arr[0])

for i in range(no_of_rows):

max1 = 0

for j in range(no_of_column):

if arr[i][j] > max1:

max1 = arr[i][j]

print(max1)

arr = [[3, 4, 1, 8],

[1, 4, 9, 11],

[76, 34, 21, 1],

[2, 1, 4, 5]]

maxelement(arr)

Output :

Time Complexity: O(N^2), where N is the number of rows in the matrix.

Space Complexity: O(1), as no extra space is required for the algorithm.

Method 2: By calculating max element Each list of list of lists using the max() function

Python3

arr = [[3, 4, 1, 8],

[1, 4, 9, 11],

[76, 34, 21, 1],

[2, 1, 4, 5]]

for i in arr:

print(max(i))

Time complexity: O(n*m), where n is the number of rows and m is the number of columns in the matrix.

Auxiliary space: O(1), as we are only using a constant amount of extra space to store the maximum value of each row.

Another approach that could be used to find the maximum element of each row in a matrix is to use the built-in map() function. The map() function applies a given function to each element of a given iterable (such as a list or a matrix). In this case, we can use the map() function to apply the max() function to each row of the matrix.

Here is an example of how this approach could be implemented:

Python3

def find_max_element(matrix):

return list(map(lambda row: max(row), matrix))

matrix = [[3, 4, 1, 8],

[1, 4, 9, 11],

[76, 34, 21, 1],

[2, 1, 4, 5]]

max_elements = find_max_element(matrix)

print(max_elements)

Time complexity: O(n * m), where n is the number of rows and m is the number of columns in the matrix.
Auxiliary Space: O(n), as we are creating a new list to store the maximum elements of each row.

Method#4: Using the Recursive method.

The find_max_recursive function takes a matrix as input, along with an optional index variable i (which is initially set to 0) and a result list res (which is initially empty). The function returns a list of the maximum element in each row of the matrix.

The function first checks if it has reached the end of the matrix (i.e., if i is equal to the length of the matrix). If so, it returns the result list. Otherwise, it finds the maximum element in the current row using the built-in max function, and appends it to the result list. It then recursively calls itself with the index of the next row and the updated result list.

Python3

def find_max_recursive(matrix, i=0, res=[]):

if i == len(matrix):

return res

max_val = max(matrix[i])

res.append(max_val)

return find_max_recursive(matrix, i+1, res)

matrix = [[3, 4, 1, 8],

[1, 4, 9, 11],

[76, 34, 21, 1],

[2, 1, 4, 5]]

max_elements = find_max_recursive(matrix)

print(max_elements)

The time complexity of this function is O(n^2), where n is the size of the input matrix. This is because the function iterates over each element in the matrix once to find the maximum value in each row, resulting in n iterations. Additionally, finding the maximum value in each row requires iterating over each element in the row, resulting in another n iterations. Therefore, the total number of iterations is n^2.

The auxiliary space of this function is also O(n^2), as the result array ‘res’ is being appended with the maximum element from each row in the matrix. Since the matrix has n^2 elements, the result array will also have a maximum of n^2 elements, leading to the O(n^2) space complexity.

Method#5: Using the lambda function + list comprehension

In this method, we define a lambda function that takes a matrix as input and uses a list comprehension to print the maximum element of each row using the NumPy max() function.

Note: Before using numpy you first need to install it by using the following command: pip install numpy

Below is the code for the following method:

Python3

import numpy as np

maxelement = lambda arr: [print(np.max(row), end = " ") for row in arr]

arr = [[3, 4, 1, 8],

[1, 4, 9, 11],

[76, 34, 21, 1],

[2, 1, 4, 5]]

maxelement(arr)

Output:

Time complexity: O(n*m), where n is the number of rows and m is the number of columns in the matrix.
Auxiliary Space: O(1)

Please refer complete article on Find maximum element of each row in a matrix for more details!

Last Updated :
29 Mar, 2023

Like Article

Save Article

Источник

Долго проболел, не ходил в универ, задали:
Определить наибольший элемент в каждой строке матрицы A[B,C], где B<=10, C<=15.

Можете объяснить, что тут вообще надо сделать?

Виталина

111 золотой знак2 серебряных знака8 бронзовых знаков

задан 10 ноя 2014 в 11:50

У тебя есть матрица [10,15]:

Делаешь цикл по строкам.
Объявляешь переменную max = первому элементу в этой строке.
Бежишь по строке и сравниваешь max с текущим элементом x[i,j].
Если max < x[i,j] то max = x[i,j].
Выводишь max (или записываешь куда-нибудь).
Переходишь к следующей строке.

ответ дан 10 ноя 2014 в 12:14

whispeerwhispeer

8994 золотых знака12 серебряных знаков30 бронзовых знаков

Ну… Как что делать? Взять тетрадь у однокурсников и порешать задачи в ней, все.

А что непонятного? Наибольший элемент в наборе чисел (например, в массиве) определить умеете? Вот и прогоните определение наибольшего элемента для каждой из строк матрицы. (Как адресуются элементы в матрице, знаете?)

Обновление

Ну хоть с однокурсницами, девочки с первой парты обычно с удовольствием всё объясняют.

Насколько я понял задание, B и C — размеры матрицы, соответственно по иксу и по игреку. А числа в матрице любые.

Обновление 2

То есть вы

заводите матрицу размера «с запасом»: 10 на 15;
запрашиваете у юзера настоящие размеры. Проверяете, вылазят ли они за границы, если да, ругаетесь на юзера;
вводите матрицу поэлементно;
пробегаетесь по строкам, в каждой находите макс. элемент и выводите;
PROFIT!

ответ дан 10 ноя 2014 в 12:04

VladDVladD

206k27 золотых знаков289 серебряных знаков521 бронзовый знак

Источник

Автор оригинала: Pankaj Kumar.

В этом руководстве мы узнаем о numpy.argmax () Функция в Python Отказ Эта функция возвращает индексы максимальных элементов в матрице. Функция позволяет пройти аргумент, упомянующий ось, наряду, на которой вам нужно найти индексы максимальных элементов.

Мы получаем три варианта при использовании функции argmax.

Найдите максимальный элемент для всей матрицы. (По умолчанию)
Получите максимальный элемент для каждой строки.
Получите максимальный элемент для каждого столбца.

Давайте посмотрим, как использовать эту функцию.

Давайте начнем с импорта Numpy и создания образца матрицы ..

import numpy as np
a = np.arange(12).reshape(4,3) + 10
print(a)

Выход:

[[10 11 12]
 [13 14 15]
 [16 17 18]
 [19 20 21]]

Теперь давайте найдем индекс максимального элемента в массиве.

Выход: 11.

Мы получаем 11 в качестве вывода. Это связано с тем, что в функции Numpy.argmax () не упоминается оси. Как только это сделано, он возвращает индекс последнего элемента в массиве.

Или в основном, без указанной оси функция Python Numpy.argmax () возвращает количество элементов в массиве.

Мы можем использовать функцию NP.UNRAVAVEL_INDEX для получения индекса, соответствующего 2D-массиве с вывода Numpy.argmax.

Примечание: В случае нескольких вхождений максимальных значений функция возвращает индексы, соответствующие первому.

Использование NP.UNRAVEL_INDEX на выходе Argmax

Использовать np.unravel_index Функция на выходе Argmax, давайте запустим следующий фрагмент кода:

index = np.unravel_index(np.argmax(a), a.shape)
print(index)
print(a[index])

Это дает следующий выход:

Мы можем объединить код из этих двух секций, чтобы напрямую печатать максимальный элемент.

Заполните код для печати максимального элемента для матрицы

Вот полный код:

import numpy as np
a = np.arange(12).reshape(4,3) + 10
print(a)
index = np.unravel_index(np.argmax(a), a.shape)
print(index)
print(a[index])

Найти максимальные элементы вдоль столбцов с помощью python numpy.argmax ()

Чтобы найти максимальные элементы для каждого использования столбцов:

import numpy as np
a = np.arange(12).reshape(4,3) + 10
print(np.argmax(a, axis=0))

Выход:

Это дает Индексное значение максимальных элементов вдоль каждого столбца.

Точно так же, если мы упомянем оси как 1, то мы можем получить индексы максимальных элементов вдоль рядов.

Найти максимальные элементы вдоль рядов

Чтобы найти максимальные элементы для каждой используемой строки:

import numpy as np
a = np.arange(12).reshape(4,3) + 10
print(np.argmax(a, axis=1))

Выход:

Заключение

В этом руководстве было функция numpy.argmax () в Python. Мы узнали, как эта функция используется для нахождения максимальных элементов вдоль разных осей матрицы.

Источник

Здравствуйте! Помогите, пожалуйста, мне с программой. Я си изучаю 2 день и у меня возникла проблема с функцией, я никак не могу понять, как её правильно вызвать. Задание звучит так: Найти максимальный элемент каждой строки матрицы и заменить его числом 1.

#include <stdio.h>
 
int max_el(int a, int n, int m)
{
    int i, j, max = 0;
    for (i=1; i<=n; i++)
    {
        for (j=1; j<=m; j++)
        {
            if (a[i][j] > a[i][max]) max = j;
        } 
        a[i][max] = 1;   
    }
}
 
int main()
{
    setlocale(0,"");
    int a[100][100], k, n, m, i, j;
    
    printf("Г‚ГўГҐГ¤ГЁГІГҐ Г°Г*Г§Г¬ГҐГ°Г*Г®Г±ГІГј n*m: ");
    scanf("%d %d", &n, &m);
    srand(time(NULL));
    for (i=1; i<=n; i++)
    {
        for (j=1; j<=m; j++)
        {
            a[i][j] = rand()%10;
            printf("%d ", a[i][j]);
        } 
        printf("n");   
    }
    
    max_el(a, n, m);
    
     for (i=1; i<=n; i++)
    {
        for (j=1; j<=m; j++)
        {
            printf("%d", a[i][j]);
        } 
        printf("n");   
    }   
    _getch();
}

Источник

Для
поиска максимального элемента матрицы
и определения его индексов нам потребуются
три дополнительные переменные. В первой
из них будем хранить значение максимального
элемента, а во второй – номер строки, к
которой он находится, а в третьей –
номер столбца. Поиск максимального
элемента в матрице традиционно начинают
с элемента, стоящего в нулевой строке
и нулевом столбце. Затем организуют
вложенные циклы, которые позволят
проанализировать все элементы матрицы.
Если значение какой-либо элемента
матрицы окажется больше ранее найденного
максимума, то значение максимума
необходимо обновить, сделав равным
этому элементу. При этом сразу запоминаются
оба его индекса. Рассмотрим особенности
программной реализации этого алгоритма.

Объявляем
необходимые переменные. Переменная maxпредназначена для хранения значения
максимального элемента. Ее тип всегда
должен совпадать с типом элементов
матрицы. В переменнойimaxмы будем запоминать номер строки, в
которой находится максимальный элемент
матрицы, а в переменнойjmaxмы будем хранить номер столбца, в котором
находится максимальный элемент. Эти
две переменные всегда будут иметь
целочисленный тип.

Dim max, imax, jmax As Integer

Поиск максимума мы начинаем с элемента,
стоящего в нулевой строке и нулевом
столбце матрицы.

max = a(0, 0)

В переменные imaxиjmaxмы записываем соответственно номера
строки и столбца, которые равны нулю.

imax = 0

jmax = 0

Организуем цикл по всем строкам матрицы.

For i = 0 To m

Организуем цикл по столбцам матрицы.
Он позволит нам перебрать все элементы
в пределах i-й
строки.

For j = 0 To n

Анализируем очередной элемент матрицы.

If a(i, j) > max Then

Если его значение больше, чем значение
ранее найденного максимума, то необходимо
обновить значение максимума (переменной
max),
записав в него значение текущего
элемента.

max = a(i, j)

Сразу же запоминаем индексы нового
максимума. Номер строки, в которой
находится данный элемент матрицы,
хранится в переменной i,
а номер столбца – в переменнойj.

imax = i

jmax = j

End If

После завершения вложенных циклов нам
остается только вывести полученные
результаты в окно списка. Сначала выведем
горизонтальную черту, чтобы зрительно
отделить исходные данные от полученных
результатов.

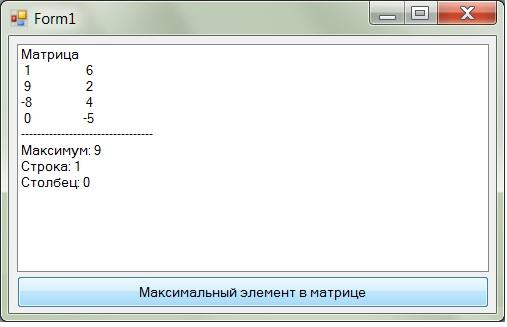
lstMatrix.Items.Add(«——————————«)

Заем выведем максимальное значение и
его индексы.

lstMatrix.Items.Add(«Максимум:»
+ Str(max))

lstMatrix.Items.Add(«Строка:»
+ Str(imax))

lstMatrix.Items.Add(«Столбец:»
+ Str(jmax))

Полный
текст программы представлен в приложении
38. Пример работы программы приведен на
рис. 53.

Рис. 53. Пример работы программы
поиска максимального элемента в
прямоугольной матрице

8.4. Обработка матрицы по строкам

Обработка
прямоугольной матрицы может вестись
двумя способами: по строкам и по столбцам.
Как правило, способ обработки определяется
условием решаемой задачи. При обработке
по строкам вложенные циклы организуются
таким образом, чтобы за один шаг внешнего
цикла полностью обрабатывалась одна
строка матрицы. В этом случае внешний
цикл будет идти по строкам матрицы, а
внутренний – по столбцам. В качестве
примера рассмотрим задачу вычисления
среднего арифметического четных
элементов в каждой строке матрицы.

Для
решения этой задачи необходимо в каждой
строке матрицы вычислить свою сумму и
количество четных элементов. Затем,
если это возможно, найти среднее
арифметическое. Если же в какой-то строке
матрицы нет четных элементов, то вместо
среднего арифметического мы будем
печатать поясняющее сообщение. Результаты
работы программы будем выводить в окно
списка.

Начнем
с объявления необходимых переменных.
Переменные sumиkol,
имеющие целочисленный тип данных,
предназначены для хранения суммы и
количества четных элементов в одной
строке матрицы.

Dim sum, kol As Integer

Так как среднее арифметическое получается
в результате деления, то соответствующая
переменная всегда будет иметь рациональный
тип данных.

Dim sred As Single

Для каждой строки матрицы мы будем
получать отдельный результат. Поэтому
удобно совместить процессы вычисления
и вывода в одном цикле. Чтобы результаты
вычислений зрительно отделялись от
исходных данных, выведем горизонтальную
черту.

lstMatrix.Items.Add(«——————————«)

Результаты вычислений мы будем выводить
в две колонки. В первой будет указываться
номер обрабатываемой строки матрицы,
а во второй – найденное значение среднего
арифметического четных элементов.
Выводим поясняющий заголовок. Константа
vbTabпозволяет организовать вывод в две
колонки.

lstMatrix.Items.Add(«Строка»
+ vbTab + _

«Сред.
арифм.»)

Так как по условию задачи требуется,
чтобы каждая строка матрицы обрабатывалась
отдельно, то обработку матрицы будем
вести по строкам. Для этого организуем
внешний цикл по строкам, а внутренний
– по столбцам.

For i = 0 To m

За один шаг внешнего цикла мы будем
полностью обрабатывать одну строку
матрицы. Для этого мы будем использовать
внутренний цикл. Следовательно, начальные
значения для суммы и количества необходимо
задать до него.

sum = 0

kol = 0

Организуем внутренний цикл. Нам необходимо
обработать все элементы, находящиеся
в i-й
строке матрицы. Для этого мы должны
пройтись по всем столбцам матрицы.
Соответственно, внутренний цикл будет
по столбцам.

For j = 0 To n

На каждом шаге цикла анализируем элемент
матрицы.

If a(i, j) Mod 2 = 0 Then

Если его значение при делении на 2 дает
в остатке ноль, значит, оно четное, и
данный элемент надо добавить к сумме.
При этом количество четных элементов
в данной строке матрицы увеличивается
на единицу.

sum += a(i, j)

kol += 1

End If

После завершения внутреннего цикла
можно приступать к вычислению среднего
арифметического четных элементов в
одной строке матрицы. Сначала анализируем
количество четных элементов.

If kol = 0 Then

Если количество четных элементов равно
нулю, значит, их в рассматриваемой строке
нет ни одного четного элемента.
Следовательно, вычислить их среднее
арифметическое невозможно. Поэтому
вместо ответа выводим номер строки и
поясняющее сообщение.

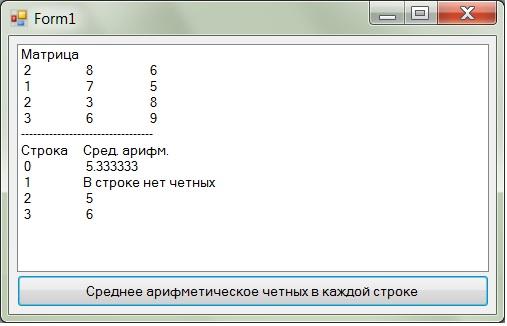
lstMatrix.Items.Add(Str(i)
+ vbTab + _

«В
строке нет четных»)

Else

Иначе мы делим сумму четных элементов
на их количество и получаем искомое
значение.

sred = sum / kol

В окно списка выводим номер строки и
найденное значение среднего арифметического
четных элементов в этой строке.

lstMatrix.Items.Add(Str(i)
+ vbTab + _

Str(sred))

End If

Полный
текст программы представлен в приложении
39. Пример работы программы приведен на
рис. 54.

Рис. 54. Пример работы программы
поиска среднего арифметического четных
элементов в каждой строке прямоугольной
матрицы

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Python

Method 2: By calculating max element Each list of list of lists using the max() function

Python3

Python3

Python3

Python3

Использование NP.UNRAVEL_INDEX на выходе Argmax

Заполните код для печати максимального элемента для матрицы

Найти максимальные элементы вдоль столбцов с помощью python numpy.argmax ()

Найти максимальные элементы вдоль рядов

Заключение

8.4. Обработка матрицы по строкам

Не пропустите также: