Как найти максимальные элементы диагоналей с

Дана квадратная матрица размером nxn. Найти минимальный элемент среди элементов, расположенных ниже главной диагонали, найти максимальный элемент, среди элементов расположенных выше побочной диагонали. Найденные минимальный и максимальный элементы поменять местами и вывести их индексы.

// main_secondary_diagonal.cpp: определяет точку входа для консольного приложения.

#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;

int main(int argc, char* argv[])
{
    srand(time(NULL));
    int size_array; // размер квадратной матрицы
    setlocale(LC_ALL, "rus");

    cout << "Введите размер квадратной матрицы: ";
    cin >> size_array;

    // динамическое создание двумерного массива
    int **arrayPtr = new int* [size_array];
    for (int count = 0; count < size_array; count++)
        arrayPtr[count] = new int [size_array];

    for (int counter_rows = 0; counter_rows < size_array; counter_rows++)
    {
        for (int counter_columns = 0; counter_columns < size_array; counter_columns++)
        {
            arrayPtr[counter_rows][counter_columns] = rand() % 100; // заполнение массива случайными числами
            cout << setw(2) << arrayPtr[counter_rows][counter_columns] << "  "; // вывод на экран двумерного массива
        }
        cout << endl;
    }
    cout << endl;

    int min = arrayPtr[1][0], // минимальный елемент массива, ниже главной диагонали
        row_min = 1,          // номер строки минимального элемента
        column_min = 0;       // номер столбца минимального элемента

    // поиск минимального элемента в массиве, ниже главной диагонали
    for (int counter_rows = 1; counter_rows < size_array; counter_rows++)
    {
        for (int counter_columns = 0; counter_columns < counter_rows ; counter_columns++)
        {
            if ( arrayPtr[counter_rows][counter_columns] < min )
            {
                min = arrayPtr[counter_rows][counter_columns];
                row_min = counter_rows;
                column_min = counter_columns;
            }
        }
    }

    cout << "min" << "[" << (row_min + 1) << "][" << (column_min + 1) << "]"  << " = " << min << endl; 

    int max = arrayPtr[0][0], // максимальный элемнет массива, выше побочной диагонали
        row_max = 0,              // номер строки максимального элемента
        column_max = 0;           // номер столбца максимального элемента

    for (int counter_rows = 0; counter_rows < size_array - 1; counter_rows++)
    {
        for (int counter_columns = 0; counter_columns < (size_array - counter_rows - 1); counter_columns++)
        {
            if ( arrayPtr[counter_rows][counter_columns] > max )
            {
                max = arrayPtr[counter_rows][counter_columns];
                row_max = counter_rows;
                column_max = counter_columns;
            }
        }
    }

    cout << "max" << "[" << (row_max + 1) << "][" << (column_max + 1) << "]"  << " = " << max << endl; 

    //////////////////перестановка элементов////////////////////////////////////////////////

    arrayPtr[row_min][column_min] = max;
    arrayPtr[row_max][column_max] = min;

    ////////////////////////////////////////////////////////////////////////////////////////

    cout << "nМассив после перестановки максимального и минимального элементов:n";

    for (int counter_rows = 0; counter_rows < size_array; counter_rows++)
    {
        for (int counter_columns = 0; counter_columns < size_array; counter_columns++)
        {
          cout << setw(2) << arrayPtr[counter_rows][counter_columns] << "  "; // вывод на экран двумерного массива
        }
        cout << endl;
    }
    cout << endl;

    cout << "min" << "[" << (row_max + 1) << "][" << (column_max + 1) << "]"  << " = " << min << endl; 
    cout << "max" << "[" << (row_min + 1) << "][" << (column_min + 1) << "]"  << " = " << max << endl; 

    // удаление двумерного динамического массива
    for (int count = 0; count < size_array; count++)
        delete []arrayPtr[count];

    system("pause");
    return 0;
}

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <iostream>
#include <conio.h>
using namespace std;
 
int main()
{    
   const int n = 3;
   int i,j,sum=0,vib=0,maxsum=0;   
        int a[n][n],s[2*n];
           printf ("Kak vvodit' elementi?n0 - randomn1 - s klaviaturin");
           scanf ("%i", &vib);
           printf ("nMi vibrali: %in",vib);
        srand(time(0));
        switch (vib)
        {
        case 0://random
                for (i=0; i<n; i++)
                        for (j=0; j<n; j++) 
                                a[i][j] = rand()%20;
                printf("n");
                break;
        case 1:// sklavi
                for (i=0; i<n; i++)
                        for (j=0; j<n; j++)
                        {
                                printf ("a[%i][%i]= ", i+1, j+1);
                                scanf ("%i", &a[i][j]);
                        }
        }
  printf("Nasha matrica: n");
  for (i=0; i<n; i++)
        {
                for (j=0; j<n; j++)
                {
                        printf ("%i ", a[i][j]);
                }
                printf ("n");
        }
printf("n");
printf ("Cymmi elementov diagonaley matrici, paralel'nie glavnoy: n");
 for (j=0;j<(2*n);j++) s[j]=0;
  for (i=0;i<n;i++)
  {
      for (j=0;j+i<n;j++)
      {
          s[j]+=a[i][i+j];
          s[n+j]+=a[i+j][i]; 
      }      
  }
  for (j=0;j<n;j++) printf("%dn",s[j]);
  for (j=n+1;j<(2*n);j++) printf("%dn",s[j]);
  maxsum=-1000;
  for (j=1;j<n;j++)
      if (maxsum<s[j]) 
          maxsum=s[j];
  printf("n");
  printf("Max sum = %dn",maxsum);
  _getch();
  return 0;
  }

Частным
случаем матрицы является квадратная
матрица,
т.е.
матрица, имеющая одинаковое количество
строк и столбцов (рис.43).

X[1,1]	X[1,2]	X[1,3]
X[2,1]	X[2,2]	X[2,3]
X[3,1]	X[3,2]	X[3,3]

Рис.43

Элементы
матрицы, выделенные на рис.43, называются
главной
диагональю.
Отличительной
особенностью этих
элементов является то, что они имеют
одинаковые
номера строки и столбца.
Поэтому в i-ой
строке индексы элемента
главной диагонали
матрицы Х будут X[i,i].
Для обработки
элементов главной
диагонали
требуется изменять только одну
переменную,
поэтому необходимо всего один
цикл, а не два,
как при обработке
всей матрицы.
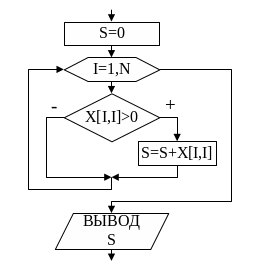
На рис.44 показан алгоритм
нахождения суммы положительных
элементов главной диагонали. Ниже
приведён фрагмент
программы к этому алгоритму.

•

• •

S:=0;

for
i:=1
to
N
do

if
X[i,i]>0 then

S:=S+X[i,i];

writeln(‘S=’
, S);

• • •

Рис.44

3.2.6. Обработка элементов побочной диагонали

Побочная
диагональ
(рис.45)
существует только в квадратной
матрице.

X[1,1]	X[1,2]	X[1,3]
X[2,1]	X[2,2]	X[2,3]
X[3,1]	X[3,2]	X[3,3]

Рис.45

Н
етрудно
заметить, что элемент побочной диагонали
матрицы Х в первой строке имеет индексы
Х[1,N],
во второй строке – Х[2, N-1], в третьей –
Х[3, N-2].
Отсюда можно заключить, что в i-ой
строке элемент побочной диагонали будет
иметь индексы Х[I,
N-I+1].

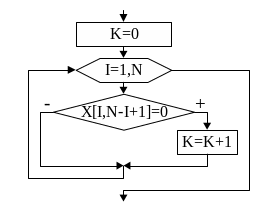
На
рис.46 показан алгоритм нахождения
количества равных
нулю элементов побочной диагонали. Ниже
представлен фрагмент
программы к этому алгоритму.

Рис.46

• • •

К:=0;

for
i:=1
to
N
do

if
X[i,N-i+1] = 0 then

K:=K+1

writeln(
‘K=’ , K) ;

• • •

3.2.7. Обработка элементов квадратных матриц, расположенных над и под главными и побочными диагоналями

На
рис. 47 приведена схема расположения
элементов относительно главной диагонали.

Г


лавная
диагональ (ГД) Элементы,
расположенные над ГД

гд
	Гд
		ГД
			гд

Элементы,
расположенные под ГД

Рис.
47

Рассмотрим
элементы, расположенные над главной
диагональю матрицы. Для матрицы А
размером 4х4 эти элементы будут иметь
следующие индексы:

в
первой строке: A[1,2],
A[1,3],
A[1,4];

во
второй строке: A[2,3],
A[2,4];

в
третьей строке: A[3,4];

в
четвертой строке элементов нет.

Проанализировав
полученные индексы, можно определить,
что для элементов, расположенных выше
главной диагонали, номер столбца всегда
больше номера строки. Поэтому при
организации циклов для обработки этих
элементов нужно учитывать, что в первой
строке нужно рассматривать элементы,
начиная со второго столбца, во второй
строке – начиная с третьего столбца, в
третьей строке – начиная с четвертого
столбца. В общем случае элементы i-ой
строки нужно обрабатывать, начиная с
элемента из i+1
столбца и заканчивая элементом последнего
(N-го)
столбца.

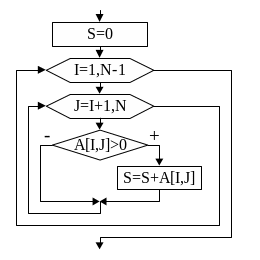
Для
примера рассмотрим алгоритм нахождения
суммы положительных элементов,
расположенных над главной диагональю
(рис.
48).

S:=0;

For
i :=1 to N-1 do

For
j:= I +1 to N do

If
A[I,j]>0 then

S:=S+A[I,j];

Рис.
48

Рассмотрим
элементы, расположенные под главной
диагональю матрицы. Для матрицы А
размером 4х4 эти элементы будут иметь
следующие индексы:

в
первой строке элементов нет;

во
второй строке: A[2,1],

в
третьей строке: A[3,1],
А[3,2];

в
четвертой строке: A[4,1],
A[4,2],
A[4,3].

Проанализировав
полученные индексы, можно определить,
что для элементов, расположенных ниже
главной диагонали, номер столбца всегда
меньше номера строки. Поэтому при
организации циклов для обработки этих
элементов нужно учитывать, что во второй
строке нужно рассматривать элементы
строки, заканчивая элементами из первого
столбца, в третьей строке – заканчивая
элементами из второго столбца, в четвертой
строке – заканчивая элементами из
третьего столбца. В общем случае элементы
i-ой
строки нужно обрабатывать, начиная с
элемента из первого столбца и заканчивая
рассмотрение элементами из i-1
столбца.

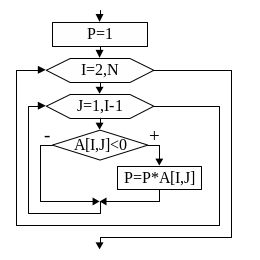
Для
примера рассмотрим алгоритм нахождения
произведения отрицательных элементов,
расположенных под главной диагональю
(рис.
49).

P:=1;

For
i :=2 to N do

For
j:= 1 to I-1 do

If
A[I,j]<0 then

P:=P+A[I,j];

Рис.
49

На
рис. 50 приведена схема расположения
элементов относительно побочной
диагонали.

Э
лементы,
Побочная диагональ(ПД)

р

асположенные
над ПД

			пд
		Пд
	Пд
пд

Элементы,
расположенные под ПД

Рис.
50

Рассмотрим
элементы, расположенные над побочной
диагональю матрицы. Для матрицы А
размером 4х4 эти элементы будут иметь
следующие индексы:

в
первой строке: A[1,1],
A[1,2],
A[1,3];

во
второй строке: A[2,1],
A[2,2];

в
третьей строке: A[3,1];

в
четвертой строке элементов нет.

В
общем случае элементы i-ой
строки нужно обрабатывать, начиная с
элемента первого столбца и заканчивая
элементом из N-i
столбца.

Для
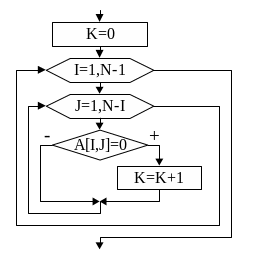
примера рассмотрим алгоритм нахождения
количества нулевых элементов, расположенных
над побочной диагональю (рис.
51).

K:=0;

For
i :=1 to N-1 do

For
j:= 1 to N-i do

If
A[I,j]=0 then

K:=K+1;

Рис.51

Теперь
рассмотрим элементы, расположенные под
побочной диагональю матрицы. Для матрицы
А размером 4х4 эти элементы будут иметь
следующие индексы:

в
первой строке элементов нет;

во
второй строке: A[2,4],

в
третьей строке: A[3,3],
А[3,4];

в
четвертой строке: A[4,2],
A[4,3],
A[4,4].

В
общем случае элементы i-ой
строки нужно обрабатывать, начиная с
элемента из столбца под номером N+2-I
и заканчивая элементом из последнего
(N-го
столбца).

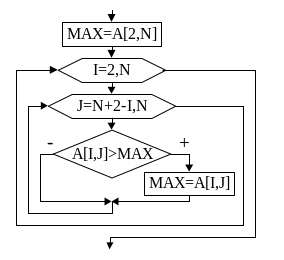
Для
примера рассмотрим алгоритм нахождения
максимального среди элементов,
расположенных под побочной диагональю
(рис. 52).

M
AX:=A[2,N];
{за начальное значения максимума берем
любой элемент, расположенный под побочной
диагональю}

For i :=2 to N do

For
j:= N+2-i to N do

If
A[I,j]>MAX then

MAX:=A[I,j];

Рис. 52

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #