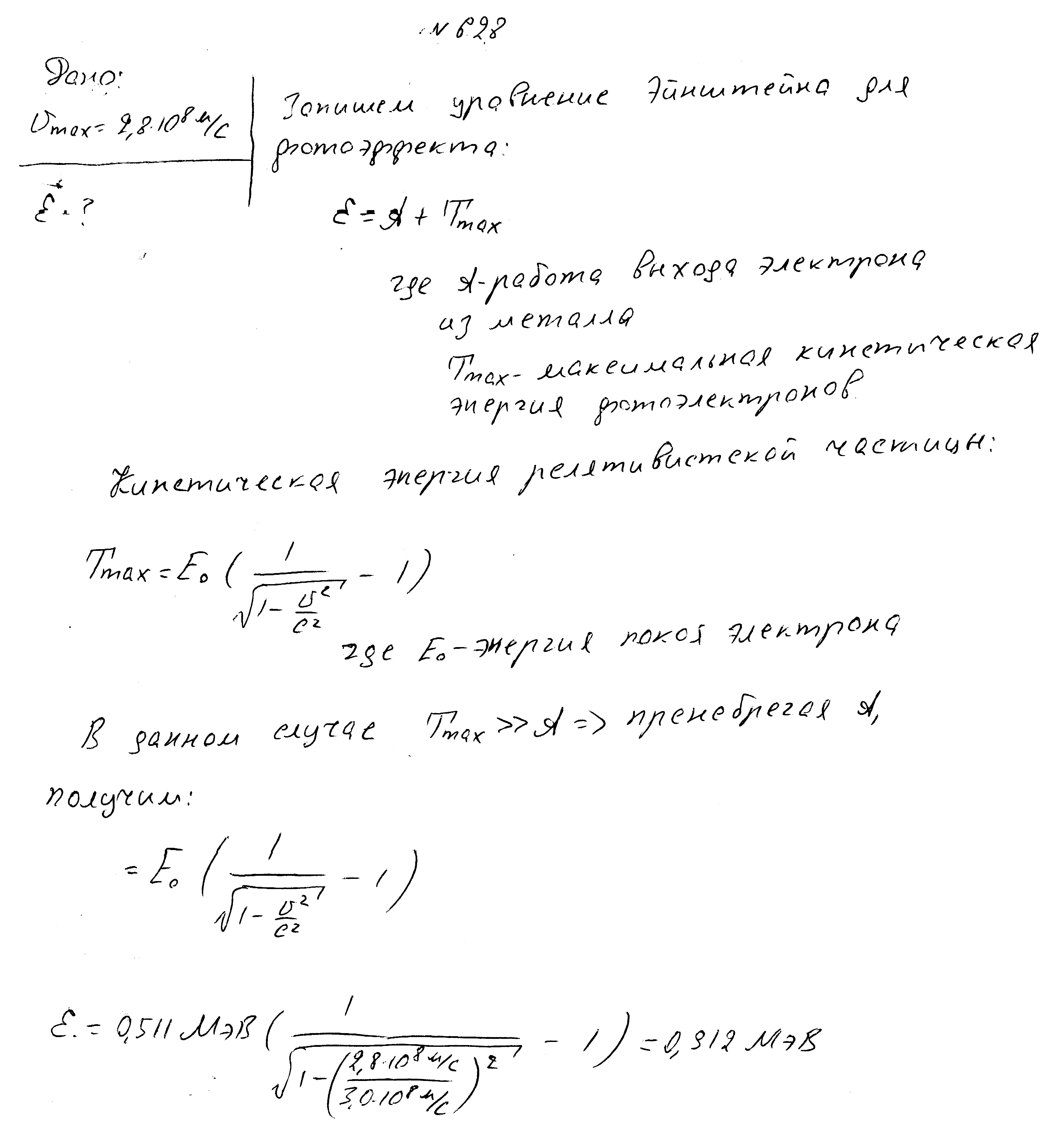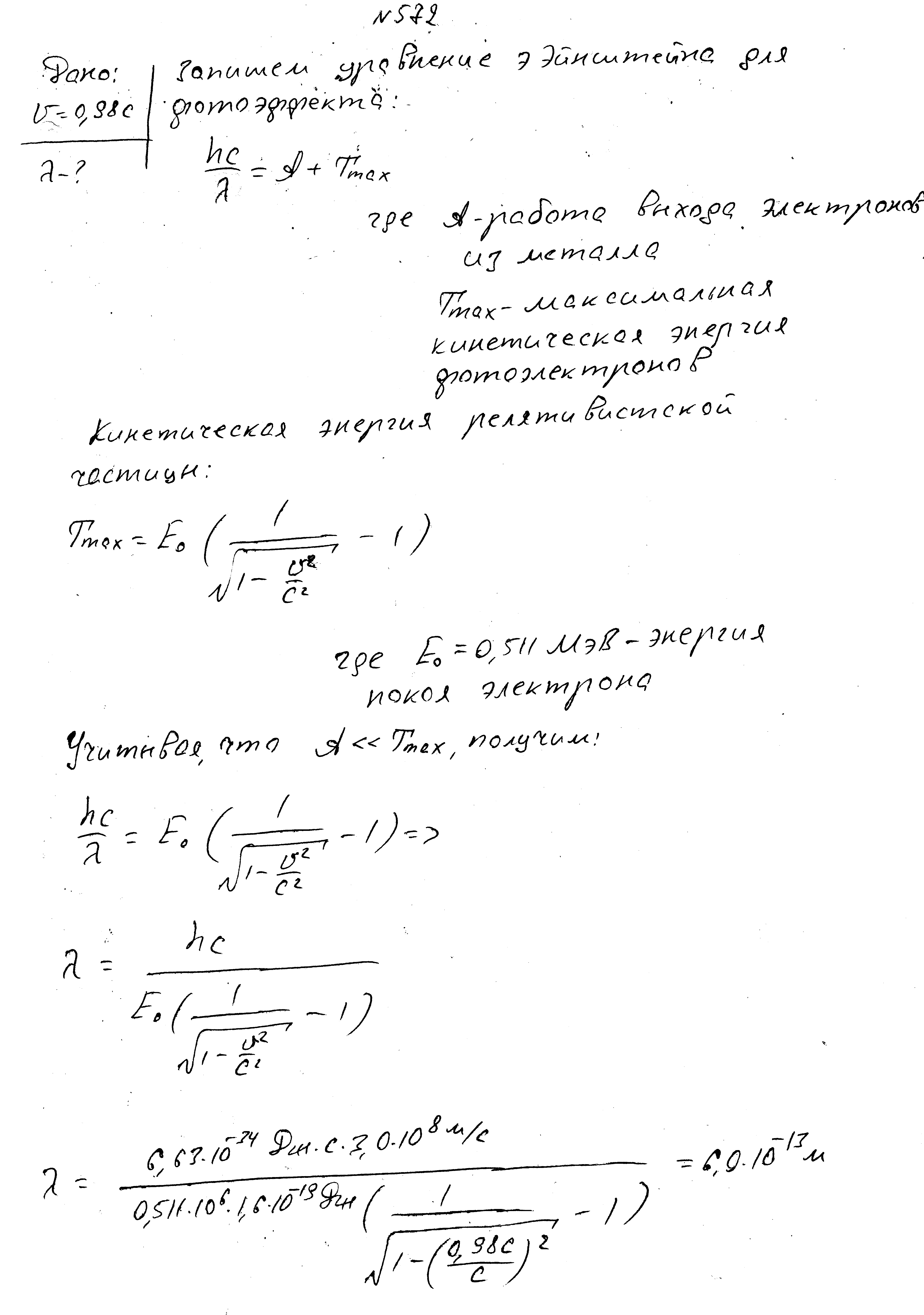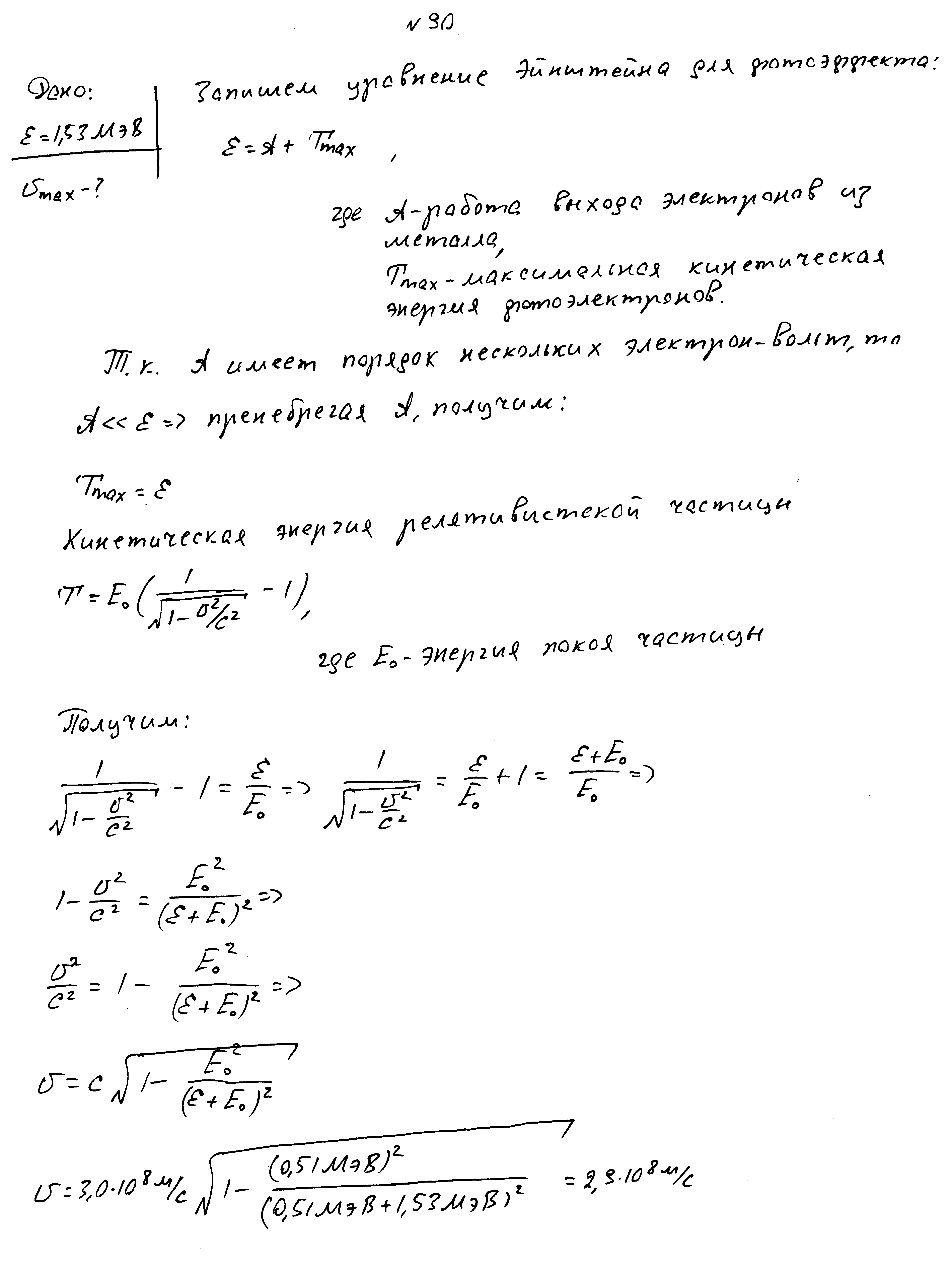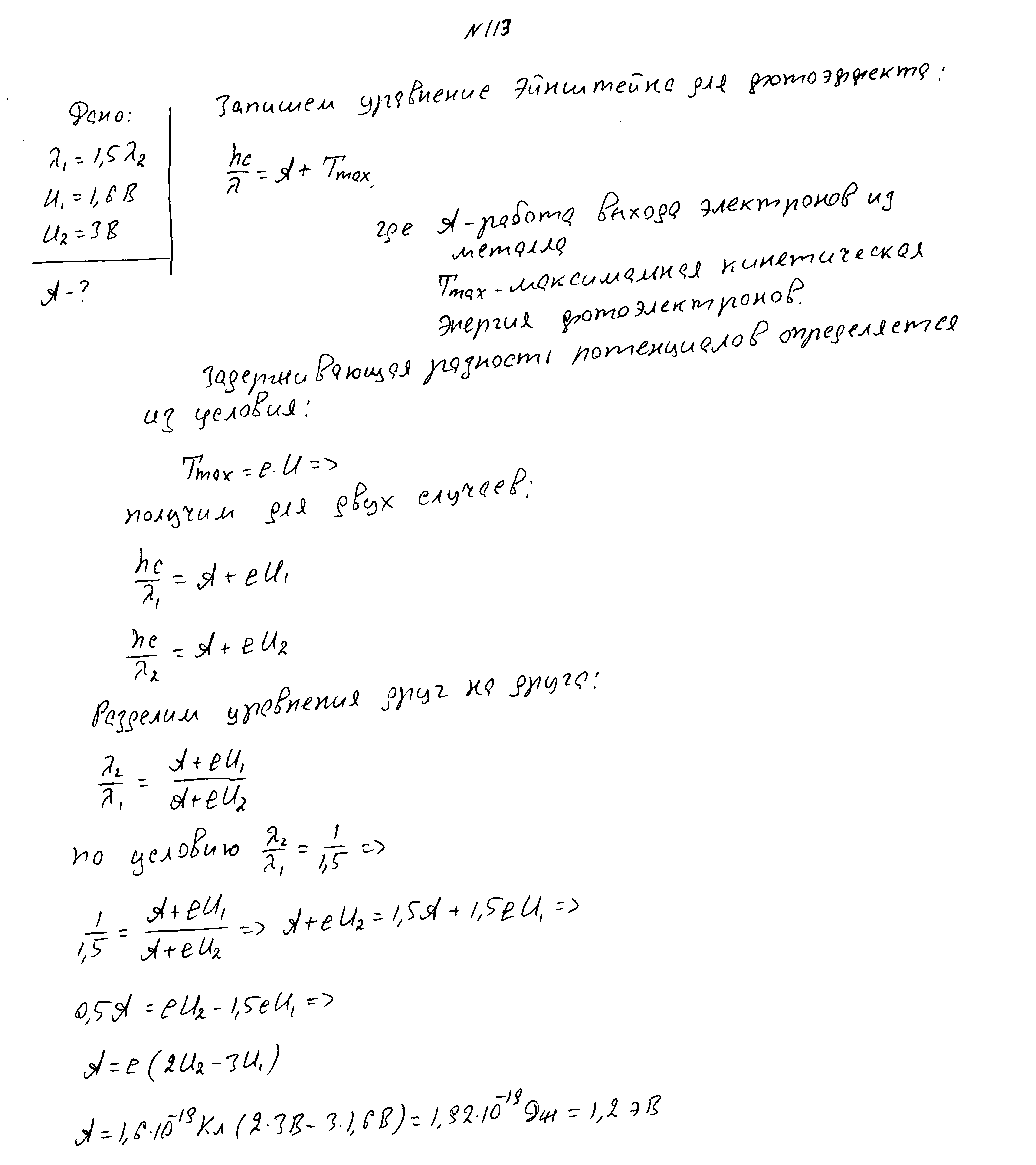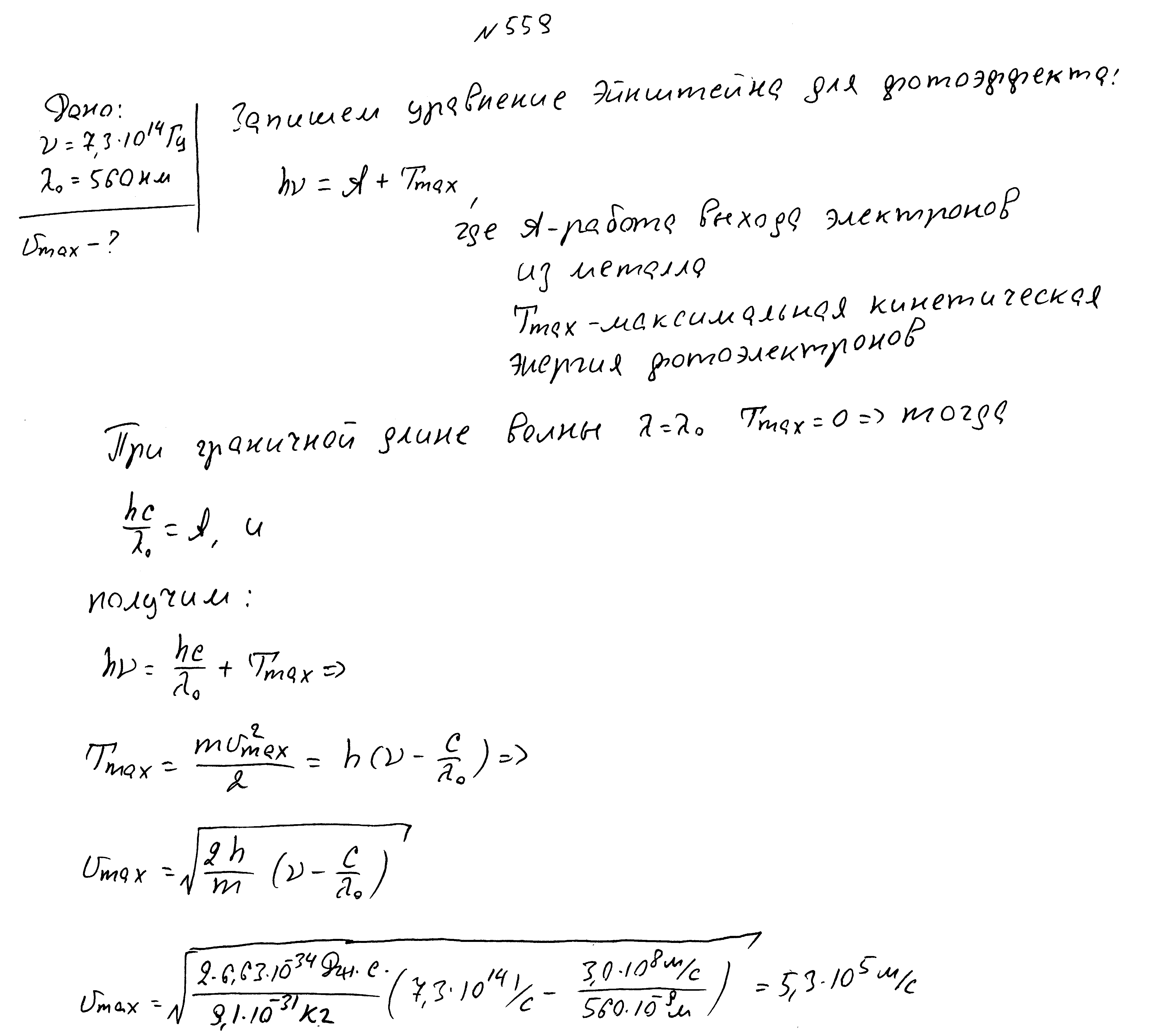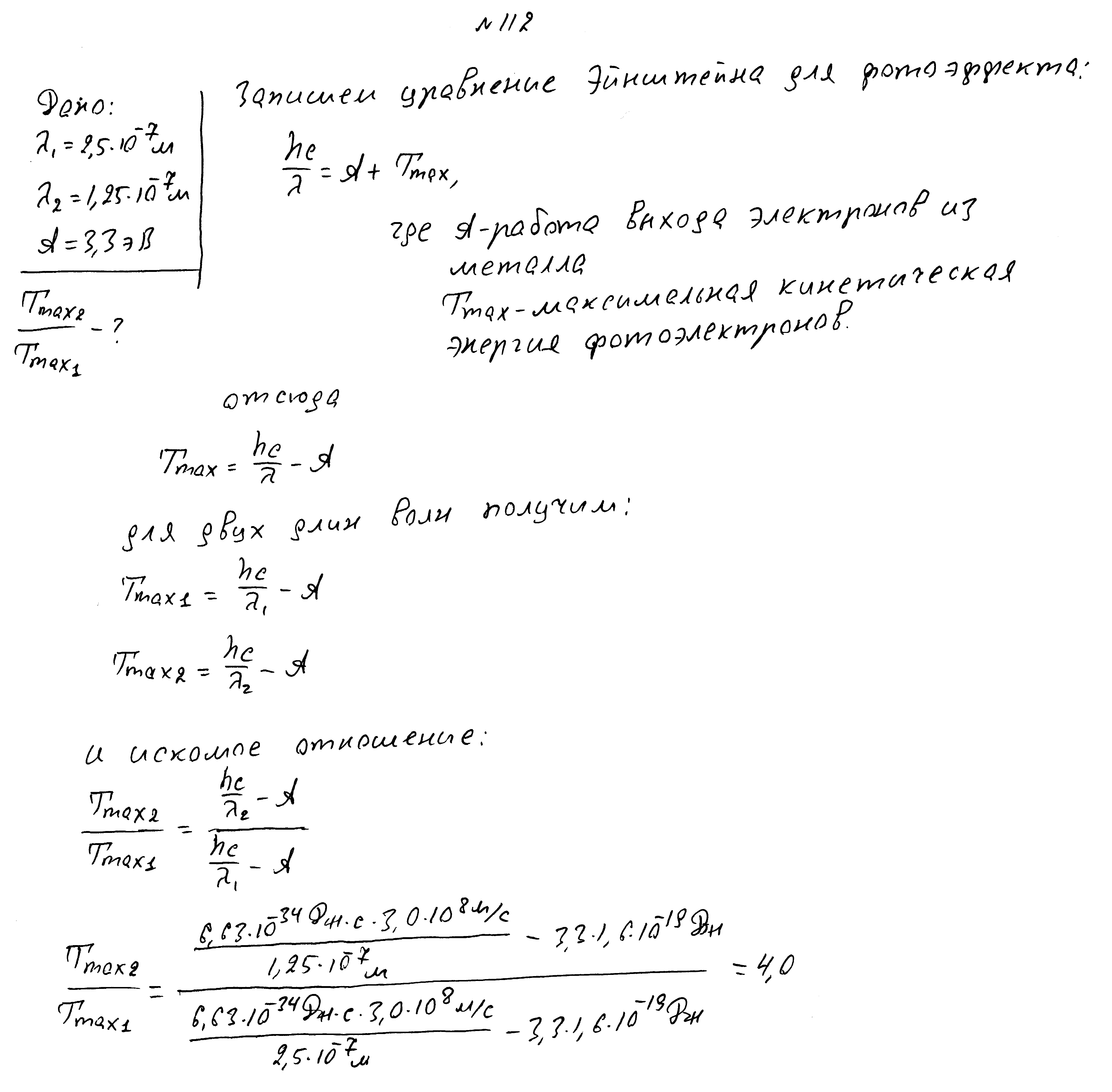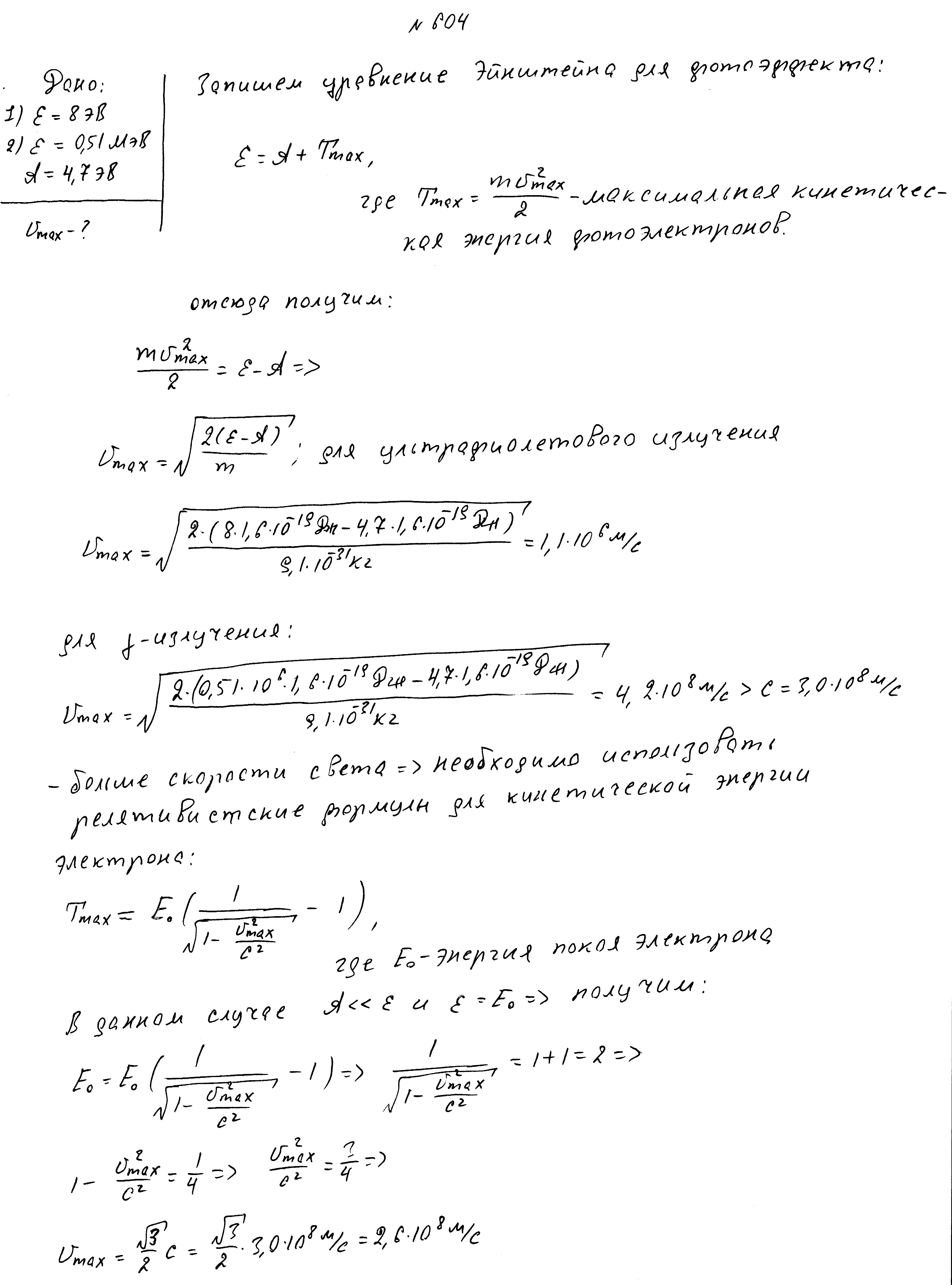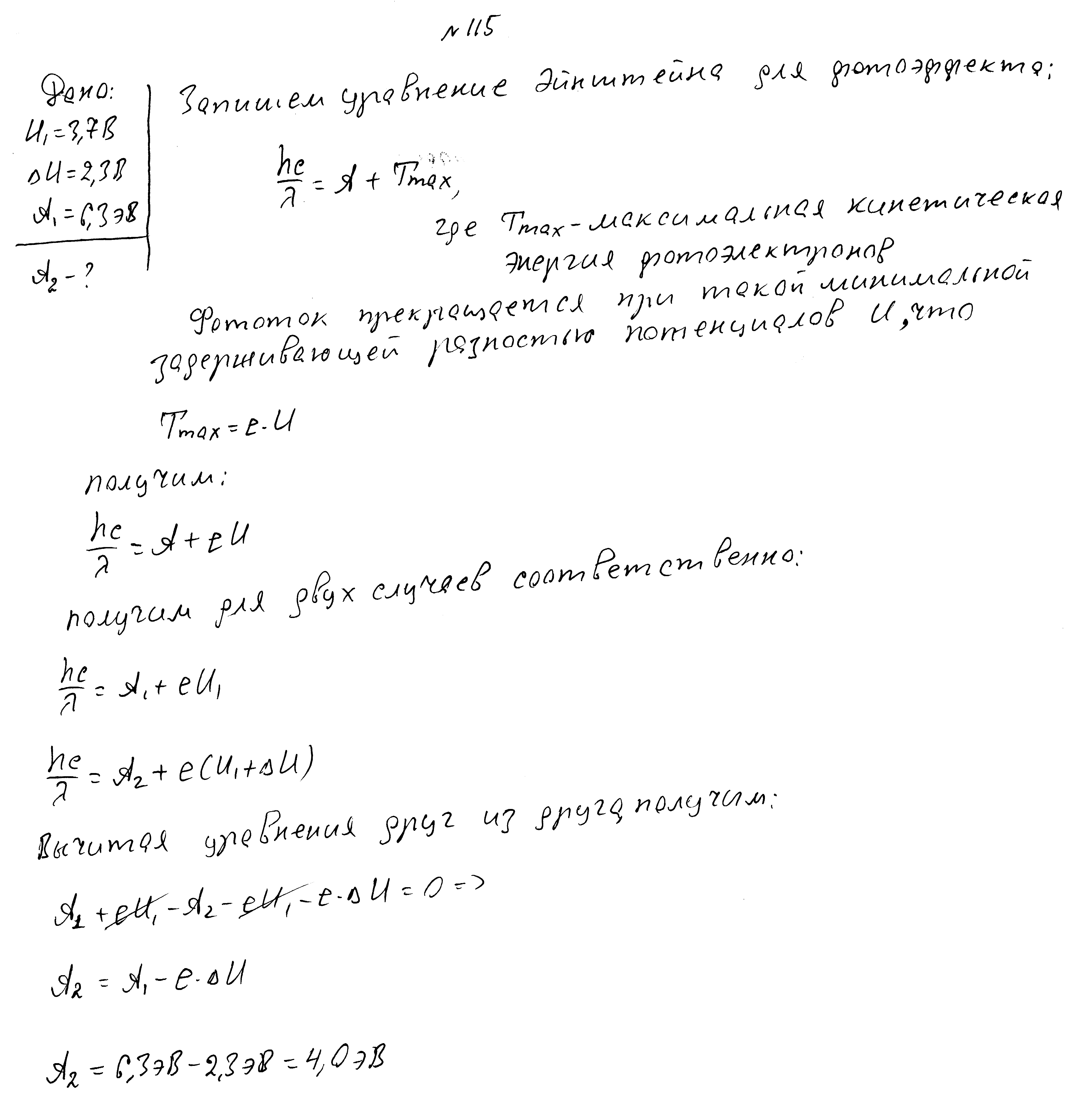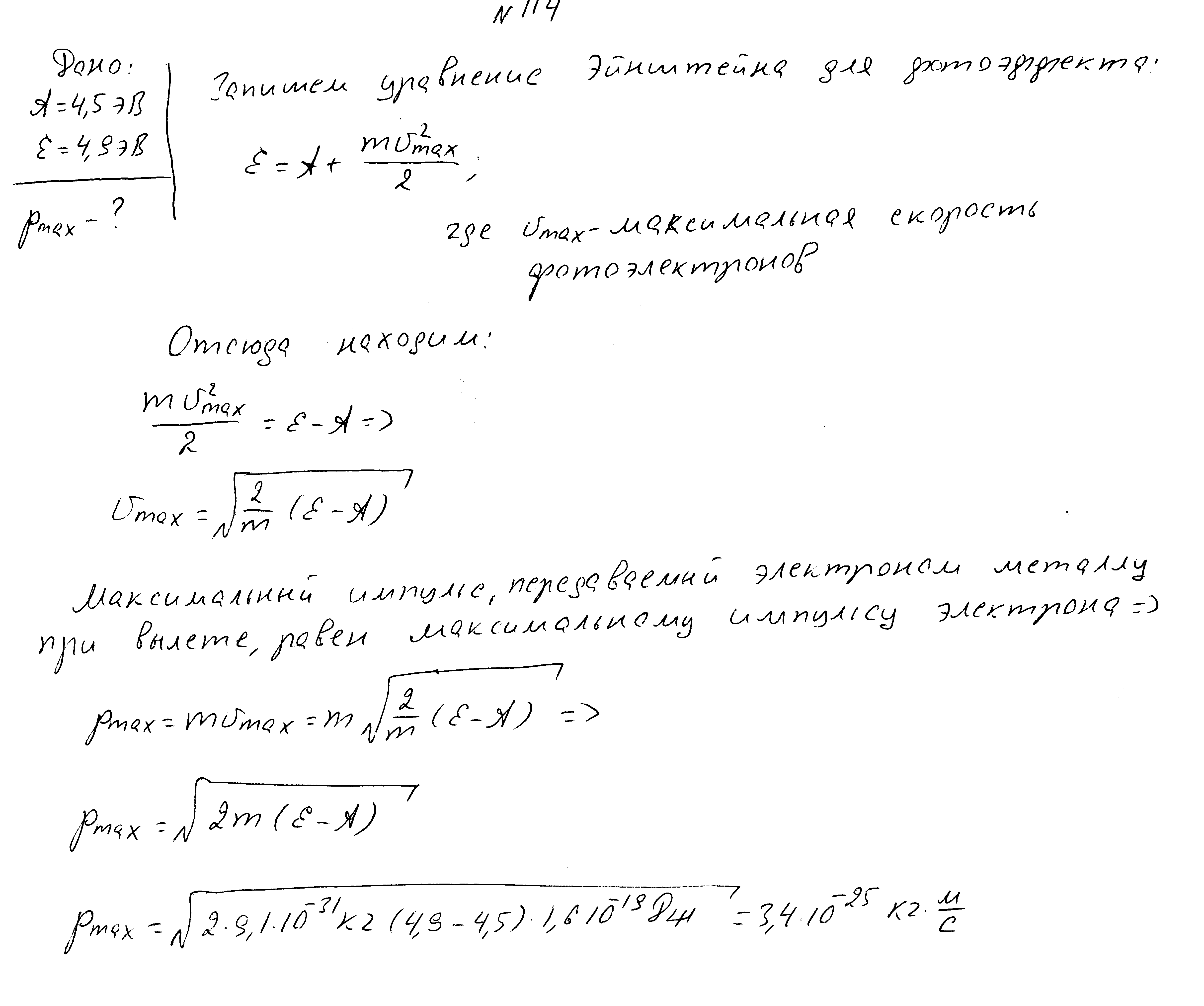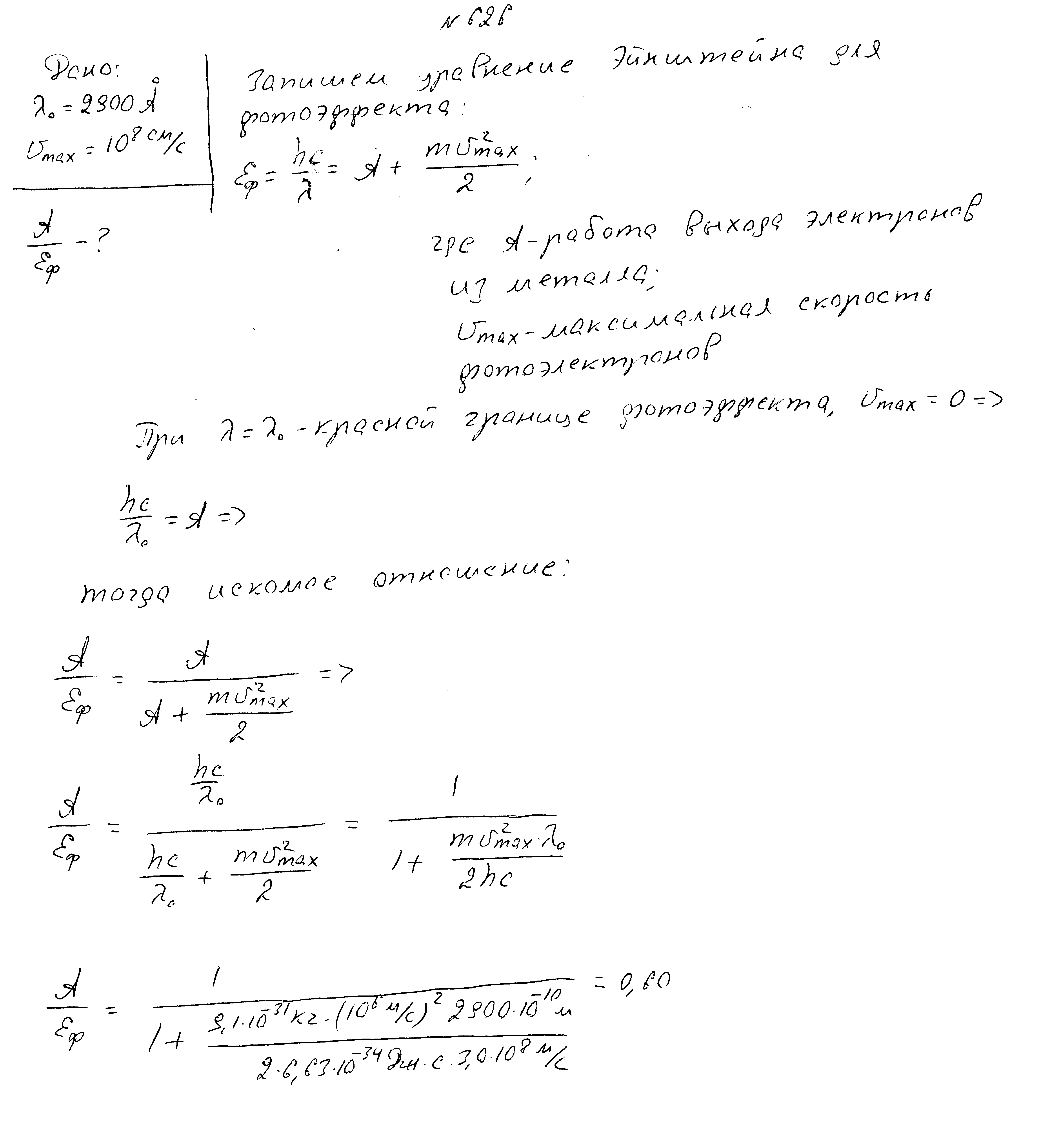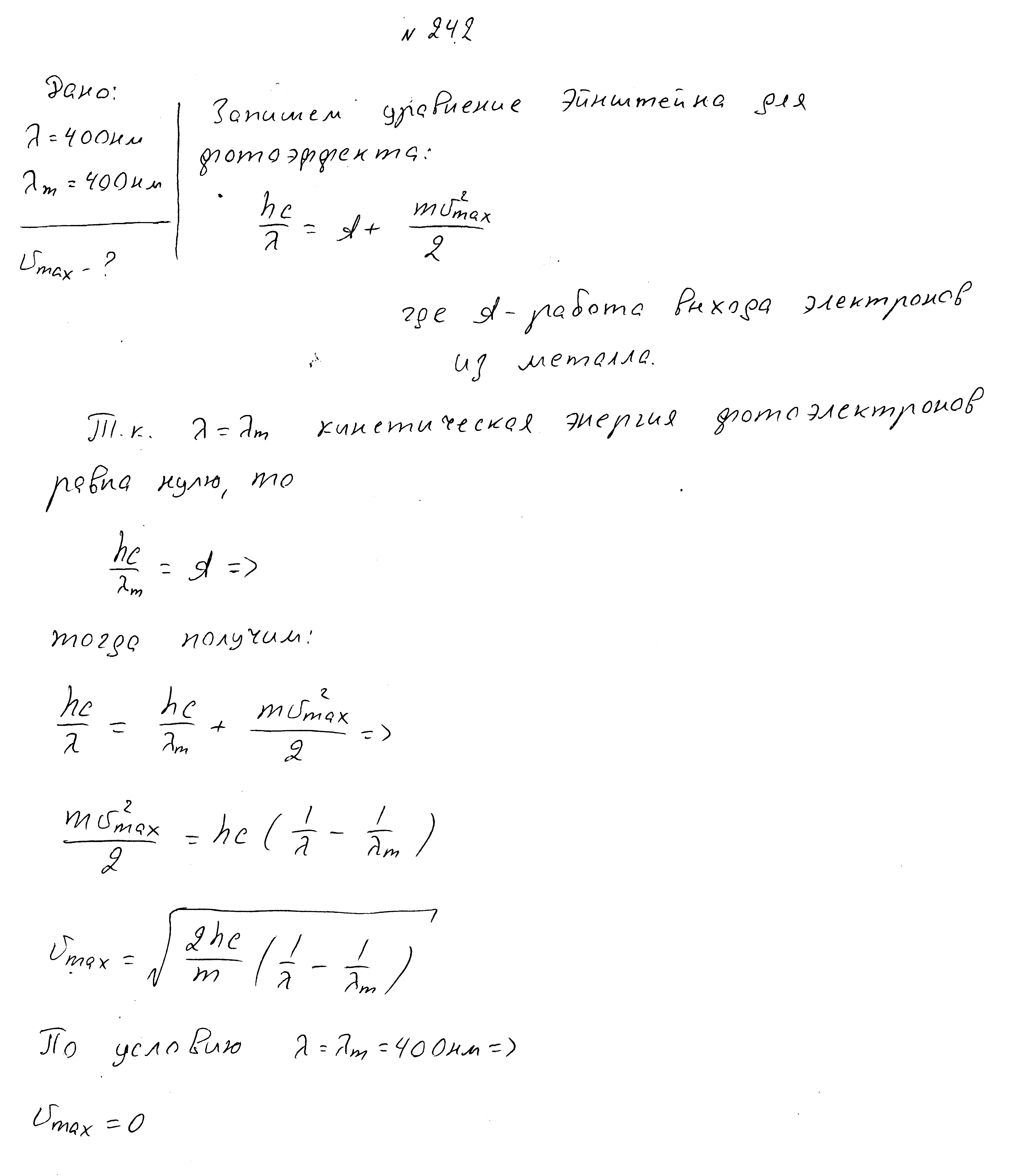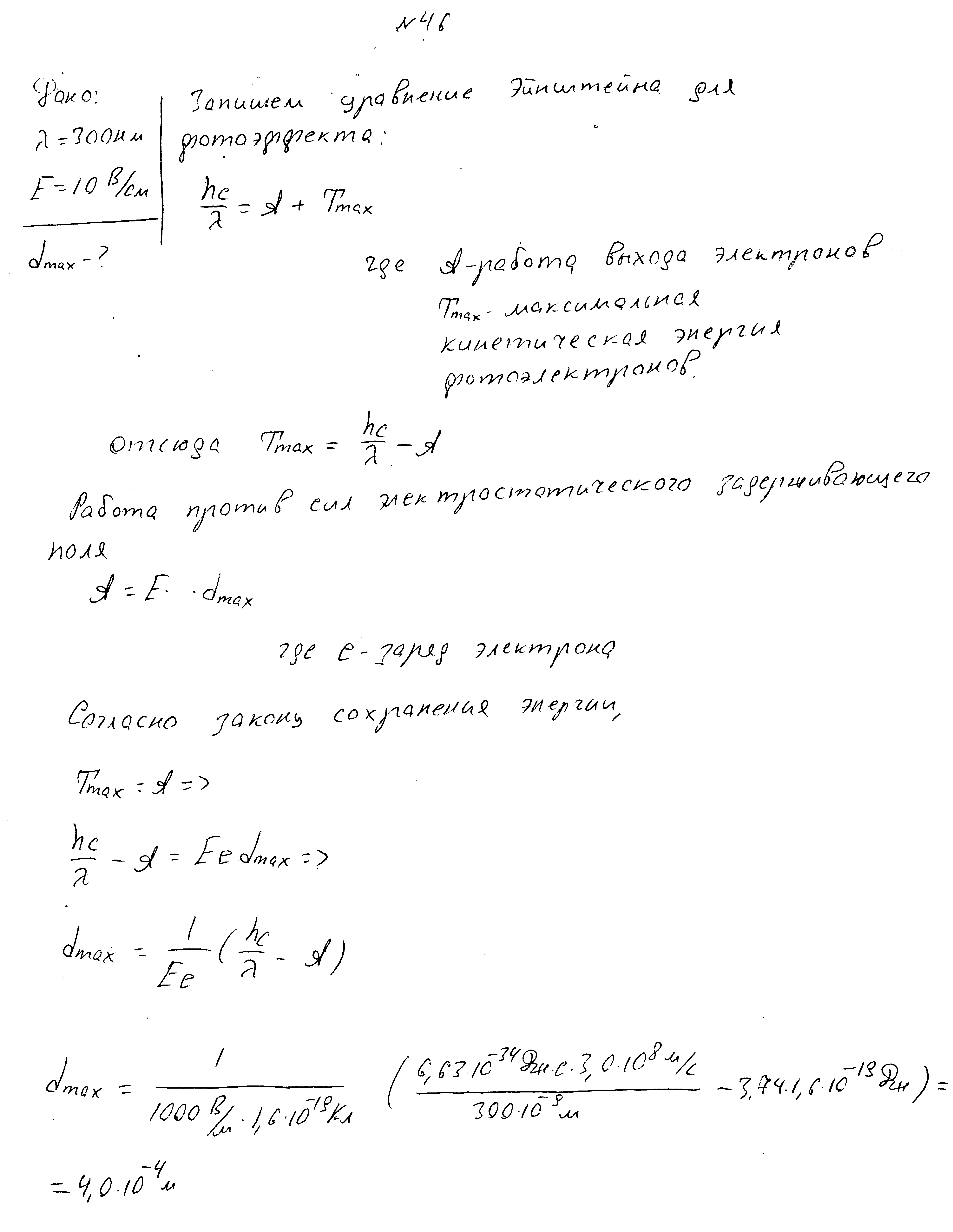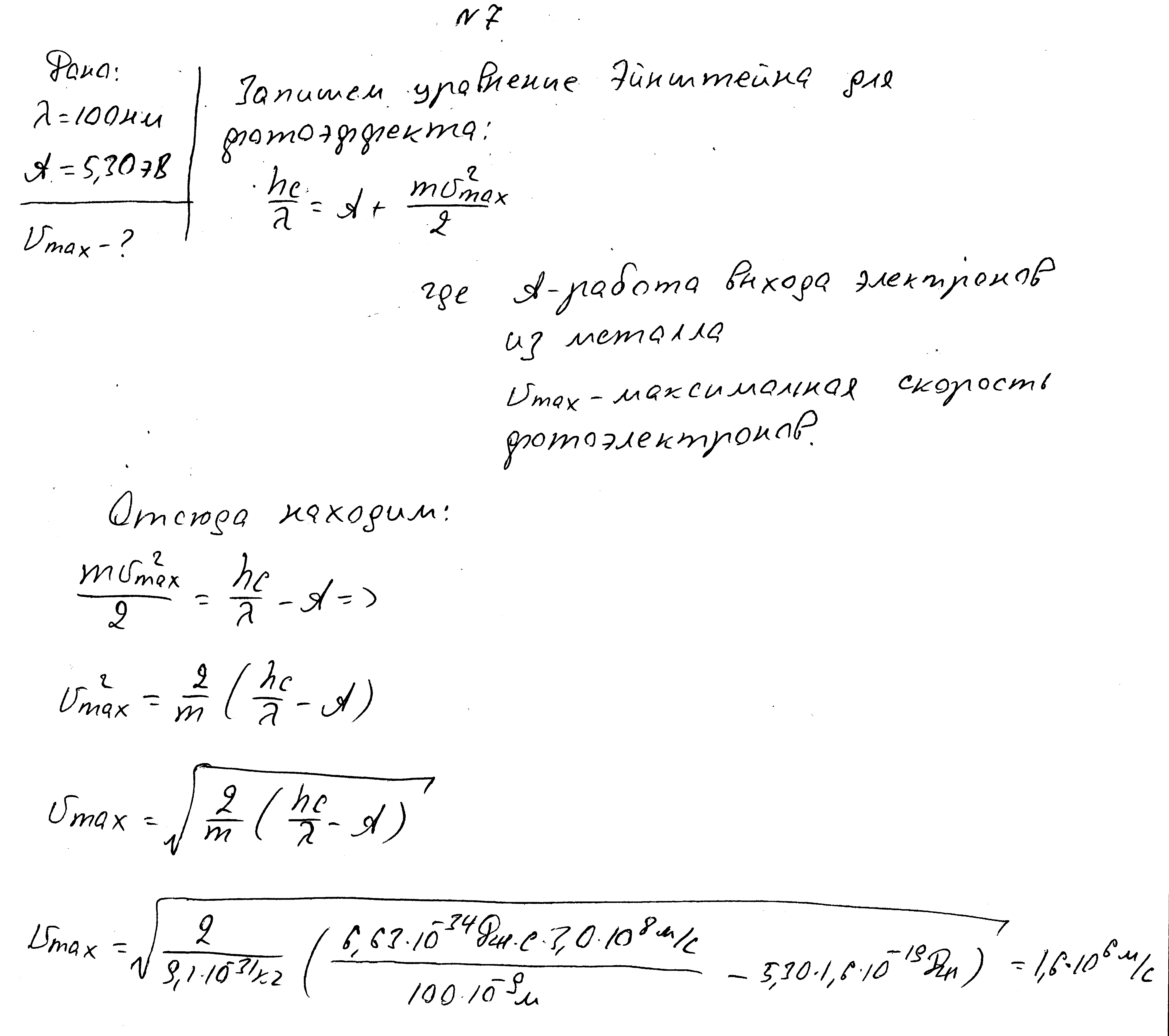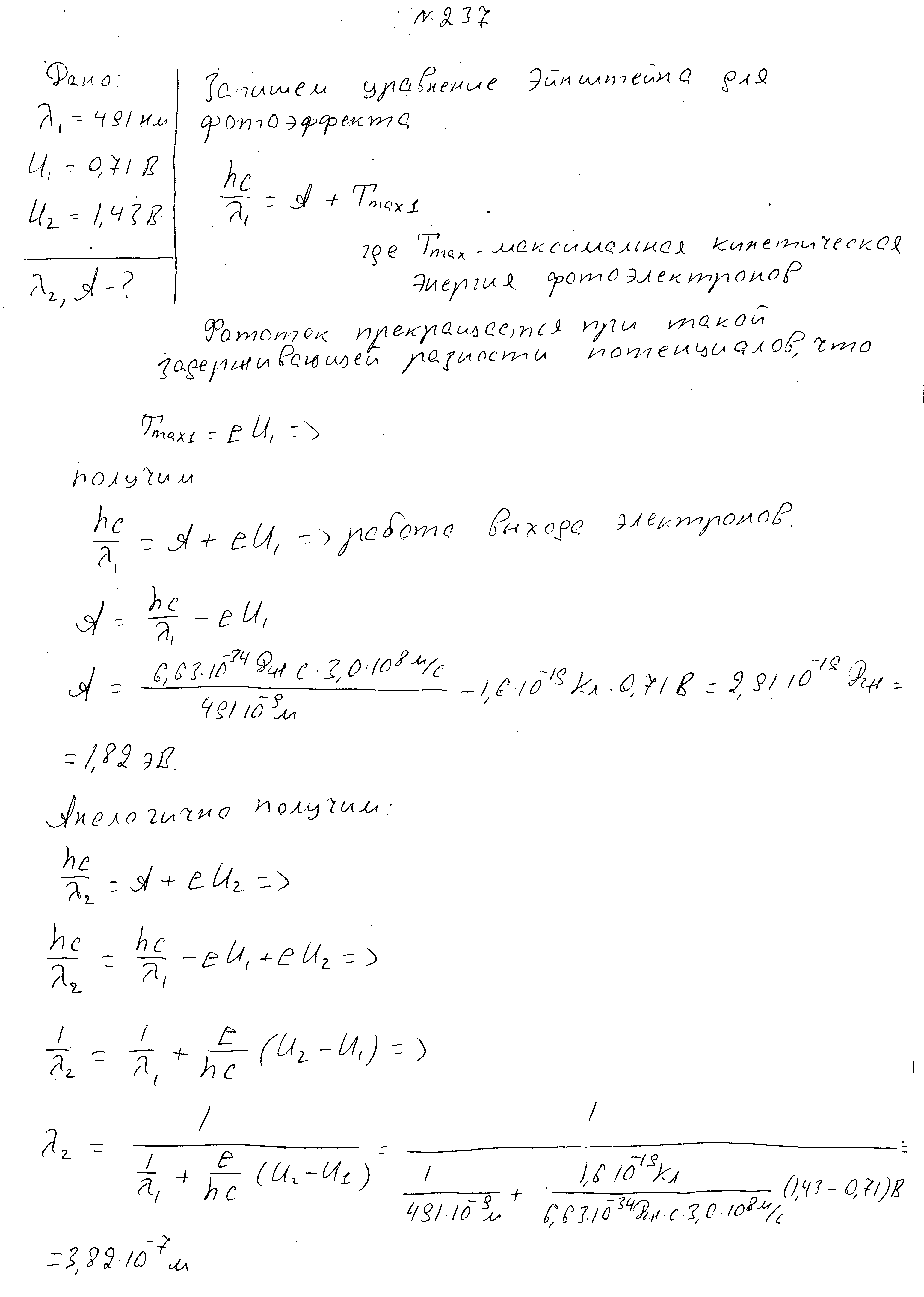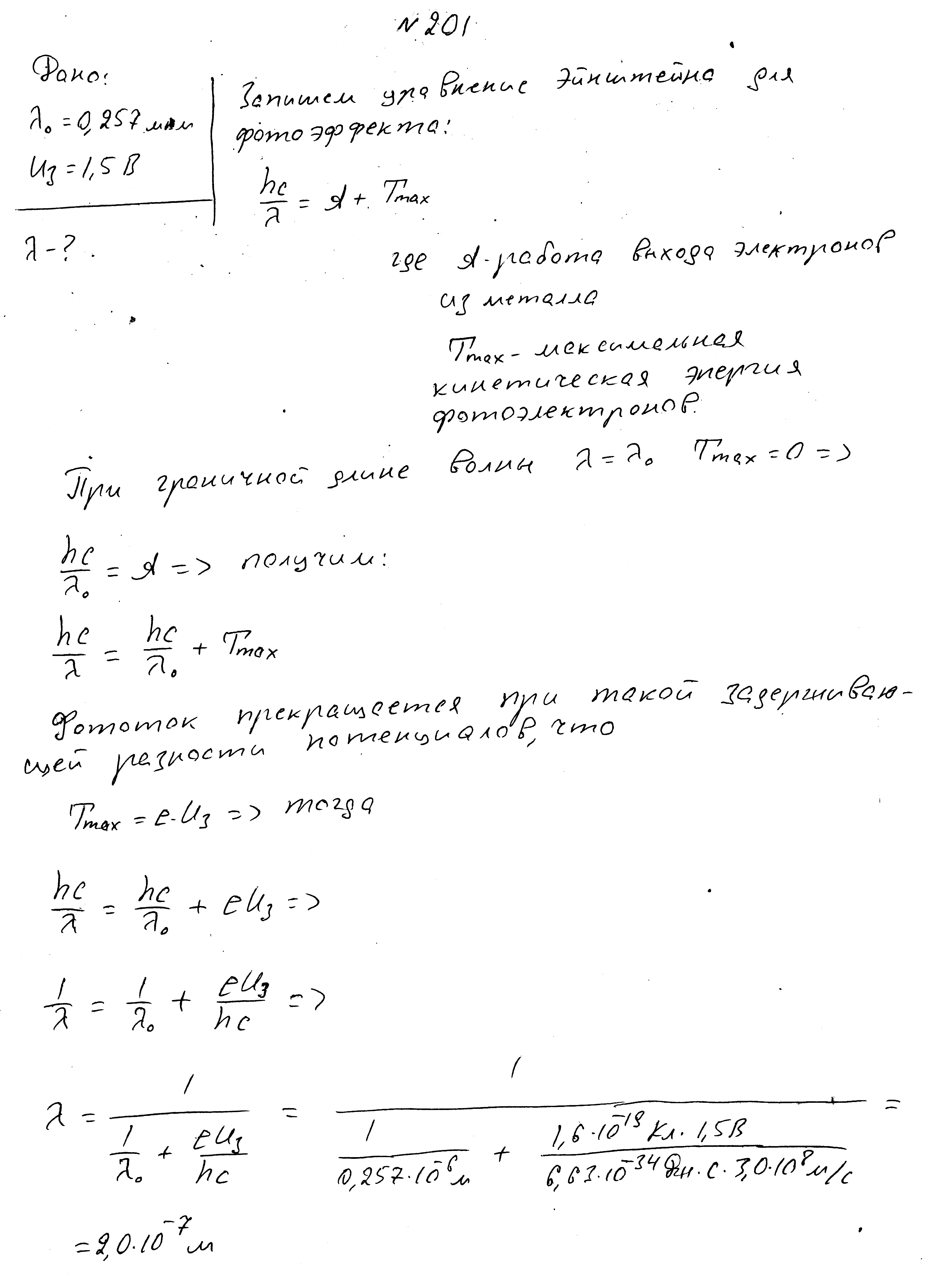Как найти максимальную скорость света при фотоэффекте

КВАНТОВАЯ ФИЗИКА.

РЕШЕНИЕ ЗАДАЧ.

ЗАДАЧА 2.

Найдите максимальную скорость электронов, освобождаемых при фотоэффекте светом с длиной волны   с поверхности материала с работой выхода 1,9 эВ.

Дано:

__________________________

Решение:

Для решения задачи воспользуемся уравнением Эйнштейна для фотоэффекта  , подставив в него выражение 

для максимальной кинетической энергии электронов.

КВАНТОВАЯ ОПТИКА И ЯДЕРНАЯ ФИЗИКА

Найти максимальную скорость фотоэлектронов, вырываемых с поверхности металла светом с длиной волны λ = 180 нм . Красная граница фотоэффекта λ = 275 нм

Дано:

λ_кр = 275 нм =275·10 -9 м

λ_кр = 180 нм =180·10 -9 м

Решение:

Зная красную границу фотоэффекта, найдем работу выхода

Уравнение Эйнштейна для внешнего фотоэффекта

Откуда максимальная кинетическая энергия

Максимальная скорость фотоэлектронов

Ответ: ;

Определение и уравнение фотоэффекта

Фотоэффект является одним из примеров проявления корпускулярных свойств света. Вылет электронов из освещенных тел, называется внешним фотоэффектом.

Сущность внутреннего фотоэффекта состоит в том, что при освещении полупроводников и диэлектриков от некоторых атомов отрываются электроны, которые, однако, в отличие от внешнего фотоэффекта, не выходят через поверхность тела, а остаются внутри него. В результате внутреннего фотоэффекта возникают электроны в зоне проводимости и сопротивление полупроводников и диэлектриков уменьшается.

При освещении границы раздела между полупроводниками с различным типом проводимости возникает электродвижущая сила. Это явление называется вентильным фотоэффектом.

Уравнение Эйнштейна для внешнего фотоэффекта

Основным уравнением, описывающим внешний фотоэффект, является уравнение Эйнштейна для внешнего фотоэффекта:

где – энергия фотона монохроматической волны света, — масса электрона, — работа выхода электрона из фотокатода.

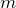
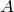
Уравнение фотоэффекта (1) является следствием закона сохранения энергии. В соответствии с законами сохранения энергии и импульса, поглощение фотона свободными электронами невозможно, и фотоэффект возможен только на электронах, связанных в атомах, молекулах и ионах, а также на электронах твердых и жидких тел.

Из уравнения фотоэффекта существует ряд важных выводов, которые характеризуют это явление:

1. Для данного фотокатода максимальная начальная скорость фотоэлектронов зависит от частоты падающего света и не зависит от его интенсивности.
2. При постоянном спектральном составе падающего света число фотоэлектронов, вырываемых светом из фотокатода за единицу времени, и фототок насыщения пропорциональны энергетической освещенности фотокатода.
3. Для каждого вещества фотокатода существует красная граница фотоэффекта (порог фотоэффекта) – минимальная частота , при которой еще возможен фотоэффект. Длина волны , соответствующая частоте , для большинства металлов находится в ультрафиолетовой части спектра.

Примеры решения задач

Вылет электронов прекратится тогда, когда потенциальная энергия электрона (U) в задерживающем поле станет равной его кинетической энергии (E), то есть:

Запишем уравнение фотоэффекта, в которое входит кинетическая энергия электрона:

Подставим (1.1) в (1.2), получим:

(1.3), откуда:

Полагая, что красная граница фотоэффекта соответствует энергии фотонов, при которой скорость вырываемых с металла электронов равна нулю, получим:

Подставим (1.5) в (1.4), получим:

Ответ
Искомая в задаче частота света может быть рассчитана по формуле:

Задание

Металлическую пластинку (работа выхода A) освещают светом с длинной волны 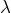. На какое максимальное расстояние от пластинки (d) может удалиться фотоэлектрон, если вне пластинки создано задерживающее однородное электрическое поле с напряженностью E?

Решение
Запишем уравнение фотоэффекта, в которое входит кинетическая энергия электрона:

По закону сохранения энергии, работа которую совершает электрическое поле при движении электрона (, равна максимальному значению кинетической энергии электрона при его максимальной удаленности от поверхности пластинки, следовательно, запишем:

Определить максимальную скорость v_max фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ ₁ =0,155 мкм; 2) γ-излучением с длиной волны λ ₂ =2,47 пм.

Решение . Максимальную скорость фотоэлектронов определим из уравнения Эйнштейна для фотоэффекта:

Энергия фотона вычисляется по формуле ε = hc / λ , работа выхода А указана в табл. 20 для серебра A =4,7 эВ.

Кинетическая энергия фотоэлектрона в зависимости от того, какая скорость ему сообщается, может быть выражена или по классической формуле

или по релятивистской

Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона ε много меньше энергии покоя электрона Е , то может быть применена формула (2); если же ε сравнима по размеру с Е , то вычисление по формуле (2) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3)

1. В формулу энергии фотона ε = hc / λ подставим значения величин h , с и λ и, произведя вычисления, для ультрафиолетового излучения получим

Это значение энергии фотона много меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть выражена

по классической формуле (2) ε ₁ = A + ½ m v 2 _max , откуда

(4)

Выпишем величины, входящие в формулу (4): ε ₁ =1,28 × 10 -18 Дж (вычислено выше); A =4,7 эВ = 4,7 × 1,6*10 -19 Дж = 0,75*10 -18 Дж; m =9,11 × 10 -31 кг (см. табл. 24).

Подставив числовые значения в формулу (4), найдем максимальную скорость:

2. Вычислим теперь энергию фотона γ-излучения:

Работа выхода электрона (A = 4,7 эВ) пренебрежимо мала по сравнению с энергией γ-фотона, поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона:

Так как в данном случае кинетическая энергия электрона сравнима с его энергией покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии,

где E = m c 2 .

Выполнив преобразования, найдем

Сделав вычисления, получим

Следовательно, максимальная скорость фотоэлектронов, вырываемых γ-излучением,

В сегодняшней статье нашей традиционной рубрики «физика» разбираем задачи на фотоэффект.

Подпишитесь на наш телеграм и не пропускайте важные новости. А на втором канале ищите скидки и приятные бонусы для клиентов.

Задачи на фотоэффект с решениями

Прежде чем приступать к решению задач, напоминаем про памятку и формулы. Эти материалы пригодятся при решении задач по любой теме.

Задача на фотоны и фотоэффект №1

Условие

Найти энергию фотона ε (в Дж) для  электромагнитного излучения с частотой ϑ=100·1014Гц.

Решение

Это типичная задача на энергию фотона. Применим формулу:

ε=hcλ=hϑ

Здесь h — постоянная Планка. Произведем расчет:

ε=6,63·10-34·10·1014=6,63·10-18Дж

Ответ: ε=6,63·10-18 Дж.

Задача на фотоны и фотоэффект №2

Условие

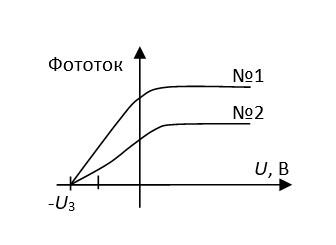
При фиксированной частоте падающего света в опытах №1 и №2 получены вольтамперные характеристики фотоэффекта (см. рис.). Величины фототоков насыщения равны I1 и I2, соответственно. Найти отношение числа фотоэлектронов N1 к N2 в этих двух опытах.

I1=13,5 мкАI2=10,6 мкА

Решение

Вольтамперная характеристика фотоэффекта показывает зависимость тока от напряжения между электродами. При выходе тока на насыщение все фотоэлектроны, выбитые из фотокатода, попадают на анод. Таким образом, величина тока насыщения пропорциональна числу фотоэлектронов. Тогда:

N1N2=I1I2=13,510,6=1,27

Ответ: 1,27.

Задача на фотоны и фотоэффект №3

Условие

На поверхность металла падают монохроматические лучи с длиной волны 0,1 мкм. Красная  граница фотоэффекта 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? 

Решение

Энергия падающего фотона равна:

ε=hcλ

Далее для решения задачи примененим уравнение Эйнштейна для фотоэффекта, которое можно записать в виде:

hcλ=hcλ0+Eк

Отсюда найдем кинетическую энергию:

Eк=hcλ-hcλ0=hcλ0-λλλ0

Чтобы найти искомую долю, разделим кинетическую энергию на энергию фотона:

W=Eкε=hcλ0-λλhc·λλ0=λ0-λλ0=3·10-7-10-73·10-7=0,667

Ответ: W=0,667.

Задача на фотоны и фотоэффект №4

Условие

Максимальная энергия фотоэлектронов, вылетающих из металла при его освещении лучами с длиной волны 325 нм, равна Tтax=2,3·10-19Дж. Определите работу выхода и красную границу фотоэффекта. 

Решение

Формула Эйнштейна для фотоэффекта имеет вид:

hϑ=hcλ=A+Tmax

Отсюда работа выхода A равна:

A=hcλ-Tmax

Красная граница фотоэффекта определяется условием Tmax=0, поэтому получаем:

A=hcλ0λ0=hcA

Найдем:

A=6,63·10-34·3·1083,25·10-7-2,3·10-9=3,81·10-19 Дж

λ0=6,63·10-34·3·1083,81·10-19=520 нм

Ответ: A=3,81·10-19Дж; λ0=520 нм.

Задача на фотоны и фотоэффект №5

Условие

Наибольшая длина волны света λ0, при которой еще может наблюдаться фотоэффект на сурьме, равна 310 нм. Найдите скорость электронов, выбитых из калия светом с длиной волны 140 нм. 

Решение

Красная граница фотоэффекта определяется условием Tmax=0, поэтому для работы выхода получаем:

A=hcλ0

Формула Эйнштейна для фотоэффекта имеет вид:

hcλ=A+Tmax

Учитывая, что Tmax=mv2max2, определим максимальную скорость электронов при фотоэффекте:

vmax=2hcm1λ-1λ0

Произведем вычисления:

vmax=2·6,63·10-349,1·10-3111,4·10-7-13,1·10-7=1,3·106 мс

Ответ: 1,3·106 мс.

Вопросы с ответами на тему «Фотоны и фотоэффект»

Вопрос 1. В чем суть фотоэффекта?

Ответ. Фотоэффект — это явление «выбивания» электронов из вещества под действием света (электромагнитного излучения).

Вопрос 2. Что такое ток насыщения?

Ответ. Ток насыщения при фотоэффекте — максимальное значение фототока.

Вопрос 3. Что такое красная граница фотоэффекта?

Ответ. Это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.

Вопрос 4. Что такое работа выхода?

Ответ. Это минимальная энергия, которую надо сообщить электрону, чтобы выбить его из металла.

Вопрос 5. Что такое квант?

Ответ. Неделимая порция какой-либо величины в физике.

Нужна помощь в решении задач и выполнении других типов заданий? Обращайтесь в профессиональный сервис для учащихся по любому вопросу.

Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь  похожее условие и решить свою по аналогии.   Загрузка страницы может занять некоторое время в связи с большим количеством рисунков.  Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.

Явление фотоэффекта заключается в испускании веществом электронов под действием падающего света. Теория фотоэффекта разработана Эйнштейном и заключается в том, что поток света представляет собой поток отдельных квантов(фотонов) с энергией каждого фотона hn. При попадании фотонов на поверхность вещества часть из них передает свою энергию электронов. Если этой энергия больше работы выхода из вещества, электрон покидает металл. Уравнение эйнштейна для фотоэффекта:  где  — максимальная кинетическая энергия фотоэлектрона. 

Длина волны красной границы фотоэффекта для некоторого металла составляет 307 нм. Максимальная кинетическая энергия фотоэлектронов – 1 эВ. Найти отношение работы выхода электрона к энергии падающего фотона. 

Частота света красной границы фотоэффекта для некоторого металла составляет 6*10¹⁴ Гц, задерживающая разность потенциалов для фотоэлектронов – 2В. Определить частоту падающего света и работу выхода электронов. 

Работа выхода электрона из металла составляет 4,28эВ. Найти граничную длину волны фотоэффекта.

На медный шарик радает монохроматический свет с длиной волны 0,165 мкм. До какого потенциала зарядится шарик, если работа выхода электрона для меди 4,5 эВ?

Работа выхода электрона из калия составляет 2,2эВ, для серебра 4,7эВ. Найти граничные длину волны фотоэффекта.

Длина волны радающего света 0,165 мкм, задерживающая разность потенциалов для фотоэлектронов 3В. Какова работа выхода электронов?

Красная граница фотоэффекта для цинка 310 нм. Определить максимальную кинетическую энергию фотоэлектронов, если на цинк падает свет с длиной волны 200нм.

На металл с работой выхода 2,4эВ падает свет с длиной волны 200нм. Определить задерживающую разность потенциалов. 

На металл  падает свет с длиной волны 0,25 мкм, задерживающая разность потенциалов при этом 0,96В. Определить работу выхода электронов из металла. 

При изменении длины волны падающего света  максимальные скорости фотоэлектронов изменились в 3/4 раза. Первоначальная длина волны 600нм, красная граница фотоэффекта 700нм. Определить длину волны после изменения. 

Работы выхода электронов для двух металлов отличаются в 2 раза, задерживающие разности потенциалов — на 3В. Определить работы выхода. 

Максимальная скорость фотоэлектронов равно 2,8*10⁸ м/с. Определить энергию фотона. 

Энергии падающих на металл фотонов равны 1,27 МэВ. Найти максимальную скорость фотоэлектронов. 

Максимальная скорость фотоэлектронов равно 0,98с, где с — скорость света в вакууме. Найти длину волны падающего света. 

Энергия фотона в пучке света, падающего на поверхность металла, равно 1,53 МэВ. Определить максимальную скорость фотоэлектронов. 

На шарик из металла падает свет с длиной волны 0,4 мкм, при этом шапик заряжается до потенциала 2В. До какого потенциала зарядится шарик, если длина волны станет равной 0,3 мкм?

После изменения длины волны падающего света в 1,5 раза задерживающая разность потенциалов изменилась с 1,6В до 3В. Какова работа выхода?

Красная граница фотоэффекта 560нм, частота падающего света 7,3*10¹⁴ Гц. Найти максимальную скорость фотоэлектронов. 

Красная граница фотоэффекта 2800 ангстрем, длина волны падающего света 1600 ангстрем. Найти работу выхода и максимальную кинетическую энергию фотоэлектрона.

Задерживащая разность потенциалов 1,5В, работа выхода электронов 6,4*10^-19 Дж. Найти длину волны падающего света и красную границу фотоэффекта.

Работа выхода электронов из металла равна 3,3 эВ. Во сколько раз изменилась кинетическая энергия фотоэлектронов. если длина волны падающего света изменилась с 2,5*10^-7м до 1,25*10^-7м?

Найти максимальную скорость фотоэлектронов для видимого света с энергией фотона 8 эВ и гамма излучения с энергией 0,51 МэВ. Работа выхода  электронов из металла 4,7 эВ.

Фототок прекращается при задерживающей разности потенциалов 3,7 В. Работа выхода электронов равна 6,3 эВ. Какая работа выхода электронов у другого металла, если там фототок прекращается при разности потенциалов, большей на 2,3В.

Работа выхода электронов из металла 4,5 эВ, энергия падающих фотонов 4,9 эВ. Чему равен максимальный импульс фотоэлектронов?

Красная граница фотоэффекта 2900 ангстрем, максимальная скорость фотоэлектронов 10⁸ м/с. Найти отношение работы выхода электронов к энергии палающих фотонов. 

Длина волны падающего света 400нм, красная граница фотоэффекта равна 400нм. Чему равна максимальная скорость фотоэлектронов?

Длина волны падающего света 300нм, работа выхода электронов 3,74 эВ. Напряженность задерживающего электростатического поля 10 В/см.Какой максимальный путь фотоэлектронов при движении в направлении задерживающего поля?

Длина волны падающего света 100 нм, работа выхода электронов 5,30эВ. Найти максимальную скорость фотоэлектронов.

При длине волны радающего света 491нм задерживающая разность потенциалов 0,71В. Какова работа выхода электронов? Какой стала длина волны света, если  задерживающая разность потенциалов стала равной 1,43В?

Кинетическая энергия фотоэлектронов 2,0 эВ, красная граница фотоэффекта 3,0*10¹⁴ Гц. Определить энергию фотонов.

Красная граница фотоэффекта 0,257 мкм, задерживающая разность потенциалов 1,5В. Найти длину волны падающего света.

Красная граница фотоэффекта 2850 ангстрем. Минимальное значение энергии фотона, при котором возможен фотоэффект?

Ниже вы можете посмотреть обучаюший видеоролик на тему фотоэффекта и его законов.

2.
Для каждого вещества существует красная
граница фотоэффекта, т.
е. минимальная частота vq
света, при
ко­торой еще возможен внешний
фотоэффект. Величина v₀
зависит от
химической природы вещества и состояния
его поверхности.

3.
Число фотоэлектронов п,
вырываемых с
единицы площади катода за единицу
времени, пропорционально интенсивности
света (фототек
насыщения пропорционален энергетической
освещенности Е_э
катода, т. е. /нас~£э).

Приведенные
первый и второй законы фотоэффекта
трудно объяснить с помощью волновой
природы света. Для объяснения этих
законов А./Эйнштейн (1879—1955) развил идеи
Планка о кванто/ом характере теплового
излучения. Он предположил, что свет не
только излучается отдельными квантами,
но распространяется и поглощается
веществом в виде квантов энергии. В
связи с этим распро­странение
электромагнитного излучения рассматривается
уже не как непрерывный волновой процесс,
а как поток дискретных квантов, движущихся
в вакууме со скоростью света с.
Эти кванты
электромагнитного излучения были
названы фотонами (1926
г.). Процесс поглощения света сводится
к тому, что фотоны передают всю свою
энергию частицам этого вещества. С
позиции квантовой природы света Эйнштейн
дал наглядное объяснение явления
фото­эффекта. Для вырывания электрона
из вещества необхо­димо совершить
работу, которая называется работой
вы-

хода
А. Поэтому, если энергия
кванта hv
> А,
то фотоэф­фект будет
наблюдаться. В соответствии с законом
сохра­нения энергии Эйнштейн предложил
следующее урав­нение: (9.22)

— уравнение
Эйнштейна для
внешнего фотоэффекта.

Величина
muLx/2
представляет собой максимально воз­можную
кинетическую энергию вырванного
электрона. Уравнение (9.22) объясняет все
экспериментально установленные законы
фотоэффекта: во-первых, из соотно­шения
(9.22) следует, что максимальная скорость
вырван­ных фотоэлектронов зависит
не от интенсивности /, а от частоты v
света и работы выхода А
(первый закон
фотоэффекта); во-вторых, внешний фотоэффект
воз­можен только в том случае, если
энергия фотона hv
боль­ше или равна
А. Поэтому
частота vo,
соответствующая красной границе
фотоэффекта (второй закон фото­эффекта),
равна

— красная граница
фотоэффекта. (9.23)

И,
наконец, общее число п
фотоэлектронов,
вылетающих из вещества за единицу
времени, пропорционально числу фотонов,
падающих за это время на поверхность
веще­ства, т. е. пропорционально
интенсивности падающего света (третий
закон фотоэффекта).

Спомощью соотношений (9.21) и (9.23) уравнение
Эйнштейна для фотоэффекта можно
переписать в виде (9.24)

Если
значения v
и v₀
известны, то, определив из опыта величину
задерживающего потенциала U₃,
можно с по­мощью
формулы (9.24) найти постоянную Планка:

(9.25)

Совпадение
найденного по этой формуле значения h
с результатами ее
измерения в других опытах, в частности
в опытах с тепловым излучением абсолютно
черного тела, подтверждает справедливость
уравнения Эйнштейна для фотоэффекта.

При
больших интенсивностях света (лазерное
излуче­ние) возможен многофотонный
фотоэффект. Он
наблюда­ется при поглощении электроном
энергии N фотонов
(N
= = 2, 3, …). Уравнение
для многофотонного фотоэффекта имеет
вид

(9.26)

Красная граница
при многофотонном эффекте опре­деляется
соотношением

(9.27)

Внешний фотоэффект
используется в фотоэлементах, которые
служат для регистрации и измерения
световых потоков путем преобразования
световых сигналов в элек­трические.