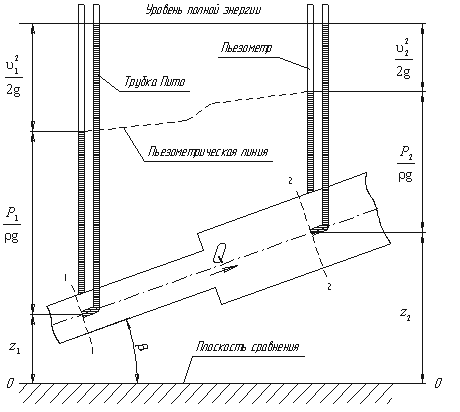
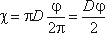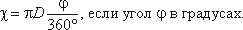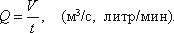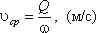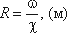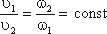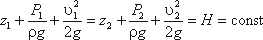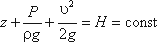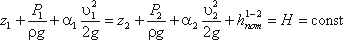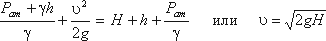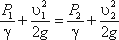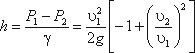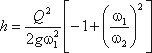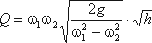Как найти максимальную скорость движения жидкости - AvtoShod.ru

3.1. Уравнение д. Бернулли без учета потерь энергии

Уравнение Д. Бернулли для потока невязкой
жидкости (без учета потерь энергии),
составленное в отношении произвольно
выбранной плоскости сравнения, имеет
следующий вид:

Левая часть уравнения представляет
собой сумму двух видов энергии:
потенциальной, состоящей из энергии
положения

и энергии давления,
и кинетической энергии,
отнесенных к единице веса движущейся
жидкости. Коэффициент кинетической
энергии потока,
входящий в уравнение Д. Бернулли при
движении невязкой жидкости, может
быть принят равным единице.

Многие практические задачи, связанные
с установившимся движением жидкости,
решаются совместным применением
уравнения Д. Бернулли и уравнения
неразрывности (сплошности) потока.

Уравнение неразрывности может быть
записано в следующем виде:

откуда

где V₁иV₂— средние скорости в сечениях потока;

и— соответствующие площади живых сечений.

Примеры

3.1.Определить расход водыв трубе диаметром,
имеющей плавное сужение до диаметра,
если показания пьезометров: до сужения;
в сужении.
Температура воды.

Решение.Составим уравнение Бернулли
для сечений 1-1 и 2-2, принимая за плоскость
сравнения ось трубы:

Учитывая, что
,
пренебрегая потерями напора, т. е.
принимая,
и полагая,получим:

Из уравнения неразрывности расхода
имеем:

Поскольку

находим:

Обозначим

Тогда уравнение Бернулли запишется в
виде

откуда найдем скорость в сечении 1-1:

Расход воды в трубе

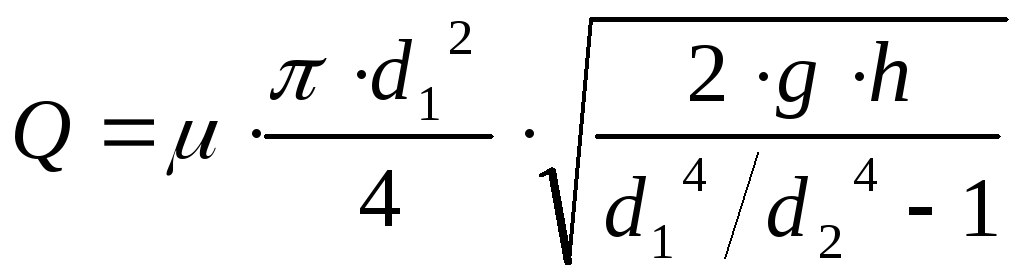
где μ – коэффициент, учитывающий
уменьшение расхода вследствие потерь
напора; в первом приближении принимаем
μ=0,98; тогда расход будет

Коэффициент μ зависит от отношения
диаметров
и числа Рейнольдса:

;

Найдем скорость в сужении трубы

Кинематическую вязкость воды примем:
(табл. П-12).

С учётом полученных данных найдем число
Рейнольдса

По табл. П-25 находим μ =0,98. Следовательно,
в первом приближении значение μ принято
верно.

Искомый расход
.

Замечание: Рассмотренное сужение трубы
с плавными переходами от большего
диаметра к малому и от малого к большому
называется водомером Вентури.

Ответ: .

3.2.Определить, на какую высоту
поднимается вода в трубке, один конец
которой присоединён к суженному сечению
трубопровода, а другой конец опущен в
воду. Расход воды в трубе,
избыточное давление,
диаметрыи.

Решение.Уравнение Бернулли для
сечений 1-1 и 2-2 относительно оси трубы
(потерями напора пренебрегаем) имеет
вид (при)

Учитывая, что скорости в сечениях 1-1 и
2-2 находятся так

и,

то после преобразований получим:

Полученная отрицательная высота –
вакуумметрическая высота. На эту высоту
и поднимается вода в трубке.

Ответ: .

3.3. Определить критическую скорость,
отвечающую переходу от ламинарного
режима к турбулентному, в трубе диаметромd= 0,03 м при движении воды
и воздуха при температуре 25˚C и глицерина
при температуре 20˚C.

Решение.Из формулы для критического
числа Рейнольдса имеем:

Для воды

Для воздуха

Для глицерина

3.4. Определить давлениер₁
в сечении1-1горизонтально
расположенного сопла гидромонитора,
необходимое для придания скорости
водеV₂ = 40м/св выходном сечении2-2, если
скорость движения воды в сечении1-1
V₁= 3м/с.

Решение.Данная задача может быть
решена при помощи уравнения Д. Бернулли
и уравнения неразрывности.

При составлении уравнения Д. Бернулли
следует выбрать два сечения в
рассматриваемом потоке и плоскость
сравнения, по отношению к которой
записывается уравнение для двух выбранных
сечений. Эти сечения и плоскость сравнения
выбираются так, чтобы наибольшее
количество величин, входящих в уравнение,
были известными, а в уравнение входили
искомые величины.

При решении данной задачи удобно
использовать сечения 1 — 1 и2 —2, поскольку скорости в этих
сечениях заданы, давлениеp₁подлежит определению, а давлениер₂в сечении на выходе из гидромонитора
равно атмосферному. Плоскость сравнения
следует провести через ось сопла, тогда
удельные энергии положенияz₁= z₂= 0 и
уравнение Д. Бернулли будет иметь
следующий вид:

откуда.

Ответ:.

3.5.Определить диаметрdсуженной части горизонтального
трубопровода, при котором вода
поднимается на высотуh
= 3,5м при расходе

Q= 6л/с и диаметреD = 10см.

Решение.Плоскость сравнения
совместим с осью трубы. Выбрав сечения1 — 1 и2 —2 и составив
уравнение Д. Бернулли, получим:

Так как плоскость сравнения проведена
по оси трубы, то z₁
=z₂= 0, и тогда

Для того чтобы вода поднялась на высоту
3,5 м, необходимо, чтобы удельная
энергия давления в сечении1 — 1была
равна,
откуда.

Так как истечение происходит в атмосферу,
то давление р₂равно атмосферному,
т.е.

Следовательно,

Для определения диаметра суженной части
воспользуемся уравнением неразрывности
движения
,
гдеи.

Подставив в уравнение найденные величины,
получим

откуда искомый диаметр

Ответ:
.

3.6.Определить расход воды в
горизонтальном трубопроводе переменного
сечения, скорость на каждом из участков
и построить пьезометрическую линию,
еслиH= 5м, d₁= 15мм, d₂= 20мм и d₃
= 10мм.

Решение.Уравнение Д. Бернулли для
сечений0 — 0 и3 —3при
совмещении плоскости сравнения с осью
трубы будет иметь вид

В данном случае
=H,= 0. В связи с тем, что в сечениях0—0
и3—3давление равно атмосферному,
то.
Учитывая, чтоH=const,
а скорость в сечении0—0 V₀= 0, скорость в выходном сечении3 —3определится из зависимости

откуда

Расход воды в трубопроводе

Скорость в сечении 1 —
1

Скорость в сечении 2 —2

Пьезометрическую линию строят, исходя
из следующих положений. Поскольку задача
решается без учета потерь энергии, то
напорная линия (линия полной энергии)
будет представлять собой горизонтальную
прямую, являющуюся продолжением свободной
поверхности воды в сечении 0 —0.
Пьезометрическая линия расположитсяниже напорной линии на величинув каждом сечении. Таким образом, отложив
вниз от напорной линии величиныв сечениях, соответствующих изменению
диаметра трубопровода, получим ряд
точек, соединив которые построим
пьезометрическую линию (см. рис). При
этом:

Ответ:
.

3.7. Определить избыточное давление
воды на входе в брандспойт и диаметр
выходного сечения , необходимые для
получения струи мощностьюQ=9
л/с, бьющей вертикально вверх на высоту
Н=15 м при диаметре входного сеченияD=60
мм и длине брандспойтаh=0,5
м.

Решение:

Составим уравнение Бернулли для сечений
1-1 и 3-3

относительно плоскости сравнения

(см.рис.):

где Z₁=0;p₁=;Z₃=(H+h);p₃=p_атм;V₃=0;V₁=.

Тогда
.

Откуда найдем давление на входе в
брандспойт:

Па=1,498Па.

Составим уравнение Бернулли для сечений
2-2 и 3-3 относительно плоскости сравнения
(см.рис.):

где Z₂=0;p₂=p_атм;
р₃=р_атм;Z₃=H;V₃=0.

Тогда получаем уравнение:

,
откуда определим скорость воды на
входеVм|c.

Из уравнения постоянства расхода Q=найдем диаметрd:

d=м=25,8 мм.

Ответ: рПа;d=25,8 мм.

3.8. Поршень в цилиндре А, двигаясь
вверх, поднимает воду из резервуара В
при разности уровней воды в цилиндре
под поршнем и в резервуаре Н=3 м. Определить
скорость движения поршня, при котором
абсолютное давление под ним р=0,65 кг/см.

Решение:

Составим уравнение Бернулли для сечений
1-1 и 2-2 относительно плоскости сравнения
0-0 (см.рис.):

где Z;p=p;V;Z=H;p=p;V=V.

Тогда
=H+.

Откуда найдем скорость поршня:

V=м/с.

Ответ: V_n=3,13
м/с.

3.9. Давление в трубопроводе диаметром
d=35 мм при закрытом кране равно p=3,2
кгс/см². Определить давление перед
краном при расходе воды в трубопроводе
Q=7,3 л/с.

Решение:

Найдём скорость движения воды в трубе
после открытия крана:

м/с.

Таким образом, часть давления
(первоначального) перейдёт в скоростной
напор:

H_v=м.

Найдём это конечное давление перед
краном:

^р^1

=

Па = 2,88 кгс/см².

Ответ:р₁=2,88 кгс/см².

3.10. Горизонтальный отстойник для
очистки сточных вод имеет ширинуb=1,5
м и глубинуh=1,0 м. Режим
движения воды в отстойнике ламинарный.
Определить максимально допустимый
расход сточных вод в отстойнике, еслиt_в=20^oC,Rе<Rе_кр

Решение: Так как режим движения воды
в отстойнике ламинарный, то число
Рейнольда длжно быть меньше критического,
которое для открытых русел может быть
найдено по зависимости:

Rе’_кр== 800 ÷ 900,

где R=— гидравлический радиус;

ω=bh–площадь
гидравлического сечения отстойника;

χ= 2h+b– смоченный периметр отстойника.

Тогда R=
=
=.

Найдём максимальное значение скорости,
соответствующее максимальному режиму
движения. При этом
=
1.01·10^-6м²/c(Приложение 2, стр 226 (1)).

Замечание : скорость получилась вполне
удовлетворительная для горизонтальных
отстойников. Теперь найдём максимально
допустимый расход сточных вод:

л/c

Ответ:
.

3.11. Под действием разности уровнейH= 2,6 м и избыточном давленииp₀= 0.3 ат по трубе
нормального сечения вода перетекает
из из верхнего резервуара в нижний(d₁=150мм,d₂=125 мм,d₃=100 мм). Определить
расход воды и построить пьезометрическую
линию без учёта потерь на трение.

Решение:

Составим уравнение Бернулли для сечений
1-1

и 2-2 относительно плоскости сравнения
0-0

( см. рис.):

где Z₁=H;Z₂= 0;p_1

=p_o+p_ат;p₂=p_ат;

V₁=V₂≈ 0.

Так как по условию задачи потери на
трение

не учитываются, то остаются только

потери напора на местных сопротивлениях:

h_w=h_l+h_м= 0 +h_м,

где h_м=h_вх+h_вн.с.1+h_вн._c_.2+h_вых.

В результате получаем:

или
(*).

Распишем местные сопротивления:

;;

где
;;

;;

Подставив исходные данные в эти формулы,
в результате получим:

;;

;

Потери напора в местных сопротивлениях
приведем к одной скорости, в частности,
к V_{3 :}

;;

Представив эти значения в уравнение
(*) , в результате получим:

Найдём напор; соответствующий давлению

Получаем уравнение:

откуда найдём скорость

Найдём величину расхода воды, протекающей
по трубе:

Для построения пьезометрической линии
найдём величину скоростного напора в
каждой из трёх труб:

;

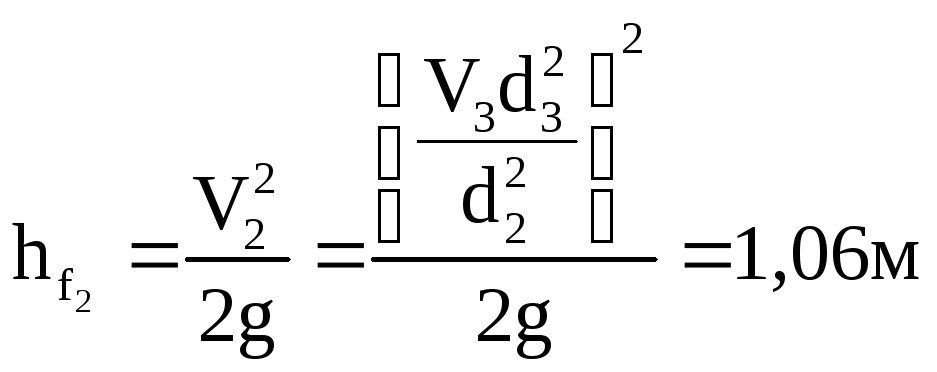
Найдём теперь потери напора на местных
сопротивлениях и от этих значений вниз
отложим величины скоростных напоров,
в результате получим линию пьезометрических
напоров p-p:

;

Замечание: если бы в решении задачи
были учтены потери напора на трение по
длине, то линияp-pна участкахd_1,d_2,d₃имела бы
наклонный характер.

3.12. Из открытого резервуара вода
вытекает по расширяющейся трубе с
диаметрамиd₁=300 мм
иd₂=350 мм , длиной
от суженной части до нижнего сеченияH₂= 2,5 м. Найти давлениеpв суженной части трубы
при напореH₁= 0,65 м.
Потерями напора пренебречь.

Решение:

З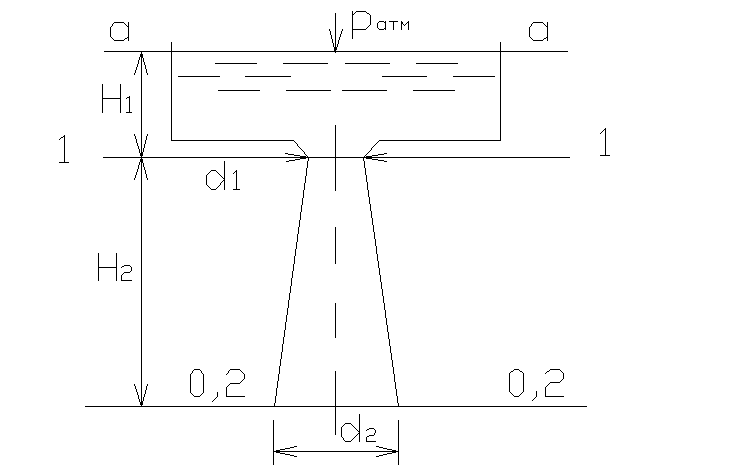апишем
уравнение Бернулли для сечений а-а и
2-2 относительно плоскости сравнения
0-0 (см. рис.):

Тогда

откуда найдем скорость истечения
:

По уравнению постоянства расхода
найдем скорость воды в сечении 1-1:

Составим уравнение Бернулли для
сечений 1-1 и 2-2 относительно плоскости
сравнения 0-0:

где
.

Тогда
откуда найдём давление

Ответ:

3.13. Определить среднюю скорость
движения воды в трубе, если разность
показаний между динамической и статической
трубками, определяемая по ртутному
дифференциальному пьезометру, составляетh=20 мм.

Решеиие:

Составим уравнение равновесия для

ртутного пьезометра:

где
—
давление в точке А.

Получаем

=h(—
1).

Следовательно, скорость на оси трубы
равна:
==

==2,22м/с

Средняя скорость в трубе при турбулентном
режиме движения составит

V=(0,850,95)=(0,850,95)2,22=
(1,892,11)м/с.

Ответ. V2,0м/с.

3.14. Из резервуара по трубе, имеющей
сужение, протекает вода. Определить
диаметр суженной частиd,
при котором образуется заданная величинаh_вак=10мм, если
известны напор Н=10м и диаметрD=100мм.

Д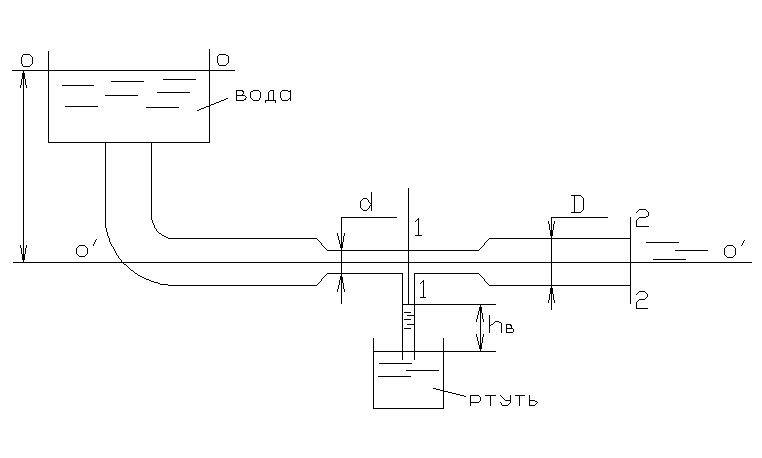ано:

Решение:

Составим уравнение Бернулли для сечений
0-0 и 2-2 относительно плоскости сравнения
—:

где

.

Тогда получаем .

Найдём скорость на выходе из трубы
.

Составим уравнение Бернулли для сечений
1-1 и 2-2 относительно плоскости сравнения
—:

где

.

Подставим и получим
,

Откуда найдём вакуум.

Поделим на удельный вес ртути и найдём
вакуумметрическую высоту

;

или

Найдём скорость в сечении 1-1

По уравнению неразрывности найдём
диаметр в сечении 1-1

Ответ:
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

На чтение 4 мин Просмотров 4.4к.

В предыдущей статье было подробно рассмотрено ключевое понятие для гидравлики – давление. Теперь, во второй части этой статьи, я постараюсь максимально просто рассказать про движение жидкости.

Для начала рассмотрим, какое бывает движение жидкости. Существует большое количество различных классификаций и подходов к математическому описанию движения, но мы практически все это опустим, упомянем лишь, что в инженерной практике преимущественно рассматривается так называемое установившееся равномерное движение.

Это означает, что мы рассматриваем поток жидкости как замороженную картинку. Обычно системы водоснабжения и канализации рассчитывают именно так, принимая при этом пиковую нагрузку (расходы). Кроме того отметим, что рассматриваем далее движение реальной жидкости (т.е. в ней действуют силы внутреннего трения).

Это означает, что жидкость испытывает сопротивление своему движению, и тратит на движение свою энергию, которую называют напором жидкости.

Для нас также важно то, что движение жидкости может быть безнапорным и напорным.

Содержание

Виды движения жидкости
Уравнение неразрывности потока жидкости
Уравнение Бернулли

Виды движения жидкости

Безнапорное движение: жидкость движется сверху вниз под действием силы тяжести. Сечение трубы (канала) при этом не полностью заполнено водой, имеется так называемая свободная поверхность жидкости. Так работает система канализации у нас дома в большинстве случаев.
Напорное движение: жидкость может двигаться не только сверху вниз, но и снизу вверх. Она движется под разницей напоров. Это подробно объясняется чуть ниже. Напорное движение характерно для системы водоснабжения.

Движение жидкости подчиняется двум основным уравнениям.

Уравнение неразрывности потока жидкости

Q = ω · v

Q – расход жидкости; объем жидкости, проходящий через живое сечение потока ω за единицу времени. В системе СИ измеряется в м³/с. Поскольку 1 кубометр – это очень много, то обычно эту единицу измерения используют для рек. В инженерной практике оперируют [л/с], величиной, в 1000 раз меньшей. Так, обычно, умываясь, из смесителя к нам в руки направляется 0,1 – 0,2 л/с воды.

ω – живое сечение потока, м². Живое сечение – та часть поперечного сечения трубопровода (или русла), которую занимает поток жидкости.

v – средняя скорость потока жидкости в живом сечении. Дело в том, что если посмотреть на распределение скоростей частиц жидкости по сечению, например в напорном трубопроводе, то получится, что по центру скорость движения максимальна, а у стенок трубы равна 0. Т.е. скорости не одинаковы, поэтому используют понятие средней скорости. Измеряется в метрах в секунду (м/c). Скорость движения воды в системах водоснабжения и водоотведения примерно 0,7 — 1,5 м/с

Пример. Какой расход движется по трубе внутренним диаметром 40 мм в напорном режиме, если средняя скорость потока составляет 1,2 м/c?

Решение: площадь живого сечения трубы = площадь круга диаметром 40 мм. Площадь круга: ω = 3,14*d²/4 = 3,14*0,04²/4 = 0,00126 м². Тогда расход: Q = ω·v = 0,00126 · 1,2 = 0,00151 м³/с = 1,51 л/с.

Здесь представим сразу упрощенный вид уравнения Бернулли для напорного движения жидкости, который используют для расчета трубопроводных систем. В нем пренебрегают скоростными напорами (кинетической энергией жидкости в сечениях потока) ввиду малости этих скоростей для систем водоснабжения и водоотведения.

Уравнение Бернулли составляют для любых двух сечений одного потока жидкости. Оно связывает между собой скорости движения жидкости и давления в этих сечениях.

Уравнение Бернулли

Z₁ + H₁ = Z₂ +H₂ + h_f

Здесь: Z₁ – положение (отметка) сечения 1-1, выражается в метрах.

H₁ – напор в сечении 1-1 (избыточное давление в сечении 1-1, выраженное в метрах столба жидкости H₁ = p₁/ρg)

Z₂ – положение (отметка) сечения 2-2, выражается в метрах.

H₂ – напор в сечении 2-2 (избыточное давление в сечении 2-2), выражается также в метрах

h_f – общая потеря напора при движении жидкости от сечения 1-1 до сечения 2-2. Происходит за счет работы сил трения в жидкости. При определенных условиях зависит от шероховатости

Пример. Какой напор будет в точке установки смесителя (точка 2) при величине напора воды в точке подключения в квартиру (точка 1) равном 5 м? Потерю напора при движении расчетного расхода по указанному пути принять 2 м. Точка 1 расположена на высоте 1 м от пола, точка 2 расположена на высоте 0,5 м от пола.

Решение: Отметки записываются относительно плоскости сравнения. Это может быть абсолютно любая горизонтальная плоскость. В данном случае удобно принять за плоскость сравнения поверхность пола.

Z₁ + H₁ = Z₂ +H₂ + h_f

1 + 5 = 0,5 + H₂ + 2, H₂ = 3,5м.

Отметим, что этот напор 3,5 м будет полностью потрачен в самом смесителе. В месте выхода воды из смесителя – атмосферное давление. Избыточное давление в этом месте равно 0 м.вод.ст.

Это выглядит довольно просто, однако сложность заключается в том, что в реальной жизни величину потери напора h_f необходимо определять. Какие бывают потери напора, и как их определять – читайте третью статью в данном цикле

Источник

Воспользовавшись данным калькулятором, вы без труда сможете определить скорость воды в трубе, зная диаметр трубы и расход воды.

Как пользоваться калькулятором для расчёта скорости жидкости в трубопроводе?

Введите диаметр трубы, через которую будет протекать жидкость. Затем заполните следующее поле калькулятора, где укажите расход воды в трубе за единицу времени. После этого останется только нажать на кнопку «Рассчитать» и сразу же узнаете скорость потока жидкости в данном трубопроводе. Как вы можете видеть всё довольно просто и легко.

В итоге, после вычислений, результат скорости будет выведен в метрах в секунду (м/с). Если вам нужны другие единицы измерения, то переводить придётся самостоятельно.

Как самостоятельно определить скорость движения воды в трубе ?

Для того чтобы рассчитать скорость протекания жидкости в трубе воспользуйтесь следующей формулой из гидравлики:

V = 4 * Q / (π * d²) , где

Q — расход воды в трубе, м³/сек,
π — просто число пи (из математики),
d — внутренний диаметр трубопровода, м

Результатом будет скорость движения жидкости в м/с. При вычислениях будьте внимательны в размерностях. А лучше всего скорость воды считайте на нашем простом онлайн-калькуляторе. Это сэкономит ваше время и нервы :).

Максимальная скорость движения жидкости в трубе обычно ограничивается из соображений шумности потока в трубах. Следует придерживаться следующих рекомендаций:

до 1,5 м/сек — скорость для общественных зданий и помещений в них,
до 2,0 м/сек — скорость для административно-бытовых зданий и помещений,
до 3,0 м/сек — максимальная скорость в производственных зданиях и помещениях.

Слишком маленькая скорость тоже противопоказана нормальной работе трубопровода. В некоторых случаях могут образовываться воздушные пробки в системе.

Как м3/ч перевести в л/с ?

Перевести метры кубические в час в литры в секунду или наоборот очень просто. Посмотрите ниже на коэффициенты перевода и вам все станет понятно. Достаточно лишь воспользоваться кнопкой умножения на калькуляторе.

1 м3/час равен 0,278 л/сек

1 л/сек равен 3,600 м3/час

Думаю такая информация будет весь полезна при любых расчётах в гидравлике. Примеры приводить нет смысла, если очень надо то посмотрите калькулятор расчета диаметра трубы по расходу воды, там всё это есть.

Было полезно? Поделитесь с друзьями!

Источник

Главная страница

Содержание

Введение

Основы гидростатики

Основы гидродинамики

Гидравлические сопротивления

Истечние жидкости из отверстий, насадков и из-под затворов

Гидравлический расчет простых трубопроводов

Гидравлические машины

Лекция 3. ОСНОВЫ ГИДРОДИНАМИКИ

Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие
с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде
такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

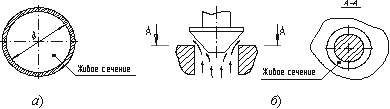
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную
к направлению течения. Например, живое сечение трубы — круг (рис.3.1, б); живое сечение клапана — кольцо с
изменяющимся внутренним диаметром (рис.3.1, б).

Рис. 3.1. Живые сечения: а — трубы, б — клапана

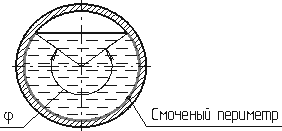
Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми
стенками (рис.3.2, выделен утолщенной линией).

Рис. 3.2. Смоченный периметр

Для круглой трубы

если угол в радианах, или

Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое
сечение ω.

Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода
жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения
и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она
равна нулю.

Гидравлический радиус потока R — отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется
такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

υ = f(x, y, z)

P = φ f(x, y, z)

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени,
называется неустановившимся или нестационарным

υ = f₁(x, y, z, t)

P = φ f₁(x, y, z, t)

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор
скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением.
Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Рис. 3.3. Линия тока и струйка

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах
без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением).
Безнапорное — течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые
каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

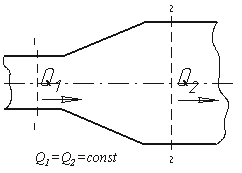
Рис. 3.4. Труба с переменным диаметром при постоянном расходе

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений.
Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении
постоянен, т.е. Q₁=Q₂= const, откуда

ω₁υ₁ = ω₂υ₂

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

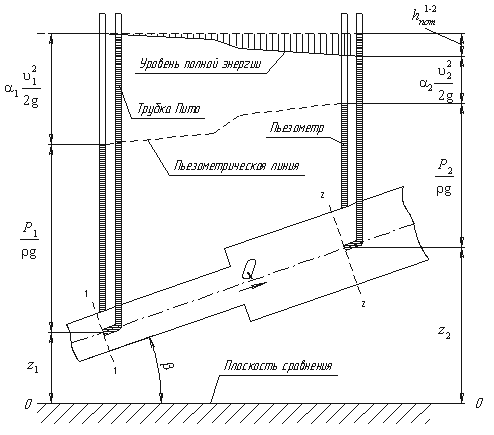
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно
дает связь между давлением P, средней скоростью υ и пьезометрической высотой z
в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого
уравнения решается большой круг задач.

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом
β (рис.3.5).

Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и
сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой
равен Q.

Для измерения давления жидкости применяют пьезометры — тонкостенные стеклянные трубки, в которых
жидкость поднимается на высоту 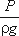. В каждом сечении установлены
пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой
направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также
поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2
поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы
получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой
плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет
отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет
следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть
величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 — удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и
2-2;
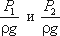
— удельные энергии давления, характеризующие потенциальную
энергию давления в тех же сечениях;
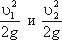
— удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении
постоянна.

Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет
линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 — геометрические высоты сечений 1-1
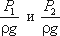
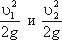
и 2-2 над плоскостью сравнения; — пьезометрические высоты;
— скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной
высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых
жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше
полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный
напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень
первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться
из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного
напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые
называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного
режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями
жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

= h_лин + h_мест

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два
сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ,
g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго
сечения используют уравнение постоянства расхода жидкости υ₁ω
₁ = υ₂ω₂.

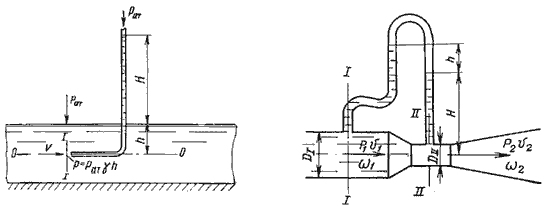
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка
Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости
в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения
1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н — столб жидкости в трубке Пито.

Рис. 3.7. Трубка Пито и pасходомер Вентури

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого
основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с
цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры,
то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и
II-II:

или

Используя уравнение неразрывности

Q = υ₁ω₁ = υ₂ω₂

сделаем замену в получено выражении:

Решая относительно Q, получим

Выражение, стоящее перед 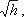, является постоянной величиной, носящей название постоянной
водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в
виде тарировочной кривой h от Q, которая имеет параболический характер.

Проверить себя ( Тест )

Наверх страницы

Источник

Занятие 7 Режимы движения жидкости. Критическая скорость Режим движения (ламинарный или турбулентный) определяется по числу Рейнольдса: для напорных потоков круглого сечения Reкр = 2320 для некруглых напорных потоков и безнапорных Reкр = 580 Тогда при Re < 2320 (580) — режим ламинарный; при Re > 2320 (580) — режим турбулентный.

Примеры решения задач Задача 1 По трубе диаметром 70 мм протекает за сутки 120000 кг нефти плотностью 820 кг/м 3, вязкость нефти = 0, 5 см 2/с. Определить режим движения нефти.

Решение: Q = 120000/820∙ 86400 = 0, 0017 м 3/с; = 3, 14∙ 0, 072/4 = 0, 0038 (м 2) v = 0, 0017/0, 0038 = 0, 45 (м/с); Re = 45∙ 7 / 0, 5 = 630 < Reкр= 2320 – режим ламинарный

Задача 2 Определить режим движения в лотке прямоугольного сечения шириной b = 120 см при уровне воды в нем h = 5 см, если V = 8 см/с, = 0, 015 см 2/с.

Решение: = b∙h /2 h + b = 120∙ 5 /2∙ 5 + 120 = 4, 62 (см) Re = 8 ∙ 4, 62 / 0, 015 = 2464 > Reкр= 580 — режим турбулентный

Задача 3 Определить режим движения в водопроводе диаметром 100 мм и длиной 2, 5 км, если расход воды 11, 8 л/с.

Решение = 3, 14∙ 0, 12 / 4 = 0, 00785 (м 2). V = 0, 0118 / 0, 00785 = 1, 5 (м/с). Принимается = 0, 01 см 2/с. = = 150∙ 10 / 0, 01 = 150000 > 2320 – режим турбулентный

Задача 4 Вода из одного бассейна в другой с расходом 12 л/с подается по трубе диаметром 50 мм. Определить режим движения и критическую скорость.

Решение Определяется скорость в трубе (м/с) Определяется режим движения при кинематической вязкости воды =0, 01 см 2/с. = 611∙ 5 / 0, 01 = 305500 — режим турбулентный. Критическая скорость соответствует критическому числу Re = 2320

Задачи для самостоятельного решения Задача 5 Какой режим движения воды будет при температуре в круглой напорной трубе диаметром d = 32 мм, если расход равен Q = 0, 5 л / с ? Задача 6 По напорной трубе диаметром d = 25 мм движется вода, температура которой составляет . Определить расход в л/с, при котором наступает смена режима движения.

Задача 7 Изучение режимов движения жидкости производится в лабораторных условиях на стеклянной трубе диаметром d = 0, 025 м, через которую пропускается вода с температурой 10 ºС. Расход воды определяется при помощи мерного цилиндра и секундомера. Подсчитать, в течение какого времени будет наполнятся мерный цилиндр емкостью W = 0, 003 м 3 при режиме движения воды, соответствующем критическому значению числа Рейнольдса.

Задача 8 Определить критическую скорость, отвечающую переходу из ламинарного течения к турбулентному, для трубы диаметром d = 0, 02 м, при движении в ней воды при температуре t = 15 ºС и глицерина при t = 20 ºС. Кинематическая вязкость глицерина = 4, 1 · 10 -4 м 2/с.

Задача 9 Определить режим движения жидкости с вязкостью в лотке прямоугольного сечения при расходе потока Q = 300 л/с. Ширина лотка 1 м, глубина безнапорного потока в нём 0, 5 м. Примечание: выполнить второе решение для движения напорного потока.

Самостоятельно: Задача 10 По трубопроводу диаметром 100 мм перекачивается нефть ( = 0, 42 см 2/с) в количестве 12 дм 3/с. Определить: а) режим движения нефти; б) критическую скорость. Задача 11 Определить потерю напора в трубопроводе длиной 500 м и диаметром 150 мм при перекачке воды расходом 20 л/с, = 0, 012 см 2/с. Как изменится потеря напора в трубопроводе, если диаметр трубы уменьшится в 2 раза? Задача 12 Задача 13 Как изменится потеря напора в трубопроводе, если вязкость уменьшится в 2 раза?