Как найти максимальную мощность цепи

Мощность переменного тока

  • Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

  • Мощность тока через резистор

  • Мощность тока через конденсатор

  • Мощность тока через катушку

  • Мощность тока на произвольном участке

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть U и I — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени dt — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины U и I можно считать постоянными в течение интервала dt.

Пусть за время dt через наш участок прошёл заряд dq = Idt (в соответствии с правилом выбора знака для силы тока заряд dq считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

dA = Udq = UIdt.

Мощность тока P — это отношение работы электрического поля ко времени, за которое эта работа совершена:

P= I_0 frac{displaystyle dA}{displaystyle dt vphantom{1^a}} = UI. (1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: P > 0. Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: P < 0. Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

к оглавлению ▴

Мощность тока через резистор

Пусть переменный ток I = I_0 sin omega t протекает через резистор сопротивлением R. Напряжение на резисторе, как нам известно, колеблется в фазе с током:

U = IR = I_0 R sin omega t = U_0 sin omega t.

Поэтому для мгновенной мощности получаем:

P = UI= U_0 I_0 sin^2 omega t = P_0 sin^2 omega t. (2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение P_0 нашей мощности связано с амплитудами тока и напряжения привычными формулами:

P_0=U_0 I_0 = I_0^2 R = frac{displaystyle U_0^2}{displaystyle R vphantom{1^a}}.

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой 50 Гц, т. е. за секунду совершается 50 колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между 0 и P_0. Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение P_0/2?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно 1/2.

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно 1/2

Итак, для среднего значения bar{P} мощности тока на резисторе имеем:

bar{P}= frac{displaystyle P_0}{displaystyle 2 vphantom{1^a}} = frac{displaystyle U_0 I_0}{displaystyle 2 vphantom{1^a}} = frac{displaystyle I_0^2 R}{displaystyle 2 vphantom{1^a}} = frac{displaystyle U_0^2}{displaystyle 2R vphantom{1^a}}. (3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

bar{U}= frac{displaystyle U_0}{displaystyle sqrt(2) vphantom{1^a}}, bar{I}= frac{displaystyle I_0}{displaystyle sqrt(2) vphantom{1^a}}. (4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

bar{P}=bar{U} bar{I} = bar{I}^2 R = frac{displaystyle bar{U}^2}{displaystyle R vphantom{1^a}}.

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения U, а затем к источнику переменного напряжения с таким же действующим значением U, то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые 220 вольт из розетки — это действующее значение напряжения бытовой электросети.

к оглавлению ▴

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение U = U_0 sin omega t. Как мы знаем, ток через конденсатор опережает по фазе напряжение на pi:

I = I_0 sin left ( omega t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = I_0 cos omega t.

Для мгновенной мощности получаем:

P = UI = U_0 I_0 sin omega t cos omega t = frac{displaystyle 1}{displaystyle 2 vphantom{1^a}}U_0 I_0 sin2 omega t = P_0 sin2 omega t.

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, 0 < t < T/4. Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, T/4 < t < T/2. Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, T/2 < t < 3T/4. Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, 3T/4 < t < T. Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

к оглавлению ▴

Мощность тока через катушку

Пусть на катушку подано переменное напряжение U = U_0 sin omega t. Ток через катушку отстаёт по фазе от напряжения на pi/2:

I = I_0 sin left ( omega t - frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = -I_0 cos omega t.

Для мгновенной мощности получаем:

P = UI = -U_0 I_0 sin omega t cos omega t = -frac{displaystyle 1}{displaystyle 2 vphantom{1^a}}U_0 I_0 sin2 omega t = -P_0 sin2 omega t.

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

к оглавлению ▴

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение U = U_0 sin omega t.

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз alpha. Мы записывали это так:

I = I_0 sin(omega t - alpha).

Тогда для мгновенной мощности имеем:

P = U_0 I_0 sin omega t sin(omega t - alpha). (5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

sin x sin y = frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} (cos (x-y) - cos (x+y)).

В результате получим:

P = U_0 I_0 frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} ( cos alpha - cos (2 omega t - alpha)). (6)

Но среднее значение величины cos (2 omega t - alpha) равно нулю! Поэтому средняя мощность оказывается равной:

bar{P} = U_0 I_0 frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} cos alpha. (7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

bar{P} = bar{U} bar{I} cos alpha.

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем alpha = 0, и мы приходим к формуле (3). Для конденсатора и катушки alpha = pi/2, и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы cos alpha у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Мощность переменного тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Формула полезной мощности в физике

Формула полезной мощности

Определение и формула полезной мощности

Определение

Мощность — это физическая величина, которую использует как основную характеристику любого устройства, которое применяют
для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.

Отношение работы ($Delta A$) к промежутку времени за которое она выполнена ($Delta t$) называют средней мощностью ($leftlangle Prightrangle $) за это время:

[leftlangle Prightrangle =frac{Delta A}{Delta t}left(1right).]

Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $Delta tto 0$:

[P={mathop{lim }_{Delta tto 0} frac{Delta A}{Delta t} }=A'(t)left(2right).]

Приняв во внимание, что:

[Delta A=overline{F}cdot Delta overline{r }left(3right),]

где $Delta overline{r }$ — перемещение тела под действием силы $overline{F}$, в выражении (2) имеем:

[P={mathop{lim }_{Delta tto 0} left(frac{overline{F}cdot Delta overline{r }}{Delta t}right) }=overline{F}{mathop{lim }_{Delta tto 0} left(frac{Delta overline{r }}{Delta t}right)= }overline{F}cdot overline{v}left(4right),]

где $ overline{v}-$ мгновенная скорость.

Коэффициент полезного действия

При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($eta $), при этом:

[eta =frac{P_p}{P}left(5right),]

где $P_p$ — полезная мощность; $P$ — затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:

[P_p=eta P left(6right).]

Формула полезной мощности источника тока

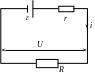
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:

[P=?I left(7right),]

где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.

Обозначим $U$ — напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:

[P=?I=UI+I^2r=P_p+P_0left(8right),]

где $P_p=UI=I^2R=frac{U^2}{R}(9)$ — полезная мощность; $P_0=I^2r$ — мощность потерь. При этом КПД источника определяют как:

[eta =frac{P_p}{P_p+P_0}left(9right).]

Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.

При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.

Примеры задач с решением

Пример 1

Задание. Коэффициент полезного действия электрического двигателя равен $eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двигатель идет ток силой $I=$10 А?

Решение. За основу решения задачи примем формулу:

[P_p=eta P left(1.1right).]

Полную мощность найдем, используя выражение:

[P=IUleft(1.2right).]

Подставляя правую часть выражения (1.2) в (1.1) находим, что:

[P_p=eta IU.]

Вычислим искомую мощность:

[P_p=eta IU=0,42cdot 110cdot 10=462 left(Втright).]

Ответ. $P_p=462$ Вт

Пример 2

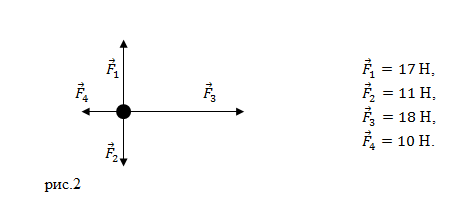
Задание. Какова максимальная полезная мощность источника тока, если ток короткого замыкания его
равен $I_k$? При соединении с источником тока сопротивления $R$, по цепи (рис.1) идет ток силой $I$.

Формула полезной мощности, пример 1

Решение. По закону Ома для цепи с источником тока мы имеем:

[I=frac{varepsilon}{R+r}left(2.1right),]

где $varepsilon$ — ЭДС источника тока; $r$ — его внутреннее сопротивление.

При коротком замыкании считаем, что сопротивление внешней нагрузки равно нулю ($R=0$), тогда сила тока короткого замыкания равна:

[I_k=frac{varepsilon}{r} left(2.2right).]

Максимальная полезная мощность в цепи рис.1 электрический ток даст, при условии:

[R=r left(2.3right).]

Тогда сила тока в цепи равна:

[I’=frac{varepsilon}{r+r}=frac{varepsilon}{2r}left(2.4right).]

Максимальную полезную мощность найдем, используя формулу:

[P_{p max}={I’}^2r={left(frac{varepsilon}{2r}right)}^2cdot r=frac{varepsilon^2}{4r}=frac{varepsilon^2}{4R}left(2.5right).]

Мы получили систему из трех уравнений с тремя неизвестными:

[left{ begin{array}{c}
I’=frac{varepsilon}{2r}, \
I_k=frac{varepsilon}{r}, \
P_{p max}={left(I’right)}^2r end{array}
left(2.6right).right.]

Используя первое и второе уравнения системы (2.6) найдем $I’$:

[frac{I’}{I_k}=frac{varepsilon}{2r}cdot frac{r}{varepsilon}=frac{1}{2}to I’=frac{1}{2}I_kleft(2.7right).]

Используем уравнения (2.1) и (2.2) выразим внутреннее сопротивление источника тока:

[varepsilon=Ileft(R+rright);; I_kr=varepsilon to Ileft(R+rright)=I_krto rleft(I_k+Iright)=IRto r=frac{IR}{I_k-I}left(2.8right).]

Подставим результаты из (2.7) и (2.8) в третью формулу системы (2.6), искомая мощность будет равна:

[P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}.]

Ответ. $P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}$

Читать дальше: формула равнодействующей всех сил.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Электрические цепи
обычно состоят из источника тока,
подводящих проводов и сопротивления
нагрузки. На рис.6.7 нарисована такая
простейшая цепь. В этой цепи R
является сопротивлением нагрузки,
– ЭДС источника тока, а через r
мы обозначили внутреннее сопротивление
источника тока; это сопротивление всегда
присутствует в электрической цепи,
содержащей источник тока.

Рис.6.7

Мощность, выделяемую
в цепи, можно вычислить, используя
определение мощности, введенное в курсе
«Механика». По определению, мощностью
называется работа, произведенная в
единицу времени. Работу, возникающую
на участке цепи, в которой течет ток i,
можно записать dA
= dqU
= idtU.
Следовательно, мощность, выделяемая в
такой цепи, равна:


.

Таким образом, мощность,
выделяемая в электрической цепи или на
ее участке, равна произведению тока,
текущего в этой цепи, на падение напряжения
на этом участке цепи. Согласно полученному
выражению, мощность, отдаваемая источником
тока, определяется произведением ЭДС
источника на силу тока, текущего в цепи:

P
= i.

По закону Ома для
замкнутой цепи (см. рис.6.7) ток равен:


.

Таким образом, мощность,
отдаваемая источником тока, равна:


.

Теперь найдем мощность,
выделяемую в нагрузке R:

PR
= URi.

По закону Ома падение
напряжения на сопротивлении нагрузки
UR
= iR.
Следовательно:


.

Мы получили выражение,
которое показывает, что мощность,
выделяемая в нагрузке, меньше мощности,
отдаваемой источником тока в электрическую
цепь. Отсюда ясно, что часть мощности
источника тратится не на нагрузку. В
связи с этим вводится понятие коэффициента
полезного действия источника тока,
который обозначается через
и определяется как отношение полезной
мощности к полной или затраченной:


.

Из этого выражения
видно, что коэффициент полезного действия
всегда меньше единицы. На рис.6.8 приведены
графики изменения полезной и затраченной
мощности и коэффициента полезного
действия при изменении сопротивления
нагрузки.

Рис.6.8

На основании этих
графиков можно сделать вывод, что
максимальный коэффициент полезного
действия равен единице, когда сопротивление
нагрузки равно бесконечности, т.е. цепь
разорвана. Но в этом случае и полезная,
и затраченная мощности стремятся к
нулю, т.е. этот режим не интересен. Когда
сопротивление нагрузки равно нулю
(короткое замыкание), источник тока
выделяет в цепь максимальную мощность,
но при этом полезная мощность и КПД
равны нулю, значит, и этот режим не
интересен. График изменения полезной
мощности имеет экстремальный характер.
Величину сопротивления, соответствующего
максимальному значению полезной
мощности, можно найти, приравняв первую
производную от нее по сопротивлению к
нулю. Тогда получаем Rmax
= r.
Для этого значения сопротивления
нагрузки коэффи­циент полезного
действия оказывается равным 0,5, а
мощность, выделяемая в нагрузке, равна:


.

Как видно из полученного
выражения, максимальная мощность,
выделяемая в нагрузке, в четыре раза
меньше максимальной мощности, выделяемой
источником тока, и в два раза меньше той
мощности, которую источник тока при
данном сопротивлении выделяет в
электрическую цепь.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник
Определение

При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Ее принято называть работой тока.

Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:

A=ΔqU

Но сила тока равна:

I=ΔqΔt

Выразим заряд:

Δq=IΔt

Тогда работа тока равна:

A=IUΔt

Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.

Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:

A=I2RΔt=U2RΔt

Работа тока измеряется в Джоулях (Дж).

Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.

A=IUΔt=16·220·10=35200 (Дж)=35,2 (кДж)

Закон Джоуля-Ленца

В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.

Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:

Закон Джоуля—Ленца

Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.

Q=I2RΔt

Количество теплоты измеряется в Джоулях (Дж).

Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.

Используем закон Ома и закон Джоуля—Ленца:

Q=I2RΔt=(UR)2Δt=U2RΔt=1222=72 (Дж)

Мощность тока

Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.

Определение

Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).

Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:

P=AΔt

Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:

P=IU=I2R=U2R

Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.

P=I2R=0,32·10=0,9 (Вт)

Выразив силу тока через заряд, прошедший за единицу времени, получим:

P=qUt

Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:

P=(εR+r)2R

Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.

Pmax=(εr+r)2r=ε24r

Мощность тока внутренней цепи:

Pвнутр=I2r=(εR+r)2r

Полная мощность:

Pполн=I2(R+r)=ε2R+r

Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?

Используем формулу для нахождения полезной мощности:

P=(εR+r)2R

Применим закон Ома для полной цепи:

I=εR+r

Выразим сопротивление внешней цепи:

R=εI−r

Отсюда:

P=(εεI−r+r)2(εI−r)=I2(εI−r)=Iε−rI2

Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:

rI2−Iε+P=0

I2−1I+0,75=0

Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.

Подсказки к задачам

Объем проводника цилиндрической формы

V=Sl
Масса проводника цилиндрической формы

m=ρV=ρSl
Количество теплоты и изменение температуры

Q=cmΔT

Конденсатор в цепи постоянного тока

Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.

Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.

Подсказки к задачам

Электроемкость, заряд и напряжение

C=qU
Напряженность и напряжение

E=Ud
Энергия конденсатора

W=q22C=CU22
Количество теплоты

Q=ΔW

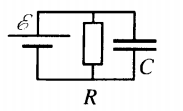
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?

Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:

I=εR+r

Применим закон Ома:

I=UR

Приравняем правые части выражений и получим:

εR+r=UR

Отсюда напряжение на конденсаторе равно:

U=εRR+r

Напряженность электрического поля равна:

E=Ud=εRd(R+r)=9·80,002(8+1)=720,018=4000 (Вм)

Задание EF17564

Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?

Ответ:

а) 5 Дж

б) 4 Дж

в) 3 Дж

г) 1 Дж

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для нахождения количества теплоты, выделенной внутри источника тока.

3.Выполнить решение в общем виде.

4.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• ЭДС источника тока: ε = 3 В.

• Внутреннее сопротивление источника тока: r = 1 Ом.

• Сила тока в цепи: I = 2 А.

• Напряжение на внешней цепи: U = 5 В.

Количество теплоты, выделенной внутри источника тока, равно:

Q=I2rt=22·1·1=4 (Дж)

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17573

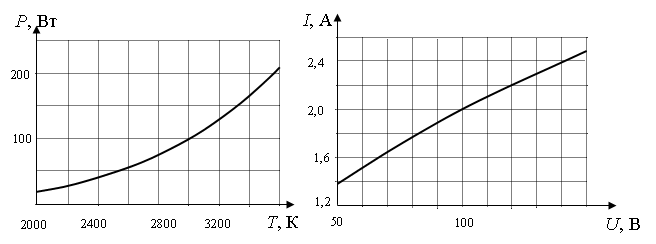
При нагревании спирали лампы накаливания протекающим по ней электрическим током основная часть подводимой энергии теряется в виде теплового излучения. На рисунке изображены графики зависимости мощности тепловых потерь лампы от температуры спирали P=P(T) и силы тока от приложенного напряжения I=I(U). При помощи этих графиков определите примерную температуру спирали лампы при силе тока I=2 A.

Ответ:

Алгоритм решения

1.Записать исходные данные.

2.С помощью графика зависимости силы тока от напряжения вычислить мощность.

3.С помощью графика зависимости мощности от температуры спирали определить ее температуру.

Решение

Нас интересует сила тока, равная 2 А. По графику зависимости силы тока от напряжения этому значение соответствует U = 100 В. Мощность определяется формулой:

P=IU=2·100=200 (Вт)

Этой мощности соответствует температура, равная около 3600 К.

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17608

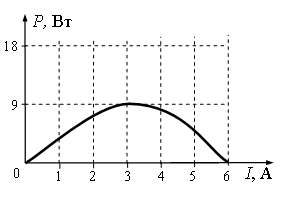
Ученик исследовал зависимость тепловой мощности Р, выделяющейся на реостате R, от силы тока в цепи. При проведении опыта реостат был подключён к источнику постоянного тока. График полученной зависимости приведён на рисунке.

Какое из утверждений соответствует результатам опыта?

А. При коротком замыкании в цепи сила тока будет равна 6 А.

Б. При силе тока в цепи 3 А на реостате выделяется минимальная мощность.

Ответ:

а) только А

б) только Б

в) и А, и Б

г) ни А, ни Б

Алгоритм решения

  1. Проверить истинность каждого из утверждений.
  2. Выбрать верный ответ.

Решение

Согласно первому утверждению, при коротком замыкании в цепи сила тока будет равна 6 А. Это действительно так, потому что при этом значении силы тока мощность равна нулю. А это значит, что сопротивление на внешней цепи было нулевым.

Согласно второму утверждению, при силе тока в цепи 3 А на реостате выделяется минимальная мощность. Это не так. На графике этой силе тока соответствует максимальная мощность.

Верно только первое утверждение  «А».

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 8.4k

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти маршрутизатор вай фай
  • Как найти жену по объявлению
  • Как найти стертые фотографии на телефоне
  • Как составить вопросы к стихотворению в бурю а плещеев
  • Как найти икс в дробном уравнении

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии