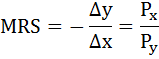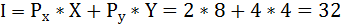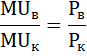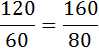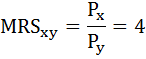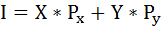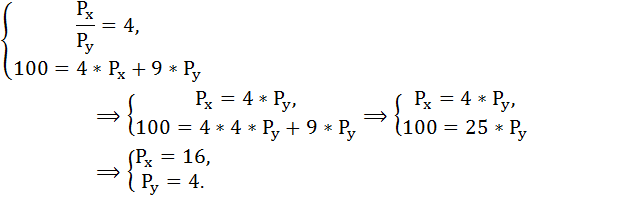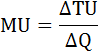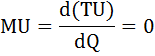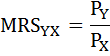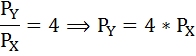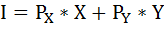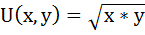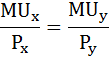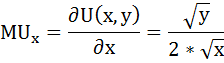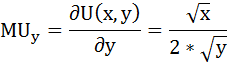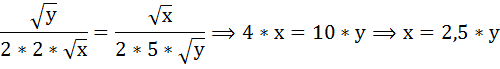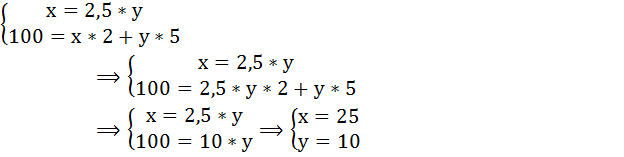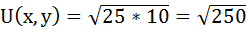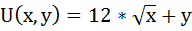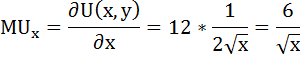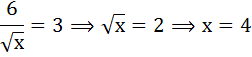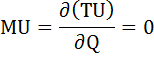Как
известно, на рынке потребитель сталкивается
с бесконечно большим количеством
товаров и услуг, однако для упрощения
нашего анализа мы предположим существование
всего двух товаров.
Пусть
потребитель выбирает первый товар в
количестве
q1,
а
второй — в количестве
q2.
Тогда
набор (q1,
q2)
определит
потребительский
набор
(потребительскую
корзину),
включающую то или иное количество
обоих товаров и обладающую для потребителя
некоторым качеством, которое можно
измерить.
Так,
если наборы пищевые, то таким качеством
будет калорийность данных благ, либо
содержание в них витамина С, либо
содержание сахара и т.д. Если рассматриваемые
товары — металлы, то таким качеством
будет прочность сплава, либо температура
его плавления, либо другая аналогичная
характеристика.
Естественно,
что не
всякое качество товара может быть
охарактеризовано числом.
Например, качество одежды оценивается
и продолжительностью носки (ее можно
охарактеризовать числом), и ее
соответствием современной моде или
красотой (а это числом охарактеризовать
невозможно). В дальнейшем будем
считать, что каждой потребительской
корзине
(q1,
q2)
соответствует
некоторое число
TU(total
utility),
называемое
совокупной полезностью.
Совокупная
полезность (TU)
есть
совокупное удовлетворение, получаемое
человеком в результате потребления
данного количества товаров или услуг
за данное время.
На
совокупную полезность блага влияют не
только его физические характеристики,
но и психология потребителя, его личный
опыт, социальная и культурная среда. И
хотя экономисты проявляют интерес
к этим факторам, однако на практике
обычно уделяют внимание только
количественным показателям (таким,
как объем продаж, количество единиц
товара, приобретенных покупателями, и
т.д.), предполагая постоянными все
прочие факторы, влияющие на поведение
человека. Допущение «при прочих равных
условиях» позволяет упростить анализ
условий максимизации полезности без
особого ущерба для модели.
Математически
это означает, что задается общая функция
полезности от потребления за определенный
период времени n-го
количества товаров:
TU=
U(q1,
q2,
…, qn).
где
q
—
количество товаров, включенных в
потребительский набор.
Функция
полезности
показывает количественную зависимость
между объемом потребления каждого из
n-благ
за данный промежуток времени и совокупной
полезностью блага, отражающей
индивидуальные предпочтения потребителя.
Как
и любая другая функция, функция полезности
может быть представлена в виде таблицы,
графика или уравнения.
Если
мы отвлечемся от отдельных случаев
функции полезности, то для большинства
товаров и услуг действует следующая
закономерность: чем
больше объем потребления, какого- либо
товара, тем больше значение совокупной
полезности, получаемой потребителем.
Изменение
(или приращение) совокупной полезности
отражается в показателе предельной
полезности.
Предельная
полезность
MU
(marginal
utility)
—
это дополнительная полезность,
получаемая человеком от потребления
одной дополнительной единицы данного
блага за единицу времени.
Математически
предельная полезность является первой
производной функции совокупной
полезности по количеству данного
блага и рассчитывается по формуле2:
MU
=
TU(q)
=
d(TU)/dq,
где
d(TU)
—
приращение совокупной полезности,
dq
—
приращение количества потребляемого
блага.
Существует
множество уравнений, которые могут
описывать функцию совокупной
полезности, однако наиболее простым
и наиболее часто применяемым является
общее уравнение
кубической функции:
TU
= а
+ bq
+
cq2—
dq3,
где
q
—
количество потребленного товара;
а,
d,
с, d
—
положительные константы.
Если
последовательное потребление какого-либо
блага постепенно приводит человека
к состоянию насыщенности, то дополнительная
полезность от использования одной
дополнительной единицы данного блага
начинает сокращаться. Эта закономерность
имеет универсальный характер и называется
законом
убывания предельной полезности или
первым законом Госсена.
Закон назван так в честь немецкого
экономиста Германа Госсена (1810-1858),
впервые сформулировавшего данный
принцип.
Начиная
с некоторого момента, дополнительная
полезность от потребления одного
дополнительного блага уменьшается по
мере того, как возрастает объем потребления
данного блага.
Математически
это означает, что вторая производная
общей полезности по количеству
данного блага является отрицательной
величиной.
Принцип
убывания предельной полезности был
использован английским экономистом
А. Маршаллом (1890) для объяснения
знаменитого
парадокса
воды и алмазов.
Суть
парадокса заключалась в том, что на
рынке алмазы ценятся неизмеримо
дороже, чем вода, и в то же время все
понимают, что если без алмазов человек
может обойтись, то без воды выжить
невозможно.
Объяснение
Маршалла состояло в следующем. Цена
товара определяется не его совокупной
полезностью для человека, а той предельной
полезностью, которую человек извлекает
из последнего глотка воды. Другими
словами, стоимость воды определяется
той суммой денег, которую индивидуум
захочет заплатить, чтобы получить
дополнительную меру воды. В силу того,
что предельная ценность убывает по мере
возрастания количества потребленной
воды, а запасов воды на земле существенно
больше, чем запасов алмазов, вода имеет
более низкую стоимость при обмене, чем
алмазы.
Рассмотрим
конкретные задачи 4.1 и 4.2.
Задача
4.1.
Определение точки насыщения
Пусть
дана функция полезности отдельного
потребителя:
TU
=
130q
—
2,5q2.
Определить
точку, при которой совокупная полезность
(TU)
является
максимальной и человек достигает
насыщения.
Решение:
Функция
совокупной полезности достигает своего
максимума при условии MU
=
0:
MU
=
dTU/dq
=
130 — 5q.
Приняв
функцию предельной полезности равной
нулю, получаем:
130 – 5q
= 0; q
= 26.
Это
и есть искомая точка насыщения.
Задача
4.2.
Закон убывания предельной полезности
Пусть
функция полезности задана уравнением:
TU=
18q
+7q2
– (l/3)
q3
Найти
объем потребления (q),
при
котором начинает действовать закон
убывания предельной полезности, т.е.
предельная полезность (MU)
начинает
уменьшаться.
Решение:
Очевидно,
что MU
начнет
уменьшаться в точке, в которой функция
предельной полезности имеет максимальное
значение:
MU
=
dTU/dq
=
18 + 14q
— q2.
Приравняв
dMU/dq
к
нулю и решая это уравнение относительно
q,
получим
q=7
это
степень потребления, при которой
начинается уменьшение MU.
Если
известны или могут быть оценены функции
потребительской полезности, то можно
судить о том, какие товары и услуги
потребители будут или не будут покупать
на рынке.
Для
дальнейшего анализа дополним наше
предположение о рациональности
потребителя допущениями о независимости
рассматриваемых нами функций полезности
(функция полезности одного товара
или услуги не зависит от степени
потребления других благ) и о полной
информированности потребителей.
Каждый потребитель обладает всей
необходимой для принятия решений
информацией, вполне определенными
вкусами и предпочтениями; знает,
какие товары и услуги доступны для
приобретения, качественные характеристики
этих товаров и их способность
удовлетворять его желания, цены, по
которым они продаются.
С
учетом представленных допущений
проанализируем поведение отдельного
потребителя, выбирающего комбинацию
из двух товаров
(q1,
q2)
и
располагающего доходом
(R),
равным
40 у.е. Эксперимент позволил выявить
следующие потребительские предпочтения
(табл. 4.1) для двух товаров (q1,
q2)
(в
баллах). Рыночные цены товаров
соответственно: p1
= 3 у.е., p2
=
5 у.е.
Таблица
4.1
Потребительские
предпочтения индивидуума
|
q1 |
TU1 |
MU1 |
MU1/P1 |
q2 |
TU2 |
MU2 |
MU2/P2 |
|
0 |
0 |
— |
— |
0 |
0 |
— |
— |
|
1 |
54 |
54 |
18 |
1 |
75 |
75 |
15 |
|
2 |
99 |
45 |
15 |
2 |
135 |
60 |
12 |
|
3 |
129 |
30 |
10 |
3 |
175 |
40 |
8 |
|
4 |
138 |
9 |
3 |
4 |
200 |
25 |
5 |
|
5 |
141 |
3 |
1 |
5 |
215 |
15 |
3 |
|
6 |
138 |
-3 |
-1 |
6 |
220 |
5 |
1 |
Как
видно из табл. 4.1, наибольшее удовольствие
потребителю принесло бы потребление
5 ед. товара
q1,
6 ед.
товара
q2.
Однако
на эти покупки пришлось бы потратить
45
у.е.
(5×3+5×6),
которых у человека нет.
Критерием
правильности
потребительского выбора является не
совокупная и даже не предельная
полезность, а предельная полезность на
1 у.е. затрат (MU/P).
Прибавочное
удовлетворение, получаемое на 1 у.е.
затрат, является наилучшим критерием,
поскольку объединяет и фактор
удовлетворения, и фактор затрат,
необходимые для обоснованного сравнения
товаров между собой.
В
нашем примере потребитель получит
наибольшее удовлетворение, распределяя
свой доход (40 у.е.) следующим образом:
4 ед. товара
q1
(4
х 3 у.е. = 12 у.е.), 5 ед. товара
q2
(5×6
у.е. = 30 у.е.).
3
у.е. (45 у.е. — (12 + 30 у.е.) = 3 у.е. останутся на
сбережениях.
С
учетом полученных результатов сформулируем
основное условие
потребительского оптимума, или второй
закон Госсена, для
двух и более товаров.
Для
максимизации полезности потребитель
должен таким образом распределить свой
ограниченный бюджет, чтобы предельные
полезности на один рубль, затраченный
на последнюю единицу каждого товара,
равнялись бы между собой
MU1/P1
=
MU2/P2
=
… = MUn
/Pn
а
сумма всех затрат потребителя на товары
и услуги плюс сбережения (S)
соответствовала
его денежному доходу (R),
т.е.
P1Q1
+P2
Q2 +…
+ PnQn
+S
= R
Если
эти предельные полезности не равны, то
совокупное удовлетворение может быть
увеличено путем уменьшения расходов
на товары с меньшей степенью полезности
и увеличения затрат на товары с большей
степенью полезности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
Запишем бюджетное ограничение:
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.
Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
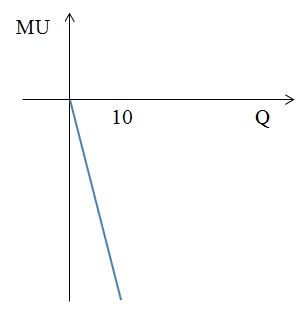
2) U(Q)= 5 + Q – Q2
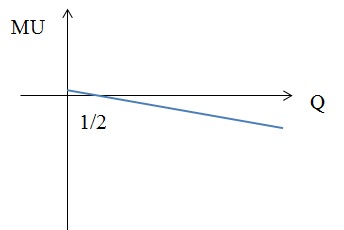
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
1) MU = –10 × Q = 0, следовательно, Q = 0;
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
Далее воспользуемся формулой бюджетного ограничения:
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
Аналогично находим предельную полезность товара y:
Далее воспользуемся бюджетным ограничением:
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
При х = 25 и у = 10 общая полезность достигнет максимума:
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
Оптимальный объём потребления будет достигнут при МU = P:
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q) = 1 – 2Q2;
2) U(Q) = 5 + Q – Q2;
3) U(Q) = Q2 – Q3.
Как будут выглядеть функции предельной полезности?
Решение:
Функции предельной полезности определим с помощью первой производной от функции общей полезности.
1) MU(Q) = (1 – 2Q2)’ = – 4Q
2) MU(Q) = (5 + Q – Q2)’ = 1 – 2Q
3) MU(Q) = (Q2 – Q3)’ = 2Q – 3Q2
Общая полезность (TU) достигает своего максимума, когда предельная полезность (MU) равна нулю:
Таким образом, оптимальный для потребителя объем:
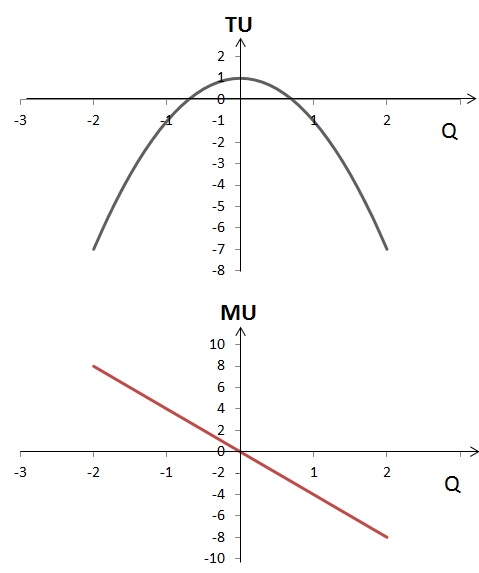
1) MU(Q)= – 4Q = 0, Q = 0
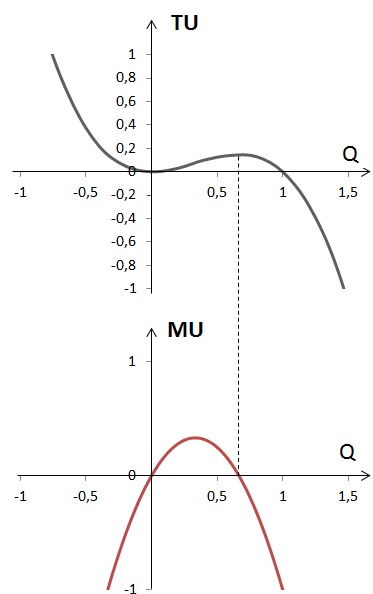
Изобразим функции общей и предельной полезности графически:
Как видно из графика, оптимальный для потребителя объем блага Q = 0. Общая полезность в этой точке максимальна.
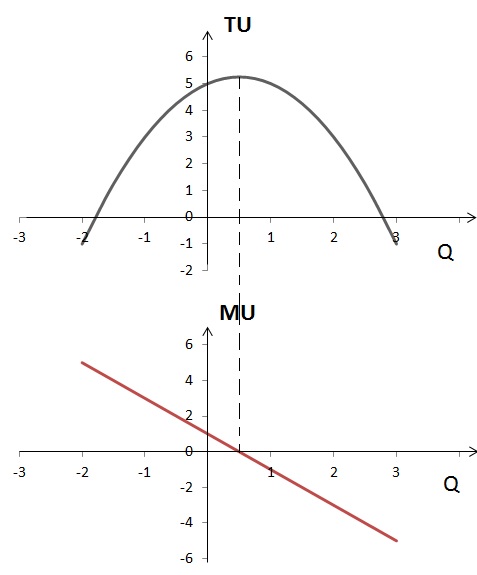
2) MU(Q) = 1 – 2Q = 0, Q = 1/2
Графически функции общей и предельной полезности для данного случая будут выглядеть следующим образом:
Как видно из графика, общая полезность максимальна при потреблении 1/2 единицы блага Q.
Внимательный читатель может возразить, что совсем необязательно было строить графики TU и MU с отрицательными значениями Q, так как значения функции при Q < 0 экономического смысла не имеют. Однако? как мы увидим далее, это окажется для нас полезным.
3) MU(Q) = 2Q – 3Q2
Приравнивая к нулю производную функции общей полезности получим квадратное уравнение:
2Q – 3Q2 = 0,
Корни этого уравнения:
Q = 0 и Q = 2/3.
Как видно из графика, максимум функции общей полезности находится лишь в точке Q = 2/3, который и будет оптимальным для потребителя.
Примеры решений задач: функция полезности
В этом разделе вы найдете подробно решенные задачи, касающиеся функции полезности, задачи выбора потребителем набора благ при заданном бюджетном ограничении, максимизации полезности, заменяемости товаров и т.д.
Понравилось? Добавьте в закладки
Функция полезности: задачи с решениями
Задача 1. Функция полезности имеет вид: $TU=4xy$, где X и Y — количество товаров. Расходы потребителя на эти два товара в месяц равны 1200 р., цена товара X — 400 р., товара Y — 300 р. Определите оптимальный объем ежемесячных закупок двух данных товаров и соответствующее ему значение общей полезности.
Задача 2. Условия: потребитель расходует 200 руб. в неделю на покупку товаров А и В.
Цена (руб.) Кол-во покупаемых единиц товаров Общая полезность Предельная полезность
А 7 20 500 20
В 5 12 1000 30
Задание: Объяснить, как должен поступать потребитель, чтобы максимизировать получаемую полезность при данном бюджете.
Задача 3. Потребитель покупает три товара Х, Y, Z, цены которых соответственно равны Px=100 руб.; Py=70 руб.; Pz=50 руб.
Функции общей полезности разных благ: $F(TU(x))=3sqrt{Qx}$, $F(TU(y))=5sqrt{Qy}$, $F(TU(z))=5sqrt{Qz}$.
Определить:
1) каким образом потребитель может использовать денежный запас 500 рублей для достижения максимальной полезности при потреблении и рассчитать её количественно;
2) то же, если при покупке более, чем 2-х товаров Px снижается на 25%, а Py – на 50%
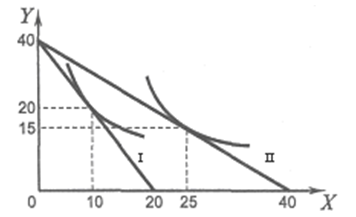
Задача 4. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии (I и II) и соответствующие им кривые безразличия.
Определить координаты (P,Q) двух точек линии спроса данного потребителя на товар Х.
Задача 5. Общая полезность благ $alpha$ и $beta$ для некоего потребителя описывается уравнениями $U_alpha = q_alpha(15 — 0,5q_alpha)$, $U_beta = q_beta(30 — q_beta)$. Допустим, потребитель располагает бюджетом для покупки $alpha$ и $beta$ в размере 120 руб., цены на $alpha$ и $beta$ равны соответственно 5 и 10 руб. Определить количество $alpha$ и $beta$, максимизирующее полезность потребителя.
Задача 6. Потребитель тратит 7 долларов в день на товары X и Y. MU товара X для него равна $10 – x$, где $x$ — количество X в шт. MU товара Y: $21 – 2y$, где $y$ — количество Y в шт. Р 1 ед. товара X = 1 доллар, P 1 ед. Y = 1 доллар. Какое количество X и Y купит рациональный покупатель?
Задача 7. В таблице представлена предельная полезность для походов в магазин.
Имея 100 руб. 80 коп. потребитель купил 3 буханки хлеба по цене 8 руб. за буханку, 4 пакета молока по 11 руб. 20 коп. за пакет и 2 пачки сахара по 16 руб. за пачку. Достиг ли он максимума полезности? Ответ обосновать и в случае отрицательного ответа определить объем покупок, обеспечивающий максимум полезности при данном бюджете.
Задача 8. Построить кривую безразличия для двух абсолютно взаимозаменяемых товаров: пепси-колы и кока-колы, если их цены за литр равны 8 и 10 ден. ед. при бюджете на их потребление, равном 40 ден. ед.
Задача 9. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна, а элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея 6 долларов и 10 долларов с вероятностями 1/3 и 2/3 и лотерея 3 доллара и 9 долларов с вероятностями 2/3 и 1/3 для него эквивалентны. Что можно сказать о склонности данного индивида к риску?
Задача 10. Пусть функция полезности наборов из двух товаров $X=(x_1,x_2)$ имеет вид $u(x_1,x_2)=x_1^{1/7}x_2^{1/6}$.
• Найти набор товаров, который имеет такую же полезность, как набор $X_1=(5,3)$ и количество второго товара равно 1.
• Для набора $X_1=(5,3)$ найти предельные полезности первого и второго товаров.
• В наборе $X_1=(5,3)$ количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.
Задача 11. Функция полезности потребителя имеет вид $u(x_1,x_2)=(x_1-50)^{1/7}(x_2-40)^{1/6}$.
1. Найти равновесный спрос и его полезность, если рыночная цена первого товара $p_1=5$, рыночная цена второго товара $p_2=3$ и потребитель выделяет на приобретение товаров сумму $M=5000$ денежных единиц.
2. Найти функции спроса на оба вида товаров.
3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.
Задача 12. Для потребителя с функцией полезности $U(x_1,x_2)=x_1^{1/3}x_2^{1/4}$
1) найдите функцию спроса на каждый товар;
2) найдите точку спроса при доходе $K=60$ и ценах $P=(2,4)$.
Задача 13. Решить прямую задачу потребителя (найти оптимальную потребительскую корзину). Дано: Функция полезности потребителя $U=sqrt{xy}$. Цена блага х равна 15, цена блага у равна 20, доход потребителя равен 300.
Найти: Оптимальный набор благ потребителя $(х, у)$.
Задача 14. Предельная полезность первой единицы блага равна 300. При потреблении первых трех единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза. Предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 5 раз. Найти совокупную полезность 5 единиц блага.
Консультируем по решению задач микроэкономики
Может быть интересно:
|
|
1. Рассмотрим модель поведения потребителей с функцией полезности ,
. Найдем оптимальные значения объемов товаров
, при которых функция полезности максимальна. При этом потребитель ограничен в покупке товаров бюджетным ограничением
, где
— свободные денежные средства потребителя;
— вектор цен за единицу товаров. В силу свойств функции полезности
(см. [5, 6]) оптимальное значение потребления
будет достигаться на неотрицательном значении и при выполнении равенства
. Тогда задача оптимизации потребления перепишется в виде
Введем функцию Лагранжа , тогда из необходимых условий экстремума получим систему уравнений для поиска оптимальной точки
:
Если функция полезности зависит только от двух видов товаров , то эта система упрощается
|
|
(12.1) |
2. Пусть , капитал
. Найти текущую стоимость первого товара
, если его оптимальное значение равно
.
Решение. Согласно пункту 1 оптимальные объемы товаров удовлетворяют системе (12.1). Найдем частные производные функции
и выпишем систему (12.1):
Теперь в первое уравнение подставим и найдем
.
3. Пусть ,
,
,
. Найти оптимальные значение объемов потребления товаров и максимальное значение функции полезности.
Решение. Поскольку производная функции
не является непрерывной в точках , то выписать функцию Лагранжа и систему (12.1) нельзя. Воспользуемся другим определением оптимальной точки, а именно: оптимальная точка является точкой касания линии уровня (множества безразличия)
и бюджетной линии.
Поскольку , то линии безразличия
представляют собой лучи параллельные осям OX и OY с точками соединения
. В этом случае точка касания бюджетной линии
и множества безразличия определяется из решения системы
.
4. Рассмотрим задачу оптимизации портфеля, состоящего из двух ценных бумаг. Матрица ковариаций эффективностей этих бумаг имеет вид . Найти все допустимые значения
, при которых оптимальный по Марковицу портфель минимального риска содержит бумаги обоих видов. Операция «short sale» запрещена.
Решение. Задача имеет вид
Здесь . Выразим из ограничения вторую переменную
и подставим в критерий. Тогда
. Поскольку переменная
должна принадлежать отрезку [0; 1], то эта задача свелась к поиску минимума параболы
на отрезке. Эта задача имеет решения или в точке безусловного экстремума
, или в одном из концов отрезка. Для того чтобы портфель ценных бумаг содержал бумаги обоих видов, необходимо, чтобы точка
попала внутрь отрезка [0; 1], т. е. должны быть выполнены неравенства
. Из этих неравенств можно
найти допустимые значения .
Найдем точку из необходимого условия экстремума
:
.
Из неравенства получаем, что
. Из неравенства
получаем, что
. Пересекаем эти множества и получаем, что
.
Осталось только учесть, что матрица V является ковариационной матрицей, а следовательно, должна быть неотрицательно определенной.
По критерию Сильвестра необходимо, чтобы и
были неотрицательны. Из неравенства
получаем, что
. Окончательно
.
Задачи для самостоятельного решения по теме 12
1. Пусть выпуск описывается производственной функцией Кобба-Дугласа (см. [5, 6]), где коэффициент эластичности по фондам на 50% больше коэффициента эластичности по труду. Вычислить стоимость единицы фондов, если известно, что инвестиционный капитал в 8,3(3) раза больше оптимального объема закупки фондов
.
2. Пусть функция полезности имеет вид и цены
,
. При какой минимальной величине денежных средств
может быть достигнуто значение
.
3. Рассмотрим задачу оптимизации портфеля, состоящего из двух ценных бумаг. Матрица ковариаций эффективностей этих бумаг имеет вид . Найти все допустимые значения
, при которых оптимальный по Марковицу портфель минимального риска содержит бумаги только
одного вида. Вычислить риск. Операция «short sale» запрещена.
4*. Рассмотрим линейную модель производства
Где технологическая матрица 

, X — объемы выпускаемой продукции. Найти все допустимые значения параметра A, при которых следует производить товары обоих видов.
5**. Рассмотрим задачу оптимизации портфеля, состоящего из трех ценных бумаг
Где матрица ковариаций эффективностей ценных бумаг имеет вид 
от неизвестного значения ожидаемой
доходности , т. е.
,
,
. Построить графики этих зависимостей.
Указание: Значение может меняться только в пределах от 2 до 9. Для решения задачи нужно выразить из двух ограничений две переменные через третью и подставить их в критерий. Учесть положительность всех переменных. В ответе должны получиться кусочно-линейные функции.
| < Предыдущая | Следующая > |
|---|