Тема: Определить максимальное значение ЭДС самоиндукции в катушке (Прочитано 3702 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Определить максимальное значение ЭДС самоиндукции в катушке, индуктивность которой L = 180 мГн, если ток в ней изменяется по закону I = 4∙cos5∙t (А). Сделать рисунок.
Записан
Решение. ЭДС самоиндукции в катушке определим по формуле
[ E=-Lcdot frac{dI}{dt}(1). ]
По условию задачи ток в катушке изменяется по закону
I = 4∙cos5∙t (2).
Подставим (2) в (1) определим зависимость ЭДС самоиндукции в катушке от времени
[ begin{align}
& E=-Lcdot frac{d4cdot cos 5cdot t}{dt}=-Lcdot 4cdot 5cdot sin 5cdot t,E=-20cdot Lcdot sin 5cdot t, \
& E=-{{E}_{max }}cdot sin 5cdot t(3). \
end{align} ]
Максимальное значение ЭДС самоиндукции в катушке равно
Еmax = 20∙L, Еmax = 20∙180∙10-3 = 3,6 Дж.
Ответ: 3,6 Дж.
« Последнее редактирование: 20 Октября 2018, 06:29 от alsak »
Записан
Примеры решения задач
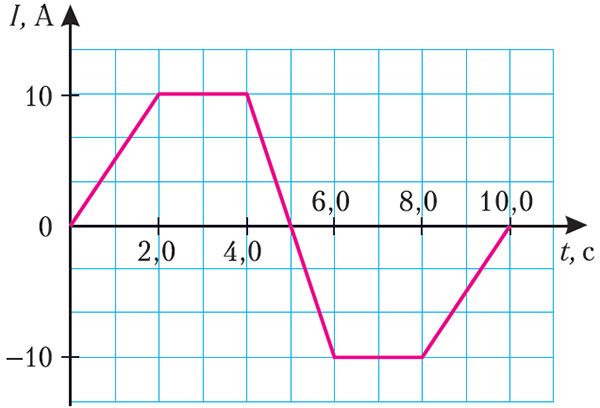
Пример 1. На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность L = 40 мГн.
Дано:
L = 40 мГн = 4,0 · 10–2 Гн
— ?
Решение: ЭДС самоиндукции 
. Анализируя график (рис. 186), можно сделать вывод, что сила тока, проходящего по соленоиду, изменяется на трёх участках:
1) от момента времени t1 = 0,0 с до момента времени t2 = 2,0 с сила тока изменяется на ΔI1 = 10 А за промежуток времени Δt1 = 2,0 с;
2) от момента времени t3 = 4,0 с до момента времени t4 = 6,0 с сила тока изменяется на ΔI2 = –20 А за промежуток времени Δt2 = 2,0 с;
3) от момента времени t5 = 8,0 с до момента времени t6 = 10,0 с сила тока изменяется на ΔI3 =10 А за промежуток времени Δt3 = 2,0 с.
Поскольку промежутки времени Δt1 = Δ t2 = Δ t3 = 2,0 с, то очевидно, что максимальное значение модуля скорости изменения силы тока, а следовательно, и максимальное значение модуля ЭДС самоиндукции, создаваемой в соленоиде, соответствует промежутку времени Δt2 = 2,0 с (от t3 = 4,0 с до t4 = 6,0 с):
Таким образом,
Ответ: = 0,40 В.
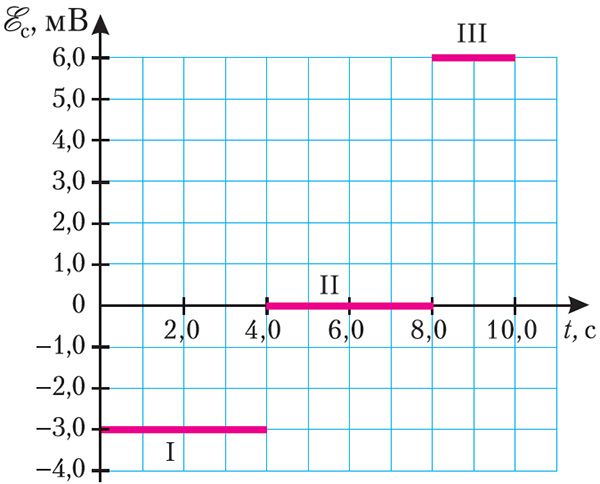
Пример 2. На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью L = 2,0 мГн, от времени. Определите изменения силы тока на участках I, II и III графика. Чему равна энергия магнитного поля в момент времени t = 4,0 с, если в начальный момент времени сила тока в катушке I = 0?
Дано:
L = 2,0 мГн = 2,0 · 10–3 Гн
t = 4,0 с
ΔII — ? ΔIII — ?
ΔIIII — ? Wм — ?
Решение: Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции 
= –3,0 мВ, на участке III — 
= 6,0 мВ. Изменение силы тока на этих участках графика можно определить, воспользовавшись законом электромагнитной индукции для явления самоиндукции:
; 
.
; 
.
На участке II графика 
= 0, следовательно, сила тока не изменялась: ΔIII = 0.
В момент времени t = 4,0 с энергия магнитного поля катушки 
.
Следовательно,
.
Ответ: ΔII = 6,0 А; ΔIII = 0; ΔIIII = –6,0 А; Wм = 36 мДж.
Пример 3. За промежуток времени Δt = 9,50 мс сила тока в катушке индуктивности равномерно возросла от I1 = 1,60 А до I2 = 2,40 А. При этом в катушке возникала ЭДС самоиндукции 
= ‒14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.
Дано:
Δt = 9,50 мс = 9,50 · 10-3 с
I1 = 1,60 А
I2 = 2,40 А
= ‒14,0 В
Фс — ?
ΔWм — ?
Решение: При изменении в катушке силы тока от I1 до I2 возникает собственный магнитный поток Фс = LI2. Индуктивность L катушки можно определить из закона электромагнитной индукции для явления самоиндукции: 
. Следовательно,
. Тогда 
.
Приращение энергии магнитного поля катушки
Ответ: Фс = 399 мВб, ΔWм = 266 мДж.
Физика, 11 класс
Урок 6. Самоиндукция. Индуктивность
Перечень вопросов, рассматриваемых на уроке:
1) индуктивность, самоиндукция, ЭДС самоиндукции;
2) использование явления электромагнитной индукции, принцип действия электрогенератора и электродинамического микрофона;
3) аналогия между самоиндукцией и инертностью;
4) закон самоиндукции, границы его применимости;
5) ЭДС индукции в движущихся проводниках.
Глоссарий по теме
Самоиндукцией называют явление возникновения ЭДС индукции в самом проводнике, по которому идет переменный ток. Эта ЭДС называется ЭДС самоиндукции 
.
Величину L называют индуктивностью контура или его коэффициентом самоиндукции.
Индуктивность проводника равна 1 Гн, если в нём при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В.
Энергия магнитного поля, созданного током, проходящим по участку цепи с индуктивностью L равна произведения индуктивности и квадрата силы тока деленная на два.
Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.
Основная и дополнительная литература по теме урока:
Обязательная литература:
Мякишев Г.Я.,Буховцев Б.Б.,Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 47 — 52.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа, 2009. – С. 121 – 125.
Целых Д. Об измерении энергии магнитного поля //Квант. — 1998. — № 1. — С. 43-44.
Основное содержание урока
Самоиндукция — это явление возникновения электромагнитной индукции в проводнике при изменении силы тока, протекающего через проводник 
.
При самоиндукции проводящий контур выполняет двойную роль: переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, то появляется ЭДС индукции 
.
По правилу Ленца, в момент нарастания тока напряженность вихревого электрического поля направлена против тока, препятствуя нарастанию тока. В момент уменьшения тока вихревое поле наоборот поддерживает его.
ЭДС самоиндукции E_si может быть больше ЭДС источника тока
.
Генератор – это устройство, преобразующее энергию того или иного вида в электрическую энергию.
Генератор состоит из подвижной части – ротора, и неподвижной части – статора.
Все генераторы состоят из магнита или электромагнита, создающего магнитное поле, и рамки (обмотки) в которой индуцируется ЭДС.
По закону электромагнитной индукции Фарадея, в условиях, когда проводник движется внутри магнитного поля, образуется эффект пересечения магнитных силовых линий. На заряды со стороны магнитного поля действует сила Лоренца и внутри проводника свободные заряды приходят в направленное движение, то есть индуцируется ЭДС (электродвижущая сила), которая имеет магнитное происхождение. Величина индуцированной электродвижущей силы проводника напрямую зависит от скорости изменения магнитного потока (от скорости вращения рамки), пронизывающий проводник. Генераторы вырабатывают переменный электрический ток.
Микрофон осуществляет превращение звуковых колебаний воздуха в колебания электрического тока. Его действие основано на явлении электромагнитной индукции.
В электродинамическом микрофоне мембрана механически жёстко соединена с катушкой, который находится в кольцевом зазоре постоянного магнита (аналогично динамикам). Линии магнитной индукции перпендикулярны виткам катушки.
Звуковая волна вызывает колебание мембраны и, соответственно, колебание звуковой катушки. Катушка движется в магнитном поле, в её витках индуцируется ток, и на концах катушки возникает переменная ЭДС индукции.
Это переменное напряжение вызывает колебание тока в цепи микрофона.
Самоиндукция является частным случаем электромагнитной индукции.
Самоиндукцию можно представить как своеобразный маховик или точнее – силу инерции. При действии на маховик внешней силы сначала сопротивляется этой силе, а при резком прекращении ее действия, когда уже маховик раскручен – еще какое-то время движется по инерции.
Явление самоиндукции используют в системах плавного включения электрических устройств, например, в осветительных приборах, цепях, содержащих трансформаторы, генераторы, электродвигатели, выключение тока проводят медленно, чтобы ЭДС самоиндукции не превысила ЭДС источника, и прибор не вышел из строя, выполняет очень важную роль в: электротехнике и радиотехнике. Индуктивность цепи оказывает существенное влияние на прохождение по цепи переменного электрического тока.
Магнитный поток 
пропорционален силе тока I:
где
— индуктивность контура, или его коэффициентом самоиндукции. Единицу индуктивности в СИ называют генри (обозначается 1 Гн). Индуктивность зависит от геометрических размеров проводника, его формы, и непосредственно не зависит от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Индуктивность одного проволочного витка меньше, чем у катушки (соленоида), состоящей из N таких же витков, так как магнитный поток катушки увеличивается в N раз.
если геометрические параметры проводника остаются неизменными и поток меняется только за счет изменения силы тока.
Электродвижущая сила самоиндукции 
прямо пропорциональна скорости изменения силы тока, протекающего сквозь проводник, взятого со знаком минус.
Источник тока, включенный в электрическую цепь, обладает запасом энергии. Источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, идет на образование магнитного поля.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока
Энергию магнитного поля можно выразить и через характеристики поля. Плотность энергии магнитного поля (то есть энергия единицы объёма) пропорциональна квадрату магнитной индукции: 
, подобно плотности энергии электрического поля пропорциональной квадрату напряженности электрического поля: 
Запас энергии магнитного поля катушки равен энергии, израсходованной источником тока на преодоление э. д. с. самоиндукции за весь тот промежуток времени, пока сила тока при замыкании цепи возрастала от нуля до некоторого значения. Часть работы ЭДС источника в катушке идет на нагревание ее проводов, а часть, равная э. д. с. самоиндукции, совершает работу против ЭДС самоиндукции.
При движении проводника длиной l в однородном магнитном поле на электроны проводника действует сила Лоренца 
.
Если концы проводника будут соединены через нагрузку друг с другом, то через проводник потечёт ток.
Сила Лоренца, совершает работу по перемещению зарядов по всей длине проводника l.
Возникающая за счет действия на заряды силы Лоренца ЭДС индукции имеет магнитное происхождение.
Электродвижущая сила индукции в проводнике равна отношению работы по перемещению заряда к этому заряду:
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью v в однородном магнитном поле
Разбор тренировочных заданий
1. Катушка индуктивностью 2 Гн подключена к источнику тока так, как показано на рисунке. Сопротивление лампы равно 70 Ом, ЭДС источника 210 В.
Внутренним сопротивлением источника и сопротивлением проводов пренебречь. Выберите два верных утверждения о процессах, наблюдаемых в опыте.
1) Сила тока в цепи равна 3 А;
2) Энергия магнитного поля равна 18 Дж;
3) Ток через лампу сначала увеличивается, затем достигнув максимального значения не меняется;
4). Магнитный поток пронизывающий катушку сначала уменьшается, потом увеличивается.
Дано:
L=2 Гн
R=70 Ом
Ԑ=210В
r=0
Решение:
1) Согласно закону Ома для полной цепи
Утверждение 1 верно.
2) Энергия магнитного поля:
Утверждение 2 неверно.
3) Согласно явлению самоиндукции, ток в проводнике нарастает постепенно и не меняется, если в проводнике установится постоянный ток.
Утверждение 3 верно.
4) При увеличении тока магнитный поток пронизывающий катушку увеличивается, потом не изменяется.
Утверждение 4 неверно.
Правильные варианты: 1); 3).
2. На рисунке представлен график зависимости силы тока в катушке от времени. Индуктивность катушки равна 2,5 Гн. Найдите два правильных ответа:
1) модуль магнитного потока через катушку в интервале времени от 0 до 1 с равна 1,25 Вб;
2) модуль ЭДС самоиндукции в интервале времени от 1 до 5 с равна 0,625 В;
3) максимальное значение модуля ЭДС самоиндукции для данного графика равна 2,5 В;
4) энергия магнитного поля катушки за 2 секунды, начиная с момента времени t = 6 c равна 0,15625 Дж.
Дано:
L=2,5 Гн
Решение:
1) Модуль магнитного потока через катушку равен:
Утверждение 1 верно.
2) ЭДС самоиндукции согласно формуле равна:
Утверждение 2 неверно.
3) Согласно графику максимальное ЭДС самоиндукции будет на интервале от 5с до 6с.
Утверждение 3 верно.
4) Энергия магнитного поля катушки:
Утверждение 4 неверно.
Правильные варианты: 1); 3).
Согласно
закону электромагнитной индукции, при
изменении магнитного потока Ф,
пронизывающего контур, в последнем
возникает ЭДС индукции ε
i,
пропорциональная скорости изменения
магнитного потока во времени :
εi
=
(3.4.1)
Знак
“минуc”
в выражении (3.4.1) соответствует правилу
Лоренца: индукционный ток всегда
направлен таким образом, чтобы
противодействовать причине, его
вызвавшей.
Если
контур содержит N
витков и каждый виток сцеплен с переменным
магнитным потоком Ф, то
ε
i
=
,
здесь
N
·
Ф = Ψ – полный магнитный поток или
потокосцепление.
Изменение
магнитного потока может быть обусловлено
равными причинами, связанными с изменением
: магнитной индукции во времени; формы
контура (площади, охватываемой им); угла
между нормалью к плоскости и вектором
В
(например, при вращении рамки в магнитном
поле); площади, описываемой проводником,
пересекающим силовые линии поля и т.д.
Поэтому при решении задач на эту тему
надо, прежде всего, установить причину
изменения магнитного потока.
Пример.
Найти заряд, протекающий по замкнутому
витку с сопротивлением R,
при удалении его из магнитного поля.
Магнитный поток сквозь виток равен
Ф.
Решение.
Причина
изменения магнитного потока –
исчезновение поля, магнитный поток
сначала был равен Ф, затем снизился до
нуля. Так как проводник замкнутый, по
нему течет индукционный ток I.
Тогда заряд, прошедший по витку, q
= I
dt΄.
По закону Ома I
= ε
i
/ R,
а ЭДС индукции ε i
= — dФ
/ dt.
Тогда :
q
=
Ответ
: q
= Ф / R.
Пример.
Прямолинейный проводник длиной l
движется в однородном магнитном поле
так, что его скорость v
составляет угол β
с направлением силовых линий. Найти ЭДС
индукции, возникающей на концах
проводника. Магнитная индукция поля В
считается известной.
Решение.
Причина изменения магнитного потока –
изменение площади, пересекаемой
проводником при его движении. Поэтому
скорость изменения магнитного потока
во времени
dФ/dt
= B(dS/dt) cosα.
dS/dt
– площадь, пересекаемая проводником в
единицу времени, равная ldx/dt
= lν,
а угол α дополняет угол β до 90 0
(рис. 13). Тогда
εi
= — B
l
ν
sin
β.
Ответ
:
ε
i
= — B l ν sin β.
Пример.
Рамка
площадью 100 см2
вращается в магнитном поле с индукцией
0,2 Тл так, что ось вращения расположена
перпендикулярно силовым линиям магнитного
поля. Рамка делает 5 оборотов в секунду.
Найти значение ЭДС индукции в момент
времени t
= 2с и максимальную ЭДС индукции в рамке.
В начальный момент времени плоскость
рамки располагалась перпендикулярно
силовым линиям поля.
Решение.
Причина
изменения магнитного потока здесь –
изменение угла между нормалью к рамке
и магнитной индукцией, причем угловая
скорость вращения ω = 2πn
(n
– число оборотов в единицу времени.).
Согласно основному закону электромагнитной
индукции :
Подставив
числовые данные, получим в момент t
= 2 c
ε
i
= — 0,2 · 10 –
2
· 2 · 3,14 · 5 · sin (2π · 5 · 2) = 0
Максимальное
значение ЭДС находим из условия, что
sin
(2πn)
=1:
ε
maх
= 0, 2 · 10 – 2
· 2 · 3,14 · 5 = 0, 0628 В.
Ответ
:
В момент времени 2 с ЭДС индукции равна
нулю.
Максимальная
ЭДС индукции 0, 0628 В.
Если по контуру
протекает изменяющийся во времени ток,
то в контуре возникает ЭДС самоиндукции
:
ε
S
=
(3.4.2)
где
L
– индуктивность
контура, определяемая отношением
потокосцепления к силе тока в контуре
:
(3.4.2
΄ )
В
СИ индуктивность измеряется в Генри
(Гн).
Выведем
формулу для индуктивности соленоида.
При протекании тока по соленоиду длиной
l
в нем возбуждается магнитное поле,
индукция которого на оси соленоида
определяется формулой (3.2.4). Потокосцепление
,
где
Ψ = BS
– поток, пронизывающий каждый из витков;
S
– площадь поперечного сечения соленоида;
N
= nl
– общее число витков. Следовательно,
индуктивность соленоида равна
,
где
IS
= V
– объем соленоида. По этой формуле
вычисляется индуктивность соленоида
без сердечника
или немагнитным
сердечником (
в том и другом случае μ = 1 ).
Если
соленоид содержит ферромагнитный
сердечник,
то надо сначала определить значение
магнитной проницаемости материала
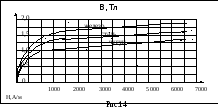
сердечника. Для этого надо знать ход
кривой B
= f(H)
(рис.14).
Определив
из условий задачи либо напряженность
поля, либо магнитную индукцию, нужно по
графику для данного материала определить
недостающую из этих двух величин и затем
найти
μ
= B/(μ0H).
Пример.
Найти
индуктивность соленоида с железным
сердечником, если обмотка соленоида
выполнена в один слой из проволоки
диаметром 0,4 мм, витки плотно прилегают
друг к другу. По соленоиду идет ток 1 А.
Объем соленоида 1500 с3
.
Решение.
Индуктивность
соленоида можно определить по формуле
(1.4.3). Так как соленоид имеет магнитный
сердечник, то сначала определим магнитную
проницаемость последнего, как отношение
B/(μ0H).
Для этого находим напряженность поля
на оси соленоида по формуле H
= In
, где n
(число витков на единицу длины)
подсчитывается следующим образом: витки
плотно прилегают друг к другу и общее
число
витков равно N
= l/d
( d
– диаметр проволоки), n
= N/l
= 1/d
.
Тогда напряженность
H
= I/d
= 1/(0,4·10-3 )
= 2500 А/м.
Из
графика (рис. 14) следует, что этому
значению для железа соответствует
магнитная индукция 1,4 Тл. Этих данных
достаточно для определения дтносительной
магнитной проницаемости сердечника и
далее индуктивности. Подставив их в
формулу (1.4.3) , получим
Ответ:
L
= 5,25 Гн.
Если по катушке идет переменный ток, то магнитный поток, пронизывающий катушку, меняется. Поэтому возникает ЭДС индукции в том же самом проводнике, по которому идет переменный ток. Это явление называют самоиндукцией.
При самоиндукции проводящий контур выполняет двойную роль. С одной стороны, переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, появляется ЭДС индукции εis. По правилу Ленца в момент нарастания тока напряженность вихревого электрического поля направлена против тока. Следовательно, в этот момент вихревое поле препятствует нарастанию тока. Наоборот, в момент уменьшения тока вихревое поле поддерживает его.
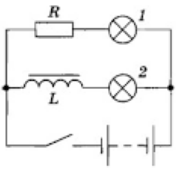
Явление самоиндукции можно наблюдать в простых опытах. На рисунке представлена схема параллельного соединения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L, снабженной железным сердечником.
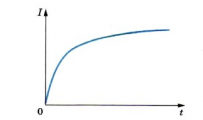
При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения (см. график ниже).
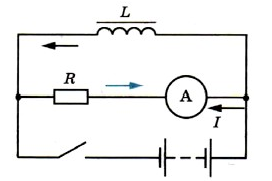
Появление ЭДС самоиндукции при размыкании можно наблюдать в опыте с цепью, схематически показанной на следующем рисунке. При размыкании ключа в катушке L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в момент размыкания через гальванометр идет ток (цветная стрелка), направленный против начального тока до размыкания (черная стрелка). Сила тока при размыкании цепи может превышать силу тока, проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции εis больше ЭДС ε батареи элементов.
Самоиндукция и инерция
Явление самоиндукции проще понять, проведя аналогию с инерцией в механике. Инерция приводит к тому, что под действием силы тело не мгновенно приобретает скорость, а постепенно. Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила. Точно так же за счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы не прекращаем ток сразу. Самоиндукция его поддерживает некоторое время, несмотря на сопротивление цепи.
Чтобы увеличить скорость тела, согласно законам механики нужно совершить работу. При торможении тело само совершает работу. Точно так же для создания тока нужно совершить работу против вихревого электрического поля, а при исчезновении тока это поле совершает положительную работу.
Индуктивность
Модуль вектора индукции В магнитного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф ~ В~ I. Это дает право утверждать, что:
Φ=LI
L — коэффициент пропорциональности между током в проводящем контуре и магнитным потоком, пронизывающим этот контур. Эту величину также называют индуктивностью контура, или его коэффициентом самоиндукции.
Применив закон электромагнитной индукции, а также считая, что форма контура остается неизменной, и поток меняется только за счет изменения силы тока, получим:
εis=−ΔΦΔt=−LΔIΔt
Эта формула позволяет дать такую формулировку L, которая точно отражает суть этой величины.
Определение
Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
Единица измерения индуктивности — генри (Гн). Индуктивность проводника равна 1 Гн, если в нем при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции в 1 В.
Индуктивность подобна электроемкости. Она зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Пример №1. При равномерном изменении силы тока в катушке на 10 А за 0,02 с в ней возникает ЭДС самоиндукции, равная 200 В. Чему равна индуктивность катушки?
Выразим индуктивность из формулы для ЭДС самоиндукции:
L=−ΔtεisΔI=0,02·20010=−0,4 (Гн)
Знак «минус» означает, что ЭДС самоиндукции действует так, что индукционный ток препятствует изменению магнитного потока. Поэтому само значение индуктивности мы можем принять за модуль полученного результата — 0,4 Гн.
Задание EF17686
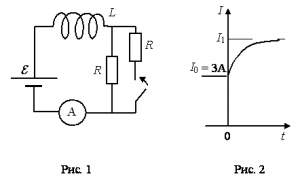
Катушка, обладающая индуктивностью L, соединена с источником питания с ЭДС ε и двумя одинаковыми резисторами R. Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.
В момент времени t=0 ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните, почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения – I1. Определите значение силы тока I1. Внутренним сопротивлением источника тока пренебречь.
Алгоритм решения
1.Установить, какими физическими законами можно описать эксперимент.
2.Описать, что происходит до замыкания ключа.
3.Определить, что произойдет после замыкания ключа.
4.Вычислить силу тока в катушке.
Решение
На рисунке 1 изображена схема, в которой катушка индуктивности подключена последовательно к двум параллельно соединенным резистором и источнику тока. Амперметр тоже соединен с катушкой последовательно, следовательно, он определяет силу тока, проходящую через нее.
Для описания процесса можно подходит закон Ома для полной цепи и формула ЭДС самоиндукции, которая будет возникать при изменении силы тока в цепи:
IRобщ=ε+εis
εis=−LΔIΔt
До замыкания ключа общее сопротивление цепи равно сопротивлению одного резистора — R. Так как ток в этом случае постоянный, ЭДС самоиндукции отсутствует. Тогда закон Ома принимает вид:
I0=εR
Когда ключ замыкается, сопротивление в цепи уменьшается вдвое, так как подключается второй резистор:
1Rобщ=1R+1R=2R
Rобщ=0,5R
Изменение сопротивления в цепи вызывает изменение силы тока. В результате возникает ЭДС самоиндукции. Она препятствует изменению силы тока через катушку в соответствии с правилом Ленца. Поэтому сила тока через катушку при замыкании ключа не претерпевает скачка.
Постепенно ЭДС самоиндукции уменьшается до нуля, а сила тока через катушку плавно возрастает до значения:
I1=ε0,5R=2I0
На рисунке 2 начальная сила тока равна 3 А. Следовательно:
I1=3·2=6 (А)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17724
В электрической цепи, показанной на рисунке, ЭДС и внутреннее сопротивление источника тока соответственно равны 12 В и 1 Ом, ёмкость конденсатора 2 мФ, индуктивность катушки 36 мГн и сопротивление лампы 5 Ом. В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Сопротивлением катушки и проводов пренебречь. Ответ записать в мДж.
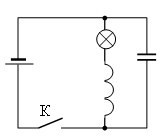
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Установить величину электромагнитного поля катушки и электрического поля конденсатора.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 12 В.
• Сопротивление источника тока: r = 1 Ом.
• Емкость конденсатора: C = 2 мФ.
• Индуктивность катушки: L = 36 мГн.
• Сопротивление лампы: R = 5 Ом.
2 мФ = 2∙10–3 Ф
36 мГн = 36∙10–3 Гн
Пока ключ замкнут, через катушку L течёт ток определяемый внутренним сопротивлением источника и сопротивлением лампочки. Его можно вычислить, используя закон Ома для полной цепи:
I=εR+r
При этом конденсатор будет заряжен до напряжения U, которое определяется законом Ома для участка цепи:
U=IR
Подставив в это выражение закон Ома для полной цепи, получим:
U=εRR+r
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22=C2(εRR+r)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22=L2(εR+r)2
После размыкания ключа начинаются затухающие электромагнитные колебания, и вся энергия, запасённая в конденсаторе и катушке, выделится на лампе:
E=Wкон+Wкат=C2(εRR+r)2+L2(εR+r)2
Ответ: 172
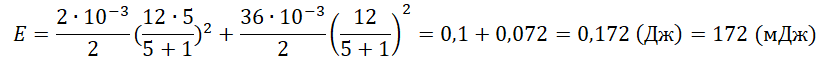
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18478
Катушка индуктивности подключена к источнику тока с пренебрежимо малым внутренним сопротивлением через резистор Ом (см. рисунок). В момент ключ К замыкают. Значения силы тока в цепи, измеренные в последовательные моменты времени
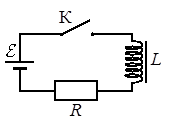
с точностью 0,01 А, представлены в таблице.
Выберите два верных утверждения о процессах, происходящих в цепи.
Ответ:
- Напряжение на резисторе в момент времени t= 1,0 c равно 1,9 В.
- Энергия катушки максимальна в момент времени t= 0 c.
- ЭДС источника тока равна 18 В.
- Напряжение на катушке максимально в момент времени t= 6,0 c.
- Модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В.
Алгоритм решения
1.Проверить истинность каждого утверждения.
2.Выбрать 2 верных утверждения.
Решение
Согласно утверждению 1, напряжение на резисторе в момент времени t = 1,0 c равно 1,9 В. Так как сила тока еще не установилась, а сопротивление источника тока пренебрежимо мало, вычислить напряжение на резисторе можно с помощью закона Ома для полной цепи:
I=ε−εisR
U=ε−εis=IR=0,19·60=11,4 (В)
Следовательно, утверждение 1 — неверно.
Согласно утверждению 2, энергия катушки максимальна в момент времени t = 0 c. Энергия катушки определяется формулой:
Wкат=LI22
Так как сила тока в начальный момент времени равна нулю, то энергия катушки в это время тоже нулевая.
Следовательно, утверждение 2 — неверно.
Согласно утверждению 3, ЭДС источника тока равна 18 В. Вычислить ЭДС источника тока можно, используя закон Ома для полной цепи в момент, когда сила тока в цепи достигнет максимального значения. В этом случае ЭДС самоиндукции будет равна 0. Тогда:
I=εR
ε=IR=0,3·60=18 (В).
Это действительно так. Следовательно, утверждение 3 — верно.
Согласно утверждению 4, напряжение на катушке максимально в момент времени t = 6,0 c. Напряжение на катушке равно разности напряжения ЭДС источника тока и напряжения на резисторе (так как они соединены последовательно):
U=ε−IR
Так как значение силы тока в момент времени t = 6,0 с максимально, то напряжение на катушке. Следовательно, утверждение 4 — неверно.
Согласно утверждению 5, модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В. Проверяя истинность утверждения 3, мы выяснили, что ЭДС источника тока равна 18 В. Следовательно, ЭДС самоиндукции равна:
εis=ε−IR
Для вычислений используем значения из таблицы для момента времени t = 2,0 с:
εis=18−0,26·60=2,4 (В)
Следовательно, утверждение 5 — верно.
Ответ: 35
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.2k