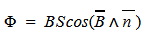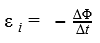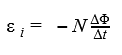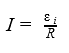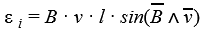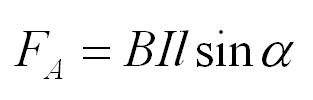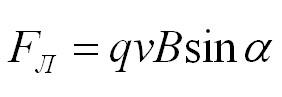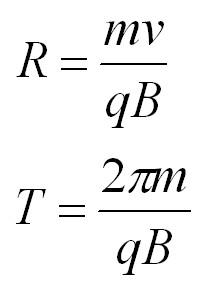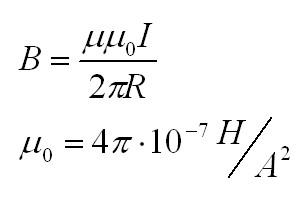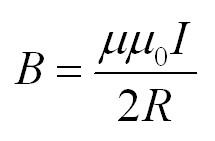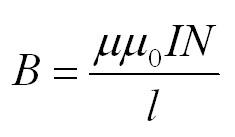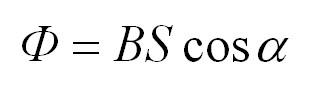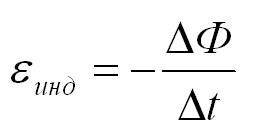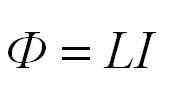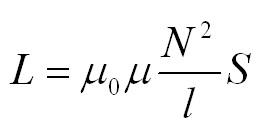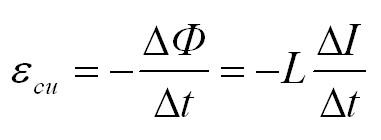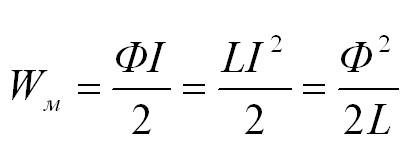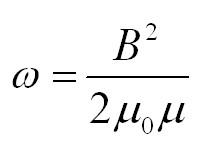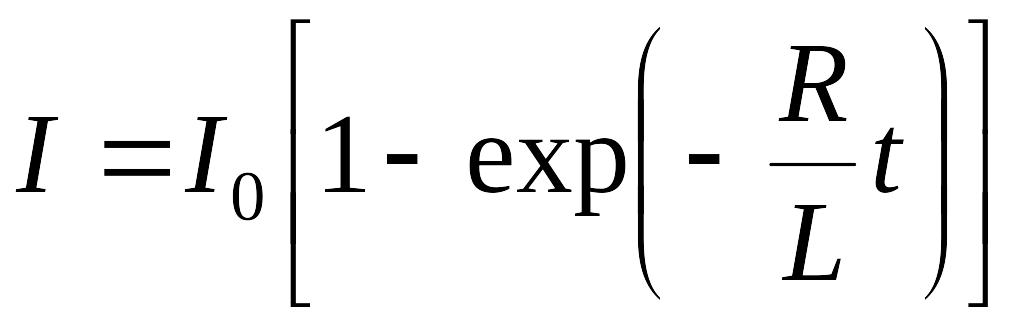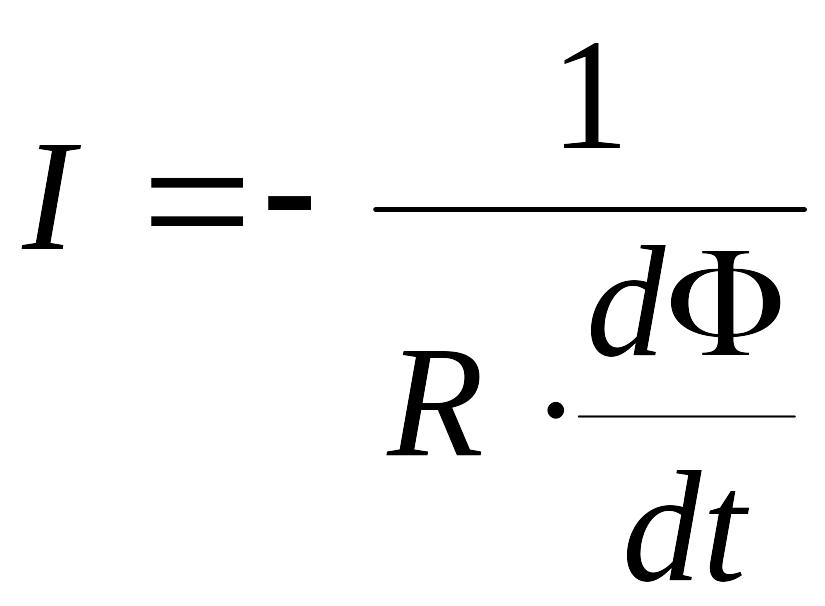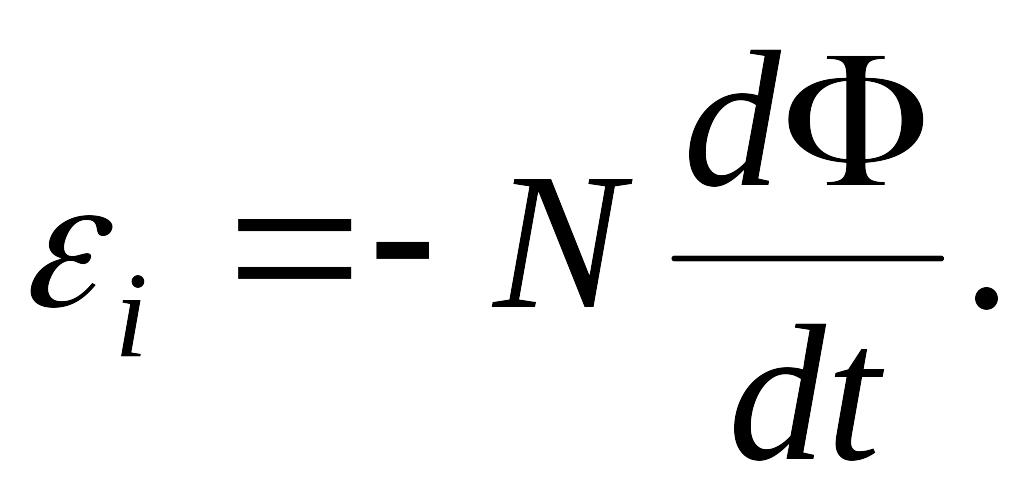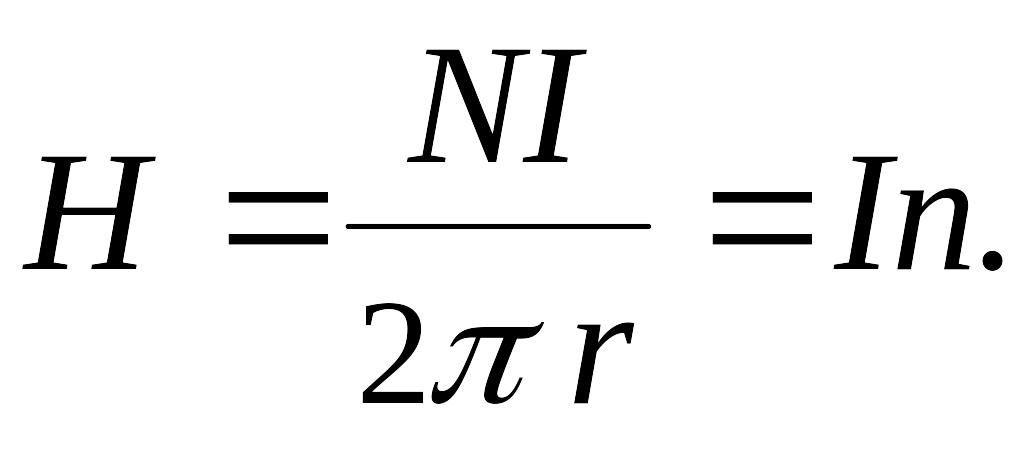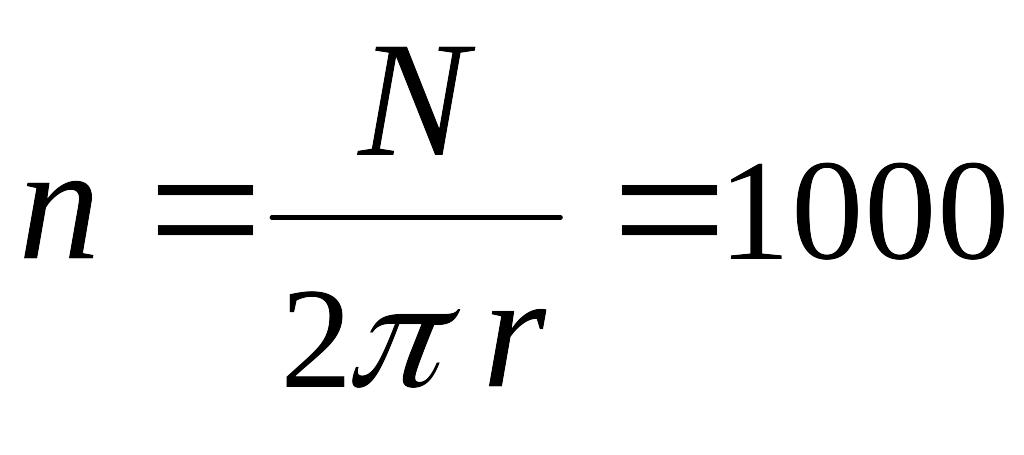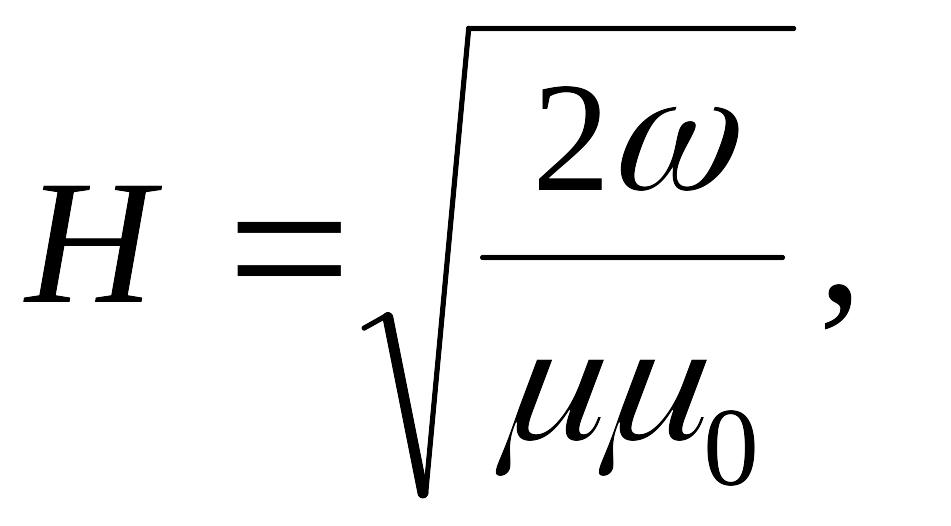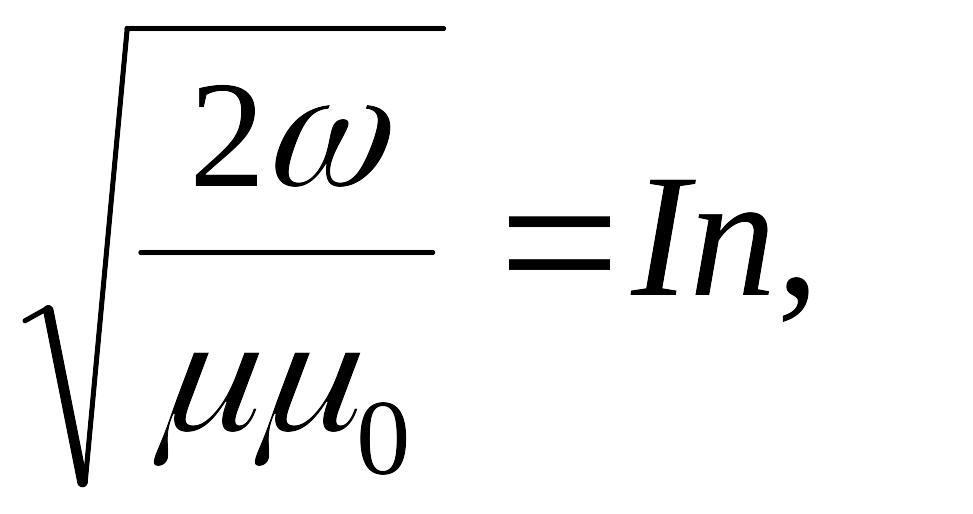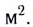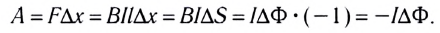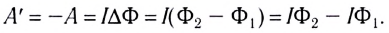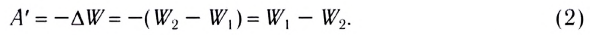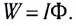Магнитный поток
Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.
Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.
Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
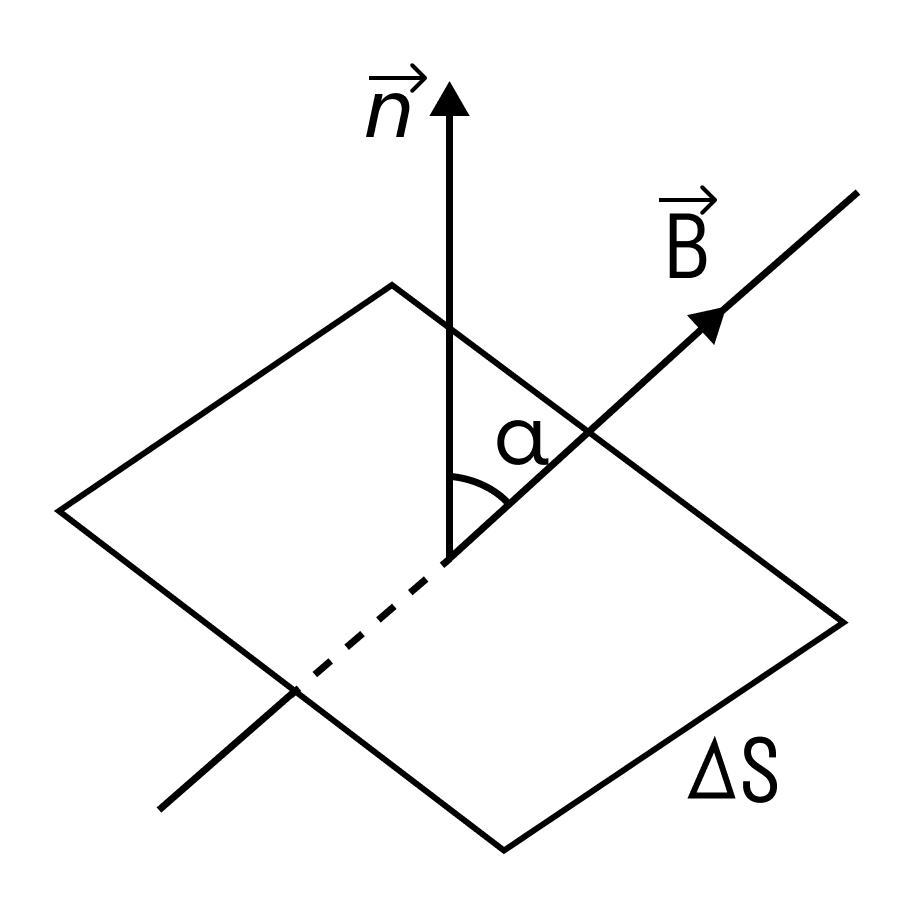
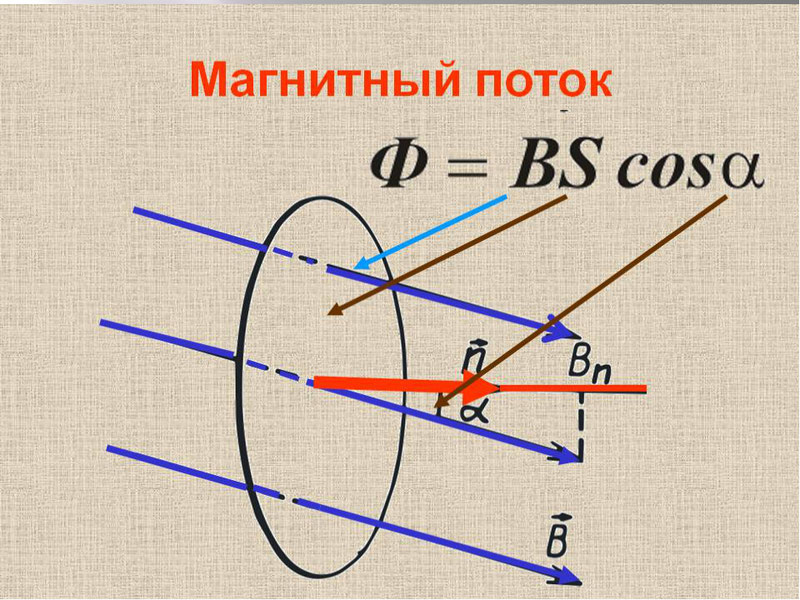
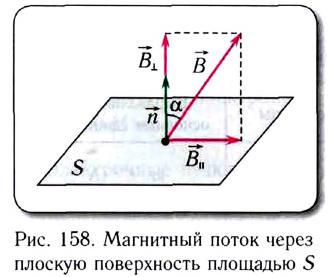
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции B, площади поверхности S, пронизываемой данным потоком, и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Магнитный поток
Ф — магнитный поток [Вб]
B — магнитная индукция [Тл]
S — площадь пронизываемой поверхности [м^2]
n — вектор нормали (перпендикуляр к поверхности) [-]
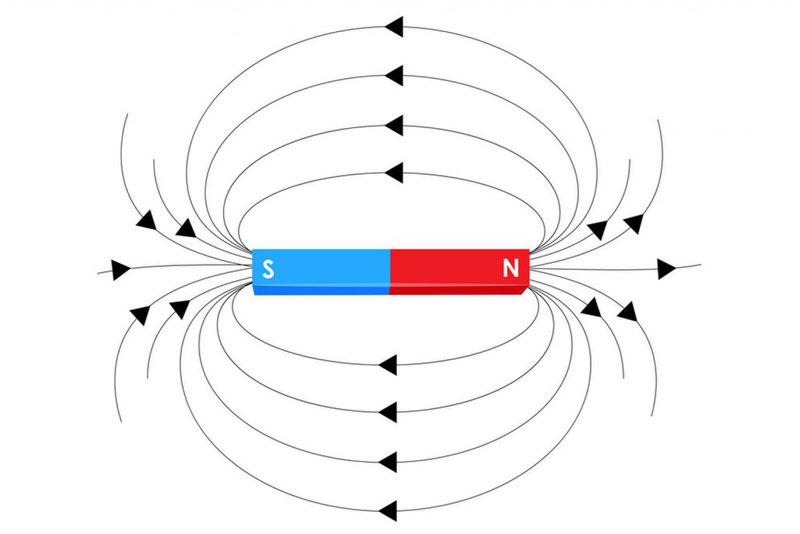
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.
Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
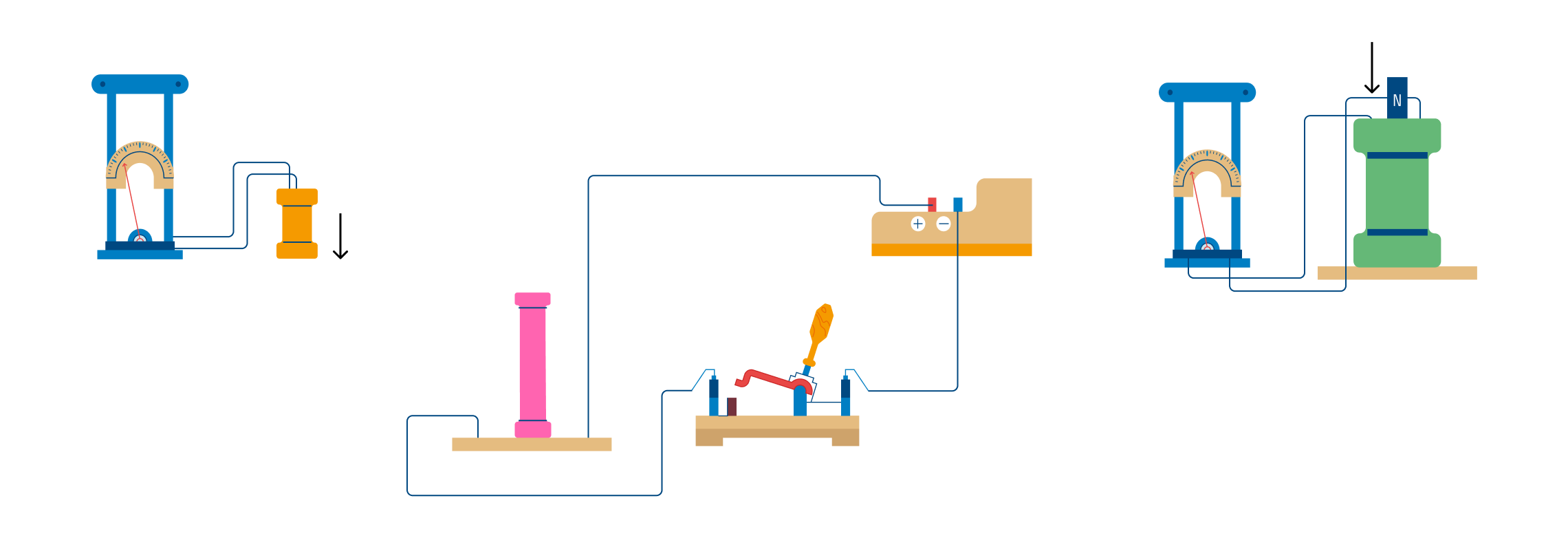
Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки
Вот, что показали эти опыты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока будет различно при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
Закон Фарадея
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
Закон Фарадея для контура из N витков
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
N — количество витков [-]
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
Закон Ома для проводящего контура
Ɛi — ЭДС индукции [В]
I — сила индукционного тока [А]
R — сопротивление контура [Ом]
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
ЭДС индукции для движущегося проводника
Ɛi — ЭДС индукции [В]
B — магнитная индукция [Тл]
v — скорость проводника [м/с]
l — длина проводника [м]
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
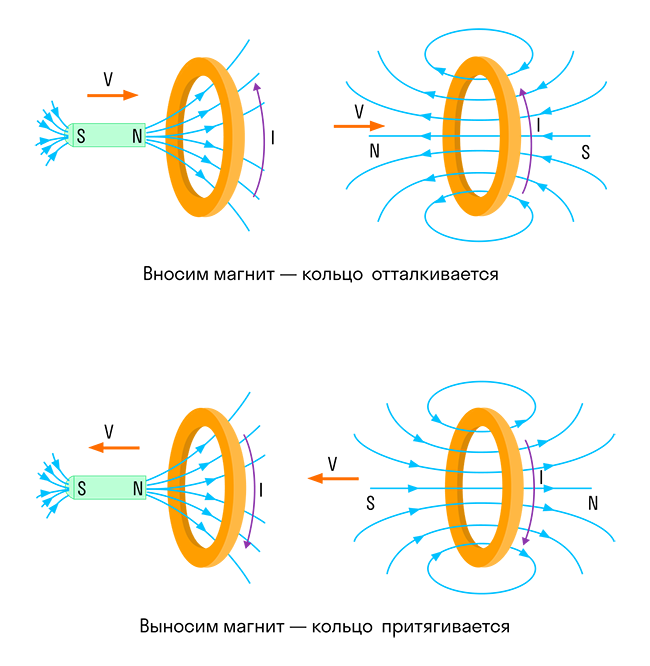
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
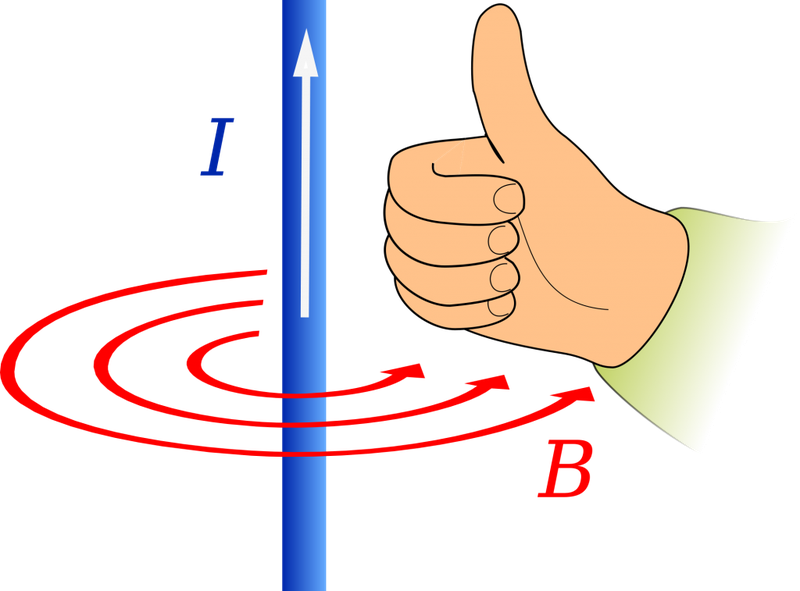
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
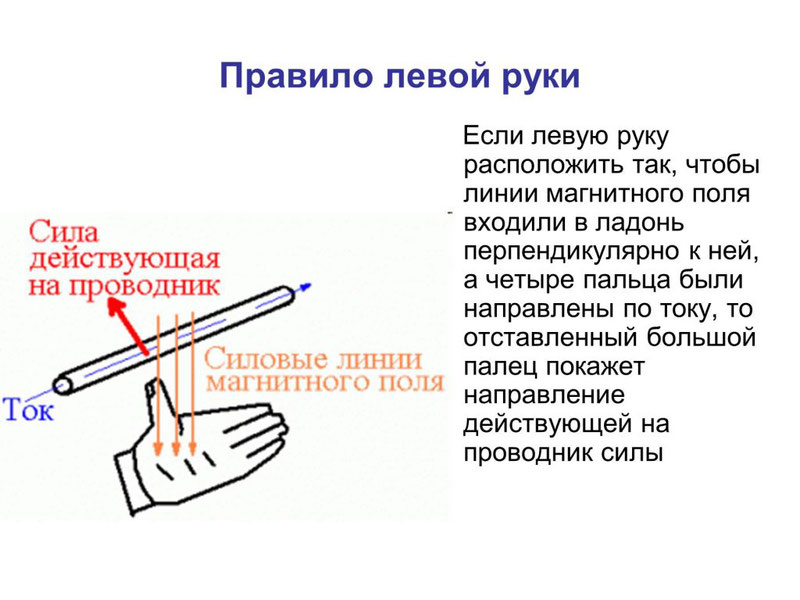
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
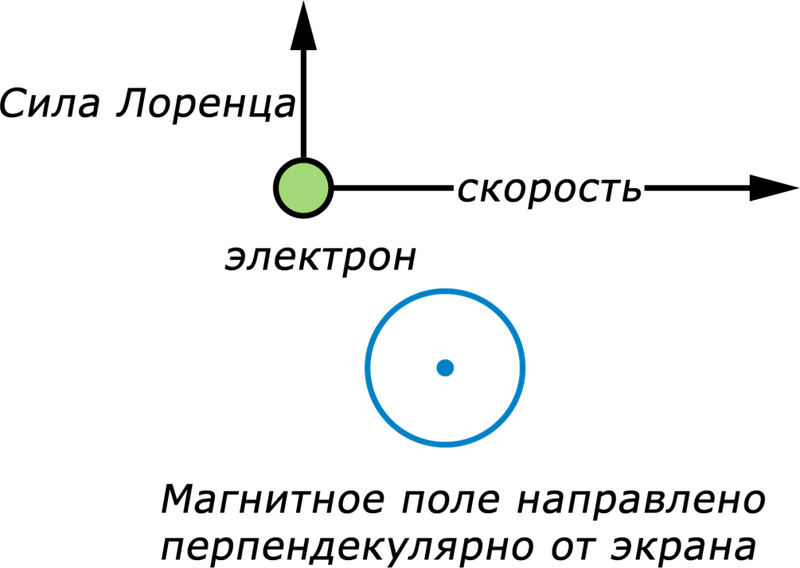
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
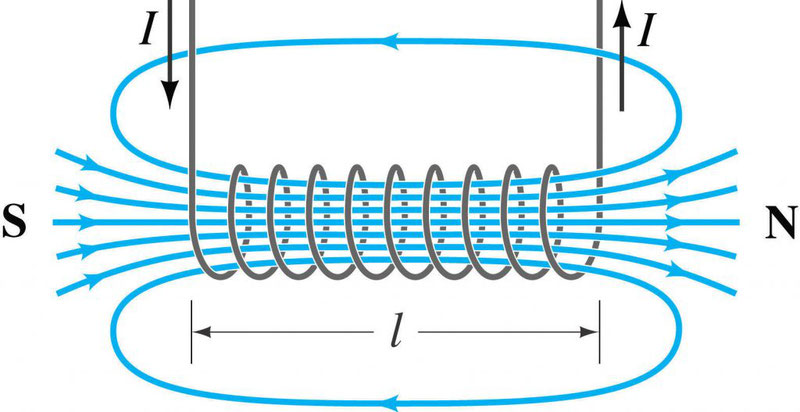
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
Электромагнитная индукция
Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.1 (62.35%) 102 votes
Краткие
теоретические сведения
Основные
формулы
Магнитный поток
через плоский контур:
а) в случае
однородного поля:
где
— угол между вектором нормали к плоскости
контура и вектором магнитной индукции;
— проекция вектора
на нормаль (
);
— площадь контура;
б) вслучае
неоднородного поля:
где
интегрирование ведется по всей
поверхности
.
Потокосцепление
(полный магнитный поток):
где
— магнитный поток через один виток;
— число витков.
Работа
по перемещению замкнутого контура с
током в магнитном поле:
где
—
изменение магнитного потока, пронизывающего
поверхность, ограниченную контуром;
—
сила тока в контуре.
Разность
потенциалов
на концах проводника длиной
,
движущегося со скоростью
в однородном магнитном поле с индукцией
,
выражается по формуле:
где
— угол между направлениями векторов
и
.
Заряд,
протекающий по замкнутому контуру при
изменении на величину
потокосцепления, пронизывающего все
витки контура:
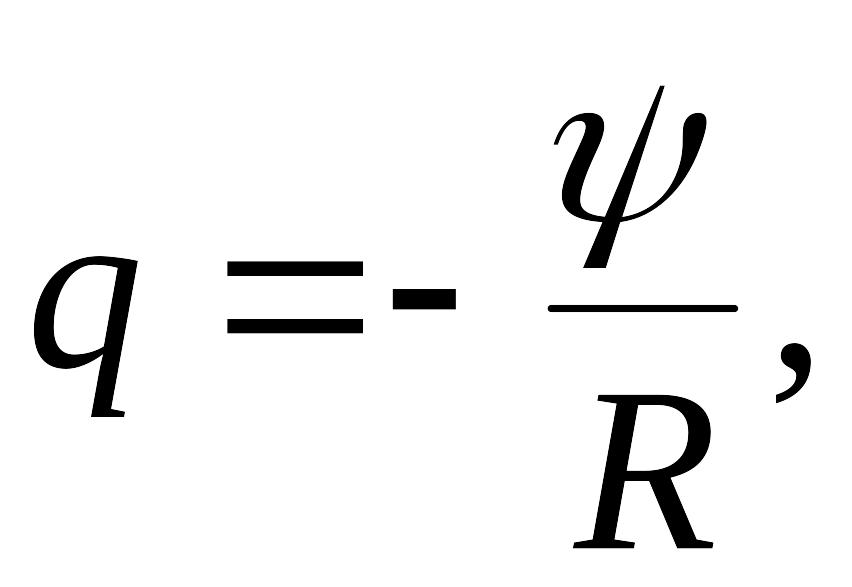
где
— сопротивление контура.
Основной
закон электромагнитной индукции
(закон Фарадея-Максвелла):
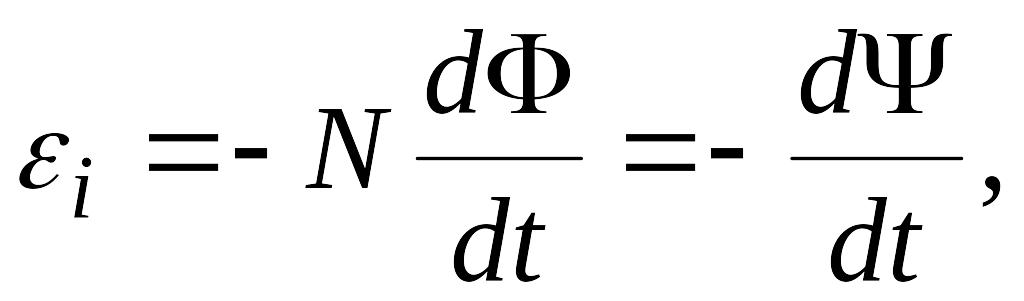
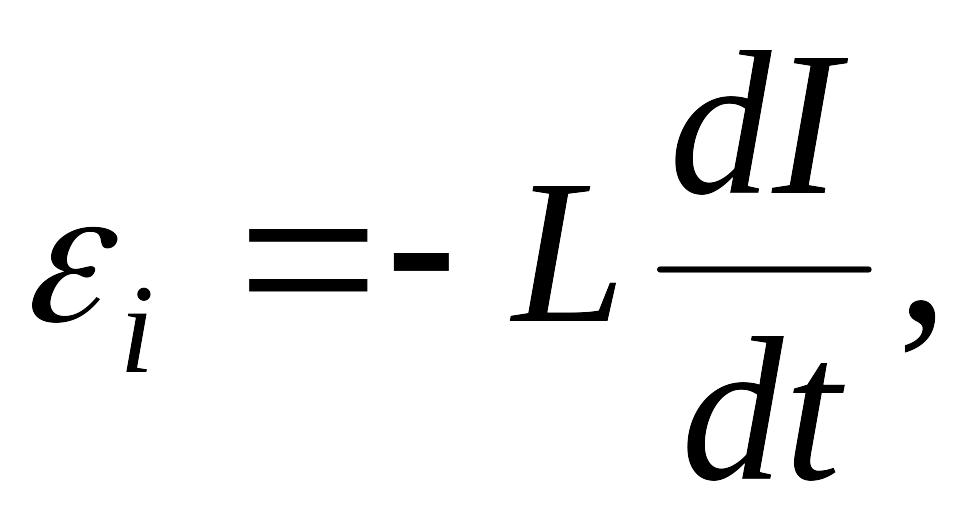
где
—
ЭДС индукции, возникающая в контуре;
— скорость изменения магнитного потока,
—
число витков контура;
— потокосцепление.
— индуктивность контура,
— скорость изменения силы тока.
Индуктивность
соленоида:
где
— длина соленоида,
— площадь его поперечного сечения,
— число витков на единицу длины.
ЭДС взаимной
индукции:

где
— взаимная индуктивность контуров.
Взаимная
индуктивность двух соленоидов,
пронизываемых общим магнитным потоком:
где
и
— числа витков на единицу длины этих
соленоидов.
Закон
изменения тока при размыкании (выключении)
цепи:
индуктивностью
и сопротивлением
:
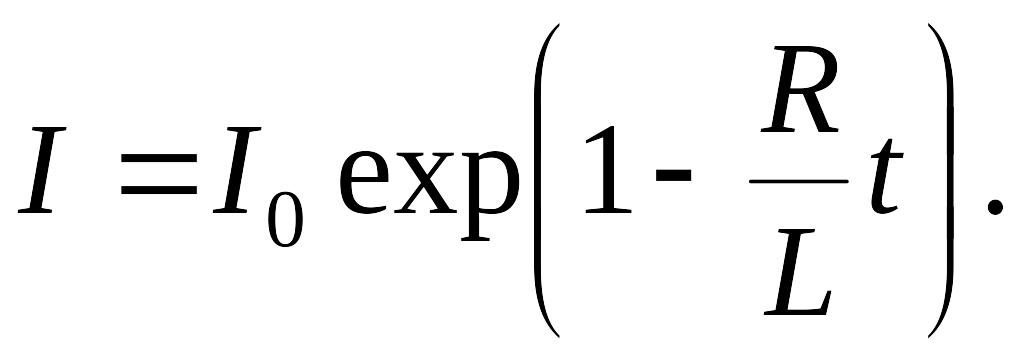
Закон изменения
тока при замыкании (включении) цепи:
.
Энергия магнитного
поля:
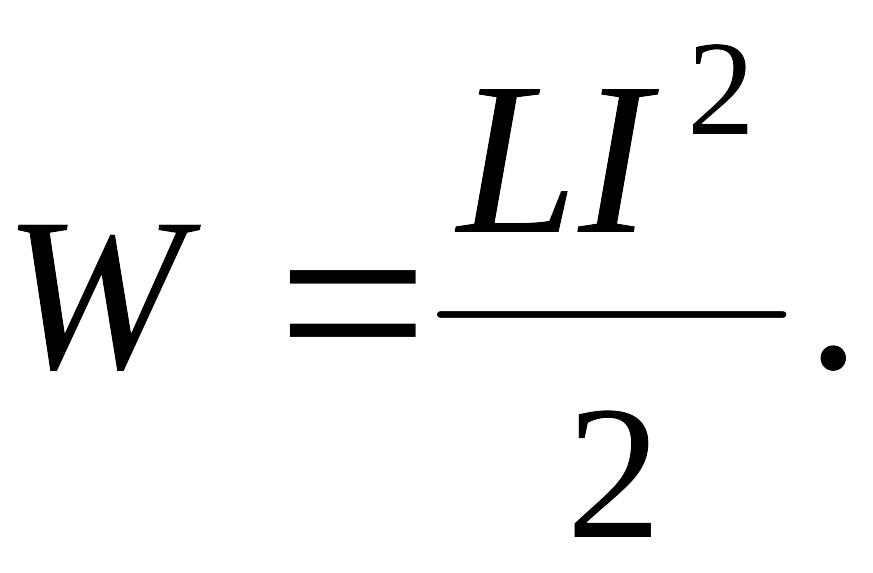
Плотность энергии
магнитного поля:
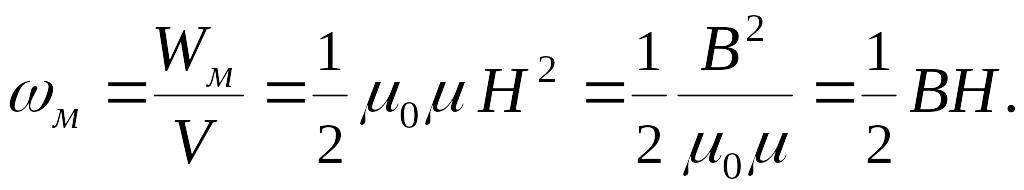
Вопросы для ответа у доски
-
ЭДС
электромагнитной индукции.
Получите
формулу для ЭДС индукции, исходя из
закона сохранения энергии. Покажите,
что ЭДС электромагнитной индукции
возникает не только в замкнутом контуре,
но и в проводнике, пересекающем при
своем движении линии магнитной индукции.
-
Ток
самоиндукции при замыкании и размыкании
электрической цепи.
Нарисуйте
соответствующие схемы электрических
цепей, составьте дифференциальные
уравнения и решите их.
Полученные
результаты проанализируйте и представьте
графически.
-
Энергия
магнитного поля. Плотность энергии.
Рассчитайте
работу, выполняемую до полного
исчезновения магнитного поля в соленоиде
при отключении источника ЭДС.
Покажите, что эта
работа равна энергии магнитного поля.
Рассчитайте
энергию магнитного поля бесконечного
соленоида и введите в рассмотрение
понятие плотности магнитной энергии.
Примеры решения задач
Задача 1.
Виток,
по которому течет ток
20А,
свободно установится в однородном
магнитном поле
16мТл.
Диаметр d
витка равен
10 см. Какую работу нужно совершать,
чтобы медленно повернуть виток на угол
/2
относительно оси, совпадающей с
диаметром?
Решение.
При
медленном повороте контура в магнитном
поле индукционными токами можно
пренебречь и считать ток в контуре
постоянным. Работа сил поля в этом
случае определяется выражением:
где
и
— магнитные потоки, пронизывающие контур
в начальном и конечном положениях.
Работа
внешних сил будет равна модулю работе
сил поля и противоположна ей по знаку:
(*)
Момент
внешних сил, действующий
на контур, равен нулю,
так как
в начальном положении контур установился
свободно (положение
устойчивого равновесия).
В
этом положении вектор магнитного
момента
контура сонаправлен с вектором
(рис.а) и магнитный поток
максимален (
0,
1),
.
В
конечном положении (рис.б)
вектор
перпендикулярен вектору
(
/2,
0)
и магнитный поток
0.
Подставляя в (*),
получаем:
где
площадь контура
С
учетом этого:
.
Подставляя числовые
значения, находим:
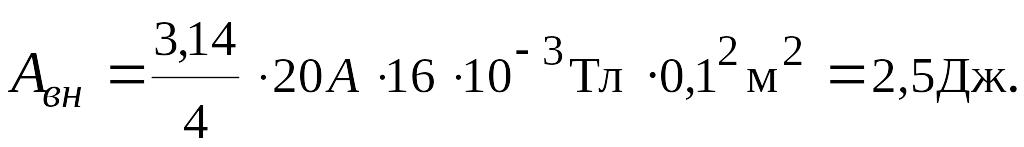
Ответ:
2,5Дж.
Задача 2.
Пусть
в магнитном поле имеется замкнутый
контур, пронизываемый потоком магнитной
индукции
.
Предположим, что этот поток уменьшается
до нуля. Вычислить величину заряда,
прошедшего по цепи.
Решение.
Мгновенное значение
ЭДС индукции в процессе исчезновения
магнитного потока выражается формулой:
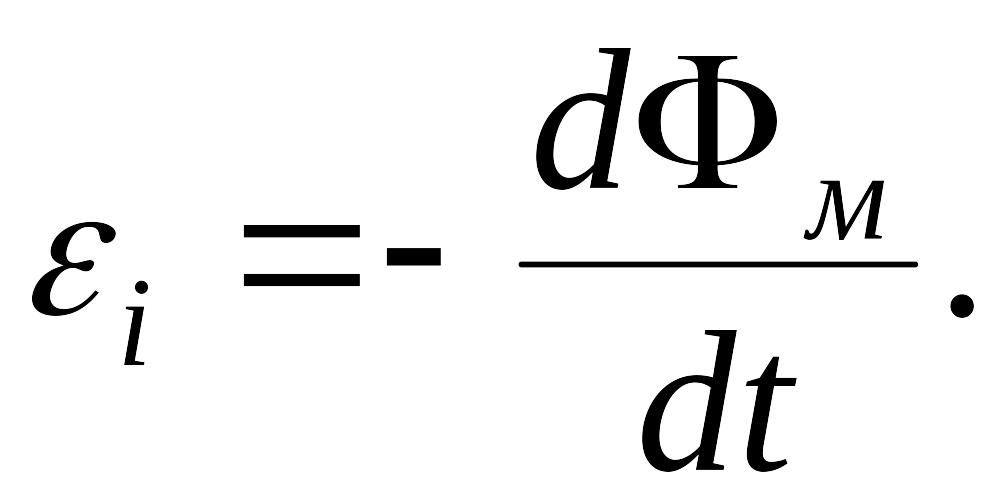
Следовательно,
мгновенное значение силы тока по закону
Ома будет равно:
,
где
— полное сопротивление контура.
Тогда величина
прошедшего заряда:
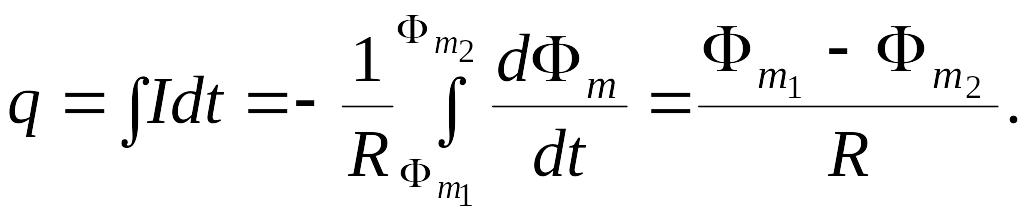
Так
как
,
то
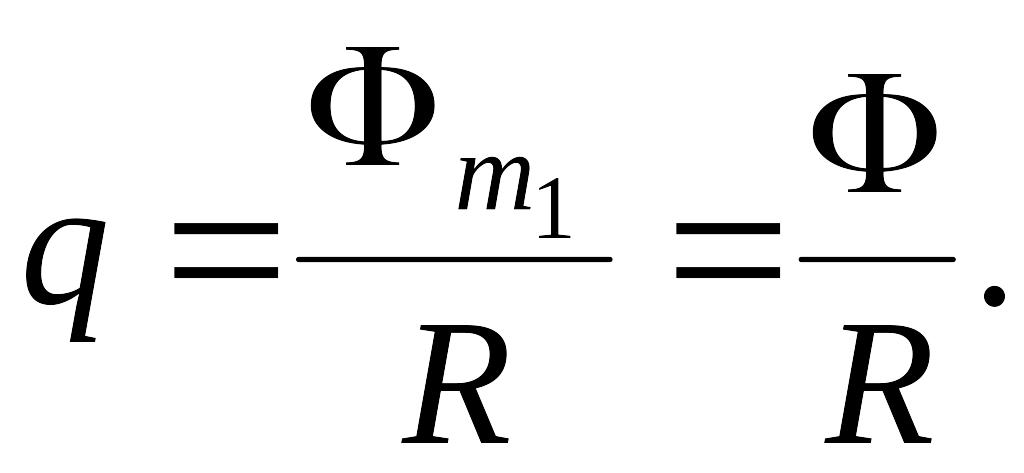
Ответ:
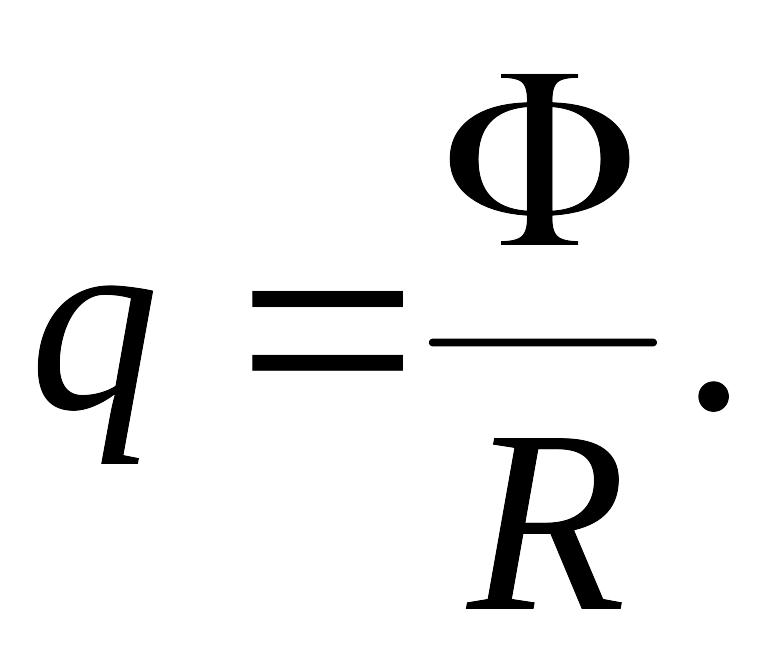
Задача 3.
В
однородном магнитном поле с индукцией
0,1Тл
равномерно вращается рамка, содержащая
1000
витков, с частотой
10с-1.
Площадь
рамки равна 150 см3.
Определить мгновенное значение ЭДС
,
соответствующее
углу поворота рамки 300.
Решение.
Мгновенное
значение ЭДС индукции
определяется
основным уравнением электромагнитной
индукции Фарадея-Максвелла:
(*)
Потокосцепление
,
где
— число витков, пронизываемых магнитным
потоком
.
Подставив выражение
в (*), получим:
(**)
При
вращении рамки магнитный поток
пронизывающий
рамку в момент времени
,
изменяется по закону:
где
— магнитная индукция;
— площадь рамки;
— угловая частота.
Подставив
в формулу (**) выражение
и
продифференцировав по времени, найдем
мгновенное значение ЭДС индукции:
(***)
Угловая
частота
связана с частотой
вращения
соотношением
.
Подставив
выражение
в формулу (***) и заменив
на угол
,
получим:
Подставляя
численные значения, находим:
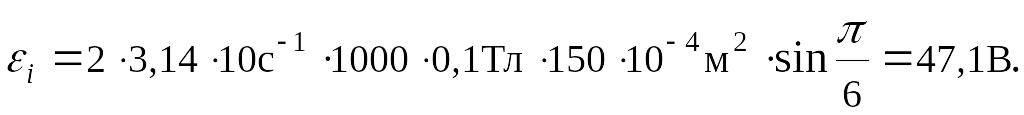
Ответ:
47,1В.
Задача
4.
Обмотка
тороида содержит
10
витков/см. Сердечник немагнитный. При
какой силе тока
плотность энергии магнитного поля
1Дж/м?
Считать, что диаметр витка обмотки
много меньше диаметра тороида.
Решение.
Силовая
линия радиусом
,
проходящая
внутри тороида охватывает число токов,
равное числу витков тороида. Сила тока
во всех витках одинакова. Поэтому по
закону полного тока (теорема о циркуляции):
где
— число витков в тороиде, отсюда:
(*)
—
это длина окружности, определяемая
средней линией тороида. По условию
задачи обмотка тороида содержит
10
витков/см,
т.е.:
витков/м.
Объемная
плотность энергии магнитного поля:
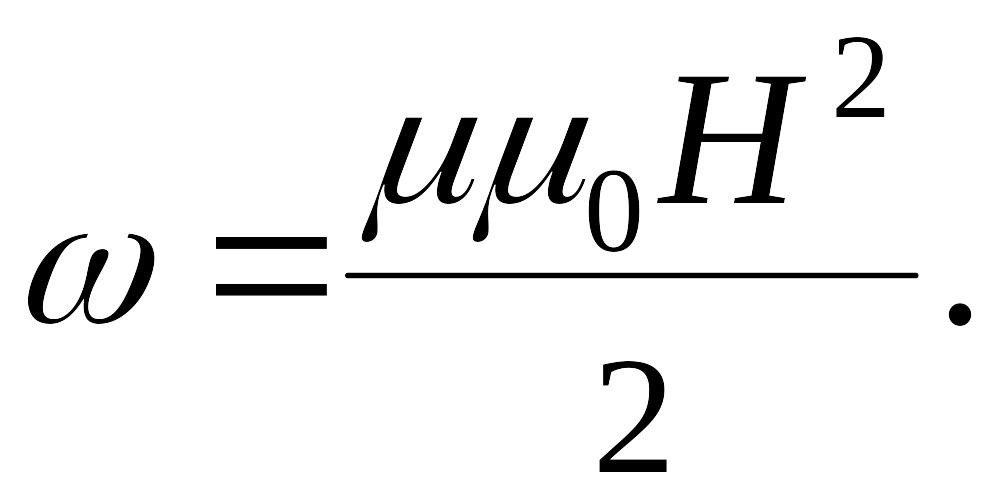
Определим
отсюда
:
согласно
(*)
Приравняв
правые части, получаем:
отсюда: 
Подставив
численные значения, находим:
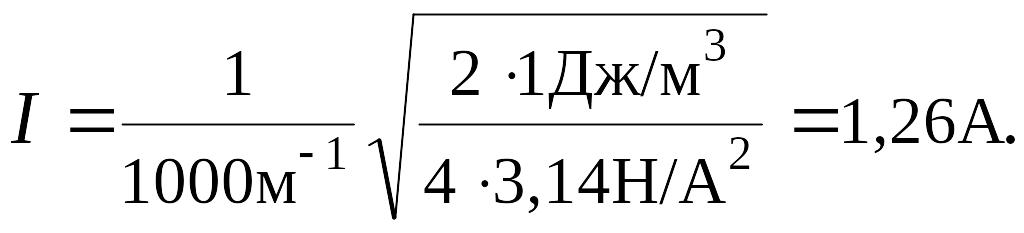
Ответ:
1,26А.
Задача
5.
Кольцо
из сверхпроводника помещено в магнитное
поле, индукция которого нарастает от
нуля до
.
Плоскость кольца перпендикулярна
линиям магнитной индукции поля.
Определите силу индукционного тока,
возникающего в кольце. Радиус кольца
равен r
, индуктивность L.
Решение.
Сопротивление
кольца равно нулю и суммарная
электродвижущая сила в нём должна быть
равна нулю. Иначе сила тока согласно
закону Ома станет бесконечной.
Следовательно, изменение магнитного
потока внешнего магнитного поля равно
по модулю и противоположно по знаку
изменению магнитного потока, созданного
индукционным током:
Учитывая, что поток
нарастает от нуля до
,
а индукционный
ток меняется при этом от 0 до I,
получим:
отсюда:
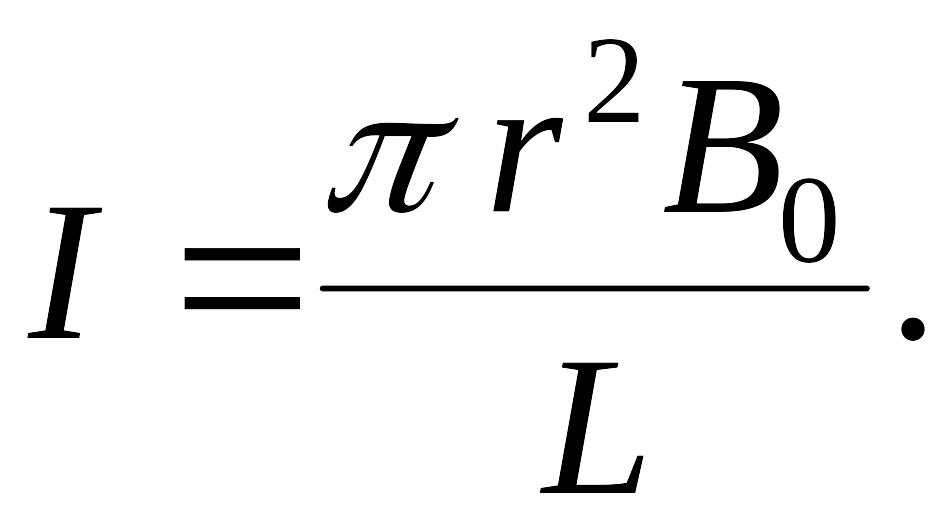
Ответ:
Задача
6.
По
обмотке длинного соленоида со стальным
сердечником течет ток силой
2А.
Определить объёмную плотность
энергии магнитного поля в сердечнике,
если число витков
на каждом сантиметре длины соленоида
равно 7см-1.
Решение.
Объёмная
плотность энергии магнитного поля
найдём по формуле:
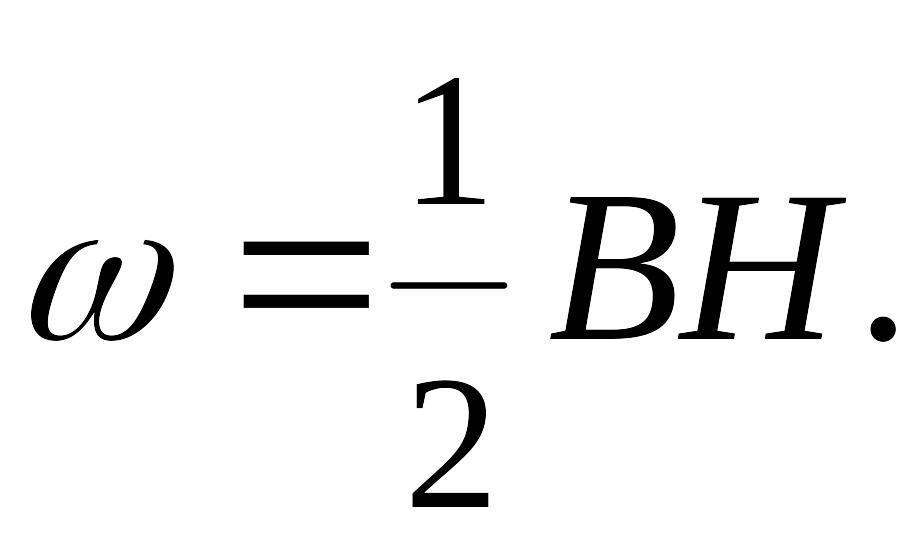
Напряженность
магнитного поля найдем как
Подставив сюда значения
(
7см-1=700м-1),
найдём:
1400А/м.
Магнитную
индукцию определим по графику зависимости
индукции от напряженности магнитного
поля:
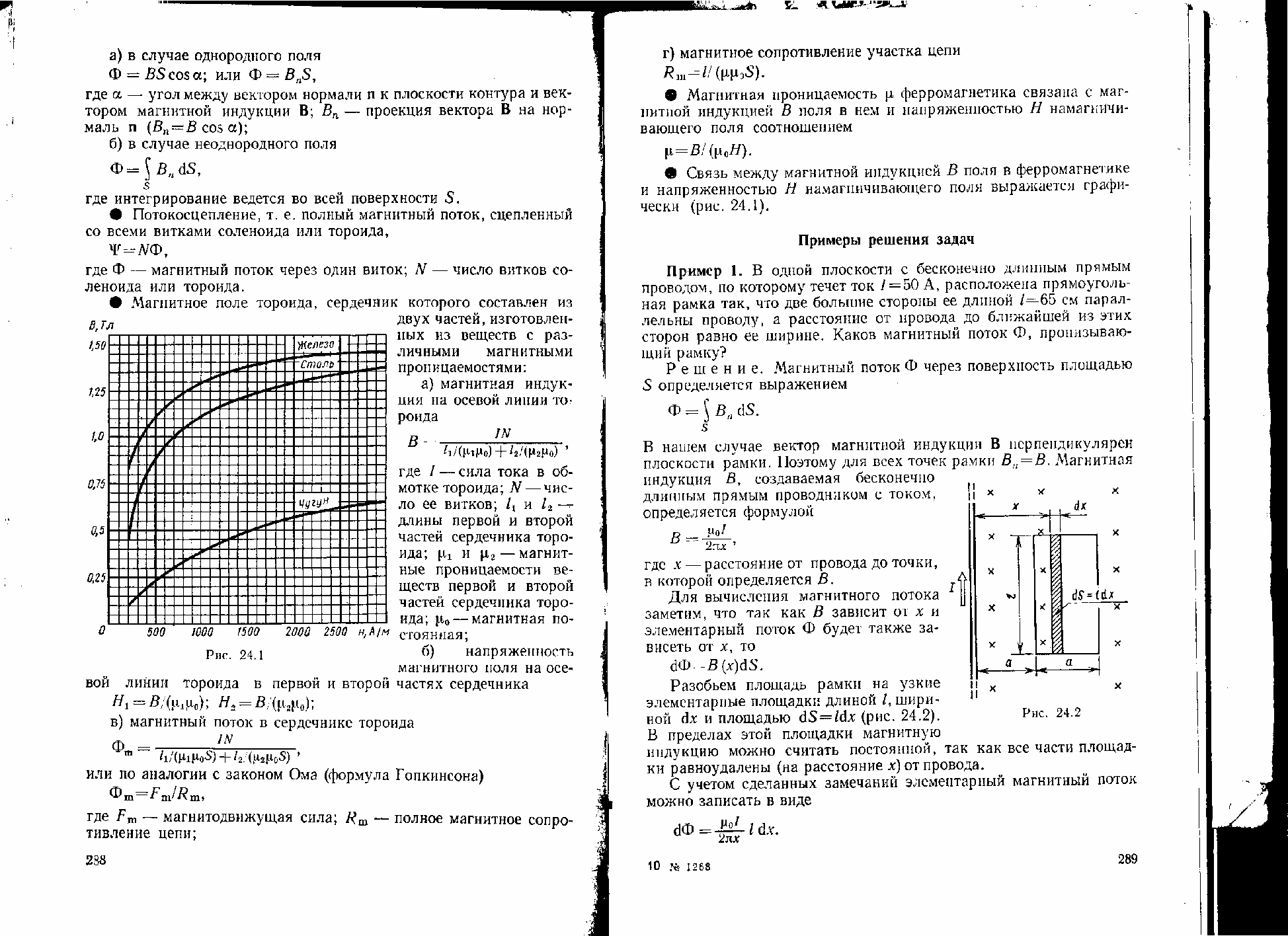
Из
справочной литературы по приведенному
графику:
1,2Тл.
Отсюда
получаем:
840Дж.
Ответ:
840Дж.
Домашнее
задание:
[Л-2]
– 11.93, 11.98, 11.104, 11.108, 11.117, 11.122, 11.126, 11.128,
11.132;
[Л-3]
– 3.125, 3.127, 3.132, 3.134, 3.137, 3.141;
[Л-4]
– 3.183, 3.186, 3.187, 3.188, 3.195, 3.198.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
Магнитный поток — формулы и определение с примерами
Магнитный поток:
Вектор индукции
Для характеристики числа линий индукции магнитного поля, пронизывающих некоторую площадку, вводится физическая скалярная величина, называемая магнитным потоком и обозначаемая греческой буквой Ф.
Магнитный поток Ф однородного поля через плоскую поверхность равен произведению модуля индукции В магнитного поля, площади поверхности S и косинуса угла 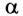
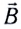
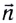
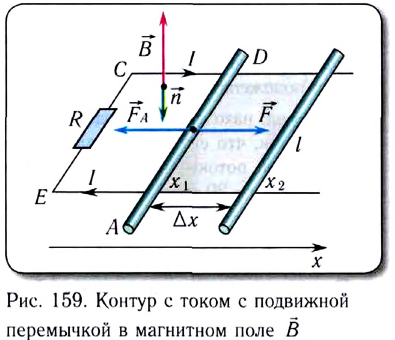
В СИ единицей магнитного потока является вебер-. 1 Вб = 1 Тл • 1
Магнитный поток в 1 Вб через плоскую поверхность площадью 1 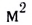
Магнитный поток через плоскую поверхность может изменяться как вследствие изменения модуля индукции В магнитного поля, так и вследствие изменения площади S плоской поверхности или угла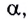
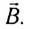
Рассмотрим прямоугольный контур AECD (рис. 159), одна из сторон AD которого длиной l не закреплена и может без трения скользить по направляющим, увеличивая площадь контура.
Если по контуру проходит постоянный ток силой I и контур находится в однородном внешнем магнитном поле индукцией 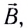
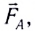
- Заказать решение задач по физике
Таким образом, для перемещения проводника вправо необходимо приложить внешнюю силу, равную по модулю и противоположную по направлению силе Ампера. При перемещении проводника на расстояние 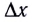
При этом работа А’, совершаемая силой Ампера, будет такой же по модулю, но противоположной по знаку:
Таким образом, работа А’ определяется изменением магнитного потока 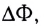
С другой стороны, работа силы Ампера определяется разностью энергий контура с током в начальном 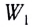
Сравнивая полученные выражения для работы А’, видим, что энергия контура с током в магнитном поле определяется силой проходящего в нем тока и магнитным потоком, пронизывающим его:
- Волны в физике
- Волновое движение в физике
- Продольные и поперечные волны в физике
- Звуковые волны в физике
- Кипение жидкостей в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Магнитные явления в физике