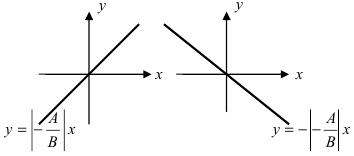
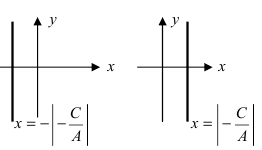
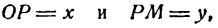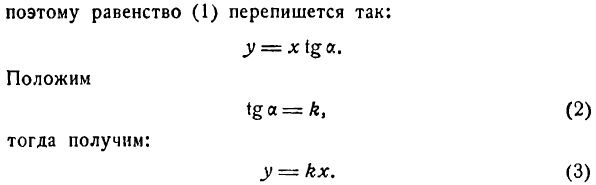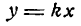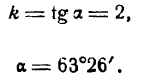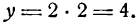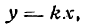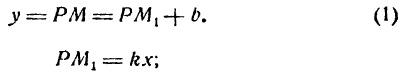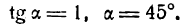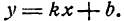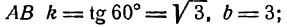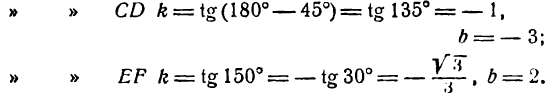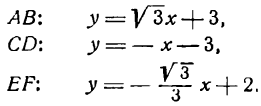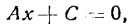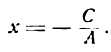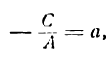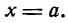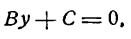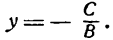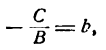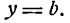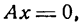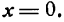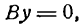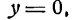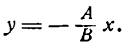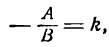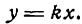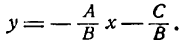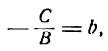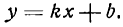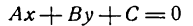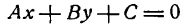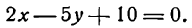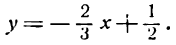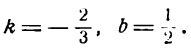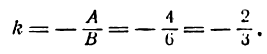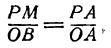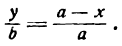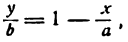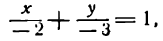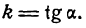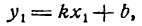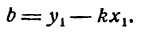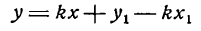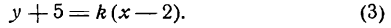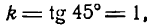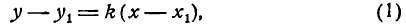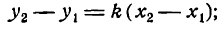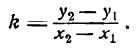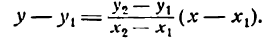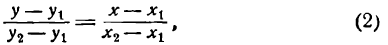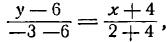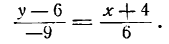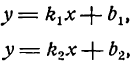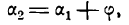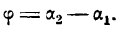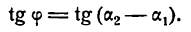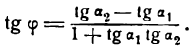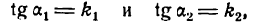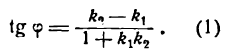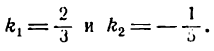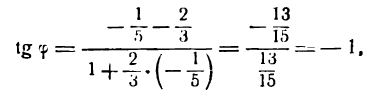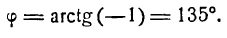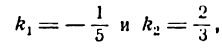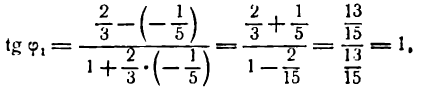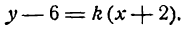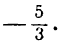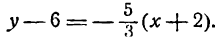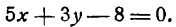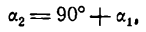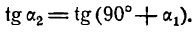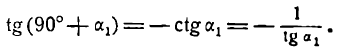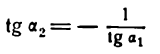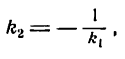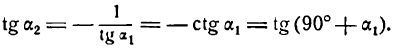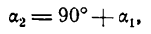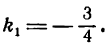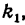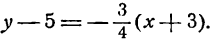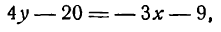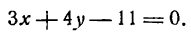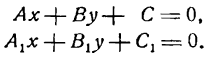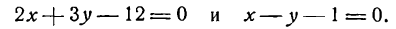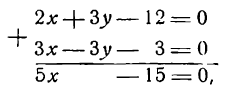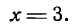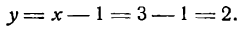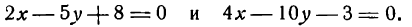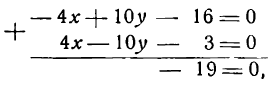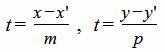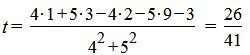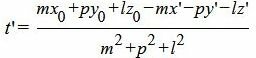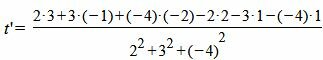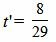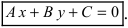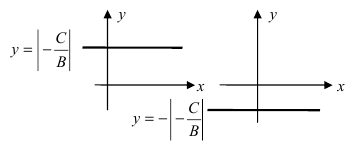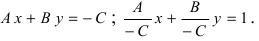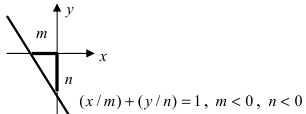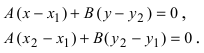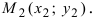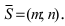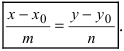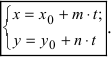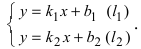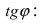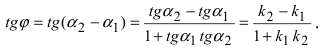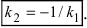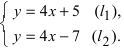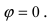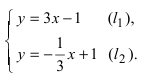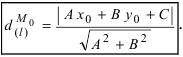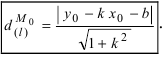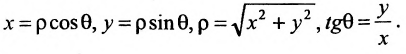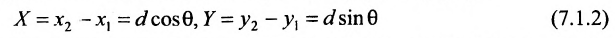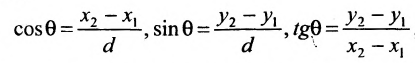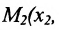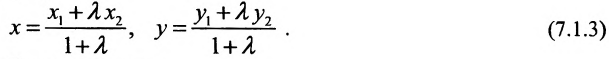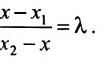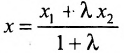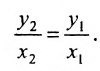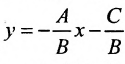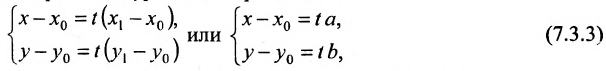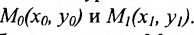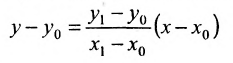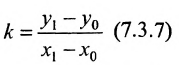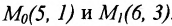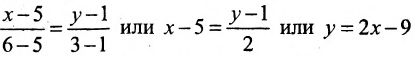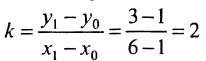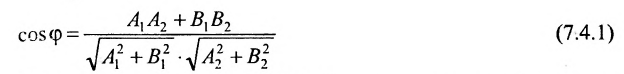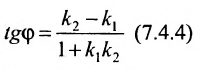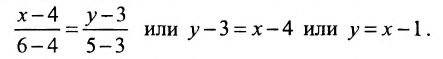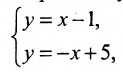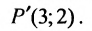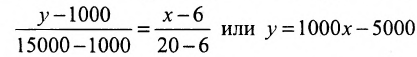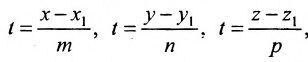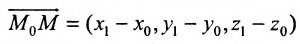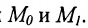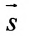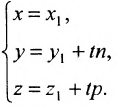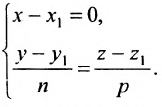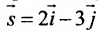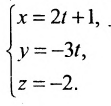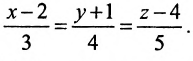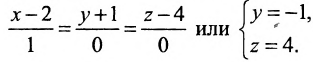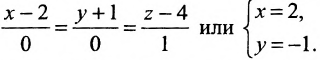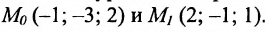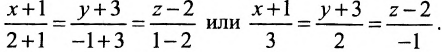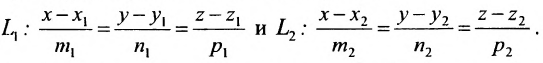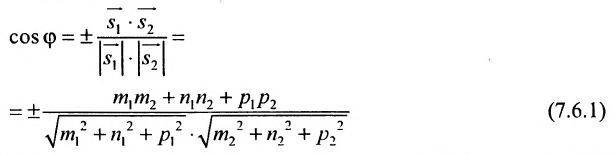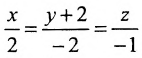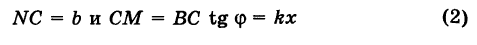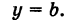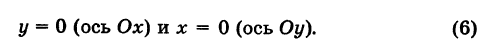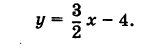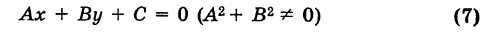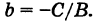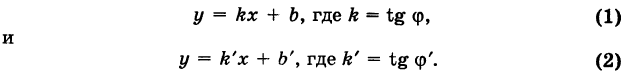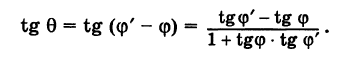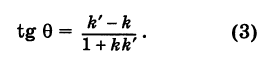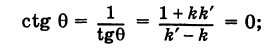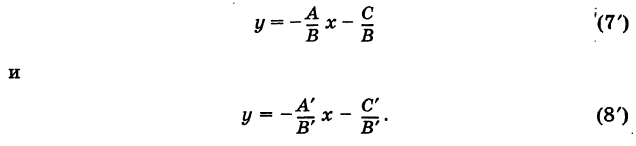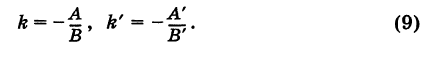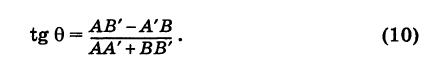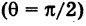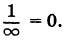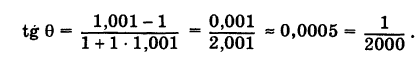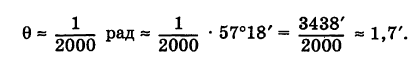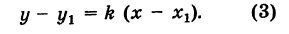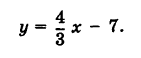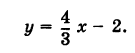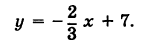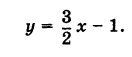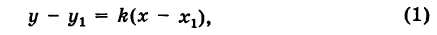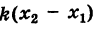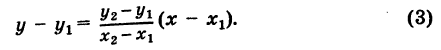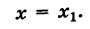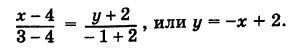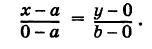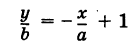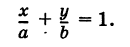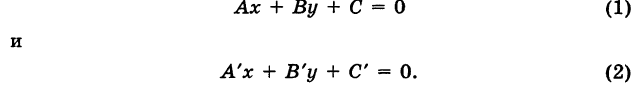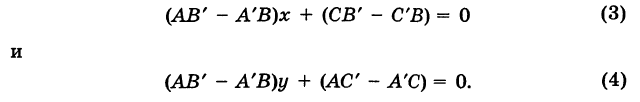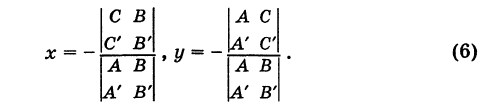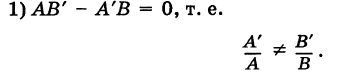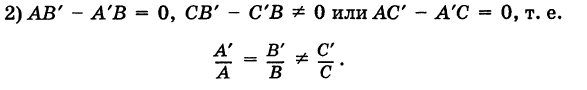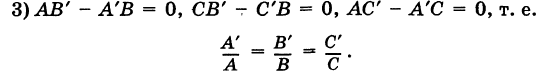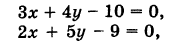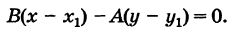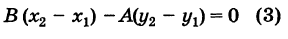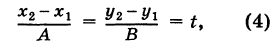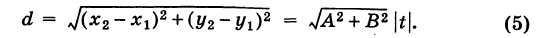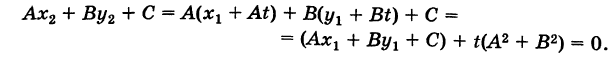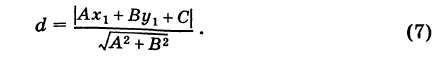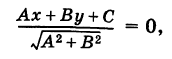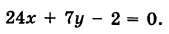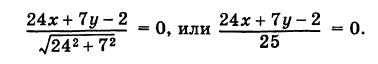Как найти точку на прямой
В современной математике точкой называются элементы весьма различной природы, из которых состоят различные пространства. Например, в n-мерном евклидовом пространстве точкой называется упорядоченная совокупность из n чисел.

Вам понадобится
- Знания по математике.
Инструкция
Прямая — одно из основных понятий в математике. Аналитически прямая на плоскости задается уравнением первого порядка вида Ax+By=C. Принадлежность точки к заданной прямой легко определить, подставив координаты точки в уравнение прямой. Если уравнение обращается в верное равенство, значит точка принадлежит прямой. Например, рассмотрим точку с координатами A(4, 5) и прямую заданную уравнением 4х+3у=1. Подставим в уравнение прямой координаты точки А и получим следующее: 4*4+3*5 = 1 или 31 = 1. Получили равенство, которое является не верным, а значит, эта точка не принадлежит прямой.
Для поиска точки на прямой достаточно взять одну из координат, и подставить в уравнение, а затем выразить из полученного уравнение вторую. Таким образом найдется точка с заданной одной из координат. Так как прямая проходит через всю плоскость, то и точек, которые ей принадлежат бесконечно много, а значит, для любой одной координаты всегда найдется другая, такая что полученная точка будет принадлежать заданной прямой. Возьмем для примера прямую с уравнением 3x-2y=2. И возьмем координату равную x=0. Тогда подставим значение x в уравнение прямой и получим следующее: 3*0-2у=2 или у=-1. Таким образом мы нашли точку лежащую на прямой и ее координаты равны (0, -1). Аналогичным образом можно найти точку, принадлежащую прямой, когда известна координата y.
В трехмерном пространстве у точки 3 координаты, а прямая задается системой из двух линейных уравнений вида Ax+By+Cz=D. Аналогичным образом, как и в двумерном случае, если вы знаете хоть одну координату точки, решив систему, найдете две остальные и эта точка будет принадлежать исходной прямой.
Видео по теме
Обратите внимание
После того как найдены все координаты точки, необходимо проверить их правильность. Подставьте найденные координаты в уравнение прямой, и если получится верное равенство, все решено корректно.
Полезный совет
Способ поиска точки по известной координате справедлив для любой размерности пространства, разница лишь в том, сколько необходимо уравнений решить, для поиска остальных координат.
Источники:
- найти точки прямой
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямых, параллельных осям координат
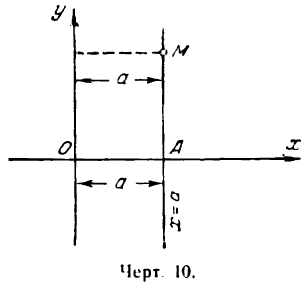
Возьмем прямую линию, параллельную оси Оу и проходящую на расстоянии а от нее (рис. 10).
Все точки этой прямой одинаково удалены от оси ординат на расстояние, равное а. Следовательно, для каждой точки прямой АМ абсцисса одна и та же, а именно:
х = а, (1)
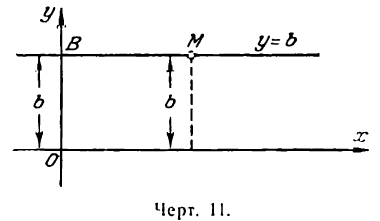
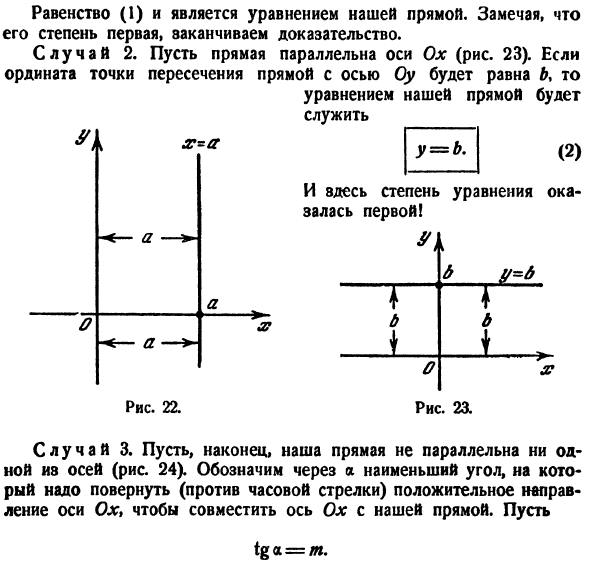
ордината же различна. Таким образом, уравнение (1) вполне определяет прямую, параллельную оси Оу, а потому оно является ее уравнением. Возьмем прямую, параллельную оси Ох, на расстоянии.
равном b от нее (рис. 11). Все точки этой прямой одинаково удалены от оси Ох на расстояние, равное b , т. е. любая точка прямой ВМ имеет постоянную ординату, а именно:
абсциссу же различную. Как видно, уравнение (2) вполне определяет прямую, параллельную оси Ох, а потому оно является ее уравнением.
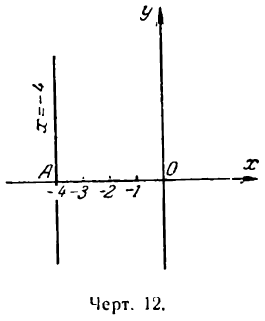
По уравнениям (1) и (2) можно построить соответствующие им прямые. Пусть, например, дана прямая х = — 4. Отложив на оси Ох отрезок ОА = — 4 (рис. 12) и проведя через точку А прямую, параллельную оси Оу, получим искомую прямую.
Уравнения осей координат
Возьмем уравнение прямой, параллельной оси Оу:
х = а
и станем в нем уменьшать абсолютную величину а, тогда прямая, определяемая этим уравнением, будет приближаться к оси Оу, оставаясь все время ей параллельной, и при а = 0 сольется с ней. Уравнение х = 0 является уравнением оси Оу.
Если же в уравнении у = b прямой, параллельной оси Ох, будем уменьшать абсолютную величину b то эта прямая станет приближаться к оси Ох, оставаясь ей параллельной, и при b = 0 с ней совпадет. Таким образом, уравнение у = 0 будет уравнением оси Ох.
Уравнение прямой, проходящей через начало координат
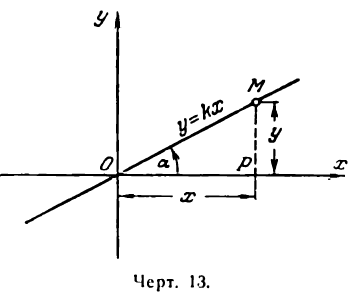
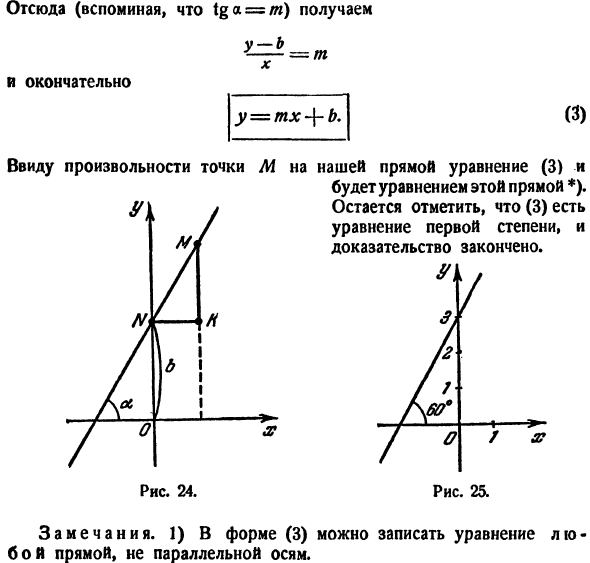
Проведем прямую через начало координат под углом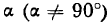
к оси Ох (рис. 13). Принято положительный угол а отсчитывать от положительного направления оси абсцисс в сторону, противоположную движению часовой стрелки (рис. 13), а отрицательный — по часовой стрелке.
Возьмем на проведенной прямой произвольную точку М (х; у). Опустив перпендикуляр МР на ось Ох, получим прямоугольный треугольник ОМР, из которого найдем:
Но
Координаты любой точки прямой ОМ удовлетворяют полученному уравнению; можно показать, что координаты любой точки, не лежащей на прямой ОМ, не удовлетворяют ему; поэтому оно является уравнением прямой ОМ. Итак,
есть уравнение прямой, проходящей через начало координат. В нем х и у — текущие координаты, а 
Определение:
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к положительному направлению оси Ох.
Величина 

Заметим, что при а = 90° углового коэффициента не существует, так как 90° не имеет числового значения.
Зная угловой коэффициент прямой у = 
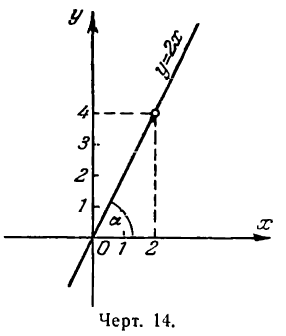
Пусть требуется построить прямую у= 2х.
Для этого найдем угол а из условия
откуда:
Построив при точке О найденный угол, мы и получим искомую прямую (рис. 14).
Построение этой прямой можно провести и проще.
Известно, что положение прямой определяется двумя точками, поэтому для решения задачи нужно знать их координаты. В нашем же случае достаточно определить координаты одной точки, так как вторая (начало координат) нам известна. Для этого дадим х произвольное значение, например х = 2, тогда из уравнения прямой найдем:
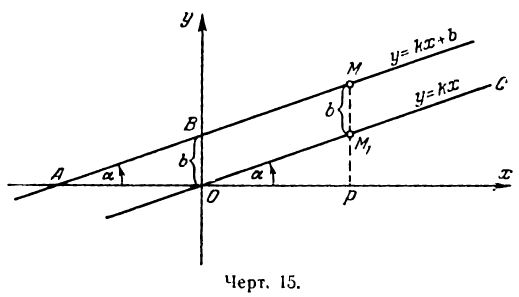
Значения х = 2 и у = 4 и будут координатами точки, лежащей на данной прямой. Построив эту точку, проведем через нее и начало координат прямую линию (рис. 14).
Уравнение прямой с угловым коэффициентом и начальной ординатой
Пусть дана прямая ОС, проходящая через начало координат под углом а к положительному направлению оси Ох (рис. 15)
Ее уравнение имеет вид
где 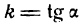
Проведем прямую 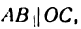
Но
Подставив значение РМ1 в равенство (1), получим уравнение прямой АВ в виде:
где 
Заметим что прямая 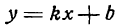
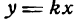
Уравнение 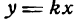
Зная угловой коэффициент 
Из данного уравнения имеем:
откуда
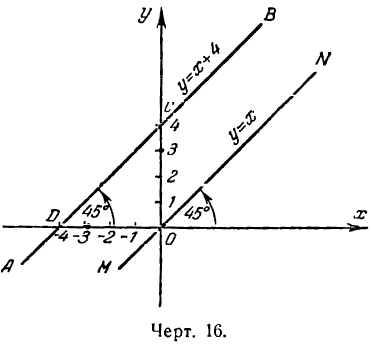
Проведем через начало координат прямую МN под углом в 45 градусов к положительному направлению оси Ох (рис. 16). На прямую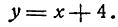
Как видно из уравнения ее пересекает ось Оу на расстоянии ОС, равном 4 единицам масштаба от начала координат.
Поэтому прямая АВ, проведенная через точку С параллельно прямой МN, и будет искомой.
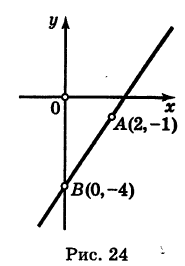
Однако проще построить указанную прямую по двум ее точкам. Удобнее для этого брать точки пересечения прямой с осями координат. Одна из них — точка С пересечения прямой с осью Оу— дается самим уравнением, а именно С(0; 4). Для нахождения точки D пересечения этой прямой с осью Ох положим в данном уравнении y = 0, получим х = — 4; значит, прямая пересекает ось Ох в точке D (-4; 0). Строим точки С и D и проводим через них искомую прямую.
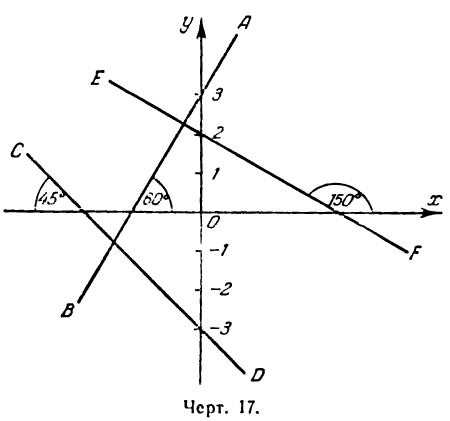
Пример:
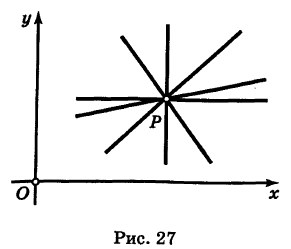
Найти уравнения прямых АВ, СD и ЕF, изображенных на рис. 17.
Решение:
Чтобы написать уравнения данных прямых, нужно определить величины 
Для прямой АВ
Следовательно, уравнения данных прямых будут:
Общее уравнение прямой
В предыдущей лекции были выведены следующие виды уравнения прямой: уравнение прямой, параллельной оси Оу:
уравнение прямой, параллельной оси Ох:
уравнение оси Оу:
уравнение оси Ох:
уравнение прямой, проходящей через начало координат:
уравнение прямой с угловым коэффициентом и начальной ординатой:
Уравнения (1) — (6) исчерпывают все возможные положения прямой, поэтому можно сказать, что
всякая прямая линия определяется уравнением первой степени относительно текущих координат.
Покажем теперь, что указанные виды уравнения прямой можно получить из уравнения
при некоторых частных значениях коэффициентов А, В и С.
I. Если В = 0, то уравнение (7) обратится в следующее:
откуда
Положив
получим
Уравнение 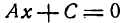
II. Если А = 0, то
отсюда
Положив
получим
Уравнение 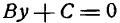
III. Если В = 0 и С = 0, то
отсюда
IV. Если А = 0 и С = 0, то
отсюда
V. Если С = 0, то
отсюда
Положим
тогда
Уравнение 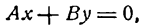
VI. Если ни один из коэффициентов уравнения (7) не равен нулю, то и в этом случае его можно преобразовать в знакомую нам форму уравнения прямой. Найдем из уравнения (7) значение у:
Положив
и
можем написать
Следовательно, уравнение
включает в себя все рассмотренные нами ранее уравнения прямой; поэтому оно называется общим уравнением прямой. Итак, всякое уравнение первой степени
при любых значениях коэффициентов А, В и С, исключая одновременное равенство А и В нулю, определяет прямую линию.
Пример:
Построить прямую
Решение:
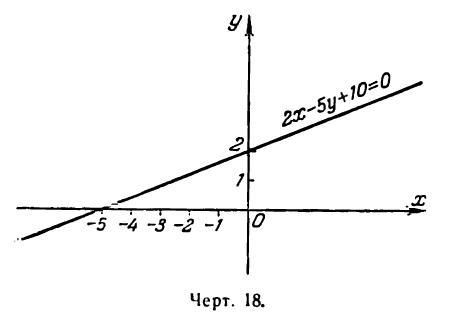
Проще всего построить прямую по двум ее точкам пересечения с осями координат. Положив в данном уравнении у = 0, получим х =- 5; координаты (-5; 0) и будут определять положение точки пересечения прямой с осью Ох. Для нахождения точки пересечения прямой с осью Оу положим в том же уравнении х = 0 тогда найдем у = 2; координаты искомой точки будут (0; 2).
Построив эти точки, проводим через них прямую 2х— 5у —10 = 0 (рис. 18).
Пример:
Найти угловой коэффициент и начальную ординату прямой 4х+ 6у — 3 = 0.
Решение:
Преобразуем это уравнение к виду
для этого находим:
6у = — 4х + 3,
отсюда
Сравнив полученное уравнение с уравнением 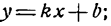
Угловой коэффициент можно найти и из равенства (8). Для этого, как видно, нужно коэффициент при х общего уравнения прямой разделить на коэффициент при у и частное
взять с противоположным знаком. Таким образом, в данном примере
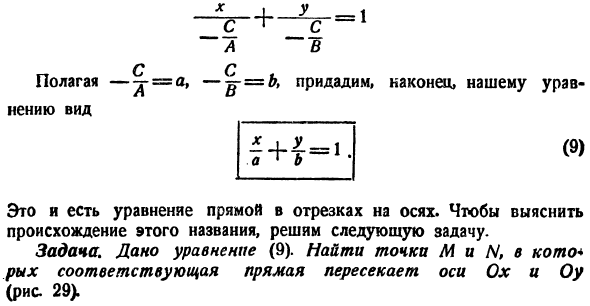
Уравнение прямой в отрезках
Как мы уже знаем, положение прямой определяется или двумя точками или одной точкой и углом наклона прямой к оси Ох. Если прямая не параллельна ни одной из координатных осей и не проходит
через начало координат, то ее положение может быть определено и другими данными, например отрезками, которые она отсекает на осях. Выведем уравнение прямой для этого случая.
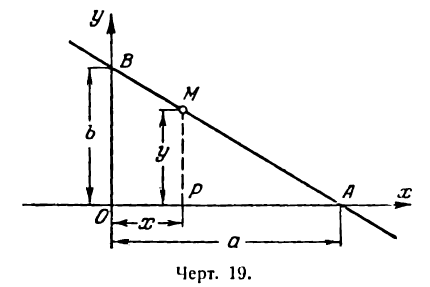
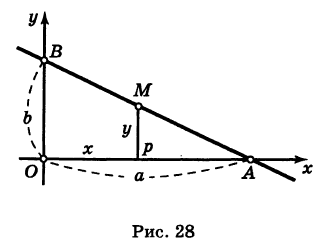
Пусть дана прямая, отсекающая на координатных осях отрезки ОА = а и ОВ = b (рис. 19).
Возьмем на этой прямой произвольную точку M (х; у) и проведем
МР 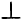
или
Разделив а — х почленно на а, будем иметь:
откуда
Можно показать, что координаты любой точки нашей прямой будут удовлетворять этому равенству, а потому его нужно рассматривать как уравнение прямой АВ.
В уравнение (1) входят отрезки а и b , отсекаемые прямой на осях; поэтому оно называется уравнением прямой в отрезках.
Величины а и b могут быть как положительными, так и отрицательными в зависимости от того, в какую сторону от начала координат откладываются отрезки а и b .
Пусть, например, дана прямая АВ (рис. 20). Здесь а = — 2, b = — 3; следовательно, уравнение прямой АВ запишется в таком виде:
По уравнению вида (1) Очень просто строится прямая. Для этого нужно только отложить на осях отрезки а и b взятые из уравнения, и через их концы провести прямую.
Заметим, что уравнение в отрезках легко получается из общего уравнения прямой: Ах + Ву + С= 0, если все коэффициенты общего уравнения отличны от нуля (иначе уравнение в отрезках не имеет смысла).
Уравнение пучка прямых
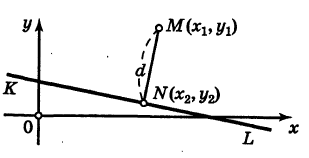
Пусть прямая АВ проходит через точку М(х1; у1) и образует угол а с положительным направлением оси Ох (рис. 21). Составим для прямой АВ уравнение вида
Для этого нужно найти величины 

Для нахождения b воспользуемся тем, что точка М лежит на прямой (1) и, следовательно, ее координаты удовлетворяют уравнению этой прямой.
Подставив в уравнение (1) вместо х и у их значения х1 и у1, а величину 
откуда
Уравнение (1) можем теперь записать в виде
или
Таково искомое уравнение прямой АВ; в нем 
Допустим, что через ту же точку M(х1; у1) проходит несколько прямых; тогда угол а наклона этих прямых к оси Ох, и также множитель 
В таком случае уравнение (2) будет определять уже не одну прямую, проходящую через данную точку M, а множество прямых, пересекающихся в эточке.
Совокупность всех прямых, проходящих через одну точку М, называется пучком прямых с центром в точке М. Таким образом, уравнение (2) с переменным 
Чтобы выделить из этого пучка прямую, образующую заданный угол с осью Ох, нужно в уравнении (2) вместо 
Выделим из этого пучка одну прямую, которая наклонена к положительному направлению оси Ох под углом а = 45°;
тогда
и уравнение (3) обратится в следующее:
или
Уравнение прямой, проходящей через две данные точки
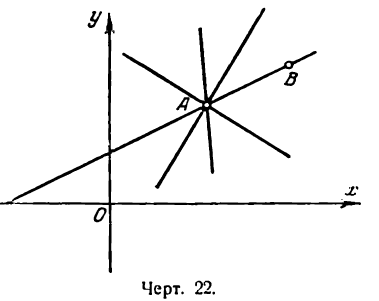
Пусть даны две точки A(х1; у1) и В(х2; у2); требуется найти уравнение прямой, проходящей через эти точки.
Если взять одну точку, например А, то через нее можно провести пучок прямых, уравнение которого будет:
где каждому значению 
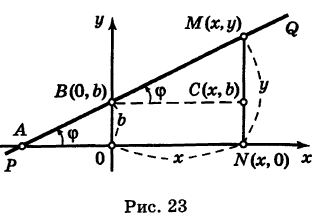
Выделим из этого пучка прямую, которая проходит и через вторую точку В (рис. 22). Чтобы найти ее уравнение, необходимо определить угловой коэффициент. Для этого примем во внимание, что точка В лежит на искомой прямой, и потому ее координаты должны обращать уравнение (1)
в тождество при 
отсюда находим угловой коэффициент искомой прямой:
Уравнение (1) можно переписать так:
Преобразуем это уравнение, разделив обе части его на у2 — у1 получим:
гле х и у — текущие координаты. Равенство (2) является уравнением прямой, проходящей через две данные точки. Это, как и уравнение в отрезках, частный случай общего уравнения прямой.
Если х1 = х2 или у1 = у2, то формула (2) теряет смысл, так как делить на нуль нельзя. В этих случаях точки А и В лежат либо на прямой, параллельной оси Оу, либо на прямой, параллельной оси Ох. В первом случае уравнение прямой запишется в виде
х = х1
а во втором — в виде
у = у1
Пример:
Написать уравнение прямой, проходящей через две точки: А(—4; 6) и В(2; —3).
Решение:
Имеем:
х1 = —- 4, х2 = 2
и
у1 = 6, у2 = — 3.
Подставим эти значения в уравнение (2); получим:
или
Умножив обе части последнего уравнения на —18, будем иметь:
2у— 12 = — 3х— 12,
откуда
Зх + 2у = 0.
Пример:
Через две точки А( 3; 2) и В (5; 2) проходит прямая. Написать ее уравнение.
Решение:
Так как ординаты данных точек равны, то заключаем, что искомая прямая параллельна оси Ох, а потому ее уравнение будет
у = 2.
Угол между двумя прямыми
Пусть даны уравнения двух прямых:
y=klx+blt
где 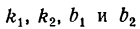
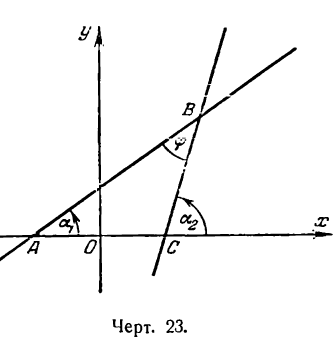
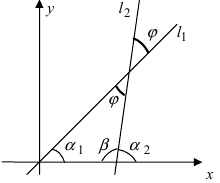
Обозначим углы, образуемые данными прямыми с положительным направлением оси Ох, через а1 и а2, а угол между этими прямыми через 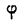
Угол а2, как внешний угол треугольника ABC, будет равен сумме внутренних, с ним не смежных, т. е.
откуда
Если углы равны между собой, то и тангенсы их равны друг другу, поэтому
Применяя формулу для тангенса разности двух углов, получим:
Но
Поэтому
Определив tg 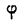
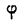
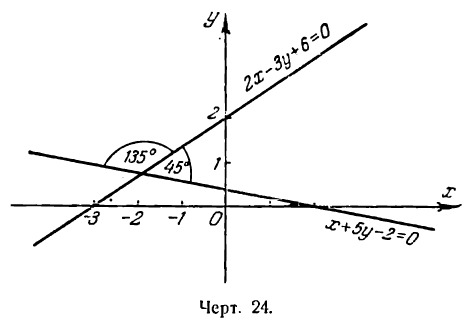
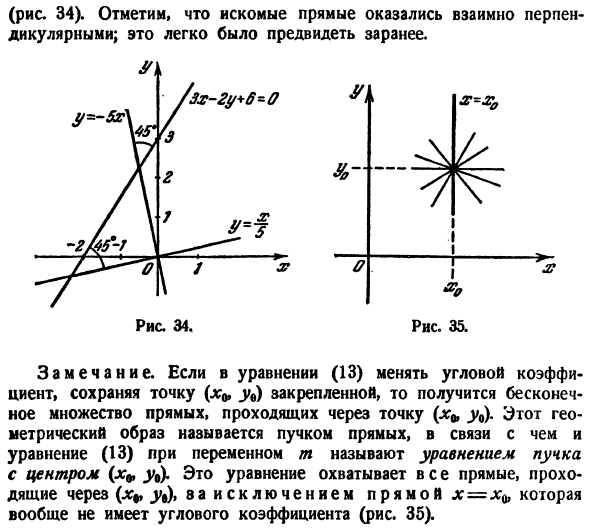
Пример:
Определить угол между прямыми:
2х — 3у + 6 =0
и
х + 5у — 2=0.
Решение:
Из данных уравнений найдем угловые коэффициенты этих прямых :
Согласно формуле (1) имеем:
откуда
Полученный угол между прямыми тупой. Но если принять
то вычисляя 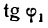
откуда 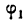
найденным тупым углом (рис. 24). Первое и второе значение угла будет ответом на вопрос задачи.
Условие параллельности прямых
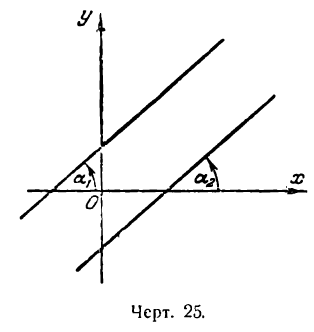
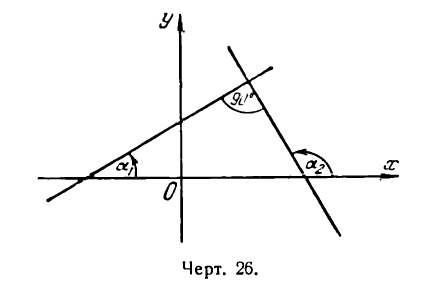
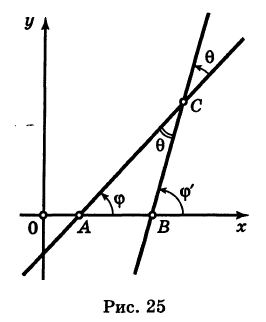
Если прямые параллельны между собой, то они образуют одинаковые углы а1 и а2 с положительным направлением оси Ох (рис. 25).
Из равенства углов а1 и а2 следует
или
Обратно, если 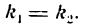
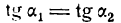
Итак, если прямые параллельны между собой, то их угловые коэффициенты равны (и наоборот).
Пример:
Написать уравнение прямой, проходящей через точку А (—2; 6) и параллельной прямой 5х—3у — 7 = 0.
Решение:
Через точку А проходит пучок прямых, среди которых находится искомая прямая. Следовательно, прежде всего пишем уравнение пучка прямых , проходящих через точку А:
Затем находим из данного в задаче уравнения прямой ее угловой коэффициент; применяя равенство (8) , получим:
Согласно условию параллельности угловой коэффициент искомой прямой тоже равен
Подставим найденное значение 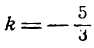
пучка:
Выполнив необходимые преобразования, получим искомое уравнение прямой:
Условие перпендикулярности прямых
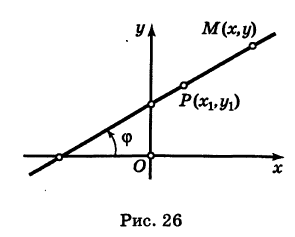
Пусть две прямые взаимно перпендикулярны и образуют с положительным направлением оси Ох углы а1 и а2 (рис. 26). В этом случае
отсюда
Но
Следовательно,
или
Обратно, если
то
Отсюда
т. е. данные прямые взаимно перпендикулярны.
Таким образом, если прямые взаимно перпендикулярны, то их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку (и наоборот).
Так, например, если у одной прямой угловой коэффициент
равен 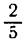
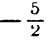
Пример:
Написать уравнение прямой, проходящей через точку А(—3; 5) и перпендикулярной прямой 4х — Зу—10 = 0.
Решение:
Через точку А проходит пучок прямых, среди которых находится и искомая прямая. Поэтому напишем сначала уравнение этого пучка
Чтобы выделить из него нашу прямую, нужно найти ее угловой коэффициент 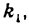
данной прямой равенством (1). Но 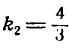
Подставив в уравнение (2) вместо 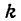
получим:
Это и есть искомое уравнение прямой. Преобразовав его, найдем:
или
Пересечение прямых
Пусть даны две прямые, определяемые уравнениями:
Требуется найти точку их пересечения.
Так как точка пересечения данных прямых есть их общая точка, то ее координаты должны удовлетворять как первому, так и второму уравнению, т. е. эти координаты должны быть общими корнями данных уравнений.
Чтобы найти эти корни, нужно, как известно из алгебры, решить совместно данные уравнения, рассматривая их как систему уравнений.
Пример:
Найти точку пересечения прямых
Решение:
Решим данные уравнения как систему. Умножив второе уравнение на 3 и сложив результат с первым уравнением, получим:
откуда
Зная х, находим у, например, из второго уравнения:
Пример:
Найти точку пересечения прямых
Решение:
Умножив все члены первого уравнения на —2 и сложив полученное уравнение со вторым, найдем:
что невозможно. Значит, данная система уравнений решений не имеет, а потому прямые, определяемые этими уравнениями, не имеют общих точек, т. е. данные прямые параллельны.
К этому же заключению можно прийти, сравнивая угловые коэффициенты данных прямых.
Дополнение к прямой линии
Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Проекция точки на прямую онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на прямую. Дается подробное решение с пояснениями. Для вычисления проекции точки на прямую, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на прямую − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
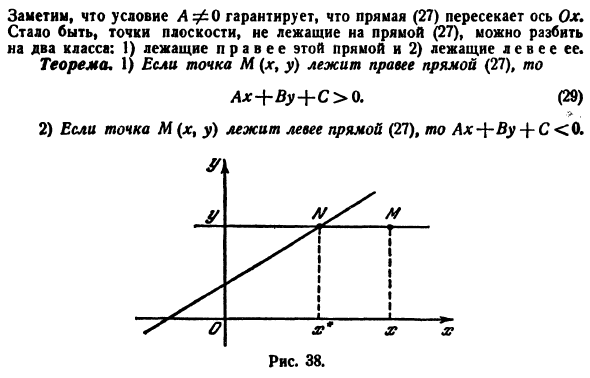
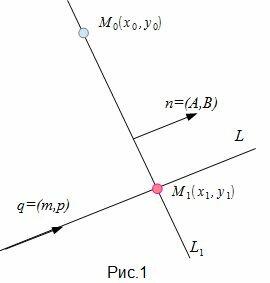
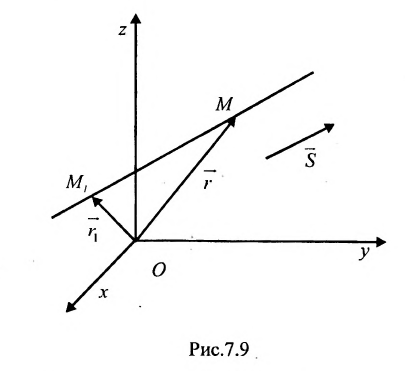
1. Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
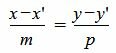 , , |
(1) |
где q=(m,p) направляющий вектор прямой L.
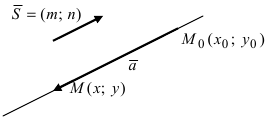
Найдем проекцию точки M0 на прямую (1)(Рис.1).
Алгоритм нахождения проекции точки на прямую L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
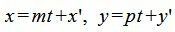 |
(5) |
Подставим значения x и y в (4):
m(mt+x’)+p(pt+y’)−mx0−py0=0
m 2 t+mx’+p 2 t+py’−mx0−py0=0
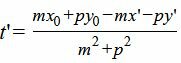 |
(5′) |
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
Пример 1. Найти проекцию точки M0(1, 3) на прямую
 |
(6) |
Направляющий вектор прямой (6) имеет вид:
Т.е. m=4, p=5. Из уравнения прямой (6) видно, что она проходит через точку M’ (x’, y’)=(2, −3)(в этом легко убедится − подставляя эти значения в (6) получим тождество 0=0), т.е. x’=2, y’=-3. Подставим значения m, p, x0, y0, x’, y’ в (5′):
Подставляя значение t в (5), получим:


Проекцией точки M0(1, 3) на прямую (6) является точка:
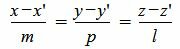 , , |
(7) |
где q=(m, p, l) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (7)(Рис.2).
Нахождение проекцию точки на прямую L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (8) |
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (8) можно записать так:
m(x−x0)+p(y−y0)+l(z−z0)=0
| mx+py+lz−mx0−py0−lz0=0 | (9) |
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (7):
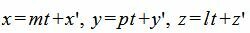 |
(10) |
Подставим значения x и y в (9):
m(mt+x’)+p(pt+y’)+l(lt+z’)−mx0−py0−lz0=0
m 2 t+mx’+p 2 t+py’+l 2 t+ly’−mx0−py0−lz0=0
 |
(10′) |
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (9). Следовательно, подставляя значение t’ в (10) получим координаты проекции точки M0 на прямую L:
Пример 2. Найти проекцию точки M0(3, −1, −2) на прямую
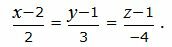 |
(11) |
Направляющий вектор прямой (11) имеет вид:
Т.е. m=2, p=3, l=−4. Из уравнения прямой (11) видно, что она проходит через точку M’ (x’, y’, z’)=(2, 1, 1)(в этом легко убедится − подставляя эти значения в (11) получим тождество 0=0=0), т.е. x’=2, y’=1, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (10′):
Подставляя значение t=t’ в (10), получим:
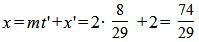
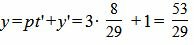
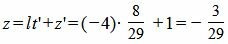
Проекцией точки M0(3, −1, −2) на прямую (11) является точка:
Проекция точки на прямую, координаты проекции точки на прямую
Данная статья рассматривает понятие проекции точки на прямую (ось). Мы дадим ему определение с использованием поясняющего рисунка; изучим способ определения координат проекции точки на прямую (на плоскости или в трехмерном пространстве); разберем примеры.
Проекция точки на прямую, определение
В статье «Проекция точки на плоскость, координаты» мы упоминали, что проецирование фигуры является обобщенным понятием перпендикулярного или ортогонального проецирования.
Все геометрические фигуры состоят из точек, соответственно проекция этой фигуры есть множество проекций всех ее точек. Поэтому, чтобы иметь возможность спроецировать фигуру на прямую, необходимо получить навык проецирования точки на прямую.
Проекция точки на прямую – это или сама точка, если она принадлежит заданной прямой, или основание перпендикуляра, опущенного из этой точки на заданную прямую.
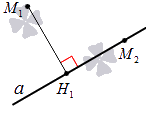
Рассмотрим рисунок ниже: точка H 1 служит проекцией точки М 1 на прямую a , а точка М 2 , принадлежащая прямой, является проекцией сама себя.
Данное определение верно для случая на плоскости и в трехмерном пространстве.
Чтобы на плоскости получить проекцию точки М 1 на прямую a , проводится прямая b , проходящая через заданную точку M 1 и перпендикулярная прямой a . Таким образом, точка пересечения прямых a и b будет проекцией точки М 1 на прямую a .
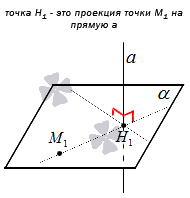
В трехмерном пространстве проекцией точки на прямую будет служить точка пересечения прямой a и плоскости α , проходящей через точку М 1 и перпендикулярной прямой a .
Нахождение координат проекции точки на прямую
Рассмотрим данный вопрос в случаях проецирования на плоскости и в трехмерном пространстве.
Пусть нам заданы прямоугольная система координат O x y , точка М 1 ( x 1 , y 1 ) и прямая a . Необходимо найти координаты проекции точки М 1 на прямую a .
Проложим через заданную точку М 1 ( x 1 , y 1 ) прямую b перпендикулярно прямой a . Точку пересечения маркируем как H 1 . Точка Н 1 будет являться точкой проекции точки М 1 на прямую a .
Из описанного построения можно сформулировать алгоритм, который позволяет находить координаты проекции точки М 1 ( x 1 , y 1 ) на прямую a :
— составляем уравнение прямой (если оно не задано). Для совершения этого действия необходим навык составления основных уравнений на плоскости;
— записываем уравнение прямой b (проходящей через точку М 1 и перпендикулярной прямой a ). Здесь поможет статья об уравнении прямой, проходящей через заданную точку перпендикулярно заданной прямой;
— определяем искомые координаты проекции как координаты точки пересечения прямых a и b . Для этого решаем систему уравнений, составляющие которой – уравнения прямых a и b .
На плоскости O x y заданы точки М 1 ( 1 , 0 ) и прямая a (общее уравнение – 3 x + y + 7 = 0 ). Необходимо определить координаты проекции точки М 1 на прямую a .
Решение
Уравнение заданной прямой известно, поэтому, согласно алгоритму, переходим к шагу записи уравнения прямой b . Прямая b перпендикулярна прямой a , а значит нормальный вектор прямой a служит направляющим вектором прямой b . Тогда направляющий вектор прямой b запишем как b → = ( 3 , 1 ) . Запишем и каноническое уравнение прямой b , поскольку нам также заданы координаты точки М 1 , через которую проходит прямая b :
Заключительным шагом определяем координаты точки пересечения прямых a и b . Перейдем от канонических уравнений прямой b к общему ее уравнению:
x — 1 3 = y 1 ⇔ 1 · ( x — 1 ) = 3 · y ⇔ x — 3 y — 1 = 0
Составим систему уравнений из общих уравнений прямых a и b и решим ее:
3 x + y + 7 = 0 x — 3 y — 1 = 0 ⇔ y = — 3 x — 7 x — 3 y — 1 = 0 ⇔ y = — 3 x — 7 x — 3 · ( — 3 x — 7 ) — 1 = 0 ⇔ ⇔ y = — 3 x — 7 x = — 2 ⇔ y = — 3 · ( — 2 ) — 7 x = — 2 ⇔ y = — 1 x = — 2
В конечном итоге мы получили координаты проекции точки М 1 ( 1 , 0 ) на прямую 3 x + y + 7 = 0 : ( — 2 , — 1 ) .
Ответ: ( — 2 , — 1 ) .
Подробнее рассмотрим случай, когда необходимо определить координаты проекции заданной точки на координатные прямые и параллельные им прямые.
Пусть заданы координатные прямые O x и O y , а также точка М 1 ( x 1 , y 1 ) . Понятно, что проекцией заданной точки на координатную прямую O x вида y = 0 будет точка с координатами ( x 1 , 0 ) . Так и проекция заданной точки на координатную прямую O y будет иметь координаты 0 , y 1 .
Любую произвольную прямую, параллельную оси абсцисс, возможно задать неполным общим уравнением B y + C = 0 ⇔ y = — C B , а прямую, параллельную оси ординат — A x + C = 0 ⇔ x = — C A.
Тогда проекциями точки М 1 ( x 1 , y 1 ) на прямые y = — C B и x = — C A станут точки с координатами x 1 , — C B и — C A , y 1 .
Определите координаты проекции точки М 1 ( 7 , — 5 ) на координатную прямую O y , а также на прямую, параллельную прямой O y 2 y — 3 = 0 .
Решение
Запишем координаты проекции заданной точки на прямую O y : ( 0 , — 5 ) .
Запишем уравнение прямой 2 y — 3 = 0 в виде y = 3 2 . Становится видно, что проекция заданной точки на прямую y = 3 2 будет иметь координаты 7 , 3 2 .
Ответ: ( 0 , — 5 ) и 7 , 3 2 .
Пусть в трехмерном пространстве заданы прямоугольная система координат O x y z , точка М 1 ( x 1 , y 1 , z 1 ) и прямая a . Найдем координаты проекции точки М 1 на прямую a .
Построим плоскость α , проходящую через точку М 1 и перпендикулярную прямой a . Проекцией заданной точки на прямую a станет точка пересечения прямой a и плоскости α . Исходя из этого, приведем алгоритм для нахождения координат проекции точки М 1 ( x 1 , y 1 , z 1 ) на прямую a :
— запишем уравнение прямой а (если оно не задано). Для решения этой задачи необходимо ознакомиться со статьей об уравнениях прямой в пространстве;
— составим уравнение плоскости α , проходящей через точку М 1 и перпендикулярной прямой a (см. статью «Уравнение плоскости, проходящей через заданную точку перпендикулярно заданной прямой»);
— найдем искомые координаты проекции точки М 1 ( x 1 , y 1 , z 1 ) на прямую a – это будут координаты точки пересечения прямой α и плоскости α (в помощь – статья «Координаты точки пересечения прямой и плоскости»).
Задана прямоугольная система координат O x y z , и в ней – точка М 1 ( 0 , 1 , — 1 ) и прямая a . Прямой a соответствуют канонические уравнения вида: x + 2 3 = y — 6 — 4 = z + 1 1 . Определите координаты проекции точки М 1 на прямую a .
Решение
Используем указанный выше алгоритм. Уравнения прямой a известны, поэтому первый шаг алгоритма пропускаем. Запишем уравнение плоскости α . Для этого определим координаты нормального вектора плоскости α . Из заданных канонических уравнений прямой a выделим координаты направляющего вектора этой прямой: ( 3 , — 4 , 1 ) , который будет являться нормальным вектором плоскости α , перпендикулярной прямой a . Тогда n → = ( 3 , — 4 , 1 ) – нормальный вектор плоскости α . Таким образом, уравнение плоскости α будет иметь вид:
3 · ( x — 0 ) — 4 · ( y — 1 ) + 1 · ( z — ( — 1 ) ) = 0 ⇔ 3 x — 4 y + z + 5 = 0
Теперь найдем координаты точки пересечения прямой а и плоскости α, для этого используем два способа:
- Заданные канонические уравнения позволяют получить уравнения двух пересекающихся плоскостей, определяющих прямую a :
x + 2 3 = y — 6 — 4 = z + 1 1 ⇔ — 4 · ( x + 2 ) = 3 · ( y — 6 ) 1 · ( x + 2 ) = 3 · ( z + 1 ) 1 · ( y — 6 ) = — 4 · ( z + 1 ) ⇔ 4 x + 3 y — 10 = 0 x — 3 z — 1 = 0
Чтобы найти точки пересечения прямой 4 x + 3 y — 10 = 0 x — 3 z — 1 = 0 и плоскости 3 x — 4 y + z + 5 = 0 , решим систему уравнений:
4 x + 3 y — 10 = 0 x — 3 z — 1 = 0 3 x — 4 y + z + 5 = 0 ⇔ 4 x + 3 y = 10 x — 3 z = 1 3 x — 4 y + z = — 5
В данном случае используем метод Крамера, но возможно применить любой удобный:
∆ = 4 3 0 1 0 — 3 3 — 4 1 = — 78 ∆ x = 10 3 0 1 0 — 3 — 5 — 4 1 = — 78 ⇒ x = ∆ x ∆ = — 78 — 78 = 1 ∆ y = 4 10 0 1 1 — 3 3 — 5 1 = — 156 ⇒ y = ∆ y ∆ = — 156 — 78 = 2 ∆ z = 4 3 10 1 0 1 3 — 4 — 5 = 0 ⇒ z = ∆ z ∆ = 0 — 78 = 0
Таким образом, проекцией заданной точки на прямую a является точка c координатами ( 1 , 2 , 0 )
- На основе заданных канонических уравнений легко записать параметрические уравнения прямой в пространстве:
x + 2 3 = y — 6 — 4 = z + 1 1 ⇔ x = — 2 + 3 · λ y = 6 — 4 · λ z = — 1 + λ
Подставим в уравнение плоскости, имеющее вид 3 x — 4 y + z + 5 = 0 , вместо x , y и z их выражения через параметр:
3 · ( — 2 + 3 · λ ) — 4 · ( 6 — 4 · λ ) + ( — 1 + λ ) + 5 = 0 ⇔ 26 · λ = 0 ⇔ λ = 1
Вычислим искомые координаты точки пересечения прямой a и плоскости α по параметрическим уравнениям прямой a при λ = 1 :
x = — 2 + 3 · 1 y = 6 — 4 · 1 z = — 1 + 1 ⇔ x = 1 y = 2 z = 0
Таким образом, проекция заданной точки на прямую a имеет координаты ( 1 , 2 , 0 )
Ответ: ( 1 , 2 , 0 )
Напоследок отметим, что проекциями точки М 1 ( x 1 , y 1 , z 1 ) на координатные прямые O x , O y и O z буду являться точки с координатами ( x 1 , 0 , 0 ) , ( 0 , y 1 , 0 ) и ( 0 , 0 , z 1 ) соответственно.
Как найти проекцию точки на плоскость: методика определения и пример решения задачи
При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.
Уравнение для описания плоскости
Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее — ниже.
Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:
Первые три коэффициента — это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.
Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.
Понятие о проекции точки и ее вычисление
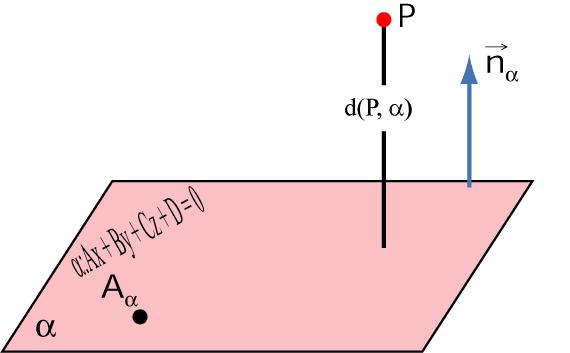
Предположим, что задана некоторая точка P(x1; y1; z1) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x2; y2; z2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.
Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:
Где λ — действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.
После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.
Вычисление расстояния от плоскости до точки
Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:
Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.
Пример задачи
Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:
Следует найти точки проекцию на плоскость и вычислить между ними расстояние.
В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90 o . Имеем:
Записывая это равенство в явном виде, приходим к следующей системе уравнений:
Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:
Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:
Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:
d = √((3 — 0 ) 2 + (-3,5 + 2 ) 2 + (4,5 — 3 ) 2 ) = 3,674.
В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/proektsija-tochki-na-prjamuju-koordinaty-proektsii/
http://fb.ru/article/440688/kak-nayti-proektsiyu-tochki-na-ploskost-metodika-opredeleniya-i-primer-resheniya-zadachi
Очень часто при решения домашней работы возникает вопрос: когда 3 точки лежат на одной прямой, ответ очень прост и он лежит в основе геометрии.
Осуществить проверку того, что три точки лежат на одной прямой можно через составления уравнения, рассматриваемой прямой, которая проходит через две наугад выбранные точки из этих трех. И проверки того, что этому уравнению удовлетворяют координаты оставшейся из этих трех точек.
Есть разные виды уравнения прямой. Воспользуемся одним из простейших способов и рассмотрим его для конкретно заданных точек.
Это сделаем лишь для того, чтобы не решать поставленную задачу в общем виде, а чтобы дать ответ на вопрос лежат ли 3 именно эти точки с этими координатами на одной прямой. Сформулируем задачу: Необходимо проверить лежат ли точки A(-2;1), Б(0;3), В (5;-7) на одной прямой.
Решим поставленную задачу
Как известно, через любые две точки можно провести прямую, причем единственную. Вот и проведем мысленно эту прямую. Допустим, прямую АБ. Значит, решение нашей задачи свелось к тому, что нужно проверить: принадлежит ли точка В прямой АБ. Если окажется, что точка В принадлежит прямой АБ, то все точки из условия будут лежать на одной прямой. Если мы выясним, что точка В не принадлежит прямой АБ, то можно будет утверждать, что точки А, Б и В на одной прямой не лежат. Составим уравнение прямой АБ как уравнение прямой проходящей через две точки:
(х+2)/(0+2)=(y-1)/(3-1)
После преобразования получим:
x-y=-3 — это уравнение прямой АБ
Проверим удовлетворяют ли координаты точки В этому уравнению, для этого достаточно выполнить подстановку координат точки В в место переменных в уравнении прямой АБ. Если получим верное числовое равенство, то точка В — это точка прямой АБ. В противном случае, неверное числовое равенство, будет свидетельствовать о не принадлежности точки В прямой АБ.
Как видим, не получили верное числовое равенство. Значит в этом случае точки А, Б, В не лежат на одной прямой.
Пример, когда 3 точки лежат на одной прямой можно легко подобрать для этой задачи. Всего лишь точка В должна иметь координаты (0;3) или (-7;-4)
Если вам даны две точки
, то вы можете отважно заявить, что они лежат на одной прямой
, потому что через всякие две точки
дозволено провести прямую. Но как же узнать, лежат ли все точки
на прямой
, если точек три, четыре либо огромнее? Подтвердить принадлежность точек одной прямой
дозволено несколькими методами.
Вам понадобится
- Точки, заданные координатами.
Инструкция
1.
Если вам даны точки
с координатами (х1, у1, z1), (х2, у2, z2), (х3, у3, z3), обнаружьте уравнение прямой
, применяя координаты всяких 2-х точек, скажем, первой и 2-й. Для этого подставьте соответствующие значения в уравнение прямой
: (х-х1)/(х2-х1)=(у-у1)/(у2-у1)=(z-z1)/(z2-z1). Если один из знаменателей равен нулю, примитивно приравняйте к нулю числитель.
2.
Обнаружить уравнение прямой
, зная две точки
с координатами (х1, у1), (х2, у2), еще проще. Для этого подставьте значения в формулу (х-х1)/(х2-х1)=(у-у1)/(у2-у1).
3.
Получив уравнение прямой
, проходящей через две точки
, подставьте значения координат третьей точки
в него взамен переменных х и у. Если равенство получилось правильное, значит все три точки
лежат на одной прямой
. Верно так же можете проверять принадлежность этой прямой
других точек.
4.
Проверьте принадлежность всех точек прямой
, проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли правильным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой
должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.
5.
Еще один метод проверить принадлежность 3 точек прямой
– посчитайте площадь треугольника, тот, что они образуют. Если все точки
лежат на прямой
, то его площадь будет равна нулю. Подставьте значения координат в формулу: S=1/2((х1-х3)(у2-у3)-(х2-х3)(у1-у3)). Если позже всех вычислений вы получили нуль – значит, три точки
лежат на одной прямой
.
6.
Дабы обнаружить решение задачи графическим методом, постройте координатные плоскости и обнаружьте точки
по указанным координатам. После этого проведите прямую через две из них и продолжите до третьей точки
, посмотрите, пройдет ли она через нее. Учтите, данный метод подходит только для точек, заданных на плоскости с координатами (х, у), если же точка задана в пространстве и имеет координаты (х, у, z), то такой метод неприменим.
Совет 2: Как проверить, что точки не лежат на одной прямой
На основании аксиомы, описывающей свойства прямой
: какова бы ни была прямая, есть точки
, принадлежащие и не принадлежащие ей. Следственно абсолютно разумно, что не все точки
будут лежать на одной прямой
линии.
Вам понадобится
- – карандаш;
- – линейка;
- – ручка;
- – тетрадь;
- – калькулятор.
Инструкция
1.
Проверить принадлежность точки
той либо другой прямой
достаточно легко. Используйте для этого уравнение прямой
. Выходит, представим, что прямая проходит через точки
А(x1,y1) и В(x2,y2). Дана точка К(x,y): необходимо проверить ее принадлежность прямой
. Уравнение линии по двум точкам имеет дальнейший вид: (x – x1) * (y2 – y1) – (x2 – x1) * (y – y1) = 0.
2.
Подставьте значение координат точки
К в уравнение. Если (x – x1) * (y2 – y1) – (x2 – x1) * (y – y1) окажется огромнее нуля, то точка К расположена правее либо ниже прямой
, проведенной по точкам А и В.
3.
В том случае, если (x – x1) * (y2 – y1) – (x2 – x1) * (y – y1) будет поменьше нуля, точка К располагается выше либо левее линии. Другими словами, только в том случае, если уравнение вида (x – x1) * (y2 – y1) – (x2 – x1) * (y – y1) = 0 объективно, точки
А, В и К будут расположены на одной прямой
.
4.
В остальных случаях лишь две точки
(А и В), которые, по условию задания, лежат на прямой
, будут ей принадлежать: через третью точку (точку К) прямая проходить не будет.
5.
Разглядите 2-й вариант определения принадлежности точки
примой: на данный раз надобно проверить принадлежит ли точка С(x,y) отрезку с концевыми точками В(x1,y1) и А(x2,y2), тот, что является частью прямой
z.
6.
Точки рассматриваемого отрезка опишите уравнением pOB+(1-p)OА=z, при условии, что 0?p?1. ОВ и ОА являются векторами. Если есть такое число p, которое огромнее либо равно 0, но поменьше либо равно 1, то pOB+(1-p)OА=С, а значит, точка С будет лежать на отрезке АВ. В отвратном случае, данная точка не будет принадлежать этому отрезку.
7.
Распишите равенство pOB+(1-p)OА=С покоординатно: px1+(1-p)x2=x и py1+(1-p)y2=y.
8.
Обнаружьте из первого уравнения число р и подставьте его значение во второе равенство. Если равенство будет соответствовать условиям 0?p?1, то точка С принадлежит отрезку АВ.
9.
Постройте точки
по заданным координатам и проведите через них прямую. Это дозволит увидеть точки
, лежащие на одной прямой
, и те точки
, что не принадлежат ей.
Обратите внимание!
Удостоверитесь в правильности расчетов!
Полезный совет
Дабы обнаружить k – угловой показатель прямой, надобно (y2 – y1)/(x2 – x1).
Построение прямых — основа технического черчения. Теперь это все почаще делается с поддержкой графических редакторов, которые предоставляют проектировщику крупные вероятности. Впрочем некоторые тезисы построения остаются теми же, что и в классическом черчении – с подмогой карандаша и линейки.
Вам понадобится
- – лист бумаги;
- – карандаш;
- – линейка;
- – компьютер с программой AutoCAD.
Инструкция
1.
Начните с классического построения. Определите плоскость, в которой вы будете строить прямую. Пускай это будет плоскость листа бумаги. В зависимости от условий задачи расположите точки. Они могут быть произвольными, но не исключено, что задана какая-то система координат. Произвольные точки поставьте там, где вам огромнее понравится. Обозначьте их как А и В. С поддержкой линейки объедините их. Согласно аксиоме, через две точки неизменно дозволено провести прямую, притом только одну.
2.
Начертите систему координат. Пускай вам даны координаты точки А (х1; у1). Дабы их обнаружить, нужно отложить по оси х надобное число и провести через подмеченную точку прямую, параллельную оси у. После этого отложите величину, равную у1, по соответствующей оси. Из подмеченной точки проведите перпендикуляр до его пересечения с первым. Место их пересечения и будет точкой А. Таким же образом обнаружьте точку В, координаты которой дозволено обозначить как (х2; у2). Объедините обе точки прямой.
3.
В программе AutoCAD прямую дозволено возвести несколькими методами. Функция «по двум точкам» обыкновенно установлена по умолчании. Обнаружьте в верхнем меню вкладку «Основная». Вы увидите перед собой панель «Рисование». Обнаружьте кнопку с изображением прямой линии и нажмите на нее.
4.
Прямую по двум точкам в этой программе дозволено возвести двумя методами. Поставьте курсор в надобную точку на экране и щелкните левой кнопкой мыши. После этого определите вторую точку, протяните туда линию и тоже щелкните мышкой.
5.
AutoCAD разрешает также задать координаты обеих точек. Наберите в находящейся внизу командной строке (_xline). Нажмите Enter. Введите координаты первой точки и тоже нажмите на ввод. Верно также определите и вторую точку. Ее дозволено указать и щелчком мыши, поставив курсор в необходимую точку экрана.
6.
В AutoCAD дозволено возвести прямую не только по двум точкам, но и по углу наклона. В контекстном меню «Рисование» выберите прямую, а после этого опцию «Угол». Начальную точку дозволено поставить щелчком мыши либо по координатам, как и в предыдущем методе. После этого задайте размер угла и нажмите на ввод. По умолчании прямая расположится под необходимым углом к горизонтали.
Видео по теме
Совет 4: Как подтвердить, что точка не лежит в плоскости треугольника
Подтвердить, что точка не лежит в плоскости треугольника, дозволено легкой проверкой всех допустимых обстановок, тем больше что их не много. Не следует только забывать, что дозволено придти и к событию противоположному, то есть случаю, когда точка является внутренней для заданного треугольника.
Инструкция
1.
Раньше чем искать решение поставленной задачи, читателю следует самому принять решение о принадлежности сторон треугольника. Считать их точки внешними для треугольника либо нет. На данной стадии считаем, что это область замкнутая, а следственно она включает свои границы. Для простоты разглядите «плоский случай», но не забывайте и о пространственном обобщении. Следственно типовые уравнения для прямых плоскости вида y=kx+b, применять не следует, по весьма мере в начале решения.
2.
Выберите метод задания для сторон треугольника. Судя по постановке задачи, это не имеет твердого значения. Следственно считайте, что даны координаты его вершин A(xa, ya), B(xb, yb), C(xc, yc) (см. рис. 1.). Обнаружьте направляющие векторы сторон треугольника AB={xb-xa, yb-ya}, BC={xc-xb, yc-yb}, AC={xc-xa, yc-ya} и запишите канонические уравнения прямых, содержащих эти стороны. Для AB – (x-xa)/(xb-xa)=(y-ya)/(yb-ya). Для BС – (x-xb)/(xc-xb)=(y-yb)/(yc-ya). Для AС – (x-xa)/(xc-xa)=(y-ya)/(yc-ya). В соответствии с рисунком проведите горизонтальные и вертикальные линии, которые дозволено записать как x=xc, x= xa, x=xb, y=yc, y=ya, y=yb. Это дозволит до минимума сократить число вычислений. Дальше следуйте предложенному алгорифму. На рисунке заданная точка М(xo,yo) помещена в самом «неблагополучном» месте.
3.
Следуя по оси 0х, проверьте выполнение неравенства xc?xo?хb. Если оно не исполнено, то точка теснее лежит вне пределов треугольника, потому что «не внутри» – это и есть «снаружи». Если же неравенство исполнено, то дальше проверьте честность xc
4.
Проверьте выполнение неравенства уc?уo?уа. Если оно не объективно, то точка не лежит внутри треугольника. В отвратном случае обнаружьте ординату прямой, содержащей АB. у1=y(xo)=[(yb-ya)(xo-xa)]/(xb-xa)+ya. Также поступите с ординатой прямой для BC. у2=у(хо)=[(yс-yb)(xo-xb)]/(xc-xb)+yc. Составьте неравенство y2?yo?y1. Его выполнение разрешает сделать завершение о том, что заданная точка находится внутри треугольника. Если же это неравенство ложно, то она лежит вне его пределов, в частности в соответствии с рисунком.
Если точки А, B и С лежат на одной прямой, то больший из отрезков AB, ВС и АС равен сумме двух других. По условию больший из данных отрезков (отрезок АС) равен 5 см, а сумма двух других (AB+BC) равна 7 см. Поэтому точки А, B и С не лежат на одной прямой.
Если точки А, В, С лежат на одной прямой, то больший из отрезков АВ, ВС и АС равен сумме двух других. По условию больший из данных отрезков (АС =5 см), а АВ + ВС = 7 см, поэтому точки А, В, С не лежат на одной прямой.
Похожие задачи:
1. Площадь ромба равна S. Найдите площадь четырехугольника, вершинами которого являются середины сторон ромба.
2. Две окружности с центрами в точках О1 и О2 пересекаются в точках А и А1, а отрезки АВ и АС — их диаметры. Найдите величины углов АА1В и АА1С и докажите, что точки В, А1 и С лежат на одной прямой.
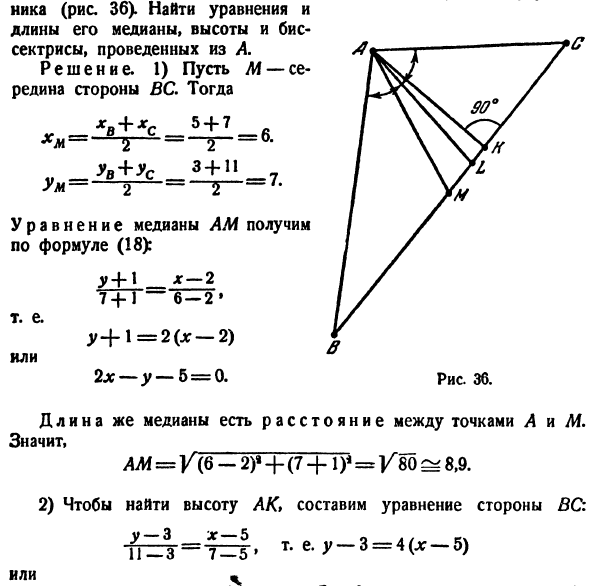
3. Медианы треугольника со сторонами 5 см, 6 см и 7 см пересекаются в точке О. Найдите расстояние от точки О до прямых, содержащих стороны треугольника.
4. Четырехугольник ABCD вписан в окружность. Известно, что угол ABD=30*, угол ACB=30*, угол BDC=20*. Найти углы четырехугольника ABCD.
1) Катеты прямоугольного треугольника равны 15см и 20см. Найдите длину окружности, диаметром которой является высота, проведенная к гипотенузе.
2) Площадь квадрата равна S. Найдите:
а) длину вписанной окружности
б) длину дуги, заключенной между двумя соседними точками касания.
в) площадь части квадрата, лежащей вне вписанной окружности.
1. Две окружности с центрами О и К имеют соответственно радиусы 4 и 8 см. Найдите радиусы окружностей, касающихся одновременно двух данных, если их центры лежат на прямой ОК, и отрезок ОК равен 6 см.
2. Высоты треугольника, пересекаясь в точке Н, образуют шесть углов с вершиной в точке Н. Определите эти углы, если углы данного треугольника равны: 50, 60, 70 градусов.
Если вам даны две точки
, то вы можете смело заявить, что они лежат на одной прямой
, так как через любые две точки
можно провести прямую. Но как же выяснить, лежат ли все точки
на прямой
, если точек три, четыре или больше? Доказать принадлежность точек одной прямой
можно несколькими способами.
Вам понадобится
- Точки, заданные координатами.
Инструкция
Если вам даны точки
с координатами (х1, у1, z1), (х2, у2, z2), (х3, у3, z3), найдите уравнение прямой
, используя координаты любых двух точек, например, первой и второй. Для этого подставьте соответствующие значения в уравнение прямой
: (х-х1)/(х2-х1)=(у-у1)/(у2-у1)=(z-z1)/(z2-z1). Если один из знаменателей равен нулю, просто приравняйте к нулю числитель.
Найти уравнение прямой
, зная две точки
с координатами (х1, у1), (х2, у2), еще проще. Для этого подставьте значения в формулу (х-х1)/(х2-х1)=(у-у1)/(у2-у1).
Получив уравнение прямой
, проходящей через две точки
, подставьте значения координат третьей точки
в него вместо переменных х и у. Если равенство получилось верное, значит все три точки
лежат на одной прямой
. Точно так же можете проверять принадлежность этой прямой
других точек.
Проверьте принадлежность всех точек прямой
, проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли верным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой
должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.
Еще один способ проверить принадлежность трех точек прямой
– посчитайте площадь треугольника, который они образуют. Если все точки
лежат на прямой
, то его площадь будет равна нулю. Подставьте значения координат в формулу: S=1/2((х1-х3)(у2-у3)-(х2-х3)(у1-у3)). Если после всех вычислений вы получили ноль — значит, три точки
лежат на одной прямой
.
Чтобы найти решение задачи графическим способом, постройте координатные плоскости и найдите точки
по указанным координатам. Затем проведите прямую через две из них и продолжите до третьей точки
, посмотрите, пройдет ли она через нее. Учтите, этот способ подходит только для точек, заданных на плоскости с координатами (х, у), если же точка задана в пространстве и имеет координаты (х, у, z), то такой способ неприменим.
Совет 2: Как проверить, что точки не лежат на одной прямой
На основании аксиомы, описывающей свойства прямой
: какова бы ни была прямая, есть точки
, принадлежащие и не принадлежащие ей. Поэтому вполне логично, что не все точки
будут лежать на одной прямой
линии.
Вам понадобится
- — карандаш;
- — линейка;
- — ручка;
- — тетрадь;
- — калькулятор.
Инструкция
Проверить принадлежность точки
той либо иной прямой
довольно просто. Используйте для этого уравнение прямой
. Итак, предположим, что прямая проходит через точки
А(x1,y1) и В(x2,y2). Дана точка К(x,y): нужно проверить ее принадлежность прямой
. Уравнение линии по двум точкам имеет следующий вид: (x — x1) * (y2 — y1) — (x2 — x1) * (y — y1) = 0.
Подставьте значение координат точки
К в уравнение. Если (x — x1) * (y2 — y1) — (x2 — x1) * (y — y1) окажется больше нуля, то точка К расположена правее или ниже прямой
, проведенной по точкам А и В.
В том случае, если (x — x1) * (y2 — y1) — (x2 — x1) * (y — y1) будет меньше нуля, точка К располагается выше или левее линии. Другими словами, только в том случае, если уравнение вида (x — x1) * (y2 — y1) — (x2 — x1) * (y — y1) = 0 справедливо, точки
А, В и К будут расположены на одной прямой
.
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 — линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) — ему не удовлетворяет;
б)
в) 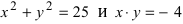
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 — уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
а) С = 0; 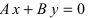
Рис. 20. Прямая, проходящая через начало координат.
б) 5 = 0; Ах+С=0 — прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
в) А = 0; Ву+С=0 — прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
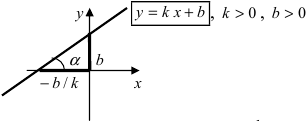
Виды уравнений прямой
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 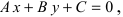
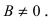
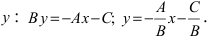
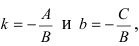
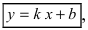
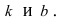
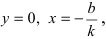
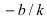
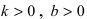
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 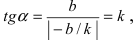
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 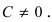
Обозначим через 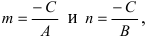
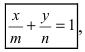
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 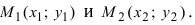
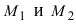
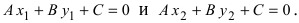
Пусть 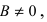
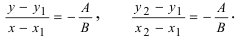
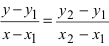
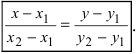
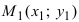
4. Уравнение прямой, проходящей через заданную точку 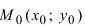
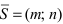
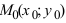
Определение: Вектор 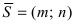
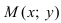
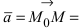
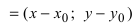
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 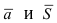
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 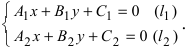
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что 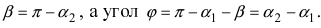
Наименьший угол между пересекающимися прямыми определим формулой 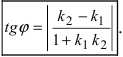
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что 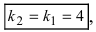
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты 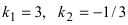
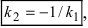
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 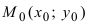
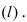
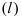
Если прямая 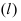
Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка 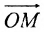
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая — второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси — координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую — осью ординат, обозначаемую Оу.
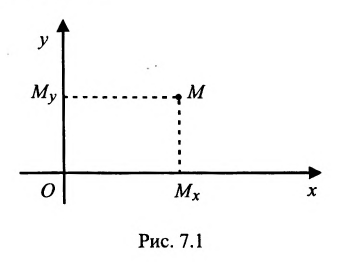
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно 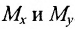
Координатами точки М в заданной системе называются числа 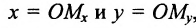
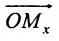
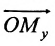
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у — М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
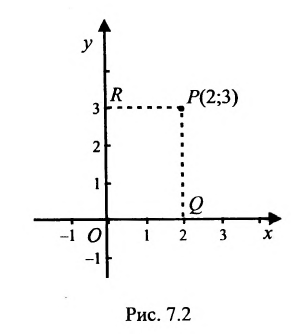
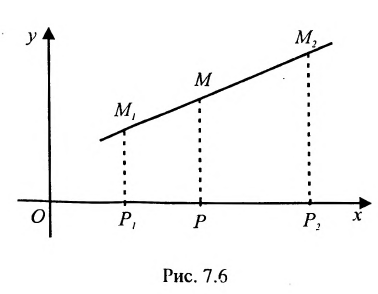
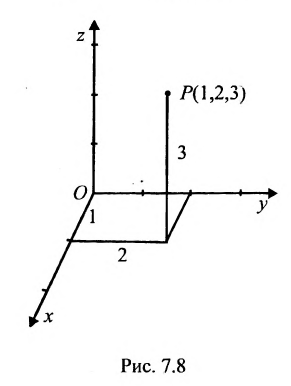
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
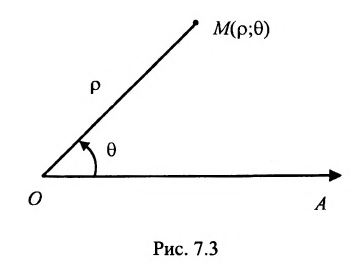
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат 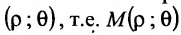
Декартова прямоугольная система координат связана с полярной системой формулами:
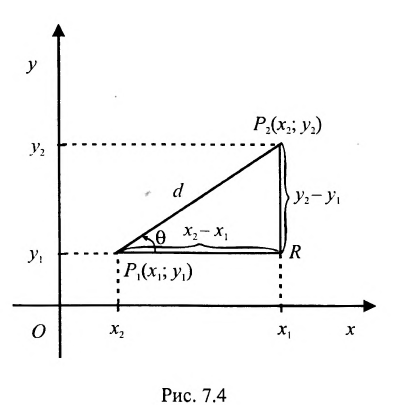
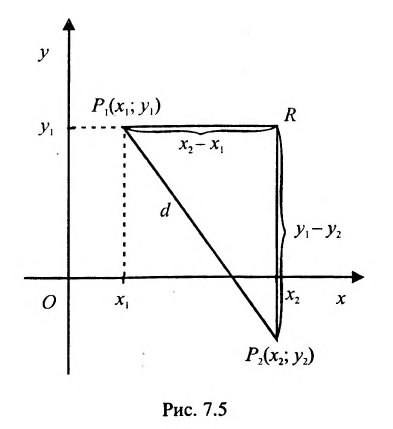
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками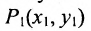
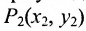
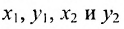
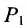
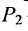
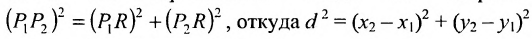
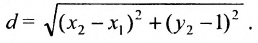
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки 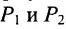
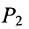
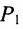
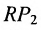
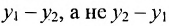
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как 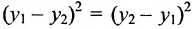
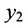
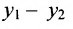
Если обозначить через 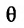
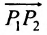
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u — произвольная ось, а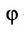
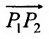
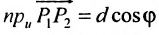
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая — второй. Обозначим их в заданном порядке через 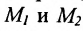
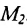
Определение 7.1.1. Число 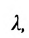
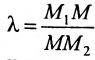
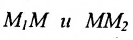
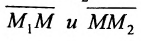
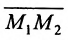
Число 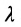
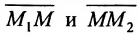
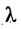
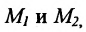
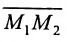
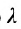
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек 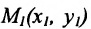
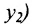
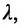
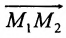
Решение задачи определяется следующей теоремой.
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок 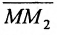
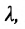
Доказательство:
Спроектируем точки 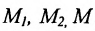
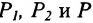
Подставив в (7.1.4) величины отрезков 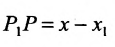
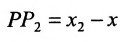
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если 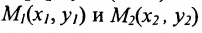
середина отрезка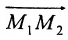
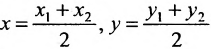
получаются из (7.1.3) при 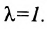
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора 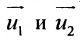
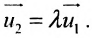
Для всех направляющих векторов 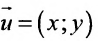
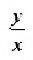
Действительно, если 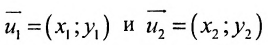
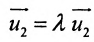
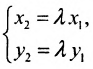
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
Доказательство: Пусть В = (О,b}- точка пересечения прямой L с осью у, а Р = (х,у) — любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р — прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то 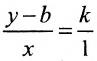
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
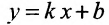
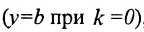
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Ах+Ву+С=0. (7.2.4)
Если 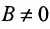
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
А х = —С,
или 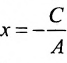
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как 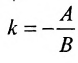
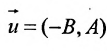
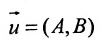
1. 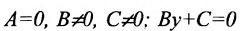
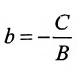
2. 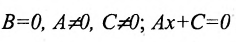
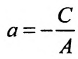
3. 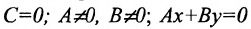
4. А=0; С=0; Ву-0 или у = 0 — это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 — это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где 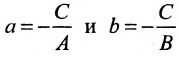
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки 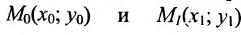
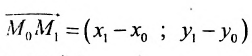
Геометрическое место концов всевозможных векторов вида 
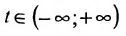
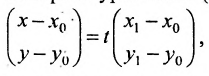
где 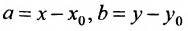
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
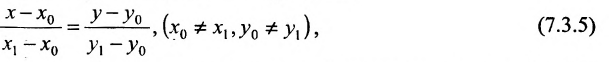
Если абсциссы точек 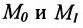

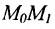
Если ординаты точек 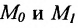
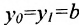
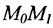
или
где
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку 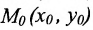
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек 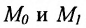
II способ. Зная координаты точек 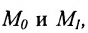
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: 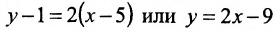
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
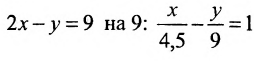
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями 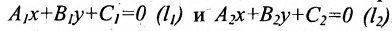
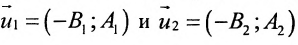
Если прямые параллельны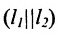
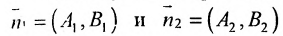
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые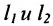
Например, прямые 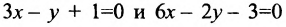
т. к.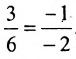
Если прямые перпендикулярны 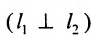
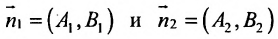
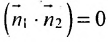
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые 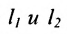
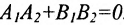
Например, прямые 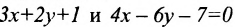
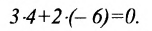
Если прямые заданы уравнениями вида 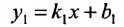
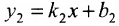
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
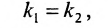
а для их перпендикулярности необходимо и достаточно, чтобы
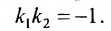
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ — это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку 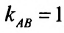
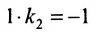
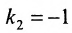
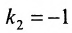
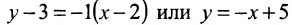
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
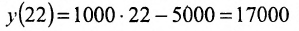
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: 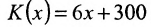
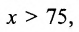
Прямая линия в пространстве
Системы координат в пространстве
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
Пусть задано пространство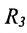
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки 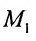
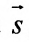
Вектор 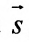
Итак, пусть прямая L проходит через точку 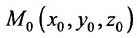
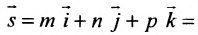
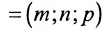
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор 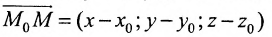
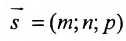
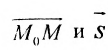
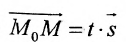
Уравнение 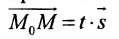
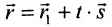
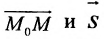
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками 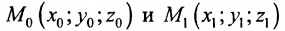
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где 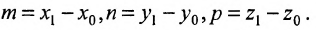
Пример:
Составить параметрические уравнения прямой, проходящей через точку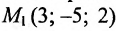
Решение:
В качестве направляющего вектора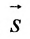
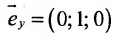
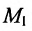
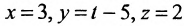
Пример:
Записать уравнения прямой 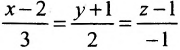
Обозначим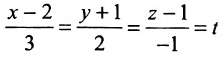
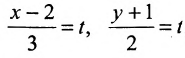
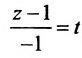
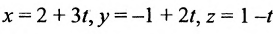
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде 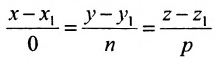
Аналогично, канонические уравнения
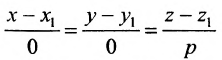
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку 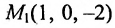
Решение:
Подставив координаты точки 
.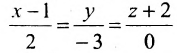
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой 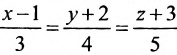
б) оси Ох;
в) оси Оу;
г) оси Oz.
Решение:
а) Поскольку направляющий вектор заданной прямой
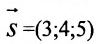
подставив координаты точки М(2; -1; 4) и вектора 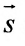
б) Поскольку единичный вектор оси О х: 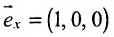
(7.5.3) координаты точки М(2; -1; 4 ) и вектора 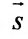
в) В качестве направляющего вектора 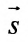
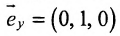
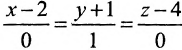
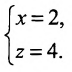
г) Единичный вектор оси Oz : 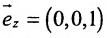
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек 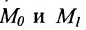
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол 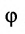
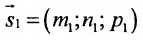
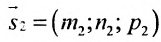
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов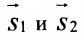
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. 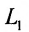
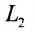
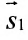
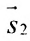
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми 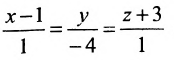
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов 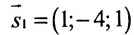
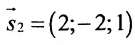
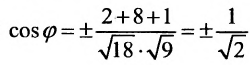
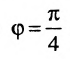
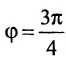
Вычисление уравнения прямой
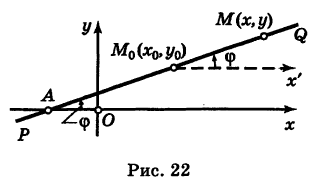
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол 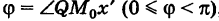
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала 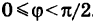
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
при х > 0.
Таким образом,
при х > 0.
Нетрудно проверить, что формула (3) остается справедливой также и при х < 0.
Мы доказали, что координаты любой точки М (х, у) прямой PQ удовлетворяют уравнению (3). Легко убедиться в обратном: если координаты какой-нибудь точки Ml 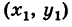
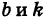
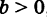
При k = 0 получаем уравнение прямой, параллельной оси Ох:
2) Если 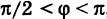
3) Если 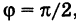
где а — абсцисса следа этой прямой на оси Ох (т. е. ее точки пересечения с осью Ох).
Замечание. Как частные случаи получаем уравнения осей координат:
Прямую легко построить по ее уравнению.
Пример:
Построить прямую, заданную уравнением
Решение:
Известно, что две точки вполне определяют положение прямой. Поэтому достаточно найти две точки, через которые проходит наша прямая. В данном уравнении b = -4. Следовательно, прямая проходит через точку В (0, -4). С другой стороны, координаты х и у любой точки, лежащей на нашей прямой, связаны заданным уравнением. Поэтому, задав абсциссу некоторой точки, лежащей на прямой, мы из уравнения прямой найдем ее ординату. Положим, например, х = 2; из уравнения прямой получим у = -1. Таким образом, наша прямая проходит через точки А (2, -1) и В (0, -4). Построив эти точки по их координатам и проведя через них прямую (рис. 24), мы получим искомую прямую.
Из предыдущего видно, что для произвольной прямой на плоскости можно составить ее уравнение; обратно, зная уравнение некоторой прямой, можно построить эту прямую. Таким образом, уравнение прямой полностью характеризует положение ее на плоскости.
Из формул (3) и (5) видно, что уравнение прямой есть уравнение первой степени относительно текущих координат х и у. Справедливо и обратное утверждение.
Теорема: Всякое невырожденное уравнение первой степени
представляет собой уравнение некоторой прямой линии на плоскости Оху (общее уравнение прямой линии).
Доказательство: 1) Пусть сначала В ^ 0. Тогда уравнение (7) можно представить в виде

2) Пусть теперь В = 0; тогда А 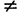
х = -С/А.
Уравнение (9) представляет собой уравнение прямой, параллельной оси Оу и отсекающей на оси Ох отрезок a = -С/А.
Так как все возможные случаи исчерпаны, то теорема доказана.
- Заказать решение задач по высшей математике
Угол между двумя прямыми
Рассмотрим две прямые (не параллельные оси Оу)у заданные их уравнениями с угловыми коэффициентами (рис. 25):
Требуется определить угол 9 между ними. Точнее, под углом 0 мы будем понимать наименьший угол, отсчитываемый против хода часовой стрелки, на который вторая прямая повернута относительно первой (0 < 0 < я). Этот угол 9 (рис. 25) равен углу АСВ треугольника ABC. Далее, из элементарной геометрии известно, что внешний угол треугольника равен сумме внутренних, с ним не смежных. Поэтому ф’ = ф + 0, или
0 = ф’ — ф;
отсюда на основании известной формулы тригонометрии получаем
Заменяя tg ф и tg ф’ соответственно на к и k окончательно будем иметь
Формула (3) дает выражение тангенса угла между двумя прямыми через угловые коэффициенты этих прямых.
Выведем теперь условия параллельности и перпендикулярности двух прямых.
Если прямые (1) и (2) параллельны, то ф’ = ф и, следовательно,
k’ = к. (4)
Обратно, если выполнено условие (4), то, учитывая, что ф’ и ф заключаются в пределах от 0 до я, получаем
Ф’ — ф, (5)
и, следовательно, рассматриваемые прямые или параллельны, или сливаются (параллельность в широком смысле).
Правило 1. Прямые на плоскости параллельны (в широком смысле) тогда и только тогдау когда их угловые коэффициенты равны между собой.
Если прямые перпендикулярны, то 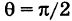
отсюда 1 + kk’ = 0 и
k’ = -l/k.
Справедливо также и обратное утверждение.
Правило 2. Две прямые на плоскости перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.
Пусть теперь уравнения прямых заданы в общем виде:
Ах + By + С = 0 (7)
и
А’х + В’у + С’ = 0. (8)
Отсюда, предполагая, что 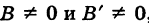
Следовательно, угловые коэффициенты этих прямых есть
Из формулы (3), производя несложные выкладки, находим тангенс угла между этими прямыми:
Отсюда получаем:
1) условие параллельности прямых (0 = 0)
2) условие перпендикулярности прямых
Отметим, в частности, что прямые
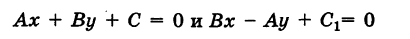
Для прямых, параллельных осям Ох и Оу, условно полагают 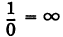
Пример:
Определить угол между прямыми у = х и у = 1,001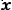
Решение:
По формуле (3) получаем
Так как для малых углов 0 справедливо приближенное равенство 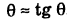
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая РМ образует угол ф с положительным направлением оси Ох (рис. 26) и проходит через заданную точку Р 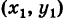
В этом случае, как мы видели, уравнение прямой имеет вид
у = kx + b, (1)
где k = tg ф — угловой коэффициент прямой, а Ь — длина отрезка, отсекаемого нашей прямой на оси Оу. Так как точка Р 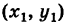
ух = kxt+ b. (2)
Вычитая из равенства (1) равенство (2), получим
Это и есть уравнение искомой прямой.
Если прямая, проходящая через точку Р 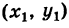
Если k — заданное число, то уравнение (3) представляет вполне определенную прямую. Если же k — переменный параметр, то это уравнение определит пучок прямых у проходящих через точку Р 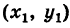
Пример:
Написать уравнение прямой, проходящей через точку Р (3, 2) и параллельной прямой:
Решение:
Так как искомая прямая параллельна данной прямой, то ее угловой коэффициент k = 4/3. Следовательно, на основании формулы (3) уравнение этой прямой имеет вид 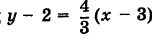
Пример:
Написать уравнение прямой, проходящей через точку Р (4, 5) и перпендикулярной к прямой:
Решение:
Так как искомая прямая перпендикулярна прямой с угловым коэффициентом k = -2/3, то ее угловой коэффициент k’ = -l/k = 3/2. Следовательно, на основании формулы (3) уравнение этой прямой таково:
Уравнение прямой, проходящей через две данные точки
Известно, что через две не совпадающие между собой точки можно провести прямую, и притом только одну. Отыщем уравнение прямой, проходящей через точки 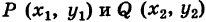
Предположим сначала, что 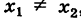
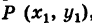
где k — неизвестный нам угловой коэффициент этой прямой. Однако так как наша прямая проходит также через точку Q 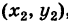
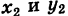
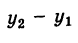
и, следовательно, при 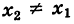
Подставляя выражение (2) для углового коэффициента k в уравнение (1), получим уравнение прямой PQ:
Это уравнение при 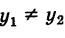
Если 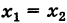
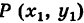
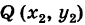
Пример:
Написать уравнение прямой, проходящей через точки Р(4, -2) и Q(3, -1).
Решение:
На основании уравнения (3) имеем
Уравнение прямой в «отрезках»
Выведем теперь уравнение прямой, положение которой на плоскости задано ненулевыми отрезками, отсекаемыми ею на осях координат. Предположим, например, что прямая АВ отсекает на оси Ох отрезок OA = а, а на оси Оу — отрезок О В = b (рис. 28), причем ясно, что тем самым положение прямой вполне определено.
Для вывода уравнения прямой АВ заметим, что эта прямая проходит через точки А (а, 0) и Б 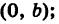
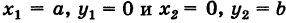
Отсюда
и окончательно
Это и есть так называемое уравнение прямой в «отрезках». Здесь х и у, как обычно, — координаты произвольной точки М (х, у), лежащей на прямой АВ (рис. 28).
Пример:
Написать уравнение прямой АВ, отсекающей на оси Ох отрезок OA = 5, а на оси Оу отрезок ОВ = -4.
Полагая в уравнении (1) а = 5 и b = -4, получим 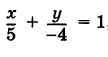
Примечание. Уравнение прямой, проходящей через начало координат или параллельной одной из осей координат, не может быть записано как уравнение прямой в «отрезках».
Точка пересечения двух прямых
Пусть имеем две прямые
Точка пересечения этих прямых лежит как на первой прямой, так и на второй. Поэтому координаты точки пересечения должны удовлетворять как уравнению первой, так и уравнению второй прямой. Следовательно, для того чтобы найти координаты точки пересечения двух данных прямых, достаточно решить совместно систему уравнений этих прямых.
Последовательно исключая из уравнений (1) и (2) неизвестные у и х, будем иметь
Отсюда если 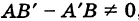
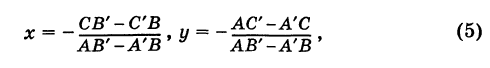
Для прямых (1) и (2) возможны следующие три случая.
На основании прямые не параллельны. Координаты их единственной точки пересечения определяются из формул (6).
Прямые параллельны и точки пересечения нет. Аналитически это видно из того, что по меньшей мере одно из уравнений (3) или (4) противоречиво и, значит, система (1) и (2) несовместна.
Прямые (1) и (2) сливаются, и, таким образом, существует бесчисленное множество точек пересечения. В этом случае левые части уравнений (1) и (2) отличаются только на постоянный множитель и, следовательно, система этих уравнений допускает бесконечно много решений.
Пример:
Решая совместно систему уравнений прямых
получаем х = 2 и у = 1. Следовательно, эти прямые пересекаются в точке N(2,1).
Расстояние от точки до прямой
Рассмотрим прямую KL, заданную общим уравнением
и некоторую точку М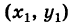
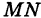
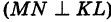
Уравнение перпендикуляра MN можно записать в виде
Отсюда для основания перпендикуляра N(x2, у2) будем иметь
и, следовательно,
где t — коэффициент пропорциональности. Поэтому
С другой стороны, учитывая, что точка N(*2, i/2) лежит на прямой KL, причем из (4) имеем 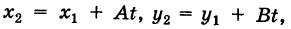
Следовательно,
Таким образом, в силу формулы (5) имеем
В частности, полагая 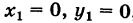
Замечание. Разделив обе части уравнения прямой (1) на 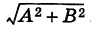
свободный член которого 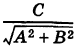
начала координат до прямой. Такое уравнение прямой будем называть нормированным.
Из формулы (7) получаем правило:
чтобы определить расстояние от точки до прямой, нужно в левую часть нормированного уравнения этой прямой подставить координаты данной точки и взять модуль полученного результата.
Пример:
Определить расстояние от точки М (-2, 7) до прямой
Решение:
Нормируя уравнение этой прямой, будем иметь
Отсюда искомое расстояние есть
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление