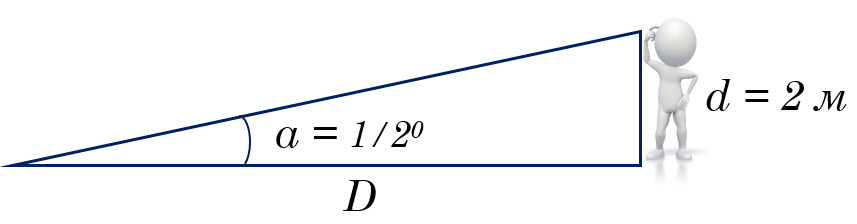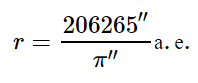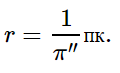Как найти линейный диаметр в астрономии

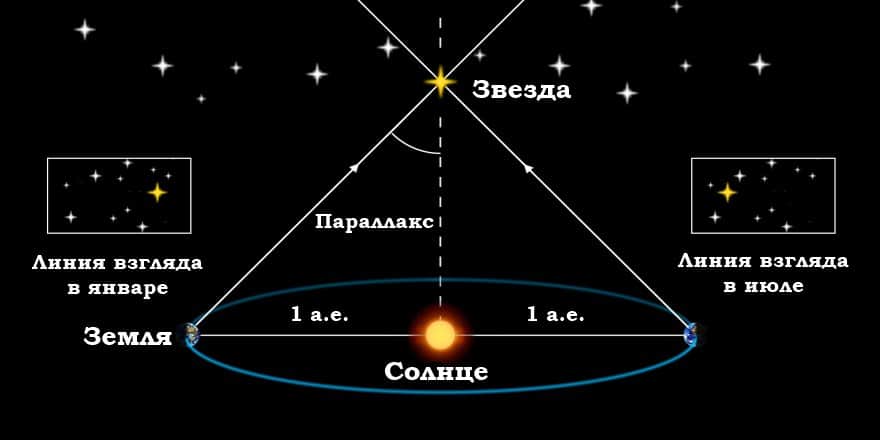
Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними. Зачастую непосредственное измерение кратчайшего расстояния между этими пунктами оказывается невозможным из-за различных естественных препятствий (гор, рек и т. п.). Поэтому применяется способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из сторон (базиса — BC) и двух углов B и C в треугольнике ABC (рис. 3.9).

Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.

Чем дальше расположен предмет, тем меньше его параллактическое смещение, и чем больше перемещение наблюдателя (базис измерения), тем больше параллактическое смещение.

Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.

Почему так трудно определить размеры небесных объектов и расстояния до них? Все дело в том, что размеры удаленных объектов мы можем определить только по сравнению размерами известных объектов, а на небе нам не с чем сравнивать. Мы видим на небе множество светящихся точек, но яркость точки может определяться как ее размером, абсолютной светимостью, так и расстоянием до нее.

Поэтому в астрономии практически невозможно определить оптическими методами линейный размер удаленного объекта, можно определить только его угловой размер.

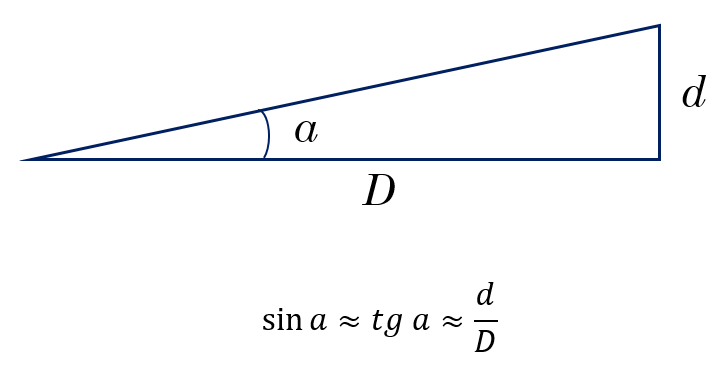
Древние греки изобрели тригонометрию, которая позволяет определить количественные соотношения между углами, линейными размерами и линейными расстояниями. С помощью простых математических соотношений, включающих базовую тригонометрию, мы можем вычислить расстояния до удаленных объектов, размеры которых известны (или размеры, если расстояния известны).

Уравнение малых углов

Если углы малые, то синус угла примерно равен тангенсу, который, в свою очередь примерно равен самому углу в радианной мере. 

Уравнение малых углов включает в себя угловой размер объекта, его линейный размер и расстояние. Если известны какие-либо две из этих величин, можно вычислить третью. Обратимся к угловому размеру с символом a, выраженному в секундах дуги. Обозначим диаметр объекта как d, а расстояние до него как D. Тогда уравнение малого угла

a / 206 265 = d / D

Число 206 265 называется константой пропорциональности. Число 206 265 на самом деле является числом секунд дуги в угле 57,3°, который является специальным углом, называемым радианом. Радиан определяется как центральный угол дуги, длина которой равна радиусу окружности. Длина окружности равна 2πr, Радиан равен 360° / 2 π = 57,3° или около шестой части полного круга. 

Вот пример использования уравнения малого угла. Предположим, что ваш друг ростом в 2 метра стоит через поле от вас, где он виден под углом ½°, или 1800″. Как он далеко от вас? Мы хотим найти расстояние D, выразим эту величину из уранения:

D = 206 265 d / a

Используя метрические единицы, найдем

D = (2.1 x 10⁵ x 2) / (1.8 x 10³) = 2.3 х 10² метра = 230 метров

Если ваш друг имеет рост 2 метра и угловой размер его составляет ½ ° (или 1800 угловых секунд), расстояние D составляет 230 метров. Обратите внимание, что мы округляем все наши оценки до двух значащих цифр, потому что измерение угла вряд ли будет очень точным.

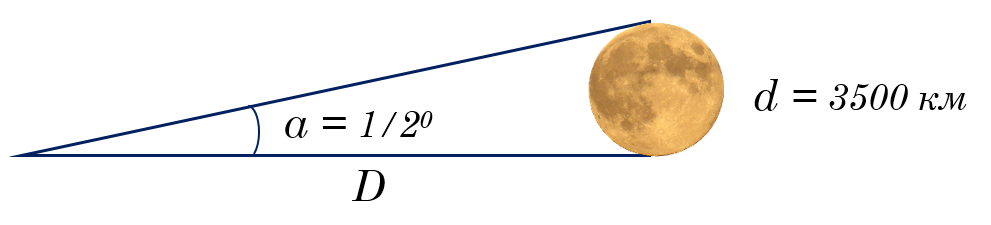
Как поняли древние греки, уравнение малого угла можно использовать для определения астрономических расстояний. Они не могли точно измерить диаметр Луны, но они знали ее угловой размер a, который также составляет примерно ½°, или 1800″.

Если мы используем современные знания о том, что диаметр Луны составляет около 3500 километров, мы можем оценить расстояние до нее так же, как мы это сделали для расстояния друга выше. В метрических единицах d будет 3,5 × 10⁶ метров. Уравнение будет гласить:

D = (2.1 × 10⁵ × 3.5 × 10⁶) / (1.8 × 10³) ≈ 4 х 10⁸ метров ≈ 4 x 10⁵ километров.

Реальное среднее расстояние до Луны 384 000 км. Неплохая точность!

Методы определения расстояний до звезд

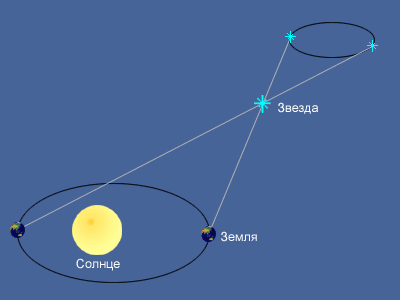
Годичный параллакс

Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом (π).

Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.

Если CT = a есть средний радиус земной орбиты, SC = r — расстояние до звезды S от Солнца C, а угол π — годичный параллакс звезды, то

Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′, то расстояние до звезды можно определить из соотношения

При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины — парсек (пк), название которой происходит от слов «параллакс» и «секунда».

Парсек — это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.

1 пк = 206 265 а. е. = 3,086 · 10¹³ км.

Таким образом, расстояние до звезд в парсеках будет определяться выражением

В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках (1 кпк = 10³ пк) и мегапарсеках (1 Мпк = 10⁶ пк), а также в световых годах (1 св. г. = 9,46 · 10¹² км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г.).

Световой год — расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.

Источник

Фотометрический метод определения расстояний

Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m — видимая, M — абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний r_ф(пк):

Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.

Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5^m. Эта погрешность соответствует относительной погрешности 30%.

Цефеиды (стандартные свечи)

Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном свойстве переменных звезд — цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5^m. Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.

Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).

Угол, под которым
с Земли виден диск светила, называется
его угловым
диаметром.
Угловые диаметры некоторых небесных
тел (Солнца, Луны, планет) можно определить
непосредственно из наблюдений.

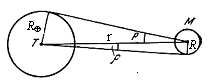
Рис. 2.4. Определение
линейных размеров светил.

Если известен
угловой диаметр (или радиус) светила и
его расстояние от Земли, то легко
вычислить его истинный диаметр (или
радиус) в линейных мерах. Действительно,
если (рис. 2.4) —
угловой радиус светила М, r
— расстояние между центрами светила и
Земли, р — горизонтальный экваториальный
параллакс светила, а R_
и R — линейные
радиусы Земли Т и светила М, то

а, учитывая, что
угол 
мал и

:

где

— угловой
радиус, выраженный в угловых секундах.

С учетом формулы (2.9) соотношение (2.13)
может быть приведено к следующему виду:

т.е.
чтобы вычислить
линейный радиус небесного тела, необходимо
измерить его угловой радиус и горизонтальный
параллакс.

Форму небесных тел можно определить,
измеряя различные диаметры их дисков.
Если тело сплющенное, то один из его
диаметров окажется больше, а один —
меньше всех других диаметров. Измерения
диаметров планет показали, что помимо
Земли сплющенную форму имеют Марс,
Юпитер, Сатурн, Уран и Нептун.

Линейные размеры
и форма небесных тел, угловые размеры
которых непосредственно измерить нельзя
(например, малые планеты и звезды),
определяются специальными методами.

§ 2.5. Измерение расстояний до звезд

Т.к. звезды удалены
от нас на огромные расстояния, то их
суточное параллактическое смещение
исключительно мало, поэтому оно не может
быть измерено.

Расстояния до
звезд определяются по их годичному
параллактическому смещению,
которое обусловлено перемещением
наблюдателя (вместе с Землей) по земной
орбите (рис. 2.5).

Рис. 2.5. Годичный
параллакс звезд.

Угол, под которым
со звезды был бы виден средний радиус
земной орбиты при условии, что направление
на звезду перпендикулярно к радиусу,
называется годичным
параллаксом звезды
.
Если СТ = а_
есть средний радиус земной орбиты, МС
= r
— расстояние звезды М
от Солнца С
(гелиоцентрическое
расстояние),
а угол 
— годичный параллакс звезды, то из
прямоугольного треугольника СТМ
имеем

Годичные параллаксы
звезд меньше 1«, и поэтому, учитывая,
что

,
получим:

где

— годичный
параллакс, выраженный в угловых секундах.

Расстояние r
по этим формулам получается в тех же
единицах, в которых выражено среднее
расстояние а_
Земли от Солнца.

Т.к. звезды находятся
на очень больших расстояниях от Земли,
то их гелиоцентрические расстояния и
расстояния от Земли будем считать
одинаковыми.

Расстояние,
соответствующее годичному параллаксу
в 1«,
называется парсеком.

Если расстояния
до звезд измерять в парсеках (пс),
то

Кроме этого,
расстояния до звезд измеряют также в
световых
годах.

Световой год
— расстояние,
которое свет проходит за один год,
распространяясь со скоростью около 300
000 км/с.

Запишем соотношения
между единицами расстояния в астрономии:

1 пс
= 3,1¹³
км
= 206 265 а.е.
= 3,26 светового
года;

1 световой
год = 9,46¹²
км =
63 240 а.е.;

1 а.е.=
149,6 
10⁶
км.

Расстояния до
небесных тел, находящихся за пределами
Солнечной системы, обычно выражаются
в парсеках, килопарсеках (1 000 пс)
и мегапарсеках (1 000 000 пс),
а также в световых годах.

Установлено, что
ближайшей к Солнцу звездой является
звезда Проксима
Центавра, которая имеет годичный
параллакс 
= 0«,772.
Следовательно, она находится от нас на
расстоянии 1,3 пс
или 4,2 светового
года.

Современные
астрономические приборы позволяют в
настоящее время измерить годичные
параллаксы, не меньшие 0«,005.
Это дает возможность определить
расстояния методом годичного параллакса,
не превышающие 200 пс.
Расстояния до более далеких объектов
определяются другими способами.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вы уже знаете, что ещё в Древней Греции учёными и мыслителями
было установлено, что наша планета не является плоской, а имеет шарообразную
форму. Представление о Земле как о шаре, который свободно, без всякой опоры
находится в космическом пространстве, является одним из величайших достижений
древнего мира.

Первый известный науке метод определения размеров Земли
применил греческий учёный Эратосфен, живший в Египте. Его идея была достаточно
проста. Итак, Эратосфен выбрал два города — Александрию и Сиену (ныне Асуан) —
расположенных на одном земном меридиане.

Далее он обозначил длину дуги меридиана между двумя городами
через l, а её
угловое значение в градусах как п.

Тогда длина дуги в 1^о выбранного меридиана равна

А длина всей окружности меридиана: L = 360^o ∙ l₀.

С другой стороны, он знал, что длина окружности равна: L =
2πR.

Приравняв правые части последних двух уравнений, легко
получить искомый радиус земного шара:

Теперь было необходимо определить длину дуги меридиана в градусной
мере. Очевидно, что она равна разности географических широт Александрии и
Сиены. Так вот, чтобы определить эту разность Эратосфен придумал хитрый способ.
Он знал, что в полдень дня летнего Солнцестояния в Сиене Солнце находится в
зените и освещает дно самых глубоких колодцев. А в Александрии Солнце до зенита
не доходит. Поэтому шест, вбитый вертикально в землю должен отбрасывать тень.
Измерив длину этой тени можно легко определить искомую длину дуги меридиана,
которая у Эратосфена оказалась равной 7,2^о.

Ну а расстояние между Александрией и Сиеной ему было хорошо
известно: оно составляло пять тысяч греческих стадий.

Подставив все данные в формулу для длины окружности
меридиана, Эратосфен получил значение в 250 000 стадий.

Стадий — это весьма неоднозначная единица измерения
расстояния. Но, как правило, за стадий принимали расстояние, которое проходит
легковооружённый воин за промежуток времени от появления первого луча солнца
при его восходе до того момента, когда весь солнечный диск окажется над горизонтом.

Однако если учесть, что расстояние между Александрией и
Асуаном по прямой примерно равно 844 километрам, то можно полагать, что одна
стадия примерно равна 169 метрам.

Тогда искомая длина всей окружности меридиана равна
42 250 километрам, что совсем не плохо для того времени.

Современная наука располагает более точными способами
измерения расстояний на земной поверхности. Одним из них является метод
триангуляций, основанный на явлении параллактического смещения.

Параллактическое смещение — это изменение направления
на предмет при перемещении наблюдателя. С его помощью можно измерить расстояние
на основе измерения длины одной из сторон (базиса) и двух прилегающих к
ней углов в треугольнике.

Суть метода триангуляций состоит в следующем. По обе стороны
дуги, длину которой нужно измерить, выбирается несколько точек на расстоянии не
более 50 километров друг от друга, на которых устанавливаются геодезические
вышки. При этом из каждой точки должны быть видны по крайней мере две другие
точки. Далее тщательным образом измеряется длина базиса (с точностью до одного
миллиметра). После этого с вершины вышки при помощи теодолита измеряются углы
между направлениями на два-три соседних пункта. Измерив углы в треугольнике,
одной из сторон которого является базис, геодезисты получают возможность
вычислить длину двух других его сторон по известным тригонометрическим
формулам. Проводя затем измерение углов из пунктов, расстояние между которыми
уже вычислено, можно узнать длину очередных двух сторон и так далее. Затем, по
вычисленным сторонам, определяется искомая длина дуги.

В XVIII веке использование триангуляционных измерений в
экваториальных широтах и вблизи северного полярного круга, показало, что длина
дуги в 1^о меридиана не одинакова и увеличивается к полюсам. Из этого
следовало, что наша планета не является идеальным шаром и её полярный радиус
почти на 21 километр короче экваториального. Поэтому в геодезии и форму Земли
считают геоидом, то есть телом с поверхностью, близкой к поверхности спокойного
океана и продолженной под материками.

В настоящее время форму Земли принято характеризовать
следующими физическими характеристиками:

·                   полярное сжатие — 0,0033528;

·                   экваториальный радиус — 6378,1 км;

·                   полярный радиус — 6356,8 км;

·                   средний радиус — 6371,0 км;

·                  
и длина окружности экватора — 40 075,017 км.

Долгое время загадкой для многих астрономов являлось истинное
расстояние от Земли до Солнца. Измерить его смогли лишь во второй половине XVIII века,
когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при
этом измеряется параллактическое смещение объекта, находящегося за пределами
Земли, а базисом является её радиус.

Горизонтальным параллаксом называется угол, под
которым со светила виден радиус Земли, перпендикулярный лучу зрения.

Зная горизонтальный параллакс светила, можно, по известным
тригонометрическим соотношениям, определить его расстояние от центра Земли:

Очевидно, что чем дальше расположено светило, те меньше его
горизонтальный параллакс. Например, наибольший параллакс, в среднем 57ʹ,
имеет спутник Земли — Луна. У Солнца он значительно меньше и примерно
составляет 8,794ʹʹ. Такому параллаксу соответствует среднее
расстояние от Земли до Солнца, примерно равное 149,6 миллиона километров.

На одном из прошлых уроков мы говорили о том, что это
расстояние в астрономии принимается за одну астрономическую единицу. С её
помощью удобно измерять расстояния между телами в Солнечной системе.

Но вернёмся к нашей формуле. Итак, из геометрии вам должно
быть известно, что при малых значениях угла его синус примерно равен самому углу,
выраженному в радианах. Если учесть, что в одном радиане содержится 206
265ʹʹ, то легко можно получить формулу, удобную для вычислений:

Для примера, давайте с вами определим расстояние от Земли до
Юпитера в момент противостояния, если его горизонтальный параллакс был равен
2,2ʹʹ. Радиус Земли примем равным 6371 километру.

Эту же задачу можно было решить несколько иначе.

В настоящее время для более точного определения расстояний до
тел в Солнечной системе применяется более точный метод измерений — радиолокационный.
Измерив время, необходимое для того, чтобы радиолокационный импульс достиг
небесного тела, отразился и вернулся на Землю, вычисляют расстояние до этого
тела по формуле:

где с — это скорость света в вакууме.

С разработкой методов определения расстояний до тел в
Солнечной системе учёным не составило большого труда придумать и способ
определения их размеров. В частности, при наблюдениях небесного тела Солнечной
системы с Земли можно измерить угол, под которым оно видно наблюдателю, то есть
его угловой размер (или угловой диаметр), а, следовательно, и угловой радиус.

А зная угловой радиус и расстояние до светила, можно
вычислить его линейный радиус:

.

Только в этой формуле угловой радиус должен быть выражен в
радианах.

Если в записанное уравнение подставить формулу для
определения расстояний методом горизонтального параллакса и упростить её,
используя тот факт, что значения углов ρ и р малы, то получим
формулу, по которой можно определять линейные размеры небесных тел:

Но помните, пользоваться ей можно тогда, когда видны диски
светил.

Для примера давайте решим с вами такую задачу. При наблюдении
прохождения Меркурия по диску Солнца определили, что его угловой радиус равен
5,5’’, а горизонтальный параллакс — 14,4’’. Чему равен линейный радиус
Меркурия?

Тема 3.2. Законы движения небесных тел. Определение расстояний и размеров тел в Солнечной системе.

3.2.1. Законы движения небесных тел.

Важную роль в формировании представлений о строении Солнечной системы сыграли также законы движения планет, которые были открыты Иоганном Кеплером (1571—1630) и стали первыми естественнонаучными законами в их современном понимании. Работы Кеплера создали возможность для обобщения знаний по механике той эпохи в виде законов динамики и закона всемирного тяготения, сформулированных позднее Исааком Ньютоном. Многие ученые вплоть до начала XVII в. считали, что движение небесных тел должно быть равномерным и происходить по «самой совершенной» кривой— окружности. Лишь Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.

В своих поисках Кеплер исходил из убеждения, что «в мире правит число», высказанного еще Пифагором. Он искал соотношения между различными величинами, характеризующими движение планет, — размеры орбит, период обращения, скорость. Кеплер действовал фактически вслепую, чисто эмпирически. Он пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон описанных и вписанных в орбиты планет многоугольников Иоганн Кеплер и т. д.

Кеплеру необходимо было построить орбиты планет, перейти от экваториальной системы координат, указывающих положение планеты на небесной сфере, к системе координат, указывающих ее положение в плоскости орбиты. Он воспользовался при этом собственными наблюдениями планеты Марс, а также многолетними определениями координат и конфигураций этой планеты, проведенными его учителем Тихо Браге.Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям. Для того чтобы построить орбиту Марса, он применил способ, который показан на рисунке 3.5.

Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты — его прямое восхождение  α₁, которое выражается углом Т₁М₁ где Т₁ — положение Земли на орбите в этот момент, а М₁ — положение Марса. Очевидно, что спустя 687 суток (таков звездный период обращения Марса) планета придет в ту же точку своей орбиты. Если определить прямое восхождение Марса на эту дату, то, как видно из рисунка 3.5, можно указать положение планеты в пространстве, точнее, в плоскости ее орбиты. Земля в этот момент находится в точке Т₂, и, следовательно, угол T₂M₁ есть не что иное, как прямое восхождение Марса — α₂. Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил еще целый ряд точек и, проведя по ним плавную кривую, построил орбиту этой планеты.

Изучив расположение полученных точек, он обнаружил, что скорость движения планеты по орбите меняется, но при этомрадиус-вектор планеты за равные промежуткивремени описывает равные площади.Впоследствии эта закономерность получила название второго закона Кеплера.

Этот закон, который часто называют законом площадей, иллюстрируется рисунком 3.6. Радиус-вектором называют в данном случае переменный по своей величине отрезок, соединяющий Солнце и ту точку орбиты, в которой находится планета. АА₁ ВВ₁ и СС₁ — дуги, которые проходит планета за равные промежутки времени. Площади заштрихованных фигур равны между собой.

Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной энергии. По мере приближения планеты к Солнцу возрастает ее скорость — увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.

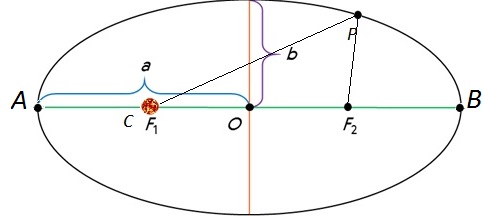
Установив закономерность изменения скорости движения планет, Кеплер задался целью определить, по какой кривой происходит их обращение вокруг Солнца. Он был поставлен перед необходимостью сделать выбор одного из двух возможных решений:     1) считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями (из-за ошибок наблюдений) на 8′; 2) считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью. Будучи уверенным в точности наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом, при этом Солнце не располагается в центре эллипса. В результате был сформулирован закон, который называется первым законом Кеплера.

Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

Как известно, эллипсом называется кривая, у которой сумма расстояний от любой точки Р до его фокусов есть величина постоянная. На рисунке 3.6 обозначены: О — центр эллипса; F и F₁ — фокусы эллипса; АВ — его большая ось. Половина этой величины (а), которую обычно называют большой полуосью, характеризует размер орбиты планеты. Ближайшая к Солнцу точка А называется перигелий, а наиболее удаленная от него точка В — афелий. Отличие эллипса от окружности характеризуется величиной его эксцентриситета: е = OS/OA. В том случае, когда эксцентриситет равен О, фокусы и центр сливаются в одну точку — эллипс превращается в окружность.

Примечательно, что книга, в которой в1609 г. Кеплер опубликовал первые два открытых им закона, называлась «Новая астрономия, или Физика небес, изложенная в исследованиях движения планеты Марс…».

Оба этих закона, опубликованные в 1609 г., раскрывают характер движения каждой планеты в отдельности, что не удовлетворило Кеплера. Он продолжил поиски «гармонии» в движении всех планет, и спустя 10 лет ему удалось сформулировать третий закон Кеплера.

Квадраты звездных периодов обращения планет относятся между собой, как кубы больших полуосей их орбит.

Формула, выражающая третий закон Кеплера, такова:

где Т₁ и Т₂ — периоды обращения двух планет; а₁ и а₂ — большие полуоси их орбит.

Вот что писал Кеплер после открытия этого закона: «То, что 16 лет тому назад я решил искать, <…> наконец найдено, и это открытие превзошло все мои самые смелые ожидания…»

Действительно, третий закон заслуживает самой высокой оценки. Ведь он позволяет вычислить относительные расстояния планет от Солнца, используя при этом уже известные периоды их обращения вокруг Солнца. Не нужно определять расстояние от Солнца каждой из них, достаточно измерить расстояние от Солнца хотя бы одной планеты. Величина большой полуоси земной орбиты — астрономическая единица (а. е.) — стала основой для вычисления всех остальных расстояний в Солнечной системе.

Пример решения задач

Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты?

3.2.2. Определение расстояний и размеров тел в Солнечной системе.

Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений науки древнего мира.

Считается, что первое достаточно точное определение размеров Земли провел греческий ученый Эратосфен (276— 194 до н. э.), живший в Египте. Идея, положенная в основу измерений Эратосфена, весьма проста: измерить длину дуги земного меридиана в линейных единицах и определить, какую часть полной окружности эта дуга составляет. Получив эти данные, можно вычислить длину дуги в 1°, а затем длину окружности и величину ее радиуса, т. е. радиуса земного шара. Очевидно, что длина дуги меридиана в градусной мере равна разности географических широт двух пунктов: φ_B – φ_A.

Для того чтобы определить эту разность, Эратосфен сравнил полуденную высоту Солнца в них в один и тот же день. Измерив высоту Солнца h_B(рис. 3.8) в полдень 22 июня в Александрии, где он жил, Эратосфен установил, что Солнце отстоит от зенита на 7,2°. В этот день в полдень в городе Сиена (ныне Асуан) Солнце освещает дно самых глубоких колодцев, т. е. находится в зените h_A.

Следовательно, длина дуги составляет 7,2°. Расстояние между Сиеной (А) и Александрией (В) около 5000 греческих стадий — l.

Стадией в Древней Греции считалось расстояние, которое проходит легко вооруженный греческий воин за тот промежуток времени, в течение которого Солнце, коснувшееся горизонта своим нижним краем, целиком скроется за горизонт.

Несмотря на кажущееся неудобство такой единицы и достаточную громоздкость словесного определения, ее введение выглядело вполне оправданным, учитывая, что строгая периодичность небесных явлений позволяла использовать их движение для счета времени.

Обозначив длину окружности земного шара через L, получим такое выражение: 

откуда следует, что длина окружности земного шара равняется 250 000 стадий.

Точная величина стадии в современных единицах неизвестна, но, зная, что расстояние между Александрией и Асуаном составляет 800 км, можно полагать, что 1 стадия = 160 м. Это означает, что результат, полученный Эратосфеном, практически не отличается от современных данных, согласно которым длина окружности Земли составляет 40 000 км.

Эратосфен ввел в практику использование терминов «широта» и «долгота». Видимо, появление этих терминов связано с особенностями формы карт того времени: они повторяли по очертаниям побережье Средиземного моря, которое длиннее по направлению запад-восток (по долготе), чем с севера на юг (по широте).

Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними. Зачастую непосредственное измерение кратчайшего расстояния между этими пунктами оказывается невозможным из-за различных естественных препятствий (гор, рек и т. п.). Поэтому применяется способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из сторон (базиса — ВС) и двух углов В и С в треугольнике ABC(рис. 3.9).

Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.

Чем дальше расположен предмет, тем меньше его параллактическое смещение, и чем больше перемещение наблюдателя (базис измерения), тем больше параллактическое смещение.

Для определения длины дуги используется система треугольников — способ триангуляции, который впервые был применен еще в 1615 г. Пункты в вершинах этих треугольников выбираются по обе стороны дуги на расстоянии 30 — 40 км друг от друга так, чтобы из каждого пункта были видны по крайней мере два других. Основой для вычисления длин сторон во всех этих треугольниках является размер базиса АС (рис. 3.10). Точность измерения базиса длиной в 10 км составляет около 1 мм. Во всех пунктах устанавливают геодезические сигналы — вышки высотой в несколько десятков метров. С вершины сигнала с помощью угломерного инструмента (теодолита) измеряют углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон. Проводя затем измерение углов из пунктов, расстояние между которыми вычислено, можно узнать длину двух очередных сторон в треугольнике. Зная длину сторон этих треугольников, можно определить длину дуги АВ.

В какой степени форма Земли отличается от шара, выяснилось в конце XVIII в. Для уточнения формы Земли Французская академия наук снарядила сразу две экспедиции. Одна из них работала в экваториальных широтах Южной Америки в Перу, другая — вблизи Северного полярного круга на территории Финляндии и Швеции. Измерения показали, что длина одного градуса дуги меридиана на севере больше, чем вблизи экватора. Последующие исследования подтвердили, что длина дуги одного градуса меридиана увеличивается с возрастанием географической широты. Это означало, что форма Земли — не идеальный шар: она сплюснута у полюсов. Ее полярный радиус на 21 км короче экваториального.

Для школьного глобуса масштаба 1:50 000 000 отличие этих радиусов будет всего 0,4 мм, т. е. совершенно незаметно.

Отношение разности величин экваториального и полярного радиусов Земли к величине экваториального называется сжатием. По современным данным оно составляет 1/298 или 0,0034. Это означает, что сечение Земли по меридиану будет не окружностью, а эллипсом, у которого большая ось проходит в плоскости экватора, а малая совпадает с осью вращения.

В XX в. благодаря измерениям, точность которых составила 15 м, выяснилось, что земной экватор также нельзя считать окружностью. Сплюснутость экватора составляет всего 1/30 000 (в 100 раз меньше сплюснутости меридиана). Более точно форму нашей планеты передает фигура, называемая эллипсоидом, у которого любое сечение плоскостью, проходящей через центр Земли, не является окружностью.

В настоящее время форму Земли принято характеризовать следующими величинами:

• экваториальный радиус — 6378,160 км;
• полярный радиус — 6356,777 км;
• сжатие эллипсоида — 1 : 298,25;
• средний радиус — 6371,032 км;
• длина окружности экватора — 40075,696 км.

13.2 Определение расстояний в Солнечной системе.

Горизонтальный параллакс

Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определен горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является ее радиус.

Горизонтальным параллаксом (р) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).

Из треугольника OASможно выразить величину — расстояние OS = D:

,

где R— радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.

Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57′. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца 8,8Ѕ. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 000 000 км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы.

Известно, что для малых углов sin p ≈ p, если угол р выражен в радианах. В одном радиане содержится 206 265Ѕ. Тогда, заменяя sin р на р и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:

или (с достаточной точностью)

Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний — необходимое условие для расчетов траекторий полета космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров.

Пример решения задач.

На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9″?

13.4. Определение размеров светил

Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус ρ (рис. 3.12).

Формула, связывающая эти величины, аналогична формуле для определения параллакса:

Учитывая, что угловые диаметры даже Солнца и Луны составляют примерно 30′, а все планеты видны невооруженному глазу как точки, можно воспользоваться соотношением: sin ρ ≈ ρ. Тогда:

 и .

Следовательно,

.

Если расстояние Dизвестно, то

где величина ρ выражена в радианах.

Пример  решения задач

Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 30′?