Формула тонкой линзы — формула, связывающая три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы.
Условные обозначения:
- расстояние от предмета до линзы — d (м);
- расстояние от изображения до линзы— f (м);
- фокусное расстояние линзы — F (м).
Вывод формулы
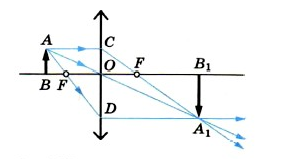
Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:
Видно, что треугольники АОВ и А1В1О подобные (по двум углам). Следовательно:
BOOB1=ABA1B1
По двум углам также являются подобными треугольники COF и FA1B1. Отсюда делаем вывод, что:
COA1B1=OFFB1
Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:
AB=CO
Следовательно:
ABA1B1=COA1B1
Отсюда следует, что:
BOOB1=OFFB1
BO является расстоянием от предмета до линзы. Обозначим его за d. OB1 является расстоянием от линзы до изображения. Обозначим его за f. OF является фокусным расстоянием линзы. Обозначим его за F. FB1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:
df=Ff−F
Избавимся от знаменателей и получим:
fd−Fd=fF
Или можно записать так:
fF+Fd=fd
Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:
Формула тонкой линзы
1d+1f=1F
Поскольку величиной, равной обратной фокусному расстоянию, является оптическая сила, формулу тонкой линзы можно записать следующим образом:
1d+1f=D
Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.
Правила расстановки знаков перед членами уравнения в формуле линзы
- Если линза собирающая, то ее фокус действительный, и перед членом 1F ставят знак «плюс» (1F).
- Если линза рассеивающая, то ее фокус мнимый, и перед членом 1F ставят знак «минус» (−1F).
- Если изображение действительное, то перед величиной 1d ставят знак «плюс» (1d).
- Если изображение мнимое, то перед величиной 1d ставят знак «минус» (−1d).
- Величина 1f всегда имеет знак «плюс», поскольку расстояние от предмета до линзы всегда положительное.
Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.
Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.
Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.
Применим формулу тонкой линзы:
1d+1f=1F
1d+115=110
Умножим выражение на 150d:
150+10d=15d
5d=150
d=30 (см)
Увеличение линзы
Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.
Определение
Линейное увеличение — отношение линейного размера изображения к линейному размеру предмета. Линейное увеличение обозначают буквой Γ.
Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А1В1 равна Н, то:
Γ=Hh
Мы уже выяснили, что треугольники АОВ и ОА1В1 подобны. Поэтому:
Hh=|f||d|
Где H — высота изображения предмета, h — высота самого предмета.
Отсюда вытекает, что увеличение линзы равно:
Γ=|f||d|
Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?
2 см = 0,02 м
Сначала применим формулы тонкой линзы:
1d+1f=1F
Она необходима, чтобы выразить фокусное расстояние линзы:
F=dfd+f
Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:
Γ=fd=Hh
Отсюда это расстояние равно:
d=fhH
Подставим полученное выражение в формулу фокусного расстояния линзы:
F=fhHffhH+f=f2hH·
Hfh+fH=fhH+h
F=fhH+h=4·0,021+0,02≈0,08 (м)=8 (см)
Задание EF17760

Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
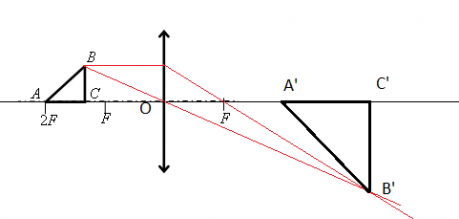
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17685
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Ответ:
а) 0,50 м
б) 0,75 м
в) 1,25 м
г) 1,50 м
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Алгоритм решения
1.Записать известные данные.
2.Записать формулу увеличения линзы и формулу тонкой линзы.
3.Выразить из обеих формул расстояние от линзы до изображения предмета.
4.Приравнять правые части выражений.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем известные данные:
• Фокусное расстояние линзы: F = 1 м.
• Увеличение линзы: Γ = 4.
Запишем формулу увеличения линзы и выразим из нее расстояние от линзы до изображения предмета:
Γ=fd
f=Γd
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Γd=dFd−F
Поделим на d и выразим расстояние от предмета до линзы:
Γ=Fd−F
d=FΓ+F=14+1=1,25 (м)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18124
Предмет высотой 6 см расположен на горизонтальной главной оптической оси тонкой собирающей линзы на расстоянии 30 см от её оптического центра. Высота изображения предмета 12 см. Найдите фокусное расстояние линзы.
Ответ:
а) 5 см
б) 10 см
в) 20 см
г) 36 см
Алгоритм решения
1.Записать известные данные.
2.Записать формулу увеличения линзы в двух вариантах и выразить из нее расстояние от изображения до линзы.
3.Записать формулу тонкой линзы и тоже выразить из нее расстояние от изображения до линзы.
4.Приравнять правые части выражений.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем известные данные:
• Расстояние от оптического центра линзы до предмета: d = 30 cм.
• Высота предмета: h = 6 см.
• Высота изображения: H = 12 см.
Так как все данные измеряются в сантиметрах, переводить единицы измерения величин в СИ нет необходимости. Просто ответ будет получен тоже в сантиметрах.
Запишем формулу увеличения линзы:
Γ=Hh=fd
Отсюда расстояние от изображения до линзы равно:
f=Hdh
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Hdh=dFd−F
Поделим на d, у множим на h(d –F) и выразим фокусное расстояние:
Hh=Fd−F
H(d−F)=hF
Hd−HF=hF
hF+HF=Hd
F(h+H)=Hd
F=Hdh+H=12·3012+6=20 (см)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF19112
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью v = 5 м/с движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе. Ответ запишите в м/с.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
3.Записать формулу тонкой линзы и определить из нее расстояние от изображения до линзы.
4.Записать формулу линейного увеличения линзы двумя способами для вычисления радиусов окружностей, по которым движутся точка и ее изображение.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Фокусное расстояние линзы: F = 10 см.
• Расстояние от линзы до плоскости, в которой вращается точка: d = 15 см.
• Скорость вращения точки: v = 5 м/с.
10 см = 0,1 м
15 см = 0,15 м
Выполним рисунок. Для его построения достаточно найти изображение точки А. Затем в противоположную сторону отложим перпендикуляр и на таком же расстоянии от главной оптической оси будет находиться изображение точки B.
Глядя со стороны, мы будем видеть вместо окружности, которую описывает точка, линию AB. Она равн диаметру окружности, по которой движется точка. Обозначим ее радиус OA за r. Изображением окружности будет окружность. Вместо нее мы со стороны также увидим отрезок — A´B´. Обозначим радиус O´A´ за R.
Запишем формулу тонкой линзы и выразим из нее расстояние от изображения до линзы:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Формулу линейного увеличения линзы можно определить как отношение радиуса окружности, по которой движется точка-изображение, к радиусу окружности, по которой движется сама точка:
Γ=Rr
Линейное увеличение также определяется формулой:
Γ=fd
Следовательно:
Rr=fd
Подставим сюда выражение, найденное для расстояния от изображения до линзы из формулы тонкой линзы:
Rr=dFd(d−F)=Fd−F
Так как изображение будет двигаться вслед за точкой, то угловые скорости этой точки и изображения будут равны. Поэтому:
ω=vr=VR
Отсюда линейная скорость движения изображения равна:
V=Rvr=Fvd−F=0,1·50,15−0,1=10 (мс)
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15k
|
Одним из простейших оптических приборов является тонкая линза (рис. 144), которая широко используется как для исправления дефектов зрения, так и для получения оптических изображений. Какие изображения дает тонкая линза? Как связаны между собой расстояние от предмета до тонкой линзы и расстояние от линзы до изображения? |
Линза называется собирающей, если после преломления в ней параллельный пучок становится сходящимся (рис. 145, а). Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей (рис. 145, б).
Величина, обратная фокусному расстоянию линзы, выраженному в метрах, называется ее оптической силой: .
Единица оптической силы — диоптрия (1 дптр). 1 дптр соответствует оптической силе линзы с фокусным расстоянием ; 1дптр = 1м-1

Линза считается тонкой, если ее толщина в центре намного меньше радиусов ограничивающих ее поверхностей. Тонкая линза дает неискаженное изображение только в том случае, если свет монохроматический и предмет достаточно мал, следовательно, лучи распространяются вблизи главной оптической оси.
Отметим условия, при одновременном выполнении которых линза является собирающей (рис. 147, а):
— толщина в центре больше толщины у краев;
— ее показатель преломления больше показателя преломления окружающей среды.
При невыполнении (или выполнении) только одного из этих условий линза является рассеивающей (рис. 147, б):
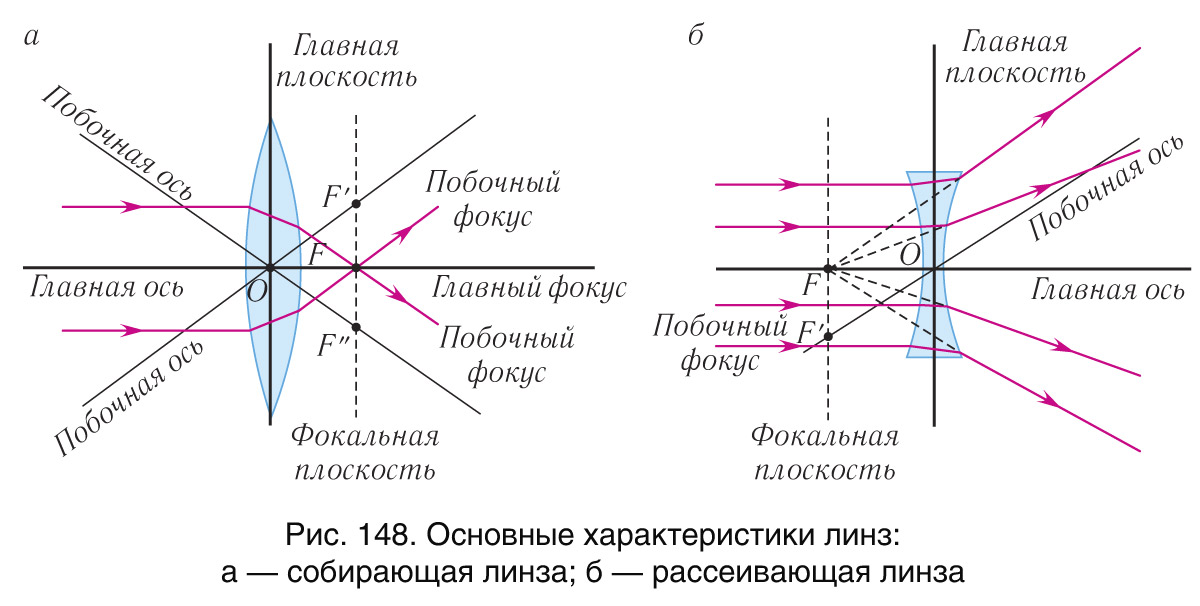
Рассмотрим основные характеристики линзы (рис. 148 а, б).
Прямая линия, на которой лежат центры обеих сферических поверхностей линзы, называется главной оптической осью.
Точка линзы, проходя через которую луч не преломляется, называется оптическим центром.
Прямая линия, проходящая через оптический центр линзы, не совпадающая с главной оптической осью, называется побочной оптической осью. Каждая линза имеет только одну главную оптическую ось и бесконечно много побочных осей.
Плоскость, проходящая через оптический центр тонкой линзы перпендикулярно главной оптической оси, называют главной плоскостью линзы.
Точка, в которую собирается узкий пучок света после преломления в линзе, распространяющийся параллельно главной оптической оси, называется главным фокусом F линзы. Расстояние OF от оптического центра линзы до ее главного фокуса, называется фокусным расстоянием линзы.
Плоскость, проходящая через главный фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость собирающей линзы является геометрическим местом точек, в которых пересекаются параллельные лучи, падающие на линзу под любым углом к главной оптической оси. Поэтому, пучок света, направленный на собирающую линзу параллельно побочной оптической оси, собирается в побочном фокусе.
Построение изображений
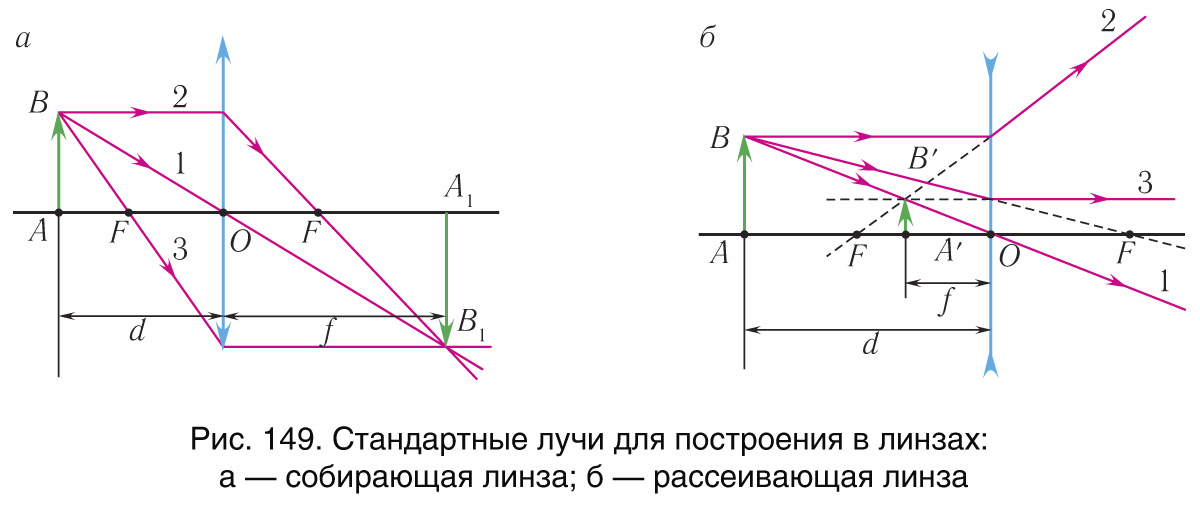
Обычно для построений в линзах используют три характерных (стандартных) луча (рис. 149 а, б):
— луч (1), идущий через оптический центр линзы, не испытывает преломления;
— луч (2), параллельный главной оптической оси, после преломления проходит через главный фокус;
— луч (3), проходящий через главный фокус, после преломления идет параллельно главной оптической оси.
Для построения изображения в линзе достаточно построить ход двух лучей от каждой точки предмета (см. рис. 149). Изображение находится в месте пересечения лучей после преломления на поверхностях линзы (действительное изображение) или в месте пересечения продолжений лучей (мнимое изображение).
Отметим, что если предмет AB расположен перпендикулярно главной оптической оси, то и его изображение будет перпендикулярно этой оси. Поэтому достаточно построить только изображение
точки предмета A, а изображение
точки B находим, опуская перпендикуляр из точки
на главную оптическую ось (см. рис. 149).
Для построения изображения точки, находящейся на главной оптической оси, кроме луча, проходящего через центр линзы, используют луч, падающий на нее параллельно какой либо побочной оптической оси (рис. 150). Этот луч после преломления в линзе пройдет через побочный фокус , лежащий на побочной оси. Такие построения приведены для собирающей и рассеивающей линз на рис. 150. На рисунке 151 приведен пример построения области видения предмета S в тонкой линзе.
Характеристики изображений
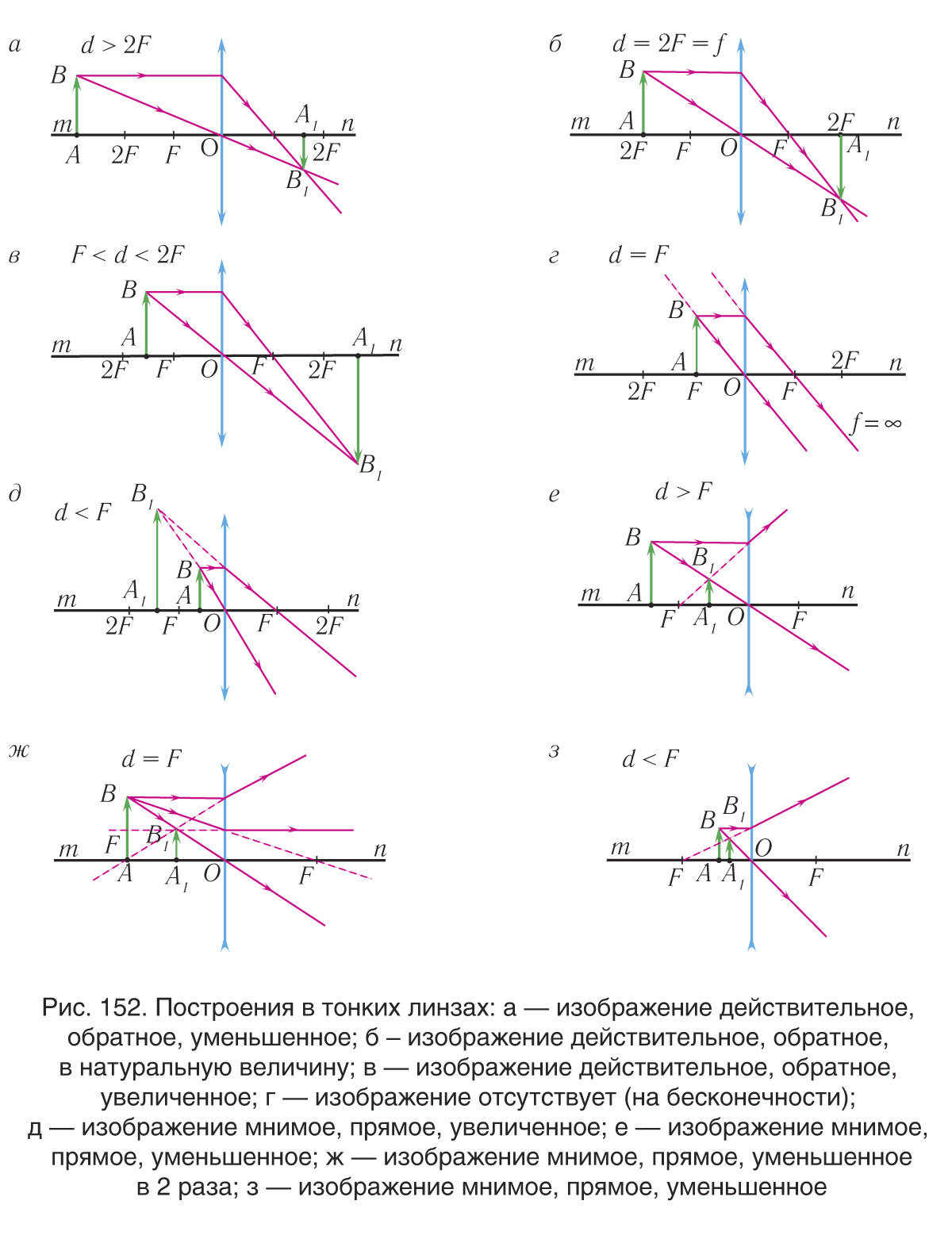
В зависимости от типа линзы и расстояния до нее можно получать изображения: увеличенные и уменьшенные, прямые и обратные (перевернутые), действительные и мнимые (рис. 152).
Между фокусным расстоянием тонкой линзы, расстоянием от предмета до линзы и от линзы до изображения существует определенная количественная зависимость, называемая формулой тонкой линзы.
Выведем формулу тонкой линзы из геометрических соображений, рассматривая ход характерных лучей. Луч, идущий через оптический центр O линзы, луч, параллельный главной оптической оси линзы, и луч, проходящий через главный фокус линзы.
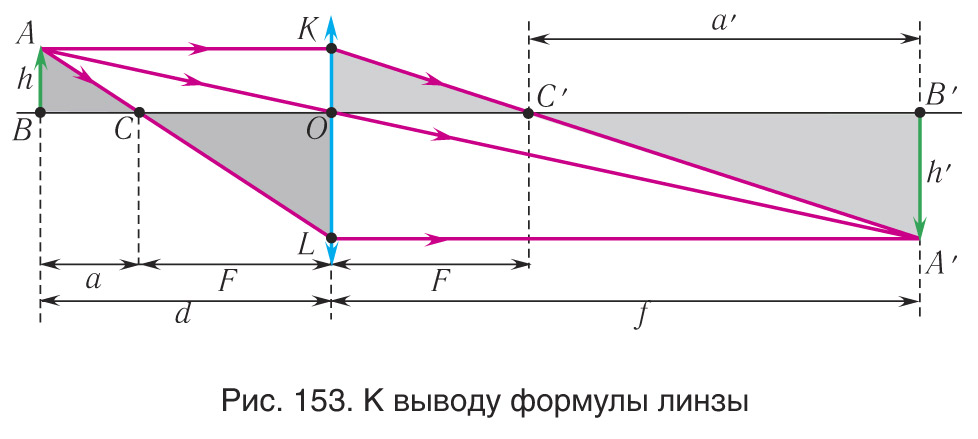
Построим изображение предмета AB в тонкой собирающей линзе (рис. 153). Пусть расстояние от предмета до линзы d, расстояние от линзы до изображения f , фокусное расстояние линзы F , расстояние от предмета до переднего главного фокуса α , расстояние от заднего главного фокуса до изображения α‘ , высота предмета h, высота его изображения h’ .
Из рисунка 153 видно, что ΔABC ~ ΔCLO, ΔA’B’C» ~ ΔKOC» , ΔABO ~ ΔA’B’O. Из подобия треугольников следует
Используя соотношения (1) и (2), получим:
С учетом того, что d = α + F, f = α′ + F (см. рис. 153), находим α = d — F и α′ = f — F и подставляем в формулу (4):
| (d — F)(f — F) = df — Ff — dF+ F2 = F2 |
Откуда получаем df = Ff + dF.
Разделив обе части последнего выражения на dfF, получаем формулу тонкой линзы:
|
|
(5) |
Для практического использования формулы линзы следует твердо запомнить правило знаков:
Для собирающей линзы, действительного источника и действительного изображения величины F, d, f считают положительными. Для рассеивающей линзы, мнимого источника и мнимого изображения — F, d, f считают отрицательными.
Заметим, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей.
Таким образом, линза с F > 0 является собирающей (положительной), а с F < 0 — рассеивающей (отрицательной).
Линейным (поперечным) увеличением Г называется отношение линейного размера изображения h’ к линейному размеру предмета h. Из соотношения (3) находим линейное увеличение тонкой линзы
|
|
(6) |
В современных оптических приборах для улучшения качества изображений используются системы линз. Оптическая сила D системы тонких линз, сложенных вместе, равна сумме их оптических сил Di
| D = D1 + D2 + … + Dn | (7) |
Фокусное расстояние и оптическая сила тонкой линзы
Расстояние между оптическим центром линзыO и главным фокусом F называется фокусным расстоянием. Оно обозначаетcя буквой F.
Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f.
Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = м–1. Формула тонкой линзы аналогична формуле сферического зеркала.
Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0.
Величины d и f также подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений;
d < 0 и f < 0 – для мнимых источников и изображений.
В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения h’ и предмета h. Величине h’, как и в случае сферического зеркала, удобно приписывать знаки плюс или минус в зависимости от того, является изображение прямым или перевернутым. Величина h всегда считается положительной. Поэтому для прямых изображений Γ > 0, для перевернутых Γ < 0. Из подобия треугольников на рисунке ниже легко получить формулу для линейного увеличения тонкой линзы:Γ=h’h=-fd.
В рассмотренном примере с собирающей линзой: d = 3F > 0, f=32F>0;следовательно, Γ=-12<0 – изображение перевернутое и уменьшенное в 2 раза.
В примере с рассеивающей линзой: d = 2|F| > 0, f=-23|F|<0; следовательно, Γ=13>0 – изображение прямое и уменьшенное в 3 раза.
Оптическая сила D линзы зависит как от радиусов кривизны R1 и R2 ее сферических поверхностей, так и от показателя преломления n материала, из которого изготовлена линза. В курсах оптики доказывается следующая формула: (D = frac{1}{F} = left( {n — 1} right)left( {frac{1}{{{R_1}}} + frac{1}{{{R_2}}}} right)).
Радиус кривизны выпуклой поверхности считается положительным, вогнутой – отрицательным. Эта формула используется при изготовлении линз с заданной оптической силой.
Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета. Это второе изображение также может быть действительным или мнимым. Расчет оптической системы из двух тонких линз сводится к двукратному применению формулы линзы, при этом расстояние d2 от первого изображения до второй линзы следует положить равным величине l – f1, где l – расстояние между линзами. Рассчитанная по формуле линзы величина f2 определяет положение второго изображения и его характер (f2 > 0 – действительное изображение, f2 < 0 – мнимое). Общее линейное увеличение Γ системы из двух линз равно произведению линейных увеличений обеих линз: Γ = Γ1 ċ Γ2. Если предмет или его изображение находятся в бесконечности, то линейное увеличение утрачивает смысл.
Частным случаем является телескопический ход лучей в системе из двух линз, когда и предмет, и второе изображение находятся на бесконечно больших расстояниях. Телескопический ход лучей реализуется в зрительных трубах – астрономической трубе Кеплера и земной трубе Галилея.
Тонкие линзы обладают рядом недостатков, не позволяющих получать высококачественные изображения. Искажения, возникающие при формировании изображения, называются аберрациями. Главные из них – сферическая и хроматическая аберрации. Сферическая аберрация проявляется в том, что в случае широких световых пучков лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула тонкой линзы справедлива только для лучей, близких к оптической оси. Изображение удаленного точечного источника, создаваемое широким пучком лучей, преломленных линзой, оказывается размытым.
Хроматическая аберрация возникает вследствие того, что показатель преломления материала линзы зависит от длины волны света λ. Это свойство прозрачных сред называется дисперсией. Фокусное расстояние линзы оказывается различным для света с разными длинами волн, что приводит к размытию изображения при использовании немонохроматического света.
В современных оптических приборах применяются не тонкие линзы, а сложные многолинзовые системы, в которых удается приближенно устранить различные аберрации.
Формирование собирающей линзой действительного изображения предмета используется во многих оптических приборах, таких как фотоаппарат, проектор и т. д.
Тонкие линзы. Построение изображений.
-
Собирающая линза: действительное изображение точки.
-
Собирающая линза: действительное изображение предмета.
-
Собирающая линза: мнимое изображение точки.
-
Собирающая линза: мнимое изображение предмета.
-
Собирающая линза: предмет в фокальной плоскости.
-
Рассеивающая линза: мнимое изображение точки.
-
Рассеивающая линза: мнимое изображение предмета.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: построение изображений в линзах, формула тонкой линзы.
Правила хода лучей в тонких линзах, сформулированные в предыдущей теме, приводят нас к важнейшему утверждению.
Теорема об изображении. Если перед линзой находится светящаяся точка , то после преломления в линзе все лучи (или их продолжения) пересекаются в одной точке
.
| Напомним ещё раз, что это касается не вообще всех лучей, а только параксиальных, то есть образующих малые углы с главной оптической осью. В предыдущей теме мы договорились, что рассматриваем только параксиальные лучи. Лишь для них работают наши правила хода лучей сквозь тонкие линзы. |
Точка называется изображением точки
.
Если в точке пересекаются сами преломлённые лучи, то изображение называется действительным. Оно может быть получено на экране, так как в точке
концентрируется энергия световых лучей.
Если же в точке пересекаются не сами преломлённые лучи, а их продолжения (так бывает, когда преломлённые лучи расходятся после линзы), то изображение называется мнимым. Его нельзя получить на экране, поскольку в точке
не сосредоточено никакой энергии. Мнимое изображение, напомним, возникает благодаря особенности нашего мозга — достраивать расходящиеся лучи до их мнимого пересечения и видеть в этом пересечении светящуюся точку.Мнимое изображение существует лишь в нашем сознании.
Теорема об изображении служит основой построения изображений в тонких линзах. Мы докажем эту теорему как для собирающей, так и для рассеивающей линзы.
к оглавлению ▴
Собирающая линза: действительное изображение точки.
Сперва рассмотрим собирающую линзу. Пусть — расстояние от точки
до линзы,
— фокусное расстояние линзы. Имеются два принципиально разных случая:
и
(а также промежуточный случай
). Мы разберём эти случаи поочерёдно; в каждом из них мы
обсудим свойства изображений точечного источника и протяжённого объекта.
Первый случай: . Точечный источник света
расположен дальше от линзы, чем левая фокальная плоскость (рис. 1).
 |
| Рис. 1. Случай a>f: действительное изображение точки S |
Луч , идущий через оптический центр, не преломляется. Мы возьмём произвольный луч
, построим точку
, в которой преломлённый луч пересекается с лучом
, а затем покажем, что положение точки
не зависит от выбора луча
(иными словами, точка
является одной и той же для всевозможных лучей
). Тем самым окажется, что все лучи, исходящие из точки
, после преломления в линзе пересекаются в точке
и теорема об изображении будет доказана для рассматриваемого случая
.
Точку мы найдём, построив дальнейший ход луча
. Делать это мы умеем: параллельно лучу
проводим побочную оптическую ось
до пересечения с фокальной плоскостью в побочном фокусе
, после чего проводим преломлённый луч
до пересечения с лучом
в точке
.
Теперь будем искать расстояние от точки
до линзы. Мы покажем, что это расстояние выражается только через
и
, т. е. определяется лишь положением источника и свойствами линзы, и не зависит тем самым от конкретного луча
.
Опустим перпендикуляры и
на главную оптическую ось. Проведём также
параллельно главной оптической оси, т. е. перпендикулярно линзе. Получим три пары подобных треугольников:
, (1)
, (2)
. (3)
В результате имеем следующую цепочку равенств (номер формулы над знаком равенства указывает, из какой пары подобных треугольников данное равенство получено).
(4)
Но , так что соотношение (4) переписывается в виде:
. (5)
Отсюда находим искомое расстояние от точки до линзы:
. (6)
Как видим, оно и в самом деле не зависит от выбора луча . Следовательно, любой луч
после преломления в линзе пройдёт через построенную нами точку
, и эта точка будет действительным изображением источника
Теорема об изображении в данном случае доказана.
Практическая важность теоремы об изображении состоит вот в чём. Коль скоро все лучи источника пересекаются после линзы в одной точке — его изображении
— то для построения изображения достаточно взять два наиболее удобных луча. Какие именно?
Если источник не лежит на главной оптической оси, то в качестве удобных лучей годятся следующие:
— луч, идущий через оптический центр линзы — он не преломляется;
— луч, параллельный главной оптической оси — после преломления он идёт через фокус.
Построение изображения с помощью этих лучей показано на рис. 2.
 |
| Рис. 2. Построение изображения точки S, не лежащей на главной оптической оси |
Если же точка лежит на главной оптической оси, то удобный луч остаётся лишь один — идущий вдоль главной оптической оси. В качестве второго луча приходится брать «неудобный» (рис. 3).
 |
| Рис. 3. Построение изображения точки S, лежащей на главной оптической оси |
Посмотрим ещё раз на выражение ( 5). Его можно записать в несколько ином виде, более симпатичном и запоминающемся. Перенесём сначала единицу влево:
Теперь разделим обе части этого равенства на a:
(7)
Соотношение (7) называется формулой тонкой линзы (или просто формулой линзы). Пока что формула линзы получена для случая собирающей линзы и для . В дальнейшем мы выведем модификации этой формулы для остальных случаев.
Теперь вернёмся к соотношению (6). Его важность не исчерпывается тем, что оно доказывает теорему об изображении. Мы видим также, что не зависит от расстояния
(рис. 1, 2) между источником
и главной оптической осью!
Это означает, что какую бы точку отрезка
мы ни взяли, её изображение будет находиться на одном и том же расстоянии
от линзы. Оно будет лежать на отрезке
— а именно, на пересечении отрезка
с лучом
, который пойдёт сквозь линзу без преломления. В частности, изображением точки
будет точка
.
Тем самым мы установили важный факт: изображением отрезка лужит отрезок
. Отныне исходный отрезок, изображение которого нас интересует, мы называем предметом и обозначаем на рисунках красной стрелочкой. Направление стрелки нам понадобится для того, чтобы следить — прямым или перевёрнутым получается изображение.
к оглавлению ▴
Перейдём к рассмотрению изображений предметов. Напомним, что пока мы находимся в рамках случая . Здесь можно выделить три характерных ситуации.
1. . Изображение предмета является действительным, перевёрнутым, увеличенным (рис. 4; двойной фокус обозначен
). Из формулы линзы следует, что в этом случае будет
(почему?).
Такая ситуация реализуется, например, в диапроекторах и киноаппаратах — эти оптические приборы дают на экране увеличенное изображение того, что находится на плёнке. Если вам доводилось показывать слайды, то вы знаете, что слайд нужно вставлять в проектор перевёрнутым — чтобы изображение на экране выглядело правильно, а не получилось вверх ногами.
Отношение размера изображения к размеру предмета называется линейным увеличением линзы и обозначается Г — (это заглавная греческая «гамма»):
.
Из подобия треугольников и
получим:
. (8)
Формула (8) применяется во многих задачах, где фигурирует линейное увеличение линзы.
2. . В этом случае из формулы (6) находим, что и
. Линейное увеличение линзы согласно (8) равно единице, т. е. размер изображения равен размеру предмета (рис. 5).
 |
| Рис. 5.a=2f: размер изображения равен размеру предмета |
3. . В этом случае из формулы линзы следует, что
(почему?). Линейное увеличение линзы будет меньше единицы — изображение действительное, перевёрнутое, уменьшенное (рис. 6).
 |
| Рис. 6.a>2f: изображение действительное, перевёрнутое, уменьшенное |
Данная ситуация является обычной для многих оптических приборов: фотоаппаратов, биноклей, телескопов — словом, тех, в которых получают изображения удалённых объектов. По мере удаления предмета от линзы его изображение уменьшается в размерах и приближается к фокальной плоскости.
Рассмотрение первого случая нами полностью закончено. Переходим ко второму случаю. Он уже не будет столь объёмным.
к оглавлению ▴
Собирающая линза: мнимое изображение точки.
Второй случай: . Точечный источник света
расположен между линзой и фокальной плоскостью (рис. 7).
 |
| Рис. 7. Случай a < f: мнимое изображение точки |
Наряду с лучом , идущим без преломления, мы снова рассматриваем произвольный луч
. Однако теперь на выходе из линзы получаются два расходящихся луча
и
. Наш глаз продолжит эти лучи до пересечения в точке
.
Теорема об изображении утверждает, что точка будет одной и той же для всех лучей
, исходящих из точки
. Мы опять докажем это с помощью трёх пар подобных треугольников:
Снова обозначая через расстояние от
до линзы, имеем соответствующую цепочку равенств (вы уже без труда в ней разберётесь):
. (9)
Отсюда
. (10)
Величина не зависит от луча
, что и доказывает теорему об изображении для нашего случая
. Итак,
— мнимое изображение источника
. Если точка
не лежит на главной оптической оси, то для построения изображения
удобнее всего брать луч, идущий через оптический центр, и луч, параллельный главной оптической оси (рис. 8).
 |
| Рис. 8. Построение изображения точки S, не лежащей на главной оптической оси |
Ну а если точка лежит на главной оптической оси, то деваться некуда — придётся довольствоваться лучом, падающим на линзу наклонно (рис. 9).
 |
| Рис. 9. Построение изображения точки S, лежащей на главной оптической оси |
Соотношение (9) приводит нас к варианту формулы линзы для рассматриваемого случая . Сначала переписываем это соотношение в виде:
,
а затем делим обе части полученного равенства на a:
. (11)
Сравнивая (7) и (11), мы видим небольшую разницу: перед слагаемым стоит знак плюс, если изображение действительное, и знак минус, если изображение мнимое.
Величина , вычисляемая по формуле (10), не зависит также от расстояния
между точкой
и главной оптической осью. Как и выше (вспомните рассуждение с точкой
), это означает, что изображением отрезка
на рис. 9 будет отрезок
.
к оглавлению ▴
Учитывая это, мы легко строим изображение предмета, находящегося между линзой и фокальной плоскостью (рис. 10). Оно получается мнимым, прямым и увеличенным.
Такое изображение вы наблюдаете, когда разглядываете мелкий предмет в увеличительное стекло — лупу. Случай полностью разобран. Как видите, он качественно отличается от нашего первого случая
. Это не удивительно — ведь между ними лежит промежуточный «катастрофический» случай
.
к оглавлению ▴
Собирающая линза: предмет в фокальной плоскости.
Промежуточный случай:. Источник света
расположен в фокальной плоскости линзы (рис. 11).
Как мы помним из предыдущего раздела, лучи параллельного пучка после преломления в собирающей линзе пересекутся в фокальной плоскости — а именно, в главном фокусе, если пучок падает перпендикулярно линзе, и в побочном фокусе при наклонном падении пучка. Воспользовавшись обратимостью хода лучей, мы заключаем, что все лучи источника , расположенного в фокальной плоскости, после выхода из линзы пойдут параллельно друг другу.
 |
| Рис. 11. a=f: изображение отсутствует |
Где же изображение точки ? Изображения нет. Впрочем, никто не запрещает нам считать, что параллельные лучи пересекаются в бесконечно удалённой точке. Тогда теорема об изображении сохраняет свою силу и в данном случае — изображение
находится на бесконечности.
Соответственно, если предмет целиком расположен в фокальной плоскости, изображение этого предмета будет находиться на бесконечности (или, что то же самое, будет отсутствовать).
Итак, мы полностью рассмотрели построение изображений в собирающей линзе.
к оглавлению ▴
Рассеивающая линза: мнимое изображение точки.
К счастью, здесь нет такого разнообразия ситуаций, как для собирающей линзы. Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.
Снова берём луч и произвольный луч
(рис. 12). На выходе из линзы имеем два расходящихся луча
и
, которые наш глаз достраивает до пересечения в точке
.
 |
| Рис. 12. Мнимое изображение точки S в рассеивающей линзе |
Нам снова предстоит доказать теорему об изображении — о том, что точка будет одной и той же для всех лучей
. Действуем с помощью всё тех же трёх пар подобных треугольников:
.
Имеем:
(12)
Отсюда
. (13)
Величина b не зависит от луча span
, поэтому продолжения всех преломлённых лучей span
пересекутся в точке
— мнимом изображении точки
. Теорема об изображении тем самым полностью доказана.
Вспомним, что для собирающей линзы мы получили аналогичные формулы (6) и (10). В случае их знаменатель обращался в нуль (изображение уходило на бесконечность), и поэтому данный случай разграничивал принципиально разные ситуации
и
.
А вот у формулы (13) знаменатель не обращается в нуль ни при каком a. Стало быть, для рассеивающей линзы не существует качественно разных ситуаций расположения источника — случай тут, как мы и сказали выше, имеется только один.
Если точка не лежит на главной оптической оси, то для построения её изображения удобны два луча: один идёт через оптический центр, другой — параллельно главной оптической оси (рис. 13).
 |
| Рис. 13. Построение изображения точки S, не лежащей на главной оптической оси |
Если же точка лежит на главной оптической оси, то второй луч приходится брать произвольным (рис. 14).
 |
| Рис. 14. Построение изображения точки S, лежащей на главной оптической оси |
Соотношение (13) даёт нам ещё один вариант формулы линзы. Сначала перепишем:
,
а потом разделим обе части полученного равенства на a:
(14)
Так выглядит формула линзы для рассеивающей линзы.
Три формулы линзы (7), (11) и (14) можно записать единообразно:
если соблюдать следующую договорённость о знаках:
— для мнимого изображения величина считается отрицательной;
— для рассеивающей линзы величина считается отрицательной.
Это очень удобно и охватывает все рассмотренные случаи.
к оглавлению ▴
Величина , вычисляемая по формуле (13), опять-таки не зависит от расстояния
между точкой
и главной оптической осью. Это снова даёт нам возможность построить изображение предмета
, которое на сей раз получается мнимым, прямым и уменьшенным (рис. 15).
 |
| Рис. 15. Изображение мнимое, прямое, уменьшенное |
Разберем задачи ЕГЭ по теме: Тонкие линзы. Построение изображений.
1. Тонкая собирающая линза с фокусным расстоянием F находится между двумя точечными источниками света на расстоянии d=15 см от одного из них. Источники расположены на главной оптической оси на расстоянии L=22,5 см друг от друга. Найдите фокусное расстояние линзы, если их изображения получились в одной точке. Ответ выразите в сантиметрах.
Дано:
= 15 см = 0,15 м
= 22,5 см=0,225 м
Найти:
Фокусное расстояние F — ?
Решение:
Тонкая собирающая линза дает различные виды изображений: увеличенные (уменьшенные), прямые (обратные), действительные (мнимые). Характеристика изображения зависит от расстояния от предмета до линзы, т.е. от соотношения d и F.
Так как в задаче говорится о получении изображений в одной точке, то один из точечных источников должен находиться за фокусом линзы – он дает действительное изображение. Второй точечный источник должен находиться перед фокусом – он дает мнимое изображение.
На рис. 1 представлено получение изображения для точечного источника света , находящегося на расстоянии больше фокусного,
— изображение точечного источника света
.
На рис. 2 представлено получение изображения для точечного источника света , находящегося на расстоянии меньше фокусного,
— изображение точечного источника света
.
После создания модели, поясняющей условие этой задачи, можно переходить к её решению. Для этого надо применить формулу тонкой линзы для двух случаев. С учетом правила знаков , так как изображение в первом случае действительное, во втором – мнимое.
Сложим эти два уравнения и учтем, что Так как изображения в двух случаях получались в одной точке, то
Определим, что (м).
(м)
(см).
Ответ: 10
2. Какая из точек (1, 2, 3 или 4) является изображением точки S, созданным тонкой собирающей линзой с фокусным расстоянием F (см. рисунок)?
Решение:
Для получения изображения точечного источника S необходимо осуществить построение двух любых лучей, исходящих от этого источника. Самым «удобным» лучом является луч, проходящий через оптический центр линзы. Такие лучи, после прохождения через линзу, не меняют своего направления. На рисунке таким лучом является луч 1-1ʹ.
Второй и третий лучи от точечного источника S попадают на линзу произвольно. Дальнейший ход таких лучей определяется следующим алгоритмом:
- необходимо построить побочные оптические оси, параллельные падающим лучам (на рисунке они проведены пунктирной линией);
- провести фокальную плоскость и найти точки пересечения этой плоскости с побочными оптическими осями;
- продолжить ход световых лучей после прохождения через линзу (на рисунке это лучи 2ʹ и 3ʹ).
Поэтому изображением точечного источника S (точки S) будет являться точка 2.
При решении этой задачи мы рассмотрели ход трех лучей сквозь линзу, для получения ответа достаточно взять любую комбинацию лучей (1-1ʹ и 2 — 2ʹ) или (1-1ʹ и 3 — 3ʹ ).
Ответ: 2
3. Спираль лампочки расположена вблизи главной оптической оси тонкой рассеивающей линзы на расстоянии а от неё перпендикулярно этой оси, причем , где F – модуль фокусного расстояния линзы. Затем рассеивающую линзу заменили на собирающую с фокусным расстоянием F. Установите соответствие между видом линзы, использованной в опыте, и свойствами даваемого ею изображения.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| Виды линз | Свойства изображения |
| А) линза рассеивающая | 1) мнимое, прямое, уменьшенное |
| Б) линза собирающая | 2) мнимое, перевёрнутое, увеличенное |
| 3) действительное, перевёрнутое, увеличенное | |
| 4) действительное, прямое, увеличенное |
Решение
Решение подобных задач опирается на умение строить изображения протяженных (имеющих размеры) предметов при прохождении лучей через линзу.
Рис.1
На рис.1 выполнено построение изображения предмета АВ в тонкой собирающей линзе. Для этого применялись следующие лучи:
1-1ʹ — луч, проходящий через оптический центр, не преломляется;
2 — 2ʹ — луч, падающий на линзу параллельно главной оптической оси, после преломления идет через фокус, расположенный за линзой .
Полученное изображение АʹВʹ имеет следующие характеристики:
увеличенное (размер изображения превышает размер предмета),
перевернутое (направления стрелок АВ и АʹВʹ противоположны),
действительное (предмет и его изображения находятся по разные стороны от линзы).
Рис.2
На рис.2 выполнено построение изображения предмета АВ в тонкой рассеивающей линзе. Для этого применялись следующие лучи:
1-1ʹ — луч, проходящий через оптический центр, не преломляется;
2 — 2ʹ — луч, падающий на линзу параллельно главной оптической оси, после преломления идет через фокус, расположенный перед линзой .
Полученное изображение АʹВʹ имеет следующие характеристики:
уменьшенное (размер изображения меньше размера предмета),
прямое (направления стрелок АВ и АʹВʹ совпадают),
мнимое (предмет и его изображения находятся с одной стороны от линзы).
Полученные изображения и их характеристики приводят к следующему ответу:
4. На рисунке показан ход лучей от точечного источника света S через тонкую линзу. Какова оптическая сила этой линзы? (Ответ дать в диоптриях.)
Решение:
На рисунке представлен ход световых лучей от точечного источника света S. Луч, проходящий через оптический центр, не меняет своего направления. Второй луч, идущий параллельно главной оптической оси, после преломления идет через фокус. Это позволяет определить фокусное расстояние линзы. Согласно рисунку, оно равно двум клеткам. С учётом указанного масштаба, длина одной клетки равна 4 см. Таким образом, фокусное расстояние этой линзы F=8 см = 0,08 м.
Так как оптическая сила линзы (дптр).
Ответ: 12,5
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Тонкие линзы. Построение изображений.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Фокусное расстояние
У центрированных оптических приборов (объективы, лупы, окуляры, очковые линзы и т.п.) есть пара замечательных точек: переднего и заднего фокусов. Эти точки на оптических схемах обозначают F и F’ соответственно. Параллельный пучок света пришедший вдоль оптической оси объектива собирается в точке заднего фокуса F’. Светящаяся точка расположенная в переднем фокусе F даст на выходе из объектива параллельный пучок света распространяющийся вдоль оптической оси. Обе эти точки лежат на оптической оси — оси симметрии центрированного оптического прибора.
Есть и еще одна пара замечательных точек на оптической оси объектива — так называемые главные точки: H — передняя и H’ — задняя. Расстояние от H до F — называют передним фокусным расстоянием f, а от H’ до F’ — задним фокусным расстоянием f’. Заметим, что для обычного объектива работающего в воздухе f’ — величина положительная, а f = -f’. Если известно положение этих точек, то возможно в приближении так называемых «нулевых лучей» построить изображение любой точки в пространстве предметов (грубо говоря, слева от оптической схемы). см. рисунок.
- cardinals.JPG (16.65 КБ) 18110 просмотров
Фокусные расстояния f’ и f (обычно выражаются в мм) — самые важные масштабные характеристики объективов. f’ определяет масштаб изображения, которое строится объективом:
y’ = f’·φ = f’·φo/57.3 = f’·φ’/(60·57.3) = f’·φ»/(60·60·57.3), (1)
где y’ — линейный размер изображения предмета небольшого углового размера φр (в радианах), или φо (в градусах), или φ’ (в угловых минутах*), или φ» (в угловых секундах).
или в обратном угловой размер предмета φ (радианы, градусы, минуты, секунды) который на приемнике имеет линейный размер y в мм:
φ (рад) = y/f’, (1.a)
φ°= 57.3*y/f’, (1.b)
φ’ = 57.3*60*y/f’ или примерно 3500*dy/f (1.c)
φ»= 57.3*60*60*y/f’ или примерно 200000*dy/f[/b] (1.d)
Например, размер диска Луны (φ = 30 угловых минут) в фокальной плоскости объектива с фокусным расстоянием f’ = 400 мм будет равен y’ = f’·φ/(60’·57.3o) = 400·30’/3438 = 3.5 мм. На кадр со сторонами 35х24 мм в фокусе астрографа с фокусным f’ = 150 мм поместится по этим формулам φ° = 57.3·y’/f’ поле зрения 13 на 9 градусов (57.3·35/150 и 57.3·24/150). Фокусное расстояние однозначно (с точностью до дисторсии) определяет доступное поле зрения объектива 2W = 2·arctg(Y’/f’), где 2W — угловое поле зрения, Y’ — половинка диагонали кадра или радиус полевой диафрагмы.
Фокусные расстояния линз (объективов) также позволяет рассчитывать ход лучей в оптических системах в так называемом нулевом приближении (см. «Полезные оптические соотношения» — формулы отрезков, Ньютона и прохождения луча через тонкую линзу).
*) В расчетной оптике величины относящиеся к пространству изображений (например заднее фокусное расстояние, задний фокус, размер изображения и т.д.) снабжают апострофом: f’, F’, y’ для того, чтобы отличать от точек и величин относящихся к пространству предметов: f, F, y.
- cardinalies.JPG (42.78 КБ) 18099 просмотров
Связь фокусного расстояния с доступным полем зрения телескопа
Для телескопа фокусное расстояние его объектива главным образом определяет величину доступного поля зрения. У более короткофокусных телескопов (обычно это рефракторы и телескопы по схеме Ньютона) доступное поле зрения шире. Более длиннофокусные телескопы (обычно это разнообразные Кассегрены) имеют более ограниченное входное поле зрения. Связь доступного поля зрения телескопа 2w (в градусах) с фокусным расстоянием его объектива f’ проста: 2w = 57.3*D/f’, где D — диаметр максимально возможной полевой диафрагмы окуляра. D ограничено диаметром окулярной трубки телескопа, в телескопах оборудованных 2″ фокусером это 46 мм, а в телескопах оборудованных 1.25″ фокусером 27 мм. На основе этой формулы получается такая вот табличка:
Доступные поля зрения в телескопах
с разными фокусными расстояниями
| fD | 2″/46 мм | 1.25″/27 мм |
| 250 мм | 10.5° | 6.2° |
| 500 мм | 5.3° | 3.1° |
| 750 мм | 3.5° | 2.1° |
| 1000 мм | 2.6° | 1.5° |
| 1250 мм | 2.1° | 1.2° |
| 1500 мм | 1.8° | 62′ |
| 1750 мм | 1.5° | 53′ |
| 2000 мм | 1.3° | 46′ |
| 2250 мм | 1.2° | 41′ |
Апертура
Апертура A и A’ другая базовая характеристика оптических приборов — она связана со способностью оптики ограничивать световые пучки, которые проходят через нее от предмета к изображению. Различают входную апертуру A (ограничение размеров световых пучков от предмета попадающих в оптических прибор) и выходную апертуру A’ (ограничение размеров световых пучков, которые строят изображение). И та и другая апертура связаны между собой и определяются явно или неявно заданной апертурной диафрагмой — механическим узлом оптического устройства выполненным в виде отверстия постоянного или переменного размера в непрозрачном материале, который максимально ограничивает осевой пучок света (который строит изображение на оптической оси). Роль апертурной диафрагмы может играть оправа линзы (не всегда первой), края зеркал и т.д. Иногда оптический узел «заимствует» апертурную диафрагму у другого, с которым он работает совместно (например, окуляр обычно не имеет своей апертурной диафрагмы). Входная (передняя) и выходная (задняя) апертура измеряются по-разному, в зависимости от того с каким предметом/изображением работает оптическое устройство. Входная апертура телескопа (удаленный предмет) это обычно диаметр осевого пучка D, а у микроскопа (близкий предмет) так называемая числовая апертура — синус угла, под которым выходит крайний луч из осевой точки предмета умноженный на показатель преломления среды. Чем апертура больше, тем меньше влияние дифракции и больше способность прибора собирать свет и строить более яркие изображения. Но чем больше апертура тем обычно больше влияние остаточных аберраций ухудшающих качество изображения, и тем более сложную конструкцию объектива приходится разрабатывать для контроля этих аберраций.
Зависимость проницания (M) и
разрешения (ф») от апертуры
телескопа (D в дюймах и мм)
| D,» | D,мм | M, зв.вел. | ф» |
| 3.1 | 80 | 12.0 | 1.50 |
| 3.9 | 100 | 12.5 | 1.20 |
| 5 | 127 | 13.0 | 0.94 |
| 6 | 152 | 13.4 | 0.79 |
| 7 | 180 | 13.8 | 0.67 |
| 8 | 203 | 14.0 | 0.59 |
| 10 | 254 | 14.5 | 0.47 |
| 12 | 305 | 14.9 | 0.39 |
| 14 | 356 | 15.3 | 0.34 |
| 16 | 407 | 15.5 | 0.29 |
| 18 | 457 | 15.8 | 0.26 |
| 20 | 508 | 16.0 | 0.24 |
В телескопе входная и выходная апертуры связаны между собой простым соотношением:
A = Г·A’, (2)
где A, мм — входная апертура (диаметр входного зрачка),
A’, мм — выходная апертура (диаметр выходного зрачка),
Г — увеличение
В объективе (фотообъективе, объективе телескопа) соотношение меняется:
A’ = 0.5·A/f’об, (3)
где A, мм — входная апертура объектива (ее диаметр),
A’, мм — выходная апертура (синус апертурного угла),
f’об — заднее фокусное расстояние объектива
Зрачки
Зрачок характеристика тесно связанная с апертурой. Выходной зрачок — это изображение апертурной диафрагмы последующей частью оптического прибора. А входной зрачок — изображение апертурной диафрагмы через предыдущую часть оптической системы в пространство предметов. Входная апертура у телескопа или объектива это диаметр входного зрачка D, выходная апертура телескопа или окуляра — диаметр его выходного зрачка D’. Так называемые главные лучи (средние лучи световых пучков) проходят через центр входного и выходного зрачка. При совместном использовании оптики, в которой есть свои апертурные диафрагмы следует добиваться совмещения соответствующих входных и выходных зрачков и согласовывать из размеры для предотвращения срезания внеосевых пучков. Простейший пример — визуальные наблюдения в телескоп, когда входной зрачок глаза наблюдателя (или просто — зрачок) следует совместить с выходным зрачком телескопа (окуляра).
Соотношения диаметров входного и выходного зрачков телескопа — см. формулу (2).
Разрешение
Разрешение — то минимальное расстояние между светящимися точками (линиями) в пространстве предметов или изображения, которое способен разрешить оптический прибор — построить изображение однозначно трактуемое как двойное. В зависимости от типа оптики это расстояние следует измерять в угловой (для «удаленных» предметов) или линейной (для «близких») мере. Для телескопа в пространстве предметов это минимальное угловое расстояние между равными по яркости компонентами двойной звезды, при котором между их изображениями еще виден темный промежуток. Обычно полагают, что звезды разрешены, если расстояние между максимумами в дифракционной картине изображения равно или больше радиусу первого темного кольца, при этом относительный провал яркости между максимумами составит 26% (критерий Рэлея). Визуальное разрешение при наблюдении в телескоп ограничено многими другими факторами кроме дифракции: недостаточным увеличением, дефектами зрения наблюдателя, аберрациями и ошибками изготовления объектива и окуляра, светорассеиванием, неоднородностями показателя преломления воздуха внутри и вне телескопа, недостаточно или избыточной яркостью объекта наблюдения, величиной центрального экранирования и т.д. Но только дифракция представляет собой по настоящему непреодолимое препятствие для разрешения, а все остальные факторы можно более или менее эффективно преодолеть. В таком идеализированном случае предел разрешения будет равен
ф» = 140″/D, (4)
где ф» — разрешение в угловых секундах, D — диаметр входной апертуры (зрачка) телескопа.
Есть и другие формулы в которых вместо 140″ используют коэффициент 120″ (5% провал яркости между максимумами), 114″ (плоская «полочка») и другие. Обычно эту величину и приводят производители телескопов, хотя, возможно, и не совсем правомерно (без учета остаточных аберраций и допусков на ошибки изготовления).
В линейной мере объектив имеет предел разрешения
д = 0.55*f’/D (мкм), (5)
где f’ — фокусное расстояние, а D — диаметр объектива.
То есть из-за дифракции на приемнике невозможно разрешить детали отстоящие друг от друга на расстояние меньшее, чем д, если середина спектрального диапазона инструмента приходится на волну с длиной λo = 0.55 мкм. В общем случае д = λo*f/D
Относительное отверстие и фокусное расстояние
Относительное отверстие, которое представляют обычно в виде дроби 1:k — это для объективов отношение диаметра входной апертуры (зрачка) к заднему фокусному расстоянию: 1/k = D/f’, где k еще называют диафрагменным числом (диафрагмой) или относительным фокусным расстоянием k = f’/D. Чем относительное отверстие объектива больше, тем более яркие изображения он строит (поэтому светосила объектива пропорциональна квадрату его относительного отверстия) и тем меньшие по линейному размеру детали он может построить в плоскости изображения. Но и тем труднее совладать в нем с остаточными аберрациями. Заметим, что предел разрешения на фотоприемнике у идеального фотообъектива пропорционален его относительному фокусному расстоянию:
д = λ·k, (6)
где λ, мкм — длина волны середины спектрального диапазона (для визуальных и бытовых фотографических приборов принимают λ = 0.546 мкм), k — относительное фокусное расстояние (с учетом всех использованных экстендеров/редьюсеров и проч.).
Поле зрения/изображения
Поле — максимальный по размеру предмет или его изображение, которые пропускает оптических прибор характеризуется обычно линейной 2Y (2Y’) или угловой 2W (2W’) величиной. Для «удаленного» предмета (как он представляется объективу телескопа или фотоаппарата) 2W и изображения (которое, например, создается окуляром телескопа или лупой) 2W’ поле измеряют в угловой мере — это удвоенный угол между осью оптического прибора и направлением на границу поля зрения, измеренный из центра входного или соответственно выходного зрачка. Для «ближнего» предмета (как он представляется объективу микроскопа или лупе) 2Y или изображения (как у фотообъектива) 2Y’ поле измеряют в линейной мере (в мм) — это удвоенное расстояние от оси прибора до дальней точки кадра.
Как входное, так и выходное поле зрения ограничивается единственной полевой диафрагмой, расположенной на предмете или изображении (возможно промежуточном) или совокупностью виньетирующих диафрагмами (элементы конструкции трубы, оправы оптических элементов, их края). Полевая диафрагма располагается в плоскости изображения и формирует резкую границу кадра (поля зрения), а виньетирующие диафрагмы (не сопряженные оптически с предметом/изображением) — нерезкую. Довольно часто узлы сложных оптических приборов наследуют полевую диафрагму у других узлов. Например, объектив телескопа обычно не имеет собственной полевой диафрагмы (хотя может иметь немало виньетирующих, предназначенных, например, для светозащиты), а «использует» полевую диафрагму окуляра. Поэтому поле зрения телескопа (до известных пределов) определяется окуляром, но может быть ограничено виньетированием на конструкциях объектива (включая размеры фокусера, диагонального зеркала и т.д.).
Значение входного (видимого, TFOV — true field of view) поля зрения телескопа можно рассчитать следующим образом:
2W = 2·arctg(Y’/f’)
или с хорошим приближением:
2W, градусы = 57.3·2Y’/f’об = 2W’ок/Г, (7)
2W, угл.минуты = 60·2Wгр = 3444·2Y’/f’об = 60·2W’ок/Г, (8)
где
2Y’, мм — диаметр полевой диафрагмы окуляра (уменьшенное на кратность линзы Барлоу, если она использовалась) или диагонали кадра на фотоприемнике;
f’об, мм — фокусное расстояние объектива;
2W’ок, градусы — угловое поле зрения окуляра;
Г — увеличение телескопа.
Значение выходного поля зрения телескопа (AFOV — apperant field of view) или углового поля зрения окуляра (при нулевой угловой дисторсии):
2W’, градусы = 57.3·2Y’/f’ок = 2W’ок·Г, (9)
где f’ок, мм — фокусное расстояние окуляра.
Часто для определения видимого поля зрения 2W телескопа используют прием «остановки часовика». Измеряют время t в секундах, за которое достаточно яркая звезда пересечет поле зрения по диаметру от одного края до другого, при остановленном часовом механизме. Тогда поле зрения в угловых минутах определяется следующим образом
2W = t·cos(б)/4, (10)
где б — склонение звезды (для звезд у небесного экватора где б = 0 и cos(б) = 1 угловое поле зрения определяется проще: 2W = t/4).
Увеличение
Увеличение Г — характеризует соотношение размеров изображения и сопряженного с ним объекта.
Для телескопа, бинокля или подзорной трубы это самая важная характеристика — отношение малого угла dw’, под которым глаз видит изображение объекта, к углу dw под которым этот объект виден объективу телескопа: Г = dw’/dw. Для небольших углов полей зрения, характерных для телескопа, более-менее верны (если не вдаваться в детали) следующие общеизвестные соотношения, следующие из этого определения увеличения:
Г = f’об/f’ок ≃ D/D’ ≃ 2W’/2W, (11)
где 2W’ — поле зрения окуляра (или угловой размер наблюдаемого изображения), 2W — поле зрения объектива (или угловой размер наблюдаемого объекта), D — диаметр входной апертуры (входного зрачка) телескопа, D’ — диаметр выходного зрачка телескопа, f’об — фокусное расстояние объектива, f’ок — фокусное расстояние окуляра (если использована линза Барлоу следует домножить на ее заявленную кратность). Увеличение телескопа численно равное D/6-D/7 (D — в мм) принято называть ночным равнозрачковым (выходной зрачок телескопа примерно равен зрачку наблюдателя ночью), 1.5·D — разрешающим (дальнейший рост увеличения не увеличивает детализацию изображения, но приводит к падению яркости).
Для проекционных систем, микро- и макрообъективов увеличение это отношение линейных размеров малого фрагмента изображения dy’, к размеру этого же фрагмента на объекте dy: Г = dy’/dy. Такое увеличение еще называют поперечным увеличением, поскольку это отношение размеров предмета/изображения поперек оптической оси прибора. Стоит обратить внимание на то, оптический прибор (как, к примеру, большинство фотообъективов) может уменьшать размер изображения по сравнению с оригинальным размером объекта (иначе как бы фотографируемые люди поместились на кадр 24х35 мм ), в этом случае оптики продолжают говорить об увеличении, но значение Г при этом меньше единицы. При оборачивании изображения (вверх ногами) величина увеличения Г отрицательная. Для расчета поперечного увеличения верны следующие формулы:
Г = z/f = f’/z’ = a’/a = y’/y, (12)
где z — расстояние от предмета до переднего фокуса изображающей оптической системы, f и f’ — переднее и заднее фокусное расстояния (для объектива в воздухе они равны между собой), z’ — расстояние от заднего фокуса до плоскости изображения, a — передний отрезок (от предмета до передней главной плоскости объектива), a’ — задний отрезок (расстояние от объектива — точнее его задней главной плоскости — до изображения).
Назад к оглавлению статей