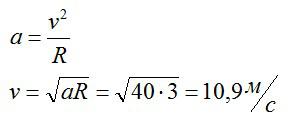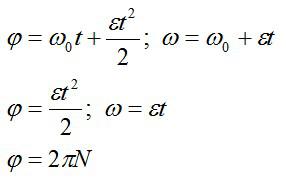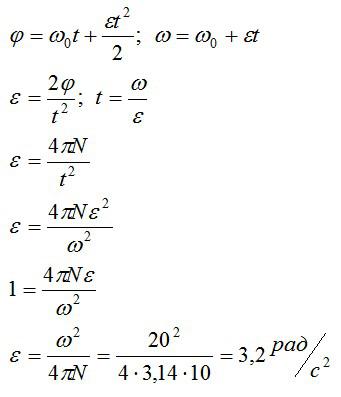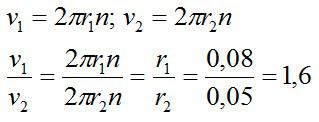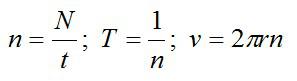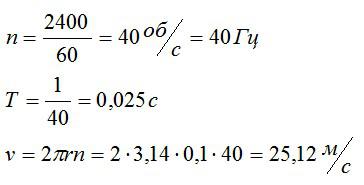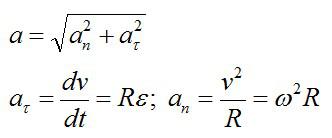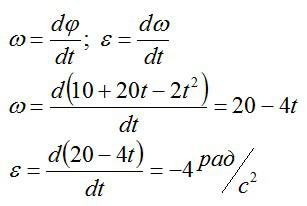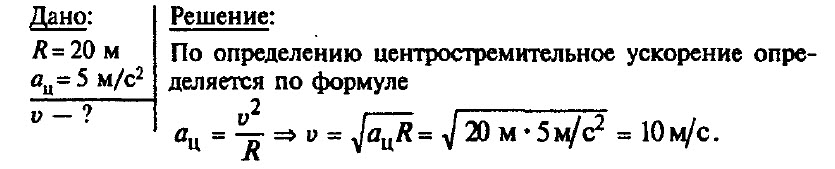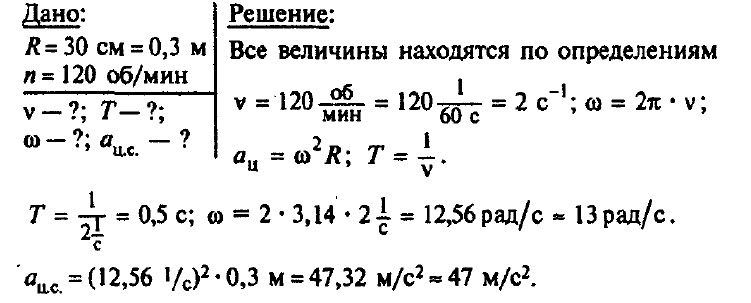Как найти линейную скорость точки обода колеса

Условие задачи:

Какова линейная скорость точек на ободе колеса паровой турбины с диаметром колеса 1 м и частотой вращения 300 об/мин?

Задача №1.8.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(D=1) м, (nu=300) об/мин, (upsilon-?)

Решение задачи:

Линейную скорость точек (upsilon) на ободе легко определить, зная угловую скорость (omega) и радиус колеса (R). Так как радиус равен половине диаметра, то:

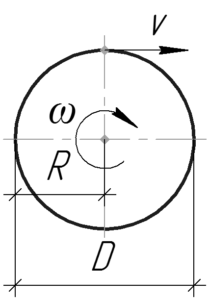
[upsilon  = omega R = frac{{omega D}}{2}]

Теперь необходимо определить угловую скорость (omega). Это можно сделать по формуле связи угловой скорости (omega) и частоты вращения (nu):

[omega  = 2pi nu ]

Подставим её в первую формулу, тогда получим ответ в общем виде.

[upsilon  = frac{{2pi nu D}}{2} = pi nu D]

Подставляя численные значения в формулу, необходимо не забывать, что их нужно переводить в систему СИ.

[300; [1/мин] = frac{{300}}{{60}}; [1/с] = 5; [1/с]]

Единицу измерения 1/с называют Гц (Герц).

Также хочется отметить, что в физике нет такого понятия как “обороты”, поэтому правильнее не 300 об/мин, а 300 1/мин. Обороты, количество молекул и т.д. в физике считаются безразмерными.

Считаем ответ:

[upsilon  = 3,14 cdot 5 cdot 1 = 15,7; м/с = 942; м/мин]

Ответ: 942 м/мин.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.7.27 При движении моторной лодки по течению реки ее скорость относительно берега
1.8.2 Какова угловая скорость вращения колеса, делающего 240 оборотов
1.8.3 Найти скорость движения автомобиля, если его колесо диаметром 1,1 м делает

Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только. 

Движение по окружности: определение, примеры

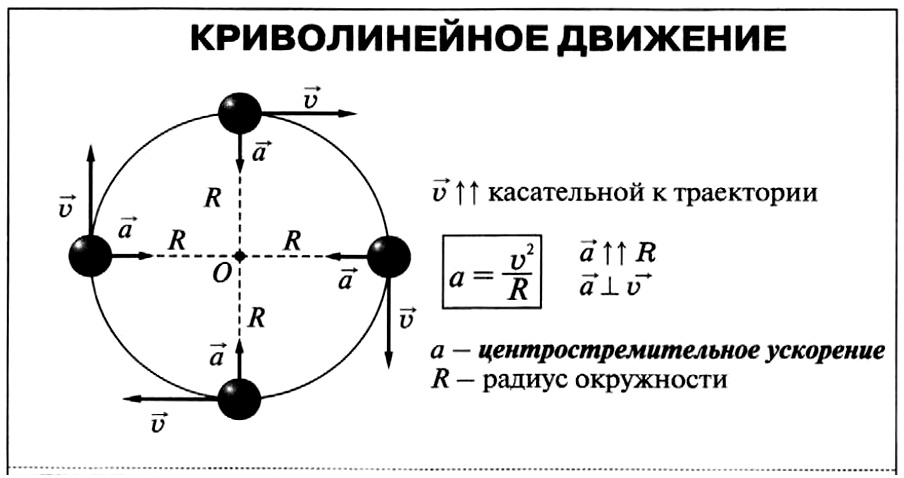
Движение по окружности – самый простой случай криволинейного движения. 

Примеры движения по окружности:

• грузовик движется по мосту с радиусом кривизны R;
• атлет крутит шар в руке, перед тем как бросить его;
• космическая станция летает по кругу над поверхностью Земли;
• катафот вращается на раскрученном колесе велосипеда.

Приведем ниже кинематические соотношения для поступательного и вращательного движений:

Вопросы на движение по окружности

Вопрос 1. Как направлено центростремительное ускорение?

Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.

Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?

Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.

Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?

Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.

Вопрос 4. Что такое линейная и угловая скорость?

Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.

Вопрос 5. При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?

Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.

Задачи на движение по окружности

Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.

Задача №1. Нахождение линейной скорости при движении по окружности

Условие

Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?

Решение

В данном случае ввиду имеется нормальное ускорение. Поэтому, для решения достаточно вспомнить всего одну формулу:

Ответ: 10,9 м/с.

Задача №2. Нахождение углового ускорения

Условие

Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

Решение

Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:

Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:

Ответ: 3,2 радиан на секунду в квадрате.

Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.

Задача №3. Нахождение скорости движения по окружности

Условие

Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?

Решение

Две точки вращаются на одном колесе, а значит, с одинаковой частотой. Используем соотношения для скорости:

Ответ: скорость точки на ободе больше в 1,6 раза.

Задача №4. Нахождение периода и частоты при движении по окружности

Условие

Маховик равномерно вращается и за время t=1 мин совершает N=2400 оборотов. Какова частота вращения маховика, период обращения и линейная скорость точки, расположенной на расстоянии 10 сантиметров от центра маховика?

Решение

По определению:

Подставим значения, предварительно переведя все величины в систему СИ, и вычислим:

Ответ: 40 Гц; 0,025 с; 25,12 м/с.

Задача №5. Нахождение полного ускорения при движении по окружности

Условие

Тело вращается вокруг стационарной оси по закону фи=10+20t-2t^2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.

Решение

Полное ускорение – векторная сумма нормального и тангенциального ускорений.

Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:

Подставляем значение t из условия и вычисляем:

 
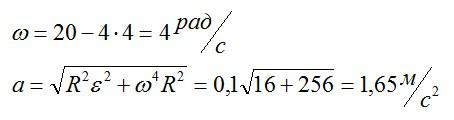
Ответ: 1,65 метра в секунду.

Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.

Задачи на Движение тела по окружности с решениями

Формулы, используемые на уроках «Задачи на Движение тела по окружности».

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с² ?

Задача № 2.
 С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?

Задача № 3.
 Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.

Задача № 4.
 Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?

Задача № 5.
 Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?

Задача № 6.
 Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.

Задача № 7.
 Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с².

Задача № 8.
 Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.

Задача № 9.
 Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.

Задача № 10.
  ОГЭ
 Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?

Задача № 11.
   ЕГЭ
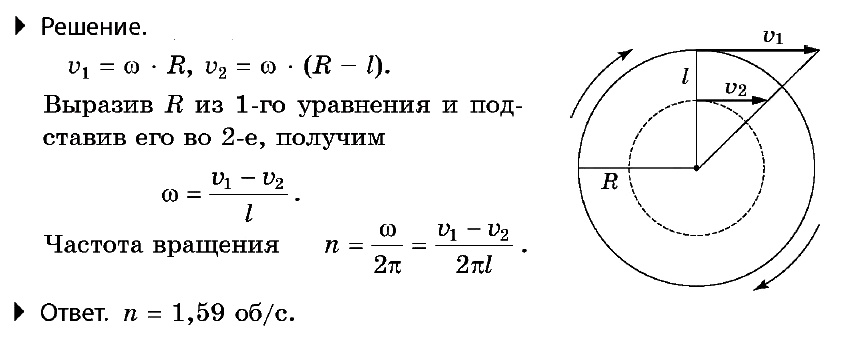
 Линейная скорость точек обода вращающегося диска v₁ = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v₂ = 2 м/с. Найти частоту вращения диска.

Задача № 12.
Груз, привязанный к шнуру длиной l = 50 см, описывает окружность в горизонтальной плоскости. Какой угол φ образует шнур с вертикалью, если частота вращения n = 1 с^-1 ?

Рассуждение: На схеме покажем груз, подвешенный на нити и движущийся по окружности некого радиуса R в горизонтальной плоскости так, что нить составляет с вертикалью угол φ. На груз действуют две силы: 1) сила тяжести mg; 2) сила натяжения нити T. Так как груз не движется вдоль оси y, то запишем первый закон Ньютона в проекции на эту ось: T⋅• cos φ = mg. Поскольку груз описывается окружность, то второй закон Ньютона запишется так: T⋅• sin φ = ma.

Ответ: 60º.

Краткая теория для решения Задачи на Движение тела по окружности.

Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на Искусственные спутники планет.
• Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Содержание книги

Предыдующая страница

§3. Криволинейное движение. Плоскопараллельное движение твердого тела

3.6 Плоскопараллельное движение

Движение твердого тела называется плоскопараллельным, если траектории движения всех его точек являются плоскими кривыми, лежащими в параллельных плоскостях.

Плоскопараллельное движение твердого тела можно представить как суперпозицию поступательного движения и вращения вокруг оси, направление которой не изменяется. Наглядными примерами такого движения являются качение колеса, движение книги без отрыва от стола и т.д.

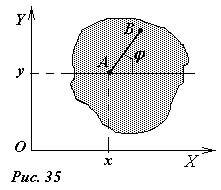
Для описания положения абсолютно твердого тела при плоскопараллельном движении необходимо задать две декартовые координаты какой-либо точки тела ^[1] и угол его поворота, то есть плоскопараллельное движение обладает тремя степенями свободы.

Выберем внутри тела две точки A, B; зададим координаты x_A, y_A точки A и угол φ, который образует отрезок AB с направлением оси X. Три числа x_A, y_A и φ однозначно определяют положение тела на плоскости, следовательно, являются его координатами. Зная эти координаты, можно определить положение в пространстве любой другой точки твердого тела путем геометрических построений.

Покажем теперь, как можно найти скорость любой точки твердого тела при плоскопараллельном движении (рис. 36).

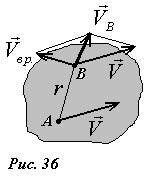
Разложим движение на две составляющих — поступательное движение, скорость которого обозначим (~vec V) , и вращение вокруг оси, проходящей через точку A, с угловой скоростью (~omega = frac{Delta varphi}{Delta t}) . Тогда скорость любой другой точки тела (например, B) является векторной суммой скоростей поступательного и вращательного движений —

(~vec V_B = vec V + vec V_{BP}) , (1)

причем вектор скорости вращательного движения направлен перпендикулярно отрезку AB и равен по абсолютной величине V_BP = ωr, где r расстояние от точки B до оси вращения.

Рассмотрим катящееся без проскальзывания колесо радиуса R (рис. 37).

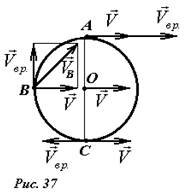
Пусть его центр движется со скоростью (~vec V). Найдем скорости некоторых других точек колеса. Для этого представим движение колеса как сумму поступательного движения его центра и вращения вокруг его оси. Так как движение происходит без проскальзывания, то угловая скорость вращения определяется формулой (~omega = frac{upsilon}{R}). Для точек, находящихся на ободе колеса линейная скорость вращательного движения равна по модулю скорости поступательного движения, так как для них расстояние до оси вращения равно радиусу колеса, поэтому (~V_{BP} = omega r = frac{V}{R} R = V) . Однако, направление этой скорости различно для разных точек. Так, для точки A скорость вращательного движения направлена горизонтально, также как и скорость поступательного движения. Поэтому суммарная скорость точки A равна 2V и направлена горизонтально. Скорость вращательного движения точки B направлена вертикально вверх, поэтому ее полная скорость направлена под углом 45° к горизонту, а ее модуль (~V_B = V sqrt{2}) . Очень интересна точка касания с поверхностью C : скорость ее вращательного движения направлена горизонтально в сторону противоположную скорости поступательного движения, поэтому ее полная скорость равна нулю.

Так как разложение движения на составляющие не является однозначным, можно теперь представить качение колеса как сумму движения точки C и вращения вокруг оси, проходящей через эту точку. Мы показали, что скорость точки C равна нулю, поэтому появляется возможность рассматривать движение колеса как чистый поворот вокруг точки C. Правда, это возможно в течение только бесконечно малого промежутка времени, потому, что в следующий момент точкой касания будет другая точка колеса. Множество точек твердого тела, скорости которых в данный момент равны нулю, образуют мгновенную ось вращения тела. Такая ось существует при любом движении твердого тела. Правда положение этой оси постоянно изменяется, поэтому для вычисления координат точек такое представление движения не дает особых преимуществ. Но для вычисления скоростей точек, рассматривать плоскопараллельное движение как чистый поворот очень удобно.

Легко доказать, что угол поворота тела не зависит от того, относительно какой оси мы его рассматриваем, следовательно, и угловая скорость не зависит от оси. С этой точки зрения, скорость любой точки колеса определяется формулой V = ωr’ , где r’ — расстояние от данной точки до мгновенной оси вращения.

Рассмотренная задача об определении скоростей точек катящегося колеса может быть легко решена, если рассматривать его движение как поворот вокруг точки C (рис. 38): точка A находится на расстоянии 2R от мгновенной оси вращения, поэтому ее скорость равна V_A = 2Rω = 2V; точка B находится на расстоянии (~R sqrt{2}) от оси, ее скорость (~V sqrt{2}). Направления векторов скоростей также совпадают с полученными ранее.

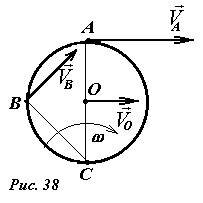
Таким образом, мы имеем два примерно одинаковых по сложности способа описания движения твердого тела: первый — суперпозиция поступательного и вращательного движений: второй — поворот вокруг мгновенной оси.

Примечания

1. ↑ С точки зрения кинематического описания выбор этой точки произволен — только следует стремиться к тому, чтобы траектория этой точки была попроще. Далее мы укажем как можно легко найти такую точку.

Следующая страница