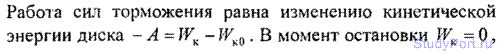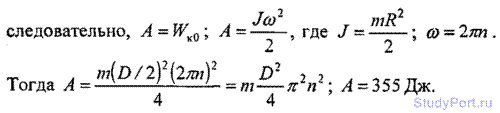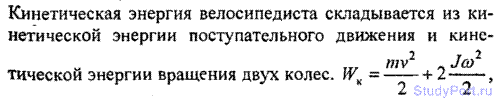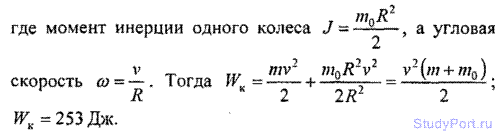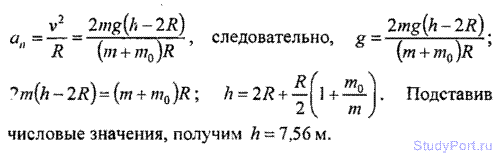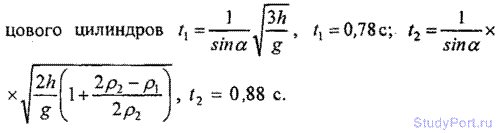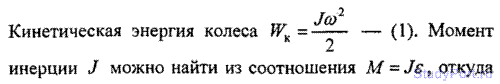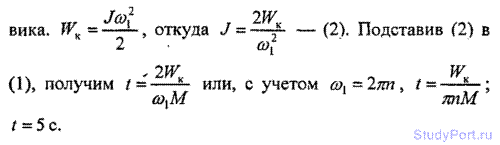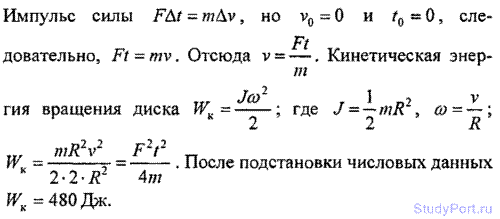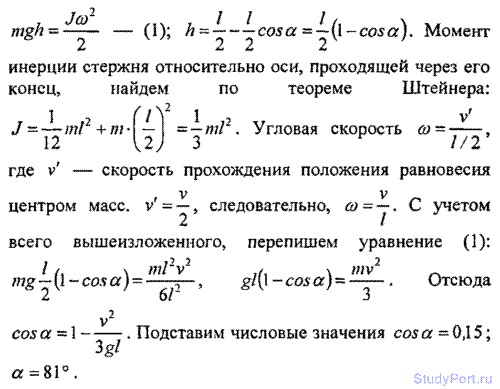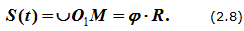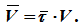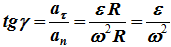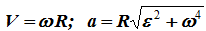Как найти линейную скорость обруча

Нашли ошибку? Сообщите в комментариях (внизу страницы)

Страница 2 из 3

3.21. Диск диаметром D = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой n = 20 об/с. Какую работу А надо совершить, чтобы остановить диск?

Решение:

3.22. Кинетическая энергия вала, вращающегося с частотой n = 5 об/с, W_K = 60 Дж. Найти момент импульса L вала.

Решение:

3.23. Найти кинетическую W_K энергию велосипедиста, еду со скоростью v = 9км/ч. Масса велосипедиста вместе с велосипедом m = 78 кг, причем на колеса приходится масса m₀ = 3 кг. Колеса велосипеда считать обручами.

Решение:

3.24. Мальчик катит обруч по горизонтальной дороге со скоростью v = 7,2 км/ч. На какое расстояние s может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен 10 м на каждые 100м пути.

Решение:

3.25. С какой наименьшей высоты h должен съехать вело, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом R = 3м*, и не оторваться от дорожки в верхней точке петли? Масса велоси вместе с велосипедом m = 75 кг, причем на колеса приходится масса m₀ = 3 кг. Колеса велосипеда считать обруча.

Решение:

3.26. Медный шар радиусом R = 10 см вращается с частотой n= 2 об/с вокруг оси, проходящей через его центр. Какую работу А надо совершить, чтобы увеличить угловую скорость w вращения шара вдвое?

Решение:

3.27. Найти линейные ускорения а центров масс шара, диска и обруча, скатывающихся без скольжения с наклонной плос. Угол наклона плоскости а = 30°, начальная скорость всех тел v₀ =0. Сравнить найденные ускорения с ускорением тела, соскальзывающего с наклонной плоскости при отсутствии трения.

Решение:

3.28. Найти линейные скорости v движения центров масс шара, диска и обруча, скатывающихся без скольжения с наклон плоскости. Высота наклонной плоскости h = 0,5 м, началь скорость всех тел v₀ = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.

Решение:

3.29. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) — одинакового радиуса R = 6 см и одина массы m = 0,5 кг. Поверхности цилиндров окрашены оди. Как, наблюдая поступательные скорости цилиндров у ос наклонной плоскости, можно различить их? Найти мо инерции J₁ и J₂ этих цилиндров. За какое время t каждый цилиндр скатится без скольжения с наклонной плоскости? Высота наклонной плоскости h = 0,5 м, угол наклона плоскости а = 30°, начальная скорость каждого цилиндра v₀ = 0.

Решение:

3.30. Колесо, вращаясь равнозамедленно, уменьшило за время   t = 1мин частоту вращения   от   n₁ =300 об/мин до n₂ = 180 об/мин. Момент инерции колеса J = 2кгм². Найти угловое ускорение е колеса, момент сил торможения М, ра А сил торможения и число оборотов N, сделанных коле за время t = 1 мин.

Решение:

3.31. Вентилятор вращается с частотой n = 900 об/мин, После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 15 об. Работа сил торможения А = 44,4 Дж. Найти момент инерции J вентилятора и момент сил торможения М.

Решение:

3.32. Маховое колесо, момент инерции которого J = 245кг*м², вращается с частотой n = 20об/с. После того как на колесо перестал действовать вращающий момент, оно оста, сделав N =1000 об. Найти момент сил трения М_тр и время t, прошедшее от момента прекращения действия враща момента до остановки колеса.

Решение:

3.33. По ободу шкива, насаженного на общую ось с маховым колесом, намотана нить, к концу который подвешен груз массой m = 1 кг. На какое расстояние h должен опуститься груз, чтобы колесо со шкивом получило частоту вращения n = 60 об/мин? Момент инерции колеса со шкивом J = 0,42 кгм², радиус шкива R = 10 см.

Решение:

3.34. Маховое колесо начинает вращаться с угловым ускоре e = 0,5 рад/с² и через время t₁ = 15 с после начала движения приобретает момент импульса L = 73,5 кгм²/с. Найти кинети энергию W_K колеса через время t₂ = 20 с после начала движения.

Решение:

3.35. Маховик вращается с частотой n = 10 об/с. Его кинети энергия W_K = 7,85 кДж. За какое время t момент сил М = 50Нм, приложенный к маховику, увеличит угловую ско со маховика вдвое?

Решение:

3.36. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 К. Какую кинетическую энергию W_K будет иметь диск через время t = 5 с после начала действия силы?

Решение:

3.37. Однородный стержень длиной l = 1 м подвешен на гори оси, проходящей через верхний конец стержня. На какой угол а надо отклонить стержень, чтобы нижний конец стержня при прохождении положения равновесия имел скорость v = 5 м/с?

Решение:

3.38. Однородный стержень длиной l = 85 см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую скорость v надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?

Решение:

3.39. Карандаш длиной l = 15 см, поставленный вертикально, падает на стол. Какую угловую скорость w и линейную ско v будет иметь в конце падения середина и верхний конец карандаша?

Решение:

3.40. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n₁ =10 об/мин. Человек массой m₀ =60 кг стоит при этом на краю платформы. С какой частотой n₂ начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека — точечной массой.

Решение:

Из условия задачи следует, что максимальный угол отклонения обруча от вертикали составляет $theta = 32^circ$.

Так как обруч движется по окружности, то его движение можно описать с помощью угловой скорости $omega$, которая равна изменению угла за единицу времени.

Мы знаем, что при максимальном отклонении диаметр обруча составляет $2Rsintheta$, где $R$ — радиус обруча. Таким образом, длина окружности, по которой движется нижняя точка обруча, равна $2pi Rsintheta$.

Время, за которое обруч проходит половину этой окружности (то есть, от максимального отклонения до положения равновесия), равно $t = frac{pi Rsintheta}{omega}$.

Линейная скорость нижней точки обруча в положении равновесия равна $v = Romega$.

Таким образом, чтобы найти линейную скорость, нам нужно сначала найти угловую скорость $omega$. Для этого воспользуемся законом сохранения энергии: потенциальная энергия обруча в положении максимального отклонения равна его кинетической энергии в положении равновесия.

Потенциальная энергия обруча в положении максимального отклонения равна $mgh$, где $m$ — масса обруча, $g$ — ускорение свободного падения, а $h$ — высота максимального отклонения, которая равна $R(1-costheta)$.

Кинетическая энергия обруча в положении равновесия равна $frac{1}{2}mv^2$, где $v$ — линейная скорость нижней точки обруча в положении равновесия.

Таким образом, мы можем записать:

$$mgh = frac{1}{2}mv^2$$

$$v = sqrt{2gh}$$

где $h = R(1-costheta)$.

Теперь мы можем найти линейную скорость нижней точки обруча в положении равновесия:

$$v = sqrt{2gR(1-costheta)} approx 2.84 text{ м/с}$$

Ответ: линейная скорость нижней точки обруча в положении равновесия составляет примерно 2.84 м/с.

Движение по окружности (кинематика, динамика)

Найти линейную скорость Земли v при ее орбитальном движении. Средний радиус земной орбиты R=1,5·10 8 км.

Ответ и решение

Пропеллер самолета радиусом 1,5 м вращается при посадке с частотой 2000 мин -1 , посадочная скорость самолета относительно Земли равна 162 км/ч. Определить скорость точки на конце пропеллера. Какова траектория движения этой точки?

Ответ и решение

v ≈ 317 м/с. Точка на конце пропеллера описывает винтовую линию с шагом h ≈ 1,35 м.

Пропеллер самолета вращается с частотой:

λ = 2000/60 с -1 = 33,33 с -1 .

Линейная скорость точки на конце пропеллера:

Скорость самолета при посадке v = 45 м/с.

Результирующая скорость точки на конце пропеллера равна сумме векторов линейной скорости при вращении пропеллера и скорости самолета при посадке:

v_рез = ≈ 317 м/с.

Шаг винтовой траектории равен:

Диск радиусом R катится без скольжения с постоянной скоростью v. Найти геометрическое место точек на диске, которые в данный момент имеют скорость v.

Геометрическим местом точек на диске, имеющих скорость v в данный момент, является дуга радиуса R, центр которой лежит в точке касания диска с плоскостью, т.е. в мгновенном центре вращения.

Цилиндрический каток радиусом R помещен между двумя параллельными рейками. Рейки движутся в одну сторону со скоростями v₁ и v₂.

Определить угловую скорость вращения катка и скорость его центра, если проскальзывание отсутствует. Решить задачу для случая, когда скорости реек направлены в разные стороны.

; .

По горизонтальной плоскости катится без скольжения с постоянной скоростью v_c обруч радиусом R. Каковы скорости и ускорения различных точек обруча относительно Земли? Выразить скорость как функцию угла между вертикалью и прямой, проведенной между точкой прикосновения обруча с плоскостью и данной точкой обруча.

v_A = 2v_Ccosα. Ускорение точек обода содержит только центростремительную составляющую, равную a_ц = v 2 /R.

Автомобиль движется со скоростью v = 60 км/ч. С какой частотой n вращаются его колеса, если они катятся по шоссе без скольжения, а внешний диаметр покрышек колес равен d = 60 см? Найти центростремительное ускорение а_цс внешнего слоя резины на покрышках его колес.

На горизонтальную плоскость кладут тонкостенный цилиндр, вращающийся со скоростью v₀ вокруг своей оси. Какой будет скорость движения оси цилиндра, когда прекратится проскальзывание цилиндра относительно плоскости?

Совершает ли работу равнодействующая всех сил, приложенных к телу, равномерно движущемуся по окружности?

Груз массой m может скользить без трения по горизонтальному стержню, вращающемуся вокруг вертикальной оси, проходящей через один из его концов. Груз соединяют с этим концом стержня пружиной, коэффициент упругости которой k. При какой угловой скорости ω пружина растянется на 50% первоначальной длины?

.

Две точечные массы m₁ и m₂ прикреплены к нити и находятся на абсолютно гладком столе. Расстояния от них до закрепленного конца нити равны l₁ и l₂ соответственно.

Система вращается в горизонтальной плоскости вокруг оси, проходящей через закрепленный конец, с угловой скоростью ω. Найти силы натяжения участков нити Т₁ и Т₂.

Человек сидит на краю круглой горизонтальной платформы радиусом R=4 м. С какой частотой n должна вращаться платформа вокруг вертикальной оси, чтобы человек не мог удержаться на ней при коэффициенте трения k=0,27?

Тело массой m находится на горизонтальном диске на расстоянии r от оси. Диск начинает раскручиваться с малым ускорением. Построить график зависимости составляющей силы трения в радиальном направлении, действующей на тело, от угловой скорости вращения диска. При каком значении угловой скорости диска начнется соскальзывание тела?

.

Камень массой m=0,5 кг, привязанный к веревке длиной l=50 см, вращается в вертикальной плоскости. Сила натяжения веревки, когда камень проходит низшую точку окружности, Т=44 Н. На какую высоту h над нижней точкой окружности поднимется камень, если веревку перерезать в тот момент, когда его скорость направлена вертикально вверх?

Спортсмен посылает молот (ядро на тросике) на расстояние l=70 м по траектории, обеспечивающей максимальную дальность броска. Какая сила Т действует на руки спортсмена в момент броска? Масса молота m=5 кг. Считать, что спортсмен разгоняет молот, вращая его в вертикальной плоскости по окружности радиусом R=1,5 м. Сопротивление воздуха не учитывать.

Автомобиль массой М=3*10 3 кг движется с постоянной скоростью v=36 км/ч: а) по горизонтальному мосту; б) по выпуклому мосту; в) по вогнутому мосту. Радиус кривизны моста в последних двух случаях R=60 м. С какой силой давит автомобиль на мост (в последних двух случаях) в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α=10° с вертикалью?

По выпуклому мосту, радиус кривизны которого R = 90 м, со скоростью v = 54 км/ч движется автомобиль массой m = 2 т. В точке моста, направление на которую из центра кривизны моста составляет с направлением на вершину моста угол α, автомобиль давит с силой F = 14 400 Н. Определить угол α.

Шарик массой m = 100 г подвешен на нити длиной l =1 м. Шарик раскрутили так, что он начал двигаться по окружности в горизонтальной плоскости. При этом угол, составляемый нитью с вертикалью, α = 60°. Определить полную работу, совершаемую при раскручивании шарика.

С какой наибольшей скоростью может двигаться автомобиль на повороте с радиусом закругления R = 150 м, чтобы его не «занесло», если коэффициент трения скольжения шин о дорогу k = 0,42?

1. Каким должен быть максимальный коэффициент трения скольжения k между шинами автомобиля и асфальтом, чтобы автомобиль мог пройти закругление радиусом R = 200 м при скорости v = 100 км/ч?

2. Автомобиль со всеми ведущими колесами, трогаясь с места, равномерно набирает скорость, двигаясь по горизонтальному участку дороги, представляющему собой дугу окружности α = 30° радиусом R = 100 м. С какой максимальной скоростью автомобиль может выехать на прямой участок пути? Коэффициент трения колес о землю k = 0,3.

Поезд движется по закруглению радиусом R = 800 м со скоростью v = 12 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего, чтобы на колесах не возникало бокового усилия. Расстояние между рельсами по горизонтали принять равным d = 1,5 м.

Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте?

1. С какой максимальной скоростью v может ехать по горизонтальной плоскости мотоциклист, описывая дугу радиусом R = 90 м, если коэффициент трения скольжения k = 0,4?

2. На какой угол φ от вертикального направления он должен при этом отклониться?

3. Чему будет равна максимальная скорость мотоциклиста, если он будет ехать по наклонному треку с углом наклона α = 30° при том же радиусе закругления и коэффициенте трения?

4. Каким должен быть угол наклона трека α₀ для того, чтобы скорость мотоциклиста могла быть сколь угодно большой?

Самолет совершает поворот, двигаясь по дуге окружности с постоянной скоростью v = 360 км/ч. Определить радиус R этой окружности, если корпус самолета повернут вокруг направления полета на угол α = 10°.

На повороте дороги радиусом R = 100 м равномерно движется автомобиль. Центр тяжести автомобиля находится на высоте h = 1 м, ширина колеи автомобиля а = 1,5 м. Определить скорость v, при которой автомобиль может опрокинуться. В поперечном направлении автомобиль не скользит.

Шофер, едущий на автомобиле, внезапно заметил впереди себя забор, перпендикулярный направлению его движения. Что выгоднее сделать, чтобы предотвратить аварию: затормозить или повернуть в сторону?

В вагоне поезда, идущего равномерно по криволинейному пути со скоростью v = 12 км/ч, производится взвешивание груза на пружинных весах. Масса груза m = 5 кг, а радиус закругления пути R = 200 м. Определить показание пружинных весов (силу натяжения пружины Т).

Найти силу F_ед.об., отделяющую сливки (плотность ρ_с = 0,93 г/см 3 ) от снятого молока (ρ_м = 1,03 г/см 3 ) в расчете на единицу объема, если отделение происходит: а) в неподвижном сосуде; б) в центробежном сепараторе, вращающемся с частотой 6000 мин -1 , если жидкость находится на расстоянии r = 10 см от оси вращения.

Самолет делает «мертвую петлю» с радиусом R = 100 м и движется по ней со скоростью v = 280 км/ч. С какой силой F тело летчика массой М = 80 кг будет давить на сиденье самолета в верхней и нижней точках петли?

Определить силу натяжения Т каната гигантских шагов, если масса человека М = 70 кг и канат при вращении образует со столбом угол α = 45°. С какой угловой скоростью со будут вращаться гигантские шаги, если длина подвеса l = 5 м?

T ≈ 990 Н; ω ≈ 1,68 рад/с.

Найти период Т вращения маятника, совершающего круговые движения в горизонтальной плоскости. Длина нити l. Угол, образуемый нитью с вертикалью, α.

.

Грузик, подвешенный на нити, вращается в горизонтальной плоскости так, что расстояние от точки подвеса до плоскости, в которой происходит вращение, равно h. Найти частоту и вращения груза, считая ее неизменной.

. Результат не зависит от длины подвеса.

Люстра массой m = 100 кг подвешена к потолку на металлической цепи, длина которой l = 5 м. Определить высоту h, на которую можно отклонить люстру, чтобы при последующих качениях цепь не оборвалась? Известно, что разрыв цепи наступает при силе натяжения Т > 1960 Н.

Шарик массой m подвешен на нерастяжимой нити. На какой минимальный угол α_мин надо отклонить шарик, чтобы при дальнейшем движении нить оборвалась, если максимально возможная сила натяжения нити 1,5 mg?

Маятник отклоняют в горизонтальное положение и отпускают. При каком угле α с вертикалью сила натяжения нити будет равна по величине действующей на маятник силе тяжести? Маятник считать математическим.

Груз массой m, привязанный к нерастяжимой нити, вращается в вертикальной плоскости. Найти максимальную разность сил натяжений нити.

Гимнаст «крутит солнце» на перекладине. Масса гимнаста m. Считая, что вся его масса сосредоточена в центре тяжести, а скорость в верхней точке равна нулю, определить силу, действующую на руки гимнаста в нижней точке.

Один грузик подвешен на нерастяжимой нити длиной l, а другой — на жестком невесомом стержне такой же длины. Какие минимальные скорости нужно сообщить этим грузикам, чтобы они вращались в вертикальной плоскости?

Для нити v_мин = ; для стержня v_мин = .

Шарик массой М подвешен на нити. В натянутом состоянии нить расположили горизонтально и отпустили шарик. Вывести зависимость силы натяжения нити Т от угла α, который образует в данный момент нить с горизонтальным направлением. Проверить выведенную формулу, решив задачу для случая прохождения шарика через положение равновесия, при α = 90°.

Математический маятник длиной l и массой М отвели на угол φ₀ от положения равновесия и сообщили ему начальную скорость v₀, направленную перпендикулярно к нити вверх. Найти силу натяжения нити маятника Т в зависимости от угла φ нити с вертикалью.

.

Грузик, подвешенный на нити, отводят в сторону так, что нить принимает горизонтальное положение, и отпускают. Какой угол с вертикалью α образует пить в тот момент, когда вертикальная составляющая скорости грузика наибольшая?

Одинаковые упругие шарики массой m, подвешенные на нитях равной длины к одному крючку, отклоняют в разные стороны от вертикали на угол α и отпускают. Шарики ударяются и отскакивают друг от друга. Какова сила F, действующая на крючок: а) при крайних положениях нитей; б) в начальный и конечный моменты удара шариков; в) в момент наибольшей деформации шариков?

Математическому маятнику с гибкой нерастяжимой нитью длиной l сообщают из положения равновесия горизонтальную скорость v₀. Определить максимальную высоту его подъема h при движении по окружности, если v₀ 2 = 3gl. По какой траектории будет двигаться шарик маятника после того, как он достиг максимальной высоты подъема h на окружности? Определить максимальную высоту H, достигаемую при этом движении маятника.

; по параболе; .

Маленький шарик подвешен в точке А на нити длиной l. В точке О на расстоянии l/2 ниже точки А в стену вбит гвоздь. Шарик отводят так, что нить занимает горизонтальное положение, и отпускают. В какой точке траектории исчезает сила натяжения нити? Как дальше будет двигаться шарик? До какой наивысшей точки поднимется шарик?

На l/6 ниже точки подвеса; по параболе; на 2l/27 ниже точки подвеса.

Сосуд, имеющий форму расширяющегося усеченного конуса с диаметром дна D = 20 см и углом наклона стенок α = 60°, вращается вокруг вертикальной оси 00₁. При какой угловой скорости вращения сосуда ω маленький шарик, лежащий на его дне, будет выброшен из сосуда? Трение не учитывать.

Сфера радиусом R = 2 м равномерно вращается вокруг оси симметрии с частотой 30 мин -1 . Внутри сферы находится шарик массой m = 0,2 кг. Найти высоту h, соответствующую положению равновесия шарика относительно сферы, и реакцию сферы N.

Внутри конической поверхности, движущейся с ускорением a, вращается шарик по окружности радиусом R. Определить период Т движения шарика по окружности. Угол при вершине конуса 2α.

.

Небольшое тело массой m соскальзывает вниз по наклонному скату, переходящему в мертвую петлю радиусом R.

Трение ничтожно мало. Определить: а) какова должна быть наименьшая высота h ската, чтобы тело сделало полную петлю, не выпадая; б) какое давление F при этом производит тело на помост в точке, радиус-вектор которой составляет угол α с вертикалью.

Лента конвейера наклонена к горизонту под углом α. Определить минимальную скорость ленты v_мин, при которой частица руды, лежащая на ней, отделяется от поверхности ленты в месте набегания ее на барабан, если радиус барабана равен R.

v_мин = .

Небольшое тело скользит с вершины сферы вниз. На какой высоте h от вершины тело оторвется от поверхности сферы радиусом R? Трением пренебречь.

Найти кинетическую энергию обруча массой m, катящегося со скоростью v. Проскальзывания нет.

Тонкий обруч без проскальзывания скатывается в яму, имеющую форму полусферы. На какой глубине h сила нормального давления обруча на стенку ямы равна его силе тяжести? Радиус ямы R, радиус обруча r.

Маленький обруч катится без скольжения по внутренней поверхности большой полусферы. В начальный момент у ее верхнего края обруч покоился. Определить: а) кинетическую энергию обруча в нижней точке полусферы; б) какая доля кинетической энергии приходится на вращательное движение обруча вокруг его оси; в) нормальную силу, прижимающую обод к нижней точке полусферы. Масса обруча равна m, радиус полусферы R.

Вода течет по трубе, расположенной в горизонтальной плоскости и имеющей закругление радиусом R = 2 м. Найти боковое давление воды. Диаметр трубы d = 20 см. Через поперечное сечение трубы в течение одного часа протекает М = 300 т воды.

Тело соскальзывает из точки А в точку В по двум искривленным наклонным поверхностям, проходящим через точки A и В один раз по выпуклой дуге, второй — по вогнутой. Обе дуги имеют одинаковую кривизну и коэффициент трения в обоих случаях один и тот же.

В каком случае скорость тела в точке B больше?

В случае движения по выпуклой дуге.

Стержень ничтожной массы длиной l с двумя маленькими шариками m₁ и m₂ (m₁ > m₂) на концах может вращаться около оси, проходящей через середину стержня перпендикулярно к нему. Стержень приводят в горизонтальное положение и отпускают. Определить угловую скорость ω и силу давления F на ось в момент прохождения стержнем с шариками положения равновесия.

; .

На виток цилиндрической спирали, ось которой вертикальна, надевают маленькое колечко массой m. Колечко без трения начинает скользить по спирали. С какой силой F будет колечко давить на спираль после того, как оно пройдет n полных витков? Радиус витка R, расстояние между соседними витками h (шаг витка). Считать h ≪ R.

.

Замкнутая металлическая цепочка лежит на гладхом горизонтальном диске, будучи свободно насажена на центрирующее ее кольцо, соосное с диском. Диск приведен во вращение. Принимая форму цепочки за горизонтальную окружность, определить силу натяжения Т вдоль цепочки, если ее масса m = 150 г, длина l = 20 см и цепочка вращается с частотой n = 20 с -1 .

Реактивный самолет m = 30 т летит вдоль экватора с запада на восток со скоростью v = 1800 км/ч. На сколько изменится подъемная сила, действующая на самолет, если он будет лететь с той же скоростью с востока на запад?

Задача на вращение обруча

Вопрос:

У меня не получается решить следующую задачу.

Задача №5.7

Тонкий жесткий обруч радиуса R , оставаясь в вертикальной плоскости, скатывается без проскальзывания с горки высотой h =4* R . Сила упругости, возникающая в обруче в результате его вращения, в конце спуска с горки равна T . Определите массу M обруча.

Рис.1. Условия задачи

Ответ

Решение №1

Давайте немного порассуждаем.

Сила упругости в обруче зависит от скорости вращения. Ведь центростремительное ускорение

Рис.2. Вращение обруча

Сила упругости зависит также и от k – жесткости упругого элемента . Но с другой стороны, если k = infinity (как и дано по условиям задачи), то при любой F упр деформация Dx =0. Значит, в этом случае F упр определится по другой формуле. Какой?

Идея! F упр – это именно та сила, которая сообщает частицам обруча a цс !

Где dM – это масса частицы обруча

Рис.3.Силы, действующие на элемент обруча

Но какого размера частица обруча?

Или имеется в виду сила упругости, действующая на весь обруч? Но это нонсенс. Потому что на каждую частицу обруча действует своя сила упругости, а в сумме они дают 0, так как равномерно распределены и все направлены к центру.

Рис.4. Распределенная сила упругости, действующая на обруч

Да, именно сила упругости, распределенная на весь обруч (то есть просуммированная по кольцу алгебраически, а не как вектор ) – это то, что нужно найти в данной задаче.

В этой формуле T определяется как int ( dT ( fi ), fi =0..2* Pi ) . Это следует из формулы

dM ( fi )* V вр^2/ R = dT ( fi ) (которая является уточненной версией формулы dM * V вр^2/ R = F упр ). Если её проинтегрировать по fi (угловой координате кольца) в интервале полного поворота, то есть от 0 до 2* Pi , то мы получим именно такое определение T и формулу M * V вр^2/ R = T .

Рис.5. Как получается парциальная равнодействующая сил упругости.

Из рис.5 видно, как получается сила dT ( fi ) – парциальная равнодействующая парциальных сил упругости, действующих на малый элемент кольца, измеряемый угловой координатой dfi . Таких парциальных сил упругости для любого элемента кольца всегда две – T ( fi ) и T ( fi + dfi )(как и для всякого упругого элемента). Таким образом, Т в данном случае — необычная сила.

Более того, сама задача становится разрешимой только после понимания того, о какой же силе упругости в данном случае идет речь.

Дальше решение продвигается просто.

Сначала находим V вр. Её можно найти из закона сохранения энергии

В начале скатывания обруча его полная энергия (она складывается только из потенциальной ):

В конце скатывания (она складывается только из кинетической ):

E2 = M*V п ^2/ R = M*V вр ^2/R,

так как V вр= V п – проскальзывания, по условию задачи, нет.

(Иными словами, проскальзывание равно 0, так как оно и определяется как разность V вр- V п . Иногда говорят об относительном проскальзывании. Вполне логично это понятие определить как ( V вр- V п)/ V вр . В более общем же случае это ( V 1- V 2)/ V 1, где v 1 и v 2 – скорости взаимодействующих, через трение, поверхностей. )

Mgh = MV вр^2/2 => V вр^2 = 2 gh => T = M *2 gh / R

Так как по условию задачи h =4* R , то

что и требовалось найти .

В некоторых источниках [например, «Сборник задач по физике» под редакцией С.Н.Дмитриева, пособие для поступающих в ВУЗЫ, учебный центр МГТУ им.Баумана, М.2004 ] подзадача отыскания силы упругости для данной задачи решается следующим образом.

Рассмотрим дугу обруча с центральным углом alfa (рад). Масса этого элемента (в предположении постоянной плотности вдоль обруча) равна M*alfa/(2*Pi), поэтому уравнение 2-го закона Ньютона (при вращении) для него запишется в виде

где F — это равнодействующая сил упругости, с которыми действует на данный элемент (с обоих концов элемента) оставшаяся часть обруча (см. рис.5). Поскольку обруч представляет из себя последовательное соединение упругостей, то сила упругости не изменяется от сечения к сечению.

Поэтому данная равнодействующая найдется по формуле

Так как угол alfa мал, то sin(alfa/2) можно приравнять alfa/2, следовательно:

Подставляя (2a) в (1), получим уравнение для определения T, из которого:

то есть величина T, в 2*pi раз меньшая, чем получилось в решении №1.

А вот в чем. В решении №2 считается (по традиции), что угол alfa мал. Но на самом деле он может быть любым, поэтому правильное решение относительно T получается при подстановке (2) в (1) и выглядит так:

Из этой формулы, в частности, выходит, что для половины обруча (то есть при alfa=pi):

T= M/4*Vвр^2/R => F=M/2*Vвр^2/R

Это же следует и из других соображений: если обруч разрезать по диаметру, то на каждую половину действует равнодействующая сил упругости, равная именно этой величине (поскольку масса каждой половины M/2)

При каком же условии допущение о малости alfa будет правомерным? Если мы будем находить равнодействующую сил упругости для бесконечно малого элемента обруча dm (соответствующего бесконечно малому углу dalfa). Уравнение 2-го закона Ньютона для него запишется так:

M*dalfa/(2*pi)*Vвр^2/R = dF = 2*T’*sin(dalfa/2)=T*dalfa

Таким образом, в решении №2 найдена не (требуемая по условию) сила упругости, а её производная по углу дуги обруча — угловое механическое «напряжение» обруча.

Чтобы найти силу упругости, нужно проинтегрировать полученную величину по центральному углу от 0 до 2*pi. Что и даст Fупр=T*2*pi= M*Vвр^2/R (см. решение №1) Именно это значение покажет динамометр, помещенный в (одинарный) разрез обруча. Поскольку в данном сечении обруч действует с силой упругости сам на себя (одним концом на другой, то есть целиком).

iSopromat.ru

Рассмотрим определение скоростей и ускорений точек вращающегося твердого тела:

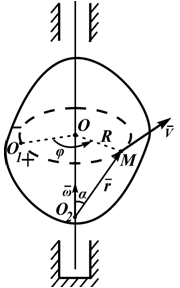
При вращении твердого тела вокруг неподвижной оси каждая точка тела движется по окружности. Радиус окружности R равен расстоянию от точки до оси вращения.

Закон движения точки может быть задан естественным способом (рисунок 2.4): траектория – окружность; начало отсчета точка O₁ и положительное направление движения выбраны, длина дуги (дуговая координата) определяется по формуле

Скорости точек

Скорость точки вращающегося твердого тела определяется выражением

где ω — угловая скорость вращения твердого тела.

Скорость направлена по касательной к траектории, поэтому можно написать

Вектор скорости можно получить векторным произведением:

Ускорения точек

Ускорение точки при естественном способе задания движения определяется как сумма касательного и нормального ускорений (см. вывод формулы (1.10)):

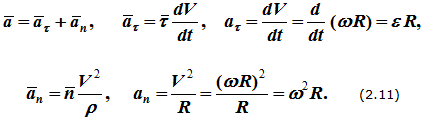
Эти же выражения можно получить, взяв производную от векторного произведения V=ω × r.

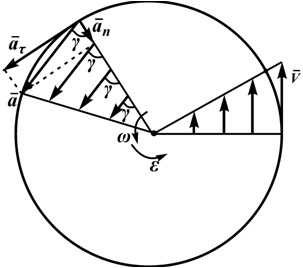
Угол, который составляет полное ускорение с радиусом, может быть определен из соотношения (рисунок 2.5)

То есть эти углы для всех точек тела одинаковы и не зависят от их расположения на теле. На этом же рисунке представлены законы распределения скоростей и ускорений точек во вращающемся теле в зависимости от расстояния их до оси вращения. Эти законы распределения соответствуют формулам:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах