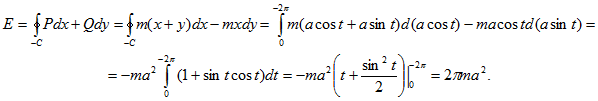Длина

Если пространственная линия задана параметрическими уравнениями

Площадь S фигуры, расположенной в плоскости Оху и ограниченной замкнутой линией L, находится по формуле

Масса /я материальной дуги

Где

Прямоугольные координаты центра тяжести материальной дуги находятся по формулам

Где
Если
Совершающая работу



Пусть сила

Ражение

Где

Замечание. Если линия

(21.18), (21.20) — (21.22) упрощаются.
Пример 21.13. Найти массу материальной дуги кривой
Точками
Пропорциональна абсциссе этой точки.
Найдем выражения линейной плотности
Условия следует, что линейная плотность выражается формулой




Пример 21.14 Найти центр тяжести дуги винтовой линии


Так как
Согласно условию, линейная плотность выражается формулой

По формуле (21.20) находим массу данной дуги
Итак,
Вычислим интегралы каждой из формул (21.21), обозначив их через
Таким
Пример 21.15. Найти работу, производимую силой
Дуги кривой

Проекции силы


По формулам (21.21) находим координаты центра тяжести:
По этой формуле получаем
Гпава 22
ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
| < Предыдущая | Следующая > |
|---|
Содержание
- Линейная плотность
- См. также
- Полезное
- Смотреть что такое «Линейная плотность» в других словарях:
- Производная в физике
- Задача о теплоемкости тела
Линейная плотность
Линейная плотность однородного тела — физическая величина, определяемая отношением массы тела к его линейному параметру (как правило, длине).
Единицей измерения является килограмм на метр(кг/м).
Линейная плотность электрического заряда — предел отношения электрического заряда, находящегося в элементе линии, к длине этого элемента линии, который содержит данный заряд, когда длина этого элемента стремится к нулю.
Единицей измерения является кулон на метр (Кл/м).
См. также
- Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).
- Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Линейная плотность» в других словарях:
линейная плотность — 3.1 линейная плотность: По ГОСТ 10878. Источник: ГОСТ 10213.1 2002: Волокно штапельное и жгут химические. Методы определения линейной плотности … Словарь-справочник терминов нормативно-технической документации
линейная плотность — ilginis tankis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydžio kiekis vienetiniame (fizikinės erdvės) ilgyje. atitikmenys: angl. line density; linear density vok. lineare Dichte, f rus. линейная плотность, f pranc. densité… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
линейная плотность — ilginis tankis statusas T sritis chemija apibrėžtis Medžiagos masės ir iš jos pagaminto gaminio (siūlo, gijos ar kt.) ilgio santykis. atitikmenys: angl. linear density rus. линейная плотность … Chemijos terminų aiškinamasis žodynas
линейная плотность — ilginis tankis statusas T sritis fizika atitikmenys: angl. line density; linear density vok. lineare Dichte, f rus. линейная плотность, f pranc. densité linéique, f … Fizikos terminų žodynas
ЛИНЕЙНАЯ ПЛОТНОСТЬ — физ. величина, равная отношению массы тела к его длине и применяемая для хар ки толщины нитей, проволок, тканей, плёнок, бумаги и др. подобных материалов, а также для хар ки балок, рельсов и т. д. В СИ Л. п. выражается в кг/м. Л. п. текст. нитей… … Большой энциклопедический политехнический словарь
Линейная плотность — косвенная характеристика толщины (масса единицы длины), или единица измерения толщины волокон и нитей, текс. Определяется по формуле: T = m/l, где m масса волокна или отрезка нити, г; l их длина, км. Во многих странах мира и у нас для… … Энциклопедия моды и одежды
линейная плотность тока — Векторная величина, равная пределу произведения плотности электрического тока проводимости, протекающего в тонком слое у поверхности тела, и толщины этого слоя, когда последняя стремится к нулю. [ГОСТ Р 52002 2003] Тематики электротехника,… … Справочник технического переводчика
ЛИНЕЙНАЯ ПЛОТНОСТЬ ЭНЕРГИИ ЗАЖИГАНИЯ — отношение энергии, выделяемой в канале разряда, к длине разрядного промежутка. См. также Источник зажигания, Минимальная энергия зажигания … Российская энциклопедия по охране труда
линейная плотность ионизации — линейная плотность ионизации; отрасл. удельная ионизация Число пар ионов, образуемых частицей или квантом излучения на единице длины пути в среде … Политехнический терминологический толковый словарь
линейная плотность заряда — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN linear charge density … Справочник технического переводчика
Источник
Производная в физике
Алгебра щедра. Зачастую она дает больше, чем у нее спрашивают.
Межпредметные связи являются дидактическим условием и средством глубокого и всестороннего усвоения основ наук в школе.
Кроме того, они способствуют повышению научного уровня знаний учащихся, развитию логического мышления и их творческих способностей. Реализация межпредметных связей устраняет дублирование в изучении материала, экономит время и создаёт благоприятные условия для формирования общеучебных умений и навыков учащихся.
Установление межпредметных связей в курсе физики повышает эффективность политехнической и практической направленности обучения.
В преподавании математики очень важна мотивационная сторона. Математическая задача воспринимается учащимися лучше, если она возникает как бы у них на глазах, формулируется после рассмотрения каких-то физических явлений или технических проблем.
Сколько бы ни говорил учитель о роли практики в прогрессе математики и о значении математики для изучения физики, развития техники, но если он не показывает, как физика влияет на развитие математики и как математика помогает практике в решении её проблем, то развитию материалистического мировоззрения будет нанесен серьёзный ущерб. Но для того, чтобы показать, как математика помогает в решении её проблем, нужны задачи, не придуманные в методических целях, а возникающие на самом деле в различных областях практической деятельности человека
Исторические сведения
Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:
- о разыскании касательной к произвольной линии;
- о разыскании скорости при произвольном законе движения.
Еще раньше понятие производной встречалось в работах итальянского математика Николо Тартальи (около 1500 – 1557гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.
В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной.
Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л.Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.
Термин «производная» является буквальным переводом на русский французского слова derive, которое ввел в1797 году Ж. Лагранж (1736-1813).
И.Ньютон называл производную функцию флюксией, а саму функцию – флюентой.
Некоторые применения производной в физике
Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции.
Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.
Таким образом,
Значит, чтобы вычислить производную функции f(x) в точке x0 по определению, нужно:
Рассмотрим несколько физических задач, при решении которых применяется эта схема.
Задача о мгновенной скорости. Механический смысл производной
Напомним, как определялась скорость движения. Материальная точка движется по координатной прямой. Координата х этой точки есть известная функция x(t) времени t. За промежуток времени от t0 до t0 + 


Обычно характер движения бывает таковым, что при малых 

Но по определению 
Поэтому считают, что мгновенная скорость в момент времени t0
Коротко говорят: производная координаты по времени есть скорость. В этом состоит механический смысл производной.
Аналогично рассуждая, получаем, что производная от скорости по времени есть ускорение, т.е.
Задача о теплоемкости тела
Чтобы температура тела массой в 1г повысилась от 0 градусов до t градусов, телу необходимо сообщить определенное количество тепла Q. Значит, Q есть функция температуры t, до которой тело нагревается: Q = Q(t). Пусть температура тела повысилась с t0 до t. Количество тепла, затраченное для этого нагревания, равно 


Т.к. средняя теплоёмкость не дает представления о теплоёмкости для любого значения температуры Т, то вводится понятие теплоёмкости при данной температуре t0 (в данной точке t0).
Теплоемкостью при температуре t0 (в данной точке) называется предел
Задача о линейной плотности стержня
Рассмотрим неоднородный стержень.
Для такого стержня встаёт вопрос о скорости изменения массы в зависимости от его длины.
Средняя линейная плотность 
Таким образом, линейная плотность неоднородного стержня в данной точке определяется следующим образом:
Рассматривая подобные задачи, можно получить аналогичные выводы по многим физическим процессам. Некоторые из них приведены в таблице.
Вывод m(t) – зависимость массы расходуемого горючего от времени. 




Практические задания:
Снаряд, вылетевший из пушки, движется по закону x(t) = – 4t 2 + 13t (м). Найти скорость снаряда в конце 3 секунды.
Количество электричества, протекающего через проводник, начиная с момента времени t = 0 c, задаётся формулой q(t) = 2t 2 + 3t + 1 (Кул) Найдите силу тока в конце пятой секунды.
Количество тепла Q (Дж), необходимого для нагревания 1 кг воды от 0 o до t o С, определяется формулой Q(t) = t + 0,00002t 2 + 0,0000003t 3 . Вычислите теплоемкость воды, если t = 100 o .
Тело движется прямолинейно по закону х(t) = 3 + 2t + t 2 (м). Определите его скорость и ускорение в моменты времени 1 с и 3 с.
Найдите величину силы F, действующей на точку массой m, движущуюся по закону х(t) = t 2 – 4t 4 (м), при t = 3 с.
Тело, масса которого m = 0,5кг, движется прямолинейно по закону х(t) = 2t 2 + t – 3 (м). Найдите кинетическую энергию тела через 7 с после начала движения.
Можно указать еще много задач из техники, для решения которых также необходимо отыскивать скорость изменения соответствующей функции.
Например, отыскание угловой скорости вращающегося тела, линейный коэффициент расширения тел при нагревании, скорость химической реакции в данный момент времени.
Ввиду обилия задач, приводящих к вычислению скорости изменения функции или, иначе, к вычислению предела отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, оказалось необходимым выделить такой предел для произвольной функции и изучить его основные свойства. Этот предел и назвали производной функции.
Итак, на ряде примеров мы показали, как различные физические процессы описываются с помощью математических задач, каким образом анализ решений позволяет делать выводы и предсказания о ходе процессов.
Конечно, число примеров такого рода огромно, и довольно большая часть из них вполне доступна интересующимся учащимся.
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.
Так сказал американский математик Морис Клайн.
Список литературы :
- Абрамов А.Н., Виленкин Н.Я. и др. Избранные вопросы математики. 10 класс. – М: Просвещение, 1980.
- Виленкин Н.Я., Шибасов А.П. За страницами учебника математики. – М: Просвещение,1996.
- Доброхотова М.А., Сафонов А.Н. Функция, её предел и производная. – М: Просвещение, 1969.
- Колмогоров А.Н., Абрамов А.М. и др. Алгебра и начала математического анализа. – М: Просвещение, 2010.
- Колосов А.А. Книга для внеклассного чтения по математике. – М: Учпедгиз, 1963.
- Фихтенгольц Г.М. Основы математического анализа, ч.1 – М: Наука, 1955.
- Яковлев Г.Н. Математика для техникумов. Алгебра и начала анализа, ч.1 – М: Наука, 1987.
Источник
Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
Рабчук Александр Викторович1, Самигуллина Ракия Гареевна2
1Уфимский государственный авиационный технический университет, к.т.н.. доцент кафедры математики
2Уфимский государственный авиационный технический университет, старший преподаватель каф. математики
Аннотация
Традиционно, такие разделы высшей математики как криволинейные и поверхностные интегралы, особенно их применение, вызывают затруднения у студентов при изучении. Поэтому в данной статье кратко дана теория и приведено много разобранных примеров взятых из различных источников, в частности из [1,2,3].
Rabchuk Aleksandr Viktorovich1, Samigullina Rakiya Gareevna2
1Ufa State Aviation Technical University, PhD in Technical Science, Assistant Professor of the Mathematic Department
2Ufa State Aviation Technical University, Senior teacher of the Mathematic Department
Abstract
By tradition, devides higher mathematics by contour and surface integrals ,particularly application, is difficult by students.Therefor in this article give theori and many look into examples from [1,2,3].
Библиографическая ссылка на статью:
Рабчук А.В., Самигуллина Р.Г. Приложения криволинейных интегралов. Часть 1 // Современная педагогика. 2014. № 10 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2014/10/2675 (дата обращения: 24.02.2023).
Приложения криволинейного интеграла первого рода
1. Если подынтегральная функция равна единиц, то криволинейный интеграл
равен длине S кривой L, т.е.
2. Пусть в плоскости Оху задана гладкая кривая L, на которой определена и непрерывна функция двух переменных z=f(x,y)≥0. Тогда можно построить цилиндрическую поверхность с направляющей L и образующей, параллельной оси Оz и заключенной между L и поверхностью z=f(x,y). Площадь этой цилиндрической поверхности можно вычислить по формуле
3. Если L=AB – материальная кривая с плотностью, равной ρ=ρ(х,у), то масса этой кривой вычисляется по формуле
(физический смысл криволинейного интеграла первого рода).
4. Статистические моменты материальной кривой L относительно координатных осей Ох и Оу соответственно равны
где ρ(х,у) – плотность распределения кривой L а
— координаты центра тяжести (центра масс) кривой L.
5. Интегралы
выражают моменты инерции кривой L с линейной плотностью ρ(х,у) относительно осей Ох, Оу и начала координат соответственно.
ПРИМЕРЫ:1. Вычислить криволинейный интеграл
где L – дуга параболы у2 = 2х, заключенная между точками (2, 2) и (8, 4).
Найдем дифференциал дуги dl для кривой
. Имеем
Следовательно, данный интеграл равен
Ответ:
2. Вычислить криволинейный интеграл
где L – контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0)
Поскольку
то остается вычислить криволинейный интеграл по каждому из отрезков АВ, ВО и ОА :
1) (АВ): так как уравнение прямой АВ имеет вид у=1 – х, то . Отсюда, учитывая, что х меняется от 0 до 1, получим
2) (ВО): рассуждая аналогично, находим х=0, 0 ≤ у ≤ 1, откуда
3) (ОА):
.
4) Окончательно
Ответ:
3. Вычислить криволинейный интеграл
где L – окружность
Введем полярные координаты
Тогда, поскольку
уравнение окружности примет вид
т.е.
а дифференциал дуги
При этом Следовательно,
Ответ:
4. Вычислить криволинейный интеграл первого рода от функции с тремя переменными
где L – дуга кривой, заданной параметрически
Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:
Теперь выразим через t дифференциал dl:
Таким образом,
Ответ:
5. Вычислить площадь части боковой поверхности кругового цилиндра , ограниченной снизу плоскостью Оху, а сверху поверхностью
Искомая площадь вычисляется по формуле
где L – окружность x2+y2=R2. Поверхность цилиндра и поверхность симметричны относительно координатных плоскостей Оxz и Oyz, поэтому можно ограничиться вычислением интеграла при условиях у≥0, х≥0, т.е. вычислить четверть искомой площади и результат умножить на 4. Имеем
Следовательно,
Получили определенный интеграл, который берем подстановкой
откуда
Ответ:
6. Найти массу четверти эллипса
расположенной в первой четверти, если линейная плотность в каждой точке пропорциональна ординате этой точки с коэффициентом k.
Поскольку р(х, у)=ky, имеем
L – четверть эллипса
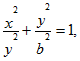
Переходим к параметрическим координатам эллипса Напомним, что
— фокусное расстояние эллипса, а
— эксцентриситет эллипса. Находим
Переходим к вычислению массы
Воспользуемся формулой
где Получаем
Учитывая, что 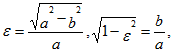
Ответ: .gif)
7. Найти координаты центра тяжести дуги окружности x2+y2=R2(0≤ x ≤R, 0≤ y ≤R).
Так как по условию задана четверть дуги окружности, то ее длина
В силу того, что биссектриса I координатного угла является осью симметрии, имеем
. Теперь находим
Ответ:
Приложения криволинейного интеграла второго рода
Интеграл
можно представить в виде скалярного произведения векторов F=Pi+Qi и ds=idx+jdy:
В таком случае
Выражает работу переменной силы F=Pi+Qj при перемещении материальной точки М=М(х,у) вдоль кривой L=AB от точки А до точки В.
При А=В кривая L замкнута, а соответствующий криволинейный интеграл по замкнутой кривой обозначается так:
В этом случае направление обхода контура иногда поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим, что в плоскости Оху имеется односвязная область D (это значит, что в ней нет «дыр»), ограниченная кривой , (
— обозначение границы области D), а в области D и на ее границе
функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными.
Теорема: Пусть А и В – произвольные точки области D, AmB и AnB – два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 2).
Тогда следующие условия равносильны:
1. (условие Грина).
2. (криволинейный интеграл не зависит от пути интегрирования).
3. (интеграл по любому замкнутому пути равен нулю).
4. (выражение
представляет собой полный дифференциал некоторой функции
).
В случае выполнения любого из равносильных условий предыдущей теоремы криволинейный интеграл по любой кривой, соединяющей точки (хо, уо) и (х1, у1) из области D, можно вычислить при помощи формулы Ньютона-Лейбница
где U(x, y) – некоторая первообразная для P dx + Q dy.
С другой стороны, первообразная U(x, y) выражения P dx + Q dy может быть найдена при помощи криволинейного интеграла
В этих же условиях на функции Р(х,у) и Q(х,у), а также на область D, имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
Здесь предполагается, что обход границы области D в криволинейном интеграле
совершается в положительном направлении, т.е. при таком обходе границы область D остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
Заметим, что площадь S=S(D) области D может быть вычислена при помощи криволинейного интеграла второговрода:
(эта формула получается из формулы Грина с ).
ПРИМЕРЫ:1. Даны функции Р(х ,у) = 8х+4у+2, Q(х ,у) = 8у+2 и точки А(3, 6), В(3,0), С(0,6). Вычислить криволинейный интеграл
где:
1) L – отрезок ОА;
2) L – ломаная ОВА;
3) L – ломаная ОСА;
4) L – парабола, симметричная относительно оси Оу и проходящая через точки О и А;
5) проверить выполнимость условия Грина.
1) Отрезок ОА может быть записан в виде: у=2х, . Тогда dy=2dx и
2) Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам ОВ и ВА. Тогда:
а) ОВ: здесь у=0, 0≤х≤3, т.е. dy=0, откуда
б) ВА: х=3, 0≤у≤6, т.е. dx=0, и
Таким образом,
3) Этот интеграл вычислим аналогично предыдущему.
а) ОС: х=0, (т.е. dx=0), 0≤y≤6, откуда
б) СА: 0≤х≤3 , у=6, dy=0, следовательно,
Окончательно
4) Подставив координаты точки А(3;6) в равенство у=ах2 найдем уравнение данной параболы . При этом 0≤х≤3 и
откуда (путь ОА по параболе обозначим
)
5) Имеем
т.е. условие Грина не выполняется. Этот факт, а также вычисления в пунктах 1) – 4) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
2. Вычислить интеграл
где L – верхняя половина эллипса .gif)
Воспользуемся параметрическими уравнениями эллипса: х=a cost, y=b sin t,
т.е. dx = – a sin t dt, dy = b cos t dt. Подставляя в интеграл и учитывая направление обхода (откуда следует, что t меняется от π до 0), получаем
.gif)
3. Вычислить криволинейный интеграл
где L – отрезок, соединяющий точку С(2, 3, -1) с точкой D(3, -2, 0).
Составим параметрические уравнения отрезка СD, используя уравнения прямой, проходящей через две точки:
Отсюда . Далее, находим
подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
Ответ:
4. Вычислить где К – отрезок прямой от А(0 ;0) до В (4; 3).
Уравнение прямой АВ имеет вид у=(3; 4)х. Находим у/= ¾ и, следовательно,
Ответ:
5. Вычислить если
Найдем
Тогда
Ответ:
6. Найти массу М дуги кривой x=t, y=t2/2, z=t3/3 (0≤ t ≤1), линейная плотность которой меняется по закону
Ответ:
7. Вычислить криволинейный интеграл от точки А(1, 0) до точки В(0, 2) (рис. 3):
1) по прямой 2х+у=2;
2) по дуге параболы 4х+у2=4;
3) по дуге эллипса x=cost, y=2sint.
1) Пользуясь данным уравнением линии интегрирования, преобразуем криволинейный интеграл в обыкновенный определенный интеграл с переменной х, затем вычисляем его:
у=2-2х, dy=-2dx,
2) Здесь удобно преобразовать криволинейный интеграл в обыкновенный интеграл с переменной у:
3) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем его: x=cost, dx=-sintdt; y=2sint; dy=2costdt:
Ответ: I1=1, I2=-1/5, I3=4/3.
8. Вычислить криволинейный интеграл между точками Е
(-1, 0) и Н (0, 1):
1) по прямой ЕН;
2) по дуге астроиды х=cos3t, y=sin3t.
1) Вначале составляем уравнение линии интегрирования – прямой ЕН, как уравнение прямой, проходящей через две известные точки: у-х=1.
Пользуясь этим уравнением и известной формулой для дифференциала дуги плоской кривой преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной х и вычисляем его:
2) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем:
ибо π/2≤ t ≤π;
Ответ:
9. Даны точки А(3, -6, 0) и В(-2, 4, 5). Вычислить криволинейный интеграл
1) по прямолинейному отрезку ОВ;
2) по дуге АВ окружности, заданной уравнениями x2+y2+z2=45, 2x+y=0.
1) Вначале составляем уравнения линии интегрирования – прямой ОВ.
Пользуясь общими уравнениями прямой, проходящей через две точки .gif)
Приравнивая эти равные отношения параметру t, преобразуем полученные канонические уравнения прямой ОВ к параметрическому виду: x=-2t, y=4t, z=5t.
Далее, пользуясь этими уравнениями, преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной t, затем вычисляем его
2) Преобразуем данные уравнения окружности к параметрическому виду. Полагая х=t, получим у=-2t (из второго данного уравнения), (из первого уравнения). Отсюда
.gif)
Ответ:
10. Вычислить криволинейные интегралы:
1)
2) вдоль периметра треугольника с
вершинами А(-1,0), В (0,2) и С (2,0)
Составив уравнение прямой АВ, у-2х=2, и исходя из этого уравнения, преобразуем криволинейный интеграл на отрезке АВ в обыкновенный интеграл с переменной х:
у=2х+2, dy=2dx,
Аналогичным путем вычисляя криволинейный интеграл на отрезках ВС и СА, получим
х=2-у, dx=-dy,
Следовательно,
2) Здесь подынтегральное выражение есть полный дифференциал функции двух переменных, ибо (уcosx)’y =(sinx)’x =cosx. Вследствии этого данный криволинейный интеграл, взятый по периметру данного треугольника равен нулю. Он будет равен нулю и по любому другому замкнутому контуру.
Ответ:
11. Найти длину кардиоиды x=2acost-acos2t, y=2asint-asin2t.
Применяем формулу
, исходя из данных параметрических уравнений кардиоиды и формулы для дифференциала дуги плоской кривой, преобразуем криволинейный интеграл формулы в обыкновенный интеграл с переменной t.
Ответ: L=16a.
12. Найти площадь, ограниченную замкнутой кривой:
1) эллипсом x=a cost, y=b sint;
2) петлей декартова листа х3+у3-3аху=0.
1) Применяем формулу
, исходя из данных параметрических уравнений эллипса, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной t и вычисляем его:
2) Вначале преобразуем данное уравнение к параметрическому виду. Полагая у=хt, получим
Геометрический параметр t=y/x есть угловой коэффициент полярного радиуса ОМ (рис. 6), точка М(х, у) опишет всю петлю кривой при изменении t от 0 до +∞.
Преобразуя криволинейный интеграл формулы в обыкновенный интеграл с переменной t , получим
Ответ: S=3a2/2.
13. Найти массу дуги АВ кривой у=lnx, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки: хА=1, хВ=3.
Применяем формулу
, исходя из данного уравнения кривой, преобразуем криволинейный интеграл в обыкновенный с переменной х
Ответ:
14. Найти координаты центра тяжести дуги АВ винтовой линии х=аcost, y=asint, z=bt, если в каждой ее точке линейная плотность пропорциональна аппликате этой точки: tA=0, tB=π.
Применяя формулы
.gif)
Следовательно,
Ответ:
15. Вычислить работу, совершаемую силой тяжести при перемещении точки массы m по дуге АВ некоторой кривой.
Если выбрать прямоугольную систему координат так, чтобы направление оси Оz совпало с направлением силы тяжести, то действующая на точку сила
а ее проекции на оси координат Fx=P=O, Fy=Q=0, Fz=R=mg.
Искомая работа согласно формуле
Она зависит только от разности аппликат начала и конца пути, но не зависит от формы пути.
16. Найти работу силового поля, в каждой точке (х,у) которого напряжение (сила, действующая на единицу массы) , когда точка массы m описывает окружность x=accost, y=asint, двигаясь по ходу часовой стрелки.
Подставляя в формулу
проекции силы
действующей на точку: Fx=m(x+y), Fy= – mx, и преобразуя криволинейный интеграл в обыкновенный с переменной t, получим
Ответ: Е=2πma2.
Библиографический список
- Лунгу К.Н. Сборник задач по высшей математике. 1 курс – 7-е изд., – М.: Айрис-пресс, 2008.
- Лунгу К.Н. Сборник задач по высшей математике. 2 курс – 5-е изд., – М.: Айрис-пресс, 2007.
- Письменный Д.Т. Конспект лекций по высшей математике: полный курс – 7-е изд. – М.: Айрис-пресс, 2008.
Все статьи автора «Рабчук Александр Викторович»
Что такое линейная массовая плотность в физике?
Линейная массовая плотность количество массы на единицу длины. Так же, как обычная плотность — это масса на единицу объема, линейная плотность — это масса на единицу длины. Линейные плотности обычно используются для длинных тонких объектов, таких как струны для музыкальных инструментов.
Что такое формула линейной плотности массы?
Размерная формула линейной плотности массы = М1Л-1Т0. Единицей СИ линейной плотности массы является кг м-1.
Что такое линейная массовая плотность стержня?
Линейная массовая плотность (λ) стержня длиной L, вытянутого вдоль оси x, изменяется как λ=α+βx, где α и β — положительные константы.
От чего зависит линейная массовая плотность?
Линейная массовая плотность (масса/длина) стержня зависит от расстояние от одного конца (скажем, A) поскольку λx=(αx+β) Здесь α и β — константы. … Длина стержня l.
Что такое линейная плотность?
3.2. 1 Линейная плотность. Линейная плотность мера массы волокна на единицу длины или длины на единицу массы. Обычно встречающиеся единицы линейной плотности включают денье (D), децитекс (dtex), количество хлопка (cc или Ne) и метрическое количество (Nm).
Что такое линейная плотность и поверхностная плотность?
Плотность площади двумерного объекта рассчитывается как масса на единицу площади. … Линейная плотность двумерного объекта равна рассчитывается как масса на единицу длины. Производная единица СИ: килограмм на метр. Объемная плотность двумерного объекта рассчитывается как масса на единицу объема.
Почему важна линейная массовая плотность?
Линейная массовая плотность количество массы на единицу длины. … Линейные плотности обычно используются для длинных тонких объектов, таких как струны для музыкальных инструментов.
Как найти плотность по линейной плотности?
Разделите массу струны на ее длину, чтобы получить линейную плотность. в килограммах на метр. Для примера струны весом 0,0025 кг и длиной 0,43 м выполните эту операцию следующим образом: 0,0025/0,43 = 0,00582 кг/м.
Что такое линейная плотность заряда?
Линейная плотность заряда (λ) равна количество заряда на единицу длины, измеряемый в кулонах на метр (C⋅m−1), в любой точке линейного распределения заряда. Плотность заряда может быть как положительной, так и отрицательной, поскольку электрический заряд может быть как положительным, так и отрицательным.
Как найти линейную массовую плотность стержня?
Линейная массовая плотность стержня определяется выражением α=Bx2 который расположен на оси x с одним из концов в начале координат.
Как найти плотность стержня?
1. Центр масс для функции линейной плотности. Удочка имеет длину 4 метра. На расстоянии метров от его левого конца плотность стержня определяется выражением δ ( х ) = 5 + 2 х г/м.
Как найти массу стержня с различной плотностью?
Рис. 2.48. Массу тонкого стержня, ориентированного вдоль оси x, можно вычислить по формуле интегрируя его функцию плотности. Если стержень имеет постоянную плотность ρ , выраженную в виде массы на единицу длины, то масса стержня — это просто произведение плотности и длины стержня: ( b — a ) ρ .
Как линейная плотность влияет на скорость волны?
Так как скорость волны на струне обратно пропорциональна квадратному корню из линейной массовой плотности, скорость будет выше при низкой линейной плотности массы струны.
Что такое производная линейной плотности?
Или р = [M1 L T] × [M L1 T]–1 = [M1 L–1 T]. Следовательно, линейная плотность размерно представлена как [M1 L–1 T].
Что такое линейная плотность в легких?
Они характеризуются линейные тени повышенной плотности на основания легких. Обычно они горизонтальные, имеют толщину 1-3 мм и длину всего несколько сантиметров. В большинстве случаев эти находки не имеют клинического значения и наблюдаются у курильщиков и пожилых людей.
Смотрите также, как сделать вулкан дымом без сухого льда
Что является переменной для линейной плотности?
Линейная плотность, представленная λ, указывает количество количества, обозначенного м, на единицу длины по одному измерению.
Как найти линейную плотность заряда?
Количество заряда на единицу длины, измеряемое в кулонах на метр (см-1), в любой точке линейного распределения заряда называется линейной плотностью заряда (λ). Предположим, что q — заряд, а l — длина, по которой он течет, тогда формула линейной плотности заряда имеет вид λ= q/lи С.И.
Масса равна плотности?
Калькулятор плотности использует формулу p=m/V или плотность (p) равна массе (m), деленной на объем (V)
. Калькулятор может использовать любые два значения для расчета третьего. Плотность определяется как масса на единицу объема.
Что такое массовый объем?
Обновлено 7 октября 2019 г. Масса и объем — это две единицы измерения объектов. Масса – это количество материи, содержащейся в объекте, а объем — это то, сколько места он занимает.
Что подразумевается, если предполагается, что линейная плотность массы объекта однородна?
Если плотность одинакова, объект не сдвинется с того места, где он находится. … Дайте определение термину «линейная массовая плотность». Кроме того, что подразумевается, если предполагается, что линейная плотность массы объекта однородна? Линейная массовая плотность = масса на единицу длины.
Как линейная плотность влияет на частоту?
Использование другой струны (как правило, той же длины) означает, что вы используете струну с другим натяжением и/или плотностью линейной массы; чем выше напряжение, тем выше скорость волны и, следовательно, частота, но чем выше линейная массовая плотность, тем ниже частота.
Какова линейная плотность струны?
Линейная плотность струны равно массе, деленной на длину струны. Основная длина волны равна удвоенной длине струны.
Какова линейная плотность воды?
Весовая плотность воды 62,4 фунта/фут3, или 9800 Н/м3. Используйте уравнение для расчета общей силы.
Как найти плотность?
Формула плотности д = М/В, где d — плотность, M — масса, V — объем. Плотность обычно выражается в граммах на кубический сантиметр.
Как рассчитать линейную плотность FCC?
Что такое объемная и линейная плотности заряда?
В зависимости от того, как распределен заряд, будем рассматривать либо объемную плотность заряда ρ = dq dV, либо поверхностную плотность заряда σ = dq dA, либо линейная плотность заряда λ = dq d A , где V, A и A обозначают объем, площадь и длину соответственно.
Каково правильное выражение для линейной плотности заряда?
линейная плотность заряда: λ≡ заряд на единицу длины (рис. 5.6. 1а); единицы – кулоны на метр (Кл/м) поверхностная плотность заряда: σ≡ заряд на единицу площади (рис. 5.6.1b); единицы — кулоны на квадратный метр (Кл/м2)
Что такое уравнение плотности заряда?
Формулы плотности заряда | Решенные примеры вопросов
Смотрите также, как называется мужская гамета у растений.
Плотность заряда зависит от распределения заряда и может быть положительным или отрицательным. В зависимости от природы формула плотности заряда может быть представлена следующим образом: (i) линейная плотность заряда; λ=ql. , где q — заряд, l. это длина, по которой он распределяется.
Как найти массу по плотности в исчислении?
Для объекта постоянной плотности D, объема V и массы m мы знаем, что m=D·V. Если плотность тела с постоянной площадью поперечного сечения (например, тонкого стержня) распределена вдоль оси согласно функции ρ(x), то мы можем найти массу тела между x=a и x=b через m=∫baρ(x)dx.
Как найти плотность стального стержня?
Если к каждому диаметру стального стержня в формуле подставить 1 метр длины, то получится удельный вес.
- ø стержня 6 мм = 6² x 1/162 = 0,222 кг/м.
- ø стержня 8 мм = 8² x 1/162 = 0,395 кг/м.
- ø стержня 10 мм = 10² x 1/162 = 0,617 кг/м.
- ø стержня 12 мм = 12² x 1/162 = 0,888 кг/м.
- ø стержня 16 мм = 16² x 1/162 = 1,580 кг/м.
Как найти центр масс, зная линейную плотность массы?
Как найти массу по плотности?
Формула плотности – это масса объекта, деленная на его объем. В форме уравнения это д = м/об , где d — плотность, m — масса, а v — объем объекта. Стандартные единицы – кг/м³.
Влияет ли линейная массовая плотность на длину волны?
То линейная массовая плотность уменьшается. Если L остается фиксированным, то комбинированные эффекты увеличения натяжения и уменьшения линейной плотности массы приводят к увеличению скорости волны, что для данной частоты возбуждения означает увеличение результирующей длины волны.
Как плотность влияет на волну?
Плотность материала влияет скорость, с которой волна будет распространяться через него. Как правило, чем плотнее прозрачный материал, тем медленнее через него проходит свет. Стекло плотнее воздуха, поэтому световой луч, проходящий из воздуха в стекло, замедляется.



























.gif)
.gif)
.gif)
.gif)
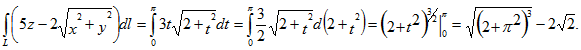
.gif)
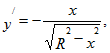
.gif)
.gif)
.gif)
.gif)
.gif)
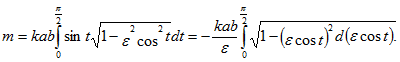
.gif)
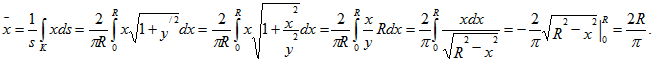
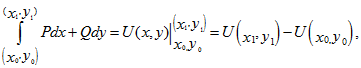
.gif)
.gif)
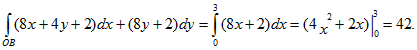
.gif)
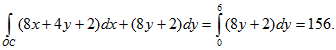
.gif)
.gif)
.gif)
.gif)
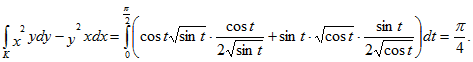
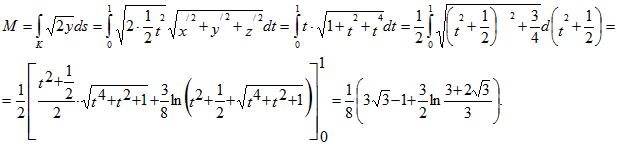
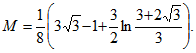
.gif)
.gif)
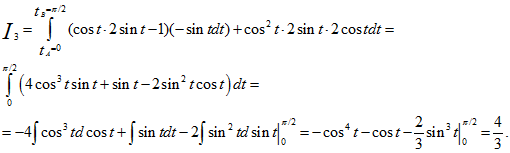
.gif)
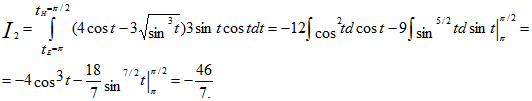
.gif)
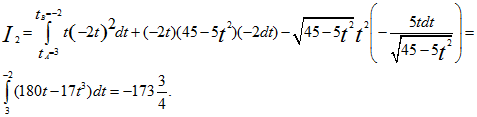
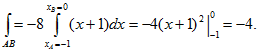
.gif)
.gif)
.gif)
.gif)
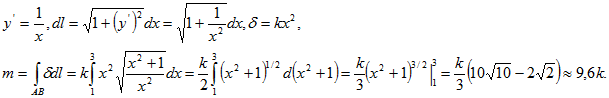
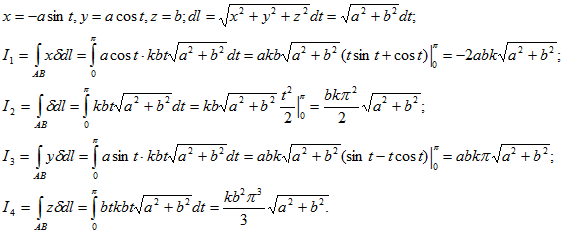
.gif)