Как найти линейно независимость векторов

Линейно зависимые и линейно независимые вектора.

Навигация по странице:

Определение линейной комбинации векторов
Определение линейно независимой комбинации векторов
Определение линейно зависимой комбинации векторов
Свойства линейно зависимых векторов
Примеры задач на линейную зависимость и линейную независимость векторов

Определение. Линейной комбинацией векторов a₁, …, a_n с коэффициентами x₁, …, x_n называется вектор

x₁a₁ + … + x_na_n.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется тривиальной, если все коэффициенты x₁, …, x_n равны нулю.

Определение. Линейная комбинация x₁a₁ + … + x_na_n называется нетривиальной, если хотя быбы один из коэффициентов x₁, …, x_n не равен нулю.

Определение. Вектора a₁, …, a_n называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору.

То есть вектора a₁, …, a_n линейно независимы если x₁a₁ + … + x_na_n = 0 тогда и только тогда, когда x₁ = 0, …, x_n = 0.

Определение. Вектора a₁, …, a_n называются линейно зависимыми, если существует нетривиальная комбинация этих векторов равная нулевому вектору.

Свойства линейно зависимых векторов:

Для 2-х и 3-х мерных векторов.

Два линейно зависимые вектора — коллинеарные. (Коллинеарные вектора — линейно зависимы.)
.
Для 3-х мерных векторов.

Три линейно зависимые вектора — компланарные. (Три компланарные вектора — линейно зависимы.)
Для n -мерных векторов.

n + 1 вектор всегда линейно зависимы.

Примеры задач на линейную зависимость и линейную независимость векторов:

Пример 1. Проверить будут ли вектора a = {3; 4; 5}, b = {-3; 0; 5}, c = {4; 4; 4}, d = {3; 4; 0} линейно независимыми.

Решение:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Пример 2. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1} линейно независимыми.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x₁ + x₂ = 0
x₁ + 2x₂ — x₃ = 0
x₁ + x₃ = 0

Решим эту систему используя метод Гаусса

1100
12-10
1010

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 — 12 — 1-1 — 00 — 0
1 — 10 — 11 — 00 — 0

1100
01-10
0-110

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 01 — 10 — (-1)0 — 0
01-10
0 + 0-1 + 11 + (-1)0 + 0

1010
01-10
0000

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x₁, x₂, x₃ таких, что линейная комбинация векторов a, b, c равна нулевому вектору, например:

—a + b + c = 0

а это значит вектора a, b, c линейно зависимы.

Ответ: вектора a, b, c линейно зависимы.

Пример 3. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 2} линейно независимыми.

x₁a + x₂b + x₃c₁ = 0

Это векторное уравнение можно записать в виде системы линейных уравнений

	x₁ + x₂ = 0
x₁ + 2x₂ — x₃ = 0
x₁ + 2x₃ = 0

Решим эту систему используя метод Гаусса

1100
12-10
1020

из второй строки вычтем первую; из третей строки вычтем первую:

1100
1 — 12 — 1-1 — 00 — 0
1 — 10 — 12 — 00 — 0

1100
01-10
0-120

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 01 — 10 — (-1)0 — 0
01-10
0 + 0-1 + 12 + (-1)0 + 0

1010
01-10
0010

из первой строки вычтем третью; к второй строке добавим третью:

1 — 00 — 01 — 10 — 0
0 + 01 + 0-1 + 10 + 0
0010

1010
0100
0010

Данное решение показывает, что система имеет единственное решение x₁ = 0, x₂ = 0, x₃ = 0, а это значит вектора a, b, c линейно независимые.

Ответ: вектора a, b, c линейно независимые.

Источник

10. Определение линейной зависимости и независимости векторов. Введем важные понятия, играющие большую роль в линейных уравнениях, например, – понятия линейной зависимости и независимости векторов

Определение 1. Линейной
комбинацией векторовназывается сумма произведений этих
векторов на скаляры:

.
(2.8)

Определение 2. Система
векторовназывается линейно зависимой системой,
если линейная комбинация их (2.8) обращается
в нуль:

=0,
(2.9)

причем среди чиселсуществует хотя бы одно, отличное от
нуля.

Определение 3. Векторыназываются линейно независимыми, если
их линейная комбинация (2.8) обращается
в нуль лишь в случае, когда все числа.

Из этих определений можно
получить следующие следствия.

Следствие 1. В линейно
зависимой системе векторов хотя бы один
вектор может быть выражен как линейная
комбинация остальных.

Доказательство. Пусть
выполнено (2.9) и пусть для определенности,
коэффициент.
Имеем тогда:.
Заметим, что справедливо и обратное
утверждение.

Следствие 2. Если система
векторовсодержит нулевой вектор, то эта система
(обязательно) линейно зависима –
доказательство очевидно.

Следствие 3. Если средиnвекторовкакие либоk()
векторов линейно зависимы, то и всеnвекторов линейно зависимы (опустим
доказательство).

2⁰. Линейные
комбинации двух, трех и четырех векторов.
Рассмотрим вопросы линейной зависимости
и независимости векторов на прямой,
плоскости и в пространстве. Приведем
соответствующие теоремы.

Теорема 1. Для того чтобы
два вектора были линейно зависимы,
необходимо и достаточно, чтобы они были
коллинеарны.

Необходимость. Пусть векторыилинейно зависимы. Это означает, что их
линейная комбинация=0
и (ради определенности).
Отсюда следует равенство,
и (по определению умножения вектора на
число) векторыиколлинеарны.

Достаточность. Пусть векторыиколлинеарны (║)
(предполагаем, что они отличны от нулевого
вектора; иначе их линейная зависимость
очевидна).

По теореме (2.7)
(см. §2.1,п.2⁰) тогдатакое, что,
или– линейная комбинация равна нулю, причем
коэффициент приравен 1 – векторыилинейно зависимы.

Из этой теоремы вытекает
следующее следствие.

Следствие. Если векторыине коллинеарны, то они линейно независимы.

Теорема 2. Для того чтобы
три вектора были линейно зависимы,
необходимо и достаточно, чтобы они были
компланарны.

Необходимость. Пусть векторы,илинейно зависимы. Покажем, что они
компланарны.

Из определения
линейной зависимости векторов следует
существование чисел
итаких, что линейная комбинация,
и при этом (для определенности).
Тогда из этого равенства можно выразить
вектор:=,
то есть векторравен диагонали параллелограмма,
построенного на векторах, стоящих в
правой части этого равенства (рис.2.6).
Это означает, что векторы,илежат в одной плоскости.

Достаточность. Пусть векторы,икомпланарны. Покажем, что они линейно
зависимы.

Исключим случай
коллинеарности какой либо пары векторов
(ибо тогда эта пара линейно зависима и
по следствию 3 (см.п.1⁰) все три
вектора линейно зависимы). Заметим, что
такое предположение исключает также
существование нулевого вектора среди
указанных трех.

Перенесем три компланарных
вектора в одну плоскость и приведем их
к общему началу. Через конец вектора
проведем прямые, параллельные векторами;
получим при этом векторыи(рис.2.7) – их существование обеспечено
тем, что векторыине коллинеарные по предположению
векторы. Отсюда следует, что вектор=+.
Переписав это равенство в виде
(–1)++=0,
заключаем, что векторы,илинейно зависимы.

Из доказанной теоремы вытекает
два следствия.

Следствие 1. Пустьине коллинеарные векторы, вектор– произвольный, лежащий в плоскости,
определяемой векторамии,
вектор. Существуют тогда числаитакие, что

=+.
(2.10)

Следствие 2. Если векторы,ине компланарны, то они линейно независимы.

Теорема 3. Любые четыре
вектора линейно зависимы.

Доказательство опустим; с
некоторыми изменениями оно копирует
доказательство теоремы 2. Приведем
следствие из этой теоремы.

Следствие. Для любых
некомпланарных векторов,,и любого вектораитакие, что

.
(2.11)

Замечание. Для векторов в
(трехмерном) пространстве понятия
линейной зависимости и независимости
имеют, как это следует из приведенных
выше теорем 1-3, простой геометрический
смысл.

Пусть имеются два линейно
зависимых вектора
и.
В таком случае один из них является
линейной комбинацией второго, то есть
просто отличается от него численным
множителем (например,).
Геометрически это означает, что оба
вектора находятся на общей прямой; они
могут иметь одинаковое или противоположное
направления (рис.2.8 хх ).

Если же два вектора расположены
под углом друг к другу (рис.2.9 хх ), то в
этом случае нельзя получить один из них
умножением другого на число – такие
векторы линейно независимы. Следовательно,
линейная независимость двух векторов
иозначает, что эти векторы не могут быть
уложены на одну прямую.

Выясним геометрический смысл
линейной зависимости и независимости
трех векторов.

Пусть векторы
,илинейно зависимы и пусть (для определенности)
векторявляется линейной комбинацией векторови,
то есть расположен в плоскости, содержащей
векторыи.
Это означает, что векторы,илежат в одной плоскости. Справедливо и
обратное утверждение: если векторы,илежат в одной плоскости, то они линейно
зависимы.

Таким образом,
векторы
,илинейно независимы в том и только в том
случае, если они не лежат в одной
плоскости.

3⁰. Понятие
базиса. Одним из важнейших понятий
линейной и векторной алгебры является
понятие базиса. Введем определения.

Определение 1. Пара векторов
называется упорядоченной, если указано,
какой вектор этой пары считается первым,
а какой вторым.

Определение 2. Упорядоченная
пара,неколлинеарных векторов называется
базисом на плоскости, определяемой
заданными векторами.

Теорема 1. Всякий векторна плоскости может быть представлен
как линейная комбинация базисной системы
векторов,:

(2.12)

и это представление единственно.

Доказательство. Пусть
векторыиобразуют базис. Тогда любой векторможно представить в виде.

Для доказательства единственности
предположим, что имеется еще одно
разложение
.
Имеем тогда=0,
причем хотя бы одна из разностей отлична
от нуля. Последнее означает, что векторыилинейно зависимы, то есть коллинеарны;
это противоречит утверждению, что они
образуют базис.

Но тогда
– разложение единственно.

Определение 3. Тройка
векторов называется упорядоченной,
если указано, какой вектор ее считается
первым, какой вторым, а какой третьим.

Определение 4. Упорядоченная
тройка некомпланарных векторов называется
базисом в пространстве.

Здесь также справедлива теорема
разложения и единственности.

Теорема 2. Любой векторможет быть представлен как линейная
комбинация базисной системы векторов,,:

(2.13)

и это представление единственно
(опустим доказательство теоремы).

В разложениях (2.12) и (2.13) величины
называются координатами векторав заданном базисе (точнее, аффинными
координатами).

При фиксированном базисе
иможно писать.

Например, если задан базис
и дано, что,
то это означает, что имеет место
представление (разложение).

4⁰. Линейные
операции над векторами в координатной
форме. Введение базиса позволяет
линейные операции над векторами заменить
обычными линейными операциями над
числами – координатами этих векторов.

Пусть задан некоторый базис
.
Очевидно, задание координат вектора в
этом базисе полностью определяет сам
вектор. Имеют место следующие предложения:

а) два вектора
иравны тогда и только тогда, когда равны
их соответственные координаты:

;
(2.14)

б) при умножении вектора
на числоего координаты умножаются на это число:

;
(2.15)

в) при сложении векторов
складываются их соответственные
координаты:

.
(2.16)

Доказательства этих свойств
опустим; докажем лишь для примера
свойство б). Имеем

==.

Замечание. В пространстве
(на плоскости) можно выбрать бесконечно
много базисов.

Приведем пример перехода от
одного базиса к другому, установим
соотношения между координатами вектора
в различных базисах.

Пример 1. В базисной системезаданы три вектора:,и.
В базисе,,векторимеет разложение.
Найти координаты векторав базисе.

Решение. Имеем разложения:,,;
следовательно,=+2+=
=,
то естьв базисе.

Пример 2. Пусть в некотором
базисечетыре вектора заданы своими координатами:,,и.

Выяснить,
образуют ли векторы
базис; в случае положительного ответа
найти разложение векторав этом базисе.

Решение. 1) векторы образуют
базис, если они линейно независимы.
Составим линейную комбинацию векторов()
и выясним, при какихиона обращается в нуль:=0.
Имеем:

=++=

По определению
равенства векторов в координатной форме
получим следующую систему (линейных
однородных алгебраических) уравнений:
;;,
определитель которой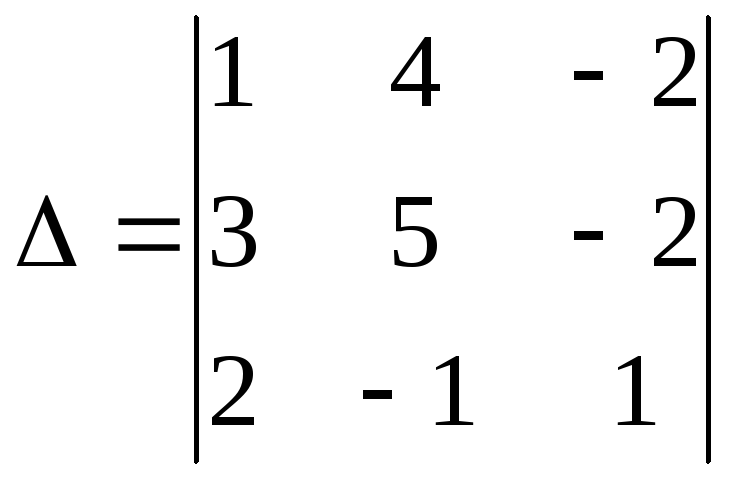=1,
то есть система имеет (лишь) тривиальное
решение.
Это означает линейную независимость
векторови, следовательно, они образуют базис.

2) разложим вектор
в этом базисе. Имеем:=или в координатной форме.

Переходя к
равенству векторов в координатной
форме, получим систему линейных
неоднородных алгебраических уравнений:
;;.
Решая ее (например, по правилу Крамера),
получим:,,и ().
Имеем разложение векторав базисе:=.

5⁰. Проекция
вектора на ось. Свойства проекций. Пусть
имеется некоторая осьl,
то есть прямая с выбранным на ней
направлением и пусть задан некоторый
вектор.Определим
понятие проекции векторана осьl.

Определение. Проекцией
векторана осьlназывается
произведение модуля этого вектора на
косинус угла между осьюlи вектором (рис.2.10):

.
(2.17)

Следствием этого определения
является утверждение о том, что равные
векторы имеют равные проекции (на одну
и ту же ось).

Отметим свойства
проекций.

1) проекция суммы векторов на
некоторую ось lравна
сумме проекций слагаемых векторов на
ту же ось:

.
(2.18)

2) проекция произведения скаляра
на вектор равна произведению этого
скаляра на проекцию вектора на ту же
ось:

=.
(2.19)

Следствие. Проекция линейной
комбинации векторов на ось равна линейной
комбинации их проекций:

.
(2.20)

Доказательства свойств опустим.

6⁰. Прямоугольная
декартова система координат в пространстве.Разложение вектора по ортам осей.
Пусть в качестве базиса выбраны три
взаимно перпендикулярных орта; для них
вводим специальные обозначения.
Поместив их начала в точкуO,
направим по ним (в соответствии с ортами)
координатные осиOx,OyиOz(ось с выбранным на ней положительным
направлением, началом отсчета и единицей
длины называется координатной осью).

Определение. Упорядоченная
система трех взаимно перпендикулярных
координатных осей с общим началом и
общей единицей длины называется
прямоугольной декартовой системой
координат в пространстве.

Ось Ox
называется осью абсцисс,Oy– осью ординат иOz
– осью аппликат.

Займемся
разложением произвольного вектора по
базису
.
Из теоремы (см.§2.2,п.3⁰, (2.13)) следует,
чтоможет быть и единственным образом
разложен по базису(здесь вместо обозначения координатупотребляют):

.
(2.21)

В (2.21)
суть (декартовы прямоугольные) координаты
вектора.
Смысл декартовых координат устанавливает
следующая теорема.

Теорема. Декартовы
прямоугольные координатывектораявляются проекциями этого вектора
соответственно на осиOx,OyиOz.

Доказательство.Поместим
векторв начало системы координат – точкуO.
Тогда его конец будет совпадать с
некоторой точкой.

Проведем через
точку
три плоскости, параллельные координатным
плоскостямOyz,OxzиOxy(рис.2.11 хх ). Получим
тогда:

.
(2.22)

В (2.22) векторы
и
называются составляющими векторапо осямOx,OyиOz.

Пусть через
иобозначены соответственно углы,
образованные векторомс ортами.
Тогда для составляющих получим следующие
формулы:

==,
==,
==(2.23)

Из (2.21), (2.22) (2.23)
находим:

==;==;==(2.23)

– координаты
вектораесть проекции этого вектора на координатные
осиOx,OyиOzсоответственно.

Замечание . Числаназываются направляющими косинусами
вектора.

Модуль вектора
(диагональ прямоугольного параллелепипеда)
вычисляется по формуле:

.
(2.24)

Из формул (2.23) и (2.24) следует,
что направляющие косинусы могут быть
вычислены по формулам:

=;=;=.
(2.25)

Возводя обе части каждого из
равенств в (2.25) и складывая почленно
левые и правые части полученных равенств,
придем к формуле:

(2.26)

– не любые три угла образуют
некоторое направление в пространстве,
но лишь те, косинусы которых связаны
соотношением (2.26).

7⁰. Радиус-вектор
и координаты точки.Определение
вектора по его началу и концу. Введем
определение.

Определение. Радиусом-вектором
(обозначается)
называется вектор, соединяющий начало
координатOс этой
точкой (рис.2.12 хх ):

.
(2.27)

Любой точке пространства
соответствует определенный радиус-вектор
(и обратно). Таким образом, точки
пространства представляются в векторной
алгебре их радиус-векторами.

Очевидно, координаты
точкиMявляются
проекциями ее радиус-векторана координатные оси:

(2.28’)

и, таким образом,

(2.28)

– радиус-вектор точки есть
вектор, проекции которого на оси координат
равны координатам этой точки. Отсюда
следует две записи:
и.

Получим формулы для вычисления
проекций вектора
по координатам его начала – точкеи конца – точке.

Проведем радиус-векторы
и вектор(рис.2.13). Получим, что

==(2.29)

– проекции вектора на координатные
орты равны разностям соответствующих
координат конца и начала вектора.

8⁰. Некоторые
задачи на декартовы координаты.

1) условия коллинеарности
векторов. Из теоремы (см.§2.1,п.2⁰,
формула (2.7)) следует, что для коллинеарности
векторовинеобходимо и достаточно, чтобы выполнялось
соотношение:=.
Из этого векторного равенства получаем
три в координатной форме равенства:,
откуда следует условие коллинеарности
векторов в координатной форме:

(2.30)

– для коллинеарности векторов
инеобходимо и достаточно, чтобы их
соответствующие координаты были
пропорциональны.

2) расстояние между
точками. Из представления (2.29)
следует, что расстояниемежду точкамииопределяется формулой

==.
(2.31)

3) деление отрезка в
данном отношении. Пусть даны точкиии отношение.
Нужно найти– координаты точкиM
(рис.2.14).

Имеем из условия коллинеарности
векторов:
,
откудаи

.
(2.32)

Из (2.32) получим в координатной
форме:

.
(2.32’)

Из формул (2.32’) можно получить
формулы для вычисления координат
середины отрезка
,
полагая:

.
(2.32”)

Замечание. Будем считать
отрезкииположительными или отрицательными в
зависимости от того, совпадает их
направление с направлением от началаотрезка к концу,
или не совпадает. Тогда по формулам
(2.32) – (2.32”) можно находить координат
точки, делящей отрезоквнешним образом, то есть так, что делящая
точкаMнаходится на
продолжении отрезка,
а не внутри его. При этом конечно,.

4) уравнение сферической
поверхности. Составим уравнение
сферической поверхности – геометрического
места точек,
равноудаленных на расстояниеот некоторого фиксированного центра –
точки.
Очевидно, что в данном случаеи с учетом формулы (2.31)

.
(2.33)

Уравнение (2.33) и есть уравнение
искомой сферической поверхности.

Источник

For linear dependence of random variables, see Covariance.

Linearly independent vectors in $mathbb{R} ^{3}$

Linearly dependent vectors in a plane in ${displaystyle mathbb {R} ^{3}.}$

In the theory of vector spaces, a set of vectors is said to be linearly independent if there exists no nontrivial linear combination of the vectors that equals the zero vector. If such a linear combination exists, then the vectors are said to be linearly dependent. These concepts are central to the definition of dimension.^[1]

A vector space can be of finite dimension or infinite dimension depending on the maximum number of linearly independent vectors. The definition of linear dependence and the ability to determine whether a subset of vectors in a vector space is linearly dependent are central to determining the dimension of a vector space.

Definition[edit]

A sequence of vectors ${displaystyle mathbf {v} _{1},mathbf {v} _{2},dots ,mathbf {v} _{k}}$ from a vector space V is said to be linearly dependent, if there exist scalars ${displaystyle a_{1},a_{2},dots ,a_{k},}$ not all zero, such that

${displaystyle a_{1}mathbf {v} _{1}+a_{2}mathbf {v} _{2}+cdots +a_{k}mathbf {v} _{k}=mathbf {0} ,}$

where denotes the zero vector.

This implies that at least one of the scalars is nonzero, say ${displaystyle a_{1}neq 0}$ , and the above equation is able to be written as

${displaystyle mathbf {v} _{1}={frac {-a_{2}}{a_{1}}}mathbf {v} _{2}+cdots +{frac {-a_{k}}{a_{1}}}mathbf {v} _{k},}$

if and ${displaystyle mathbf {v} _{1}=mathbf {0} }$ if

Thus, a set of vectors is linearly dependent if and only if one of them is zero or a linear combination of the others.

A sequence of vectors ${displaystyle mathbf {v} _{1},mathbf {v} _{2},dots ,mathbf {v} _{n}}$ is said to be linearly independent if it is not linearly dependent, that is, if the equation

${displaystyle a_{1}mathbf {v} _{1}+a_{2}mathbf {v} _{2}+cdots +a_{n}mathbf {v} _{n}=mathbf {0} ,}$

can only be satisfied by a_i=0 for This implies that no vector in the sequence can be represented as a linear combination of the remaining vectors in the sequence. In other words, a sequence of vectors is linearly independent if the only representation of as a linear combination of its vectors is the trivial representation in which all the scalars $a_{i}$ are zero.^[2] Even more concisely, a sequence of vectors is linearly independent if and only if can be represented as a linear combination of its vectors in a unique way.

If a sequence of vectors contains the same vector twice, it is necessarily dependent. The linear dependency of a sequence of vectors does not depend of the order of the terms in the sequence. This allows defining linear independence for a finite set of vectors: A finite set of vectors is linearly independent if the sequence obtained by ordering them is linearly independent. In other words, one has the following result that is often useful.

A sequence of vectors is linearly independent if and only if it does not contain the same vector twice and the set of its vectors is linearly independent.

Infinite case[edit]

An infinite set of vectors is linearly independent if every nonempty finite subset is linearly independent. Conversely, an infinite set of vectors is linearly dependent if it contains a finite subset that is linearly dependent, or equivalently, if some vector in the set is a linear combination of other vectors in the set.

An indexed family of vectors is linearly independent if it does not contain the same vector twice, and if the set of its vectors is linearly independent. Otherwise, the family is said linearly dependent.

A set of vectors which is linearly independent and spans some vector space, forms a basis for that vector space. For example, the vector space of all polynomials in x over the reals has the (infinite) subset {1, x, x², …} as a basis.

Geometric examples[edit]

Geographic location[edit]

A person describing the location of a certain place might say, «It is 3 miles north and 4 miles east of here.» This is sufficient information to describe the location, because the geographic coordinate system may be considered as a 2-dimensional vector space (ignoring altitude and the curvature of the Earth’s surface). The person might add, «The place is 5 miles northeast of here.» This last statement is true, but it is not necessary to find the location.

In this example the «3 miles north» vector and the «4 miles east» vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third «5 miles northeast» vector is a linear combination of the other two vectors, and it makes the set of vectors linearly dependent, that is, one of the three vectors is unnecessary to define a specific location on a plane.

Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, n linearly independent vectors are required to describe all locations in n-dimensional space.

Evaluating linear independence[edit]

The zero vector[edit]

If one or more vectors from a given sequence of vectors ${displaystyle mathbf {v} _{1},dots ,mathbf {v} _{k}}$ is the zero vector then the vector ${displaystyle mathbf {v} _{1},dots ,mathbf {v} _{k}}$ are necessarily linearly dependent (and consequently, they are not linearly independent).
To see why, suppose that is an index (i.e. an element of ) such that ${displaystyle mathbf {v} _{i}=mathbf {0} .}$ Then let ${displaystyle a_{i}:=1}$ (alternatively, letting $a_{i}$ be equal any other non-zero scalar will also work) and then let all other scalars be (explicitly, this means that for any index other than (i.e. for j neq i ), let ${displaystyle a_{j}:=0}$ so that consequently ${displaystyle a_{j}mathbf {v} _{j}=0mathbf {v} _{j}=mathbf {0} }$ ).
Simplifying ${displaystyle a_{1}mathbf {v} _{1}+cdots +a_{k}mathbf {v} _{k}}$ gives:

${displaystyle a_{1}mathbf {v} _{1}+cdots +a_{k}mathbf {v} _{k}=mathbf {0} +cdots +mathbf {0} +a_{i}mathbf {v} _{i}+mathbf {0} +cdots +mathbf {0} =a_{i}mathbf {v} _{i}=a_{i}mathbf {0} =mathbf {0} .}$

Because not all scalars are zero (in particular, ${displaystyle a_{i}neq 0}$ ), this proves that the vectors ${displaystyle mathbf {v} _{1},dots ,mathbf {v} _{k}}$ are linearly dependent.

As a consequence, the zero vector can not possibly belong to any collection of vectors that is linearly independent.

Now consider the special case where the sequence of ${displaystyle mathbf {v} _{1},dots ,mathbf {v} _{k}}$ has length (i.e. the case where k=1 ).
A collection of vectors that consists of exactly one vector is linearly dependent if and only if that vector is zero.
Explicitly, if $mathbf{v}_1$ is any vector then the sequence $mathbf{v}_1$ (which is a sequence of length ) is linearly dependent if and only if ${displaystyle mathbf {v} _{1}=mathbf {0} }$ ; alternatively, the collection $mathbf{v}_1$ is linearly independent if and only if ${displaystyle mathbf {v} _{1}neq mathbf {0} .}$

Linear dependence and independence of two vectors[edit]

This example considers the special case where there are exactly two vector and from some real or complex vector space.
The vectors and are linearly dependent if and only if at least one of the following is true:

is a scalar multiple of (explicitly, this means that there exists a scalar such that ) or
is a scalar multiple of (explicitly, this means that there exists a scalar such that ).

If then by setting we have (this equality holds no matter what the value of is), which shows that (1) is true in this particular case. Similarly, if then (2) is true because
If (for instance, if they are both equal to the zero vector ) then both (1) and (2) are true (by using for both).

If then is only possible if and ; in this case, it is possible to multiply both sides by ${textstyle {frac {1}{c}}}$ to conclude ${textstyle mathbf {v} ={frac {1}{c}}mathbf {u} .}$
This shows that if and then (1) is true if and only if (2) is true; that is, in this particular case either both (1) and (2) are true (and the vectors are linearly dependent) or else both (1) and (2) are false (and the vectors are linearly independent).
If but instead then at least one of and must be zero.
Moreover, if exactly one of and is (while the other is non-zero) then exactly one of (1) and (2) is true (with the other being false).

The vectors and are linearly independent if and only if is not a scalar multiple of and is not a scalar multiple of .

Vectors in R²[edit]

Three vectors: Consider the set of vectors ${displaystyle mathbf {v} _{1}=(1,1),}$ ${displaystyle mathbf {v} _{2}=(-3,2),}$ and ${displaystyle mathbf {v} _{3}=(2,4),}$ then the condition for linear dependence seeks a set of non-zero scalars, such that

${displaystyle a_{1}{begin{bmatrix}1\1end{bmatrix}}+a_{2}{begin{bmatrix}-3\2end{bmatrix}}+a_{3}{begin{bmatrix}2\4end{bmatrix}}={begin{bmatrix}0\0end{bmatrix}},}$

${displaystyle {begin{bmatrix}1&-3&2\1&2&4end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}\a_{3}end{bmatrix}}={begin{bmatrix}0\0end{bmatrix}}.}$

Row reduce this matrix equation by subtracting the first row from the second to obtain,

${displaystyle {begin{bmatrix}1&-3&2\0&5&2end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}\a_{3}end{bmatrix}}={begin{bmatrix}0\0end{bmatrix}}.}$

Continue the row reduction by (i) dividing the second row by 5, and then (ii) multiplying by 3 and adding to the first row, that is

${displaystyle {begin{bmatrix}1&0&16/5\0&1&2/5end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}\a_{3}end{bmatrix}}={begin{bmatrix}0\0end{bmatrix}}.}$

Rearranging this equation allows us to obtain

${displaystyle {begin{bmatrix}1&0\0&1end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}end{bmatrix}}={begin{bmatrix}a_{1}\a_{2}end{bmatrix}}=-a_{3}{begin{bmatrix}16/5\2/5end{bmatrix}}.}$

which shows that non-zero a_i exist such that ${displaystyle mathbf {v} _{3}=(2,4)}$ can be defined in terms of ${displaystyle mathbf {v} _{1}=(1,1)}$ and ${displaystyle mathbf {v} _{2}=(-3,2).}$ Thus, the three vectors are linearly dependent.

Two vectors: Now consider the linear dependence of the two vectors ${displaystyle mathbf {v} _{1}=(1,1)}$ and ${displaystyle mathbf {v} _{2}=(-3,2),}$ and check,

${displaystyle a_{1}{begin{bmatrix}1\1end{bmatrix}}+a_{2}{begin{bmatrix}-3\2end{bmatrix}}={begin{bmatrix}0\0end{bmatrix}},}$

${displaystyle {begin{bmatrix}1&-3\1&2end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}end{bmatrix}}={begin{bmatrix}0\0end{bmatrix}}.}$

The same row reduction presented above yields,

${displaystyle {begin{bmatrix}1&0\0&1end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}end{bmatrix}}={begin{bmatrix}0\0end{bmatrix}}.}$

This shows that ${displaystyle a_{i}=0,}$ which means that the vectors v₁ = (1, 1) and v₂ = (−3, 2) are linearly independent.

Vectors in R⁴[edit]

In order to determine if the three vectors in ${displaystyle mathbb {R} ^{4},}$

${displaystyle mathbf {v} _{1}={begin{bmatrix}1\4\2\-3end{bmatrix}},mathbf {v} _{2}={begin{bmatrix}7\10\-4\-1end{bmatrix}},mathbf {v} _{3}={begin{bmatrix}-2\1\5\-4end{bmatrix}}.}$

are linearly dependent, form the matrix equation,

${displaystyle {begin{bmatrix}1&7&-2\4&10&1\2&-4&5\-3&-1&-4end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}\a_{3}end{bmatrix}}={begin{bmatrix}0\0\0\0end{bmatrix}}.}$

Row reduce this equation to obtain,

${displaystyle {begin{bmatrix}1&7&-2\0&-18&9\0&0&0\0&0&0end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}\a_{3}end{bmatrix}}={begin{bmatrix}0\0\0\0end{bmatrix}}.}$

Rearrange to solve for v₃ and obtain,

${displaystyle {begin{bmatrix}1&7\0&-18end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}end{bmatrix}}=-a_{3}{begin{bmatrix}-2\9end{bmatrix}}.}$

This equation is easily solved to define non-zero a_i,

${displaystyle a_{1}=-3a_{3}/2,a_{2}=a_{3}/2,}$

where $a_{3}$ can be chosen arbitrarily. Thus, the vectors ${displaystyle mathbf {v} _{1},mathbf {v} _{2},}$ and ${displaystyle mathbf {v} _{3}}$ are linearly dependent.

Alternative method using determinants[edit]

An alternative method relies on the fact that vectors in $mathbb {R} ^{n}$ are linearly independent if and only if the determinant of the matrix formed by taking the vectors as its columns is non-zero.

In this case, the matrix formed by the vectors is

${displaystyle A={begin{bmatrix}1&-3\1&2end{bmatrix}}.}$

We may write a linear combination of the columns as

${displaystyle ALambda ={begin{bmatrix}1&-3\1&2end{bmatrix}}{begin{bmatrix}lambda _{1}\lambda _{2}end{bmatrix}}.}$

We are interested in whether AΛ = 0 for some nonzero vector Λ. This depends on the determinant of , which is

{displaystyle det A=1cdot 2-1cdot (-3)=5neq 0.}

Since the determinant is non-zero, the vectors (1,1) and are linearly independent.

Otherwise, suppose we have vectors of coordinates, with Then A is an n×m matrix and Λ is a column vector with entries, and we are again interested in AΛ = 0. As we saw previously, this is equivalent to a list of equations. Consider the first rows of , the first equations; any solution of the full list of equations must also be true of the reduced list. In fact, if ⟨i₁,…,i_m⟩ is any list of rows, then the equation must be true for those rows.

${displaystyle A_{langle i_{1},dots ,i_{m}rangle }Lambda =mathbf {0} .}$

Furthermore, the reverse is true. That is, we can test whether the vectors are linearly dependent by testing whether

${displaystyle det A_{langle i_{1},dots ,i_{m}rangle }=0}$

for all possible lists of rows. (In case m=n , this requires only one determinant, as above. If m>n , then it is a theorem that the vectors must be linearly dependent.) This fact is valuable for theory; in practical calculations more efficient methods are available.

More vectors than dimensions[edit]

If there are more vectors than dimensions, the vectors are linearly dependent. This is illustrated in the example above of three vectors in ${displaystyle mathbb {R} ^{2}.}$

Natural basis vectors[edit]

Let ${displaystyle V=mathbb {R} ^{n}}$ and consider the following elements in , known as the natural basis vectors:

$begin{matrix} mathbf{e}_1 & = & (1,0,0,ldots,0) \ mathbf{e}_2 & = & (0,1,0,ldots,0) \ & vdots \ mathbf{e}_n & = & (0,0,0,ldots,1).end{matrix}$

Then ${displaystyle mathbf {e} _{1},mathbf {e} _{2},ldots ,mathbf {e} _{n}}$ are linearly independent.

Proof

Suppose that $a_{1},a_{2},ldots ,a_{n}$ are real numbers such that

${displaystyle a_{1}mathbf {e} _{1}+a_{2}mathbf {e} _{2}+cdots +a_{n}mathbf {e} _{n}=mathbf {0} .}$

Since

${displaystyle a_{1}mathbf {e} _{1}+a_{2}mathbf {e} _{2}+cdots +a_{n}mathbf {e} _{n}=left(a_{1},a_{2},ldots ,a_{n}right),}$

then a_i = 0 for all

Linear independence of functions[edit]

Let be the vector space of all differentiable functions of a real variable . Then the functions e^t and ${displaystyle e^{2t}}$ in are linearly independent.

Proof[edit]

Suppose and are two real numbers such that

${displaystyle ae^{t}+be^{2t}=0}$

Take the first derivative of the above equation:

${displaystyle ae^{t}+2be^{2t}=0}$

for all values of We need to show that a=0 and In order to do this, we subtract the first equation from the second, giving ${displaystyle be^{2t}=0}$ . Since ${displaystyle e^{2t}}$ is not zero for some , It follows that a=0 too. Therefore, according to the definition of linear independence, ${displaystyle e^{t}}$ and ${displaystyle e^{2t}}$ are linearly independent.

Space of linear dependencies[edit]

A linear dependency or linear relation among vectors v₁, …, v_n is a tuple (a₁, …, a_n) with n scalar components such that

${displaystyle a_{1}mathbf {v} _{1}+cdots +a_{n}mathbf {v} _{n}=mathbf {0} .}$

If such a linear dependence exists with at least a nonzero component, then the n vectors are linearly dependent. Linear dependencies among v₁, …, v_n form a vector space.

If the vectors are expressed by their coordinates, then the linear dependencies are the solutions of a homogeneous system of linear equations, with the coordinates of the vectors as coefficients. A basis of the vector space of linear dependencies can therefore be computed by Gaussian elimination.

Generalizations[edit]

Affine independence[edit]

A set of vectors is said to be affinely dependent if at least one of the vectors in the set can be defined as an affine combination of the others. Otherwise, the set is called affinely independent. Any affine combination is a linear combination; therefore every affinely dependent set is linearly dependent. Conversely, every linearly independent set is affinely independent.

Consider a set of vectors $mathbf{v}_1, ldots, mathbf{v}_m$ of size each, and consider the set of augmented vectors ${textstyle left(left[{begin{smallmatrix}1\mathbf {v} _{1}end{smallmatrix}}right],ldots ,left[{begin{smallmatrix}1\mathbf {v} _{m}end{smallmatrix}}right]right)}$ of size n+1 each. The original vectors are affinely independent if and only if the augmented vectors are linearly independent.^[3]^: 256

Linearly independent vector subspaces[edit]

Two vector subspaces and of a vector space are said to be linearly independent if ^[4]
More generally, a collection ${displaystyle M_{1},ldots ,M_{d}}$ of subspaces of are said to be linearly independent if ${textstyle M_{i}cap sum _{kneq i}M_{k}={0}}$ for every index where ${textstyle sum _{kneq i}M_{k}={Big {}m_{1}+cdots +m_{i-1}+m_{i+1}+cdots +m_{d}:m_{k}in M_{k}{text{ for all }}k{Big }}=operatorname {span} bigcup _{kin {1,ldots ,i-1,i+1,ldots ,d}}M_{k}.}$ ^[4]
The vector space is said to be a direct sum of ${displaystyle M_{1},ldots ,M_{d}}$ if these subspaces are linearly independent and ${displaystyle M_{1}+cdots +M_{d}=X.}$

References[edit]

^ G. E. Shilov, Linear Algebra (Trans. R. A. Silverman), Dover Publications, New York, 1977.
^ Friedberg, Insel, Spence, Stephen, Arnold, Lawrence (2003). Linear Algebra. Pearson, 4th Edition. pp. 48–49. ISBN 0130084514.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Lovász, László; Plummer, M. D. (1986), Matching Theory, Annals of Discrete Mathematics, vol. 29, North-Holland, ISBN 0-444-87916-1, MR 0859549
^ ^a ^b Bachman & Narici 2000, pp. 3−7.

Bachman, George; Narici, Lawrence (2000). Functional Analysis (Second ed.). Mineola, New York: Dover Publications. ISBN 978-0486402512. OCLC 829157984.

External links[edit]

«Linear independence», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Linearly Dependent Functions at WolframMathWorld.
Tutorial and interactive program on Linear Independence.
Introduction to Linear Independence at KhanAcademy.

Источник

10. Линейная зависимость и независимость векторов

Рассмотрим далее основополагающие в линейной алгебре понятие о линейной зависимости и независимости векторов, а также определение базиса системы векторов.

Любую конечную последовательность векторов Будем называть системой векторов, а любую ее подпоследовательность – подсистемой векторов. Линейной комбинацией векторов назовем вектор , равный сумме произведений произвольных чисел на векторы системы, т. е. .

Система векторов называется линейно независимой, если их линейная комбинация равна нулевому вектору только в том случае, когда все числа равны нулю. В обратном случае система векторов называется линейно зависимой. Отсюда, система векторов является линейно зависимой в том случае, когда линейная комбинация векторов равна нулевому вектору, а хотя бы один числовой коэффициент отличен от нуля.

Линейная зависимость и независимость есть свойства системы векторов. Однако часто соответствующие прилагательные относят и к самим векторам. Поэтому вместо «линейно независимая система векторов» допустимо говорить «линейно независимые векторы».

Например, двумерные арифметические векторы И Линейно независимы. Их линейная комбинация равна вектору , который обращается в нулевой вектор Только тогда, когда и .

Если взять векторы И , то они являются линейно зависимыми, так как их линейная комбинация равна нулевому вектору при И , не равных нулю.

Из определения линейной зависимости (независимости) системы векторов вытекают следующие утверждения.

1) Если некоторая система векторов содержит нулевой вектор, то она является линейно зависимой.

Пусть для определенности первый вектор системы является нулевым, т. е.

Тогда линейная комбинация векторов вида равна нулевому вектору, что и доказывает наше утверждение.

2) Если среди векторов системы есть такие, которые сами образуют линейно зависимую подсистему, то вся система также линейно зависима.

Так как исходная подсистема линейно зависима, то среди коэффициентов линейной комбинации векторов подсистемы имеется хотя бы один отличный от нуля. Добавим к этой линейной комбинацию линейную комбинацию векторов, не вошедших в исходную подсистему, с числовыми коэффициентами, равными нулю. Мы получим линейную комбинацию из векторов полной системы, которая равна нулевому вектору, причем имеется хотя бы один коэффициент отличный от нуля. Таким образом, наше утверждение доказано.

3) Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Если предположить обратное, т. е. существование некоторой линейно зависимой подсистемы, то по предыдущему утверждению отсюда следует зависимость исходной системы, что противоречит условию доказываемой теоремы. Полученное противоречие доказывает сформулированное утверждение.

4) Для того чтобы система из 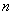Ненулевых векторов была линейно зависима необходимо и достаточно, чтобы хотя бы один из векторов системы мог быть представлен как линейная комбинация предшествующих векторов.

Необходимость. Пусть система векторов линейно зависима. Тогда равенство выполняется при том условии, что хотя бы одно из чисел в левой части равенства отлично от нуля. Будем перебирать эти числа, начиная с большего номера, и остановимся на некотором номере таком, что соответствующий коэффициент отличен от нуля, т. е. . Номер не может быть равен единице, так как иначе из условий И теоремы о нулевом произведении следовало бы равенство , что противоречит правилу выбора номера и условию теоремы. Таким образом , и справедливо равенство. Отсюда находим вектор Таким образом, чтобы он является линейной комбинацией предшествующих ему векторов, а именно .

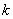
Достаточность. Пусть имеется некоторый вектор , который представлен в виде линейной комбинации предшествующих ему векторов . Тогда выполняется условие , что по определению означает линейную независимость исходной системы векторов.

По аналогичной схеме доказывается следующее утверждение.

5) Система векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов системы может быть представлен в виде линейной комбинации остальных векторов.

Как найти подсистему системы векторов

Определение 1. Система векторов 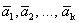называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой — в противном случае.

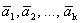
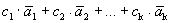
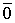
Определение 1´. Система векторов называется линейно зависимой, если найдутся числа с ₁ , с ₂ , …, с _k , не все равные нулю, такие, что линейная комбинация векторов с данными коэффициентами равна нулевому вектору: = , в противном случае система называется линейно независимой.

Покажем, что эти определения эквивалентны.

Пусть выполняется определение 1, т.е. один из векторов системы равен линейной комбинации остальных:

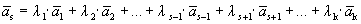
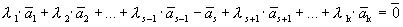
Линейная комбинация системы векторов равна нулевому вектору, причем не все коэффициенты этой комбинации равны нулю, т.е. выполняется определение 1´.

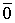
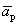
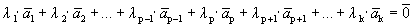
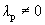
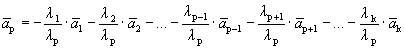
Пусть выполняется определение 1´. Линейная комбинация системы векторов равна , причем не все коэффициенты комбинации равны нулю, например, коэффициенты при векторе .

Один из векторов системы мы представили в виде линейной комбинации остальных, т.е. выполняется определение 1.

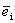
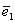
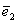
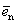
Определение 2. Единичным вектором, или ортом, называется n -мерный вектор , у которого i -я координата равна единице, а остальные — нулевые.

. (1, 0, 0, …, 0),

(0, 1, 0, …, 0),

(0, 0, 0, …, 1).

Теорема 1. Различные единичные векторы n -мерного пространства линейно независимы.

Доказательство. Пусть линейная комбинация этих векторов с произвольными коэффициентами равна нулевому вектору.

= .

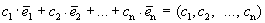
Из этого равенства следует, что все коэффициенты равны нулю. Получили противоречие.

Каждый вектор n -мерного пространства ā(а ₁ , а ₂ , . а _n ) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора

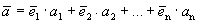
Теорема 2. Если системы векторов содержит нулевой вектор, то она линейно зависима.

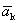
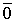
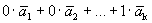
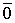
Доказательство. Пусть дана система векторов и один из векторов является нулевым, например = . Тогда с векторами данной системы можно составить линейную комбинацию, равную нулевому вектору, причем не все коэффициенты будут нулевыми:

= .

Следовательно, система линейно зависима.

Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.

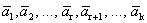
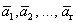
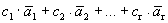
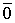
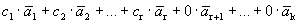
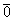
Доказательство. Дана система векторов . Предположим, что система линейно зависима, т.е. найдутся числа с ₁ , с ₂ , …, с _r , не все равные нулю, такие, что = . Тогда

= .

Получилось, что линейная комбинация векторов всей системы равна 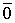, причем не все коэффициенты этой комбинации равны нулю. Следовательно, система векторов линейно зависима.

Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Предположим противное, т.е. некоторая подсистема линейно зависима. Из теоремы следует, что вся система линейно зависима. Мы пришли к противоречию.

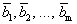
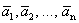
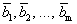
Теорема 4 (теорема Штейница). Если каждый из векторов является линейной комбинацией векторов и m > n , то система векторов линейно зависима.

Следствие. В любой системе n -мерных векторов не может быть больше чем n линейно независимых.

Доказательство. Каждый n -мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m > n , то, по теореме, данная система линейно зависима.

Как найти подсистему системы векторов

1.4. РАНГ СИСТЕМЫ ВЕКТОРОВ

Рассмотрим систему векторов (1.1), где . Максимальной линейно независимой подсистемой системы векторов (1.1) называется любой набор векторов последней, удовлетворяющий следующим условиям: векторы этого набора линейно независимы; всякий вектор из системы (1.1) линейно выражается через векторы этого набора. В общем, система векторов (1.1) может иметь несколько разных максимальных линейно независимых подсистем.

Теорема 1. 6. Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов.

Число векторов в максимальной линейно независимой подсистеме системы векторов (1.1) называется рангом последней. Системы векторов (1.1) и (1.2) называются эквивалентными, если векторы системы (1.1) линейно выражаются через систему векторов (1.2) и наоборот.

Теорема 1. 7. Ранги эквивалентных систем векторов равны.

Операции, переводящие систему векторов (1.1) в систему, ей эквивалентную, следующие:

1) изменение нумерации векторов в системе;

2) удаление нулевого вектора;

3) удаление вектора, являющегося линейной комбинацией остальных векторов системы;

4) умножение произвольного вектора системы на любое, не равное нулю число;

5) прибавление к одному из векторов системы линейной комбинации остальных векторов системы.

источники:

http://lms2.sseu.ru/courses/eresmat/course1/razd8z1/par8_5z1.htm

http://www.math.mrsu.ru/text/courses/method/rang_sist_vect.htm

Источник

Линейно зависимые и линейно независимые вектора.

Свойства линейно зависимых векторов:

Примеры задач на линейную зависимость и линейную независимость векторов:

Definition[edit]

Infinite case[edit]

Geometric examples[edit]

Geographic location[edit]

Evaluating linear independence[edit]

The zero vector[edit]

Linear dependence and independence of two vectors[edit]

Vectors in R²[edit]

Vectors in R⁴[edit]

Alternative method using determinants[edit]

More vectors than dimensions[edit]

Natural basis vectors[edit]

Linear independence of functions[edit]

Proof[edit]

Space of linear dependencies[edit]

Generalizations[edit]

Affine independence[edit]

Linearly independent vector subspaces[edit]

See also[edit]

References[edit]

External links[edit]

10. Линейная зависимость и независимость векторов

Как найти подсистему системы векторов

Как найти подсистему системы векторов

Не пропустите также:

Линейно зависимые и линейно независимые вектора.

Свойства линейно зависимых векторов:

Примеры задач на линейную зависимость и линейную независимость векторов:

Definition[edit]

Infinite case[edit]

Geometric examples[edit]

Geographic location[edit]

Evaluating linear independence[edit]

The zero vector[edit]

Linear dependence and independence of two vectors[edit]

Vectors in R2[edit]

Vectors in R4[edit]

Alternative method using determinants[edit]

More vectors than dimensions[edit]

Natural basis vectors[edit]

Linear independence of functions[edit]

Proof[edit]

Space of linear dependencies[edit]

Generalizations[edit]

Affine independence[edit]

Linearly independent vector subspaces[edit]

See also[edit]

References[edit]

External links[edit]

10. Линейная зависимость и независимость векторов

Как найти подсистему системы векторов

Как найти подсистему системы векторов

Не пропустите также:

Vectors in R²[edit]

Vectors in R⁴[edit]