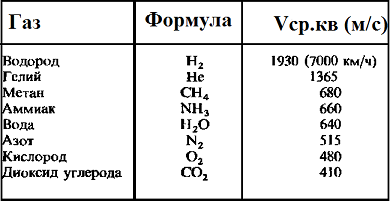
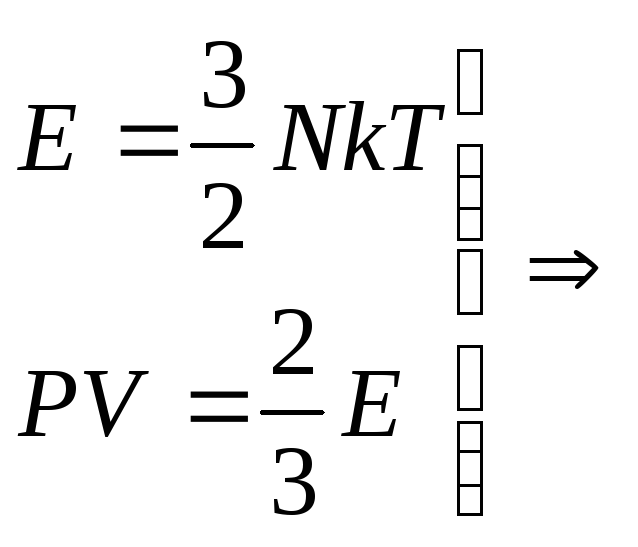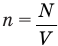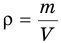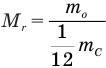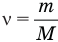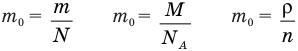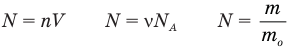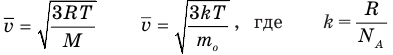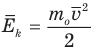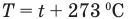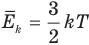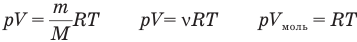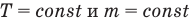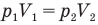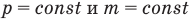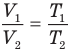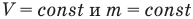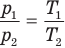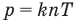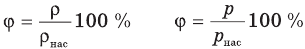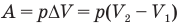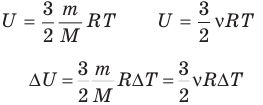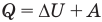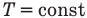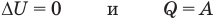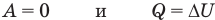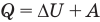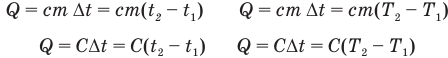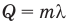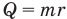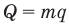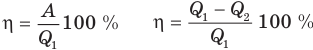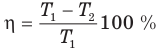Как найти квадратичную скорость через массу - AvtoShod.ru

Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа

$Large vecupsilon =sqrt{frac{3kT}{m}}=sqrt{frac{3RT}{M}}$

Таблица значений средней квадратичной скорости молекул некоторых газов

Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):

Где у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:

Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):

$large PV=frac{2}{3}vec E_k$

Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:

$large vec E_k =frac{3}{2}RT$

Но средняя кинетическая энергия, так же находится, как :

$large vec E_k =frac{1}{2}N_a m vecupsilon^2$

А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы , получается Молярная масса то у нас и получится формула для средней квадратичной скорости молекулы газа:

$Large vecupsilon =sqrt{frac{3RT}{M}}$

А если расписать универсальную газовую постоянную, как , и за одно молярную массу , то у нас получится?

$Large vecupsilon =sqrt{frac{3kT}{m}}$

В Формуле мы использовали :

— Средняя квадратичная скорость молекул

$k=1.38cdot10^{-23}$ — Постоянная Больцмана

— Температура

— Масса одной молекулы

— Универсальная газовая постоянная

— Молярная масса

— Количество вещества

— Средняя кинетическая энергия молекул

$N_a=6,02cdot10^{23}$ — Число Авогадро

Источник

Так как
,
то, следовательно,
…(11.12)

где
–
кинетическая энергия всех молекул газа.

Массу газа можно
выразить как
,
тогда (12.12) запишется как
;
для одного моля газа, то есть m
= M, а V = V_


,
отсюда

Так как молярную
массу можно выразить через массу одной
молекулы m₀
и число Авогадро —
,
то квадратичную скорость можно представить
как

где

— постоянная Больцмана.

При комнатной
температуре молекулы кислорода, например,
имеют среднеквадратическую скорость
480м/с, водорода – 1900м/с.

6. Средняя кинетическая энергия поступательного движения молекул газа.

Средняя кинетическая
энергия поступательного движения одной
молекулы идеального газа

– она пропорциональна термодина-мической
температуре и зависит только от нее, то
есть
температура тела есть количественная
мера энергии движения молекул, из которых
состоит это тело. Кроме
того, связи между абсолютной температурой
и средней кинетической энергией
показывает, что при
одинаковой температуре средние
кинетические энергии молекул всех газов
одинаковы, несмотря на различие масс
молекул разных газов.

Кинетическая
энергия газа состоящего из

молекул, равна

,
то есть
,
отсюда
,
где

— концентрация молекул, тогда

– получили уравнение состояния идеального
газа. Из этих выражений видно, что если

то <E₀>
= 0, то есть прекращается поступательное
движение молекул идеального газа, а, ,
его давление равно нулю.

Не следует думать,
что при абсолютном нуле температуры,
прекращается всякое движение частиц
вещества. Даже если все молекулы газа
остановятся, то внутри них будут двигаться
электроны, будут участвовать в движении
протоны и нейтроны ядер.

Абсолютный ноль
температур означает для реальной системы
не отсутствие движения, но такое состояние
тела, при котором дальнейшее уменьшение
интенсивности этого движения за счет
отдачи его энергии окружающим телам
невозможно. Следовательно, при абсолютном
нуле система находится в состоянии с
наименьшей возможной энергией.
Характер этого состояния зависит от
конкретных свойств составляющих систему
частиц.

7. Любая
молекулярная система состоит из большого
числа составных частиц (идеальный газ).
Эти частицы беспорядочно движутся.
Скорости каждой частицы в произвольный
момент времени неизвестны. Но, оказываются
разные
скорости различных частиц встречаются
с разными вероятностями.
В этом можно убедится на опыте Штерна
(1888 – 1970):

	Раскаленная током нить расположена на оси двух имеющих общую ось цилиндров. Нить покрыта серебром., атомы которого
испаряясь, покидают нить и по радиусу разлетаются в разные
стороны. Во внутреннем цилиндре сделана узкая щель. Только
те атомы, которые попали в щель, достигают внутренней

поверхности
внешнего цилиндра, они создают изображение
щели, которое можно увидеть, если через
некоторое время развернуть внутреннюю
поверхность большого цилиндра. Если
прибор привести во вращение вокруг
общей оси, то атомы серебра, прошедшие
сквозь щель, будут оседать не прямо
напротив него, а с некоторым смещением.
Если бы всех молекул серебра была
одинакова, то и это смещение было бы
одинаковым, но опыт показал распределение
по скоростям.

	Существует некая скорость
около которой расположе-
ны наиболее населенные
интервалы, она называется
наиболее вероятной скоро-
стью U_в и ей соответству-
ет максимум на рисунке.

Чем больше скорость
частиц отличается от U_в,
тем меньше число таких частиц. С
увеличением

возрастает наиболее вероятная скорость,
больше появится быстрых частиц, вся
кривая сместится вправо. Однако площадь
под кривой остается постоянной (так как
постоянно число частиц), кривая
растягивается. Сама кривая называется:
распределение
Максвелла молекул по скоростям.

Применив методы
теории вероятностей, Максвелл нашел
функцию распределения по скоростям
f
(1)

Значение наиболее
вероятной скорости можно найти,
продифференцировав (1):

(2)

Средняя скорость
молекул определяется по формуле:

(3)

Таким образом,
состояние газа характеризуется следующими
скоростями:

1) наиболее вероятная

2) средняя

3) Средняя квадратичная

Исходя из
распределения молекул по скоростям
можно определить функцию
распределения молекул по энергиям
теплового движения

(4)

Тогда средняя
кинетическая энергия :

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.

Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см³ при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.

Что такое средняя скорость движения молекул

Среднюю скорость движения молекул часто именуют скоростью их теплового движения.

Определение 1

Вид формулы средней относительной скорости молекул в физике можно представить выражением:

[text { Vотн }=sqrt{2} sqrt{frac{8 R T}{pi m_{0}}}]

Выражение под корнем – средняя скорость молекул идеального газа.

Как определить среднюю квадратичную скорость движения молекул

Определение 2

Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.

Средняя скорость молекул равна:

[leftlanglemathrm{V}_{mathrm{KB}}rightrangle=sqrt{frac{1}{N} sum_{i=1}^{N} v_{i}^{2}}]

Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:

[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]

Ещё одно выражение для среднеквадратичной скорости:

[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории

P = (1/3)nm*<Vкв>

Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.

Пример. 1.

Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:

Где P — давление, ρ — плотность

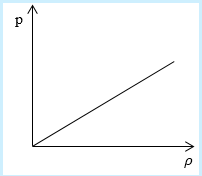
Напомним, что средняя скорость частиц:

[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]

Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ‎. Эти две величины можно связать соотношением

P=C*ρ‎

Где С – некоторая постоянная величина, константа.

Далее считаем m₀= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.

Нужно лишь подставить эти значения в формулу для средней скорости:

[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]

В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.

Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.

Нет времени решать самому?

Наши эксперты помогут!

Пример. 2.

Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).

Воспользуемся формулой:

[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Также нам потребуется уравнение Менделеева-Клайперона

Здесь мы воспользовались тем, что:

m/μ = N/N_a

PV = (m/μ)*RT = (N/N_a)*RT

Если обе части этого уравнения поделить на V и принять во внимание, что

(N/V) = n, то можно получить

P = (n/N_a)*RT. Отсюда находим, что RT = (p*N)/n

Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:

[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Источник

Формулы молекулярной физики

Формула концентрации молекул

Здесь n — концентрация , N — количество молекул (безразмерное), V — объем .

Формула плотности

Здесь — плотность вещества , m — масса вещества (кг), V — объем .

Формула относительной молекулярной массы

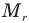
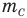
Здесь — относительная молекулярная масса (безразмерная), — масса одной молекулы (кг), — масса атома углерода (кг).

Формула количества вещества (количества молей)

Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).

Формулы массы одной молекулы

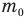
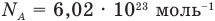
Здесь — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), — число Авогадро, — плотность вещества , n — концентрация молекул .

Формулы количества молекул

Здесь A — количество молекул (безразмерное), п — концентрация молекул , V— объем , v — количество вещества (количество молей) (моль), — число Авогадро , m — масса вещества (кг), — масса одной молекулы.

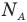
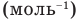
Формулы средней квадратичной скорости молекул

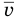
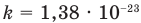
Здесь — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), Дж/К — постоянная Больцмана, — масса одной молекулы (кг).

Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па), — масса одной молекулы (кг), n — концентрация молекул , — средняя квадратичная скорость молекул (м/с), — средняя кинетическая энергия молекул (Дж).

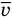
Формула средней кинетической энергии молекул

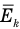
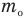
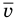
Здесь — средняя кинетическая энергия молекул (Дж), — масса одной молекулы (кг), — средняя квадратичная скорость молекул (м/с).

Связь шкал Цельсия и Кельвина

Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.

Связь средней кинетической энергии молекул идеального газа с абсолютной температурой

Здесь — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).

У равнение состояния идеального газа — уравнение Клапейрона — Менделеева

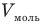
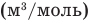
Здесь р — давление газа (Па), V — объем , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), — объем моля .

Объединенный газовый закон — уравнение Клапейрона

при

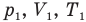
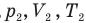
Здесь — давление (Па), объем и абсолютная температура (К) газа в первом состоянии, — давление (Па), объем и абсолютная температура (К) газа во втором состоянии.

Закон Бойля — Мариотта (изотермический процесс)

при

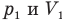
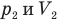
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), — давление (Па) и объем газа в первом состоянии, — давление (Па) и объем газа во втором состоянии.

Закон Гей-Люссака (изобарный процесс)

при

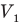
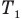
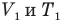
Здесь р — давление газа (Па), m — масса газа (кг), и — объем и абсолютная температура (К) газа в первом состоянии, — объем и абсолютная температура (К) газа во втором состоянии.

Закон Шарля

при

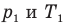
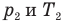
Здесь V — объем газа , m — масса газа (кг), — давление (Па) и абсолютная температура (К) газа в первом состоянии, — давление (Па) и абсолютная температура (К) газа во втором состоянии.

Связь давления идеального газа с концентрацией его молекул и температурой

Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа , абсолютная температура Т (К).

Формулы относительной влажности

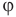
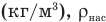
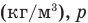
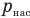
Здесь — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре — плотность насыщенного водяного пара при той же температуре — давление водяного пара в воздухе при данной температуре (Па), — давление насыщенного водяного пара в воздухе при той же температуре (Па).

Работа при изобарном изменении объема газа

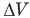
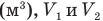
Здесь А — работа (Дж), р — давление газа (Па), — изменение объема газа — соответственно начальный и конечный объемы газа .

Внутренняя энергия идеального одноатомного газа

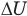
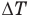
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), — изменение внутренней энергии (Дж), — изменение температуры (К).

Первый закон термодинамики

Здесь Q — количество теплоты, переданное термодинамической системе (Дж), — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)

Применение первого закона термодинамики к термодинамическим процессам

к изотермическому: при

к изохорному: при V = const

к изобарному: при р = const

к адиабатному: при Q = 0

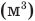
Здесь Т — абсолютная температура (К), — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем , р — давление (Па).

Формулы количества теплоты при нагревании или охлаждении тел

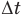
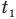
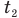
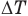
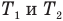
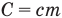
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), — изменение температуры тела по шкале Цельсия, и — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, — изменение абсолютной температуры тела (К), — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), — теплоемкость тела (Дж/К).

Формула количества теплоты при плавлении или кристаллизации

Здесь Q — количество теплоты (Дж), т — масса тела (кг), 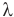— удельная теплота плавления вещества (Дж/кг).

Формула количества теплоты при парообразовании или конденсации

Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).

Формула количества теплоты при сгорании топлива

Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).

Коэффициент полезного действия теплового двигателя

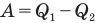
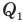
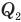
Здесь — коэффициент полезного действия (безразмерный или в %), — работа, совершенная двигателем (Дж), — количество теплоты, полученное рабочим веществом от нагревателя (Дж), — количество теплоты, отданное рабочим веществом холодильнику (Дж).

Коэффициент полезного действия идеального теплового двигателя

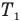
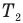
Здесь — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), — абсолютная температура нагревателя (К), — абсолютная температура холодильника(К).

Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

Источник

Условие задачи:

Определить среднеквадратичную скорость молекул газа при давлении 100 кПа и плотности 1,25 кг/м³.

Задача №4.1.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(p=100) кПа, (rho=1,25) кг/м³, (upsilon_{кв}-?)

Решение задачи:

Запишем основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

[p = frac{1}{3}{m_0}nupsilon _{кв}^2;;;;(1)]

Вспомним формулу определения концентрации молекул (n) идеального газа:

[n = frac{N}{V}]

Подставим это выражение в формулу (1), получим:

[p = frac{1}{3}frac{{{m_0}N}}{V}upsilon _{кв}^2]

Произведение массы одной молекулы (m_0) на количество молекул (N) равно массе газа (m), поэтому:

[p = frac{1}{3}frac{m}{V}upsilon _{кв}^2]

Отношение массы (m) к объему (V) – это физическая величина, называемая плотностью газа (rho), поэтому:

[p = frac{1}{3}rho upsilon _{кв}^2]

Осталось сделать последнее действие – выразить искомую скорость (upsilon_{кв}):

[{upsilon _{кв}} = sqrt {frac{{3p}}{rho }} ]

Посчитаем численный ответ задачи:

[{upsilon _{кв}} = sqrt {frac{{3 cdot 100 cdot {{10}^3}}}{{1,25}}} = 489,9;м/с approx 0,49;км/с]

Ответ: 0,49 км/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.1.33 Вычислить среднюю квадратичную скорость молекул углекислого газа
4.1.35 В баллоне емкостью 40 л находится 10 кг кислорода под давлением 20 МПа. Найти
4.1.36 Энергия поступательного движения, которой обладают все молекулы газа, находящегося

Источник

6. Средняя кинетическая энергия поступательного движения молекул газа.

Что такое средняя скорость движения молекул

Как определить среднюю квадратичную скорость движения молекул

Условие задачи:

Дано:

Решение задачи:

Ответ: 0,49 км/с.

Смотрите также задачи:

Не пропустите также: