В данной публикации мы рассмотрим, как можно вычислить радиус шара и разберем примеры решения задач для закрепления материала.
-
Формулы вычисления радиуса шара
- 1. Через объем
- 2. Через площадь поверхности
- Примеры задач
Формулы вычисления радиуса шара
1. Через объем
Радиус шара вычисляется по формуле:
V – объем шара; равен трем четвертым произведения его радиуса в кубе и числа π.
π – число, приближенное значение которого равняется 3,14.
2. Через площадь поверхности
Радиус шара рассчитывается таким образом:
S – площадь поверхности шара; равна четырем его радиусам в квадрате, умноженным на число π.
S = 4πR2
Примеры задач
Задание 1
Объем шара составляет 904,32 см3. Найдите его радиус.
Решение:
Воспользовавшись первой формулой получаем:
Задание 2
Вычислите радиус шара, если площадь его поверхности равна 314 см2.
Решение:
В данном случае рассчитать радиус шара можно, применив 2-ю формулу (через площадь поверхности):
|
Как вычислить радиус шара по объему? Для вычисления параметров шара существуют формулы. В частности, чтобы вычислить радиус шара при известном объеме, следует использовать такую формулу:  Где R — радиус шара (искомое значение), V — объем (известное значение), пи — константа, значение которой принимается как 3,14, при этом для более точных вычислений следует брать большее количество знаков после запятой. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Радиус шара по объему Шар представляет собой геометрическое тело, являющееся совокупностью всех точек пространства, которые находятся от центра шара на расстоянии не больше заданного. Данное расстояние называется радиусом шара. Для того, чтобы выразить радиус шара через объём, нужно вспомнить формулу: Объём шара V равен произведению 4/3 на число π (которое является константой и равно 3,14) и на радиус в кубе. Из этой формулы можно сначала выразить куб радиуса: Конечная формула получится такой: Радиус шара будет равен кубическому корню из дроби; числитель дроби — объем, умноженный на 3; знаменатель дроби — число π, умноженное на 4. Пример Предположим, объем шара равен 9 кубическим метрам. Радиус шара находим по формуле, приведенной выше: R ≈ ³√((3 * 9) / (4 * 3,14)) ≈ ³√(27 / 12,56) ≈ 3 / ³√12,56 ≈ 3 / 2,29 ≈ 1,31 метр. Таким образом, если объём шара составляет 9 куб. метров, то его радиус будет равен приблизительно 1,31 метра. Бархатные лапки более года назад Такие задания иногда встречаются на ЕГЭ, с одной стороны вроде ничего сложного, но все же извилины придется напрячь, чтобы ее решить. Лично мне такие задачки давались с трудом, так как я не сильно любила геометрию, но все же формулы приходилось заучивать, чтобы решать задачки. Давайте для начала вспомним по какой формуле мы находим объем шара. Итак, эта формула выглядит следующим образом: Значит радиус шара мы можем вычислить по такой формуле: В данном случае мы выражаем одну величину через другую. Так что все оказалось не так уж и запутанно и ученикам вполне под силу справится с такой заковыристой задачкой. bezdelnik 5 лет назад Радиус шара по известному объёму вычисляется по формуле R равен корню кубическому из 3*V}/4*pi, где V — объём шара, pi- трансцендентное число равное отношению длины половины окружности к её радиусу. Поэтому точно вычислить радиус не возможно, а только с определённой погрешностью. Некоторую сложность представляет извлечение кубического корня. Для этого можно воспользоваться таблицей кубов. Например, при V=1000 куб.мм. и pi=3,14 подкоренное выражение равно 238,8535… и по таблице находим R равен примерно 6,2 мм. Марина Вологда более года назад Надо вспомнить формулу и проблем с вычислением радиуса шара не возникнет. Итак, сначала укажем формулу: R — это как раз искомый нами радиус. 3 и корень — это кубический корень из полученной дроби. ? — это пи (оно всегда едино и составляет 3.14). V — объем шара, который нам известен. Ну а теперь не сложно высчитать радиус, зная его объем, подставляя в формулу известные нам данные. Simple Ein 3 года назад Найти радиус шара, зная объем очень легко. Объем шара находится по формуле: Выразим из данной формулы значение радиуса шара. Для этого необходимо объем разделить на число «Пи», умножив на ¾. Из полученного числа необходимо найти кубический корень. -Александр— 5 лет назад Формула объема шара: V=4/3*п*(R в степени 3) отсюда R = корень третей степени из (3/4*V/п) Лара Изюминка 2 года назад Достаточно простая задача для тех, кто помнит, чему равен обьем шара. А он равен четыре третьх умножить на пи умножить на радиус в кубе. Далее нужно уметь просто выражать одну величину через другую. В итоге у нас радиус равен корень кубический из ( 3 умножить на обьем и это разделить на 4 пи.) Итак еще нужно вспомнить, что пи это 3,14 приблизительно. Если нужна большая точность, берут больше знаков после запятой в числе пи. Это имеет смысл при нахождении радиуса в больших сооружениях, в архитектуре. Обычно хватает точности два знака после запятой. Эта формула нужна при решении задач по стереометрии . Vodila более года назад Зная, что обьем шара равен 43 пи умножить на радиус в квадрате совсем нетрудно выразить радиус. Очевидно, что он будет равен корень кубический из три четвертых обьема, деленного на пи. Вот собственно и вся формула. Такая задача иногда встречается в ЕГЭ по математике. Hamster1337 2 года назад Для того, что бы найти радиус шара при наличии объёма, следует воспользоваться следующей формулой: Где число «П» равно 3,14. Так же существуют другие формулы для поиска радиуса шара (из данной формулы можно вывести другую формулу). Для того, чтобы отыскать радиус шара при том, что объем известен воспользуйтесь формулой, а именно, в качестве основной применима такая. R является искомым значением, а также радиусом шара. V отображает значение, являющееся известным, объем. Пи является константа, у которой значение = 3,14. Так, когда делаются точные расчеты следует брать большее количество знаков, которые находятся после запятой. Знаете ответ? |
Радиус шара
Радиус
Отрезок, соединяющий центр шара с любой точкой на его поверхности, является радиусом шара, обозначается как r или R. В зависимости от исходных данных радиус шара можно вычислить:
— по диаметру. Как известно, радиус шара равен половине его диаметра:
г = D/2,
где г — радиус, D — диаметр шара.
— по длине окружности.
Длина окружности © равна произведению пи на диаметр (D), через радиус шара — удвоенному произведению пи на радиус ®:
C = πD = 2πr
Отсюда, радиус равен частному от деления длины окружности © на 2 пи:
r = С / 2π
π — величина постоянная, равна отношению длины окружности к диаметру. Число Пи, равное 3,141592653… обычно округляется до 3,14.
— по площади шара.
Площадь шара равна произведению четырех пи на квадрат радиуса:
S=4πr2,
где S — площадь шара, r — радиус.
Из этой формулы выводим форму радиуса:
r = √S / 4π,
т.е. радиус равен корню квадратному из площади шара деленной на четыре пи.
— по объему шара.
Объем шара равен произведению четырех третьих на число пи и на радиус шара в кубе:
V = 4/3 πr3,
где V — объем, r — радиус шара.
Отсюда, радиус шара равен корню кубическому из объема шара деленного на три четвертых Пи:
r = ∛(V / (¾π))
Рассчитать радиус шара через объем
Советы
- Не забывайте про порядок выполнения математических операций. Если вы не помните этот порядок, а ваш калькулятор умеет работать с круглыми скобками, пользуйтесь ими.
- В этой статье рассказывается о вычислении радиуса шара. Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.
- π (Пи) – это буква греческого алфавита, которая обозначает постоянную, равную отношению диаметра круга к длине его окружности. Число Пи является иррациональным числом, которое не записывается как отношение действительных чисел. Существует множество приближений, например, отношение 333/106 позволит найти число Пи с точностью до четырех цифр после десятичной запятой. Как правило, пользуются приблизительным значением числа Пи, которое равно 3,14.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра. 2. Любое сечение сферы плоскостью является окружностью. 3. Любое сечение шара плоскостью есть кругом. 4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности. 5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара. 6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара. 7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.
Видео
Одиннадцать свойств
В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:
- Точки на сфере находятся на одинаковом расстоянии от одной фиксированной, называемой центром. Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
- Контуры и плоские участки сферы являются кругами. Это однозначное свойство, которое определяет шар.
- Сфера имеет постоянную ширину и обхват. Ширина поверхности — это расстояние между парами параллельных касательных плоскостей. Множество других замкнутых выпуклых поверхностей имеют постоянную ширину, например, тело Мейснера. Обхват поверхности — это окружность границы её ортогональной проекции на плоскость. Каждое из этих свойств подразумевает другое.
- Все точки сферы омбилические. В любой точке поверхности вектор нормали расположен под прямым углом к ней, поскольку шар — это линии, выходящие из его центра. Пересечение плоскости, которая содержит нормаль с поверхностью, сформирует кривую — нормальное сечение. Любая замкнутая поверхность будет иметь как минимум четыре точки, называемых омбилическими. Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
- У шара нет центра поверхности. Например, два центра, соответствующие минимальной и максимальной секционной кривизне, называются фокальными точками, а совокупность всех таких точек образует одноимённую поверхность. И только у шара она преобразуется в единую точку.
- Все геодезические сферы являются замкнутыми кривыми. Для этой фигуры они большие круги. Многие другие поверхности разделяют это свойство.
- Имеет наименьшую площадь при наибольшем объёме. Это определяет шар однозначно. Например, мыльный пузырь: его окружает фиксированный объём, поверхностное натяжение минимизирует площадь его поверхности для такого объёма. Конечно, пузырь не будет идеальным шаром, поскольку внешние силы, такие как гравитация, будут искажать его форму.
- Сфера — единственная вложенная поверхность, у которой нет границы или сингулярностей с постоянной положительной средней кривизной.
- Сфера имеет наименьшую общую среднюю кривизну среди всех выпуклых тел с заданной площадью поверхности.
- Шар имеет постоянную гауссову кривизну. Это внутреннее свойство, которое определяется путём измерения длины и углов и не зависит от того, как поверхность встроена в пространство.
Сфера превращается в себя трёхпараметрическим семейством жёстких движений. Любое вращение вокруг линии, проходящей через начало координат, может быть выражено как комбинация вращений вокруг трёхкоординатной оси.
Определение основных величин
- 1
Запомните основные величины, которые имеют отношение к вычислению радиуса шара. Радиус шара – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Радиус шара можно вычислить по данным значениям диаметра, длины окружности, объема или площади поверхности. Диаметр (D) – это отрезок, который соединяет две точки на поверхности шара и проходит через его центр (то есть это наибольшее расстояние между противоположными точками, лежащими на поверхности шара). Диаметр равен удвоенному радиусу. Длина окружности (С) представляет собой длину окружности большого круга, то есть круга, который образует секущая плоскость, проходящая через центр шара. Объем (V) – это значение трехмерного пространства, занимаемого шаром.[6] Площадь поверхности (А) – это значение двумерного (плоского) пространства, ограниченного поверхностью шара. Пи (π) – это постоянная, которая равна отношению длины окружности к ее диаметру. Первыми десятью цифрами этой постоянной являются 3,141592653, но зачастую число Пи округляется до 3,14.
- 2
Воспользуйтесь значениями данных величин, чтобы найти радиус. Радиус можно вычислить по данным значениям диаметра, длины окружности, объема и площади поверхности. Более того, указанные величины можно найти по данному значению радиуса. Чтобы вычислить радиус, просто преобразуйте формулы для нахождения указанных величин. Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности. D = 2г. Как и в случае круга , диаметр шара в два раза больше его радиуса. C = πD = 2πr. Как и в случае круга , длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара. V = (4/3)πr3. Объем шара равен произведению 4/3 на π и на радиус в кубе.[7] А = 4πr2. Площадь поверхности шара равна учетверенному произведению π на радиус в квадрате. Так как площадь круга равна πr2, то площадь поверхности шара в четыре раза больше площади круга, который образует секущая плоскость, проходящая через центр шара.
Радиус шара
Единственной величиной, определяющей шар является радиус. Определяющая величина это величина, через которую можно найти все значения для фигуры. Через радиус шара можно найти площадь сечения шара, площадь поверхности шара и объем шара.
Приведем все формулы с участием шара:
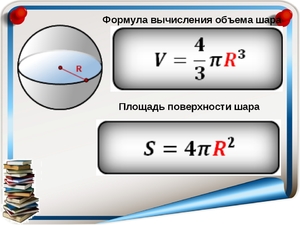
- $V={4over{3}}{pi}R^{3}$ – формула объема шара
- $S=4{pi}R^2$ – площадь шара
И на этом все. На основании этих формул можно вывести формулы радиуса через площади или объем, а так же формулы секторов и сегментов шара.
Важным моментом является понимание происхождения числа пи. Ведь в расчетах повсеместно используется это значение, но пока никто не смог рассчитать его полностью. Счет идет уже на тысячи знаков, но точного значения числа до сих пор неизвестно. Как же вычисляют число пи? Это отношение длины окружности к ее диаметру. Причем интересно, что для любой окружности эта величина будет иметь одинаковое значение.
Теги
Имея при себе всего одну формулу и зная изначально, чему равен диаметр или радиус, можно с лёгкостью вычислить площадь поверхности шара. Формула будет иметь вид S =4πR2, где число «пи» умножается на 4, затем на радиус шара в квадратной степени. Но перед непосредственными вычислениями следует сразу разобраться в терминах.
Трактовка значений
Это следует знать:
- Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
- Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
- Число «пи» — это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
- Радиус шара равен ½ его диаметру. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
- Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
- Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
- Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.
Занимательные факты
Это интересно:
- У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
- Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
- Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.
Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Рождение формулы
Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара, был Архимед. Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.
Именно Архимед определил границы числа «пи» и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.
Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.
Видео
На примере этого видео вам будет легко понять, как найти площадь поверхности шара.