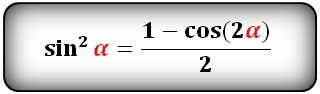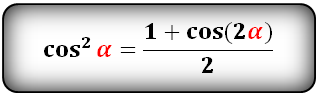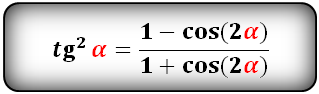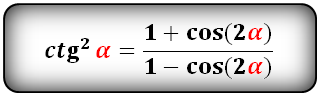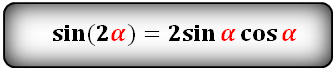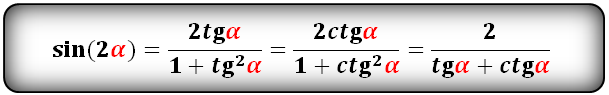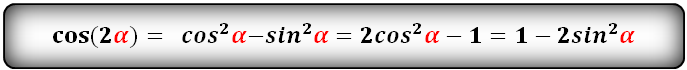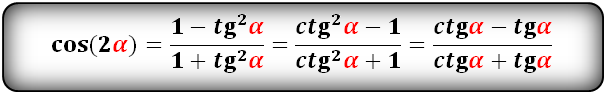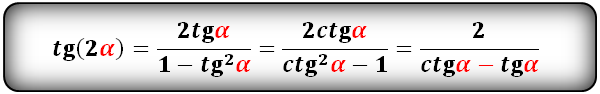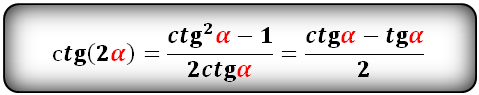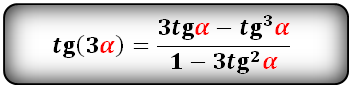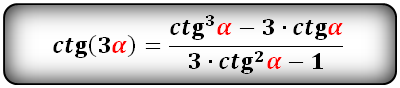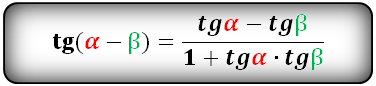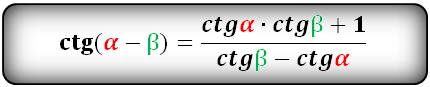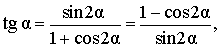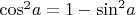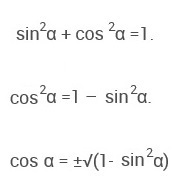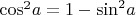Для того, чтобы выразить косинус через синус, вспомним основное тригонометрическое тождество:
sin²α + cos²α = 1.
Таким образом, если известен синус, то косинус найти можно так:
cos²α = 1 — sin²α.
Возможны 2 варианта:
1) cosα = √(1 — sin²α), если угол α находится в 1 четверти (0 < α < 90) или в 4 четверти (270 < α < 360).
2) cosα = — √(1 — sin²α), если угол α находится во 2 четверти (90 < α < 180) или в 3 четверти (180 < α < 270).
Пример
1) Синус угла α = 0,3 и 90 < α < 180. Нужно найти, чему равен косинус угла α.
Так как угол α находится во второй четверти, то косинус будет отрицательным. Выразим его по формуле:
cosα = — √ (1 — 0,09) = -√0,91 = — 0,95.
2) Синус угла α = 0,7 и 270 < α < 360. Выразим косинус.
Так как угол α находится в 4 четверти, то косинус будет положительным.
cosα = √ (1 — 0,49) = √0,51 = 0,71.
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
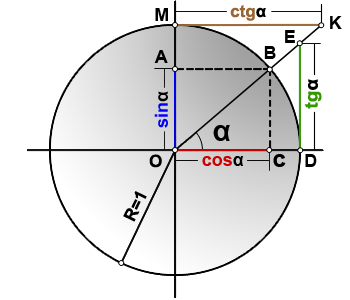
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
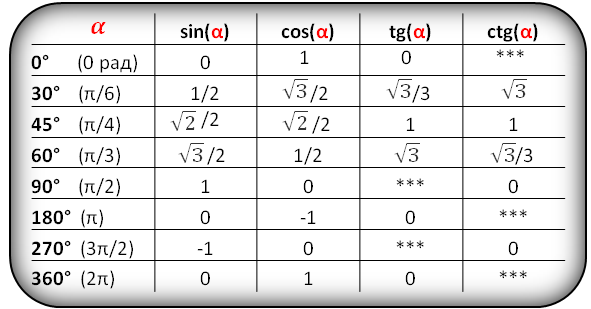
Значения функций для некоторых углов, α
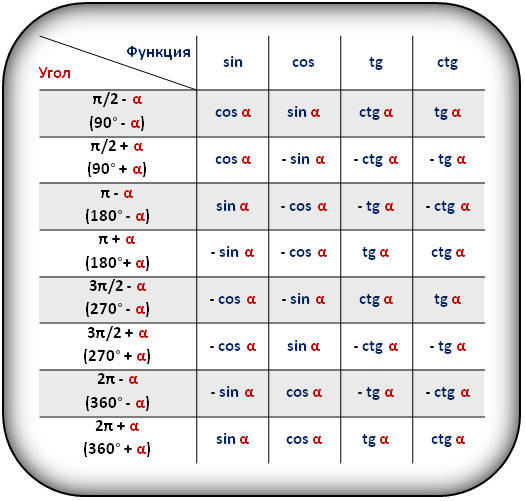
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
Основные тригонометрические формулы
Содержание
 Связи между тригонометрическими функциями одного угла |
| Тригонометрические функции суммы и разности двух углов |
| Тригонометрические функции двойного угла |
| Формулы понижения степени для квадратов тригонометрических функций |
| Формулы понижения степени для кубов синуса и косинуса |
| Выражение тангенса угла через синус и косинус двойного угла |
| Преобразование суммы тригонометрических функций в произведение |
| Преобразование произведения тригонометрических функций в сумму |
| Выражение тригонометрических функций через тангенс половинного угла |
| Тригонометрические функции тройного угла |
Связи между тригонометрическими функциями одного угла
Тригонометрические функции суммы и разности двух углов
Тригонометрические функции двойного угла
| Формула | Название формулы |
| sin 2α = 2 sin α cos α | Синус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
Косинус двойного угла |
 |
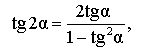Тангенс двойного угла |
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
|
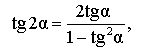Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
 |
Выражение квадрата синуса через косинус двойного угла |
 |
Выражение квадрата косинуса через косинус двойного угла |
 |
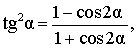Выражение квадрата тангенса через косинус двойного угла |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
 |
Выражение куба синуса через синус угла и синус тройного угла |
 |
Выражение куба косинуса через косинус угла и косинус тройного угла |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
|
Выражение тангенса через синус и косинус двойного угла
Преобразование суммы тригонометрических функций в произведение
| Сумма синусов |
|
|
| Разность синусов |
|
|
| Сумма косинусов |
|
|
| Разность косинусов |
|
|
| Сумма тангенсов |
 |
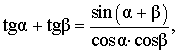| Разность тангенсов |
 |
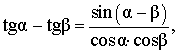Преобразование произведения тригонометрических функций в сумму
| Произведение синусов |
|
|
| Произведение косинусов |
|
|
| Произведение синуса и косинуса |
|
|
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
 |
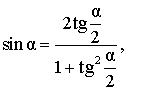Выражение синуса угла через тангенс половинного угла |
 |
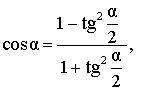Выражение косинуса угла через тангенс половинного угла |
 |
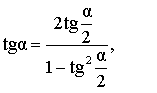Выражение тангенса угла через тангенс половинного угла |
Тригонометрические функции тройного угла
| Формула | Название формулы |
| sin 3α = 3sin α – 4sin3α | Синус тройного угла |
| cos 3α = 4cos3α –3cos α | Косинус тройного угла |
 |
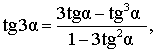Тангенс тройного угла |
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
|
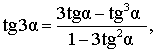Синус в квадрате
Синус (sin) — это тригонометрическая функция, геометрически представляющая отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
sin 2 (x)=sin(x)*sin(x)
Значение синуса находится в диапазоне от -1 до +1.
Смотрите также калькулятор вычисления синуса угла.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата синуса (синуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат синуса любого угла.
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
Формулы двойного угла в тригонометрии
Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .
Ниже приведены формулы двойного угла:
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α
Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что
sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .
Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .
Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .
Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .
Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и
sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что
2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3
и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3
Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .
Представить sin 2 α 3 через тригонометрические функции, при α 6 .
Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6
Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α
При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .
Так же приводится формула косинуса тройного угла:
cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α
При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
2
Как найти косинус угла, если известен синус?
11 ответов:
10
0
Ответ мой будет аналогичным ответу на похожий вопрос (см. здесь).
Из основного тригонометрического тождества:
выразим косинус в квадрате угла а:
Значит косинус угла равен либо корню квадратному из этого выражения, либо ему же, только со знаком -.
<hr />
Знак перед корнем зависит от ограничения, которое накладывается для определенности в условии задачи.
Если дано положительное значение синуса,то угол находится в 1-й или во 2-й четверти. В первой четверти (0< a< 90) значение косинуса будет положительным. Здесь выбираем знак плюс. Во второй четверти (90< a< 180) значение косинуса будет отрицательным. Тогда перед корнем выбираем знак минус.
Если значение синуса отрицательное, то угол расположен в 3-й или 4-й четверти. В 3 четверти (180< a< 270) косинус угла будет меньше нуля.
В 4 четверти (270< a< 360) косинус угла будет больше нуля.
<hr />
Примеры.
Пример 1. Найти косинус угла, если sina = -0,6. 180<a<270 (в градусах)
Решение. Находим разность 1 и квадрата значения sina, т.е. квадрата (-0,6).
-0,6 в квадрате находится так: (-0,6)*(-0,6) = 0,36. Подставим его в искомую разность:
1-0,36=0,64
Получили квадрат значения косинуса. Для нахождения значения самого косинуса, извлечем корень квадратный из 0,64 и возьмем его со знаком + или со знаком — . Получим 0,8 или -0,8.
Так как по условию угол находится в 3 четверти, то искомое значение косинуса будет также меньше нуля. Значит выбираем -0,8.
Ответ: cos a =-0,8.
Рассмотрим пример для случая, когда угол находится в 4 четверти:
Пример 2. Найти косинус угла, если sina = -0,6. 270<a<360 (в градусах)
Решение такое же (см. пример 1).
Перед выбором ответа рассуждаем так:
Т. к. по условию угол расположен в 4 четверти, то значение косинуса будет больше нуля. Значит выбираем 0,8.
Ответ: cos a =0,8.
2
0
Что-то из них по тригонометрии равен отношению того к отношению этого, т.е надо перевернуть доску другой стороной кверху если синус угла наклона внизу и вернуть в исходное положение для того чтобы найти косинус угла наклона!
2
0
Всё предельно просто и основные вычисления строятся на базе одного всем известного уравнения, при котором сумма квадратов cos и sin одного и того же угла дают в итоге единицу.
Основным моментом, который может вызвать затруднения станет постановка положительного или отрицательного знак перед корнем.
1
0
Для таких случаев нужно помнить всегда главное тригонометрическое тождество
косинус квадрат альфа+ синус квадрат альфа=1
cos^2альфа+sin^2альфа=1
и вот отсюда уже выводим
cos^2альфа=1-sin^2альфа
соsальфа=sqrt(1-sin^2альфа)
1
0
Будем считать, что основное тригонометрическое тождество помнят все.
Если кто — то забыл, то напоминаю:
Сумма квадратов синуса и косинуса какого — то (одного) угла Альфа равняется одному (1).
Формулу вспомнили, а дальше все легко.
В левой части уравнения оставляем косинус угла в квадрате, а в правую часть (где уже присутствует единица) перекидываем квадрат синуса угла. Получается следующее:
Нам нужен не квадрат косинуса, а косинус, поэтому уравнение выше преобразовываем и получаем:
Косинус угла равен квадратному корню единицы минус квадрат синуса (cos=sqrt(1-sin^2)).
1
0
Найти косинус угла можно из этого выражения:
cos^2альфа+sin^2альфа=1
То есть для того чтобы найти косинус нужно оставить косинус на левой стороне. Получится вот такое выражение — cos=sqrt(1-sin^2), косинус найден.
0
0
Как называется формула не помню:
cos^2+sin^2=1
cos=sqrt(1-sin^2).
0
0
С уроков в школе примерно 10-11 класс, я помню формулу основного тригонометрического тождества, которую мы учили наизусть:
Получаем искомую функцию:
Таким несложным способом можно найти косинус, если известен синус. И использовать его при решении задач.
0
0
Формулы по тригонометрии — это тема, которую изучают ученики в 10 и 11 классах. Чтобы найти косинус угла, зная синус, нужно воспользоваться основной формулой.
Сначала воспользуемся теоремой Пифагора
теперь подставляем полученные данные
0
0
Вычислить косинус угла, зная его синус очень просто. Для этого стоит знать основу основ тригонометрии — сумма квадратов синуса и косинуса равна единице. Зная эту формулу, легко вычислить косинус угла. Тригонометрическое тождество визуально представлено в следующих формулах, по которым можно вычислить в том числе и косинус.
Не стоит забывать, что при нахождении косинуса, следует убрать его квадрат и вычислить его квадратный корень. То есть те же значения после цифры равно поставить в квадратный корень при вычислении.
0
0
Между синусом и косинусом для одного и того же угла можно найти взаимосвязь, которая позволит найти косинус, зная синус. Вот так выглядит эта взаимосвязь:
Получается чтобы найти косинус в данном случае нам просто напросто будет нужно произвести извлечение корня из выражения (1-sin в квадрате конкретного угла).
Читайте также
Большинство школьников не разбираются даже в тангенсах и котангенсах, а Вы надеетесь что они знают и понимают, что такое секанс и косеканс. Я сам, конечно, знаю ответ, и пришлю его Вам на личную почту (Я не знаю, нужен ли Вам ответ, или вопрос задан с иной целью). Мне просто любопытно, дадут ли правильный ответ, и как скоро это произойдет.
По правде сказать, я практически ничего не помню про синусы, косинусы и тангенсы с котангенсами. Какие-то формулы смутно маячат на задворках моей памяти, но вспомнить их для меня уже затруднительно. А все потому, что после окончания школы я ими не занималась, поскольку дальнейшее мое образование было гуманитарного толка, и математику я уже больше не изучала.
Тем не менее я считаю, что изучение всех этих функций в школе пользу приносит. В частности, мозги развивает. Так что, может быть, эти синусы и косинусы мне и пригодились в некоторым смысле. Как знать, вдруг мое мышление было бы другим без их изучения.
Перепишем ваше неравенство следующим образом
y=cosx-sgrt2*sin(x/2)>1 (1)
Здесь sgrt2=2^(1/2) – квадратный корень из 2. Сокращение sgrt происходит от английских слов square root – квадратный корень. Так часто пишут в интернете. Удобно произвести такую замену
х=2А (2)
Тогда неравенство (1) запишется так cos(2A)-sgrt2*sinA>1. Вспомним хорошо известную в тригонометрии формулу для косинуса двойного угла cos(2A)=1-2sin^2(A), где sin^2(A) – синус А в квадрате. Тогда наше неравенство сводится к виду 1-2sin^2(A)-sgrt2*sinA>1.
Перепишем его так (единицы сокращаются)
2sin^2(A)+sgrt2*sinA<0 (3)
Удобно сделать еще одну замену
у= sgrt2*sinA (4)
Тогда у^2=2sin^2(A). Уравнение (3) приобретает вид у^2+у<0. Или у(у+1)<0. При каких у это выражение меньше нуля? 1) Если у<0 и y+1>0. То есть у<0 и у>-1. Эти 2 неравенства можно свети к такому виду -1<y<0. 2) Если у>0 и y+1<0. То есть у>0 и у<-1. Нет такого у, чтобы оно было одновременно и больше нуля и меньше -1. Остается только первый случай
-1<y<0 (5)
Но у дается выражением (4). То есть -1<sgrt2*sinA<0. Отсюда имеем –(1/2)sgrt2<sinA<0. Мы знаем, что sin(-45°)=–(1/2)sgrt2 и sin0=0. Тогда имеем такой интервал для величины А
-45°<A<0 или -pi/4<A<0 (6)
Из уравнения (2) имеем А=х/2. Тогда из (6) получим диапазон значений для величины х
-pi/2<х<0 (7)
Это третья и четвертая координатная четверть.
Проверка. Возьмем правый предел х=0. Тогда cos0=1, sin0=0. Из нашего уравнения (1) имеем у=1. И для уравнения (1) это есть предельное значение у. Но должно быть у>1. Так что, как видно и из (7), х=0 не входит в диапазон значений для переменной х. Возьмем левый предел для величины х, х=-pi/2. Тогда cosx=cos(-pi/2)=0, sin(x/2)=sin(-pi/4)=-(sgrt2)/2 и тогда имеем из неравенства (1) у=1. Это такое же предельное значение для у. Можно убедиться, что при х внутри диапазона (7) величина у больше 1.
Итак, ответ -pi/2<х<0.
Можно воспользоваться основным геометрическим тождеством.
***Основное геометрическое тождество
Sin^2 (x)+cos^2 (x)=1****
Следовательно
Cos (x) = Корень (1-sin^2 (x))
Cos (x) = корень (1-1^2) = корень (1-1) = корень (0) = 0
Ответ: 4) 0
Если область определения множество всех действительных чисел, то в записи функции не должно быть квадратных корней, переменной в знаменателе дроби. Если область значений отрезок от -3 до 3, то это точно не тангенс или котангенс, а коэффициент перед синусом или косинусом равен 3.
Например, y = sinx или y = cosx или y = sin(k*x) или y = cos(k*x), где к — какое либо действительное число.