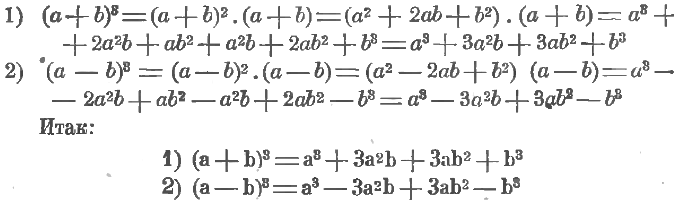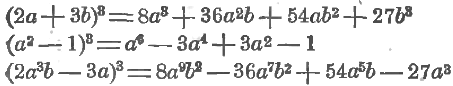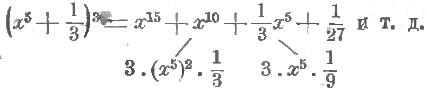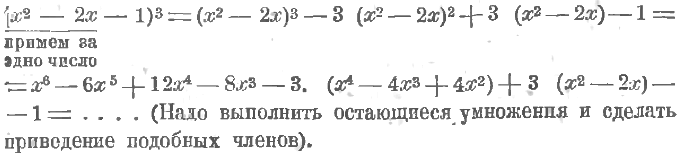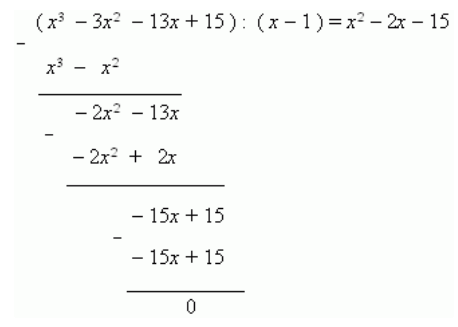Как найти куб многочлена - AvtoShod.ru - решение различных проблем

Загрузить PDF

В кубическом уравнении наивысшим показателем степени является 3, у такого уравнения 3 корня (решения) и оно имеет вид $ax^{3}+bx^{2}+cx+d=0$ . Некоторые кубические уравнения не так просто решить, но если применить правильный метод (при хорошей теоретической подготовке), можно найти корни даже самого сложного кубического уравнения — для этого воспользуйтесь формулой для решения квадратного уравнения, найдите целые корни или вычислите дискриминант.

1
2
3

Разложите на множители (на произведение двух биномов) квадратное уравнение (если возможно). Многие квадратные уравнения вида $ax^{2}+bx+c=0$ можно разложить на множители. Такое уравнение получится, если вынести за скобки. В нашем примере:^[4]
4
5

Используйте ноль и корни квадратного уравнения в качестве решений кубического уравнения. У квадратных уравнений два корня, а у кубических — три. Два решения вы уже нашли — это корни квадратного уравнения. Если же вы вынесли «х» за скобки, третьим решением будет .^[6]

Реклама

1
2
3
Разделите каждый множитель на каждый множитель . В итоге получится множество дробей и несколько целых чисел; корнями кубического уравнения будет одно из целых чисел или отрицательное значение одного из целых чисел.^[9]
- В нашем примере разделите множители (1 и 2) на множители (1, 2, 3 и 6). Вы получите: , ${frac {1}{2}}$ , ${frac {1}{3}}$ , ${frac {1}{6}}$ , и ${frac {2}{3}}$ . Теперь в этот список добавьте отрицательные значения полученных дробей и чисел: , , ${frac {1}{2}}$ , $-{frac {1}{2}}$ , ${frac {1}{3}}$ , $-{frac {1}{3}}$ , ${frac {1}{6}}$ , $-{frac {1}{6}}$ , , , ${frac {2}{3}}$ и $-{frac {2}{3}}$ . Целыми корнями кубического уравнения являются какие-то числа из этого списка.
4

Подставьте целые числа в кубическое уравнение. Если при этом равенство соблюдается, подставленное число является корнем уравнения. Например, подставьте в уравнение :^[10]
5

Реклама

1
2

Вычислите нулевой дискриминант по специальной формуле. Чтобы решить кубическое уравнение с помощью дискриминанта, нужно произвести ряд непростых вычислений, но если правильно выполнять все действия, этот метод станет незаменимым для решения наиболее сложных кубических уравнений. Сначала вычислите $Delta _{0}$ (нулевой дискриминант) — это первая необходимая нам величина; для этого подставьте соответствующие значения в формулу $Delta _{0}=b^{2}-3ac$ .^[13]
3

Вычислите первый дискриминант по формуле $Delta _{1}=2b^{3}-9abc+27a^{2}d$ . Первый дискриминант $Delta _{1}$ — это вторая важная величина; чтобы ее вычислить, подставьте соответствующие значения в указанную формулу.^[14]
4
5
6

Реклама

Об этой статье

Эту страницу просматривали 409 893 раза.

Была ли эта статья полезной?

Источник

Возведение многочленов в куб

Станем опять сначала на точку зрения арифметики и рассмотрим возведение в куб суммы и разности двух чисел. Получим:

Словами эти равенства читаются так:

1) Куб суммы двух чисел равняется кубу первого числа, плюс произведение тройки на квадрат первого числа и на второе число, плюс произведение тройки на первое число и на квадрат второго числа, плюс куб второго числа.

2) Куб разности двух числе равен кубу первого числа, минус произведение тройки на квадрат первого числа и на второе, плюс произведение тройки на первое число и на квадрат второго, минус куб второго числа.

Теперь мы можем сразу написать, что, например,

Здесь сначала написан куб первого числа, т. е. (2a³b)³, а это = 8a⁹b³, затем «минус произведение 2 на квадрат первого числа и на второе», т. е. –3 ∙ (2a³b)² ∙ (3a)= –3 ∙ 4a⁶b² ∙ 3a = – 36a⁷b², затем «плюс произведение тройки на первое число и на квадрат второго», т. е. +3 ∙ (2a³b) ∙ (3a)² = +3 ∙ 2a₃b ∙ 9a² = 54a⁵b, наконец, «минус куб второго числа», т. е. –(3a)³ = –27a³.

Мы можем наши равенства переписать в виде:

1) (a + b)³ = (+a)³ + (+3) (+a)² (+b) + (+3) (+a) (+b)² + (+b)³

2) (a – b)³ = (+a)³ + (+3) (+a)² (–b) + (+3) (+a) (–b)² + (–b)³

и читаем их так:

Куб двучлена равен кубу первого члена, плюс произведение числа (+3) на квадрат первого члена и на второй, плюс произведение числа (+3) на первый член и на квадрат второго, плюс куб второго члена.

Например: (–3a⁴ – ab)³ = (–3a⁴)³ + (+3) (–3a⁴)² (–ab) + (–3a⁴) (–ab)² + (–ab)³ = –27a¹² – 27a⁹b – 3a⁵b² – a³b³ и т. п.

Если потребуется возвести в куб трехчлен, то можно или сводить дело к умножению

[Например: (x² – 2x – 1)³ = (x² – 2x – 1)(x² – 2x – 1)(x² – 2x – 1) = …]

или, приняв временно два члена (лучше первые два) за одно число, свести дело к возведению в куб двучлена:

Источник

Кубическим называют уравнение, в котором только одна переменная представлена в третьей степени. Такие выражения в любом случае имеют от одного до трех корней. Значения, которые получаются при решении таких уравнений, могут быть равными друг другу или комплексными, если их не более двух.

Решение кубических уравнений – это решение уравнений, имеющих вид: [boldsymbol{a y^{3}+b y^{2}+c y+d=0}].

В уравнении такого типа a не равно 0, вместо b,c,d могут быть любые однозначные числа.

Данный вид уравнения имеет как минимум один корень – y₁.

Решение таких равнений может осуществляться разными способами. Оно может преобразовываться в стандартное квадратное уравнение. В таком случае предстоит выбрать один из трех вариантов решения квадратного уравнения:

разложение на множители;
применение формул для квадратных уравнений;
метод дополнения.

Решение кубических уравнений может осуществляться посредством формулы Кардано, а также теоремы Виета. Теорема Виета применяется для решения последней, четвертой степени.

Решение кубических уравнений с двумя членами

Уравнение будет иметь вид: [boldsymbol{a y^{3}+b=0}]

Для решения необходимо преобразовать его: [y^{3}=b / a=0]

Деление на a предполагает вместо нее любую цифру, кроме 0. После преобразования можно применить формулы для решения кубических уравнений, например, сокращенного умножения суммы кубов:

y3=b/a=0

(y+³√b/a)(y²—³√b/a*y+³√(b/a)²)=0

В результате из первой скобки выводим:

y=-³√b/a

во второй скобке получаем выражение – трехчлен:

y2-3√b/a*y+3√(b/a)2

Методы решения кубических уравнений возвратного вида

Алгоритм решения кубического уравнения возвратного вида отличается от предыдущего, так как оно выглядит следующим образом:

[boldsymbol{a y^{3}+b y^{2}+b y+a=0}]

В этом уравнении переменные a и b – это коэффициенты.

Первым делом при решении таких уравнений в математике выполняется группировка:

ay3+by2+by+a=a(y³+1)+b(y²+y)=a(y+1)(y²-y+1)+by(y+1)=(y+1)(ay²+y(b-a)+a)

В полученном выражении корень равен y=-1. Исходя из этого, чтобы получить корень квадратного трехчлена ay²+y(b-a)+a, потребуется найти дискриминант.

Определение

Дискриминант – произведение квадратов разностей корней в различных вариаций.

Решение кубических уравнений в составе которых рациональные корни

Предположим, что y=0. В этом случае он будет корнем уравнения, которое выглядит следующим образом:

ay³+by²+cy+d=0

При условии, что в уравнении свободные члены, d=0. Преобразуем уравнение и получим:

ay3+by2+cy=0

Решение кубических уравнений такого вида предполагает вынесение y за скобку. В итоге получается уравнение вида:

y(ay²+by+c)=0

Рассмотрим на конкретном примере, как решить кубическое уравнение с подробным решением:

5y³+2y²+4y=0

Решение:

Первым делом стоит упростить уравнение.

5y³+2y²+4y=0

Получим уравнение вида:

y(5y²+2y+4)=0

y=0, так как является корнем выражения.

Следующий шаг – поиск корней квадратного трехчлена 5y²+2y+4, который мы получили после упрощения. Для поиска приравняем к нулю и будем использовать дискриминант.

В ходе решения кубического уравнения с дискриминантом получим:

D=2²-2*5*4=-38

Так как в ответе мы получили отрицательное значение, корней у данного трехчлена нет, значит x=0.

Если в уравнениях вида ay³+by²+cy+d=0 коэффициентами являются целые числовые значения, то при решении таких уравнений и нахождении его значения мы может получить иррациональные корни.

В случае, когда a не равно 0, при умножении на a² каждой составляющей уравнения происходит замещение переменных, и получается: x=ay

ay³+by²+cy+d=0

Каждую составляющую выражения умножаем на a²:

a³*y³+b*a²*y²+c*a*a*y+d*a²=0

Учитывая, что решение кубических уравнений с подробным решением предполагает замещение переменных x=ay, то:

x²+b*x²+c*a*x+d*a²

Полученное уравнение является кубическим. В таких уравнениях корни могут быть разными – и целыми, и рациональными. Чтобы привести такое уравнение к тождественному равенству, потребуется подставить делители в полученное равенство. В этом случае полученный x₁ будет корнем, и в то же время корнем начального уравнения:

x₁=y₁/a

Чтобы найти значение корней квадратного трехчлена, потребуется многочлен ay3+by2+cy+d разделить на y-y_1.

Рассмотрим решение кубических уравнений такого вида на примере.

Пример:

Решить уравнение [x 3-3 x 2-13 x+15=0].

Решение:

Ищем первый корень перебором чисел: [0, pm1, pm2, pm3, pm5, pm15] и подстановкой в уравнение. В результате находим, что 1 является корнем. Тогда делим левую часть этого уравнения на двухчлен x-1 и получаем:

Теперь, решая квадратное уравнение: [x 2-2 x-15=0], находим оставшиеся два корня: x1=-3 и x2=5.

Ответ: 1; -3; 5.

Такой способ решения кубических уравнений используется для преобразования и решения возвратных уравнений. Из приведенного примера видно, что корнем является -1, значит, левую часть можно разделить на x+1. После того, как эти действия выполнены, можно находить корни квадратного трехчлена. Если рациональные корни отсутствуют, необходимо находить иные методы решения и разложения многочлена на множители.

Решение кубического уравнения с помощью формулы Кардано

Есть еще один способ — формула Кардано для решения кубических уравнений.

Если взять уравнение вида B₀y³+B₁y²+B₂y+B₃=0, то A₁=B₁/B₀, A₂=B₂/B₀, A₃=B₃/B₀.

Z=-A²₁/3+A₂

P=2A³₁/27-A₁A₂/3+A₃.

Выведенные значение Z и P подставим в формулу Кардано.

X=³√-P/2+√P²/4+Z³/27+³√-P/2-+√P2/4+Z3/27

В итоге подбор кубических корней должен соответствовать значению –Z/3. В этом случае корни исходного уравнения будут выглядеть следующим образом:

y=x-A₁/3

Применить формулу Кордано можно на примере для наглядности.

Пример

Решить уравнение [x^{3}+6 x^{2}+3 x-10=0]

Решение

Данное уравнение легко решается и без применения формулы Кардано. Легко подобрать корень [x=1]. Делением
[x=1] левой части уравнения по схеме Горнера получаем:

[begin{array}{r}+begin{array}{r}1&6&3&-10\0&1*1=1&7*1=7&10*1=10\end{array}
\hlinebegin{array}{r}1quadquadquad&7quadquadquad&10quadquadquadquad&0end{array}end{array}]

Следовательно, [x^{2}+7 x+10=0]. Решая это квадратное уравнение, получаем

[x=frac{-7 pm sqrt{7^{2}-4 * 1 * 10}}{2} Leftrightarrow x_{1}=-2, quad x_{2}=-5]

А теперь найдем корни исходного уравнения по формуле Кардано. Для данного уравнения [a=1, b=6, c=3, d=-10].
Замена переменной [x=y-frac{b}{3 a}=y-frac{6}{3}=y-2] приводит исходное уравнение к виду [y^{3}+p
y+q=0], где:

[p=frac{3 a c-b^{2}}{3 a^{2}}=frac{3 * 1 * 3-6^{2}}{3 * 1^{2}}=-9, quad q=\frac{2 b^{3}-9 a b c+27 a^{2}
d}{27 a^{3}}=frac{2 * 6^{3}-9 * 1 * 6 * 3+27 * 1^{2} *(-10)}{27 * 1^{3}}=0]

Вычислим дискриминант этого уравнения:

[Delta=left(frac{q}{2}right)^{2}+left(frac{p}{3}right)^{3}=left(frac{0}{2}right)^{2}+left(-frac{9}{3}right)^{3}=-27]

Так [Delta] каноническое уравнение имеет 3 действительных корня. Поскольку [q=0 Rightarrow
varphi=frac{pi}{2}=>]

[y_{1}=2 sqrt{-frac{p}{3}} * cos left(frac{varphi}{3}right)=2 sqrt{-frac{-9}{3}} * cos
left(frac{frac{pi}{2}}{3}right)=2 sqrt{3} * cos left(frac{pi}{6}right)=2 sqrt{3} *
frac{sqrt{3}}{2}=3,\y_{2}=2 sqrt{-frac{p}{3}} * cos left(frac{varphi}{3}+frac{2 pi}{3}right)=2
sqrt{3} * cos left(frac{frac{pi}{2}}{3}+frac{2 pi}{3}right)=2 sqrt{3} * cos left(frac{5
pi}{6}right)=-2 sqrt{3} * frac{sqrt{3}}{2}=-3,\y_{3}=2 sqrt{-frac{p}{3}} * cos
left(frac{varphi}{3}+frac{4 pi}{3}right)=2 sqrt{3} * cos left(frac{frac{pi}{2}}{3}+frac{4
pi}{3}right)=2 sqrt{3} * cos left(frac{3 pi}{2}right)=0.]

В данном случае для корней начального уравнения мы получим:

x₁=y₁-2=3-2=1;

x₂=y₂-2=-3-2=-5;

x₃=y₃-2=0-2=-2.

Получаем ответы: 1, -5, -2.

Нет времени решать самому?

Наши эксперты помогут!

Общее решение кубического уравнения, если известен один из корней

За исходное уравнение возьмем следующее:

y³+ay²+by+c=0

Предположим, что a,b,c являются действительными цифровыми значениями. Известный корень пометим, как y₁. В таком случае, если произвести деление начального уравнения y³+ay²+by+c=0 на y-y₁получим квадратное уравнение. При решении такого уравнения удастся найти еще два корня – y₂и y₃.

Чтобы доказать это, преобразуем кубический многочлен следующим образом:

y₃+ay₂+by+c=(y-y₁)(y-y₂)(y-y₃)

При решении таких уравнений часто допускаются ошибки. Их решение – это сложное, многократное преобразование, которое требует точного знания формул и математических законов. Чтобы избежать ошибок и погрешностей, потребуется применить не только практические навыки, но и теоретические знания. Для решения кубических уравнений можно использовать специальный онлайн калькулятор. Принцип его действия основан на формуле Кардано. В том случае, если один или несколько коэффициентов такого уравнения равны нулю, или между ними присутствует определенная зависимость, решение будет более простым.

Чтобы научиться решать подобные уравнения, необходимо рассматривать примеры и тренироваться на их решении разными способами.

Источник

Определение

Рассмотрим произвольное уравнение вида

[a_nx^n+a_{n-1}x^{n-1}+dots+a_1x+a_0=0 qquad qquad (1)]

где (a_n, a_{n-1},dots,a_0) – некоторые числа, причем (a_nne 0), называемое алгебраическим уравнением (с одной переменной) (n)-ой степени.

Обозначим (P_n(x)=a_nx^n+a_{n-1}x^{n-1}+dots+a_1x+a_0). Таким образом, сокращенно уравнение ((1)) можно записать в виде (P_n(x)=0).

Замечание

Заметим, что квадратное уравнение — это алгебраическое уравнение, степень которого равна (2), а линейное — степень которого равна (1).
Таким образом, все свойства алгебраических уравнений верны и для квадратных уравнений, и для линейных.

Теорема

Если уравнение ((1)) имеет корень (x=x_0), то оно равносильно уравнению

[(x-x_0)cdot P_{n-1}(x)=0]

где (P_{n-1}(x)) – некоторый многочлен степени (n-1).

Для того, чтобы найти (P_{n-1}(x)), необходимо найти частное от деления многочлена (P_n(x)) на ((x-x_0))
(т.к. (P_n(x)=(x-x_0)cdot P_{n-1}(x))).

Следствие: количество корней уравнения

Любое алгебраическое уравнение степени (n) может иметь не более (n) корней.

Замечание

В частности, квадратное уравнение действительно имеет всегда не более двух корней: два, один (или два совпадающих) или ни одного корня.

Для того, чтобы найти частное от деления одного многочлена на другой, удобно пользоваться следующим способом, который мы рассмотрим на примере.

Пример

Известно, что (x=2) является корнем уравнения (2x^3-9x^2+x^4-x+6=0). Найдите частное от деления (2x^3-9x^2+x^4-x+6) на (x-2).

Решение.
Будем делить многочлен на многочлен в столбик. Запишем

[begin{array}{rr|l}
x^4+2x^3-9x^2-x+6&&negthickspaceunderline{qquad x-2 qquad}\
&&\
end{array}]

Заметим, что записывать слагаемые в делимом необходимо по убыванию их степеней: в данном случае сначала (x^4), затем (2x^3) и т.д.
Подбирать слагаемые в частном будем таким образом, чтобы при вычитании уничтожить сначала четвертую степень, затем третью и т.д.
Т.к. делитель (x-2) состоит из двух слагаемых, то при делении в столбик будем сносить по два слагаемых.

Посмотрим, на что необходимо домножить (x-2), чтобы после вычитания из (x^4+2x^3) полученного многочлена уничтожилось слагаемое (x^4,).
На (x^3). Тогда после вычитания (x^4+2x^3-x^3(x-2)) останется (4x^3). Снесем слагаемое (-9x^2):

[begin{array}{rr|l}
x^4+2x^3-9x^2-x+6&&negthickspaceunderline{qquad x-2 qquad}\
underline{x^4-2x^3,} phantom{000000000000}&&negthickspace quad
x^3\[-3pt]
4x^3 -9x^2phantom{0000000}&&\
end{array}]

Теперь посмотрим, на что необходимо домножить (x-2), чтобы после вычитания из (4x^3-9x^2) полученного многочлена уничтожилось слагаемое (4x^3).
На (4x^2): (quad 4x^3-9x^2-4x^2(x-2)=-x^2).
Опять снесем следующее слагаемое (-x):

[begin{array}{rr|l}
x^4+2x^3-9x^2-x+6&&negthickspaceunderline{qquad x-2 qquad}\
underline{x^4-2x^3,} phantom{000000000000}&&negthickspace quad
x^3+4x^2\[-3pt]
4x^3 -9x^2phantom{0000000}&&\
underline{4x^3 — 8x^2,};phantom{000000}&&\[-3pt]
-x^2 — xphantom{000};&&\
end{array}]

Рассуждая аналогично, определяем, что третье слагаемое в частном должно быть (-x)

[begin{array}{rr|l}
x^4+2x^3-9x^2-x+6phantom{0}&&negthickspaceunderline{qquad x-2 qquad}\
underline{x^4-2x^3,} phantom{0000000000000}&&negthickspace quad
x^3+4x^2-x\[-3pt]
4x^3 -9x^2phantom{00000000}&&\
underline{4x^3 — 8x^2,}phantom{0000000};;&&\[-3pt]
-x^2 — ,xphantom{0000};&&\
underline{-x^2+2x},phantom{000};&&\[-3pt]
-;3x+6&&\
end{array}]

Четвертое слагаемое в частном должно быть (-3):

[begin{array}{rr|l}
x^4+2x^3-9x^2-x+6phantom{0}&&negthickspaceunderline{qquad x-2 qquad}\
underline{x^4-2x^3,} phantom{0000000000000}&&negthickspace quad
x^3+4x^2-x-3\[-3pt]
4x^3 -9x^2phantom{00000000}&&\
underline{4x^3 — 8x^2,}phantom{0000000};;&&\[-3pt]
-x^2 — ,xphantom{0000};&&\
underline{-x^2+2x},phantom{000};&&\[-3pt]
-;3x+6&&\
underline{-;3x+6}&&\[-3pt]
0&&\
end{array}]

Таким образом, можно сказать, что (x^4+2x^3-9x^2-x+6=(x-2)(x^3+4x^2-x-3)).

Замечание

1) Если (x=x_0) действительно является корнем уравнения, то после такого деления в остатке должен быть (0). В противном случае это означает, что деление в столбик выполнено неверно.

2) Если многочлен делится без остатка (то есть остаток равен (0)) на (x+a), то он также будет делиться без остатка на (c(x+a)) для любого числа (cne 0). Например, в нашем случае, если бы мы поделили многочлен, к примеру, на (2x-4), то получили бы в частном (frac12
x^3+2x^2-frac12x-frac32).
Заметим, что также происходит и с числами: если мы разделим (10) на (2), то получим (5); а если разделим (10) на (3cdot 2), то получим (frac53).

3) Деление в столбик помогает найти другие корни уравнения: теперь для того, чтобы найти остальные корни уравнения (x^4+2x^3-9x^2-x+6=0), необходимо найти корни уравнения (x^3+4x^2-x-3=0).
Поэтому рассмотрим несколько фактов, часто помогающих подобрать корни алгебраического уравнения.

Теорема

Если число (x=1) является корнем уравнения ((1)), то сумма всех коэффициентов уравнения равна нулю:

[a_n+a_{n-1}+dots+a_1+a_0=0]

Доказательство

Действительно, так как (x=1) является корнем уравнения ((1)), то после подстановки (x=1) в него мы получим верное равенство. Так как (1) в любой степени равен (1), то слева мы действительно получим сумму коэффициентов (a_i), которая будет равна нулю.

Пример

У уравнения (x^2-6x+5=0) сумма коэффициентов равна нулю: (1-6+5=0). Следовательно, (x=1) является корнем этого уравнения. Это можно проверить просто подстановкой: (1^2-6cdot
1+5=0quadLeftrightarrowquad 0=0).

Теорема

Если число (x=-1) является корнем уравнения ((1)), то сумма коэффициентов при четных степенях (x) равна сумме коэффициентов при нечетных степенях (x).

Доказательство

1) Пусть (n) – четное. Подставим (x=-1):

(a_ncdot (-1)^n+a_{n-1}cdot (-1)^{n-1}+a_{n-2}cdot
(-1)^{n-2}+dots+a_1cdot (-1)+a_0=0 quadRightarrow)

(a_n-a_{n-1}+a_{n-2}-dots-a_1+a_0=0 quad Rightarrow)

(a_n+a_{n-2}+dots+a_0=a_{n-1}+a_{n-3}+dots+a_1)

2) Случай, когда (n) – нечетное, доказывается аналогично.

Пример

В уравнении (x^3+2x^2-8x+5=0) сумма коэффициентов равна нулю:

[1+2-8+5=0]

Значит, число (x=1) является корнем данного уравнения.

Можно разделить в столбик (x^3+2x^2-8x+5) на (x-1):

[begin{array}{rr|l}
x^3+2x^2-8x+5&&negthickspaceunderline{qquad x-1 qquad}\
underline{x^3- x^2,} phantom{00000000}&&negthickspace
quad x^2 + 3x -5\[-3pt]
3x^2 — 8x,phantom{000}&&\
underline{3x^2 — 3x,}phantom{000}&&\[-3pt]
-5x + 5&&\
underline{-5x +5}&&\[-3pt]
0&&\
end{array}]

Таким образом, (x^3+2x^2-8x+5=(x-1)(x^2 + 3x -5)). Значит, остальные корни исходного уравнения — это корни уравнения (x^2+3x-5=0).

А это (x_{1,2}=-dfrac 32pm dfrac{sqrt{29}}2).

Таким образом мы нашли все корни исходного уравнения.

Пример

В уравнении (x^3-x^2+x+3=0) сумма коэффициентов при четных степенях (-1+3=2), а при нечетных: (1+1=2). Таким образом, число (x=-1) является корнем данного уравнения.

Можно разделить в столбик (x^3-x^2+x+3) на (x+1):

[begin{array}{rr|l}
x^3-,x^2+ x+3phantom{0}&&negthickspaceunderline{qquad x+1 qquad}\
underline{x^3+x^2;} phantom{00000000}&&negthickspace
quad x^2 -2x +3\[-3pt]
-2x^2 + xphantom{0000}&&\
underline{-2x^2 -! 2x},phantom{000}&&\[-3pt]
3x + 3&&\
underline{3x +3}&&\[-3pt]
0&&\
end{array}]

Таким образом, (x^3-x^2+x+3=(x+1)(x^2 — 2x +3)). Значит, остальные корни исходного уравнения — это корни уравнения (x^2-2x+3=0).
Но это уравнение не имеет корней ((D<0)), значит, исходное уравнение имеет всего один корень (x=-1).

Замечание

Подбор корней таким образом, деление в столбик и разложение многочлена на множители помогают найти корни уравнения.

Существует еще одна очень важная теорема, позволяющая подобрать рациональный корень алгебраического уравнения, если таковой имеется.

Теорема

Если алгебраическое уравнение

[a_nx^n+a_{n-1}x^{n-1}+dots+a_1x+a_0=0,] где (a_n, dots, a_0) — целые числа,
имеет рациональный корень (x=dfrac pq), то число (p) является делителем свободного члена (a_0), а число (q) — делителем старшего коэффициента (a_n).

Пример

Рассмотрим уравнение (2x^4-5x^3-x^2-5x-3=0).

В данном случае (a_0=-3, a_n=2). Делители числа (-3) — это (pm 1,
pm 3). Делители числа (2) – это (pm 1, pm 2). Комбинируя из полученных делителей дроби, получаем все возможные варианты рациональных корней:

[pm 1, pm dfrac12, pm 3, pmdfrac32]

По предыдущим теоремам можно быстро понять, что (pm1) не являются корнями. Подставив (x=-dfrac12) в уравнение, получим:

[2cdot dfrac1{16}+5cdot dfrac18-dfrac 14+5cdot dfrac12-3=0
quad Leftrightarrow quad 0=0]

Значит, число (x=-frac12) является корнем уравнения.

Можно перебрать остальные варианты: таким образом мы найдем еще один рациональный корень уравнения (x=3). Значит, уравнение можно представить в виде

[left(x+frac12right)(x-3)cdot Q_2(x)=0 quad text{или}quad (2x+1)(x-3)cdot P_2(x)=0] (тогда (P_2(x)=frac12 Q_2(x))). Заметим, что второй вид записи уравнения более удобный, т.к. нам не придется при делении в столбик работать с дробями.

После деления в столбик (2x^4-5x^3-x^2-5x-3) на ((2x+1)(x-3)=2x^2-5x-3):

[begin{array}{rr|l}
2x^4-5x^3- x^2-5x-3phantom{0}&&negthickspaceunderline{qquad 2x^2-5x-3 qquad}\
underline{2x^4-5x^3-3x^2;} phantom{00000000}&&negthickspace
qquad
x^2+0x+1\[-3pt]
0x^3 +2x^2-5xphantom{0000}&&\
underline{0x^3 + 0x^2+0x}phantom{0000}&&\[-3pt]
2x^2 — 5x-3,&&\
underline{2x^2-5x-3};&&\[-3pt]
0&&\
end{array}]

получим, что (P_2(x)=x^2+1). Данный многочлен не имеет корней, значит, уравнение имеет только два корня: (x=-frac12) и (x=3).

Замечание

Заметим, что если, пользуясь предыдущей схемой, не удалось подобрать рациональный корень уравнения, это вовсе не значит, что уравнение не имеет корней.
Например, уравнение (x^3-2=0) имеет корень — это (x=sqrt[3]2), и он не рациональный.
Для подбора иррациональных корней не существует универсального алгоритма.

Пример

Найдите корни уравнения (4x^3-3x^2-frac{23}6x-1=0).

Заметим, что в данном уравнении не все коэффициенты – целые числа (коэффициент при (x) равен (-frac{23}6)). Но мы можем преобразовать данное уравнение к нужному нам виду: необходимо умножить правую и левую части уравнения на (6):

[24x^3-18x^2-23x-6=0]
Делители свободного члена: (pm 1, pm 2, pm 3, pm 6).
Делители старшего коэффициента: (pm 1, pm 2, pm 3, pm4, pm 6,
pm 8,
pm 12, pm 24).
Получилось достаточно много (:))
Выпишем некоторые возможные рациональные корни уравнения:

[pm 1, pm dfrac12, pm dfrac13, pm dfrac 16, pmdfrac18,
pm2, pmdfrac23, pm dfrac14, pm3quad text{small{и
т.д.}}]

Перебирая варианты, убеждаемся, что (frac32) подходит. Значит, многочлен (24x^3-18x^2-23x-6) должен без остатка поделиться на (x-frac32). Для удобства разделим на (2(x-frac32)=2x-3) (чтобы не работать с дробями):

[begin{array}{rr|l}
24x^3-18x^2-23x-6phantom{0}&&negthickspaceunderline{qquad 2x-3 qquad}\
underline{24x^3-36x^2};; phantom{000000000}&&negthickspace
quad 12x^2 +9x +2\[-3pt]
18x^2 -23xphantom{0000}&&\
underline{18x^2 -27x},;phantom{000}&&\[-3pt]
4x -6&&\
underline{4x -6}&&\[-3pt]
0&&\
end{array}]

Таким образом, (24x^3-18x^2-23x-6=(2x-3)(12x^2 +9x +2)). Уравнение (12x^2 +9x +2=0) в свою очередь корней не имеет. Значит, (x=frac32) – единственный корень исходного уравнения.

Теорема

Любой многочлен (P_n(x)=a_nx^n+a_{n-1}x^{n-1}+dots+a_1x+a_0) можно разложить на произведение множителей: линейных ((ax+b, ane 0)) и квадратичных ((cx^2+px+q, cne 0)) с отрицательным дискриминантом.

Следствие

Кубическое уравнение (Ax^3+Bx^2+Cx+D=0) всегда имеет как минимум один вещественный корень, т.к. его левую часть всегда можно представить как

[Ax^3+Bx^2+Cx+D=A(x+r)(x^2+px+q)=0]

Замечание

На самом деле, такой вывод можно сделать о любом алгебраическом уравнении нечетной степени. Но, как правило, в школьном курсе математики крайне редко встречаются уравнения степени выше (4).

Источник

Download Article

In a cubic equation, the highest exponent is 3, the equation has 3 solutions/roots, and the equation itself takes the form $ax^{3}+bx^{2}+cx+d=0$ . While cubics look intimidating and unlike quadratic equation is quite difficult to solve, using the right approach (and a good amount of foundational knowledge) can tame even the trickiest cubics. You can try, among other options, using the quadratic formula, finding integer solutions, or identifying discriminants.

1
2

Advertisement
3
4
5

Use zero and the quadratic answers as your cubic’s answers. While quadratic equations have two solutions, cubics have three. You already have two of these — they’re the answers you found for the «quadratic» portion of the problem in parentheses. In cases where your equation is eligible for this «factoring» method of solving, your third answer will always be .^[6]

1
2
3
4

Plug in the integers manually for a simpler but possibly time-consuming approach. Once you have your list of values, you can find the integer answers to your cubic equation by quickly plugging each integer in manually and finding which ones equal . For instance, if you plug in , you get:^[10]
5

1
2

Calculate the discriminant of zero using the proper formula. The discriminant approach to finding a cubic equation’s solution requires some complicated math, but if you follow the process carefully, you’ll find that it’s an invaluable tool for figuring out those cubic equations that are hard to crack any other way. To start, find $Delta _{0}$ (the discriminant of zero), the first of several important quantities we’ll need, by plugging the appropriate values into the formula $Delta _{0}=b^{2}-3ac$ .^[13]
3
4
5
6

Practice Problems and Answers

Add New Question

Question

How do you solve a simple cubic equation?

David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

Academic Tutor

Expert Answer

If you only have x³ in an equation, you can isolate it and find the cube root of both sides. This only works with really simple equations, though—factoring is the best way to solve more complex equations.
Question

How would I solve xy+z+z^3=1?

That equation has numerous answers because you’ve got three variables. To get one answer for three variables you need three equations. One possible answer would be x=1, y=-1, z=1 => (1)(-1)+1+1^3=1.
Question

The question is: if 3 consecutive even numbers are multiplied and the result would be 960. What are those numbers and how did you did with the step?

Elvis Kiprotich

Community Answer

Solve the equation using the discriminant approach you will get three values of x. X=8, X=-7+(-1i)√71, X=-7+i√71. Easy from here, you pick the real value of x, that’s 8 and your three numbers were 8, 10 and 12.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

References

About This Article

Article SummaryX

To solve a cubic equation, start by determining if your equation has a constant. If it doesn’t, factor an x out and use the quadratic formula to solve the remaining quadratic equation. If it does have a constant, you won’t be able to use the quadratic formula. Instead, find all of the factors of a and d in the equation and then divide the factors of a by the factors of d. Then, plug each answer into the equation to see which one equals 0. Whichever integer equals 0 is your answer. Read on to learn how to solve a cubic equation using a discriminant approach!

Did this summary help you?

Thanks to all authors for creating a page that has been read 925,638 times.

Reader Success Stories

«The content has been written in a very easy way so that any one can understand what is told.»

Did this article help you?

Источник

Об этой статье

Была ли эта статья полезной?

Возведение многочленов в куб

Решение кубических уравнений с двумя членами

Методы решения кубических уравнений возвратного вида

Решение кубических уравнений в составе которых рациональные корни

Решение кубического уравнения с помощью формулы Кардано

Общее решение кубического уравнения, если известен один из корней

Practice Problems and Answers

Video

References

About This Article

Reader Success Stories

Did this article help you?

Не пропустите также: