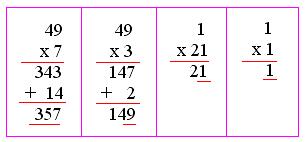Объяснение этого «фокуса» (или как там его назвать?) еще в самом начале 20 века дал Советский Я́ков Иси́дорович Перельма́н — российский и советский математик, физик и мировед, журналист и педагог, популяризатор точных наук, основоположник жанра занимательной науки. Правда не скажу в какой-именно книге я об этом прочитал. Оказывается на эту тему он начал издавать книги ещё в 1913 году («Занимательная физика) и занимался этим всю жизнь до гибели в блокадном Ленинграде. По данным Всесоюзной книжной палаты, с 1918 по 1973 год его книги только в СССР издавались 449 раз; их общий тираж составил более 13 миллионов экземпляров.
Так вот секрет заключается вот в чём.
При возведении любого числа в «куб», последняя цифра этого куба определяется только последней цифрой исходного двузначного числа. Вот смотрите: 1^3=1, 2^3=8, 3^3=27, 4^3=64, 5^3=125, 6^3=216, 7^3=343, 8^3==515, 9^3=729. Итак если двузначное число заканчивается на 1, 4, 5, 6, 9, то его куб заканчивается на ту же цифру, и только 2 и 3 (и их дополнения до десятки, т.е. 8 и 7) меняются местами. (А для пятых степеней последние цифры вообще совпадают). Теперь, разделим исходное число на 10, соответственно куб на 1000, т.е. рассмотрим первую цифру двузначного и первые 3 цифры куба. Нужно выбрать такое однозначное число, чтобы его куб не превышал первые 3 цифры «куба». А запомнить кубы первой десятки чисел — не проблема. Итак, то число будет первой цифрой исходного числа, а насчёт второй мы уже выяснили.
Например: а^3=110592. Последняя цифра куба — 2, значит в исходном числе последняя цифра — 8. Смотрим первую тройку цифр куба — 110. Вспоминаем таблицу кубов: 4^3=64<110, 5^3=125>110. Значит первая цифра исходного числа 4, а само число а=48.
Ещё пример: а^3=438976. вторая цифра исходного числа 6, а первая цифра 7, так как 7^3=343>438, а 8^3=512>438. Значит а=76.
Всего-то нужно запомнить таблицу кубов чисел от 1 до 10. А это совсем нетрудно.
P.S. Вчера я был в «бане» и не мог сразу ответить.
Для успешного выполнения упражнения ознакомьтесь с теорией и проработайте предыдущие уроки
Возведение двузначных чисел в куб | Теория
Возведение в уме двузначного числа X в куб (третью степень) удобно производить по формуле: Х3=(X+Y)X(X-Y)X+XY2*, где Y — число, на которое нужно уменьшить или увеличить число X, чтобы получить округлённое до десятков (заканчивающееся на 0) число.
Задача: 133
Решение:
Круглое число получается при вычитании 3 из 13. Поэтому за Y принимаем число 3.
(X+Y) = 13 + 3 = 16
(X-Y) = 13 — 3 = 10
Подставляем полученные числа в формулу:
133 = 16 x 13 x 10 + 13 x 32
Умножение 16 на 13 удобно выполнить с помощью факторизации числа 16.
16 x 13 x 10 = 13 x 4 x 4 x 10 = 52 x 4 x 10 = 208 x 10 = 2080
13 x 33 = 13 x 9 = 117
2080 + 117 = 2197
Задача: 453
Решение:
453 = 50 x 45 x 40 + 45 x 52
50 x 45 x 40 = 45 x 40 x 50 = 1800 x 50 = 90000
45 x 52 = 45 x 5 x 5 = 225 x 5 = 1125
90000 + 1125 = 91125
Задача: 693
Решение:
693 = 70 x 69 x 68 + 69 x 12
Так как числа 69 и 68 близки к круглому числу 70, то их удобно перемножить с помощью формулы (C-a)(C-b) = (C-a-b)C+ab, где “C” – близкое к двум перемножаемым числам круглое число, а “а” и “b” – это разницы между круглым числом и перемножаемыми числами (см. урок 10).
68 x 69 = (70 – 2) x (70 – 1) = (70 – 2 – 1) x 70 + 2 x 1 = 67 x 70 + 2 x 1 = 4690 + 2 = 4692
4692 x 70 = 4692 x 70 = 328440 (см. урок 13)
69 x 12 = 69 x 1 = 69
328440 + 69 = 328509
Задача: 923
Решение:
923 = 94 x 92 x 90 + 92 x 22
Так как числа 94 и 92 близки к круглому числу 90, то их можно перемножить с помощью формулы (C+a)(C+b) = (C+a+b)C+ab, где “C” – близкое к двум перемножаемым числам круглое число, а “а” и “b” – это разницы между перемножаемыми числами и круглым числом (см. урок 10).
94 x 92 = (90 + 4) x (90 + 2) = (90 + 4 + 2) x 90 + 4 x 2 = 96 x 90 + 4 x 2 = 8640 + 8 = 8648
8648 x 90 = 778320 (см. урок 13)
92 x 22 = 92 x 4 = 368
778320 + 368 = 778688
Задача: 963
Решение:
963 = 100 x 96 x 92 + 96 x 42
Перемножить 96 и 92 можно следующими способами (в порядке снижения сложности):
1) Обычное перемножение слева направо: 96 x 92 = 96 x 90 + 96 x 2 = 8640 + 192 = 8832
2) Метод вычитания: 92 x (100 – 4) = 9200 – 368 = 8832
3) С использованием факторизации: 92 x 6 x 4 x 4 = 552 x 4 x 4 = 2208 x 4 = 8832
4) Вычисление по формуле (C+a)(C+b) = (C+a+b)C+ab: 96 x 92 = (90 + 6) x (90 + 2) = (90 + 6 + 2) x 90 + 6 x 2 = 98 x 90 + 6 x 2 = 8820 + 12 = 8832
5) Вычисление по формуле (C-a)(C-b) = (C-a-b)C+ab: 96 x 92 = (100 – 4) x (100 – 

8832 x 100 = 883200
Операцию 42 x 96 также можно выполнить несколькими методами, включая:
1) С использованием факторизации: 42 x 96 = 96 x 4 x 4 = 384 x 4 = 1536
2) Метод вычитания: 42 x 96 = 16 x (100 – 4) = 1600 – 64 = 1536
883200 + 1536 = 884736
* Формула получена путём умножения формулы для квадрата числа X (из урока 11) на число X: X3=X2X=((X+Y)(X-Y)+Y2)X=(X+Y)X(X-Y)+XY2
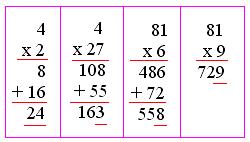
We will learn the short-cut method for finding the cube of a two-digit number.
Suppose, we have (a + b)³ = a³ + 3a²b + 3ab² + b³.
METHOD:
For finding the cube of a two-digit number with the tens digit = a
and the units digit = b, we make four columns, headed by
a³, (3a² × b), (3a × b²) and b³
The rest of the procedure is the same as followed in squaring a number by the column method.
We simplify the working as;
a² × a = a³;
a² × 3b = 3a²b;
b² × 3a = 3ab²;
b² × b = b³;
Examples on the method for finding the cube of a two-digit number:
1. Find the value of (29)³ by the short-cut method.
Solution:
Here, a = 2 and b =9.
a² × a = a³;
b² × 3a = 3a × b²;
b² × b = b³
2. Find the value of (71)³ by the short-cut method.
a² × a = a³;
a² × 3b = 3a² × b;
b² × 3a = 3a × b²;
b² × b = b³
Therefore, (71)³ = 357911
By following the above examples on the method for finding the cube of a two-digit number; we can try to find the value of each of the following using the short-cut method;
1. (25)³
2. (47)³
3. (68)³
4. (84)³
● Cube and Cube Roots
Cube
To Find if the Given Number is a Perfect Cube
Cube Root
Method for Finding the Cube of a Two-Digit Number
Table of Cube Roots
● Cube and Cube Roots — Worksheets
Worksheet on Cube
Worksheet on Cube and Cube Root
Worksheet on Cube Root
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Таблица Кубов натуральных чисел
Таблица кубов натуральных двузначных чисел от 0 до 10, до 100. Несколько версий для печати таблицы кубов. Удобный калькулятор кубов любых чисел
Таблица кубов от 0 до 100
Десятки от 0 до
9
Десятичных знаков — 4
Округление — 5/4
Добавить нули — нет
Экспоненциал. вид — нет
Сбросить настройки —
1000
1331
1728
2197
2744
3375
4096
4913
5832
6859
8000
9261
10648
12167
13824
15625
17576
19683
21952
24389
27000
29791
32768
35937
39304
42875
46656
50653
54872
59319
64000
68921
74088
79507
85184
91125
97336
103823
110592
117649
125000
132651
140608
148877
157464
166375
175616
185193
195112
205379
216000
226981
238328
250047
262144
274625
287496
300763
314432
328509
343000
357911
373248
389017
405224
421875
438976
456533
474552
493039
512000
531441
551368
571787
592704
614125
636056
658503
681472
704969
729000
753571
778688
804357
830584
857375
884736
912673
941192
970299
[an error occurred while processing the directive]
03 = 0
13 = 1
23 = 8
33 = 27
43 = 64
53 = 125
63 = 216
73 = 343
83 = 512
93 = 729
103 = 1000
113 = 1331
123 = 1728
133 = 2197
143 = 2744
153 = 3375
163 = 4096
173 = 4913
183 = 5832
193 = 6859
203 = 8000
213 = 9261
223 = 10648
233 = 12167
243 = 13824
253 = 15625
263 = 17576
273 = 19683
283 = 21952
293 = 24389
303 = 27000
313 = 29791
323 = 32768
333 = 35937
343 = 39304
353 = 42875
363 = 46656
373 = 50653
383 = 54872
393 = 59319
403 = 64000
413 = 68921
423 = 74088
433 = 79507
443 = 85184
453 = 91125
463 = 97336
473 = 103823
483 = 110592
493 = 117649
503 = 125000
513 = 132651
523 = 140608
533 = 148877
543 = 157464
553 = 166375
563 = 175616
573 = 185193
583 = 195112
593 = 205379
603 = 216000
613 = 226981
623 = 238328
633 = 250047
643 = 262144
653 = 274625
663 = 287496
673 = 300763
683 = 314432
693 = 328509
703 = 343000
713 = 357911
723 = 373248
733 = 389017
743 = 405224
753 = 421875
763 = 438976
773 = 456533
783 = 474552
793 = 493039
803 = 512000
813 = 531441
823 = 551368
833 = 571787
843 = 592704
853 = 614125
863 = 636056
873 = 658503
883 = 681472
893 = 704969
903 = 729000
913 = 753571
923 = 778688
933 = 804357
943 = 830584
953 = 857375
963 = 884736
973 = 912673
983 = 941192
993 = 970299
Таблица кубов для печати
таблица кубов
список кубов
книжная ориентация
альбомная ориентация
Вы можете распечатать таблицу или скачать таблицу кубов и сохратить в формате Pdf.
Для более точных настроек используйте блок настроек в шапке таблицы кубов.