В этой статье начнем говорить о кручении. Это одна из базисных тем в сопромате, как и растяжение-сжатие. Знания этой темы помогут тебе при изучении более сложных тем курса «сопротивление материалов».
Кручение – это такой вид деформации, при котором в сечениях стержня возникают крутящие моменты (T).
На кручение, как правило, работают детали, которые называются валами. Детали, которые широко используются в машиностроении.
Что такое крутящий момент?
Крутящий момент – это внутренний силовой фактор, возникающий в сечениях стержней испытывающих деформацию кручения.
На практике же стержни не работают исключительно на кручение, они могут и растягиваться, и изгибаться. Но это уже более продвинутые темы – сложное сопротивление. В этом же разделе будем рассматривать чистое кручение.
В чем измеряется крутящий момент и как обозначается?
Крутящие моменты обозначаются буквой – T (сокращённое с английского: Torque – крутящий момент), однако, часто в другой литературе ты можешь встретить обозначение — Мкр. Ты можешь использовать любое обозначение, какое больше нравиться, либо которое использует твой преподаватель.
В задачах тебе будут даны крутящие моменты, скорее всего, в Н·м либо кН·м.
Построение эпюры крутящих моментов
В этой статье расскажу, как строить эпюры при кручении: крутящих моментов, максимальных касательных напряжений и углов закручивания (углов поворотов).
На самом деле, многие рассматриваемые здесь принципы сильно похожи на те, что мы изучали ранее в уроке про построение эпюр при растяжении (сжатии). Здесь фактически будем делать всё то же самое, только оперировать другими обозначениями и названиями. После изучения того урока, с кручением у тебя точно не возникнет никаких трудностей.
В качестве примера, возьмём следующую расчётную схему:

Будем считать, что стержень изготовлен из стали (G = 8 · 1010 Па), а диаметры ступеней равны: d1=150 мм, d2=200 мм, d3=300 мм.
Под действием внешних моментов (M), их еще часто называют вращающими или скручивающими моментами, в поперечных сечениях стержня возникают внутренние моменты – крутящие (T).

Правило знаков для крутящих моментов
Чтобы построить эпюру крутящих моментов, необходимо задаться каким-то правилом знаков для крутящих моментов. В этой статье я буду использовать следующее правило:
- Если внешний момент (M), в плоскости сечения, поворачивает ПРОТИВ часовой стрелки, то крутящий момент (T) – положительный.

- Если внешний момент (M), в плоскости сечения, поворачивает ПО часовой стрелке, то крутящий момент (T) – отрицательный.

Можно учитывать знак крутящего момента ровно наоборот. Главное, придерживаться этого правила при расчёте всех участков и ориентироваться по полученным эпюрам: в какую сторону у тебя будут направлены внешние моменты, внутренние – крутящие моменты, куда будут поворачиваться сечения. Как видишь, знаки здесь нам нужны, чтобы задать определённые правила игры, а правило знаков – условное и не имеет физического смысла.
Расчёт крутящих моментов
Что же, давай, наконец, приступим к расчёту крутящих моментов. Пронумеруем расчётные участки:

Используя правило знаков, описанное выше, рассчитаем крутящие моменты на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры касательных напряжений при кручении
Касательные напряжения по высоте круглого сечения, будут распределены следующим образом:

Как видишь, касательные напряжения будут максимальны на поверхности стержня, они нас и будут интересовать больше всего, т. к. по ним выполняются прочностные расчёты, для них и будем строить эпюру – максимальных касательных напряжений.
Расчёт максимальных касательных напряжений
Максимальные касательные напряжения в поперечном сечении, можно определить по формуле:

где Wp — полярный момент сопротивлния, T — крутящий момент.
Полярный момент сопротивления для круглого сечения определяется по формуле:

Поэтому формулу для нахождения максимальных касательных напряжений для круглого поперечного сечения, можно записать в следующем виде:

По условию задачи диаметры участков известны. Осталось вычислить максимальные касательные напряжения на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры углов закручивания (поворотов)
Под действием внешних – скручивающих моментов, поперечные сечения стержня будут поворачиваться на определенный угол (φ). В этом разделе будем учиться определять эти углы закручивания (поворотов) поперечных сечений и строить эпюру.
Обозначим точки в характерных сечениях стержня:

Расчёт начинаем от жёсткой заделки и сразу можем записать, что в точке A, угол поворота равен нулю, т. к. здесь заделка ограничивает любые повороты сечения:
Чтобы рассчитать поворот сечения B, нужно учесть поворот предыдущего сечения:
А также, угол закручивания участка между расчётными сечениями:
Угол закручивания участка можно посчитать по формуле:

где l – длина участка; Ip – полярный момент инерции; G – модуль сдвига.
G – модуль сдвига (модуль упругости 2 рода) – определяется при испытании образцов на кручение, тем самым зависит от материала образца.
Модуль сдвига (G) известен, по условию задачи.
Формула для определения полярного момента инерции для круглого сечения следующая:

Зная диаметры, сразу вычислим полярные моменты инерции для каждого участка:

Определим угол закручивания сечения B, с учётом вышеуказанных формул:

Также можно перевести это значение в привычные градусы:

Для двух других сечений расчёт производится аналогичным образом.
Угол поворота сечения С

Угол поворота сечения D

По рассчитанным значениям, построим эпюру углов закручивания поперечных сечений:

Таким образом, свободный торец стержня, повернётся на 0.58 градуса, относительно неподвижного сечения A.
Расчеты на прочность при кручении
При кручении расчёты на прочность в целом похожи на расчёты при растяжении. Только здесь вместо нормальных напряжений расчёт ведётся по касательным напряжениям.
На кручение, как правило, работают детали, которые называются валами. Их назначение – передача крутящего момента от одного элемента к другому. При этом вал по всей длине имеет либо круглое сечение, либо кольцевое.
Условие прочности
За допустимое касательное напряжение [τ], часто в задачах по сопромату, принимают напряжение в два раза меньше, чем допустимое нормальное напряжение [σ]:

Максимальные касательные напряжения (τmax) в сечениях можно найти по формуле:

где T – крутящий момент в сечении;
Wp – полярный момент сопротивления сечения.
Полярные моменты сопротивления можно посчитать этим формулам.
Кручением
называется такой вид деформации стержня,
при котором в его поперечных сечениях
возникает только один внутренний силовой
фактор – крутящий
момент. Все
остальные внутренние усилия – нормальная
и поперечная силы, изгибающи й момент
при кручении отсутствуют. Кручение
испытывают многие детали машин и
сооружений: валы двигателей и станков,
оси моторных вагонов и двигателей,
элементы пространственных конструкций
и т.д. Как показали исследования, характер
деформации скручиваемого стержня
зависит от формы его поперечного сечения.
Особое место среди стержней, подвергаемых
кручению, принадлежит стержням с круглым
поперечным сечением. Такие стержни,
испытывающие кручение, называют валами.
К скручиваемому
стержню в разных его сечениях может
быть приложено несколько внешних
моментов. Рассмотрим случай, когда все
внешние моменты взаимно уравновешены
и действуют в плоскостях, прерпендикулярных
оси стержня (Рис.11.9,а):
(11.25)
Рис.11.9
Для
определения крутящего момента в
каком-либо сечении стержня воспользуемся
правилом, полученном при использовании
метода сечений, изложенном в теме №1.
На основании этого правила главный
вектор и главный момент всех внутренних
сил, действующих в рассматриваемом
сечении на оставшуюся часть тела,
равняются соответственно главному
вектору и главному моменту всех внешних
сил, приложенных к отброшенной части
тела.
Таким
образом, чтобы определить крутящий
момент
,
необходимо просуммировать все внешние
моменты, действующие по одну сторону
от рассматриваемого сечения. Слева от
сеченияIII,
в котором определяется крутящий момент,
действуют внешние моменты
и
.
Следовательно, крутящий момент в сеченииIII
будет равен:
.
Здесь
и в дальнейшем при построении эпюр
крутящих моментов следует пользоваться
следующим правилом знаков: если смотреть
на отброшенную часть со стороны сечения,
в котором определяется крутящий момент,
то при вращении внешним моментом стержня
по часовой
стрелке его
следует брать со знаком “минус”,
и наоборот – при вращении внешним
моментом вала против
часовой стрелки
его следует брать со знаком “плюс”.
Рассмотрим пример
построения эпюры крутящих моментов.
Пример
11.1. Построить
эпюру крутящих моментов для стержня,
изображенного на рис.11.10а.
Рис.11.10
Решение:
1.
Разобьем вал на участки: I,
II, III, IV и
V.
2. Пользуясь
правилом для определения крутящих
моментов, изложенным выше, находим:
;
кНм;
кНм;
кНм;
.
Крутящие
моменты на участках I,
II, III опредеделялись
слева, на участках IV,
V
справа.
3. Откладываем
полученные моменты от базисной линии
и строим эпюру крутящих моментов
(Рис.11.10б).
11.9. Вывод формул для напряжений и деформаций при кручении валов
Рассмотрим
стержень круглого поперечного сечения,
на поверхности которого нанесена сетка,
образованная системой образующих и
окружностей, сотавляющих внешние контуры
сечений (Рис.11.11).
Рис.11.11
Наблюдения
показывают, что после закручивания
прямоугольники, образованные сеткой,
перекашиваются, ось стержня остается
прямолинейной, контуры поперечных
сечения, круглые и плоские до деформации,
не меняют своих очертаний и после
деформации. При кручении происходит
поворот одного сечения по отношению к
другому на угол, называемый углом
закручивания. Расстояние между поперечными
сечениями практически не меняется, а
это указывает на отсутствие продольных
деформаций. Если провести прямую линию
вдоль
радиуса поперечного сечения стержня в
торцовом сечении, то в процессе
закручивания эта прямая линия не
искривляется.
Приведенные
наблюдения отражают лишь те деформации,
которые происходят на поверхности
стержня, но не позволяют делать какие-либо
заключения о деформации внутренних
волокон. В связи с этим сформулируем
ряд гипотез, которые затем положим в
основу последующих выводов. Эти гипотезы
следующие:
1. Сечения плоские
до закручивания, остаются плоскими
после закручивания.
2. Радиусы, проведенные
мысленно в любом поперечном сечении, в
процессе кручения не искривляются.
3. Поперечные
сечения, не удаляясь друг от друга в
процессе деформации, лишь скользят одно
относительно другого, в связи с чем при
кручении наблюдается деформация чистого
сдвига.
Принятые гипотезы
позволяют предположить, что при кручении
круглого стержня в результате сдвига
возникают только касательные напряжения,
а нормальные равны нулю.
Для
вывода формулы для касательных напряжений
при кручении валов рассмотрим стержень
радиуса
,
заделанный одним концом (Рис.11.12), на
свободном конце которого приложим пару
сил с моментом.
Рис.11.12
На
боковой поверхности стежня проведем
образующую AD, которая после кручения
займет положение АD1.
Под действием скручивающего момента
сечениеI
– I повернется
на угол
относительно жесткой заделки. СечениеII –
II повернется
на угол
.
Таким образом, взаимный угол поворота
сеченийI
– I и II
– II составит
.
Рассмотрим
отдельно элемент стержня длиной
.
Левое сечение элемента будем считать
неподвижным (Рис.11.13). Образующая ВС
наклонится на малый уголи займет положение ВС1.
Угол сдвига волокна, принадлежащего
поверхности вала, найдем из равенства:
.
Для
произвольного волокна, отстоящего от
центра тяжести на расстоянии
угол сдвига будет равен:
.
Рис.11.13
Применяя
для двух точек С1
и D1
закон Гука
при сдвиге (11.6), запишем выражения для
касательных напряжений:
;
(11.26)
.
(11.27)
Сравнивая
формулы (11.26) и (11.27), приходим к выводу,
что касательные напряжеения при кручении
вала пропорциональны расстоянию от оси
вала. Наибольшие напряжения будут в
точках, наиболее удаленных от центра
тяжести сечения.
Формула (11.27)
представляет собой закон изменения
касательных напряжений в поперечном
сечении вала. На рис.11.14 представлен
график изменения касательных напряжений.
Рис.11.14
Выделим
вокруг точки на расстоянии
от центра тяжести площадку
и вычислим момент силы, действующей на
этой площадке,
относительно оси стержня:
.
Полный крутящий
момент будет равен:
.
(11.28)
Подставляя
в формулу (11.28) значение
из формулы (11.27), получим:
.
(11.29)
В
формуле (11.29) величина
для всех точек поперечного сечения
одинакова, поэтому ее можно вынести за
знак интеграла. Под знаком интеграла
останется величина,
представляющая собой полярный момент
инерции поперечного сечения.
Тогда выражение (11.29) преобразуется к
виду:
или
.
(11.30)
Подставляя
выражение для
в формулу (11.27), получим:
.
(11.31)
Выражение
(11.31) представляет собой закон распределения
касательных напряжений вдоль радиуса
сечения и позволяет определить касательное
напряжение в любой точке поперечного
сечения. При
,
т.е. в центре тяжести поперечного сечения,
касательные напряжения равны нулю.
Максимальные
напряжения в сечении возникают в наиболее
удаленных точках сечения при
:
.
(11.32)
Выражение
(11.31) так же, как и выражение (11.27)
устанавливают прямо пропорциональную
зависимость величины касательных
напряжений от расстояния точки до центра
тяжести сечения. Графически этот закон
представлен на рис.11.14.
Величина
называетсяполярным моментом
сопротивления круглого сечения при
кручении и характеризуетвлияние
размеров сечения на способность
скручиваемого элемента сопротивляться
внешним нагрузкам, не разрушаясь.
Угол
закручивания поперечного сечения
можно определить из формулы (11.30):
.
Интегрируя это
выражение по всей длине стержня, получим:
.
(11.33)
Если вал имеет
постоянный диаметр, а крутящий момент
по всей длине стержня не меняется, то
после интегрирования выражения (11.33),
угол закручивание будет иметь вид:
.
(11.34)
Величина
называется жесткостью поперечного
сечения вала при кручении и характеризует
влияние геометрических размеров
поперечного сечения и физических
характеристик материала на способность
вала сопротивляться закручиванию.
Для ступенчатых
стержней или же стержней, у которых
крутящий момент меняется по длине
скачкообразно, угол закручивания между
начальным и конечным сечениями вала
определяется как сумма углов закручивания
с постоянным отношением
:
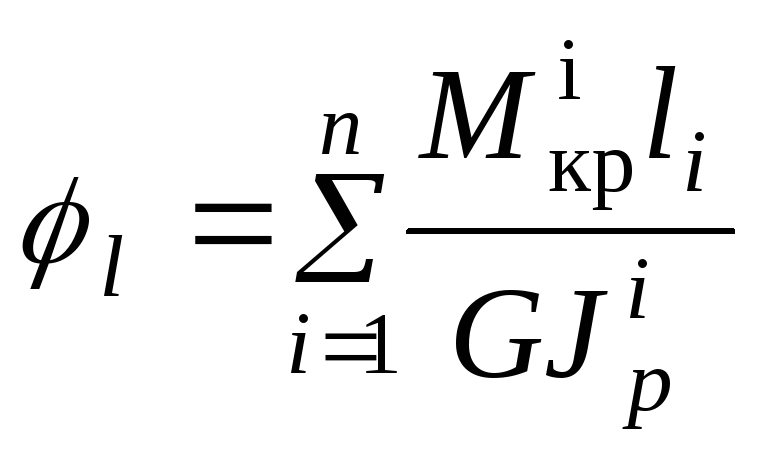
(11.35)
где
число участков вала.
Полный угол
закручивания не всегда может характеризовать
жесткость вала при кручении. Если на
протяжении длины вала крутящие моменты
имеют разные знаки, то полный угол
закручивания может оказаться небольшим,
в то время как на отдельных участках
угол закручивания может быть значительным.
В связи с этим для оценки жесткости
скручиваемого стержня применяется
другая мера – относительный угол
закручивания
.
(11.36)
Размерность
относительного угла закручивания
или
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.
Брусья, испытывающие кручение, принято называть валами.
Внутренний крутящий момент
Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.
Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.
Величина крутящего момента в любом сечении вала определяется методом сечений:
т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.
Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.
В технике наиболее широко используются валы круглого поперечного сечения.
Теория кручения круглых валов основана на следующих гипотезах:
- поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
- радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.
Напряжения при кручении
В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:
где Iρ — полярный момент инерции.
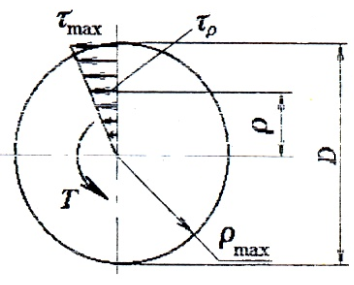
Эпюра касательных напряжений при кручении имеет следующий вид:
Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρmax:
Здесь:
— полярный момент сопротивления.
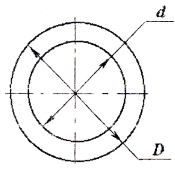
Геометрические характеристики сечений:
а) для полого вала:
б) для вала сплошного сечения (c=0)
в) для тонкостенной трубы (t<0,9)
где
— радиус срединной поверхности трубы.
Деформации
Деформации валов при кручении заключаются в повороте одного сечения относительно другого.
Угол закручивания вала на длине Z определяется по формуле:
Если крутящий момент и величина GIρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:
Расчет валов сводится к одновременному выполнению двух условий:
- условию прочности:
- условию жесткости:
Для стальных валов принимается:
Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:
- проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
- Проектировочный расчет, при котором вычисляются диаметры:
при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ. - Определение грузоподъемности вала:
Из двух найденных значений крутящего момента необходимо принять меньшее.
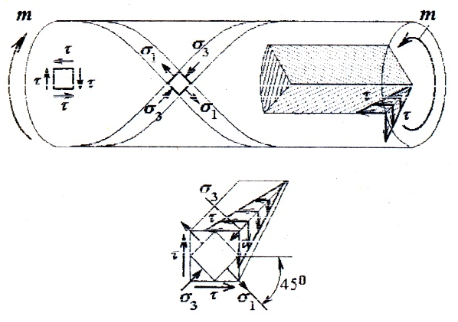
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.
Главные напряжения σ1 = τ, σ3 = -τ наклонены под углом α=±45о к образующей.
Потенциальная энергия упругой деформации определяется по формуле
или для участка вала при постоянном T и GIρ
Лекции по сопромату >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
§1. Основные понятия. Крутящий момент
§1. Основные понятия. Крутящий момент
Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент Mk, (другое обозначение T, Mz), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.
Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).
Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.
Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси
В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.
Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.
При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Mk), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.
При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.
В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов (n- частота вращения, единицы измерения — об/мин.), то вращающий момент можно найти по формуле: Мвр=P/n,
эта формула дает значение момента в Н·м, если мощность выражена в Вт, а частота вращения n — об/мин.
§2. Построение эпюр крутящих моментов
Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов Mk (Mz) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
Содержание:
- Пример решения задачи 78.
- Вычисление моментов, передаваемых на вал. построение эпюр крутящих моментов для валов
- Пример решения задачи 79.
- Пример решения задачи 80.
- Напряжения и перемещения при кручении брусьев круглого поперечного сечения
- Пример решения задачи 81.
- Пример решения задачи 82.
- Пример решения задачи 83.
- Пример решения задачи 84.
- Пример решения задачи 85.
- Пример решения задачи 86.
- Пример решения задачи 87.
- Пример решения задачи 88.
- Пример решения задачи 89.
- Пример решения задачи 90.
- Статически неопределимые задачи кручения
- Пример решения задачи 93.
- Пример решения задачи 94.
- Кручение стержней прямоугольного поперечного сечения
- Пример решения задачи 95.
- Пример решения задачи 96.
Под кручением понимается такой вид иагруження бруса, при котором в его поперечных сечениях возникают только крутящие моменты.
Кручение имеет место при действии па брус внешних пар сил, плоскости которых перпендикулярны к оси стержня.
Моменты этих внешних пар, являющиеся нагрузкой для бруса, называют внешними, вращающими или скручивающими моментами.
Простейший случай кручения показан на рис. 79: брус находится под действием двух равных и противоположных скручивающих моментов, приложенных по концам. Моменты пар, приложенных к брусу, должны удовлетворять условию равновесия
В общем случае на брус может действовать несколько скручивающих моментов, приложенных в различных сечениях и взаимно уравновешивающихся. Для случая, представленного па рис. 80,
При действии на брус скручивающих моментов в его поперечных сечениях возникают крутящие моменты 

Крутящий момент, действующий на одну часть бруса (левую), равен Рис. 82 и противоположно направлен крутящему моменту, действующему в том же сечении на его другую часть (правую) (рис. 82).
Возможно вам будут полезны данные страницы:
В простейшем случае, когда брус нагружен по концам двумя равными и противоположно направленными скручивающими моментами 
Если к брусу приложено несколько скручивающих моментов, то крутящий момент будет оставаться постоянным в пределах каждого участка между местами приложения скручивающих моментов и меняется скачком на границах участков. Изменение крутящих моментов по длине бруса изображают графически в виде эпюры крутящих моментов.
Пример решения задачи 78.
Для бруса 
величины крутящих моментов в поперечных сечениях участков 
Решение:
Определим реактивный момент 
откуда
Знак «плюс» указывает, что направление момента в заделке предварительно было выбрано правильно.
Для определения крутящих моментов и построения эпюры применим метод сечений для каждого из трех участков бруса. Проведем сечение 





или
Если взять сечение
(на участке
), то крутящий момент
(рис. 83, в), возникающий в этом сечении, должен уравновешивать сумму скручивающих моментов
действующих на отсеченную левую часть, т. е.
откуда
Ту же величину крутящего момента 


Но из условия равновесия
Знак крутящего момента физического смысла не имеет. Условимся считать крутящий момент положительным, если он при взгляде на сечение со стороны отброшенной части направлен по часовой стрелке.
Для левой части бруса, отсеченной любой плоскостью в пределах участка
откуда
По найденным данным строим эпюру крутящих моментов (рис. 83, г). Для этого проводим ось абсцисс 







Далее, от точки 








Следует обратить внимание на то, что наибольший крутящий момент равен 1,4 кн-м, в то время как наибольший скручивающий момент равен 1,6 кн-м. Это общее положение — лишь в частных случаях величины наибольшего крутящего момента и наибольшего скручивающего момента совпадают. В дальнейшем следует учесть, что .расчет бруса на прочность и на жесткость ведут по наибольшему крутящему моменту.
Вычисление моментов, передаваемых на вал. построение эпюр крутящих моментов для валов
На практике обычно известны не моменты, действующие на вал, а передаваемая валом мощность и его угловая скорость. В СИ единицей мощности является ватт (вт) — работа в один джоуль, совершенная в одну секунду 
Как известно из теоретической механики, между моментом, мощностью и угловой скоростью существует зависимость
где 


Пример решения задачи 79.
Изображенный на рис. 84 трансмиссионный вал .получает движение при помощи ременной передачи от шкива, насаженного на валу двигателя (на




Построить эпюру крутящих моментов без учета трения в подшипниках.
Решение:
Машина, соединенная ременной передачей со шкивом 

Скручивающий момент, передаваемый через шкив
Через шкив 
Скручивающий момент, передаваемый валу двигателем через шкив
На участках вала между шкивами будут действовать крутящие моменты следующей величины: момент в любом поперечном сечении на участке 
отсюда
Аналогично для сечения 
откуда
для сечения
откуда
Для построения эпюры крутящих моментов проведем ось абсцисс, параллельную оси вала. От точки 






На участке 





Из уравнения равновесия
следует, что за шкивом 



Пример решения задачи 80.
Сохраняя данные предыдущего примера, построить эпюру крутящих моментов для вала с расположением шкивов, показанном на рис. 85, а.
Решение:
Применим метод сечений к каждому участку вала в отдельности. На участке вала слева от шкива 



Этот момент на рис. 85, б представлен в масштабе ординатой 


Этот момент представлен на эпюре ординатой
Крутящий момент 
Знак «минус» показывает, что крутящий момент 



Сравнивая эпюры, представленные на рис. 84, б и 85, б, видим, что наибольший крутящий момент в первом случае равен 2781 


Напряжения и перемещения при кручении брусьев круглого поперечного сечения
При кручении брусьев круглого (сплошного и кольцевого) поперечного сечения:
а) поперечные сечения, плоские до деформации бруса, остаются плоскими и перпендикулярными к оси бруса и после деформации;
б) диаметр бруса не изменяется; не изменяется также и его длина и расстояния между поперечными сечениями;
в) образующие цилиндра из прямых линий превращаются в винтовые.
Угол поворота 
•Взаимный угол поворота 


где 

где 


Для круга
для кольца
где 
где 
Для сплошного круглого сечения
для кольцевого сечения
Угол закручивания бруса постоянного диаметра при одинаковом во всех поперечных сечениях крутящем моменте
Произведение 
Пример решения задачи 81.
Стальной брус диаметром 







касательное напряжение 

Решение:
Угол сдвига, как видно из чертежа, равен отношению длины 

Зная величину угла сдвига 
Полный угол закручивания
Наибольшее касательное напряжение 
Крутящий момент в любом поперечном сечении бруса
Пример решения задачи 82.
Стальной вал диаметром 




Решение:
Наибольшее касательное напряжение определим по формуле
где 
Зная 
Тогда относительный угол закручивания
Пример решения задачи 83.
Круглый дюралевым стержень длиной 


Решение:
Наибольшее касательное напряжение определяют по формуле
Из этой формулы можно было бы определить 

Нетрудно видеть, что величину этого отношения легко определить из формулы



Крутящий момент
в любом поперечном сечении вала
Пример решения задачи 84.
Для определения модуля сдвига 

поворота 

Решение:
Приращение угла закручивания на длине 

Полярный момент инерции сечения
Модуль упругости определим из формулы для угла закручивания:
Пример решения задачи 85.
Стальная проволока длиной 



Решение:
Зная величину наибольшего касательного напряжения 

Угол закручивания 
Эту задачу можно решить иначе, а именно: определим крутящий момент:
Тогда угол закручивания

Условие прочности при кручении бруса круглого поперечного сечения имеет вид
где 



Зная диаметр бруса и допускаемое напряжение для его материала при данных условиях работы, можно определить максимальный допускаемый крутящий момент:
При проектном расчете требуемый «полярный момент сопротивления поперечного сечения бруса определяется но формуле
Во многих случаях расчет валов должен быть выполнен не только на прочность, но и на жесткость. Условие жесткости
здесь 
Если величина 





При определении диаметра вала из условия жесткости («гири проектном ‘расчете) находят требуемую величину полярного момента инерции:
Допускаемый по условию жесткости крутящий момент определяется но формуле
Пример решения задачи 86.
При 

Решение:
Определяем крутящий момент, равный моменту, передаваемому валу 
Наибольшее напряжение
Пример решения задачи 87.
Ступенчатый стальной брус 
Требуется определить максимальные касательные’напряжения в сечениях 

Решение:
Составив уравнение равновесия, определим-реактивный момент в заделке:
откуда


Крутящий момент в произвольном сечении 
Крутящий момент в произвольном сечении 
Строим эпюру крутящих моментов (рис. 88, б). Определим полярные моменты сопротивления поперечных сечений бруса: на участке
на участке
на участке
Искомые напряжения:
Коэффициент запаса определяем для наиболее нагруженного участка бруса
Пример решения задачи 88.
Проверить ‘прочность валов зубчатой передачи от электродвигателя к станку (рис. 89), приняв допускаемое напряжение 


Решение:
Угловая скорость ведущего вала
Вычислим вращающий момент на валу
Крутящий момент в любом (расположенном левее шестерни 

Проверяем прочность этого вала

Крутящий момент в любом (расположенном между зубчатыми колесами) поперечном сечении вала 2
Проверим прочность вала 2:
Пример решения задачи 89.
Определить диаметр вала, передающего мощность 
Допускаемое напряжение 
Решение:
Крутящий момент, возникающий в любом -поперечном сечении вала, равен передаваемому валом вращающему моменту:
Из условия прочности 
Из условия жесткости
следует
(здесь
Окончательно принимаем
Пример решения задачи 90.
На валу насажены три шкива, из которых шкив 









Решение:
В этой задаче вал имеет ступенчатую форму. Чтобы определить диаметры вала 
моменты в сечениях на участках 

Крутящий момент в любом сечении участка 
Крутящий момент в любом сечении участка 
Строим эпюру крутящих моментов (рис. 90, б). Зная величины крутящих моментов, а также величину допускаемого напряжения 
тогда
тогда 

принимаем
Для определения углов закручивания будем руководствоваться правилом: угол закручивания отсчитывает ся от сечения вала в месте расположения главного шкива
Определим угол поворота сечения 
Так как вал вращается, то неподвижных сечений здесь нет. Но пас интересуют .не повороты сечений вообще, а углы поворота отдельных сечений, получающиеся в результате деформации вала. «Поэтому, приняв условно сечение 
На участке 






При
т. е. угол поворота сечения 

На участке 





Эпюра углов закручивания показана на рис. 90, в
Статически неопределимые задачи кручения
т. е. на основе применения лишь метода сечении. Так же как и при решении .статически неопределимых задач на растяжение (сжатие), дополнительно к уравнениям статики должны быть составлены уравнения перемещении.
Пример решения задачи 93.
В сечении 

Решение:
В заделках бруса возникают реактивные моменты 
Неизвестных величии две, а уравнение статики можно составить лишь одно и, следовательно, задача статически неопределима.
Составим второе уравнение, т. е. уравнение перемещений. При этом учтем, что угол поворота сечения 
где
После подстановки значений 
Решая совместно уравнения (1) и (2), найдем
откуда
Взяв произвольное поперечное сечение на расстоянии 
В произвольном поперечном -сечении вала на расстоянии 
Эпюра крутящих моментов показана на рис. 93, б. Диаметр бруса определим по наибольшему крутящему моменту из формулы
откуда
Пример решения задачи 94.
Стальной валик и дюралевая трубка жестко заделаны на одном конце, а на другом скреплены с диском, к которому приложен скручивающий момент 

Модули сдвига: стали 
Решение:
В поперечных сечениях валика возникает крутящий момент 


Задача статически неопределима, так как уравнение статики можно составить только одно, а неизвестных моментов два.
Угол поворота диска, к которому приложен -скручивающий момент, равен углу закручивания валика. Точно так же можно утверждать, что угол поворота диска равен углу закручивания трубки. Следовательно, углы закручивания валика и трубки одинаковы:
Используя формулу для угла закручивания, получаем
или
где
После несложных преобразований получаем
или
Используя уравнение статики, получаемм
откуда
и
Кручение стержней прямоугольного поперечного сечения
Задачу об определении касательных-напряжений при кручении стержней ‘прямоугольного поперечного сечения Методами сопротивления материалов решить нельзя. Это связано с тем, что в данном случае ‘первоначально плоские поперечные сечения искривляются, как это видно из рис. 95, а. По степени перекашивания сетки квадратиков, нанесенных на боковых гранях стержня, можно судить о величине касательных напряжений в различных точках. Квадратики, лежащие у ребер стержня, не перекашиваются — в этом месте касательные напряжения равны нулю. Наибольшее искажение квадратиков возникает в средних точках -боковых граней бруса— здесь касательные напряжения достигают своего наибольшего значения. На рис. 95, б представлено поперечное сечение бруса. Наибольшие касательные напряжения возникают в точках 
где 


Величины этого коэффициента приведены в табл. 5.
Таблица 5
Наибольшее .напряжение 
где 

Угол закручивания
где 


Пример решения задачи 95.
Определить максимальное напряжение, возникающее в поперечном сечении стального стержня и его угол закручивания. Поперечное сечение — прямоугольник со сторонами 


Решение:
Выбор коэффициентов 
Такого значения 
После этого определим 
Угол закручивания
Значение коэффициента (

Пример решения задачи 96.
Определить размеры прямоугольного сечения стержня с отношением сторон 


Решение:
Из условия прочности

где 
Но 
Найдем значения 

-где 



Из последнего выражения

Принимаем размеры, полученные из условия жесткости.








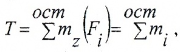
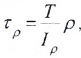
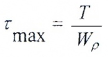
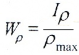
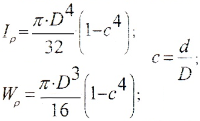
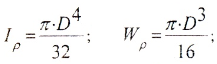
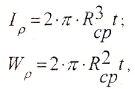
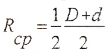
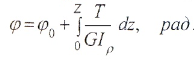
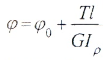
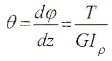
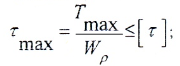
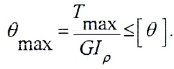
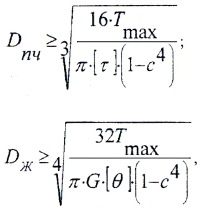
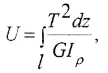
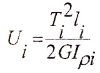












 (на участке
(на участке  ), то крутящий момент
), то крутящий момент  (рис. 83, в), возникающий в этом сечении, должен уравновешивать сумму скручивающих моментов
(рис. 83, в), возникающий в этом сечении, должен уравновешивать сумму скручивающих моментов  действующих на отсеченную левую часть, т. е.
действующих на отсеченную левую часть, т. е.

























































 в любом поперечном сечении вала
в любом поперечном сечении вала























































































































