В этой статье мы рассмотрим задачи, связанные с определением различных скоростей тел. При этом, в том числе, будем пользоваться понятием истинная аномалия. Это всего лишь угол между радиус-вектором тела и направлением на перицентр орбиты. То есть, если тело находится в перицентре, то истинная аномалия – ноль градусов, а если в апоцентре – то . По тому, на сколько отличается скорость тела от вычисленной для него параболической или круговой скорости, можно судить о форме орбиты: если скорость меньше параболической, но приближается к ней по значению, форма орбиты – сильно вытянутый эллипс с большим эксцентриситетом. Если скорость достаточно близка к круговой – то и форма орбиты почти круговая или с очень небольшим эксцентриситетом.
В частном случае задачи двух тел рассматривается движение тела меньшей массы относительно тела большей массы
, принимаемого за неподвижное и называемого центральным телом.
Линейная скорость движущегося тела относительно центрального определяется интегралом энергии
где ,
— большая полуось орбиты тела меньшей массы,
— радиус-вектор того же тела,
— гравитационная постоянная.
Если масса движущегося тела пренебрежимо мала в сравнении с массой
центрального тела, то задача двух тел называется ограниченной и тогда
.
Согласно интегралу энергии, чтобы тело меньшей массы обращалось вокруг центрального тела по круговой орбите (эксцентриситет ) радиусом
, оно должно на этом расстоянии иметь скорость
называемую круговой скоростью. Как средняя скорость движения тела, она может быть также подсчитана по периоду обращения и большой полуоси
орбиты тела:
Если движущееся тело на расстоянии от центрального тела имеет скорость
то орбитой будет парабола (,
). Поэтому скорость
называется параболической.
Если , то движущееся тело пройдет мимо центрального тела по гиперболе (
).
В каждой точке орбиты с радиус-вектором скорость тела
Точка эллиптической орбиты, ближайшая к центральному телу, называется перицентром, а наиболее удаленная от него—апоцентром. Эти точки получают конкретные наименования но названию центрального тела, например, для Земли – апогей и перигей, для Луны — апоселений и периселений.
В перицентре, при , тело-спутник обладает наибольшей скоростью
а в апоцентре, при , — наименьшей скоростью
Скорость небесных тел всегда выражается в км/с, а расстояния могут быть заданы в астрономических единицах, километрах или радиусах центрального тела. Поэтому в формулы необходимо подставлять значения расстояний в одинаковых единицах измерения.
В поле тяготения Солнца, на произвольном от него расстоянии , выраженном в астрономических единицах (а. е.), круговая скорость (км/с)
Если расстояния заданы в километрах, а масса центрального тела выражена в массах Земли, то круговая скорость (км/с)
Наконец, при измерении масс в массах Земли и расстояний в радиусах Земли круговая скорость (км/с)
Средняя или круговая скорость тела, обращающегося вокруг центрального тела по эллиптической орбите с большой полуосью
, вычисляется по тем же формулам с подстановкой в них
.
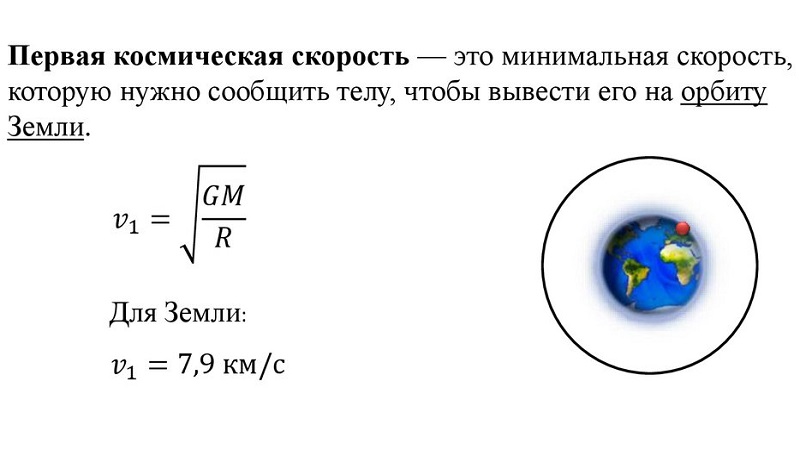
Подстановка в последние формулы (
— радиус небесного тела) дает значение круговой скорости
у поверхности этого тела, называемой в космонавтике первой космической скоростью. Вторая космическая скорость
. Очевидно, что
где отсчитывается от центра небесного тела и выражается в его радиусах.
Третий обобщенный закон Кеплера
применим к любым системам тел с массами и
, обращающихся с периодами
и
вокруг своих центральных тел (с массами
и
) по эллиптическим орбитам, большие полуоси которых соответственно равны
и
.
Массы планет и их спутников выражаются обычно в массах Земли (реже — в массах Солнца, в тоннах и килограммах), большие полуоси орбит — в астрономических единицах или в километрах, а периоды обращения- в годах и сутках, а иногда — в часах и минутах.
При вычислениях по формуле закона Кеплера выбор системы единиц не имеет значения, лишь бы однородные величины были выражены в одинаковых единицах. Если же этот закон используется в виде
то решение задач проводится обязательно в определенной системе единиц, так как в разных системах численное значение гравитационной постоянной различно.
Если периоды обращения заданы в земных средних сутках, расстояния — в километрах и массы тел — в массах Земли, то третий закон Кеплера имеет вид
Задача 1.
Чему равна круговая и параболическая скорость относительно Солнца на средних расстояниях Венеры (0,723 а. е.), Земли (1,00 а. е.), Юпитера (5,20 а. е.) и Плутона (39,5 а. е.)? По общим результатам найти и объяснить найденную закономерность. Расстояния планет от Солнца указаны в скобках.
Для Венеры
Для Земли
Для Юпитера
Для Плутона
Ответ: для Венеры круговая скорость равна 35,02 км/с, параболическая – 49,5 км/с; для Земли круговая 29,78 км/с, параболическая 42,11 км/с; для Юпитера круговая 13,06 км/с, параболическая 18,47 км/с; для Плутона круговая 4,74 км/с, параболическая 6,70 км/с. С удалением от Солнца скорость падает.
Задача 2.
Вычислить скорость малых планет Ахиллеса и Гектора в перигелии и афелии, если их круговая скорость близка к 13,1 км/с, а эксцентриситеты орбит соответственно равны 0,148 и 0,024. Примерно на каком среднем гелиоцентрическом расстоянии находятся эти планеты?
Скорость в перигелии можно вычислить по формуле:
Для Ахиллеса
Для Гектора
Скорость в афелии можно вычислить по формуле
Для Ахиллеса
Для Гектора
Так как
То среднее гелиоцентрическое расстояние равно
Ответ: для Ахиллеса скорость в перигелии 15,2 км/с, в афелии 11,2 км/с. Для Гектора скорость в перигелии 13,41 км/с, в афелии 12,7 км/с. Среднее гелиоцентрическое расстояние 5,48 а.е.
Задача 3.
Большая полуось и эксцентриситет opбиты Меркурия равны 0,387 а. е. и 0,206, а орбиты Марса — 1,524 а. е. и 0,093. Найти среднюю скорость этих планет, их скорость в перигелии и в афелии.
Рассчитаем перигельное и афелийное расстояния для Меркурия:
Определим круговую скорость:
Определяем скорость в перигелии:
И скорость в афелии:
Теперь все то же проделаем для Марса:
Рассчитаем перигельное и афелийное расстояния:
Определим круговую скорость:
Определяем скорость в перигелии:
И скорость в афелии:
Ответ: для Меркурия км/с,
км/с,
км/с; для Марса
км/c,
км/с,
км/c.
Задача 4.
Считая орбиты планет круговыми и лежащими в плоскости эклиптики, найти лучевую скорость Меркурия, Венеры и Марса во время их основных конфигураций. Необходимые для решения данные заимствовать из задач 1 и 3. (Лучевой скоростью называется проекция пространственной скорости на луч зрения наблюдателя, т. е. в данном случае на направление от Земли к планете.)
Для Венеры и Меркурия основной конфигурацией будет нижнее соединение, так как это внутренние планеты. Также можно рассмотреть восточную и западную элонгации. Для Марса, который является внешней планетой, можно рассмотреть противостояние и обе квадратуры, восточную и западную.
Рисунок 1
Лучевая скорость во всех случаях, когда планеты расположены радиально, равна нулю: это соединения и противостояния. При элонгациях лучевую скорость можно найти как разность круговой скорости планеты и проекции скорости земли на линию, соединяющую планеты. Это хорошо поясняет рисунок ниже.
Рисунок 2
Для Венеры круговая скорость– 35,02 км/c, для Меркурия – 47,87 км/с.
Определим косинус угла для Меркурия:
Определим косинус угла для Венеры:
Проекция скорости земли на линию, соединяющую планеты, будет равна
Определяем проекцию скорости Земли на линию, соединяющую планеты, для Меркурия:
Для Венеры:
Таким образом, лучевая скорость Меркурия в элонгациях
Лучевая скорость Венеры в элонгациях:
Примерно так же обстоит дело с квадратурами. Чтобы определить скорость планеты в квадратурах – а она будет одинакова и для западной, и для восточной квадратуры, надо найти проекцию круговой скорости планеты на линию, соединяющую обе планеты.
Рисунок 3
Определим для этого из треугольника расстояний между планетами и Солнцем:
Тогда проекция скорости Марса равна
Таким образом, лучевая скорость Марса в квадратурах
Ответ: лучевые скорости внутренних планет в соединениях равны 0, в элонгациях для Меркурия – 20,41 км/с, для Венеры – 14,45 км/с . Для внешних планет лучевые скорости в противостояниях равны 0, в квадратуре для Марса лучевая скорость равна 13,97 км/с.
Задача 5.
Вычислить скорость астероидов Лидии и Адониса на их среднем, перигельном и афелийном расстояниях, а также круговую и параболическую скорость на этих расстояниях. Большая полуось и эксцентриситет орбиты первого астероида равны 2,73 а. е. и 0,078, а второго— 1,97 а. е. и 0,778.
Сначала сделаем расчет для Лидии, а затем повторим все действия для Адониса.
Рассчитываем круговую скорость:
Перигельное расстояние:
Рассчитываем афелийное расстояние:
Скорость в перигелии:
И скорость в афелии:
Круговая скорость Лидии на среднем гелиоцентрическом расстоянии км/с, параболическая скорость на этом расстоянии
км/с.
На перигельном расстоянии круговая скорость астероида
Параболическая скорость:
На афелийном расстоянии круговая скорость астероида
Параболическая скорость:
Повторим все действия для Адониса.
Рассчитываем круговую скорость:
Перигельное расстояние:
Рассчитываем афелийное расстояние:
Скорость в перигелии:
И скорость в афелии:
Круговая скорость Адониса на среднем гелиоцентрическом расстоянии км/с, параболическая скорость на этом расстоянии
км/с.
На перигельном расстоянии круговая скорость астероида
Параболическая скорость:
На афелийном расстоянии круговая скорость астероида
Параболическая скорость:
Ответ: Лидия: круговая скорость 18,02 км/с, в перигелии 19,27 км/с, в афелии 16,85 км/c, круговая скорость на среднем расстоянии 18,02 км/с, в перигелии 18,57 км/с, в афелии 17,36 км/с, параболическая скорость на среднем расстоянии 25,38 км/с, в перигелии 26,2 км/с, в афелии 24,49 км/с.
Адонис: круговая скорость 21,21 км/с, в перигелии 60,51 км/с, в афелии 7,43 км/c, круговая скорость на среднем расстоянии 21,21 км/с, в перигелии 45,4 км/с, в афелии 15,92 км/с, параболическая скорость на среднем расстоянии 29,9 км/с, в перигелии 64,03 км/с, в афелии 22,44 км/с.
Задача 6.
На каких гелиоцентрических расстояниях скорость Меркурия равна 56,1 км/с и 41,7 км/с? Большая полуось орбиты планеты 0,387 а. е.
Сначала определим круговую скорость на среднем гелиоцентрическом расстоянии:
Теперь воспользуемся формулой
Из нее следует, что
Теперь подставим в нее числовые значения скоростей и определим оба расстояния:
Ответ: а.е.,
а.е.
Задача 7.
С какой скоростью относительно Солнца проходил Марс в эпоху великого противостояния при геоцентрическом расстоянии в км? Сопоставить эту скорость с круговой и параболической скоростью на том же расстоянии от Солнца. Большая полуось орбиты Марса равна 1,524 а. е.
Рассчитываем круговую скорость:
Рассчитаем скорость прохождения:
Переведем расстояние между Землей и Марсом в астрономические единицы: а.е. Таким образом, расстояние от Солнца до Марса в этот момент
а.е.
Определим круговую скорость на этом расстоянии
Определим параболическую скорость:
Ответ: скорость прохождения Марса 26,46 км/с. Это больше круговой скорости (25,3 км/с) и меньше параболической (35,74 км/с).
Задача 8.
Решить предыдущую задачу для астероида Эрота, если он в эпоху великого противостояния проходил свой перигелий 23 января 1975 г. на расстоянии км от Земли. Период обращения Эрота вокруг Солнца равен 1,76 года.
Так как сказано, что астероид находился в противостоянии, то его гелиоцентрическое расстояние, очевидно, больше, чем у Земли.
Переведем расстояние между Землей и астероидом в астрономические единицы: а.е. Таким образом, расстояние от Солнца до астероида в этот момент
а.е.
Определим большую полуось орбиты по закону Кеплера:
Определим круговую скорость на этом расстоянии
Рассчитаем скорость прохождения:
На перигельном расстоянии круговая скорость астероида
Определим параболическую скорость:
Ответ: скорость прохождения 30,55 км/с, круговая скорость 27,75 км/c, параболическая 39,1 км/с.
Задача 9.
На каком расстоянии от Солнца прошла комета, если ее скорость на этом расстоянии равнялась 65 км/с и комета двигалась по параболической орбите?
Зная параболическую скорость, определим круговую на этом расстоянии:
Откуда расстояние прохождения
Ответ: 0,417 а.е.
Задача 10.
Комета 1931 IV прошла свой перигелий на расстоянии 0,07 а. е. от Солнца со скоростью 160 км/с, а комета 1945 II —на расстоянии 1,24 а. е. со скоростью 36,5 км/с. Определить род орбит, по которым двигались эти кометы и установить, вернутся ли они к Солнцу и когда именно.
Комета 1931 IV:
На перигельном расстоянии круговая скорость кометы
Определим параболическую скорость:
Так как параболическая скорость меньше той, которую имела комета, то траектория – парабола и комета более к Солнцу не вернется.
Комета 1945 II:
На перигельном расстоянии круговая скорость кометы
Определим параболическую скорость:
Так как скорость кометы меньше, чем параболическая, то траектория – эллипс. Определим большую полуось с помощью формулы:
Откуда
Зная большую полуось, определим период обращения по закону Кеплера:
Ответ: первая комета имеет параболическую траекторию и не вернется к Солнцу, вторая вернется через 27 лет, траектория – эллипс.
Задача 11.
Синодический период обращения астероида Колхиды равен 1,298 года, а его скорость в перигелии — 20,48 км/с. Чему равны сидерический период обращения астероида, большая полуось и эксцентриситет его орбиты, перигельное и афелийное расстояния, а также скорость на среднем гелиоцентрическом расстоянии и в афелии?
По формуле
Определим сидерический период :
Теперь можно найти большую полуось орбиты, а.е.:
Круговую скорость найдем, зная большую полуось:
Скорость в перигелии дает возможность найти перигельное расстояние:
Из этой формулы следует, что
Тогда можно определить эксцентриситет:
Далее можно найти афелийное расстояние:
Скорость в афелии:
Ответ: сидерический период — 4,356 года, большая полуось – 2,667 а.е., эксцентриситет – 0,116, перигелий – 2,358 а.е., афелий – 2,976 а.е., скорость на среднем расстоянии км/с, скорость в афелии 16,22 км/c.
Задача 12.
Эксцентриситет орбиты астероида Узбекистании равен 0,092, а его скорость в афелии— 15,21 км/с. Найти большую полуось орбиты астероида, его звездный и синодический периоды обращения, скорость в перигелии и при истинной аномалии в и
.
По скорости в афелии и эксцентриситету найдем круговую скорость на среднем расстоянии:
Теперь найдем большую полуось:
Синодический период
Звездный период:
Или 443 дня.
Перигельное расстояние:
Скорость в перигелии
Для определения скоростей в точках с указанными истинными аномалиями найдем расстояния до этих точек:
При :
При :
При :
Определяем скорости:
Дано:
a п = 2,77
e = 0,235
a⊕ = 1 а.е.
T⊕ = 1 год
g п = 0,194 м/с²
R п = 512 км = 512000 м
——————————————-
Найти:
q — ?
Q — ?
T п — ?
S п — ?
υ п — ?
Решение:
1) Запишем сначала формулы перигельное и афелийное расстояния:
(1) q = a(1-e) — перигельное расстояние
(2) Q = a(1+e) — афелийное расстояние
Далее мы их находим перигельное и афелийное расстояния:
q = 2,77 а.е. × (1-0,235) = 2,77 а.е. × 0,765 = 2,11905 а.е.
Q = 2,77 а.е. × (1+0,235) = 2,77 а.е. × 1,235 = 3,42095 а.е.
2) Теперь мы находим сидерический период обращения астероида Паллада, по третьему закону Кеплера:
T п²/T⊕² = a п³/a⊕³
Так как a⊕ = 1 а.е. , T⊕ = 1 год , следовательно мы получаем:
T п² = a п³ ⇒ T п = √a п³
Теперь решаем:
T п = √2,77³ = √21,253933 ≈ 4,61 года
3) Дальше мы находим синодеричечкий период обращения астероида Паллада для верхних по такой формуле:
1/S = 1/T⊕ — 1/T п ⇒ 1/S = T п — T⊕/T⊕×Tп
Следовательно мы получим:
S = T⊕×T п/Tп — T⊕
Далее считаем:
S = 1 год × 4,61 года/4,61 года — 1 год = 4,61 года/3,61 года ≈ 1,277 года
4) Теперь мы находим круговую скорость или как говорят первой космической скорости по такой формуле что бы найти скорость астероида Паллада:
υ п = √g п × R п
Теперь считаем:
υ п = √0,194 м/с² × 512000 м = √99328 м²/с² ≈ 315,16 м/с ≈ 0,31516 км/с
Ответ: q = 2,11905 а.е. ; Q = 3,42095 а.е. ; T п = 4,61 года ; S = 1,277 года ; υ п = 315,16 м/с или 0,31516 км/с.
Скорость астероида и движение самых крупных из них
Сегодня мы поговорим про скорость астероида, точнее его перемещения по бескрайним просторам нашей Вселенной. Как известно, эти твёрдые небесные тела движутся вокруг Солнца по своей определённой орбите, так же как и планеты. Но у каждого особый характер передвижения.
Что такое скорость?
По сути, это расстояние, пройденное объектом за единицу времени. Обычно, чтобы узнать скоростное значение, необходимо пройденное расстояние разделить на время, затраченное на преодоление этого расстояния.
Правда, в физике и астрономии бывают разные виды этой величины. Например, выделяют первую космическую или круговую скорость. Это наименьшая горизонтальная скорость для заданной высоты над поверхностью планеты, которую нужно придать объекту, чтобы он смог двигаться по круговой орбите вокруг планеты.
Стоит отметить, такой темп для ближайшей земной орбиты равен 7,91 км/с. Вообще, учёные смогли найти круговую скорость практически каждого известного астероида.
Движение большинства астероидов
В космическом пространстве астероид летит со средней скоростью, которая составляет примерно 20 км/с. В среднем, период обращения вокруг Солнца занимает 3-9 лет.
Конечно, динамика движения отдельных астероидов различается. Однако она всегда выше второй космической скорости (11,2 км/с). При таких значениях космическое тело может пересиливать гравитационное притяжение планет.
Помимо этого, астероиды вращаются вокруг своей оси. Чаще всего на один полный оборот затрачивается около 7 часов. В сравнении с планетным это вращение небыстрое. Ведь астероидные объекты намного меньше планет. Собственно, поэтому сам оборот занимает меньше времени.
Самые большие астероиды и их скорость движения
Давайте рассмотрим как движутся некоторые крупные астероиды.
Прежде всего, нужно отметить астероид, а вернее карликовую планету, Церера. Она летит по орбите со скоростью 17,882 км/с и обращается вокруг Солнца примерно за 4,6 лет.
Хотя орбитальная скорость крупнейшего астероида Веста 19,346 км/с. При этом период обращения вокруг главной звезды составляет 3,628 лет.
А вот другой крупный астероид Паллада летит в темпе 17,645 км/с. Её полный оборот относительно Солнца практически соответствует Церере: он равен 4,618 годам.
Гигея перемещается со средней скоростью 16,753 км/с, а на один цикл вращения по окружности Солнца ей требуется 5,562 лет.
В то же время, астероид Европа обладает чуть большим показателем: 16,876 км/с. Соответственно, период обращения занимает немного меньше времени — 5,451 год.
Также определили среднюю скорость Гектора 13,012 км/с, который обращается вокруг Солнца за 11,989 лет.
Разумеется, здесь указан характер движения лишь самых известных астероидных тел. Вообще, их открыто около 300 тысяч. Но мы не будем перечислять все.
Церера Паллада Гектор
Как уже было сказано, скоростные показатели превышают вторую космическую скорость и обладают необходимым темпом для удержания на планетных орбитах. По предположению учёных, могут быть не обнаруженные объекты, которые проворно и быстро проносятся по Вселенной (на огромных скоростях).
В любом случае, астероиды резво путешествуют в космосе. Наверное, поэтому они часто сталкиваются друг с другом, а также с другими небесными телами.
Оценка статьи:
Загрузка…
Синодический период астероида S составляет ровно 59 лет, при этом он внешний, радиус его орбиты больше 1 а.е. Такое может быть, только если астероид обращается вокруг Солнца в том же направлении, что и Земля, а период обращения Т связан с периодом обращения Земли Т0 соотношением:
Отсюда получаем, что период обращения астероида составляет 1.0172 года. По III закону Кеплера получаем, что радиус орбиты астероида равен 1.0115 а.е. В момент противостояния астероид находился в 0.0115 а.е. или в 1.7 млн км от Земли. Это в 4.4 раза дальше Луны, при этом астероид светит на 20m или в 10^8 раз слабее полной Луны. Астероид и Луна находятся примерно на одинаковом расстоянии от Солнца, альбедо их также одинаково. Следовательно, отношение их радиусов составляет
Радиус астероида получается равным примерно 750 метрам.
Круговая орбитальная скорость астероида составляет 0.9943 от орбитальной скорости Земли, его скорость относительно Земли v — 0.0057 от орбитальной скорости Земли или всего 170 м/с, однако взаимодействием астероида с Землей мы пренебрегаем. Угловая скорость астероида на расстоянии 1.7 млн км составит 10^-7 рад/с или 0.5 градуса в день. Пренебрегая параллактическим смещением спутника, получаем, что рассеянное звездное скопление Ясли астероид будет пересекать в течение 3 дней и 4 часов.
Verified answer
Ответ: Синодический период обращения астероида = 2,(1)года
Объяснение: Дано:
Сидерический (звездный) период обращения астероида
Тсид = 1,9 года.
Сидерический период обращения Земли Тз = 1 год.
Найти синодический период обращения астероида Тсин — ?
Так как сидерический период обращения астероида больше сидерического периода обращения Земли, то по отношению к Земле астероид является внешней «планетой».
Синодический и сидерический периоды обращения внешней планеты, связаны с сидерическим периодом обращения Земли соотношением: 1/Тсин = 1/Тз– 1/Тсид.
Из этого соотношения: Тсин = Тз*Тсид/(Тсид — Тз) =
= 1*1,9/(1,9 — 1) = 1,9/0,9 = 2,(1) года