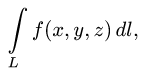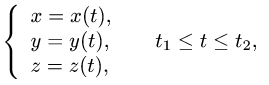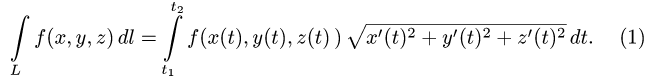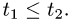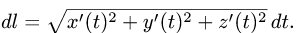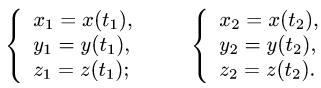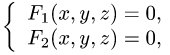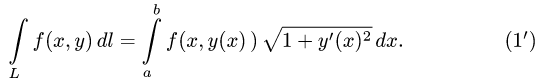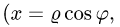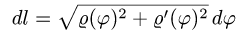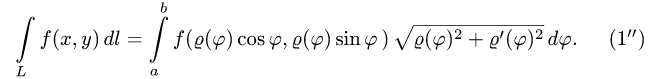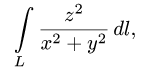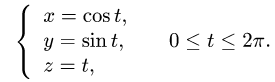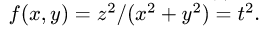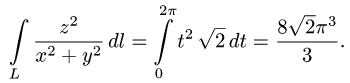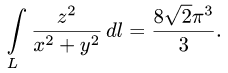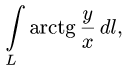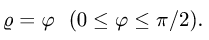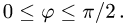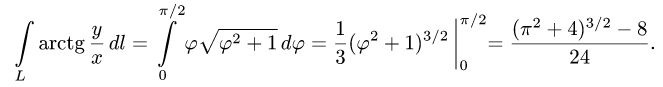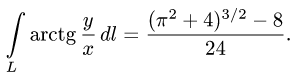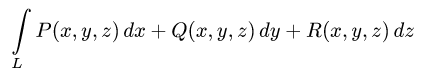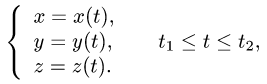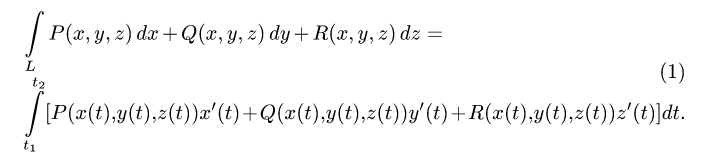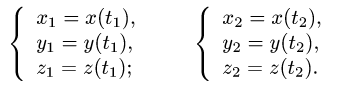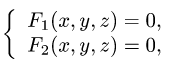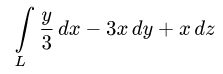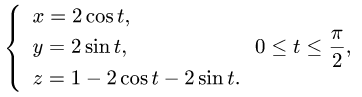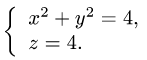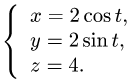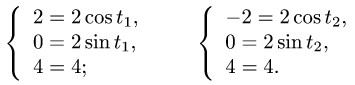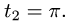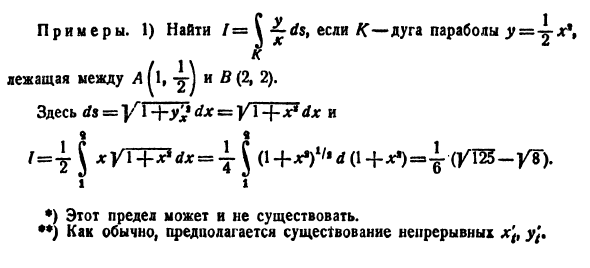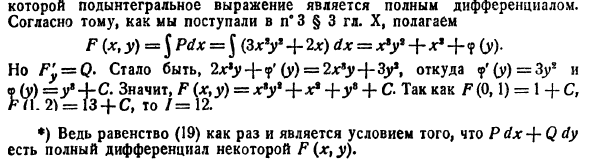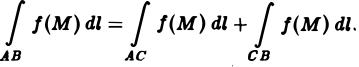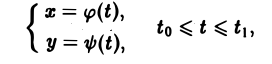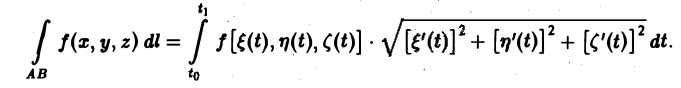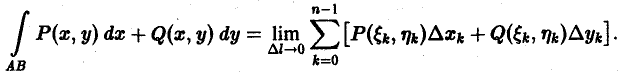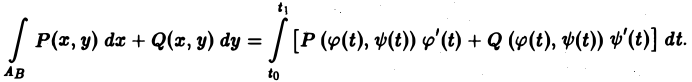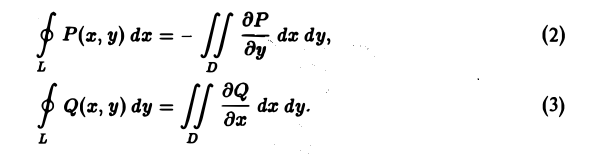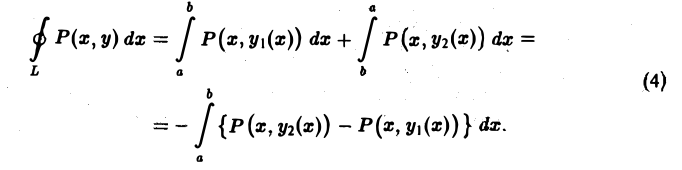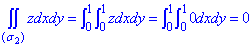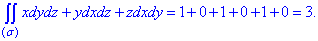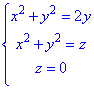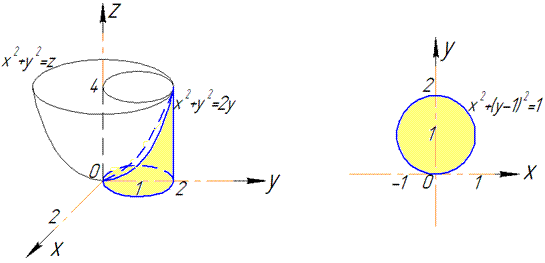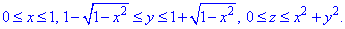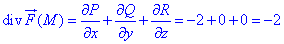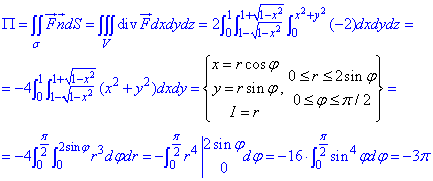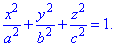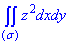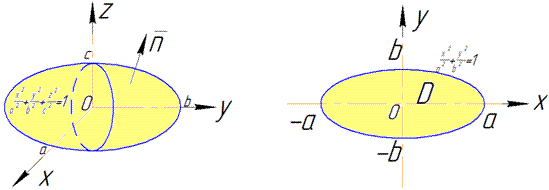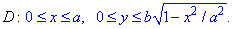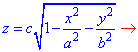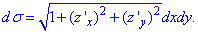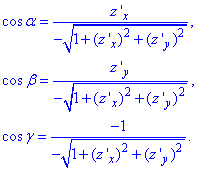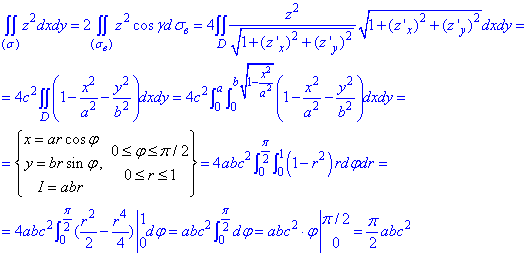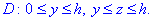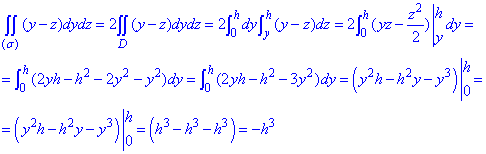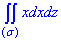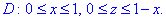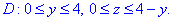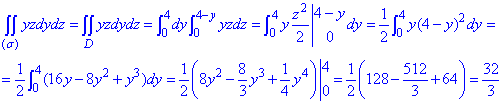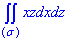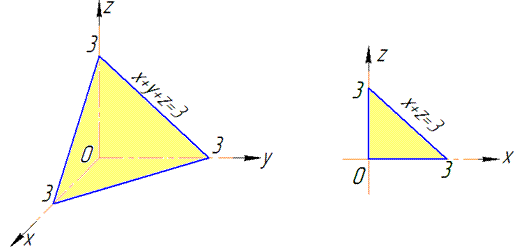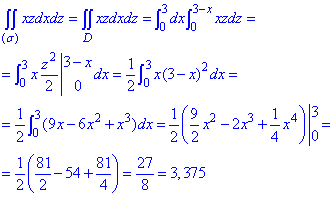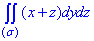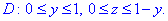Содержание:
- Двойной интеграл
- Двойной интеграл в прямоугольных декартовых координатах
- Двойной интеграл в полярных координатах
- Двойной интеграл в декартовых координатах. Определение, теорема существования
- Геометрический смысл двойного интеграла
- Свойства двойного интеграла
- Вычисление двойного интеграла в декартовых координатах
- Двойной интеграл в полярных координатах
- Вычисление площади плоской фигуры с помощью двойного интеграла
- Вычисление объема тела с помощью двойного интеграла
Двойной интеграл
В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл
На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным интегралом.
Задача.
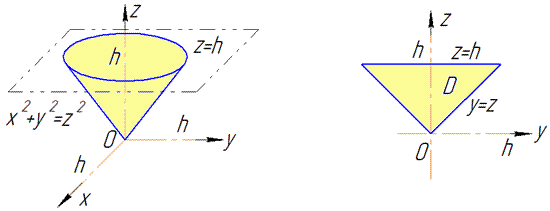
Найти объем тела, ограниченного сверху непрерывной поверхностью 




По этой ссылке вы найдёте полный курс лекций по высшей математике:
Тело указанного вида для краткости называется цилиндроидом. В частном случае, когда верхнее основание цилиндроида есть плоскость, параллельная нижнему основанию его, то цилиндроид называется цилиндром.
Примером цилиндра служит круговой цилиндр, рассматриваемый в средней школе.
Обобщая рассуждение, обычно применяемое для нахождения объема кругового цилиндра, нетрудно доказать, что объем 


Для вычисления объема 






Объем такого столбика на основании формулы объема цилиндра, очевидно, равен
где 

Формула (2) дает возможность найти объем 








Из данного определения следует, что фигура 





Пусть 





Выражение, стоящее в правой части формулы (3), называется двойным интегралом от функции 

Поэтому для объема цилиндроида окончательно имеем
Обобщая конструкцию, примененную для вычисления объема цилиндроида, приходим к следующим определениям.
Возможно вам будут полезны данные страницы:
Опрелеление 1. Двумерной интегральной суммой (2) от данной функции 






Опрелеление 2. Двойным интегралом (4) от функции 









Справедлива следующая теорема:
ТЕОРЕМА. Если область 







В дальнейшем мы будем предполагать, что условия этой теоремы выполнены.
В формуле (6) нет необходимости указывать, что 

Если 


Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем при решении задач мы будем использовать это обстоятельство, выбирая наиболее подходящие сетки. Весьма часто удобной оказывается прямоугольная сетка, образованная пересечением двух систем прямых, параллельных соответственно координатным осям 

В этом случае элементарными ячейками 










В следующих параграфах мы рассмотрим основные способы вычисления двойного интеграла.
Примеры с решением
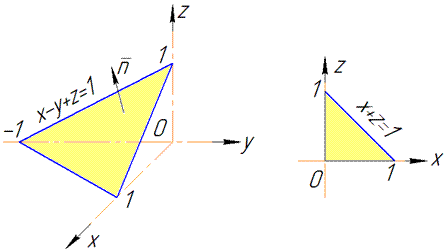
Пример 1.
Найти


Расставляя пределы интегрирования, будем иметь 


Пример 2.
Вычислить двойной интеграл

где 

Расставляя пределы интегрирования и разделяя переменные, будем иметь
Пример 3.
Вычислить 


Область 


Для вертикали 













Аналогично, для горизонтали 










Мы пришли, как и следовало ожидать, к тому же самому результату, причем второй способ вычисления оказался несколько более сложным.
Пример 4.
Изменить порядок интегрирования в повторном интеграле
Область интегрирования 


Следовательно,
Пример 5.
Расставить пределы интегрирования в двойном интеграле 







имеем
Аналогичная формула получится, если мы будем расставлять пределы интегрирования в другом порядке.
Двойной интеграл в прямоугольных декартовых координатах
Предположим для определенности, что область интегрирования 
где 









Пусть 


1) Предположим сначала, что 




Для вычисления объема 




Тогда имеем
Но 

Поэтому
Можно доказать, что при наших условиях 
Подставляя выражение (4) в формулу (3), получим окончательно
Таким образом, двойной интеграл равен соответствующему повторному интегралу (5), т. е. вычисление двойного интеграла сводится к двум квадратурам. Заметим, что при вычислении внутреннего интеграла в формуле (5) 
2) В случае знакопеременной функции 







т. е. 
Отметим один важный случай: пусть 







В силу формулы (5) имеем
Но внутренний интеграл в формуле (7) есть постоянное число, поэтому его можно вынести за знак внешнего интеграла и мы получим
т. е. двойной интеграл (8) равен произведению двух однократных интегралов.
Замечание 1. Если область


В частности, если область 

Отсюда получаем
т е. если пределы интегрирования в повторном интеграле от непрерывной функции конечны и постоянны, то результат интегрирования не зависит от порядка интегрирования.
Двойной интеграл в полярных координатах
Пусть в двойном интеграле
при обычных предположениях мы желаем перейти к полярным координатам 

Область интегрирования 





Введем обозначения 



Что касается ячеек 


В качестве точки 





и, следовательно,
Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, причем можно показать, что на значение этого предела не влияют добавки к слагаемым интегральной суммы, являющиеся бесконечно малыми высшего порядка малости. Поэтому, учитывая формулы (3) и (3′)» получаем
где 

С другой стороны, величины 


соответствующая прямоугольной сетке с линейными элементами 

Выравнивая формулы (4) и (5), получаем окончательно
Выражение 
Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты 


Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования 
где 

где
Пример 6.
Переходя к полярным координатам 






Область 


Пример 7.
В интеграле

Область интегрирования здесь есть треугольник.


В полярных координатах уравнения этих прямых записываются следующим образом: 



Двойной интеграл в декартовых координатах. Определение, теорема существования
Понятие «двойной интеграл» является естественным обобщением понятия «определенный интеграл» на случай функции двух переменных. Поэтому его определение принципиально не отличается от определения определенного интеграла и вводится аналогичным образом.
Пусть функция 






Выполним такую (стандартную) процедуру:
1) разобьем область 





2) выберем на каждой из плоскостей произвольным образом по точке 

3) составим сумму всех таких произведений
которую назовем интегральной суммой для функции 
4) вычислим границу (если она существует) интегральной суммы (26.1) при условии, что диаметр разбиения стремится к нулю при неограниченном росте 

Рис. 26.1
Конечна граница 






где 





Следовательно, по определению
Теорема 26.1 (существование двойного интеграла). Если задана функция двух переменных непрерывна в рассматриваемой замкнутой области, то существует конечное предел интегральной суммы (то есть двойной интеграл), и она не зависит ни от способа разбиения области на плоскости, ни от выбора точек в них для составления интегральной суммы.
Теорему приводим без доказательства.
Функция 

Согласно теореме 26.1 разбиения области 

Рис. 26.2
В этом случае плоскость — прямоугольник со сторонами 





Таким образом, можно записать:
Геометрический смысл двойного интеграла
В дальнейшем тело, ограниченное поверхностью 





Анализируя с геометрической точки зрения процедуру, которая предшествовала определению двойного интеграла для неотъемлемой в области 







Рис. 26.3
Свойства двойного интеграла
Сравнивая определение двойного интеграла и определение определенного интеграла функции одной переменной, можно сделать вывод, что по структуре эти определения аналогичны. Поэтому свойства двойного интеграла, а также их доведения почти повторяют соответствующие свойства определенного интеграла. Приведем эти свойства.
1. Двойной интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме двойных интегралов от слагаемых:
2. Постоянный множитель можно выносить за знак двойного интеграла:
3. Если область 




4. Если 

5. Если в каждой точке области 



6. Если функция 






где 
7. Если функция 


где 
Значение 

Вычисление двойного интеграла в декартовых координатах
Установим формулы для вычисления двойного интеграла 





Область 







Рис. 26.4
Рассмотрим цилиндрическое тело для функции 







Согласно формуле (26.11) объем данного цилиндрического тела равна:
Рис. 26.5
С другой стороны, на основании геометрического смысла двойного интеграла имеем:
Сопоставляя последние две формулы, окончательно получаем:
или в более удобной (для использования) форме:
Правую часть формулы (26.12) как определенный интеграл от определенного интеграла называют двукратным или повторным интегралом от функции 


Согласно формуле (26.12) сначала проводят интегрирования по переменной 






Аналогично область 









Рис. 26.6
Для правильной в направлении оси 
Как итог рассматриваемого наведем порядок нахождения двойного интеграла:
1) строим область интегрирования 
2) анализируем ее с целью установления того, является ли она правильной в направлении хотя бы одной из осей координат, и определяем границы интегрирования;
3) применяем одну из формул, (26.12) или (26.13), и находим сначала внутренний интеграл (как правило, со сменными пределами интегрирования), а затем — внешний (с постоянными пределами интегрирования).
Рис. 26.7
Если область 
Формулы приведения двойного интеграла к повторным (26.12) и (26.13) существенно упрощаются, если область 
В этом случае пределы интегрирования являются постоянными не только для внешнего, но и для внутреннего интеграла:
и в каком порядке интегрировать сначала по переменной 

Вычислим 


По формуле (26.15) имеем:
Если подынтегральная функция является произведением функции от 

Вычислим 


Построим область интегрирования 


Рис. 26.8
Вычислим 


Построим область 
Рис. 26.9
Она является правильной в направлении оси 

Вычислим 


Построим область 
Находим точки взаимного пересечения каждой пары линий, ограничивающих 
Линии 
Рис. 26.10
Область 






Двойной интеграл в полярных координатах
При переходе в двойном интеграле от декартовых координат 





и выражение для дифференциала площади в полярных координатах:
Соответствующая формула перехода имеет вид:
где 

Вычисление двойного интеграла в полярных координатах сводится к вычислению двукратного (повторного) интеграла по переменными 

Если область 






Рис. 26.11
Если область 

Переход к полярным координатам в двойном интеграле целесообразно делать, если область интегрирования представляет собой круг, кольцо или их частями, то есть граница области 
Вычислим 

Пределом области 
Применим формулы перехода от декартовых координат к полярным:
В координатах 

Построим в декартовых координатах круг 




Рис. 26.12
По формуле (26.17) имеем:
Вычислим с помощью двойного интеграла в полярных координатах несобственный интеграл Эйлера-Пуассона:
Для этого рассмотрим двойной интеграл 






Если теперь неограниченно увеличивать радиус 

Рис. 26.13
расширяется так, что любая точка первой четверти 


С другой стороны, при 


поскольку определенный интеграл (а с ним и несобственный) не зависит от обозначения переменной интегрирования.
Таким образом, 
Вычисление площади плоской фигуры с помощью двойного интеграла
Если в формуле (26.3): 



а за ее точное значение принимается значение интеграла:
Если область 


Найдем площадь фигуры, ограниченной линиями:
Построим плоскую фигуру (рис. 26.14) и определим точки пересечения заданных линий — гиперболы и прямой, — решив систему их уравнений:
Рис. 26.14
Решим первое уравнение: 




Заданная фигура является областью, правильной и в направлении оси 






Вычислим площадь плоской области 

Построим область 


Площадь заданной области целесообразно вычислить в полярных координатах:







Вычисление объема тела с помощью двойного интеграла
По определению двойного интеграла и его геометрическим смыслом было доказано, что двойной интеграл 





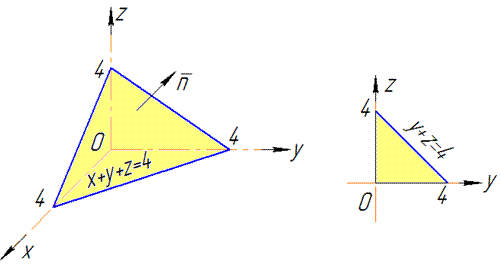
Найдем объем тела, ограниченного поверхностями:
Проанализируем уравнение поверхностей и построим область интегрирования 







Рис. 26.16
По формуле (26.3) получаем:
Найдем объем тела, ограниченного параболоидом 

Построим область интегрирования 
Вычислим объем 







Рис. 26.17
Итак, по формуле (26.17) получим:
Рассмотрим две задачи, в которых двойной интеграл применяется для вычислений в сфере экономики.
1. Пусть 




2. Аналогично, если функция 



В обоих задачах аналитическое выражение подынтегральной функции устанавливается как эмпирическая формула.
Подводя итоги темы «двойной интеграл», отметим, что рядом с двойными существуют также и многомерные (




Лекции:
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Прямая линия на плоскости
- Выпуклость и вогнутость графика функции
- Матанализ для чайников
- Производные некоторых элементарных функций
- Система показательных уравнений
- Поверхность второго порядка
- Уравнения с одной переменной
- Найдите координаты точки пересечения графиков
- Геометрический смысл производной в точке
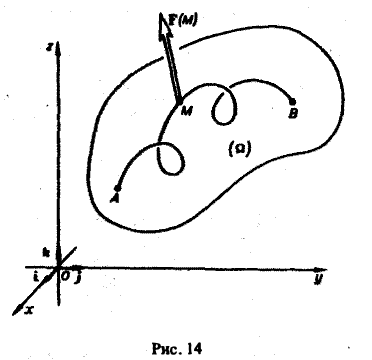
Вычисление криволинейных интегралов: теория и примеры
Понятие криволинейного интеграла
Криволинейные интегралы — обобщение понятия определённого интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:
где f(x, y) — функция двух переменных, а L — кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB.
Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?
Пусть на плоскости расположен отрезок AB некоторой кривой L, а функция двух переменных f(x, y) определена в точках кривой L. Пусть мы выполняем с этим отрезком кривой следующий алгоритм.
- Разделить кривую AB на части точками (рисунки ниже).
- В каждой части свободно выбрать точку M.
- Найти значение функции в выбранных точках.
- Значения функции умножить на
- длины частей в случае криволинейного интеграла первого рода;
- проекции частей на ось координат в случае криволинейного интеграла второго рода.
- Найти сумму всех произведений.
- Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.
Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f(x, y) по кривой AB.
Случай криволинейного интеграла
первого рода
Случай криволинейного интеграла
второго рода
Введём следующие ообозначения.
M i (ζ i ; η i ) — выбранная на каждом участке точка с координатами.
f i (ζ i ; η i ) — значение функции f(x, y) в выбранной точке.
Δs i — длина части отрезка кривой (в случае криволинейного интеграла первого рода).
Δx i — проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).
d = maxΔs i — длина самой длинной части отрезка кривой.
Криволинейные интегралы первого рода
Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:
.
Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл. Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:
.
В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B) считать началом отрезка, а какую концом, то есть
.
Криволинейные интегралы второго рода
Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:
.
В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:
.
При составлении интегральной суммы криволинейного интеграла второго рода значения функции f i (ζ i ; η i ) можно умножать также на проекции частей отрезка кривой на ось Oy. Тогда получим интеграл
.
На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P(x, y) и f = Q(x, y) и интегралы
,
а сумма этих интегралов
называется общим криволинейным интегралом второго рода.
Вычисление криволинейных интегралов первого рода
Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.
Кривая дана в декартовых прямоугольных координатах
Пусть на плоскости задана кривая y = y(x) и отрезку кривой AB соответствует изменение переменной x от a до b. Тогда в точках кривой подынтегральная функция f(x, y) = f(x, y(x)) («игрек» должен быть выражен через «икс»), а дифференциал дуги и криволинейный интеграл можно вычислить по формуле
.
Если интеграл проще интегрировать по y, то из уравнения кривой нужно выразить x = x(y) («икс» через «игрек»), где и интеграл вычисляем по формуле
.
Пример 1. Вычислить криволинейный интеграл
,
где AB — отрезок прямой между точками A(1; −1) и B(2; 1) .
Решение. Составим уравнение прямой AB , используя формулу (уравнение прямой, проходящей через две данные точки A(x 1 ; y 1 ) и B(x 2 ; y 2 ) ):
.
Из уравнения прямой выразим y через x :
.
Тогда и теперь можем вычислять интеграл, так как у нас остались одни «иксы»:
Кривая дана в параметрической форме
Пусть в пространстве задана кривая
Тогда в точках кривой функцию нужно выразить через параметр t () а дифференциал дуги , поэтому криволинейный интеграл можно вычислить по формуле
Аналогично, если на плоскости задана кривая
,
то криволинейный интеграл вычисляется по формуле
.
Пример 2. Вычислить криволинейный интеграл
,
где L — часть линии окружности
,
находящаяся в первом октанте.
Решение. Данная кривая — четверть линии окружности, расположенная в плоскости z = 3 . Она соответствует значениям параметра . Так как
,
то дифференциал дуги
Подынтегральную функцию выразим через параметр t :
.
Теперь, когда у нас всё выражено через параметр t , можем свести вычисление данного криволинейного интеграла к определённому интегралу:
Вычисление криволинейных интегралов второго рода
Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.
Кривая дана в декартовых прямоугольных координатах
Пусть дана кривая на плоскости уравнением функции «игрек», выраженной через «икс»: y = y(x) и дуге кривой AB соответствует изменение x от a до b . Тогда в подынтегральную функцию подставим выражение «игрека» через «икс» и определим дифференциал этого выражения «игрека» по «иксу»: . Теперь, когда всё выражено через «икс», криволинейный интеграл второго рода вычисляется как определённый интеграл:
Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции «икс», выраженной через «игрек»: x = x(y) , . В этом случае формула для вычисления интеграла следующая:
Пример 3. Вычислить криволинейный интеграл
, если
а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке — синяя). Напишем уравнение прямой и выразим «игрек» через «икс»:
.
Получаем dy = dx . Решаем данный криволинейный интеграл:
б) если L — дуга параболы y = x² , получим dy = 2xdx . Вычисляем интеграл:
В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.
Теорема. Если функции P(x,y) , Q(x,y) и их частные производные , — непрерывные в области D функции и в точках этой области частные производные равны, то криволинейный интеграл не зависит от пути интегрирования по линии L , находящейся в области D .
Кривая дана в параметрической форме
Пусть в пространстве дана кривая
.
,
а в подынтегральные функции подставим
—
выражения этих функций через параметр t . Получаем формулу для вычисления криволинейного интеграла:
Пример 4. Вычислить криволинейный интеграл
,
если L — часть эллипса
отвечающая условию y ≥ 0 .
Решение. Данная кривая — часть эллипса, находящаяся в плоскости z = 2 . Она соответствует значению параметра .
,
можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:
Если дан криволинейный интеграл и L — замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина.
Больше примеров вычисления криволинейных интегралов
Пример 5. Вычислить криволинейный интеграл
,
где L — отрезок прямой между точками её пересечения с осями координат.
Решение. Определим точки пересечения прямой с осями координат. Подставив в уравнение прямой y = 0 , получим , . Подставив x = 0 , получим , . Таким образом, точка пересечения с осью Ox — A(2; 0) , с осью Oy — B(0; −3) .
Из уравнения прямой выразим y :
.
, .
Теперь можем представить криволинейный интеграл в виде определённого интеграла и начать вычислять его:
В подынтегральном выражении выделяем множитель , выносим его за знак интеграла. В получившемся после этого подынтегральном выражении применяем подведение под знак дифференциала и окончательно получаем:
Пример 6. Вычислить криволинейный интеграл
,
где L — дуга параболы между точками О(0; 0) и B(2; 2) .
Решение. Так как , то .
Теперь можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:
Пример 7. Вычислить криволинейный интеграл
,
где L — дуга астроиды
в первом квадранте.
Решение. В первом квадранте . Определим дифференциал дуги:
Представляем криволинейный интеграл в виде определённого интеграла и вычисляем его:
Пример 8. Вычислить криволинейный интеграл
,
где L — первая арка циклоиды
Решение. Циклоида образует первую арку при изменении параметра t от 0 до 2π . Определим дифференциал дуги:
.
Подставим в криволинейный интеграл dl и y , выраженные через параметр t и получаем:
Пример 9. Вычислить криволинейный интеграл
,
где L — отрезок прямой от точки A(1; 1) до точки B(3; 5) .
Решение. Составим уравнение прямой AB :
.
Из полученного уравнения прямой выразим «игрек»:
Поэтому и теперь можем вычислить данный криволинейный интеграл:
Пример 10. Вычислить криволинейный интеграл
,
где L — первая арка циклоиды
Решение. Из уравнений кривой следует
.
Так как циклоида образует первую арку при изменении параметра t от 0 до 2π , то получаем соответствующие пределы интегрирования. Решаем данный криволинейный интеграл:
.
Уравнением кривой M 0 M 1 является y = 1 , тогда dy = 0 , на кривой M 1 M x — константа, значит, dx = 0 . Продолжаем и завершаем решение:
Вычисление длины дуги кривой
Если подынтегральная функция равна единице, то криволинейный интеграл первого рода равен длине дуги кривой L:
.
Пример 12. Вычислить длину дуги кривой
,
где .
Решение. Составляем криволинейный интеграл первого рода:
.
Определим производную «игрека»:
.
Продолжаем и завершаем решение:
Вычисление площади участка плоскости
Если границей участка D плоскости является кривая L, то площадь участка D можно вычислить в виде криволинейного интеграла второго рода
.
Пример 13. Вычислить площадь участка плоскости, ограниченного эллипсом
.
Решение. Площадь участка плоскости можно вычислить как криволинейный интеграл второго рода
,
где L — замкнутая линия, ограничивающая участок. Так как
.
Вычисление площади цилиндрической поверхности
Пусть на плоскости xOy дана гладка кривая L, в точках которой определена непрерывная функция двух переменных . Построим цилиндрическую поверхность, образующая которой параллельна оси Oz, и которая заключена между кривой L и поверхностью . Площадь этой цилиндрической поверхности можно вычислить по формуле
.
Вычисление массы материальной кривой
Если L — материальная кривая с плотностью , то массу материальной кривой можно вычислить по формуле
Определение статических моментов материальной кривой
Статические моменты материальной кривой с плотностью относительно осям координат вычисляются по формулам
,
.
Вычисление моментов инерции материальной кривой
Моменты инерции материальной кривой с плотностью относительно осей координат и начала системы координат можно вычислить по формулам
,
,
.
Вычисление координат центра тяжести материальной кривой
Координаты центра тяжести материальной кривой с плотностью можно определить по формулам
,
.
Вычисление работы силы
Если под воздействием переменной силы материальная точка перемещается из точки M в точку N по кривой L=MN, то приложенную работу можно вычислить по формуле
.
Пример 14. В каждой точке плоскости действует сила . Вычислить работу, совершаемую силой при перемещении единицы массы по дуге параболы из точки O(0;0) в точку А(4;2) .
Решение. Работу силы вычислим как криволинейный интеграл второго рода
.
Используя уравнение параболы, производим замену переменной
Примеры решений криволинейных интегралов
В этом разделе вы найдете подробные решения криволинейных интегралов первого и второго рода (непосредственное вычисление, по разным путям, по формуле Грина), а также применение к вычислению моментов инерции, массы, работы, силы притяжения и т.п.
Криволинейные интегралы 1-го рода: примеры решений
Задача 1. Вычислить криволинейный интеграл первого рода по указанной кривой $L$:
Задача 2. Вычислить криволинейный интеграл I рода $int_L y^2 dl$, $L$ — арка циклоиды $x=(t-sin t)/2$, $y=(1-cos t)/2$, $0 le t le pi$.
Задача 3. Вычислить криволинейный интеграл $int_L y^2 dl$, где $L$ – дуга параболы $y^2=2x$ от точки $(0;0)$ до точки $(1;sqrt<2>)$.
Если вам нужна помощь в нахождении интегралов, выполнении домашней работы, будем рады принять ваш заказ на решение. Стоимость от 100 рублей, срок от нескольких часов.
Криволинейные интегралы 2-го рода: примеры решений
Задача 4. Вычислить криволинейный интеграл второго рода, взятый вдоль ориентированной кривой $L$: $int_L x^2 dy -xydx$, где $L$ — часть кривой $x^4-y^4=6x^2y$ от точки $A=(-4sqrt<2>;4)$ до точки $B=(0;0)$
Задача 5. Вычислить интеграл $$int_L z^2x dx +(z+x+y)dy +y^2zdz,$$ где $L$ — кривая $a^2+y^2=ax, x^+y^2=z^2$ положительно ориентированная на внешней стороне цилиндра.
Задача 6. Вычислить криволинейный интеграл $int_ (y^2+x)dx+2x/y dy$ вдоль кривой $y=e^x$ от точки $A(0;1)$ до точки $B(1;e)$.
Задача 7. Проверить, что криволинейный интеграл не зависит от пути интегрирования и найти его значение.
Задача 8. Проверить криволинейный интеграл, который не зависит от пути интегрирования, и найти его значение (двумя способами – непосредственно и с помощью потенциала).
Задача 9. Вычислить криволинейный интеграл по замкнутому контуру в положительном направлении, используя формулу Грина
$$int_l (x-y^2)dy + (x^3+3y)dx, quad l: x=y, y=x^2.$$
Трудности с задачами? МатБюро поможет с интегралами.
Моменты инерции: примеры решений
Задача 10. Найти моменты инерции относительно осей однородных дуг $L$ плотности $rho$.
Задача 11. Вычислить момент инерции верхней половины окружности $x^2+y^2=a^2$ относительно оси $Oy$, если плотность $delta=1$.
Другие задания: примеры решений
Задача 12. Найти координаты силы притяжения дугой астроиды $x=a cos^3 t$, $y=a sin^3 t$, $0 le t le pi/2$ единичной массы, помещенной в начале координат, если плотность астроиды в каждой ее точке равна кубу расстояния этой точки от начала координат.
Задача 13. Вычислить работу силы $F(z,-x,y)$ вдоль дуги винтовой линии $z=2cos t$, $y=3sin t$, $z=4t$, $0 le t le 2pi$.
Задача 14. Доказать, что данное выражение $P(x,y)dx+Q(x,y)dy$ является полным дифференциалом функции $Ф(x,y)$ и найти ее с помощью криволинейного интеграла.
Задача 15. Вычислить работу силы $overline$ при перемещении точки приложения силы вдоль заданной кривой $L$ от точки $B$ до точки $C$, если значения параметра $t$ в точках $B$ и $C$ заданы.
$$ overline=-x overline+2y^2overline, quad x=2cos t, y=sint, quad t_B=0, t_C=pi/6. $$
Задача 16. Вычислить массу кривой $y=x^2/2$, где $xin (sqrt<3>, 2sqrt<2>)$, если линейная плотность задана функцией $f(x,y)=6y/x$.
Криволинейные интегралы в математике с примерами решения и образцами выполнения
При изучении темы «Криволинейные интегралы» вы познакомитесь с понятиями криволинейных интегралов первого рода (по длине дуги) и второго рода (по координатам) от функций двух и трех переменных и научитесь вычислять их вдоль различных плоских и пространственных кривых, заданных параметрически, в декартовых и в полярных координатах, приводя криволинейные интегралы к определенным.
Криволинейные интегралы первого рода
Постановка задачи. Вычислить криволинейный интеграл
где L — часть гладкой кривой, заданной параметрически
и dl — дифференциал длины дуги.
План решения. Криволинейный интеграл первого рода по кривой L определяется формулой
Подчеркнем, что криволинейный интеграл первого рода не зависит
от направления обхода кривой и всегда
1.Вычисляем и
2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.
Замечание:
Если граничные точки кривой L и
заданы в декартовых координатах, то и определяем, решая системы уравнений
Замечание:
Если кривая задана как линия пересечения двух
поверхностей:
то ее необходимо параметризовать.
Замечание:
Если плоская кривая задана уравнением у = у(х)
то дифференциал длины дуги равен и формула (1) имеет вид
Если плоская кривая задана в полярных координатах уравнением то дифференциал длины дуги равен
и формула (1) имеет вид
Пример:
Вычислить криволинейный интеграл
где L — первый виток винтовой линии
Решение:
1.Вычисляем: x'(t) = — sin t, y'(t) = cos t, z'(t) = 1, и
2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:
Ответ.
Пример:
Вычислить криволинейный интеграл
где L — отрезок прямой от точки А(0, 0) до точки В(4, 3).
Решение:
1.В данном случае уравнение прямой есть и, следовательно, и
2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:
Ответ.
Пример:
Вычислить криволинейный интеграл
где L — часть спирали Архимеда
Решение:
1.Вычисляем: так как при
2.Подставляем эти результаты в формулу (1″) и вычисляем определенный интеграл:
Ответ.
Криволинейные интегралы второго рода
Постановка задачи. Вычислить криволинейный интеграл
где L — часть гладкой кривой, заданной параметрически
План решения. Криволинейный интеграл второго рода по кривой L определяется формулой
1.Вычисляем x'(t), y'(t) и z'(t).
2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.
Замечание:
Если граничные точки кривой L и
заданы в декартовых координатах, то и определяем, решая системы уравнений
Замечание:
Если кривая задана как линия пересечения двух
поверхностей:
то ее необходимо параметризовать.
Пример:
Вычислить криволинейный интеграл
по части кривой L, заданной параметрически
Решение:
1.Вычисляем: x'(t) = — 2sin t, y'(t) = 2cos t и
2.Вычисляем криволинейный интеграл по формуле (1):
Ответ.
Пример:
Вычислить криволинейный интеграл
от точки М(2,0, 4) до точки N(—2,0,4) по кривой L, образованной пересечением параболоида и плоскости z = 4,
Решение:
В сечении получается окружность
Поэтому параметрические уравнения кривой L имеют вид
1.Вычисляем: х'(t) = -2sin t, у'(t) = 2cos t и z'(t) = 0.
Определяем из условий
Учитывая, что получаем и
2.Вычисляем криволинейный интеграл по формуле (1):
Ответ.
Дополнение к криволинейному интегралу
Решение криволинейных интегралов
Кривая АВ, заданная параметрическими уравнениями
называется гладкой, если функции φ(t) и ψ(t) имеют на отрезке [tо, t1] непрерывные производные φ'(t) и ψ'(t), причем
Если в конечном числе точек отрезка [tо, t1] эти производные не существуют или одновременно обращаются в нуль, то кривая называется кусочно-гладкой.
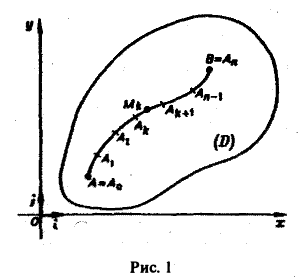
Пусть АВ — плоская кривая, гладкая или кусочно-гладкая. Пусть f(M) — функция, заданная на кривой АВ или в некоторой области D, содержащей эту кривую. Рассмотрим разбиение кривой АВ на части точками
Выберем на каждой из дуг AkAk+1 произвольную точку Мk и составим сумму
где ∆lk — длина дуги AkAk+1 и назовем ее интегральной суммой для функции f(M) по длине дуги кривой. Пусть ∆l — наибольшая из длин частичных дуг, т.е.
Определение:
Если при ∆l —► 0 интегральная сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ на части, ни от выбора точек на каждой из дуг разбиения, то этот предел называется криволинейным интегралом 1 -го рода от функции f(M) по кривой АВ (интеграл по длине дуги кривой) и обозначается символом
(точка М(х, у) лежит на кривой АВ).
В этом случае функция f(M) называется интегрируемой вдоль кривой АВ, кривая АВ называется контуром интегрирования, А — начальной, В — конечной точками интегрирования. Таким образом, по определению,
(2)
Пример:
Пусть вдоль некоторой гладкой кривой L распределена масса с переменной линейной плотностью f(M). Найти массу т кривой L.
Разобьем кривую L на п произвольных частей MkMk+1 (k = 0,1,… , n —1) и вычислим приближенно массу каждой части, предполагая, что на каждой из частей MkMk+1 плотность постоянна и равна плотности в какой-нибудь из ее точек, например, в крайней левой точке f(Mk). Тогда сумма
где ∆lk — длина k-ой части, будет приближенным значением массы т. Ясно, что погрешность будет тем меньше, чем мельче разбиение кривой L. В пределе при ∆l → 0 () получим точное значение массы всей кривой L, т.е.
Но предел справа есть криволинейный интеграл 1-го рода. Значит,
Существование криволинейного интеграла 1-го рода
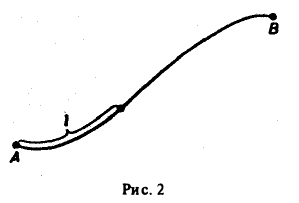
Примем на кривой АВ за параметр длину дуги I, отсчитываемую от начальной точки А (рис. 2). Тогда кривую АВ можно описать уравнениями
(3)
где L — длина кривой АВ.
Уравнения (3) называются натуральными уравнениями кривой АВ. При переходе к натуральным уравнениям функция f(x, у), заданная на кривой АВ, сведется к функции переменной l: f(x(l), y(l). Обозначив через lk (k = 0, 1,…, п — 1) значение параметра l, отвечающее точке Мk, перепишем интегральную сумму (1) в виде
Это — интегральная сумма, отвечающая определенному интегралу
Поскольку интегральные суммы (1) и (4) равны между собой, то равны и отвечающие им интегралы. Таким образом,
(5)
Теорема:
Если функция f(M) непрерывна вдоль гладкой кривой АВ, то существует криволинейный интеграл
(поскольку при этих условиях существует определенный интеграл, стоящий в равенстве (5) справа ).
Свойства криволинейных интегралов 1-го рода
1, Из вида интегральной суммы (1) следует, что
т.е. величина криволинейного интеграла 1-го рода не зависит от направления интегрирования.
2. Линейность. Если для каждой из функций f(M) и д(М) существует криволинейный интеграл по кривой АВ, то для функции af(M) + βg<М), где а и β — любые постоянные, также существует криволинейный интеграл по кривой АВ, причем
3. Аддитивность. Если кривая АВ состоит из двух кусков АС и С В и для функции f(М) существует криволинейный интеграл по AВ, то существуют интегралы
4. Если f(M) ≥ 0 на кривой AB, то
5. Если функция f(M) интегрируема на кривой АВ, то функция |f(М)| также интегрируема на АВ, и при этом
6. Формула среднего значения. Если функция f(M) непрерывна вдоль кривой АВ, то на этой кривой найдется точка Мс такая, что
где L — длина кривой AB.
Вычисление криволинейного интеграла 1-го рода
Пусть кривая АВ задана параметрическими уравнениями
причем точке А соответствует значение t = t0, а точке В — значение t = t1. Будем предполагать, что функции φ(t) и ψ(t) непрерывны на [to, t1] вместе со своими производными φ'(t) и ψ'(t) и выполнено неравенство
Тогда дифференциал дуги кривой вычисляется по формуле
В частности, если кривая АВ задана явным уравнением
причем функция g(х) непрерывно дифференцируема на [а, b] и точке А соответствует значение х = а, а точке В — значение х = b, то, принимая х за параметр, получаем
Криволинейные интегралы 1-го рода для пространственных кривых
Определение криволинейного интеграла 1-го рода, сформулированное выше для плоской кривой, дословно переносится на случай, когда функция f(M) задана вдоль некоторой пространственной кривой АВ.
Пусть кривая АВ задана параметрическими уравнениями
Тогда криволинейный интеграл 1-го рода от функции f, взятый вдоль этой кривой, можно свести к определенному интегралу при помоши следующей формулы:
Пример:
Вычислить криволинейный интеграл
где L — контур треугольника с вершинами в точках O(0,0), A(1,0), B(0, I) (рис. 3).
По свойству аддитивности имеем
Вычислим каждый из интегралов в отдельности. Так как на отрезке OA имеем: 0 ≤ x ≤ 1, у = 0 и dl = dx, то
На отрезке АВ имеем х + у = 1, откуда у = 1 — х, т.е.
причем 0 ≤ х ≤ 1, тогда
Замечание:
При вычислении интегралов
мы воспользовались свойством 1, согласно которому
Криволинейные интегралы 2-го рода
Пусть АВ — гладкая или кусочно-гладкая ориентированная кривая на плоскости хОу и пусть
F(M) = Р(М) i + Q(M) j
— вектор-функция, определенная в некоторой области D, содержащей кривую АВ. Разобьем кривую АВ на части точками
координаты которых обозначим соответственно через
На каждой из элементарных дуг АkАk+1, возьмем произвольно точку Мk(ξk, ηk) и составим сумму
Пусть ∆l — длина наибольшей из дуг АkАk+1.
Определение:
Если при ∆l → 0 сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ. ни от выбора точек (ξk, ηk) на элементарных дугах, то этот предел называется криволинейным интегралом 2-го рода от вектор-функции F(M) по кривой АВ и обозначается символом
Так что по определению (2)
Теорема:
Если в некоторой области D, содержащей кривую АВ, функции Р(х,у) и Q(х, у) непрерывны, то криволинейный интеграл 2-го рода
r(М) = xi + yj
— радиус-вектор точки М(х, у). Тогда
dr = i dx + j dy,
и подынтегральное выражение
Р(х, у) dx + Q(x, у) dy
в формуле (2) можно представить в виде скалярного произведения векторов F(Af) и dr. Так что интеграл 2-го рода от вектор-функции
по кривой АВ можно записать коротко так:
Вычисление криволинейного интеграла 2-го рода
Пусть кривая АВ задана параметрическими уравнениями,
где функции φ(t) и ψ(t) непрерывны вместе с производными φ'(t), ψ'(t) на отрезке [to, t1] причем изменению параметра t от to до t1 соответствует движение точки М(х, у) по кривой АВ от точки А к точке В.
Если в некоторой области D, содержащей кривую АВ, функции Р(х, у) и Q(x, у) непрерывны, то криволинейный интеграл 2-го рода
сводится к следующему определенному интегралу:
(3)
Таким образом, вычисление криволинейного интеграла 2-го рода также может быть сведено к вычислению определенного интеграла.
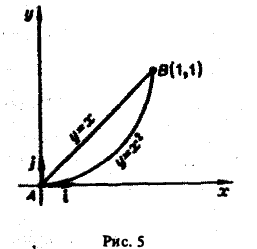
Пример:
1) вдоль прямолинейного отрезка, соединяющего точки A(0,0) и В<1, 1);
2) вдоль параболы у = х , соединяющей те же точки (рис.5).
1) Уравнение линии АВ: у = х (х — параметр, 0 ≤ х ≤ 1), откуда dy = dx. Так что
2) Уравнение линии AB:
dy = 2х dx,
x dy = 2x 2 dx
Рассмотренный пример помазывает, что величина криволинейного интеграла 2-го рода, вообще говоря, зависит от формы пути интегрирования.
Свойства криволинейного интеграла 2-го рода
1. Линейность. Если существуют криволинейные интегралы
то при любых действительных а и β существует и интеграл
2. Аддитивность. Если кривая АВ разбита на части АС и С В и криволинейный интеграл
существует, то существуют интегралы
Криволинейный интеграл второго рода (в отличие от криволинейного интеграла 1-го рода) зависит от того, в каком направлении (от A к В или от В к А) проходится кривая АВ, и меняет знак при изменении направления движения по кривой, т. е.
Замечание:
Последнее свойство cotrmrrayer физической интерпретации криволинейного интеграла 2-го рода как работы силового паля F вдоль некоторого путь: при изменении направления движения по кривой работа силового поля вдоль этой кривой меняет знак на противоположный.
Связь между криволинейными интегралами 1-го и 2-го рода
Рассмотрим криволинейный интеграл 2-го рода
где ориентированная кривая АВ (А — начальная точка, В — конечная точка) задана векторным уравнением
r = r(l)
(здесь l — длина кривой, отсчитываемая в том направлении, в котором ориентирована кривая АВ) (рис. 6).
где т = т(l) — единичный вектор касательной к кривой АВ в точке М(l). Тогда
Заметим, что последний интеграл в этой формуле — криволинейный интеграл 1-го рода. При изменении ориентации кривой АВ единичный вектор касательной т заменяется на противоположный вектор (—т), что влечет изменение знака его подынтегрального выражения и, значит, знака самого интеграла.
Формула Грина
Выведем формулу Грина, связывающую криволинейный интеграл
по границе L некоторой плоской области D с двойным интегралом по этой области.
Теорема:
Если в замкнутой области D, ограниченной кусочно-гладким контуром L, функции Р(х, у) и Q и то справедливо равенство (формула Грина):
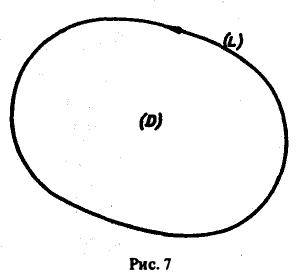
Здесь символ означает интегрирование по границе L области D, причем граница L проходится так, что область D остается слева (рис. 7).
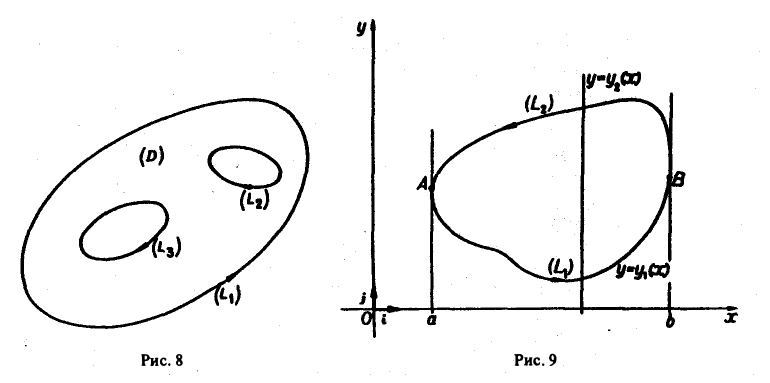
Граница L плоской области D может состоять из одной или нескольких простых замкнутых кривых (компонент). В первом случае она называется односвязной, а во втором — многосвязной. Если граница L состоит из конечного числа кусочно-гладких замкнутых кривых Li, то кривые L, называются связными компонентами границы. На рис. 8 изображена трехсвязная область.
Односвязная область D (область «без дырок») обладает тем свойством, что любая лежащая в ней замкнутая кривая может быть стянута в точку Р ∈ D, оставаясь в процессе стягивания в области D.
Доказательство теоремы проведем для односвязной области.
В силу свойства линейности достаточно доказать, что
Докажем первую из этих формул.
Предположим сначала, что кривая L пересекается каждой прямой, параллельной оси Оу, не более чем в двух точках или по целому отрезку (рис. 9). Если каждая такая прямая пересекает кривую L не более чем в двух точках, то кривую L можно разбить на две части L1 и L2 (верхнюю и нижнюю), каждая из которых проектируется взаимно однозначно на некоторый отрезок [а, b] оси Ох. В силу аддитивности криволинейного интеграла имеем
На каждой из кривых L1 и L2 возьмем в качестве параметра абсциссу х и запишем уравнения этих кривых соответственно в виде
По предположению производная непрерывна в D, и значит, в силу известной формулы интегрального исчисления, приращение функции можно записать через интеграл от производной этой функции:
Из формул (4) и (5) получаем
Повторный интеграл в правой части последнего соотношения равен двойному интегралу от функции по области D, так что окончательно имеем
Формула (2) доказана.
Соотношение (3) доказывается аналогично. Складывая почленно соотношения (2) и (3), получаем формулу Грина (1).
Отметим, что формула Грина имеет место и для более сложных контуров L, и для неодносвязных областей D. Рассмотрим, например, случай двухсвязной области (рис. 10). Сделаем разрез АВ этой области, превращающий ее в односвязную. Тогда
Отсюда, учитывая, что
где интегрирование по кривой L1 ведется в направлении против движения часовой стрелки, а по кривой L2 — в направлении движения часовой стрелки. Отметим, что при этом кривые L1 и L2 проходятся так, что область D остается слева. Такое направление обхода контура принимается за положительное.
Площадь плоской области
Р(х, y) = -y и Q(x,y) = x.
и по формуле Грина (1) получаем
где S — площадь области D.
Отсюда получаем формулу для вычисления площади S плоской области D с помощью криволинейного интеграла по границе L этой области: (7)
Пример:
Вычислить площадь области, ограниченной эллипсом L:
Запишем уравнение эллипса в параметрической форме
Искомая площадь находится no формуле (7), где криволинейный интеграл берется по эллипсу при обходе контура в положительном направлении, что соответствует изменен ию параметра t от 0 до 2 π. Так как
то отсюда получаем, что
Замечание:
Пусть в пространстве задана ориентированная кусочно-гладкая кривая АВ и пусть, кроме того, в некоторой области Ω, содержащей кривую А В, задана вектор-функция
где Р, Q, R — непрерывные в Ω функции. Аналогично плоскому случаю криволинейный интеграл от вектор-функции F по ориентированной кривой АВ определим выражением
Это — криволинейный интеграл 2-го рода в пространстве.
Приложения криволинейных интегралов
Масса кривой
В примере 1 из § 1 было показано, что масса кривой L вычисляется с помощью интеграла 1-го рода
где f(M) — переменная линейная плотность на кривой L. (Мы предполагаем, что f(М) — непрерывная функция на АВ.)
Площадь цилиндрической поверхности
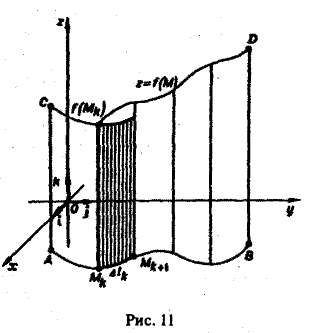
Пусть в плоскости хОу задана некоторая спрямляемая (т. е. имеющая длину) кривая АВ и на этой кривой определена непрерывная функция f(М) ≥ 0. Тогда совокупность точек (х, y, f(x, у)), или (М, f(M)), составит некоторую кривую, лежащую на цилиндрической поверхности, для которой кривая АВ является направляющей, а ее образующая параллельна оси Oz. Требуется определить площадь цилиндрической поверхности ABDC, ограниченной снизу кривой АВ, сверху — кривой z = f(M), где М ∈ АВ, и вертикальными прямыми АС и BD (рис. 11).
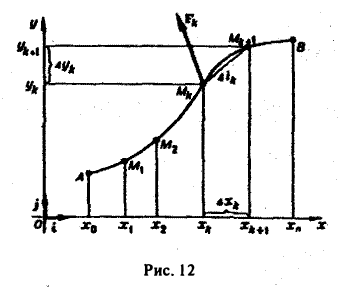
Для решения этой задачи поступим так:
1) разобьем кривую АВ на п частей точками
так, как показано на рис. 11;
2) из каждой точки Мk проведем перпендикуляр к плоскости хОу высотой f(Mk) (при этом цилиндрическая поверхность ABDC разобьется на n полосок);
3) каждую полоску заменим прямоугольником с основанием ∆lk, где ∆lk — длина дуги МkМk+1, и высотой, равной значению функции f
Тогда площадь k-ой полоски будет приближенно равна f(Mk) ∆lk, а площадь всей поверхности ABDC
Это приближенное равенство будет тем точнее, чем мельче будут частичные дуги МkМk+1, на которые разбита кривая АВ. Пусть ∆l — наибольшая из длин ∆lk частичных дуг MkMk+1. Тогда при ∆l —> 0 в пределе получим точное значение искомой площади
Предел справа по определению есть криволинейный интеграл первого рода от функции f(М) по кривой АВ. Итак, (2)
Пример:
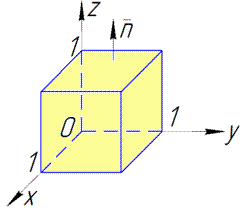
Вычислить площадь части боковой поверхности цилиндра
срезанного сверху поверхностью
ху = 2Rz.
Сведем задачу к вычислению криволинейного интеграла 1-го рода от функции
вдоль дуги окружности, расположенной в первой четверти. Будем иметь
Параметрические уравнения линии АВ —
Площадь плоской фигуры
Ранее мы установили, что площадь S плоской фигуры D, ограниченной линией L, вычисляется по формуле
Правая часть есть криволинейный интеграл 2-го рода.
Работа силы:
Пусть в некоторой плоской области D, содержащей кривую АВ, задана сила
F(M) = P(M)i + Q(M)J, (4)
где функции Р(М) и Q(M), а следовательно, и F(M) предполагаются непрерывными функциями точки М. Требуется найти работу силы F, если под действием этой силы материальная точка М, имеющая единичную массу, переместилась из точки А в точку В по кривой АВ.
Для решения этой задачи разделим кривую АВ на п частей точками
(рис. 12), заменим каждую дугу хордой MkMk+1 и, предполагая для простоты, что на участке кривой (а значит, и на хорде MkMk+1) сила Fk имеет постоянное значение, например, равное ее значению в точке Мk,
получим приближенное выражение работы силы на участке пути :
где |Fk| — длина вектора Fk, |∆lk| — длина вектора ∆lk
Из формулы (4) с учетом (5) получим
Так как правая часть формулы (6) есть скалярное произведение векторов Fk и ∆lk, то, учитывая (7) и (8), будем иметь
Суммируя по всем значениям k(k = 0,1,2,…, п — 1), получим величину
приближенно выражающую работу силы F(M) на всем пути от А до В.
Предел этой суммы при ∆хk → 0 и ∆уk → 0 принимают за точное значение работы. Но с другой стороны, предел этой суммы есть криволинейный интеграл 2-го рода от вектор-функции F(M) по кривой АВ. Итак, работа силы вычисляется по формуле
(9)
Пример:
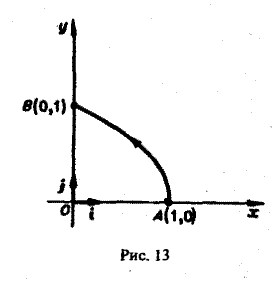
Найти работу силы
при перемещении единичной массы по параболе
от точки A(1,0) до точки В(0,1) (рис. 13). 4 Применим формулу (9), положив в ней
то искомую работу можно вычислить так:
Обобщение на случай пространственной кривой(рис. 14),
Если в некоторой пространственной области Ω, содержащей пространственную кривую АВ, задана сила
F(M) = Р(М)i + Q(M)j + R(M)k,
где Р(М), Q(M) и R(M) — непрерывные функции в области Ω, то работа, совершаемая силой F(М) по перемещению материальной точки М с единичной массой из точки А в точку В по пространственной кривой АВ, равна
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://www.matburo.ru/ex_ma.php?p1=makrint
http://lfirmal.com/krivolinejnye-integraly/
Краткая теория
Пусть
функция
непрерывна в каждой точке
гладкой кривой
. Разбив произвольным
образом кривую
на
частей
и выбрав в каждой из них произвольно точку
, построим интегральные
суммы:
где
– длины проекций частичных дуг
, на соответствующие
координатные оси. Тогда пределы:
называются
криволинейными интегралами II рода или криволинейными
интегралами по координатам.
Сумма
интегралов:
обозначается
как криволинейный интеграл
Если
кривая замкнутая, то обозначают:
Основные свойства криволинейных интегралов II рода
При
изменении направления интегрирования интеграл меняет свой знак:
Сказанное
верно и для замкнутой кривой, при этом выбор точки начала обхода безразличен.
Положительным направлением обхода считается то, при котором область,
ограниченная этой кривой, остается слева (для плоской кривой это движение против
часовой стрелки).
Остальные свойства такие же, как и у криволинейного интеграла I рода.
Вычисление криволинейного интеграла II рода
1. Если
пространственная кривая
задана параметрическими уравнениями
причем
перемещение от точки
к точке
происходит при изменении параметра
от
до
, то
2. В частном случае для плоской кривой
причем
перемещение от точки
к точке
происходит при изменении параметра
от
до
. Криволинейный интеграл
вычисляется по формуле:
3. Если
плоская кривая
определена уравнением
, причем перемещение от
точки
к точке
происходит при изменении
от
до
, то
Формула Грина
Интеграл по замкнутому контуру
можно
преобразовать в двойной интеграл по области
, ограниченной этим контуром, и наоборот, используя
формулу Грина:
где функции
и
и их частные производные первого порядка
должны быть непрерывными в области
и на контуре
.
При этом обход контура
выбирается таким образом, что область
остается слева.
Условие независимости криволинейного интеграла от пути интегрирования
Для того, чтобы
криволинейный интеграл
не зависел от пути
интегрирования, необходимо и достаточно, чтобы выполнялось равенство
Если же, кроме
того,
есть замкнутая кривая, то
Примеры решения задач
Задача 1
Вычислить
криволинейный интеграл
вдоль
дуги циклоиды
,
от точки
до точки
Решение
Искомый
криволинейный интеграл можно вычислить по формуле:
Получаем:
Ответ:
Задача 2
Вычислить
данный криволинейный интеграл вдоль линии
. Сделать чертеж.
где
— дуга кривой
от точки
до точки
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Криволинейный интеграл можно вычислить
по формуле:
Получаем:
Ответ:
Задача 3
Вычислить
криволинейный интеграл:
вдоль отрезка
прямой от точки
до точки
. Сделать чертеж.
Решение
Вычислим уравнение
прямой
:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
Задача 4
Вычислить
непосредственно и с помощью формулы Грина:
где
-контур четырехугольника
Решение
Сделаем
чертеж области:
Вычислим
криволинейный интеграл непосредственно:
Криволинейный интеграл можно
вычислить по формулам:
или
Уравнение прямой
:
Уравнение прямой
:
Уравнение прямой
:
Уравнение прямой
:
Искомый
интеграл:
По формуле
Грина:
Искомый
интеграл:
Ответ:
Задача 5
Применяя
формулу Грина, вычислить интеграл
для
заданной линии
(пробегаемой в положительном направлении) и
подынтегральных функций
и
.
Решение
По формуле
Грина:
Сделаем чертеж
области
:
Искомый
интеграл:
Ответ:
При изучении темы «Криволинейные интегралы» вы познакомитесь с понятиями криволинейных интегралов первого рода (по длине дуги) и второго рода (по координатам) от функций двух и трех переменных и научитесь вычислять их вдоль различных плоских и пространственных кривых, заданных параметрически, в декартовых и в полярных координатах, приводя криволинейные интегралы к определенным.
Криволинейные интегралы первого рода
Постановка задачи. Вычислить криволинейный интеграл
где L — часть гладкой кривой, заданной параметрически
и dl — дифференциал длины дуги.
План решения. Криволинейный интеграл первого рода по кривой L определяется формулой
Подчеркнем, что криволинейный интеграл первого рода не зависит
от направления обхода кривой и всегда
1.Вычисляем 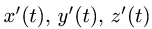
2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.
Замечание:
Если граничные точки кривой L 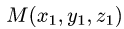
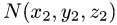
Замечание:
Если кривая задана как линия пересечения двух
поверхностей:
то ее необходимо параметризовать.
Замечание:
Если плоская кривая задана уравнением у = у(х)
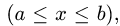
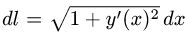
Если плоская кривая задана в полярных координатах 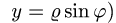
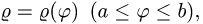
и формула (1) имеет вид
Пример:
Вычислить криволинейный интеграл
где L — первый виток винтовой линии
Решение:
1.Вычисляем: x'(t) = — sin t, y'(t) = cos t, z'(t) = 1, 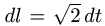
2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:
Ответ.
Пример:
Вычислить криволинейный интеграл
где L — отрезок прямой от точки А(0, 0) до точки В(4, 3).
Решение:
1.В данном случае уравнение прямой есть 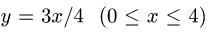
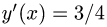
2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:
Ответ.
Пример:
Вычислить криволинейный интеграл
где L — часть спирали Архимеда
Решение:
1.Вычисляем: 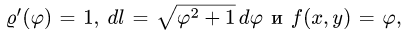
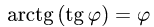
2.Подставляем эти результаты в формулу (1″) и вычисляем определенный интеграл:
Ответ.
Криволинейные интегралы второго рода
Постановка задачи. Вычислить криволинейный интеграл
где L — часть гладкой кривой, заданной параметрически
План решения. Криволинейный интеграл второго рода по кривой L определяется формулой
1.Вычисляем x'(t), y'(t) и z'(t).
2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.
Замечание:
Если граничные точки кривой L 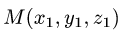
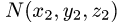
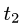
Замечание:
Если кривая задана как линия пересечения двух
поверхностей:
то ее необходимо параметризовать.
Пример:
Вычислить криволинейный интеграл
по части кривой L, заданной параметрически
Решение:
1.Вычисляем: x'(t) = — 2sin t, y'(t) = 2cos t и
2.Вычисляем криволинейный интеграл по формуле (1):
Ответ.
Пример:
Вычислить криволинейный интеграл
от точки М(2,0, 4) до точки N(—2,0,4) 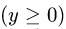
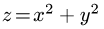
Решение:
В сечении получается окружность
Поэтому параметрические уравнения кривой L имеют вид
1.Вычисляем: х'(t) = -2sin t, у'(t) = 2cos t и z'(t) = 0.
Определяем 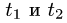
Учитывая, что 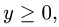
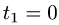
2.Вычисляем криволинейный интеграл по формуле (1):
Ответ.
Дополнение к криволинейному интегралу
Смотрите также:
Предмет высшая математика
Решение криволинейных интегралов
Кривая АВ, заданная параметрическими уравнениями
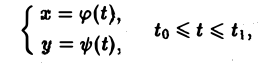
называется гладкой, если функции φ(t) и ψ(t) имеют на отрезке [tо, t1] непрерывные производные φ'(t) и ψ'(t), причем
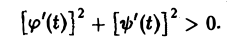
Если в конечном числе точек отрезка [tо, t1] эти производные не существуют или одновременно обращаются в нуль, то кривая называется кусочно-гладкой.
Пусть АВ — плоская кривая, гладкая или кусочно-гладкая. Пусть f(M) — функция, заданная на кривой АВ или в некоторой области D, содержащей эту кривую. Рассмотрим разбиение кривой АВ на части точками
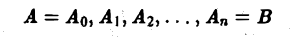
(рис. 1).
Выберем на каждой из дуг AkAk+1 произвольную точку Мk и составим сумму
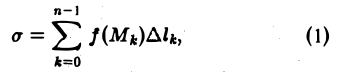
где ∆lk — длина дуги AkAk+1 и назовем ее интегральной суммой для функции f(M) по длине дуги кривой. Пусть ∆l — наибольшая из длин частичных дуг, т.е.
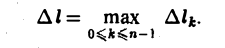
Определение:
Если при ∆l —► 0 интегральная сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ на части, ни от выбора точек на каждой из дуг разбиения, то этот предел называется криволинейным интегралом 1 -го рода от функции f(M) по кривой АВ (интеграл по длине дуги кривой) и обозначается символом
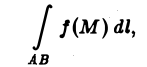
или
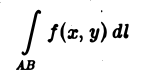
(точка М(х, у) лежит на кривой АВ).
В этом случае функция f(M) называется интегрируемой вдоль кривой АВ, кривая АВ называется контуром интегрирования, А — начальной, В — конечной точками интегрирования. Таким образом, по определению,
(2)
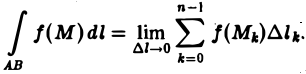
Пример:
Пусть вдоль некоторой гладкой кривой L распределена масса с переменной линейной плотностью f(M). Найти массу т кривой L.
Разобьем кривую L на п произвольных частей MkMk+1 (k = 0,1,… , n —1) и вычислим приближенно массу каждой части, предполагая, что на каждой из частей MkMk+1 плотность постоянна и равна плотности в какой-нибудь из ее точек, например, в крайней левой точке f(Mk). Тогда сумма
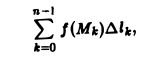
где ∆lk — длина k-ой части, будет приближенным значением массы т. Ясно, что погрешность будет тем меньше, чем мельче разбиение кривой L. В пределе при ∆l → 0 (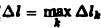
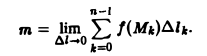
Но предел справа есть криволинейный интеграл 1-го рода. Значит,
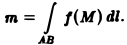
Существование криволинейного интеграла 1-го рода
Примем на кривой АВ за параметр длину дуги I, отсчитываемую от начальной точки А (рис. 2). Тогда кривую АВ можно описать уравнениями
(3)
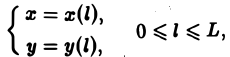
где L — длина кривой АВ.
Уравнения (3) называются натуральными уравнениями кривой АВ. При переходе к натуральным уравнениям функция f(x, у), заданная на кривой АВ, сведется к функции переменной l: f(x(l), y(l). Обозначив через lk (k = 0, 1,…, п — 1) значение параметра l, отвечающее точке Мk, перепишем интегральную сумму (1) в виде
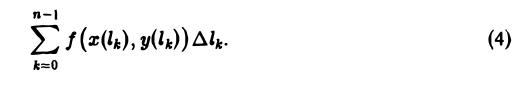
Это — интегральная сумма, отвечающая определенному интегралу
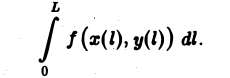
Поскольку интегральные суммы (1) и (4) равны между собой, то равны и отвечающие им интегралы. Таким образом,
(5)
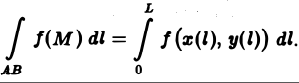
Теорема:
Если функция f(M) непрерывна вдоль гладкой кривой АВ, то существует криволинейный интеграл
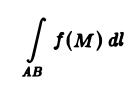
(поскольку при этих условиях существует определенный интеграл, стоящий в равенстве (5) справа ).
Свойства криволинейных интегралов 1-го рода
1, Из вида интегральной суммы (1) следует, что
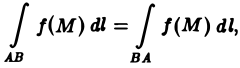
т.е. величина криволинейного интеграла 1-го рода не зависит от направления интегрирования.
2. Линейность. Если для каждой из функций f(M) и д(М) существует криволинейный интеграл по кривой АВ, то для функции af(M) + βg{М), где а и β — любые постоянные, также существует криволинейный интеграл по кривой АВ, причем
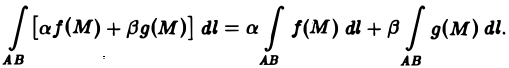
3. Аддитивность. Если кривая АВ состоит из двух кусков АС и С В и для функции f(М) существует криволинейный интеграл по AВ, то существуют интегралы
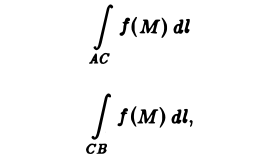
причем
4. Если f(M) ≥ 0 на кривой AB, то
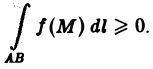
5. Если функция f(M) интегрируема на кривой АВ, то функция |f(М)| также интегрируема на АВ, и при этом
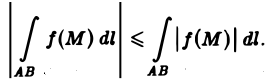
6. Формула среднего значения. Если функция f(M) непрерывна вдоль кривой АВ, то на этой кривой найдется точка Мс такая, что
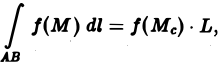
где L — длина кривой AB.
Вычисление криволинейного интеграла 1-го рода
Пусть кривая АВ задана параметрическими уравнениями
причем точке А соответствует значение t = t0, а точке В — значение t = t1. Будем предполагать, что функции φ(t) и ψ(t) непрерывны на [to, t1] вместе со своими производными φ'(t) и ψ'(t) и выполнено неравенство
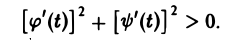
Тогда дифференциал дуги кривой вычисляется по формуле
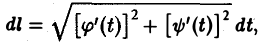
и
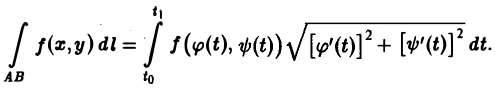
В частности, если кривая АВ задана явным уравнением
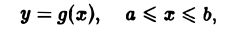
причем функция g(х) непрерывно дифференцируема на [а, b] и точке А соответствует значение х = а, а точке В — значение х = b, то, принимая х за параметр, получаем
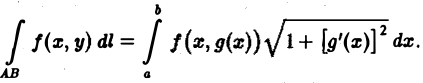
Криволинейные интегралы 1-го рода для пространственных кривых
Определение криволинейного интеграла 1-го рода, сформулированное выше для плоской кривой, дословно переносится на случай, когда функция f(M) задана вдоль некоторой пространственной кривой АВ.
Пусть кривая АВ задана параметрическими уравнениями
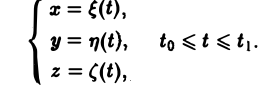
Тогда криволинейный интеграл 1-го рода от функции f, взятый вдоль этой кривой, можно свести к определенному интегралу при помоши следующей формулы:
Пример:
Вычислить криволинейный интеграл
где L — контур треугольника с вершинами в точках O(0,0), A(1,0), B(0, I) (рис. 3).
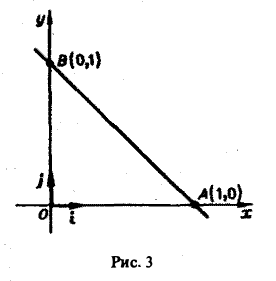
По свойству аддитивности имеем
Вычислим каждый из интегралов в отдельности. Так как на отрезке OA имеем: 0 ≤ x ≤ 1, у = 0 и dl = dx, то
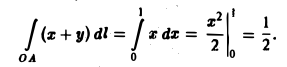
На отрезке АВ имеем х + у = 1, откуда у = 1 — х, т.е.
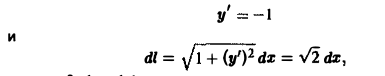
причем 0 ≤ х ≤ 1, тогда
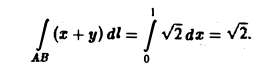
Наконец,
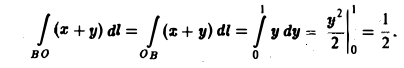
Следовательно,
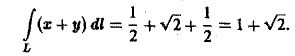
Замечание:
При вычислении интегралов
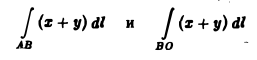
мы воспользовались свойством 1, согласно которому
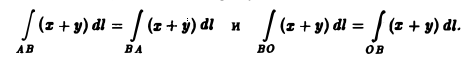
Криволинейные интегралы 2-го рода
Пусть АВ — гладкая или кусочно-гладкая ориентированная кривая на плоскости хОу и пусть
F(M) = Р(М) i + Q(M) j
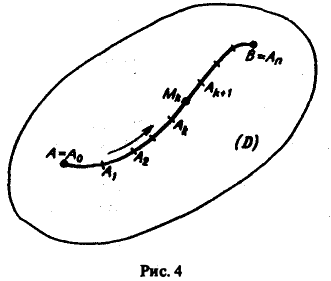
— вектор-функция, определенная в некоторой области D, содержащей кривую АВ. Разобьем кривую АВ на части точками
координаты которых обозначим соответственно через
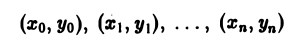
(рис. 4).
На каждой из элементарных дуг АkАk+1, возьмем произвольно точку Мk(ξk, ηk) и составим сумму
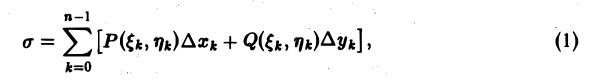
где
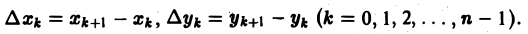
Пусть ∆l — длина наибольшей из дуг АkАk+1.
Определение:
Если при ∆l → 0 сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ. ни от выбора точек (ξk, ηk) на элементарных дугах, то этот предел называется криволинейным интегралом 2-го рода от вектор-функции F(M) по кривой АВ и обозначается символом
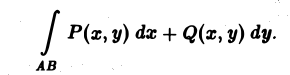
Так что по определению (2)
Теорема:
Если в некоторой области D, содержащей кривую АВ, функции Р(х,у) и Q(х, у) непрерывны, то криволинейный интеграл 2-го рода
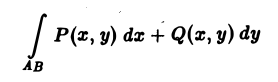
существует.
Пусть
r(М) = xi + yj
— радиус-вектор точки М(х, у). Тогда
dr = i dx + j dy,
и подынтегральное выражение
Р(х, у) dx + Q(x, у) dy
в формуле (2) можно представить в виде скалярного произведения векторов F(Af) и dr. Так что интеграл 2-го рода от вектор-функции
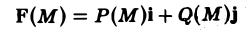
по кривой АВ можно записать коротко так:
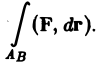
Вычисление криволинейного интеграла 2-го рода
Пусть кривая АВ задана параметрическими уравнениями,
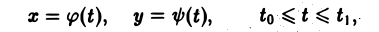
где функции φ(t) и ψ(t) непрерывны вместе с производными φ'(t), ψ'(t) на отрезке [to, t1] причем изменению параметра t от to до t1 соответствует движение точки М(х, у) по кривой АВ от точки А к точке В.
Если в некоторой области D, содержащей кривую АВ, функции Р(х, у) и Q(x, у) непрерывны, то криволинейный интеграл 2-го рода
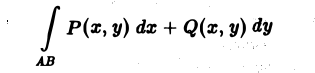
сводится к следующему определенному интегралу:
(3)
Таким образом, вычисление криволинейного интеграла 2-го рода также может быть сведено к вычислению определенного интеграла.
Пример:
Вычислить интеграл
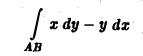
1) вдоль прямолинейного отрезка, соединяющего точки A(0,0) и В{1, 1);
2) вдоль параболы у = х , соединяющей те же точки (рис.5).
1) Уравнение линии АВ: у = х (х — параметр, 0 ≤ х ≤ 1), откуда dy = dx. Так что
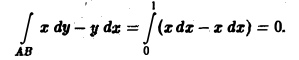
2) Уравнение линии AB:
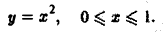
Отсюда
dy = 2х dx,
поэтому
x dy = 2x2 dx
Рассмотренный пример помазывает, что величина криволинейного интеграла 2-го рода, вообще говоря, зависит от формы пути интегрирования.
Свойства криволинейного интеграла 2-го рода
1. Линейность. Если существуют криволинейные интегралы
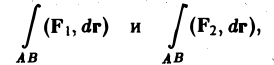
то при любых действительных а и β существует и интеграл
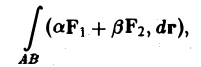
причем
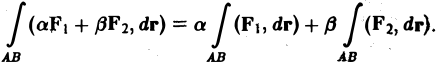
2. Аддитивность. Если кривая АВ разбита на части АС и С В и криволинейный интеграл
существует, то существуют интегралы
причем
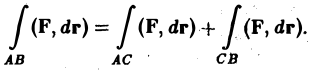
Криволинейный интеграл второго рода (в отличие от криволинейного интеграла 1-го рода) зависит от того, в каком направлении (от A к В или от В к А) проходится кривая АВ, и меняет знак при изменении направления движения по кривой, т. е.
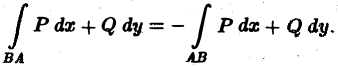
Замечание:
Последнее свойство cotrmrrayer физической интерпретации криволинейного интеграла 2-го рода как работы силового паля F вдоль некоторого путь: при изменении направления движения по кривой работа силового поля вдоль этой кривой меняет знак на противоположный.
Связь между криволинейными интегралами 1-го и 2-го рода
Рассмотрим криволинейный интеграл 2-го рода
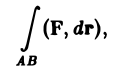
где ориентированная кривая АВ (А — начальная точка, В — конечная точка) задана векторным уравнением
r = r(l)
(здесь l — длина кривой, отсчитываемая в том направлении, в котором ориентирована кривая АВ) (рис. 6).
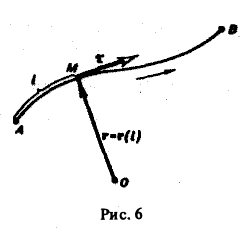
Тогдa
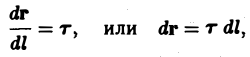
где т = т(l) — единичный вектор касательной к кривой АВ в точке М(l). Тогда
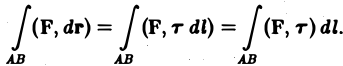
Заметим, что последний интеграл в этой формуле — криволинейный интеграл 1-го рода. При изменении ориентации кривой АВ единичный вектор касательной т заменяется на противоположный вектор (—т), что влечет изменение знака его подынтегрального выражения и, значит, знака самого интеграла.
Формула Грина
Выведем формулу Грина, связывающую криволинейный интеграл
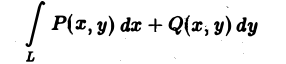
по границе L некоторой плоской области D с двойным интегралом по этой области.
Теорема:
Если в замкнутой области D, ограниченной кусочно-гладким контуром L, функции Р(х, у) и Q{x, у) непрерывны и имеют непрерывные частные производные 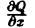
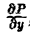
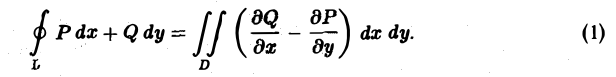
Здесь символ 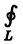
Граница L плоской области D может состоять из одной или нескольких простых замкнутых кривых (компонент). В первом случае она называется односвязной, а во втором — многосвязной. Если граница L состоит из конечного числа кусочно-гладких замкнутых кривых Li, то кривые L, называются связными компонентами границы. На рис. 8 изображена трехсвязная область.
Односвязная область D (область «без дырок») обладает тем свойством, что любая лежащая в ней замкнутая кривая может быть стянута в точку Р ∈ D, оставаясь в процессе стягивания в области D.
Доказательство теоремы проведем для односвязной области.
В силу свойства линейности достаточно доказать, что
Докажем первую из этих формул.
Предположим сначала, что кривая L пересекается каждой прямой, параллельной оси Оу, не более чем в двух точках или по целому отрезку (рис. 9). Если каждая такая прямая пересекает кривую L не более чем в двух точках, то кривую L можно разбить на две части L1 и L2 (верхнюю и нижнюю), каждая из которых проектируется взаимно однозначно на некоторый отрезок [а, b] оси Ох. В силу аддитивности криволинейного интеграла имеем
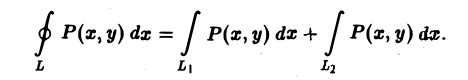
На каждой из кривых L1 и L2 возьмем в качестве параметра абсциссу х и запишем уравнения этих кривых соответственно в виде
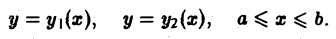
Тогда
По предположению производная 
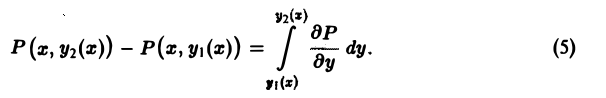
Из формул (4) и (5) получаем
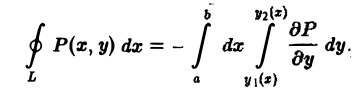
Повторный интеграл в правой части последнего соотношения равен двойному интегралу от функции 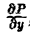
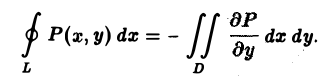
Формула (2) доказана.
Соотношение (3) доказывается аналогично. Складывая почленно соотношения (2) и (3), получаем формулу Грина (1).
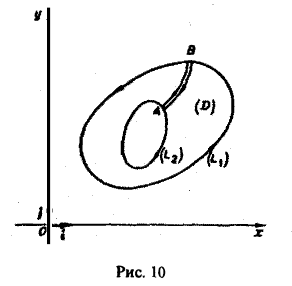
Отметим, что формула Грина имеет место и для более сложных контуров L, и для неодносвязных областей D. Рассмотрим, например, случай двухсвязной области (рис. 10). Сделаем разрез АВ этой области, превращающий ее в односвязную. Тогда
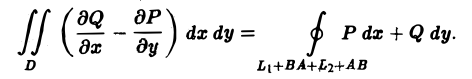
Отсюда, учитывая, что
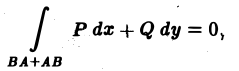
получим
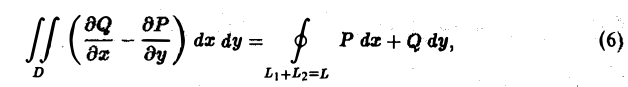
где интегрирование по кривой L1 ведется в направлении против движения часовой стрелки, а по кривой L2 — в направлении движения часовой стрелки. Отметим, что при этом кривые L1 и L2 проходятся так, что область D остается слева. Такое направление обхода контура принимается за положительное.
Площадь плоской области
Возьмем
Р(х, y) = -y и Q(x,y) = x.
Тогда
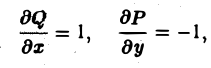
и по формуле Грина (1) получаем
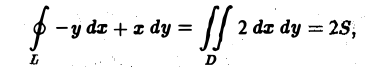
где S — площадь области D.
Отсюда получаем формулу для вычисления площади S плоской области D с помощью криволинейного интеграла по границе L этой области: (7)
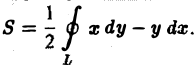
Пример:
Вычислить площадь области, ограниченной эллипсом L:
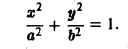
Запишем уравнение эллипса в параметрической форме
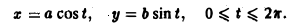
Искомая площадь находится no формуле (7), где криволинейный интеграл берется по эллипсу при обходе контура в положительном направлении, что соответствует изменен ию параметра t от 0 до 2 π. Так как
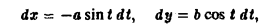
то отсюда получаем, что
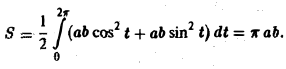
Замечание:
Пусть в пространстве задана ориентированная кусочно-гладкая кривая АВ и пусть, кроме того, в некоторой области Ω, содержащей кривую А В, задана вектор-функция
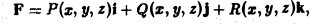
где Р, Q, R — непрерывные в Ω функции. Аналогично плоскому случаю криволинейный интеграл от вектор-функции F по ориентированной кривой АВ определим выражением
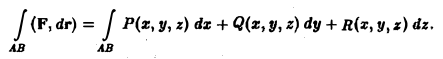
Это — криволинейный интеграл 2-го рода в пространстве.
Приложения криволинейных интегралов
Масса кривой
В примере 1 из § 1 было показано, что масса кривой L вычисляется с помощью интеграла 1-го рода

где f(M) — переменная линейная плотность на кривой L. (Мы предполагаем, что f(М) — непрерывная функция на АВ.)
Площадь цилиндрической поверхности
Пусть в плоскости хОу задана некоторая спрямляемая (т. е. имеющая длину) кривая АВ и на этой кривой определена непрерывная функция f(М) ≥ 0. Тогда совокупность точек (х, y, f(x, у)), или (М, f(M)), составит некоторую кривую, лежащую на цилиндрической поверхности, для которой кривая АВ является направляющей, а ее образующая параллельна оси Oz. Требуется определить площадь цилиндрической поверхности ABDC, ограниченной снизу кривой АВ, сверху — кривой z = f(M), где М ∈ АВ, и вертикальными прямыми АС и BD (рис. 11).
Для решения этой задачи поступим так:
1) разобьем кривую АВ на п частей точками
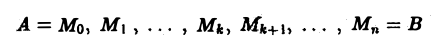
так, как показано на рис. 11;
2) из каждой точки Мk проведем перпендикуляр к плоскости хОу высотой f(Mk) (при этом цилиндрическая поверхность ABDC разобьется на n полосок);
3) каждую полоску заменим прямоугольником с основанием ∆lk, где ∆lk — длина дуги МkМk+1, и высотой, равной значению функции f{M) в какой-нибудь точке этой дуги, например, в точке Мk.
Тогда площадь k-ой полоски будет приближенно равна f(Mk) ∆lk, а площадь всей поверхности ABDC
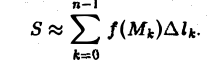
Это приближенное равенство будет тем точнее, чем мельче будут частичные дуги МkМk+1, на которые разбита кривая АВ. Пусть ∆l — наибольшая из длин ∆lk частичных дуг MkMk+1. Тогда при ∆l —> 0 в пределе получим точное значение искомой площади
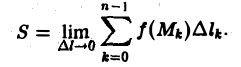
Предел справа по определению есть криволинейный интеграл первого рода от функции f(М) по кривой АВ. Итак, (2)
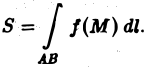
Пример:
Вычислить площадь части боковой поверхности цилиндра
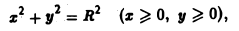
срезанного сверху поверхностью
ху = 2Rz.
Сведем задачу к вычислению криволинейного интеграла 1-го рода от функции
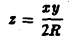
вдоль дуги окружности, расположенной в первой четверти. Будем иметь
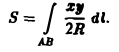
Параметрические уравнения линии АВ —
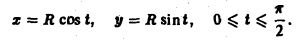
Тогда
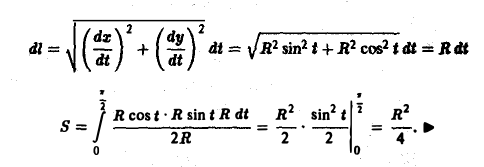
Площадь плоской фигуры
Ранее мы установили, что площадь S плоской фигуры D, ограниченной линией L, вычисляется по формуле

Правая часть есть криволинейный интеграл 2-го рода.
Работа силы:
Пусть в некоторой плоской области D, содержащей кривую АВ, задана сила
F(M) = P(M)i + Q(M)J, (4)
где функции Р(М) и Q(M), а следовательно, и F(M) предполагаются непрерывными функциями точки М. Требуется найти работу силы F, если под действием этой силы материальная точка М, имеющая единичную массу, переместилась из точки А в точку В по кривой АВ.
Для решения этой задачи разделим кривую АВ на п частей точками
(рис. 12), заменим каждую дугу 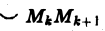
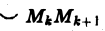

получим приближенное выражение работы силы на участке пути 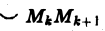
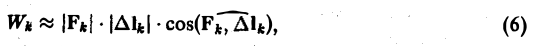
где |Fk| — длина вектора Fk, |∆lk| — длина вектора ∆lk
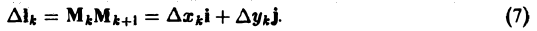
Из формулы (4) с учетом (5) получим
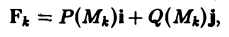
ИЛИ
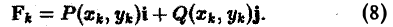
Так как правая часть формулы (6) есть скалярное произведение векторов Fk и ∆lk, то, учитывая (7) и (8), будем иметь
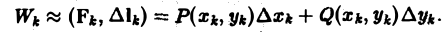
Суммируя по всем значениям k(k = 0,1,2,…, п — 1), получим величину
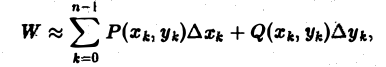
приближенно выражающую работу силы F(M) на всем пути от А до В.
Предел этой суммы при ∆хk → 0 и ∆уk → 0 принимают за точное значение работы. Но с другой стороны, предел этой суммы есть криволинейный интеграл 2-го рода от вектор-функции F(M) по кривой АВ. Итак, работа силы вычисляется по формуле
(9)
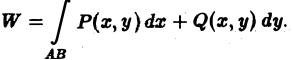
Пример:
Найти работу силы
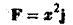
при перемещении единичной массы по параболе
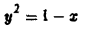
от точки A(1,0) до точки В(0,1) (рис. 13). 4 Применим формулу (9), положив в ней
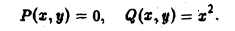
Так как
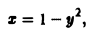
то искомую работу можно вычислить так:
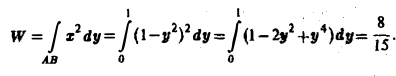
Обобщение на случай пространственной кривой(рис. 14),
Если в некоторой пространственной области Ω, содержащей пространственную кривую АВ, задана сила
F(M) = Р(М)i + Q(M)j + R(M)k,
где Р(М), Q(M) и R(M) — непрерывные функции в области Ω, то работа, совершаемая силой F(М) по перемещению материальной точки М с единичной массой из точки А в точку В по пространственной кривой АВ, равна
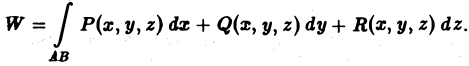
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Вычисления поверхностного интеграла второго рода заключается в нахождении двойных интегралов по ориентированным поверхностям от заранее заданных функций. Теория двойных интегралов детально расписана в учебниках и методичках, больше трудностей возникает у студентов с самим интегрированием, вернее с переходом к двойным интегралам, правильным нахождением пределов интегрирования.
На эти вопросы Вы можете найти ответы, пересмотрев готовые ответы к практикуму из высшей математики.
Пример 6.2 Вычислить поверхностный интеграл int(x*dy*dz+y*dx*dz+z*dx*dy, ds) по поверхности сигма — внешняя сторона куба, ограниченного плоскостями z=0, y=0, x=0, x=1, y=1, z=1.
Решение: Построим куб, который ограничен заданными плоскостями:
Вычисляем поверхностный интеграл ІІ рода по всем шести поверхностям, поэтому формула примет вид
Для каждой поверхности куба запишем уравнение плоскости и ее предела по граням:
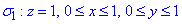
На плоскости Oxz и Oyz поверхность z=1 проектируется в прямые, где dydz=0, dxdz=0
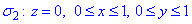
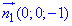
На плоскости Oxz и Oyz поверхность z=0 проектируется в прямые, где dydz=0.
Поскольку в условии куб ограничен плоскостями z=0, y=0, x=0, x=1, y=1, z=1, то по соответствующим плоскостям ситуация будет аналогична, поэтому поверхностный интеграл равен сумме
Пример 6.4 Вычислить поток векторного поля 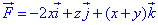
(нормаль внешня).
Решение: Уравнение x^2+y^2=2y сводим к каноническому виду x^2+(y-1)^2=1 — цилиндр вытянут вдоль оси Oz и радиусом R=1;
z=x^2+y^2 — эллиптический параболоид с вершиной в начале координат (0;0;0) ветками вытянут вверх вдоль оси Oz.
Построим цилиндр и параболоид
Это вносит определенную ясность в условие задания да и Вам более приятно читать ответы с рисунками, чем голые формулы.
Как видим из рисунка половина области V задается следующими пределами:
Рассматриваем половины в силу четности всех функций, поэтому конечный результат умножим на 2.
Вычислим дивергенцию векторного поля 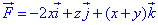
где P=P(x;y;z)=-2x, Q=Q(x;y;z)=z, R=R(x;y;z)=x+y множители при направляющих векторного поля.
Найдем поток векторного поля 
Тройной интеграл сводим к двойному, а дальнейше, перейдя к полярной системе координат, находим значение интеграла.
Пример 6.6 Вычислить поверхностный интеграл int(z2*dy*dz, ds) по поверхности сигма, где 
Решение: Построим эллипсоид и его проекцию в декартовую плоскость:
Проекция плоскости на Oxy ограничена следующим образом
(Взяли четверть области).
Дальше выражаем поверхность как функцию z(x, y)
z^2=(1-x^2/a^2-y^2/b^2) *c^2
затем находим дифференциал поверхности по формуле
Этот интеграл будем вычислять для верхней половины эллипсоида, поскольку для нижней значение поверхностного интеграла будет таким же. Таким образом, результат умножим на 2.
Вычислим направляющие косинусы поверхности:
Перед радикалами поставим знак » — «, поскольку внешняя нормаль 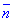
Следовательно, сводим поверхностный интеграл к повторному, дальше делаем замену переменных и находим якобиан перехода.
Все превращения дают возможность без вычисления тяжелых интегралов найти компактный ответ.
Пример 6.9 Вычислить поверхностный интеграл int((y-z)*dy*dz, ds) по поверхности сигма, где сигма — внешняя сторона конической поверхности x^2+y^2=z^2 (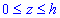
Решение: Построим конус, который ограничен сверху:
x^2+y^2=z^2 (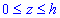
Его проекция в плоскость Oyz дает равнобедренный треугольник, ограниченный линиями
При расстановке пределов учли четность функций, поэтому результат нужно будет умножить на 2.
Находим поверхностный интеграл ІІ рода :
Проинтегрировать приведенные функции по силам каждому студенту.
Пример 6.13 Вычислить поверхностный интеграл int(x*dx*dz, ds) по поверхности сигма, где сигма — внешняя сторона треугольника, образованного пересечением плоскости x-y+z=1 с координатными осями.
Решение: Построим пространственный треугольник x-y+z=1 и его проекцию.
Проектировать всегда следует в ту плоскость Oxz по которой идет интегрирование
Вычисляем поверхностный интеграл ІІ рода:
Пример 6.15 Вычислить поверхностный интеграл int(yz*dy*dz, ds) по поверхности сигма — внешняя сторона треугольника, образованного пересечением плоскости x+y+z=4 с координатными осями.
Решение: Построим плоскость сигма: x+y+z=4.
Видим, что проекция треугольника в Oyz имеет такие пределы
Поверхностный интеграл ІІ рода сводим к повторному и вычисляем
Брать подобные интегралы не сложно, вся проблема сводится к правильному построению поверхности и корректной расстановки пределов интегрирования.
Интегрировать не трудно, поскольку, как правило, заданы самые простые функции.
Пример 6.16 Вычислить поверхностный интеграл int(xz*dx*dz, ds) по поверхности сигма- внешняя сторона треугольника, образованного пересечением плоскости x+y+z=3 с координатными осями.
Решение: Построим пространственный треугольник: x+y+z=3.
Заданная плоскость проектируется на область D в Oxz следующим образом
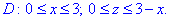
Имея пределы сводим поверхностный интеграл ІІ рода к повторному
Пример 6.23 Вычислить поверхностный интеграл int((x+z)*dy*dz, ds) по поверхности 
Решение: Выполняем рисунок к задаче
Плоскость проектируется треугольником в Oyz
Поверхностный интеграл ІІ рода вычисляем с учетом уравнения поверхности x=1-y-z.
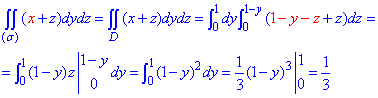
Вычисления сами по себе тяжелые, потому на практических и экзаменах эта тема не должна создавать Вам трудностей.