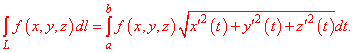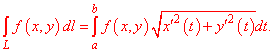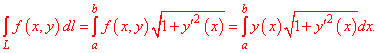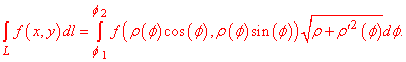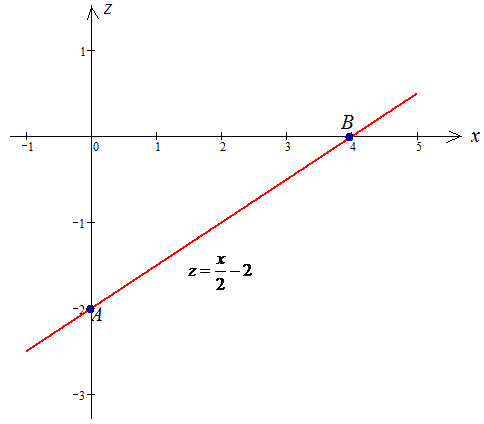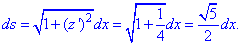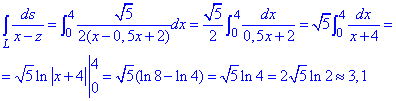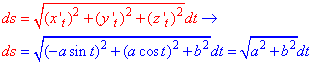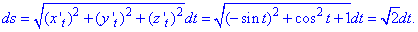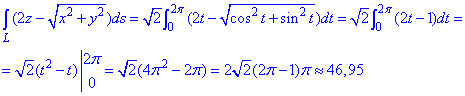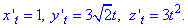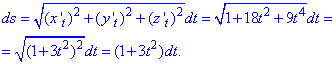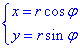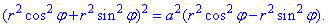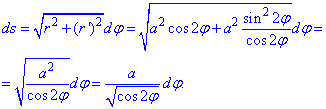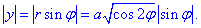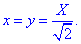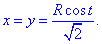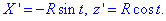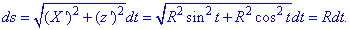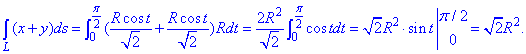Определенные интегралы в случаях когда интегрирование проводится не вдоль отрезка, а некоторой кривой (на плоскости или в пространстве) называются криволинейными. Различают криволинейные интегралы І и ІІ рода.
Формулы криволинейного интегралу первого рода
Пусть в пространстве (на плоскости) задано параметрическое уравнение гладкой кривой f (x, y, z)
x=x(t), y=y(t), z=z(t).
tє[a, b].
Каждая из функций непрерывна на промежутке интегрирования.
Функция f(x, y, z)=0 описывает кривую в пространстве.
В таком случае криволинейный интеграл первого рода равен интегралу за параметром от функции умноженной на корень квадратный из суммы квадратов производных координат за параметром
Для случая кривой на плоскости формула неопределенного интегралу I роду упрощается
Когда кривая интегрирования задана явно y=y(x), формула перехода к определенному интегралу имеет вид
Пусть функция задана полярными координатами rho=rho(phi), phi1<phi<phi2. Тогда криволинейный интеграл первого рода вдоль кривой вычисляется по формуле
На этом все формулы, что Вам нужны для вычисления интегралов, однако без готовых ответов трудно представить их приложение, поєтому перейдем к практической части.
Примеры подобрано из учебной программы для студентов ЛНУ им. И. Франко. Они охватывают широкий класс заданий, которые непременно встретите на контрольной работе и экзаменах. Поэтому внимательно разберите ответы к примерам и выучите приведенные наверху формулы вічисления криволинейных интегралов.
Пример 1.7 Вычислить криволинейный интеграл 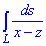
Решение: Построим графически прямую и нанесем на нее точки ограничивающие дугу
За видом видим, что необходимо вычислить криволинейный интеграл I рода.
z=x/2-2, z’=1/2.
Подынтегральная функция примет значение
1/(x-z)=1/(x -(x/2-2))=1/(0,5x+2).
Найдем дифференциал дуги заданной кривой по формуле
Подставляем и находим криволинейный интеграл
Неопределенный интеграл сводится к логарифму, который не имеет особенностей (гладкая функция) на промежутке интегрирования.
Пример 1.10 Вычислить криволинейный интеграл вдоль дуги L:
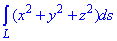
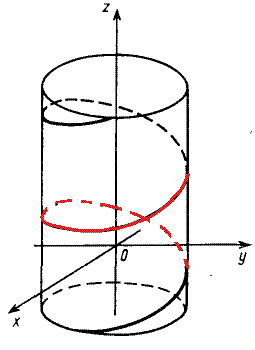
Решение: Параметрическая кривая x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi] описывает часть винтовой линии.
Ее график на цилиндрической поверхности имеет вид.
Часть винтовой линии, которая отвечает промежутку [0;2pi] изображена красным цветом.
Подынтегральная функция равна x2+y2+z2.
Нужно вычислить криволинейный интеграл I рода.
Находим производные координат по параметру
x’t=a*sin(t), y’t=a*sin(t), z’t=b.
Дальше вычисляем дифференциал дуги параметрически заданной кривой согласно формуле:
Формулы дифференциалу дуги в декартовой, полярной и пространственной системах координат приведены в теоретическом материале и поэтому здесь на них задерживаться не будем.
Интегрированием вычисляем криволинейный интеграл
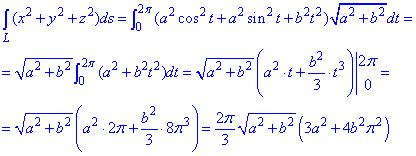
Интеграл не сложен в плане расчетов.
Пример 1.12 Вычислить криволинейный интеграл 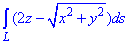
Решение: Имеем идентичное уравнение x=cos(t), y=sin(t), z=t — винтовой линии.
Для вычисления криволинейного интеграла I рода находим производные координат
x’t=-sin(t), y’t=cos(t), z’t=1.
Подставляем их в дифференциал дуги винтовой линии:
Превращаем подінтегральную функцию и находим криволинейный интеграл
Пример 1.14 Вычислить криволинейный интеграл int(x+y, dS)
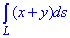
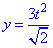
Решение: Прежде чем вычислить криволинейный интеграл I рода находим производные за параметром.
Подставляем их в формулу дифференциала дуги:
Определенный интеграл вычисляем в указанных пределах
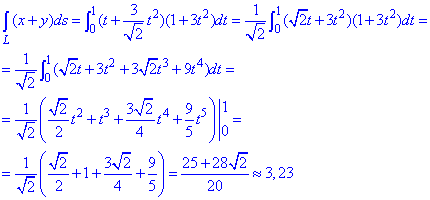
Под интегралом раскрыли скобки и применили простые формулы интегрирования.
Пример 1.18 Вычислить криволинейный интеграл int (1/x2+y2+z2,ds)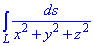
x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi].
Решение: Интегрировать опять придется вдоль винтовой линии.
Производные за параметром имеют вид
x’t=-a*sin(t), y’t=a*sin(t), z’t=b.
Вычисляем дифференциал дуги кривой:
Дальше превращаем криволинейный интеграл к определенному и находим его значение
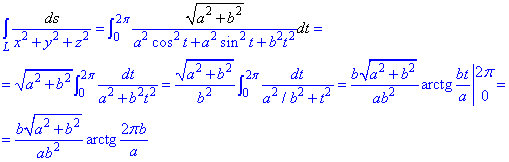
При интегрировании будем иметь арктангенс.
В результате вычислений получили компактную формулу через параметры формы цилиндра.
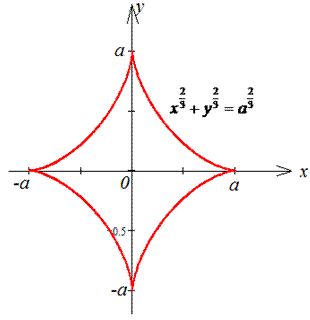
Пример 1.20 Вычислить криволинейный интеграл int(x4/3+y4/3,ds) вдоль дуги L:
дуга астроиды x2/3+y2/3=a2/3.
Решение: Запишем параметрическое уравнение астроиды:
x=a*cos3(t), y=a*sin3(t), где t[0;2pi].
График астроиды в декартовой системе координат имеет вид
Для вычисления криволинейного интеграла I рода вычисляем производные за параметром
x’t=-3a*cos2(t)*sin(t), y’t=3a*cos(t)*sin2(t).
и подставляем в дифференциал дуги астроиды:
Криволинейный интеграл 1 рода находим методом замены переменной
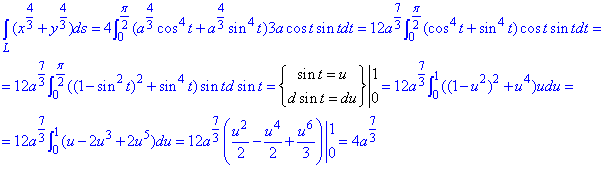
Это позволяет перейти к простому понятному виду подынтегральной функции.
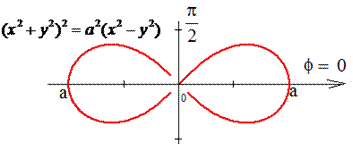
Пример 1.21 Вычислить криволинейный интеграл 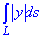
Решение: Для лемнискаты раньше рассматривали интегралы на нахождение площади.
Запишем уравнение лемнискаты в полярной системе координат, используя превращение координат:
Тогда из уравнения дуги
выражаем радиус-вектор и вычисляем производную за углом
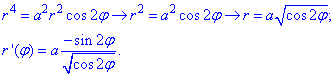
Найдем дифференциал дуги по формуле:
Запишем подынтегральную функцию:
Вычисляем криволинейный интеграл первого роду как 4 интеграла по 1 четверти
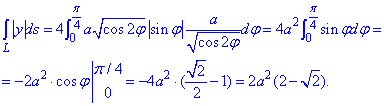
Синус в первой четверти положителен, поэтому модуль опускаем.
Пример 1.25 Вычислить криволинейный интеграл вдоль дуги L:
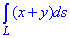
Решение: Имеем сферу x2+y2+z2=R2 и плоскость y=x, которая ее пересекает.
График дуги в пространстве имеет вид как на рисунку
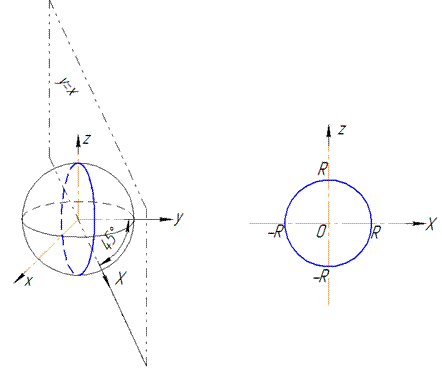
В сечении получим круг, который проектируется на плоскость y=x уравнением X2+z2=R2, где
Такие манипуляции необходимы, чтобы параметризовать круг
Параметрическое уравнение круга:
x=R*cos(t), z=R*sin(t) и t[0;Pi/2] (I октант).
Тогда переменные выражаются зависимостью
Вычисляем производные
затем находим дифференциал дуги:
Подставляем все в интеграл и выполняем вычисление
Как Вы могли убедиться, ничего сложного в нахождении криволинейных интегралов первого рода нет. В теории известны формулы как переходить от криволинейных к определенным интегралам, ими и воспользовались. Сами же интегралы не сложны, да и кривые на практике подбираются таким образом, чтобы Вы с ними долго не возились на практических занятиях.
Все сводится к умению интегрировать, что в свою очередь требует знания таблицы основных интегралов.
3. Криволинейные интегралы
И чтобы у вас сразу отлегло от сердца: криволинейные интегралы – это всего лишь однократные интегралы. Они похожи на «обычные» определённые интегралы.
Уже из самого названия нетрудно догадаться, что путём интегрирования криволинейных интегралов являются кривые линии (в общем случае).
Итак, паркет вашей комнаты – это координатная плоскость , в углу стоИт
эльф ось , а сверху «зависло» расправленное одеяло, заданное функцией
.
Возьмите в руки мел и начертите на полу под одеялом произвольную кривую . Как вариант, у неё могут быть углы – такая линия называется кусочно-гладкой. Можно изобразить даже ломаную. ВажнА спрямляемость и непрерывность пути интегрирования. Теперь суть:
Представьте, что от одеяла осталась всего лишь нитка, лежащая над кривой . Вертикальная поверхность, расположенная между кривой «эль» на полу и этой «ниткой» представляет собой фрагмент криволинейного цилиндра. …Получилась такая стоячая изогнутая ширма. …Представили? Отлично!
3.1. Криволинейный интеграл первого рода
имеет вид и по модулю* равен площади
данной «ширмы» (фрагмента криволинейного цилиндра).
* Если график целиком или бОльшей частью расположен ниже плоскости
, то площадь получится со знаком «минус».
В частности, если подынтегральная функция задаёт плоскость , то криволинейный интеграл равен площади «ленты» единичной высоты, а также и длине самой линии интегрирования:
.
…Чего только не придумаешь, чтобы не делать чертежей 
Значок называют дифференциалом дуги кривой
. Во многих источниках его обозначают через
, но, на мой взгляд, это не слишком удачный выбор.
Если на плоскости вместо кривой начертить отрезок прямой, то получится не что иное, как плоская криволинейная трапеция, параллельная оси
. Соответствующий интеграл хоть и каламбурно, но с полным правом можно назвать «прямолинейным», и это двоюродный брат определённого интеграла.


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Содержание:
- Криволинейный интеграл
- Вычисление криволинеиного интеграла
- Криволинейный интеграл второго рода
Криволинейный интеграл
Используя понятие длины кривой, а также формулы для ее вычисления при различных способах задания кривой, можно ввести понятие интеграла вдоль спрямляемой (в частности, гладкой или кусочно гладкой) кривой так же, как вдоль прямолинейного отрезка.
Пусть на плоскости 



в точках которой задана действительная функция 








Отметим, что подобное разбиение можно построить и в случае замкнутой кривой, если за точку 




По этой ссылке вы найдёте полный курс лекций по высшей математике:
Составим сумму вида

которую называют интегральной суммой функции 

Пусть существует предел 










Такой предел называют криволинейным интегралом первого рода (иногда — первого типа) вдоль кривой (или дуги) 

Итак,

Отметим, что в определении криволинейного интеграла первого рода направление обхода кривой не играет никакой роли, так как от выбора направления не зависит интегральная сумма.
Пусть, например, кривая 





Аналогично можно ввести понятие интеграла вдоль пространственной кривой. Пусть на пространственной кривой 


Как и в плоском случае, проведем разбиение 






Составив интегральную сумму и перейдя к пределу при 

где 


Возможно вам будут полезны данные страницы:
Вычисление криволинеиного интеграла
Если плоская кривая 






где 




Выберем разбиение 











Правая часть равенства есть интегральная сумма, соответствующая определенному интегралу 

Поэтому
причем существование одного из интегралов в этом равенстве означает существование и другого. Выявленная связь позволяет получить условия существования криволинейного интеграла первого рода.
Если кривая 







Теорема 5.1. Если кривая 




Итак, криволинейный интеграл первого рода можно свести к определенному интегралу с помощью формулы (5.6). Однако эта формула с практической точки зрения не очень удобна, поскольку в качестве параметра кривой далеко не всегда (а точнее, редко) выбирают натуральный параметр.
Пусть кривая 
где функции 










При этом значение 






Таким образом, для вычисления криволинейного интеграла первого рода следует заменить в подынтегральной функции переменные 






Если плоская кривая 



Аналогично при задании кривой функцией в виде 

Пусть кривая 



находим
Примеры с решением
Пример 1.
Вычислим криволинейный интеграл первого рода 



и в соответствии с (5.10)
Пример 2.
Найдем криволинейный интеграл первого рода 

В соответствии с (5.8) имеем
Кроме того, 

Пример 3.
Вычислим криволинейный интеграл первого рода от функции 


Для вычисления интеграла необходимо кривую задать параметрическими уравнениями. Астроиду можно описать следующим образом:
Находим 



т.е. астроида является кусочно гладкой кривой.
Переходя от криволинейного интеграла к определенному, получаем




Пример 4.
Найдем криволинейный интеграл первого рода от функции 




Пример 5.
Пусть 


Так как 
Учитывая, что в данном случае 

Условия существования криволинейного интеграла переносятся и на пространственный случай. Если пространственная кривая 
где функции 






Пример 6.
Вычислим криволинейный интеграл первого рода 


Предварительно находим

Далее в соответствии с формулой (5.13) получаем

В заключение отметим следующее. Так как криволинейный интеграл первого рода, согласно формуле (5.6), фактически есть определенный интеграл, на него переносятся основные свойства определенного интеграла: линейность, аддитивность, оценка интеграла по модулю (модуль интеграла не превосходит интеграла от модуля функции), теорема о среднем. Последняя позволяет ввести понятие среднего значения функции 




Криволинейный интеграл второго рода
Пусть на плоскости 















вдоль кривой 






Если существуют пределы 







Итак, по определению

В приложениях часто встречается сумма интегралов (5.27) и (5.28) от двух функций 

К криволинейному интегралу второго рода приводит задача вычисления работы силы при перемещении материальной точки по криволинейному пути.
Действительно, предел в правой части формулы (5.25) можно представить в виде суммы двух пределов, каждый из которых есть криволинейный интеграл второго рода по соответствующему переменному.
Следовательно, вместо (5.25) можем записать

где 



Отметим, что работу силы на криволинейном пути можно представить и криволинейным интегралом первого рода в виде (5.24). Это позволяет записать равенство
которое устанавливает связь между криволинеиными интегралами двух видов.
Криволинейные интегралы первого и второго рода имеют много общего. Однако у них есть и существенное различие: если первый из этих интегралов не зависит от выбора направления обхода кривой (от выбора ориентации этой кривой), то второй при изменении направления обхода на противоположное меняет знак. Это связано с тем, что в интегральной сумме интеграла первого рода значения функции 







причем из существования интегралов в правых частях этих равенств вытекает существование интегралов в левых частях, и наоборот..
Понятие криволинейного интеграла второго рода можно перенести на случай пространственной кривой. Если на кривой 




и рассмотреть их пределы при стремлении к нулю величины 





В приложениях часто встречается сумма этих интегралов, которую объединяют общим знаком интеграла:
Для пространственной кривой 
где 

являются координатными функциями в прямоугольной декартовой системе координат 





Криволинейный интеграл второго рода по замкнутому контуру 

В плоском случае для простейших контуров (окружность, эллипс) направление обхода часто сравнивают с движением часовой стрелки. При этом обход контура против хода часовой стрелки (или просто против часовой стрелки) называют положительным, а обход контура по ходу часовой стрелки (по часовой стрелке) — отрицательным (рис. 5.5, а).
В приложениях зачастую контур фигурирует как граница некоторой плоской области (в этом случае контур простой). Тогда обход контура можно соотнести с этой областью: при положительном обходе контура область все время остается слева, а при отрицательном — справа (рис. 5.5, б).
Однако описанные способы указания направления обхода контура приемлемы лишь в относительно простых ситуациях. В каком смысле следует понимать обход контура на рис. 5.6
против часовой стрелки? В таких непростых ситуациях направление обхода можно задать, выбрав на контуре три различные точки и указав, в каком порядке они проходятся. Для контурных интегралов, в которых направление обхода контура задано как положительное (против часовой стрелки),иногда используют специальное обозначение 


предполагается обход 

Пример 9.
Вычислим криволинейный интеграл второго рода

вдоль пространственной кривой 
В данном случае 

Пример 10.
Найдем криволинейный интеграл второго рода
вдоль параболы 


Лекции:
- Вычислить объем тела
- Метод наименьших квадратов
- Интеграл произведения
- Вычеты. Основная теорема о вычетах
- Оператор Гамильтона. Оператор Лапласа. Понятие о криволинейных координатах
- Свойства непрерывного отображения множеств
- Линейные дифференциальные уравнения
- Дифференцирование функций многих переменных
- Дифференцирование суммы, произведения и частного
- Система логарифмических уравнений