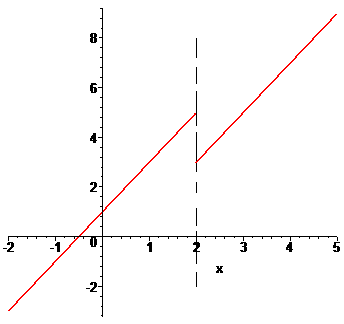
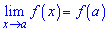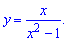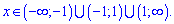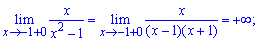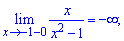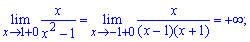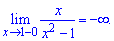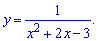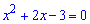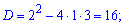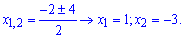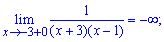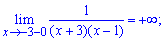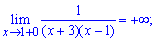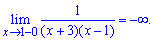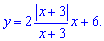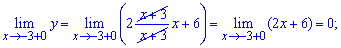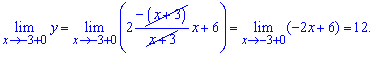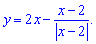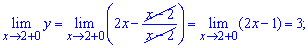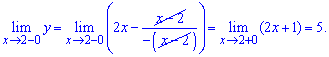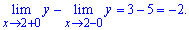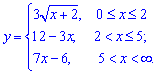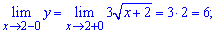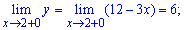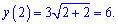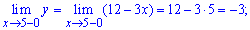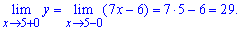(схема 31)
Точка x0 называется точкой максимума (минимума) функции y=f (x), если существует такая δ–окрестность точки x0, что для всех 
выполняется неравенство 
Точки максимума и минимума функции называются
точками экстремума (рис. 3.5).
Теорема 3.15 (необходимое условие существования точек экстремума функции одной переменной). Если дифференцируемая
функция y=f (x) имеет
экстремум в точке x0,
то её производная в этой точке равна
нулю или не существует
Точки, в которых производная функции
либо равна нулю, либо не
существует, называют критическими точками 1-го рода.
Критические точки, в которых производная функции равна
нулю, называются точками стационарности.
Функция y=f (x) называется возрастающей
на некотором интервале (a;b), если на этом интервале большему значению
аргумента x соответствует большее
значение переменной y, и убывающей, если большему
значению аргумента x соответствует меньшее значение
переменной y.
Для
дальнейшего исследования критические точки помещают на числовую ось, которая
делится этими точками на интервалы, после чего
поверяют выполнение следующих достаточных условий.
Теорема 3.16 (достаточное условие возрастания и убывания
функции одной переменной). Если
на некотором интервале (a;b) функция y=f (x) дифференцируема и при этом ее производная 
интервале возрастает (убывает)
Теорема 3.17 (достаточное условие существования точек экстремума функции ). Если функция y=f (x) непрерывна и
дифференцируема в некоторой δ –окрестности критической точки x0 и при переходе через нее
производная 
с минуса на плюс, то точка x0 является точкой минимума функции
Те критические
точки функции, для которых достаточное условие не выполняется, остаются просто
критическими точками 1-го рода.
Критические точки 1-го рода, в которых
производная не существует, делятся на классы:
– точки, в которых функция непрерывна, но при выполнении теоремы 3.17 имеет в этих точках «острый» экстремум (угловые
точки или точки излома) (рис. 3.6);
– точки, в которых функция непрерывна, но касательная в них к графику
функции параллельна оси 0y (угловой коэффициент такой касательной


– точки, в которых функция терпит разрыв (всегда переходят в класс
критических точек 2-го рода).
Но проведенное таким образом исследование, не дает ответ на очень важный
вопрос: как возрастает (убывает) функция – выпукло или вогнуто? Ответ на
поставленный вопрос дает дальнейшее рассмотрение функции с помощью второй
производной. Дадим ряд необходимых определений.
Функция называется выпуклой (выпуклой вверх) на некотором интервале (a;b), если касательная, проведенная к графику
функции в каждой точке этого интервала, лежит выше графика функции.
Функция называется вогнутой (выпуклой вниз) на некотором интервале (a;b), если касательная, проведенная к графику функции в каждой точке этого интервала, лежит
ниже графика функции.
Точки, отделяющие участки выпуклости от участков вогнутости функции,
называются ее точками перегиба (см. рис. 3.5).
Теорема 3.18 (необходимое
условие существования точек перегиба функции). Если дважды дифференцируемая функция y=f (x) имеет перегиб в точке x0,
то в этой точке вторая производная
равна нулю или не существует
Точки, в которых вторая производная функции либо равна нулю, либо не
существует, называют критическими точками 2-го рода.
Для дальнейшего исследования критические точки 2-го
рода помещают на числовую ось, которая делится этими точками на интервалы,
после чего поверяют выполнение следующих
достаточных условий.
Теорема 3.19 (достаточное
условие выпуклости и вогнутости
функции). Если на некотором интервале (a;b) функция y=f(x) дважды
дифференцируема и при этом ее вторая производная 
(выпукла)
Примечание. Очевидно,
что на интервале выпуклости функция имеет точку максимума, а на интервале
вогнутости – точку минимума (см. рис. 3.5).
Теорема 3.20 (достаточное условие существования точек
перегиба функции). Если функция y=f(x) непрерывна и дважды дифференцируема в некоторой окрестности критической
точки 2-го рода и при переходе через нее
вторая производная меняет знак, то данная точка
является точкой перегиба функции
Те критические точки функции, для которых достаточное условие 3.19 не
выполняется, остаются просто критическими точками 2-го рода. Критические точки
2-го рода, в которых вторая производная не существует, делятся на классы:
– точки,
в которых функция непрерывна и при выполнении теоремы 3.20 имеет в этих точках
«острый» перегиб, – в них можно провести
к графику функции бесконечное множество касательных (рис.
3.7);
– угловые точки (переходят из критических точек первого рода);
– точки, в которых функция терпит разрыв (в точках разрыва 2-го рода график функции имеет вертикальную асимптоту).
Для окончательного перечисления точек экстремума и перегиба функции
необходимо найти их ординаты, после чего выписать указанные точки двумя
координатами.
Для завершения исследования функции и построения графика необходимо
проверить наличие у нее асимптот. Напомним,
что асимптотой кривой называется прямая, расстояние до
которой от точки, лежащей на кривой, стремится к нулю при неограниченном
удалении от начала координат точки по кривой (рис. 3.8).
Асимптоты могут быть вертикальными, наклонными,
горизонтальными.
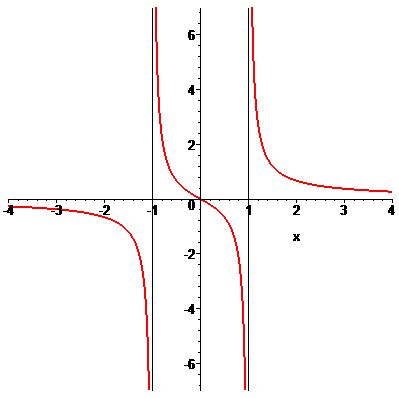
Говорят, что прямая x=a является вертикальной асимптотой графика

Например, кривая 
асимптоту x=-1, так как 
Уравнение наклонной асимптоты ищем в виде
y=kx+b (рис. 3.8).
Коэффициенты
k и b находятся
по формулам:

и 
Верно и
обратное: если существуют конечные пределы (3.41) и (3.42), то прямая y=kx+b является
наклонной асимптотой.
Если хотя бы
один из пределов (3.41) или (3.42) не существует или равен бесконечности, то
кривая y=f (x) наклонной
асимптоты не имеет.
В частности,
если k=0, то . Поэтому y=b
– уравнение горизонтальной асимптоты.
Примечание. Асимптоты графика функции y=f (x) при ∆x→+∞ и ∆x→–∞ могут быть разными. Поэтому при нахождении
пределов (3.41) и (3.42) следует отдельно рассматривать случай, когда ∆x→+∞ и когда ∆x→–∞.
Пример 3.16.
Исследовать методами дифференциального
исчисления и построить график функции 
Решение.
1. Область
определения: 
2. Исследуем функцию на непрерывность и классифицируем
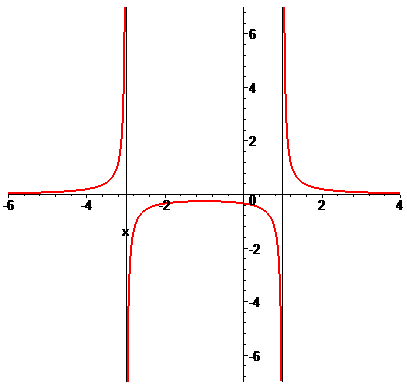
ее точки разрыва. Заданная функция непрерывна всюду, кроме точки x=4. Вычислим
односторонние пределы в этой точке:

Таким образом, точка x=4 является для заданной функции точкой разрыва второго
рода, а прямая x=4 – вертикальной асимптотой графика.
3. Проведем исследование функции методами
дифференциального вычисления. Для исследования на экстремум и промежутки
монотонности вычислим первую производную:
первого рода, в которых производная равна нулю или не существует

Результаты исследования заданной функции с помощью
первой производной занесем в таблицу 3.1,
основываясь на теоремах 3.16, 3.17.
Таблица 3.1
Исследование
функции с помощью первой производной

точка минимума функции.
4. Исследуем функцию на выпуклость, вогнутость и точки
перегиба с помощью второй производной, основываясь на теоремах 3.23, 3.24:

Так как 
Остается выяснить вопрос об интервалах его выпуклости и вогнутости. Результаты
исследования занесем в следующую таблицу 3.2.
Таблица 3.2
Исследование
функции с помощью второй производной
5. Исследуем график
функции на наличие наклонных и горизонтальных асимптот, уравнение которых как
прямых линий y=kx+b.
Согласно (3.41) 

Согласно (3.42) 
Таким образом, прямая y=x+4 –
наклонная асимптота графика.
Очевидно, график заданной функции пересекает ось 0y в точке (0; –5) и, на основе обобщения
результатов всех предыдущих исследований, имеет вид, представленный на рисунке 3.9
Содержание:
- Схема исследования функции и построение ее графика
- Условия возрастания и убывания функции.
- Экстремумы функции
- Наибольшее и наименьшее значения функции
- Условия выпуклости. Точки перегиба
Схема исследования функции и построение ее графика
График заданной функции можно строить по произвольно взятым точкам. При таком способе можно не обнаружить всех особенностей ее графика.
Проведя предварительно исследования, мы ищем характерные для данного графика точки и тем упрощаем решение задачи о построении графика.
При исследовании функции и построении ее графика целесообразно придерживаться следующей схемы:
Первый этап (использование вида заданной функции).
1) Находим область определения функции, точки разрыва.
2) Исследуем функцию на четность или нечетность, периодичность.
3) Находим асимптоты графика функции.
4) Находим точки пересечения графика функции с осями координат.
Второй этап (использование производной первого порядка).
5) Находим критические точки первого рода, интервалы возрастания и убывания, точки экстремумов и экстремальные значения функции.
Третий этап (использование производной второго порядка).
6) Находим критические точки второго рода, интервалы выпуклости и вогнутости, точки перегиба и значения функции в этих точках.
Четвертый этап. Составим таблицу результатов исследования.
Наносим полученные точки, асимптоты на координатную плоскость и строим график функции с учетом точек разрыва, интервалов возрастания и убывания функций, промежутков выпуклости и вогнутости графика функций.
Пример 1. Исследовать функцию y = x3 – 3x2 и построить ее график.
Решение.
1) Область определения функции: вся числовая ось 
2) Функция ни четная ни нечетная, поскольку y (-x) = -x3 — 3x2, поэтому y (-x) ≠ y (x) ≠ — y (x).
Функции не периодическая.
3) Вертикальных асимптот график не имеет, потому что нет точек разрыва.
Исследуем, имеет ли график наклонные асимптоты y = kx + b:
Наклонных асимптот график также не имеет.
4) Найдем точки пересечения графика функции с осями координат: при x = 0, y = 0; то есть точка O (0; 0);
при y = 0: x3 — 3x2 = 0⇒ x2 (x – 3) = 0⇒ x = 0 и x = 3, то есть точка M (3; 0).
Второй этап.
5) Находим производную первого порядка:
y ‘= 3x2 – 6 x = 3x (x – 2).
Находим критические точки первого рода:
3x (x – 2) = 0, x1 = 0, x2 = 2.
Критические точки разбивают область определения на промежутки (-∞, 0) ∪ (0,2) ∪ (2, ∞) (рис. 19).

Рис. 19. Рис. 20.
Находим знаки производной в этих промежутках:
y’ (3) = 3⋅ 3 (3 – 2) = 9 > 0,
y’ (1) = 3 ⋅ 1 (1 – 2) = –3 < 0,
y’ (1) = 3 (–1) (–1 – 2) = 9 > 0.
Следовательно, функция возрастает на промежутках (–∞; 0) ∪ (2; ∞), убывает на
промежутке (0; 2).
В точке x = 0 функция имеет максимум, ymax = y (0) = 0.
В точке x = 2 функция имеет минимум,
Третий этап.
6) Находим производную второго порядка:
y»= 6 x – 6 = 6 (x – 1). Находим критические точки второго рода: 6 (x — 1) = 0, x = 1 . Критическая точка x = 1 разбивает область определения на промежутки: (-∞, 1) ∪ (1, ∞) (рис. 20). Находим знаки второй производной в этих промежутках:
y» (0) = 6 (0 – 1) = –6 < 0,
y» (2) = 6 (2 – 1) = 6 > 0.
Следовательно, график функции выпуклый на промежутке (-∞, 1), вогнутый на промежутке (1; ∞). Точка x = 1 является точкой перегиба,
7) Составим таблицу, где занесем все результаты исследования.
Найдем еще дополнительно
y (-1) = (-1) 3 – 3 ⋅ (–1) 2 = 4.
Наносим все характерные точки на координатную плоскость и строим график (рис.21).
Рис. 21.
Пример 2. Исследовать функцию
Решение.
Первый этап.
1) Область определения функции (

2) Функция ни четная, ни нечетная, поскольку

Функция непериодическая.
3) Поскольку в точке разрыва x = 2,

то прямая x = 2 — вертикальная асимптота.
Исследуем, имеет ли график наклонные асимптоты y = kx + b:
Итак, y = 0 — горизонтальная асимптота.
4) Найдем точки пересечения графика функции с осями координат: при x = 0, 


Переходим ко второму этапу:
5) Найдем производную первого порядка:
Находим критические точки первого рода:
Учитывая точку x = 2, где производная не существует, разобьем область определения на промежутки (

Следовательно, функция возрастает на промежутке (2; 4), убывает на промежутках (



Рис. 22. Рис. 23
Переходим к третьему этапу:
6) Находим вторую производную:
Найдем критические точки второго рода:

Учитывая точку x = 2, где y» не существует, разбиваем область определения на промежутки: (

Установим знаки второй производной в этих промежутках:
Следовательно, график функции выпуклый на промежутках: (

Имеем точку
Строим график (рис. 24).
Рис. 24.
Условия возрастания и убывания функции.
1) Для того чтобы дифференцируемая на интервале 





2) Для того чтобы дифференцируемая на интервале 





3) Аналогично, достаточным условием строгого убывания дифференцируемой функции 



необходимым и достаточным условием убывания — условие


По этой ссылке вы найдёте полный курс лекций по высшей математике:
Экстремумы функции
1) Точка 



Если для всех 


то точка 

Аналогично, если в некоторой окрестности точки 

то точка 



то точка 
Для краткости слово “локальный” часто опускают и пишут просто “точка минимума” или “точка строгого максимума”.
Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках — ее экстремумами.
2) Необходимые условия экстремума. Если точка 



Эти условия не являются достаточными.
Точки, в которых функция определена, а производная функции равна нулю или не существует, называют критическими точками функции. Экстремумы функции следует искать среди ее критических точек.
3) Достаточные условия строгого экстремума (с использованием первой производной). Пусть функция 








При выполнении условий (1) принято говорить, что производная функции при переходе через точку 
Если же



т. е. если производная при переходе через точку 

4) Условия строгого экстремума (с использованием производных высших порядков). Пусть функция 



то при четном 





В частности, если


то в точке 


Возможно вам будут полезны данные страницы:
Наибольшее и наименьшее значения функции
функции, непрерывной на отрезке, существуют на этом отрезке точка, в которой функция принимает наибольшее значение, и точка, в которой функция принимает наименьшее значение (теорема Вейерштрасса).
Пусть функция 





Аналогично, если функция 



Условия выпуклости. Точки перегиба
1) Функция 






Геометрический смысл выпуклости вниз функции 

Если при тех же условиях относительно 
то функция 
В том случае, когда при 




Например, функция 
Всякий интервал, на котором функция (строго) выпукла вниз, называется интервалом (строгой) выпуклости вниз этой функции; интервал, на котором функция (строго) выпукла вверх — интервалом (строгой) выпуклости вверх этой функции.
Интервалы выпуклости вверх и интервалы выпуклости вниз называют интервалами выпуклости.
2) Условия выпуклости функции. Для того чтобы функция 



Условие
является достаточным условием строгой выпуклости вниз функции
на интервале
.
Условие (7) не является необходимым для строгой выпуклости. В самом деле, функция 


Аналогично, для функции 

а достаточным условием строгой выпуклости вверх — условие
Пусть функция 





на одном из которых 


3) Пусть функция 








Если 


На рис. 20.2 и рис. 20.3 представлены график функции 




Функция (рис. 20.4)
при переходе через точку 






не меняется (это так называемая точка возврата). При переходе через точку 
меняет направление выпуклости, но точка 
4) Необходимые условия существования точки перегиба. Если точка 



Эти условия не являются достаточными. В самом деле, для функции 

вторая производная в точке 



Точки перегиба функции следует искать среди критических точек ее первой производной.
5) Достаточные условия существования точки перегиба (с использованием второй производной). Пусть функция 









либо



В этом случае принято говорить, что при переходе через точку 
6) Условия существования точки перегиба (с использованием производных высших порядков). Пусть функция 


тогда если 



В частности, если
то 

Примеры с решением
Пример 1.
Найти интервалы возрастания и убывания функции:
1) 
3)
1) Данная функция всюду дифференцируема, причем
Так как 







2) Функция дифференцируема на всей числовой прямой, причем
Так как 



3) Данная функция является четной, поэтому достаточно найти интервалы монотонности при 

получаем



откуда



Таким образом, на интервалах 










Следует обратить внимание на то, что данная функция не является монотонной ни в какой окрестности точки 
Пример 2.
Найти точки экстремума функции 
Функция имеет производную при всех 
Следовательно, у функции может быть только один экстремум в точке 





Пример 3.
Найти экстремумы функции
Так как
то критические точки функции — 




Тот же результат можно получить, используя вторую производную. Так как 




Вычислив значения функций в точках 



Пример 4.
Исследовать на экстремум функцию:
1)
2)
3)
1) Функция определена и дифференцируема при всех 

и находим критические точки: 



переходе через точку 




2) Функция определена и непрерывна при всех 
В точках 












3) Функция дифференцируема при всех 





Поскольку 

Таким образом, первой не равной нулю оказалась производная четного порядка. Следовательно, в точке 


Пример 5.
Исследовать на экстремум функцию 
Функции 


при 



то
Производная 












В некоторой правой окрестности точки 







Лекции:
- Внесение под знак дифференциала: подведение
- Свойства логарифмов
- Линейные дифференциальные уравнения первого порядка
- Скрещивающиеся прямые
- Скалярное призведение двух векторов
- Уравнения касательной и нормали
- Наименьшее значение функции
- Найти угол между прямыми: примеры решения
- Объем шара и его частей
- Производная тангенса
С
учетом изложенного в настоящей главе
можно рекомендовать следующую схему
исследования функции в
построения
ее графика:
1)найти
область определения функции;
2)
исследовать функцию на четность и
нечетность;
3)
исследовать функцию на периодичность;
4)
исследовать функцию на непрерывность,
найти точки разрыва;
5) найти
критические точки первого рода;
6)
найти интервалы монотонности и
экстремумы
функции;
7) найти
критические точки второго рода;

интервалы выпуклости и точки перегиба;
9) найти
асимптоты графика функции;
10)
найти точки пересечения графика функции
с осями координат (если это возможно);
11)
построить график функции.
Пример
1. Построить график функции
.
Решение.
1) Данная функция определена на всей
числовой оси, кроме точек х
=
-2 и х
=
2.
-
Функция
нечетна, так как
.
3) Функция
непериодическая.
4)
Функция непрерывна во всей области ее
определения.
Точки х
= -2
и х
=
2 являются точками разрыва.
5) Находим
.
Очевидно,
что f‘(x)
= O
при
x
= 0 и x=±2.
Крометого,
f‘(x)
не
существует при х
=
±2. Следовательно,
f(x)
имеет следующие критические точки
первого рода:
.
6)
Методом пробных точек определяем знак
про_из« водной в каждом из интервалов:
,
(рис.
15).
Следовательно,
функция f
(x)
в интервалах
-возрастает,а в интервалах
—
убывает.
В точке
функция
имеет максимум, а в точке-минимум.
Так как при переходе
Рис
15
через
критическую точку х3
= 0 производная
не
меняет знак, то в этой
точке
экстремума нет. Имеем:
и
7)
Находим
Так
как f
» (х) = 0
при х
= 0
и f
«(x)
не существует при x
= ±2, то х2
=
-2, х3
= 0 и x4
= 2 являются критическими точками
второго рода.

Определяем знак второй производной
f«(x)
в
каждом из интервалов ]-;
-2[, ]-2; 0[, ]0; 2[ и ]2; +[ (рис. 16).
Рис. 16
Мы
видим, что в интервалах ]-
;
-2[ и ]0; 2[ график функции обращен
выпуклостью вверх, а в интервалах]-2;
0[ и ]2; +[—
выпуклостью вниз. Вторая производная
меняет свой знак в каждой из критических
точек второго рода, однако точких=2
не принадлежат области определения
функций и
поэтому
лишь точка х
= 0
является точкой перегиба. Имеем f(0)
= 0, следовательно, точкой перегиба
является начало координат.
9) Так
как
и
то
х
=
-2 и x
= 2 являются вертикальными асимптотами.
Далее, находим:
Следовательно,
у
= х является
наклонной асимптотой
Результаты
исследования заносим в таблицу 4.
Таблица 4
По
полученным
данным строим график функции (рис. 17).
Рис
17
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Функция f(x) называется непрерывной в точке х = а если:
1) она определена в этой точке;
2) существует предел функции в этой точке
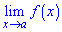
3) значение предела равно значению функции в точке х = а, т.е.
Если одно из условий нарушается то функция называется разрывной в точке х = а, а сама точка х = а называется точкой разрыва. Все элементарные функции являются непрерывными на интервалах определенности.
Классификация точек разрыва
Точка х0 называется точкой разрыва первого рода функции у = f(x) если существуют конечные односторонние пределы справа
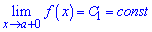
и слева
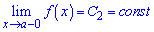
Если, кроме этого, выполняется хотя бы одно из условий
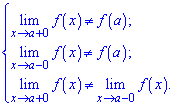
то функция в точке х = а имеет неустранимый разрыв первого рода.
Если пределы равны, однако функция не существует
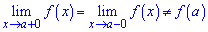
то имеем устранимый разрыв первого рода.
Точка х0 называется точкой разрыва второго рода функции у= f(x) если граница справа 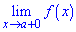
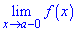
Скачком функции в точке разрыва х = х0 называется разность ее односторонних границ
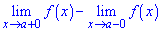
если они разные и не равны бесконечности.
При нахождении точек разрыва функции можно руководствоваться следующими правилами:
1) элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной на определенном интервале.
2) элементарная функция может иметь разрыв в точке где она не определена при условии, что она будет определена хотя бы с одной стороны от этой точки.
3) Неэлементарные функция может иметь разрывы как в точках где она определена, так и в тех где она определена.
Например, если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов, то на границе стыка может быть разрывной.
Рассмотрим несколько задач по данной теме.
Задача 1.
Найти точки разрыва функции
а)
Решение:
Функция определена во всех точках кроме тех где знаменатель обращается в нуль x = 1, x = 1. Область определения функции следующая
Найдем односторонние пределы в точках разрыва
При нахождении односторонних границ подобного вида достаточно убедиться в знаке функции и в том, что знаменатель стремится к нулю. В результате получим границу равную бесконечности или минус бесконечности.
Поскольку в точках x = 1, x = -1 функция имеет бесконечные односторонние пределы, то аргументы 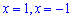
——————————————————-
б)
Решение:
Задача достаточно простая. В первую очередь находим нули знаменателя
Таким образом функция определена на всей действительной оси за исключением точек 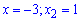
Пределы бесконечны поэтому, по определению, имеем точки разрыва 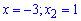
Из графиков приведенных функций видим что для ряда из них отыскания точек разрыва сводится до нахождения вертикальных асимптот. Но бывают функции которые и без вертикальных асимптот имеют разрывы первого или второго рода.
——————————————————-
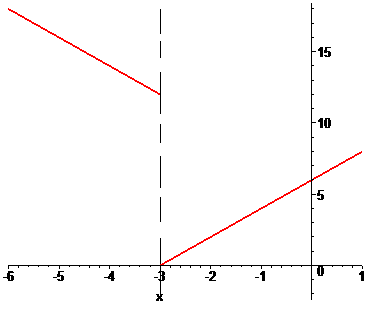
в)
Решение:
Заданная функция непрерывна на всей числовой оси кроме точки x = -3. Вычислим односторонние границы в этой точке
Они различаются по значениям, однако есть конечными. Итак точка x = -3 является неустранимой точкой разрыва І рода.
——————————————————-
Задача 2.
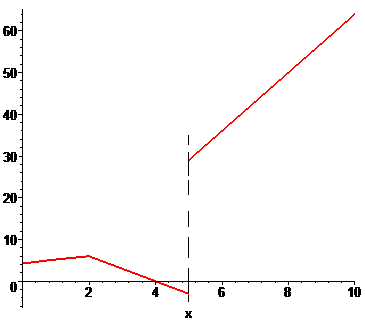
Найти точки разрыва функции если они существуют. Вычислить скачок функции в точке разрыва. Построить график функции.
а)
Решение:
Для заданной функции точка x = 2 является точкой разрыва. Найдем предел функции , чтобы определить характер разрыва
По определению, точка x = 2 является неустранимой точкой разрыва первого рода. Вычислим скачок функции при x=2
График функции на интервале который нас интересует приведен далее
——————————————————-
б)
Решение:
Неэлементарная функция y (x) определена для всех положительных значений аргумента. Точки которые разбивают функцию на интервалы могут быть разрывами. Для проверки найдем соответствующие пределы
Поскольку предел функции в точке x = 2 равен значению функции в этой точке то функция — непрерывная.
Отсюда также следует, что для непрерывной функции скачок равен 6-6 = 0.
Исследуем на непрерывность вторую точку
По определению функция в точке x = 2 имеет неустранимый разрыв І рода.
Прыжок функции равен 29 — (- 3) = 31.
По условию задания построим график функции.
Из приведенного материала Вы должны научиться находить разрывы первого и второго рода, а также различать их. Для этого подобрано немного примеров, которые в полной мере раскрывают все важные вопросы темы. Все остальное сводится к нахождению простых односторонних пределов и не должно быть для Вас сложным.
Инфоурок
›
Математика
›Презентации›Презентация по математике «Критические точки первого рода»
Презентация по математике «Критические точки первого рода»
Скачать материал

Скачать материал


- Сейчас обучается 28 человек из 10 регионов


- Сейчас обучается 27 человек из 13 регионов


- Сейчас обучается 42 человека из 30 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Критические точки I рода. Автор: Подкорытова Дарья
-
2 слайд
Теорема Если функция у=f(х) имеет в точке хо локальный экстремум и дифференцируема в этой точке, то f`(хо)=0. Такие точки называются критическими точками I рода.
Краткое описание документа:
Современный математический анализ является основной областью математики, вобравшей в себя дифференциальные уравнения, интегральные уравнения, дифференциальную геометрию, теорию функции комплексного переменного и многое другое. Математический анализ в настоящее время является незаменимым инструментом исследования в самых различных областях науки и техники. Знание дифференциального и интегрального исчисления необходимы каждому, оно способствует формированию современного научного мышления и является условием дальнейшего прогресса науки и техники.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 833 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 18.11.2014
- 1111
- 0
- 18.11.2014
- 1318
- 0
- 18.11.2014
- 591
- 0
- 18.11.2014
- 442
- 0
- 18.11.2014
- 1857
- 0
- 18.11.2014
- 772
- 0
- 18.11.2014
- 913
- 0
-
Настоящий материал опубликован пользователем Вуйлова Марина Анатольевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 12955
-
Всего материалов:
10