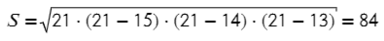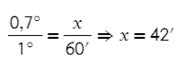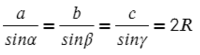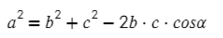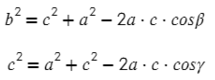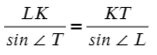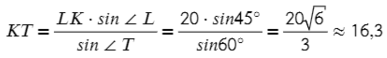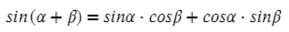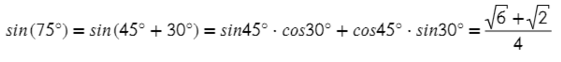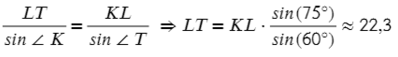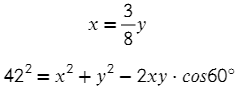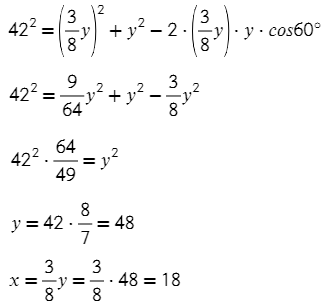Как найти косинус угла в равностороннем треугольнике

Теорема косинусов и синусов

О чем эта статья:

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

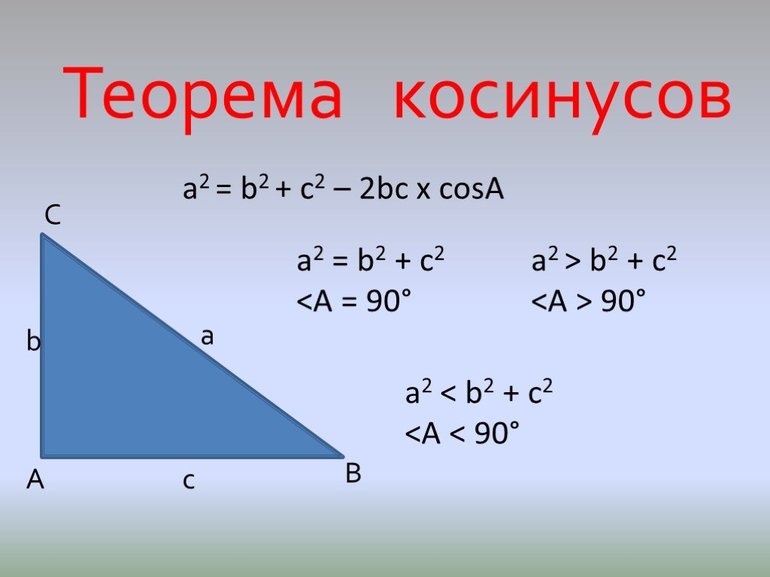
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
• Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
• Когда b 2 + c 2 — a 2

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h 2 = b 2 — (b × cos α) 2
• h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

• b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2

• a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b 2 = a 2 + c 2 — 2ac × cos β;
• c 2 = a 2 + b 2 — 2ab × cos γ.

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

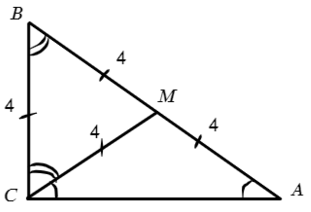
Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.

• Если c 2 2 + b 2 , то ∠C — острый.

Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.

Формула косинуса:

• a² = b² + c² – 2b.c.cosα
• b² = a² + c² – 2a.c.cosβ
• c² = a² + b² – 2a.b.cosγ

Например:

Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.

Решение по формуле a² = b² + c² – 2b.c.cosα:

b = 12 см

c = 8 см

cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)

a² = 12² + 8² – 2×12×8×(- 1/2)

a² = 144 + 64 – (–96)

a² = 304

a = √304

a ≈ 17,436

Длина третьей стороны — примерно 17,436 см.

Следствия

Следствие косинуса угла треугольника

При помощи теоремы косинусов можно найти косинус угла треугольника.

Формула:

Либо

Либо

Например:

сторона c = 6

сторона b = 7

сторона a = 8

Используйте теорему косинусов, чтобы найти угол β.

Решение:

Будем использовать эту версию формулы:

cos β = (6² + 8² − 7²) / 2×6×8

= (36 + 64 − 49) / 96

= 51 / 96

= 0,53125

= cos¯¹(0,53125)

≈ 57,9°

Следствие верхней части формулы cos α

Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):

• b²+c²−a²<0, значит угол α — тупой;
• b²+c²−a²=0, значит угол α — прямой;
• b²+c²−a²>0, значит угол α — острый.

Доказательство теоремы косинусов

Нужно доказать, что c² = a² + b² − 2a.b.cos C

1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a <=> CD = a.cos C.

2. Вычитаем это из стороны b, так мы получим DA:

DA = b − a.cosC

3. Мы знаем из определения синуса, что в том же треугольнике BCD:

sin C = BD/a <=> BD = a.sinC.

4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²

5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²

6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C

6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC

7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC

8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C

Q.E.D.

Теорема косинусов для равнобедренного треугольника

В равнобедренном треугольнике:

• две его стороны равны;
• углы при основании равны.

Рассмотрим пример:

Используем формулу теоремы косинусов

a² = b² + c² – 2b.c.cosα

Подставляем все известные:

x² = 8² + 8² – 2×8×8×cos140º

x² = 64 + 64 – 128 × (-0,766)

x² ≈ √226,048

x ≈ 15,035.

Теорема синусов

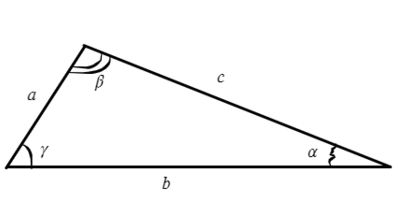
Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:

Узнайте также, что такое Теорема Пифагора и Теорема Менелая.

Площадь треугольников.

Свойства треугольников. 

Тригонометрия в прямоугольных треугольниках.

Что такое синус/косинус.

Таблицы Брадиса. Как пользоваться.

Теорема синусов и косинусов.

Геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах.

Г. Абель

С основными свойствами разобрались, теперь рассмотрим формулы и их приминение.

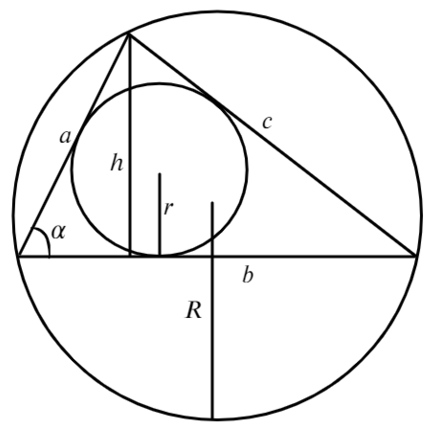
Площадь произвольного треугольника

Нет, это не кривая пентаграмма, нужны на этом рисунке только обозначения. Рассмотрим формулы школьной программы.

Высоту умножаем на ту сторону, на которую приходит высота:
В эту формулу подставляем угол между сторонами a и b:

Удобно использовать эту формулу, когда известны все стороны треугольника, p — полупериметр (половина суммы длин всех сторон):

Данная формула отлично помогает найти радиус вписанной окружности для любого треугольника, если известна площадь:

А эта формула помогает найти радиус описанной окружности для любого треугольника:

А зачем такое количество формул? К каждой задаче будут предоставлять разное дано, удобно знать и применять все формулы, чтобы максимально быстро решать задачи.

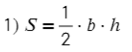
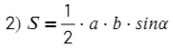
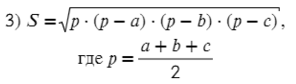
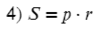
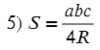
Полезные формулы для прямоугольного и равностороннего треугольника:

В данном случае получается, что один катет «b» — высота треугольника, а катет «а» — основание. 

Эту формулу можно вывести большим количеством способов, самый простой через формулу №2

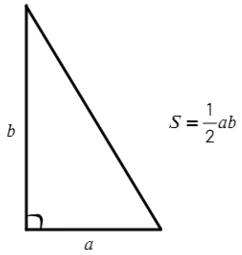
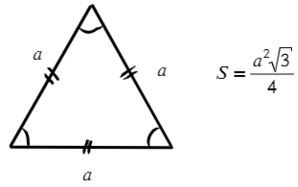
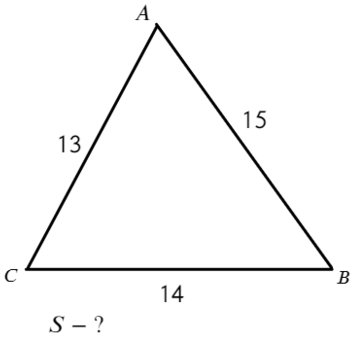
Задача №1. Дано на рисунке:

Оттолкнемся от вопроса: нужно найти площадь. Помимо 5 формул для произвольного треугольника, нам подойдет формула нахождения площади через полупроизведение катетов. 

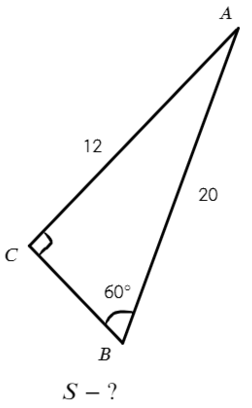
Вариантов здесь много (можно через т. Пифагора), но самый быстрый — найти ∠А = 180°− 90° − 60° = 30°, тогда площадь найдем по (2) формуле: S = ½absinα

Ответ: 60 

Задача №2. Дано на рисунке: 

Снова оттолкнемся от вопроса: нужно найти площадь. Дан обычный треугольник, значит, наш выбор ограничен первыми 5−ью формулами. В первой нужна высота, во второй угол, а в третьей полупериметр, но мы же знаем все стороны! Для начала найдем периметр и полупериметр:

Теперь можно подставить все числа в формулу площади:

Главное — правильно определиться с формулой. 

Ответ: 84

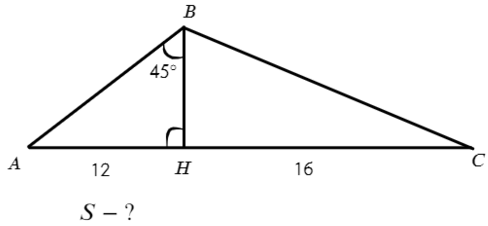
Задача №3. Дано на рисунке: 

В ΔABH: ∠A = 180°− 90° − 45° = 45°, значит, ∠A = ∠B => BH = AH = 12. 

Тогда площадь можно найти по формуле (1) S=½bh. Высота AH = 12, основание AC = 16+12 = 28. => S = ½×12×28 = 168

Ответ: 168.

Задача №4. Дано на рисунке: 

Оттолкнемся от отношения, которое нам дано. Мы знаем, что сумма данных углов равна 90°, если ∠ACM = х и ∠ВCM = 2х, тогда 2х+х = 90°

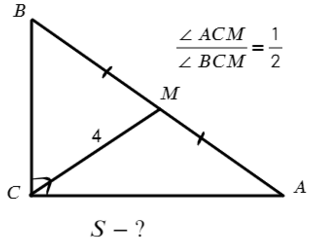
∠ACM = х = 30° => ∠ВCM = 60°. А что у нас равно 4-ем? Да, медиана! А медиана, проведенная из прямого угла, равна половине гипотенузы (2−ое свойство). Тогда отметим равные углы: 

В ΔBCM получается ∠ВCM = ∠СВM = 60°, тогда ∠СМВ = 60° и ΔBCM — правильный:

Площадь найдем по (2) формуле: S = ½absinα:

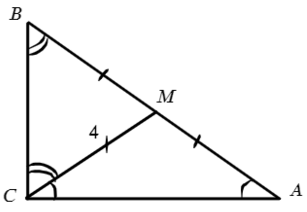
Ответ: 8√3

Задача №5. Дано на рисунке: 

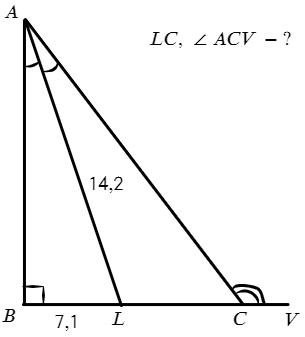
В дано есть только стороны, а найти нужно угол. Как это сделать? Вот стороны 14,2 и 7,1 во сколько раз отличаются? Да, в 2 раза, а значит угол ∠BAL = 30° (против угла в 30° лежит катет, который в два раза меньше гипотенузы). 

Значит, ∠A = 60° => ∠ACB = 180° − 90° − 60° = 30°, а ∠ACB — смежный с ∠ACV => ∠ACV = 180° − 30° = 150°. 

 Что касается LC: внимательно рассмотрим ΔALC, можно даже лупой воспользоваться. Что видишь? ∠LAC = ∠ACL = 30° => ΔALC — равнобедренный, LC = AL = 14,2. 

Ответ: 14,2 и 150°

Тригонометрия в прямоугольных треугольниках

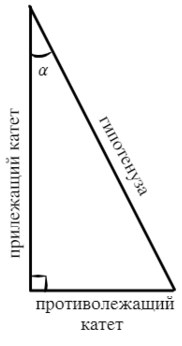
В прямоугольном треугольнике три стороны: 2 катета и гипотенуза.

Катеты меньшие стороны треугольника. Гипотенуза большая сторона, которая лежит напротив угла в 90°.

Относительно угла α:

Катет, который составляет угол, называют прилежащим. Катет, который находится напротив угла, называют противолежащим. Логично? Замечательно!

Тригонометрические функции (синус, косинус…) задают связь между углом и длинами сторон.

Но хорошо бы знать какие-то значения тригонометрических функций при определенных углах. Все значения вместе образуют таблицу Брадиса. С ее помощью можно вычислить почти любое значение тригонометрической функции при заданом угле. Но как с ней работать?

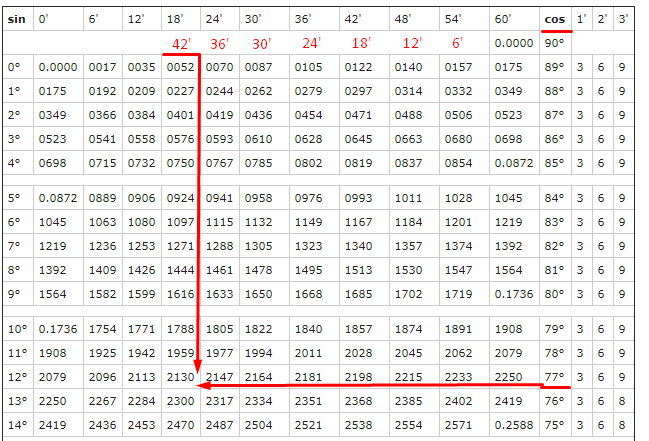
Найдем sin(10°). Для этого выберем столбец sin и в нем найдем 10°. Ближайшее значение — это то, что нам нужно — 0,1736.

А что за столбец 0′; 6′; 12′ и т.д. Это минуты! Не те, которых мы ждем в конце урока, а градусные минуты. 

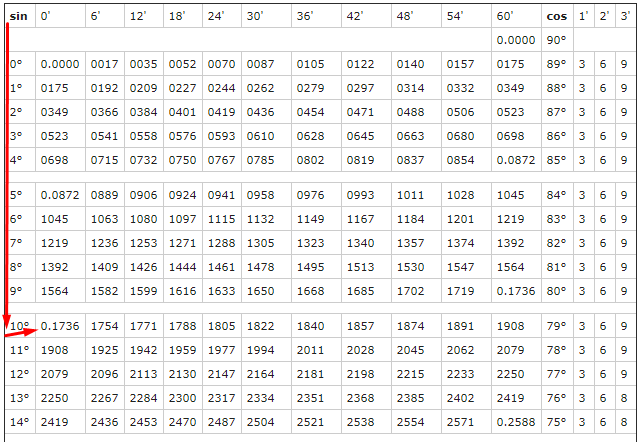
Из общего: и те, и другие минуты измеряются в промежутке от 0 до 60. 

Градусные минуты делят один градус на 60 минут (1°=60′), нужны они для большей точности задания угла.

p.s. Есть еще и градусные секунды, и в одной градусной минуте 60 градусных секунд, знакомо? 1° = 60′ = 3600».

Найдем cos(77,7°) 

Семь десятых градуса нужно перевести в минуты. Можно через пропорцию:

Теперь в таблице нужно найти 77°42′ для косинуса. Для синуса минуты прописаны, а для косинуса нет. Но мы же люди не гордые, сами напишем, но в обратном порядке. На пересечении 77° и 42′ получаем наше значение:

Но чтобы не загромождать таблицу 0, его в начале пишут только в первых строчках, поэтому ответ cos(77,7°) = 0,213.

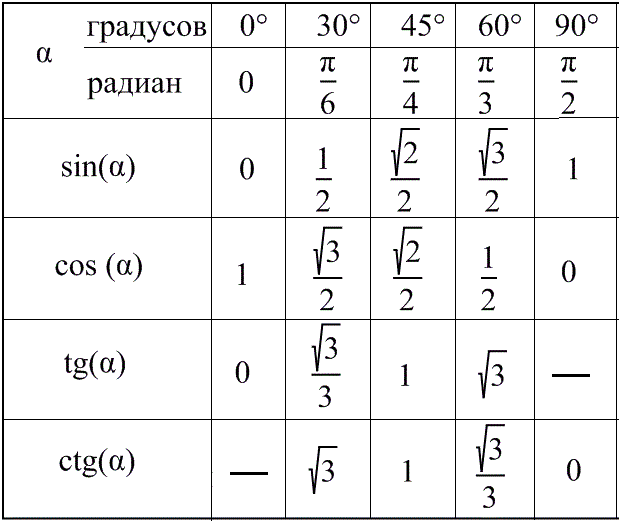
В задачах же таким обилием углов похвастаться нельзя, достаточно знать значения для 30°; 45°; 60°; 90°.

Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов — иногда, 

даже зная решение задачи, трудно понять, как можно было до него додуматься.

И.Д. Новиков

Задача №6. Дано на рисунке: 

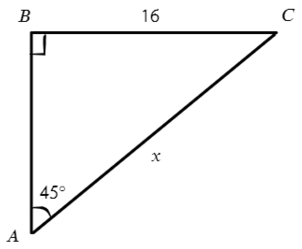
В этой задаче известен противолежащий катет относительно угла в 45°, а найти нужно гипотенузу. Смотрим, где у нас есть противполежащий катет и гипотенуза? Это синус! 

Смотрим в таблице, чему равен синус 45°, и подставляем в отношение:

Ответ: 16√2

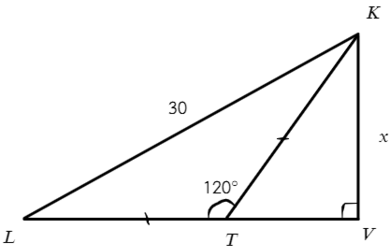
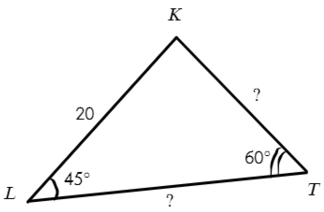
Задача №7. Дано на рисунке: 

Мы разобрались с тригонометрическими функциями в прямоугольных треугольниках, значит, и в этой задаче нужно перейти к прямоугольному треугольнику.

В ΔLTK — равнобедренный : ∠L = ∠LKT = (180° − 120°)/2 = 30°

Отлично, в прямоугольном ΔLVK: ∠L = 30° и известна гипотенуза, а нам нужно найти противолежащий катет, чем воспользуемся? Опять синусом!

Ответ: 15

Теорема синусов и теорема косинусов

Сразу возникает вопрос, а теорема тангенсов тоже есть? Конечно, есть, но она очень редко используется.

Для любого треугольника можно записать такое соотношение, это будет теорема синусов:

Запомни, что сторона относится к синусу противолежащего угла.

Следствие из теорма синусов гласит, что любое соотношение равно двум радиусам описанной окружности:

Для любого треугольника можно записать такое соотношение, это будет теорема косинусов:

А что будет, если α = 90°, а cos(90) = 0? Получится:

Теорема Пифагора, вот так просто можно запомнить теорему косинусов. Начать как теорему Пифагора, а затем вычесть удвоенное произведение на косинус угла между ними.

Можно записать и для других сторон в этом же треугольнике:

Задача №8. Дано на рисунке:

Запишем теорему синусов для двух отношений:

Выразим отсюда KT:

∠K = 180° − 60° − 45° = 75°. Чтобы найти синус угла 75°, советую посмотреть эту статью, нужно воспользовать формулой суммы синусов:

Тогда представим 75° в виде двух табличных значений:

Аналогично выразим LT:

Ответ: 16,3 и 22,3

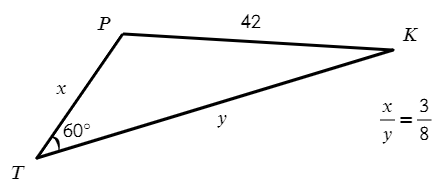
Задача №9. Дано на рисунке:

Найти нужно x и y. Запишем теорему косинусов для этого треугольника:

Икс выразим через игрек:

Ответ: 48; 18

Отлично, поздравляю тебя с Elementary по геометрии! 

Что нужно знать: 

1. Вертикальные, смежные, соответственные, накрест лежащие углы. 
2. Равенство и подобие треугольников. 
3. Что такое медиана, биссектриса, высота. 
4. Свойства треугольников. 
5. Площадь треугольников.
   
6. Синус/косинус в треугольнике.
7. Теорему синусов и косинусов.

Задачи для закрепления по треугольникам

Нашел опечатку, или что-то непонятно — напиши.

Группа с полезной информацией и легким математическим юмором.

Как найти косинус угла в равностороннем треугольнике?

Косинусом ( c o s ) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Теорема синусов. = 2 R , где R — радиус описанной около треугольника окружности.

Как найти косинус угла в равнобедренном треугольнике?

cosα= b/2a Одним из его катетов (b) будет половина длины основания равнобедренного треугольника, другим катетом (а) — высота равнобедренного треугольника.

Какие углы могут быть в равнобедренном треугольнике?

Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.

Какие углы равны в равнобедренном треугольнике?

Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектрисы, медианы и высоты, проведённые из этих углов. Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой.

Почему в равнобедренном треугольнике углы при основании равны?

В равнобедренном треугольнике углы при основании равны. Углы при основании в равнобедренном треугольнике — всегда острые. Сумма углов равнобедренного треугольника равна 180 градусам.

Каким свойством обладают углы равностороннего треугольника?

Биссектриса равнобедренного треугольника, проведенная к основанию, является его медианой и высотой. 2. Углы треугольника, лежащие против равных сторон, равны. … Все углы равностороннего треугольника равны.

Каким свойством обладает Медиана равнобедренного треугольника?

Свойства медиан равнобедренного треугольника В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой.

Чему равна биссектриса в равнобедренном треугольнике?

Свойство 1 В равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой. AB = BC, т.

Чему равна медиана в равнобедренном треугольнике?

Свойство 1 Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена. BD – медиана и высота, опущенная на основание AC, а также биссектриса угла ABC.

Как пересекаются высоты в равнобедренном треугольнике?

Так же как медианы и биссектрисы, треугольник имеет три высоты. Высоты треугольника пересекаются в одной точке.

Как найти площадь равнобедренного треугольника по двум сторонам?

Формула площади равнобедренного треугольника

1. Площадь равнобедренного треугольника можно найти, зная его сторону и основание. …
2. Вторая формула позволяет найти его площадь через боковые стороны и угол между ними — это половина квадрата боковой стороны, умноженная на синус угла между боковыми сторонами

Геометрическая фигура

Прежде чем рассматривать теорему косинусов для треугольника и формулу, которая математически ее выражает, следует познакомиться с самим геометрическим объектом подробнее.

Треугольник представляет собой плоскую фигуру, которая состоит из двух типов элементов:

• трех отрезков, являющихся сторонами;
• трех вершин, образованных на пересечении отрезков и определяющих углы фигуры.

Если две стороны треугольника равны между собой и отличаются от третьей, его называют равнобедренным. Если все имеют одинаковую длину, речь идет о равностороннем объекте. Важным свойством любого треугольника является равенство суммы его трех углов 180°. Этот факт справедлив для всех типов фигуры на плоскости.

Важные линии

Для описания характеристик объекта в геометрии используют специальные линии. Основными из них являются:

• биссектриса — прямая, выходящая из произвольной вершины и делящая ее угол на 2 равные части;
• высота — перпендикуляр, который начинается на произвольной вершине и с противоположной стороной образует прямой угол;
• медиана — линия, которая делит на 2 одинаковые по площади части треугольник, пересекает противоположную сторону фигуры ровно посередине.

Для равносторонней фигуры все 3 типа линий совпадают друг с другом, для равнобедренного треугольника только для угла, образованного равными сторонами, они являются одинаковыми.

Основные законы

О треугольнике человечеству известно все, поскольку это самая простая геометрическая фигура. Кроме того, до настоящего времени дошли некоторые работы греческих мыслителей и даже древних египтян, которые были посвящены рассмотрению ее свойств. В общем случае можно назвать 3 основные теоремы, которые в полной мере описывают главные характеристики треугольника. К ним относятся:

1. Равенство площади фигуры половине произведения высоты на длину стороны, на которую она падает — ее принято называть основанием. Помимо этой формулы, существует еще одно выражение, которое позволяет получить тот же результат, но с использованием длин трех сторон и без проведения дополнительных геометрических построений.
2. Теорема синусов.
3. Закон косинусов.

Эти 3 теоремы и соответствующие им математические выражения являются независимыми и применяются для решения многих практических проблем.

Теорема косинусов

Она также звучит как закон косинусов для треугольника и представляет собой обобщение теоремы Пифагора на фигуру произвольного типа. Ее формулировка связывает 3 стороны и угол в единое равенство. Закон косинусов заключается в следующем: квадрат произвольной стороны треугольника равен сумме квадратов двух оставшихся его сторон за вычетом удвоенного произведения их длин, которые умножены на косинус угла между ними.

Чтобы записать соответствующее математическое выражение, следует ввести некоторые обозначения. Пусть в фигуре ABC сторона, которая лежит напротив угла C, то есть AB = c, по аналогии, BC = a и AC=b. Углы при вершинах A, B и C удобно обозначать малыми греческими буквами α, β и γ, соответственно. Тогда формула теоремы косинусов запишется в следующем математическом виде:

c² = a² + b² — 2*a*b*cos (γ).

Зная 3 любых элемента фигуры, можно вычислить все остальные ее характеристики. При этом хотя бы одна из известных величин должна быть линейным параметром. Это утверждение доказать несложно, если представить 2 подобных треугольника, которые имеют попарно равные углы, но разную длину сторон (одна фигура является миниатюрной копией другой).

Иными словами, знание трех углов не является достаточным условием для определения свойств треугольника.

Историческая справка

Практически во всех языках мира теорема носит название закона косинусов и не имеет конкретного автора. Однако, во французском языке она носит имя персидского математика Аль-Каши, жившего в конце XIV — начале XV веков. Согласно историческому анализу, именно с теориями этого философа связана современная формулировка теоремы.

Взаимоотношением между сторонами треугольника человечество интересовалось с давних времен. В труде греческого философа Евклида, который называется «Элементы» и датируется III веком до н. э., появляется впервые некое подобие рассматриваемого закона. Однако Евклиду не были известны тригонометрические функции, поэтому в своем труде он отдельно рассматривал тупоугольные и остроугольные фигуры и приводил для их сторон соответствующие равенства через известные длины, например, высоту.

В начале X века, когда в мире правили Средние века, арабский математик и астроном Аль-Баттани использовал работы Евклида для сферической геометрии. Его достижения сделали возможным проведения некоторых космических расчетов, например, вычисление расстояния от Земли до Солнца.

Первые таблицы тригонометрических функций синуса и косинуса появились приблизительно в XV веке. Эти достижения в математике позволили Аль-Каши, математику из школы Самарканда, переформулировать закон косинусов в удобном для использования виде. Впоследствии француз Франсуа Виет независимо от Аль-Каши получил то же самое математическое выражение для сторон треугольника с использованием тригонометрических функций.

Начиная с конца XVII столетия, когда швейцарец Леонард Эйлер ввел в математику новую нотацию, теорема Аль-Каши приобрела современную форму.

Способы доказательства

Кратко следует отметить, что существуют несколько способов доказательства теоремы. Среди них можно перечислить следующие:

• через разложение площадей многоугольников;
• с использованием теоремы Пифагора, свойств высоты и формулы косинуса в треугольнике;
• применяя окружность и ее геометрические свойства;
• с помощью векторов и их скалярного произведения.

Последний способ доказательства теоремы косинусов является самым простым и носит общий характер. Его может реализовать каждый школьник, который умеет вычитать вектора друг из друга и знает, как рассчитывается их скалярное произведение.

Применение для разных видов треугольников

Закон косинусов служит для определения неизвестных длин сторон либо углов в треугольнике. Однако общая математическая формулировка имеет ряд частных случаев в зависимости от типа фигуры, к которой ее применяют.

Для равнобедренного треугольника, у которого стороны a и b равны, нахождение c сведется к вычислению следующего равенства:

c = a*(2*(1- cos (γ)))^0,5.

В случае равностороннего треугольника все стороны равны a = b = c. Все углы также являются одинаковыми и соответствуют 60°(180°/3). Для такой фигуры нет смысла в использовании теоремы, поскольку в ней всегда существует лишь одна неизвестная — сторона a.

Прямоугольный треугольник по отношению к теореме косинусов является специальным случаем. Благодаря этой фигуре появились понятия синуса, косинуса, тангенса и котангенса как функций, отражающих взаимоотношения между катетами и гипотенузой.

Каждый школьник знает, что возведенная длина гипотенузы в квадрат эквивалентна сумме квадратов длин двух других сторон, называемых катетами. Однако, мало кто понимает, что это математическое равенство является не чем иным, как частным случаем закона косинусов. Показать это несложно, если записать изучаемую теорему для гипотенузы c. Тогда получается следующее равенство:

c ² = a ² + b ² — 2*a*b*cos (90 °).

Если обратится к таблице тригонометрических функций, в ней видно, что косинус прямого угла равен нулю. В результате вычитаемое в правой части равенства обращается в ноль, и равенство сводится к типичной теореме Пифагора.

Пример решения задачи

Известно, что стороны треугольника равны 6 см, 8 см и 10 см. Необходимо найти площадь этой фигуры.

Для решения задачи можно воспользоваться ресурсами интернета, которые предлагают множество сайтов, где с использованием онлайн-калькуляторов можно по известным данным найти нужную величину. Тем не менее представляет интерес решить эту задачу с использованием теоремы косинусов.

Площадь любого треугольника может быть вычислена так:

S = ½*a*h.

Здесь h — высота, проведенная к a. Известные стороны a = 6 см, b = 8 см, c = 10 см. Чтобы найти высоту h следует сначала рассчитать угол между a и c. Для этого можно применить закон косинусов:

β = arccos ((a ² + c ² — b ² )/(2*a*c)) = arccos ((6 ² + 10 ² — 8 ² )/(2*6*10)) = 53,13 °.

Теперь, если рассмотреть треугольник, образованный высотой h, стороной c и частью стороны a, можно увидеть, что он является прямоугольным (c — гипотенуза). В нем h может быть найдена через синус угла β:

h = c*sin (β) = 10* sin (53,13 °) = 8 см.

Длина высоты h равна таковой для стороны b. Это означает, что исходный треугольник являлся прямоугольным (можно проверить через теорему Пифагора). Его площадь составляет:

S = ½*a*h = ½*a*b = ½*6*8 = 24 см ² .

Таким образом, теорема косинусов является универсальным инструментом для решения геометрических задач с треугольниками. С помощью нее по трем известным параметрам можно найти все остальные характеристики фигуры, включая ее площадь.