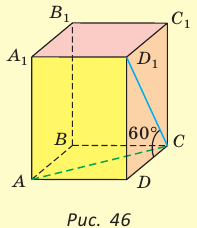
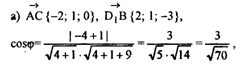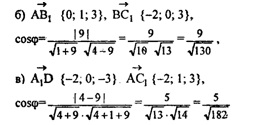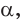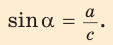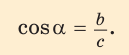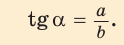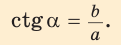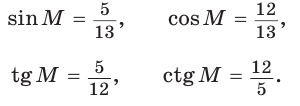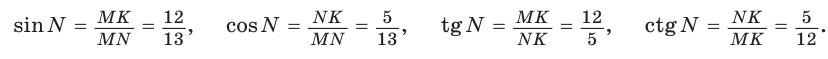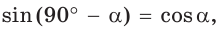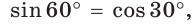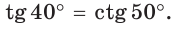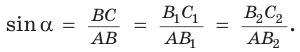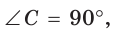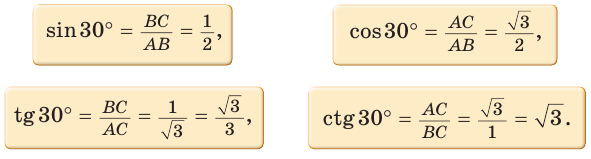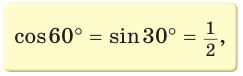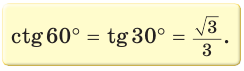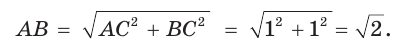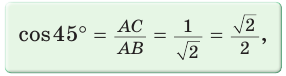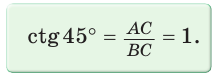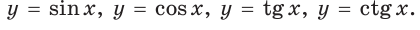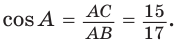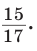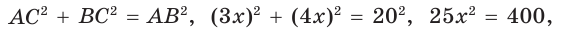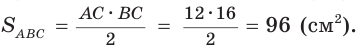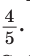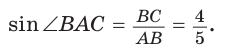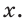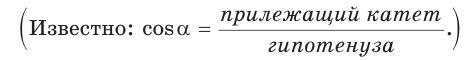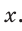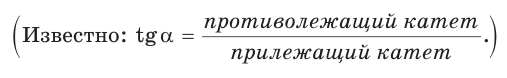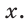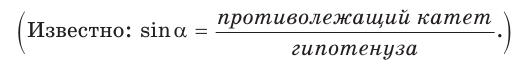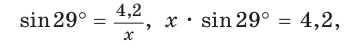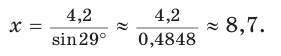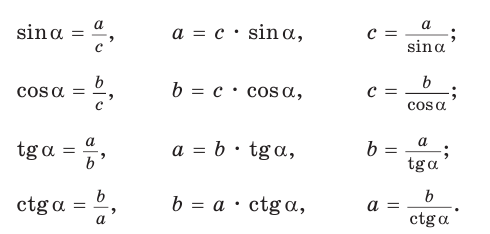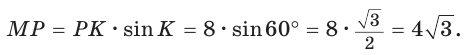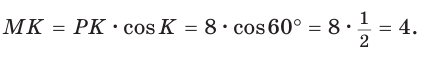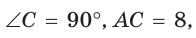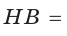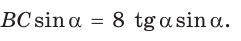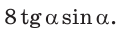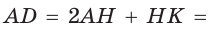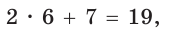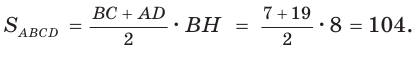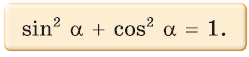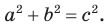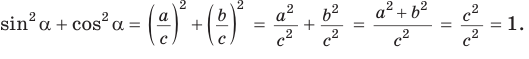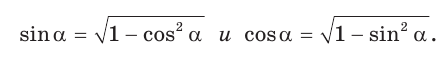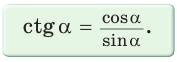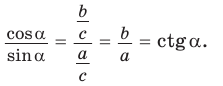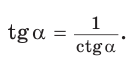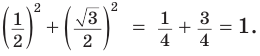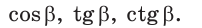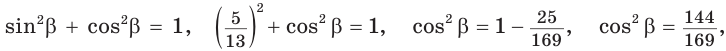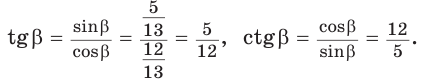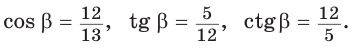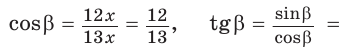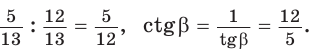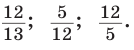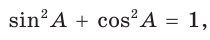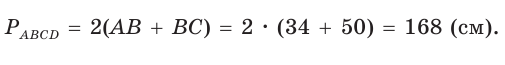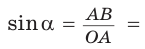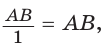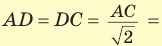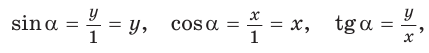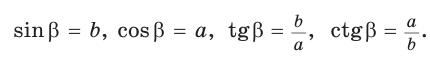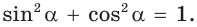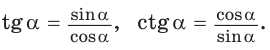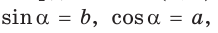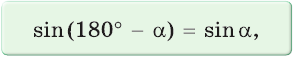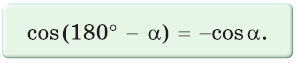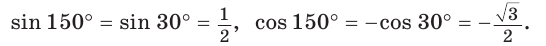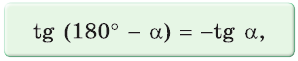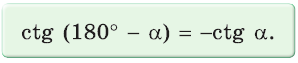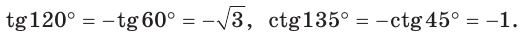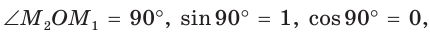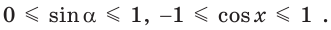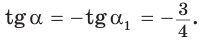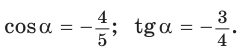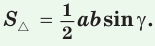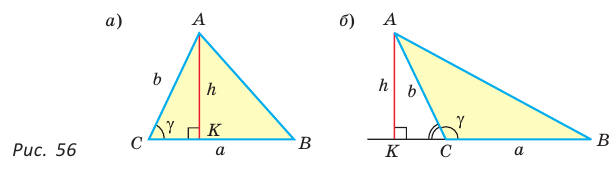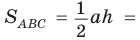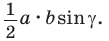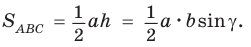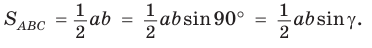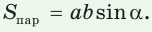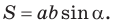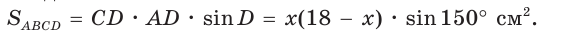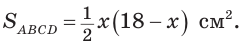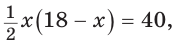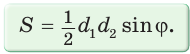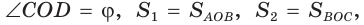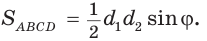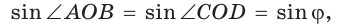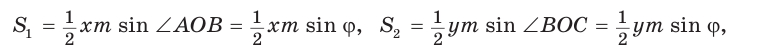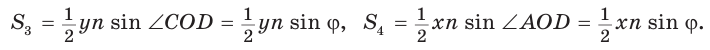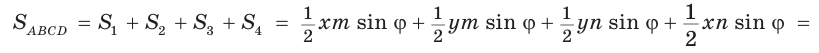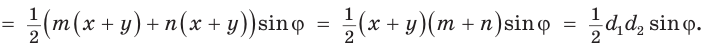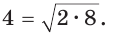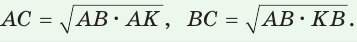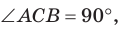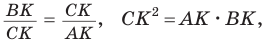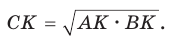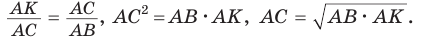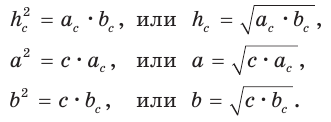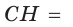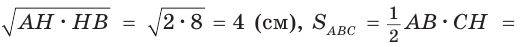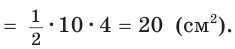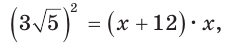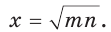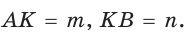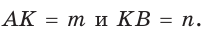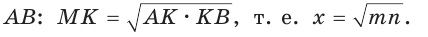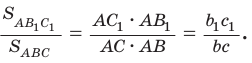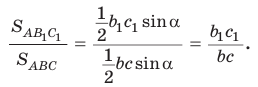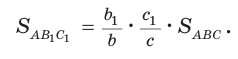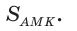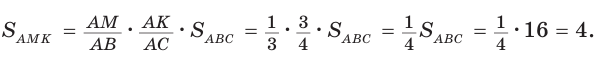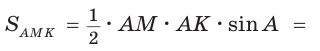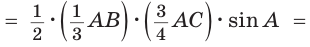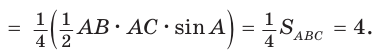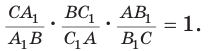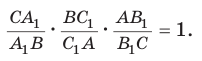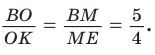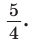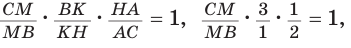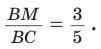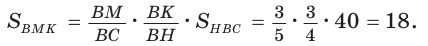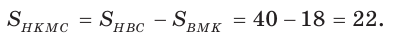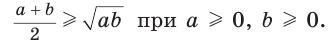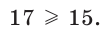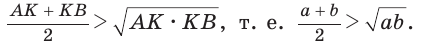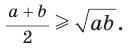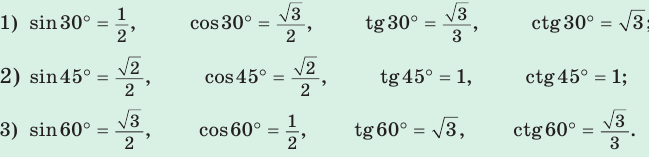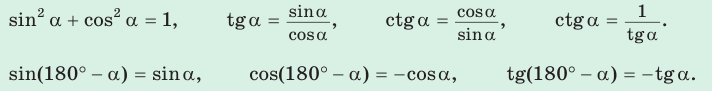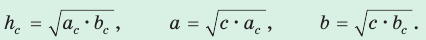Введем прямоугольную систему координат аналогично заданию № 467. Тогда А (2; 0; 0), В (2; 1; 0), С (0; 1; 0), D (0: 0: 0), А1 (2; 0; 3), В1 (2; 1; 3), С1 (0; 1; 3), D1 (0;0;3).
Тема: Перпендикулярность прямых и плоскостей
Урок: Прямоугольный параллелепипед (продолжение)
Прямоугольный параллелепипед
Определение. Параллелепипед АВСDА1В1С1D1 называется прямоугольным, если:
1. АА1 ⊥ АВСD (то есть, параллелепипед прямой).
2. АВ ⊥ АD, т. е. в основании тоже лежит прямоугольник.
Рис. 1
Основные элементы: грани, ребра, вершины, диагонали и др.
Свойства прямоугольного параллелепипеда
1. Все свойства произвольного параллелепипеда.
2. В прямоугольном параллелепипеде все шесть граней прямоугольники.
3. Все двугранные углы прямоугольного параллелепипеда прямые.
4. (см. рис. 2).
5. Диагонали равны.
Рис. 2
Определение. Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.
Все грани куба – это равные квадраты.
Задача 1
Найдите тангенс угла между диагональю куба и плоскостью одной из его граней.
Рис. 3
Дано: АВСDА1В1С1D1 – куб
Найти:
Решение:
Угол между прямой и плоскостью – это угол между прямой и ее проекцией. Проекцией прямой B1Dна плоскость АВС является прямая BD, так как ВВ1 ⊥ ABC. Поэтому: ∠(B1D; ABC) = ∠BDB1 = α. Ребро куба обозначим за а: AD = a. Тогда:
Ответ:
Задача 2
В прямоугольном параллелепипеде АВСDА1В1С1D1 дано:
D1B = d, AC = m, AB = n.
Найдите расстояние между:
а) прямой А1С1 и плоскостью АВС;
б) плоскостями АВВ1 и DCC1:
в) прямой DD1 и плоскостью ACC1;
Найдите:
г) косинус угла между прямой D1B и плоскостью АВС;
д) расстояние между прямыми DD1 и AC.
Дано: АВСDА1В1С1D1 – прямоугольный параллелепипед.
D1B = d, AC = m, AB = n.
Рис. 4
а) ρ (А1С1, АВС)
Решение:
Пусть ВС = х, DD1 = y.
Найдем ВС из прямоугольного треугольника АВС с помощью теоремы Пифагора:
. То есть, х
.
BD = AC = m (как диагонали в прямоугольнике). Найдем DD1из прямоугольного треугольника BDD1с помощью теоремы Пифагора:
. То есть, у
.
Прямая А1С1параллельна плоскости АВС. Значит, расстоянием между прямой и плоскостью является перпендикуляр, опущенный с точки прямой А1С1 на плоскость АВС, например, АА1. Значит, ρ (А1С1, АВС) = АА1 = = у
.
Ответ:
б) ρ (АВВ1, DCC1)
Плоскости АВВ1 и DCC1 параллельны. Значит, расстоянием является перпендикуляр, опущенный с любой точки одной плоскости на другую плоскость. Например, перпендикуляр ВС. Из пункта а) имеем:.
Ответ:
в) ρ (DD1, ACC1).
Прямая DD1параллельна прямой АА1 из плоскости АА1С1, а значит, прямая DD1параллельна плоскости АА1С1. Опустим с точки Dпрямой DD1 перпендикуляр DH к прямой АС (рис. 5).
Рис. 5
Прямая АА1 перпендикулярна плоскости АВС, а значит, и прямой DH, так как .
Получаем, что прямая DHперпендикулярна двум пересекающимся прямым АА1 и АС из плоскости АА1С1. Значит, прямая DH– есть перпендикуляр к плоскости ACC1. Тогда, DH = ρ (DD1, ACC1).
Рис. 6
Из прямоугольного треугольника DHC выразим DH:
Из прямоугольного треугольника ADC имеем:
Получаем:
Ответ: .
г)
Решение:
Угол между прямой D1Bи плоскостью АВС равен углу между прямой D1B и ее проекцией на плоскость АВС. DD1 – перпендикуляр к плоскости АВС. Значит, проекция D1Bна плоскость АВС – это DB. Значит, ∠(D1B, ABC) = ∠DBD1 = φ.
Ответ: .
д) ρ (DD1, AC).
Решение:
Прямая АС лежит в плоскости АВС, а прямая DD1 пересекает плоскость АВС в точке, не лежащей на прямой АС. Значит, прямые DD1 и AC скрещиваются. Прямая DD1 параллельна плоскости АСС1, в которой лежит прямая АС.
Значит, ρ (DD1, AC) = ρ (DD1, ACC1) = .
Ответ: .

Итоги урока
Итак, мы повторили основные свойства прямоугольного параллелепипеда и решили задачи с использованием этих свойств. Следующий урок мы посвятим повторению перпендикулярности прямой и плоскости.
Список литературы
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
- Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Домашнее задание
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
- Задания 12, 13 стр. 68.
- Найдите диагонали прямого параллелепипеда АВСDА1В1С1D1 , где ∠BAD = 120°, AB = 4 см, AD = 8 см, AA1 = 6 см.
- Вспомните, какие фигуры могут получиться в результате сечения параллелепипеда плоскостью.
- Найдите косинус двугранного угла при ребре ВВ1 прямого параллелепипеда ABCDA1B1C1D1(см. рис.), если АА1 = 5 см, BD = 3 см, площадь грани АА1В1В =
см2, а площадь грани AA1D1D = 25 см2.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- ФМ Класс (Источник).
- Интернет-портал Webmath.exponenta.ru (Источник).
- Я Класс (Источник).
Угол между векторами.
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
Содержание:
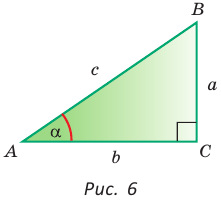
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен
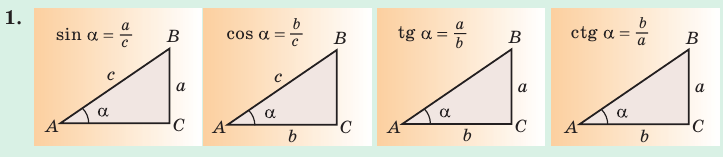
Определения синуса, косинуса, тангенса и котангенса острого угла
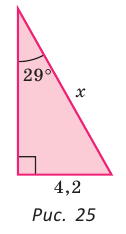
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
Пример:
Угол К в 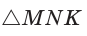
Тогда:
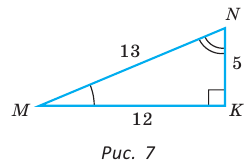
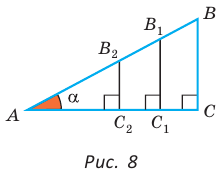
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего 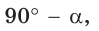
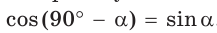
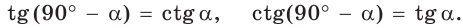
А теперь выполните Тест 1 и Тест 2.
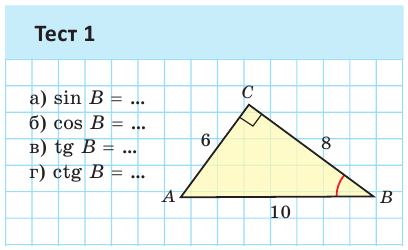
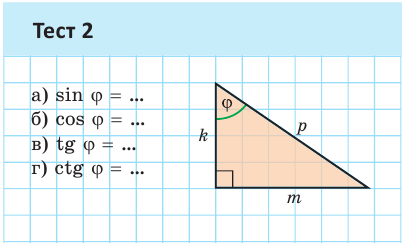
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в 

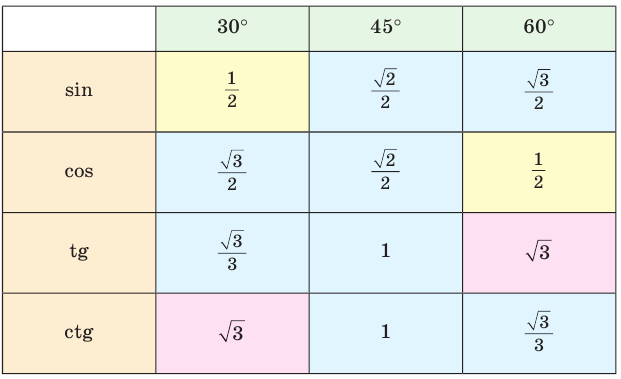
Значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
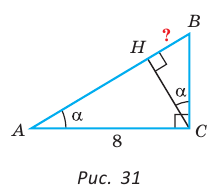
Рассмотрим прямоугольный треугольник АВС, у которого 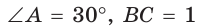
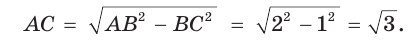
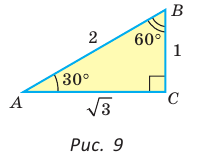
Так как 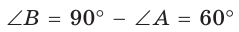

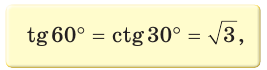
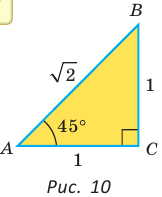
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого 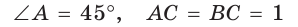
Тогда:
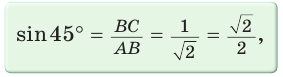
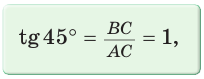
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
Нахождение значений тригонометрических функций
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно 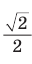
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно 
А теперь выполните Тест 3.
Тригонометрические функции острого угла
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу 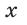
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла 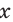
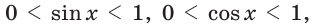
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
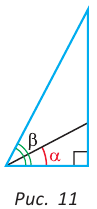
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если 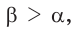
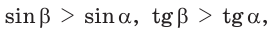
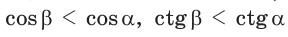
Пример №1
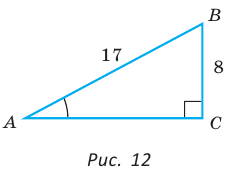
В прямоугольном треугольнике АВС, где 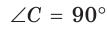
Решение:
По теореме Пифагора найдем катет 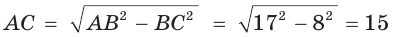
Ответ:
Пример №2
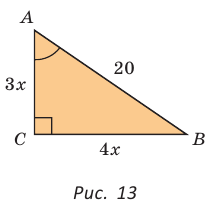
Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, 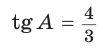
Решение:
Так как 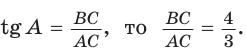
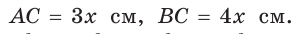
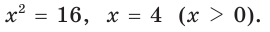
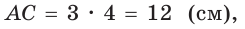
Ответ: 96
Пример №3
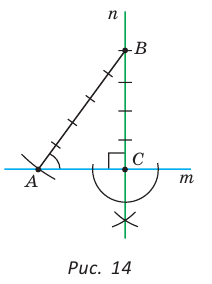
При помощи циркуля и линейки построить угол, синус которого равен
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен
Построение. 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую 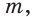
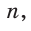
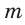
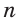
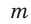
Угол ВАС — искомый.
Доказательство:
Из 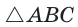
Алгоритм решения прямоугольного треугольника
Под решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.
Пример №4
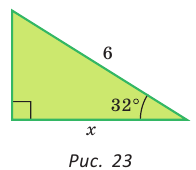
Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
Решение:
Примем длину искомого катета за
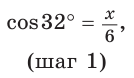

Ответ: 5,1.
Пример №5
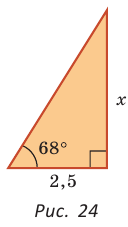
Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за
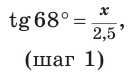
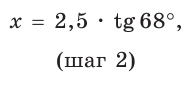
Ответ: 6,2.
Пример №6
Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за
Ответ: 8,7.
Правила решения прямоугольного треугольника
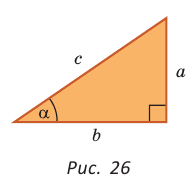
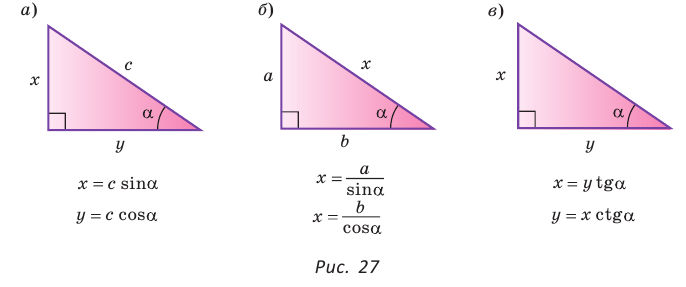
Преобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
Удобно пользоваться следующими правилами:
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис. 27, а).
- Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
Пример №7
В 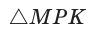
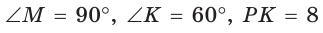
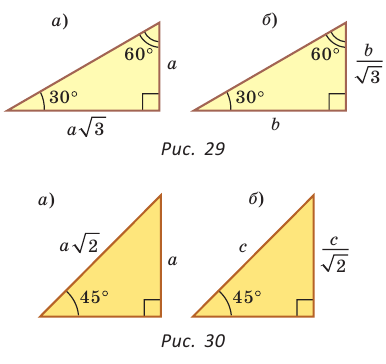
Полезно запомнить!
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет 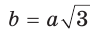
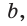
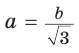
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза 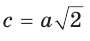
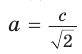
Пример №8
В прямоугольном треугольнике АВС известно: 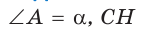
Решение:
Заметим, что 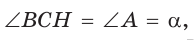
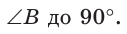
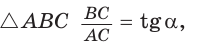
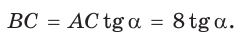
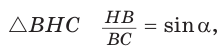
Ответ:
Пример №9
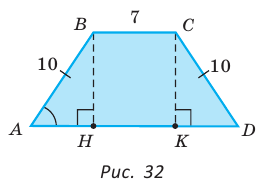
В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле 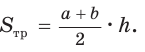
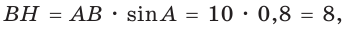
Ответ: 104.
Тригонометрические формулы
Используя формулы 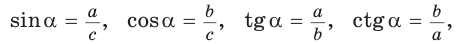
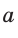
1. Основное тригонометрическое тождество
Доказательство:
По теореме Пифагора
Тогда
Следствие:
Так как синус и косинус острого угла а положительны, то
2. Выражение тангенса и котангенса через синус и косинус
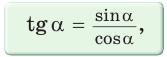
Доказательство:
a)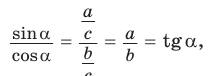
Следствие:
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что 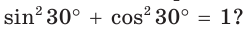
3. Основная задача
Дано: 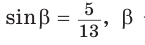
Найти:
Решение:
Способ 1. Используем основное тригонометрическое тождество: 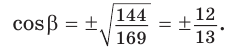
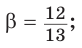
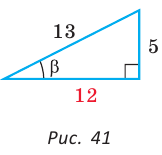
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен 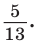
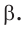
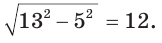
Способ 3. Пусть катет, противолежащий углу 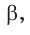
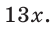
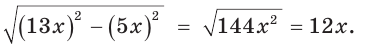
Ответ:
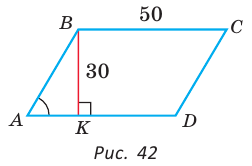
Пример №10
В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, 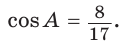
Решение:
Из треугольника АВК находим: 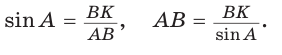
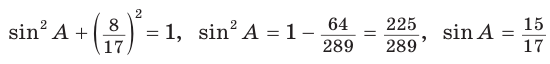
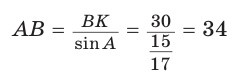
Ответ: 168 см.
Пример №11
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
Решение:
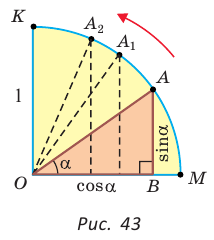
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть 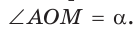
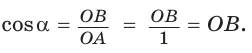
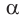
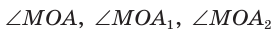
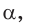
Из формулы 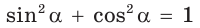
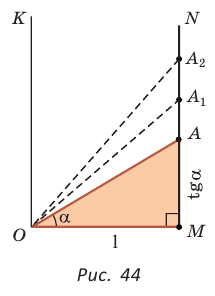
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, 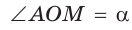
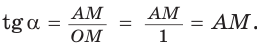
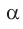
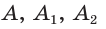
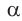
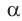
К такому же выводу можно прийти, рассматривая формулу 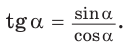
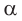
Пример №12
В основании прямоугольного параллелепипеда 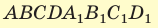
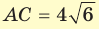
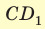
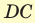

Решение:
Объем прямоугольного параллелепипеда находится по формуле 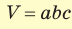
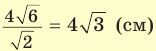
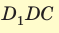
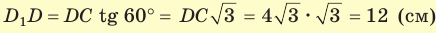
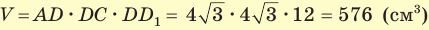
Ответ: 576 см3.
Синус, косинус, тангенс и котангенс тупого угла
1. Определение значений 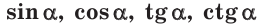
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
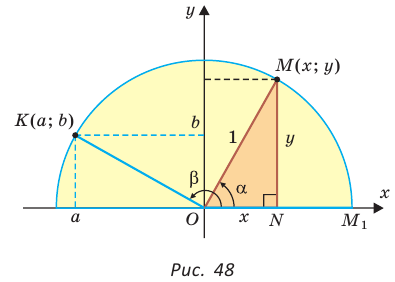
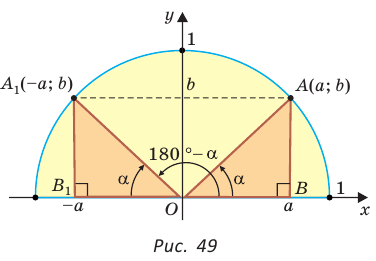
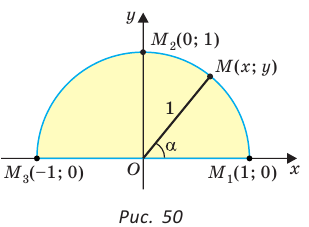
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси 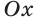
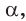
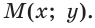
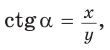
тангенс и котангенс острого угла а выражаются через координаты 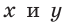
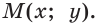
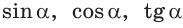
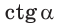
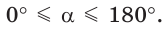
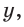
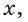
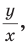
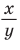
Например, для тупого 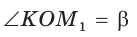
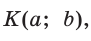
Для любого положения точки 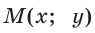
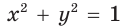
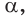

Также верны тождества:
Нахождение синуса, косинуса, тангенса и котангенса тупых углов
Пусть 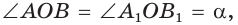
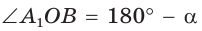
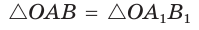
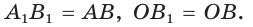
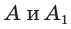
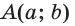
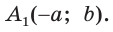
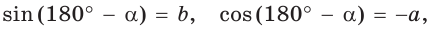
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1.
Разделив почленно равенство 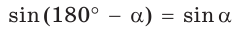
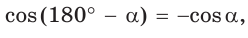
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».
Пример 2.
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
Значения тригонометрических функций для углов 0°, 90°, 180°
Если луч ОМ совпадет с лучом 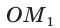
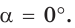
а) 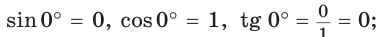
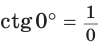
б) 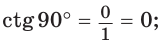
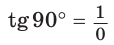
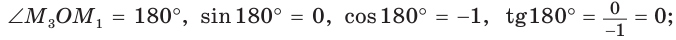
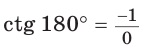
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов 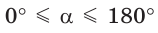
Пример №13
Найти 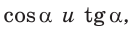
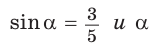
Решение:
Способ 1. Так как 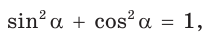
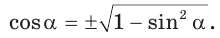
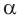
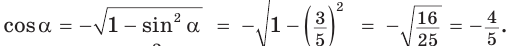
Способ 2. Синус острого угла 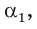
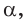
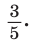
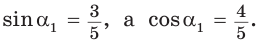
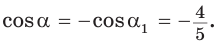
Ответ:
Формулы площади треугольника и площади параллелограмма
Тригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е.
Доказательство:
Пусть в треугольнике 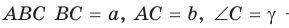
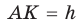
Из прямоугольного треугольника 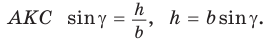
Если угол 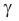
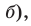
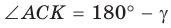
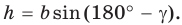
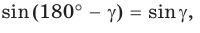
Если 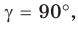
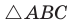
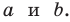

Теорема доказана.
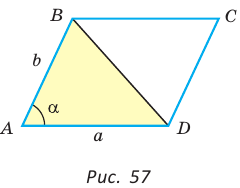
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е.
Используя рисунок 57, докажите эту теорему самостоятельно.
Замечание. Если 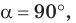
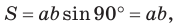

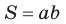
Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
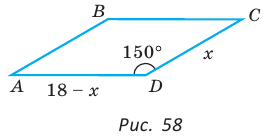
Пример №14
Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
Решение:
Полупериметр параллелограмма равен 18 см. Если 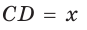
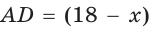
Тогда
Так как 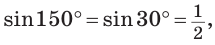
По условию 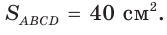
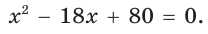
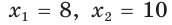
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
Пример №15
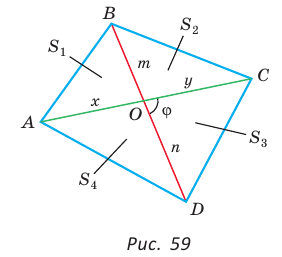
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е.
Доказательство:
Пусть диагонали 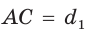
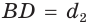
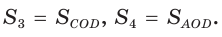
Обозначим 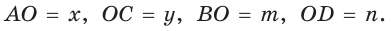
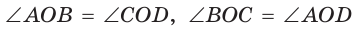
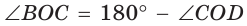
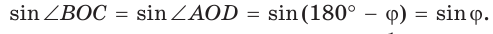
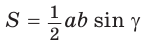
Утверждение доказано
Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольнике
Если для положительных чисел 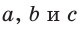
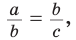
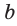
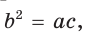
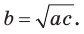
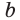
Пример №16
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = 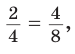
В прямоугольном треугольнике АВС, где 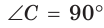
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
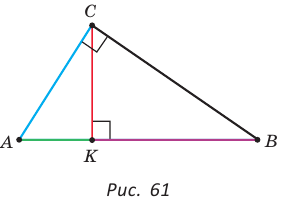
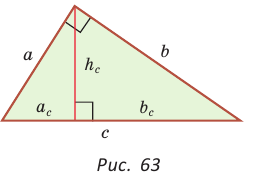
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 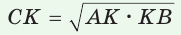
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т. е.
Доказательство:
а)3аметим, что если 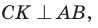
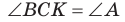
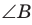
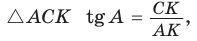
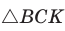
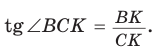
б) Из 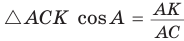
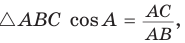
Аналогично доказывается, что 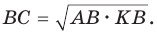
Обозначив катеты 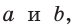
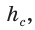
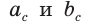
Пример №17
Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
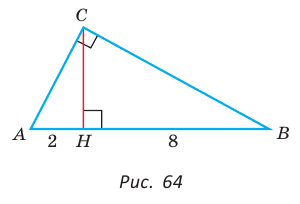
Пусть СН — высота прямоугольного треугольника АВС 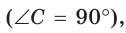
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то
Ответ: 20 см2.
Пример №18
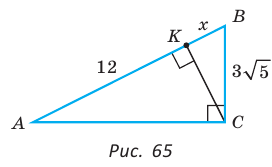
В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота 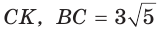
Решение:
Пусть 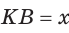
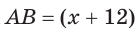
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому 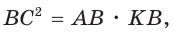
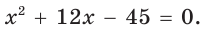
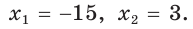
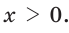
Ответ: 15 см.
Пример №19
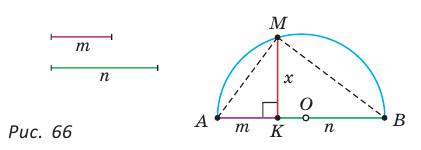
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок
Построение.
1) На произвольной прямой откладываем данные отрезки:
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
Отрезок 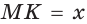
Доказательство:
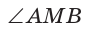
Повторение*
В 8-м классе мы доказали следующую теорему:
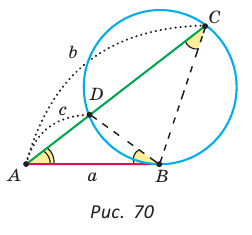
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. 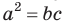
Как видим, отрезок 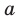
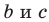
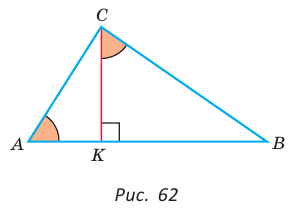
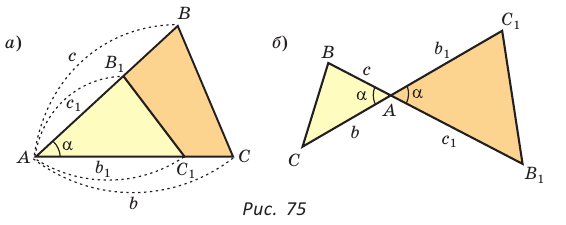
Теорема о площадях треугольников с общим (равным) углом
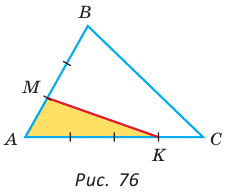
Площади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис. 75),
т.е.
Доказательство:
Следствие: Верно:
Пример №20
Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
Способ 2.
Ответ: 4.
Теорема Менелая
Если дан треугольник АВС и прямая 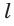
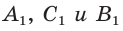
Доказательство:
Проведем отрезок 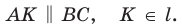
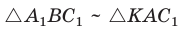

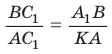
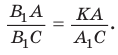
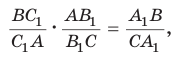
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой 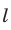
Пример №21
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
Решение:
Способ 1 (теорема Менелая). Рассмотрим 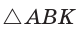
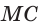
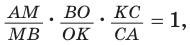
Способ 2 (теорема Фалеса обобщенная). Проведем 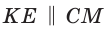
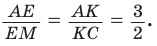
Но 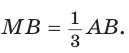
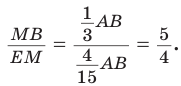
по теореме Фалеса
Ответ:
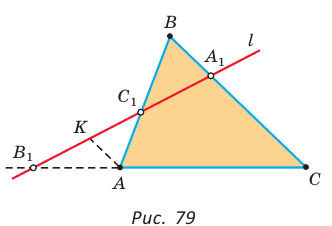
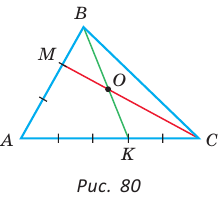
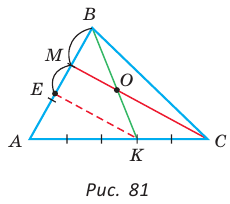
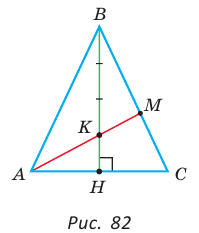
Пример №22
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
Решение:
1) 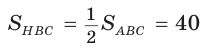
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке 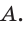
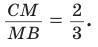
3)
4)
Ответ: 22.
Неравенство Коши
Среднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
Например, 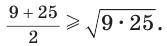
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства 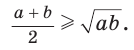
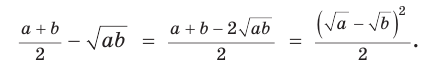
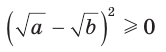
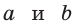
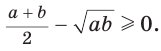
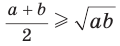
Неравенство 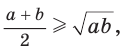
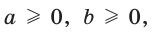
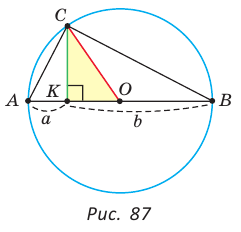
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть 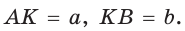

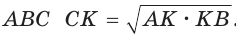
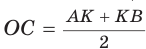
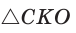
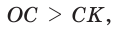
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и 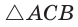
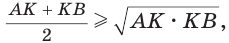
ЗАПОМИНАЕМ
2. Значения тригонометрических функций углов 30 45°, 60°:
3. Тригонометрические формулы (тождества):
Примеры:
4. Формулы площади треугольника и параллелограмма:
5. Среднее пропорциональное в прямоугольном треугольнике:
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
468. В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ = 1, ВС=2, BB1=3. Вычислите косинус угла между прямыми: а) АС и D1B; б) AB1 и ВС1; в) A1D и АС1.
Введем прямоугольную систему координат аналогично п. № 467.
Тогда
а)
б)