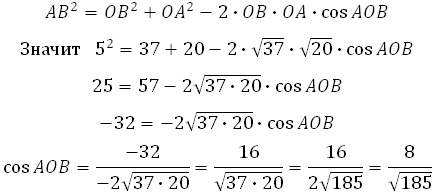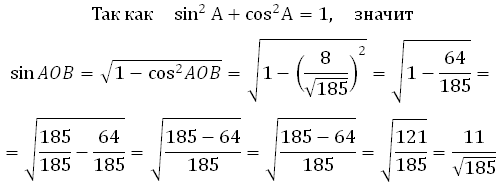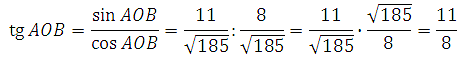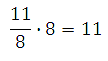Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.
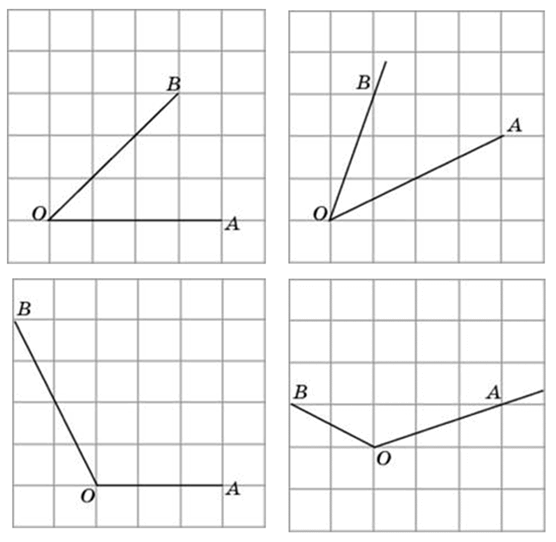
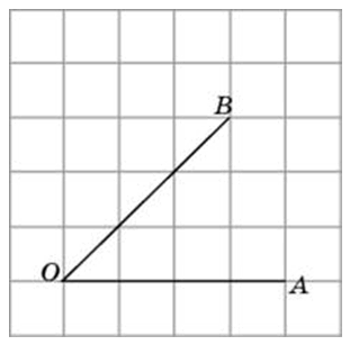
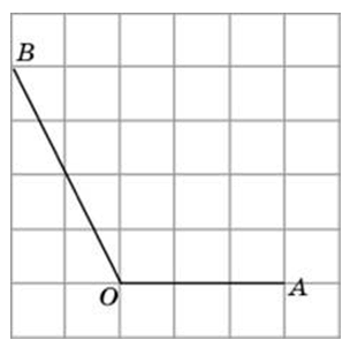
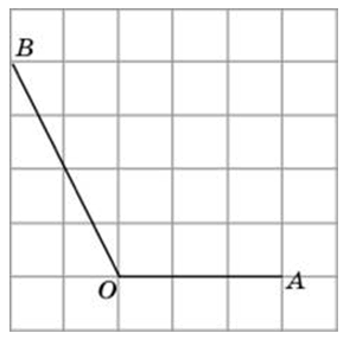
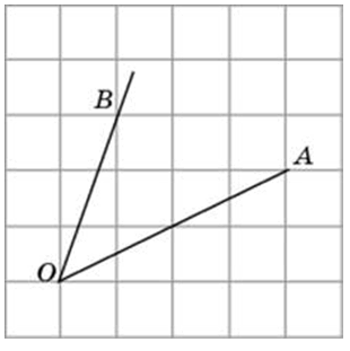
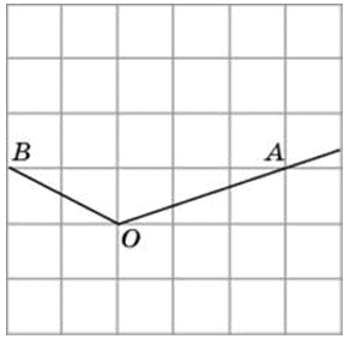
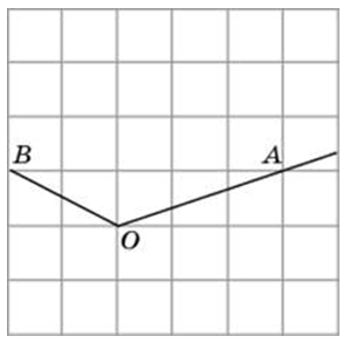
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):
Итак, рассмотрим задание:
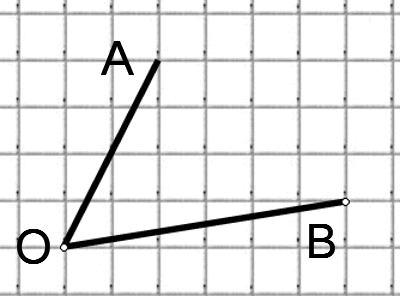
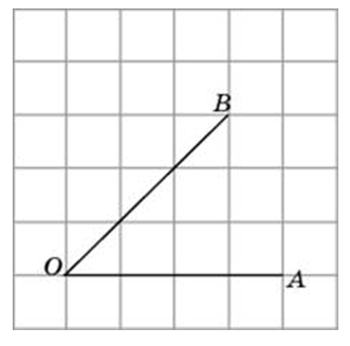
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
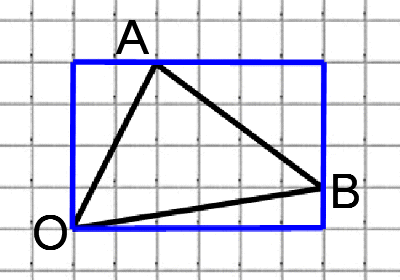
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Из основного тригонометрического тождества можем найти sin AOB:
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
Умножим результат на 8 и запишем ответ:
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
Посмотреть решение
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях )
Найти угол, построенный на листке в клетку
Учитель математики МАОУ «ССОШ№2»
Королева Е.И.
2015-2016гг.
Давайте рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задачи входят в состав ЕГЭ по математике
(задание №6 в профильном уровне.)
Способы решения существуют разные, их более трёх.
Подход изложенный ниже можно было бы назвать универсальным
Углы могут быть построены следующим образом (примеры):
Задача№1.
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Из основного тригонометрического тождества можем найти sin AOB:
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
Умножим результат на 8 и запишем ответ:
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Задача№2
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Задача№3
Найдите тангенс угла AOB.
Задача№4
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
Задача№5
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
Задача№6
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Задача№7
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
Задача№8
Найдите тангенс угла AOB.
Литература , сайты:
- ЕГЭ 4000 задач. под редакцией И.В.Ященко.
2.МАТЕМАТИКА ЕГЭ 2016 -50 вариантов.
3.ФИПИ открытый банк заданий.
4. http://matematikalegko.ru
+приложение.
Удачи!!!
04
Окт 2012
03 Задание (2022)ПЛАНИМЕТРИЯ
Косинус угла между прямыми по клеточкам.
Натолкнулась в Открытом банке заданий по математике на задачу, которую в прошлом году не встречала:
Задание B7 (№ 27458) из Открытого банка заданий для подготовки к ЕГЭ по математике:
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на 
Давайте сделаем дополнительное построение:
Величина угла АОВ равна сумме углов 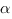
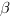
Примем размер клетки равным 1, и найдем длину ОВ из треугольника ОВС и длину АО из треугольника АОС:

По формуле для косинуса суммы имеем:
Вспомним соотношения для сторон и углов в прямоугольном треугольнике:
косинус угла равен отношению прилежащего катета к гипотенузе;
синус угла равен отношению противолежащего катета к гипотенузе.
Тогда из треугольника ВОС:
Из треугольника АОС:
Подставим эти значения в формулу для косинуса суммы:
В ответе запишем значение косинуса, умноженное на 
Ответ: -2
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ГЕОМЕТРИЯ. Часть В»

senghiesien313
Вопрос по алгебре:
найдите косинус угла АОВ, изображенного на рисунке

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
pomounthithi755
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Здесь линии клеток помогают получить такой прямоугольный треугольник. я выделил его красным во вложении.
Гипотенуза рассчитывается по теореме Пифагора:
Значит

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Найдите косинус угла АОВ изображенного на рисунке.

Вы зашли на страницу вопроса Найдите косинус угла АОВ изображенного на рисунке?, который относится к
категории Геометрия. По уровню сложности вопрос соответствует учебной
программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.