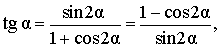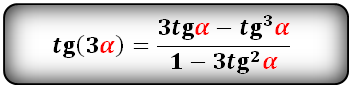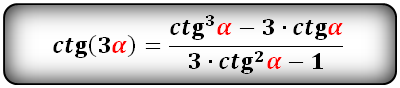Как найти косинус тройного угла - AvtoShod.ru - решение различных проблем

Косинус тройного угла, формула

Данная формула позволяет найти Косинус тройного угла зная косинус одинарного угла:

[
cos(3α) = 4cos^3(α) — 3cos(α)
]

Вычислить, найти косинус тройного угла, по формуле (1)

α° (градусов)

α´ (минут)

α˝ (секунд)

Вычислить

нажмите кнопку для расчета

Косинус тройного угла	стр. 222

Источник

Основные тригонометрические формулы

Содержание

Справочник по математике для школьников тригонометрия связи между тригонометрическими функциями

Связи между тригонометрическими функциями одного угла

Тригонометрические функции суммы и разности двух углов

Тригонометрические функции двойного угла

Формулы понижения степени для квадратов тригонометрических функций

Формулы понижения степени для кубов синуса и косинуса

Выражение тангенса угла через синус и косинус двойного угла

Преобразование суммы тригонометрических функций в произведение

Преобразование произведения тригонометрических функций в сумму

Выражение тригонометрических функций через тангенс половинного угла

Тригонометрические функции тройного угла

Связи между тригонометрическими функциями одного угла

Тригонометрические функции суммы и разности двух углов

Тригонометрические функции двойного угла

Формула	Название формулы
sin 2α = 2 sin α cos α	Синус двойного угла
cos 2α = cos ²α – sin²α cos 2α = 2cos ²α – 1 cos 2α = 1 – 2sin ²α	Косинус двойного угла
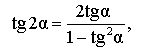	Тангенс двойного угла

Синус двойного угла

sin 2α = 2 sin α cos α

Косинус двойного угла

cos 2α = cos ²α – sin²α

cos 2α = 2cos ²α – 1

cos 2α = 1 – 2sin ²α

Тангенс двойного угла

Основные тригонометрические формулы тригонометрические функции двойного угла

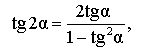Формулы понижения степени для квадратов тригонометрических функций

Формула	Название формулы
	Выражение квадрата синуса через косинус двойного угла
	Выражение квадрата косинуса через косинус двойного угла
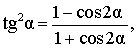	Выражение квадрата тангенса через косинус двойного угла

Формулы понижения степени для кубов синуса и косинуса

Формула	Название формулы
	Выражение куба синуса через синус угла и синус тройного угла
	Выражение куба косинуса через косинус угла и косинус тройного угла

Выражение куба синуса через синус угла и синус тройного угла

Выражение куба косинуса через косинус угла и косинус тройного угла

Выражение тангенса через синус и косинус двойного угла

Преобразование суммы тригонометрических функций в произведение

Сумма синусов

Разность синусов

Сумма косинусов

Разность косинусов

Сумма тангенсов

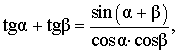Основные тригонометрические формулы преобразование суммы тригонометрических функций в произведение

Разность тангенсов

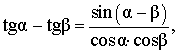Преобразование произведения тригонометрических функций в сумму

Произведение синусов

Произведение косинусов

Произведение синуса и косинуса

Выражение тригонометрических функций через тангенс половинного угла

Формула	Название формулы
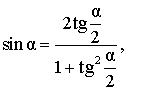	Выражение синуса угла через тангенс половинного угла
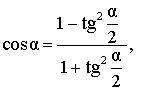	Выражение косинуса угла через тангенс половинного угла
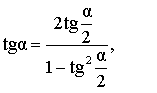	Выражение тангенса угла через тангенс половинного угла

Тригонометрические функции тройного угла

Формула	Название формулы
sin 3α = 3sin α – 4sin³α	Синус тройного угла
cos 3α = 4cos³α –3cos α	Косинус тройного угла
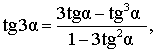	Тангенс тройного угла

Синус тройного угла

sin 3α = 3sin α – 4sin³α

Косинус тройного угла

cos 3α = 4cos³α –3cos α

Тангенс тройного угла

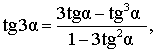Основные тригонометрические формулы тригонометрические функции тройного угла

Источник

Формулы двойного угла — это формулы, связывающие тригонометрические функции угла (синус, косинус, тангенс) с тригонометрическими функциями угла .

Формулы двойного и тройного угла (аргумента) выводятся из формул сложения.

Синус двойного угла

Доказательство. Воспользуемся формулой сложения для синуса

Из этой формулы получаем

Косинус двойного угла

$[cos{2alpha} = cos^2{alpha} - sin^2{alpha} = 2cos^2{alpha}-1 =1 - 2 sin^2{alpha}.]$

Доказательство. Применим формулу суммы агументов косинуса:

Получим

Тангенс двойного угла

$[operatorname{tg}2alpha = frac{2operatorname{tg}alpha}{1- operatorname{tg} ^2{alpha}}.]$

Доказательство этой формулы аналогично, поэтому эту формулу мы предлагаем вам доказать самостоятельно :).

Синус, косинус и тангенс тройного угла

$[sin 3alpha = 3sinalpha - 4sin^3{alpha}.]$

$[cos 3alpha = 4cos^3alpha - 3cos{alpha}.]$

$[operatorname{tg}3alpha=frac{3operatorname{tg}alpha - operatorname{tg}^3alpha }{1 - 3operatorname{tg}^2alpha}.]$

Доказательство. Формулы тройного угла можно получить из формул сложения, зная формулы двойного угла. Покажем это на примере синуса:

$[=sin{alpha}left(1 - 2 sin^2{alpha}right) + cosalpha(2sin{alpha}cos{alpha}).]$

Используя основное тригонометрическое тождество $cos^2alpha = 1 - sin^2{alpha}$ и приводя подобные члены, получаем формулу тройного угла для синуса.

Аналогично получаются формулы тройного угла для косинуса и тангенса.

Источник

Косинус тройного угла

ОПРЕДЕЛЕНИЕ

Косинус тройного угла выражается через косинус этого угла следующим образом. (
cos 3 alpha=4 cos ^{3} alpha-3 cos alpha
)

Примеры решения проблем

ПРИМЕР 1

Задача

Чтобы найти значение выражения(
5 cos 3 alpha-3
) , если (
sin alpha=frac{4}{5}
) , угол (
alpha
) лежит в первой четверти.

Решение

Преобразуйте выражение следующим образом: (
5 cos 3 alpha-3=5left(4 cos ^{3} alpha-3 cos alpharight)-3
)

Из основного тригонометрического тождества находим значение косинуса угла (
boldsymbol{alpha}
) : (
cos alpha=sqrt{1-sin ^{2} alpha}=sqrt{1-frac{16}{25}}=sqrt{frac{9}{25}}=pm frac{3}{5}
)

Так как угол (
alpha
) лежит в первой четверти, мы выбираем положительное косинусное значение (
cos alpha=frac{3}{5}
) и подставляем его в нужное выражение:

(
5 cos 3 alpha+3=5left(4 cos ^{3} alpha-3 cos alpharight)+3=5left(4 cdot frac{27}{125}-3 cdot frac{3}{5}right)+3==5 cdotleft(-frac{117}{125}right)+3=-frac{117}{25}+3=-frac{42}{25}
)

Ответ

(
5 cos 3 alpha+3=-frac{42}{25}
)

ПРИМЕР 2

Задача

Рассчитать: (
sin 135^{circ}
)

Решение.

Представьте угол (
135^{circ}
) в виде (
3 cdot 45^{circ}
), тогда мы можем написать

(
cos 135^{circ}=cos left(3 cdot 45^{circ}right)=4 cos ^{3} 45^{circ}-3 cos 45^{circ}=4 cdotleft(frac{sqrt{2}}{2}right)^{3}-3 cdot frac{sqrt{2}}{2}=4 cdot frac{2 sqrt{2}}{8}-3 cdot frac{sqrt{2}}{2}=-frac{sqrt{2}}{2}
)

Ответ: (
cos 135^{circ}=-frac{sqrt{2}}{2}
)

Источник