Как найти корни уравнения принадлежащие отрезку онлайн

В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.

а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]

Решим пункт а.

Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)

sqrt(2)cos^2x = cosx

sqrt(2)cos^2x — cosx = 0

cosx(sqrt(2)cosx — 1) = 0

cosx = 0

x1 = Pi/2 + Pin, n ∈ Z

sqrt(2)cosx — 1 = 0

cosx = 1/sqrt(2)

cosx = sqrt(2)/2

x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Решим пункт б.

1) Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.

-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi

Сразу делим все на Pi

-7/2 меньше или равно 1/2 + n меньше или равно -2

-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2

-4 меньше или равно n меньше или равно -5/2

Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Аналогично делаем еще два неравенства

-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8

Целых n в этом промежутке нет

-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8

Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.

Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4

2) Отбор корней с помощью тригонометрической окружности

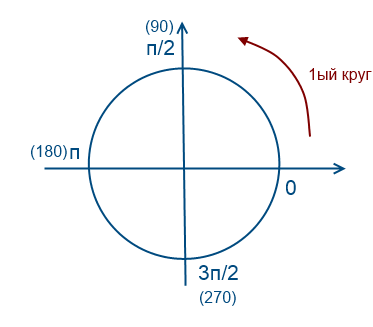
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.

Обойдем раз против часовой стрелки

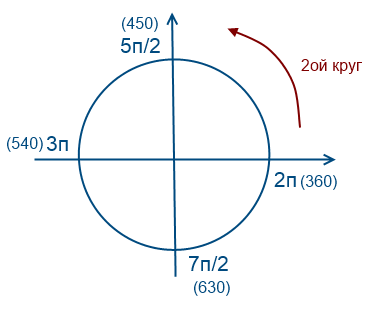
Обойдем 2 раза против часовой стрелки

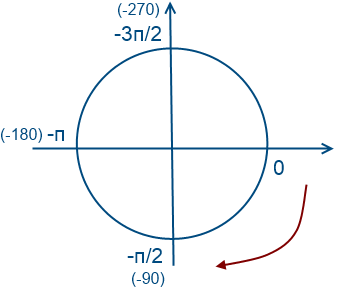
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

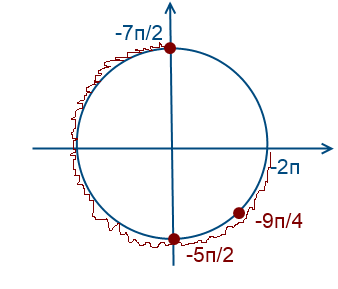
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]

Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.

Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

Сравнение двух методов.

Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.

Просмотры: 159005 |
Статью добавил: slava191 |
Категория: математика

Тригонометрические уравнения

В данной статье мы расскажем об основных типах тригонометрических уравнений и методах их решения. Тригонометрические уравнения чаще всего встречаются в задаче 12 ЕГЭ.

В вариантах ЕГЭ задача, где нужно решить уравнение, состоит из двух пунктов. Первый пункт – решение самого уравнения. Второй – нахождение его корней на некотором отрезке.

Некоторые из методов (например, замена переменной или разложение на множители) являются универсальными, то есть применяются и в других разделах математики. Другие являются специфическими именно для тригонометрии.

Необходимых формул по тригонометрии не так уж и много. Учите наизусть!
Тригонометрические формулы.

Любой метод решения тригонометрических уравнений состоит в том, чтобы привести их к простейшим, то есть к уравнениям вида sin x = a, cos x = a, tg x = a, ctg x = a.

Если вы не помните, как решать простейшие тригонометрические уравнения, — читайте материал на нашем сайте: Простейшие тригонометрические уравнения, часть 1.

О том, что такое арксинус, арккосинус, арктангенс и арккотангенс, — еще одна статья на нашем сайте: Простейшие тригонометрические уравнения,часть 2.

Теперь — сами методы. Теория и примеры решения задач.

к оглавлению ▴

Замена переменной и сведение к квадратному уравнению

Это универсальный способ. Применяется в любых уравнениях — степенных, показательных, тригонометрических,  логарифмических, каких угодно. Замена не всегда видна сразу, и уравнение нужно сначала преобразовать.

1. а) Решите уравнение:
б) Найдите корни уравнения, принадлежащие отрезку

Решение:

а) Рассмотрим уравнение

Преобразуем его, применив основное тригонометрическое тождество:

Заменяя sin x на t, приходим к квадратному уравнению:

Решая его, получим:

Теперь вспоминаем, что мы обозначили за t. Первый корень приводит нас к уравнению 
Оно не имеет решений, поскольку

Второй корень даёт простейшее уравнение

Решаем его:

б) Найдем корни уравнения на отрезке с помощью двойного неравенства.

Разделим обе части неравенства на

Вычтем из обеих частей неравенства:

Разделим на 2 обе части неравенства:

Единственное целое решение – это n=0. Тогда — это единственный корень, который принадлежит отрезку

Ответ:

2. а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку

Решение:

а)

Выразим косинус двойного угла по формуле

Получим:

Заменяя cos⁡x на t, приходим к квадратному уравнению:

1)

2) нет решений, т. к.

Получим:

б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежит только точка

Ответ: а)
б)

3. а) Решите уравнение: 
б) Найдите все корни этого уравнения, принадлежащие отрезку 

Решение:

а)  Чтобы упростить уравнение  применяем формулу приведения.

Так как  получим:

Сделаем замену:    Получим квадратное уравнение:

Сделаем обратную замену.

1)  — нет решений, т. к.  

2) 

б) Найдем корни уравнения, принадлежащие отрезку , с помощью двойного неравенства.

Для серии решений получим:

Так как то

Для серии решений получим:

отсюда

У этого неравенства нет целых решенией, и значит, из второй серии ни одна точка в указанный отрезок не входит.

Ответ: а)
б)

к оглавлению ▴

Разложение на множители

Во многих случаях уравнение удаётся представить в таком виде, что в левой части стоит произведение двух или нескольких множителей, а в правой части — ноль. Произведение двух или нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю. Сложное уравнение, таким образом, распадается в совокупность более простых.

4. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

а) Применяем формулу синуса двойного угла:

Ни в коем случае не сокращайте на косинус! Ведь может случиться, что cos x обратится в нуль, и мы потеряем целую серию решений. Переносим всё в одну часть, и общий множитель выносим за скобки:

Полученное уравнение равносильно совокупности двух уравнений: cosx = 0 и 2sinx — 1 = 0.

Получим:

Все эти три серии решений являются ответом в части (а).

б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежат точки

Ответ: а)
б)

5. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Применим формулу суммы синусов:

Дальше действуем так же, как и в предыдущей задаче:

Решаем уравнение :

(1)

Решаем уравнение :

(2)

Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).

Поэтому ответ в пункте (а):

б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:

Этот промежуток содержит 8 целых чисел: -2; -1; 0; 1; 2; 3; 4; 5.

Для каждого из этих n найдем x. Получим 8 решений на данном промежутке:

Ответ: а)
б)

6. В следующей задаче также применяется метод разложения на множители. Но это заметно не сразу.

а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Используем формулу понижения степени:

Получаем:

Применяем формулу суммы косинусов:

Получаем:

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:

б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:

1)

Решив неравенство, получим:

Так как n ∈ Z, получим для n целые значения: 0, 1, 2.

Им соответствуют решения:

2) Из серии решений на указанном отрезке лежит только корень Но он уже входит в первую серию решений.

Можно также заметить, что вся вторая серия решений является подмножеством первой.

Ответ: а)
б)

к оглавлению ▴

Однородные уравнения

7. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Такое уравнение называется однородным.

Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене степень каждого слагаемого равна двум. Мы помним, что степень одночлена — это сумма степеней входящих в него сомножителей.

Для однородных уравнений существует стандартный приём решения — деление обеих его частей на .

Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?

Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.

Предположим, что cosx = 0. Тогда в силу уравнения и sinx = 0, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию cosx 0, и мы можем поделить обе его части на .

В результате деления приходим к равносильному квадратному уравнению относительно тангенса:

Сделаем замену: получим:

б) Отметим отрезок  и найденные серии решений на единичной окружности.

О том, как отметить на единичной окружности точки из первой серии решений, то есть арктангенс минус трех, читайте здесь: Простейшие тригонометрические уравнения, часть 2.

Видим, что данному отрезку принадлежат  точки:

Ответ: а) 
б) 

8. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение

Получили однородное уравнение второй степени.

Так как не существует такой точки на единичной окружности, в которой одновременно синус и косинус равнялись бы нулю, мы разделим обе части уравнения на .

Получим: 

Выполним замену: tgx = y, получим:

Обратная замена: 

Ответом в пункте (а) являются  две серии решений.

б) Найдем корни уравнения, принадлежащие отрезку  с помощью единичной окружности. Для этого отметим на ней данный отрезок и  найденные серии решений.

Видим, что данному отрезку принадлежит только точка 

Ответ: а)
б) 

к оглавлению ▴

Введение дополнительного угла

Этот метод применяется для уравнений вида acosx + bsinx=c. Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.

9. а) Решим уравнение: 
б) Найдите все корни уравнения на отрезке 

Решение:

Делим обе части на 2:

Замечаем, что

В левой части получили синус суммы:

отсюда 

б) Отметим на единичной окружности отрезок  и найденные серии решений.

Обратите внимание, что в этой задаче отрезок больше, чем полный круг. Как нам поступить? Один из способов – нарисовать рядом две окружности.

Видим, что данному отрезку принадлежат точки:

Ответ: а) 
б)

Другой пример.

10. а) Решите уравнение: 
б) Найдите все корни уравнения на отрезке 

Решение:

Делим обе части на 

Сделаем теперь для разнообразия в левой части косинус разности:

б) Найдем корни уравнения, принадлежащие отрезку  с помощью единичной окружности. Отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежат  точки 0 и 

Ответ: а) 
б)  

Покажем, как применяется метод введения дополнительного угла в общем случае.

Рассмотрим  уравнение 

Делим обе части на

(4)

Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:

Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :

Соотношение (4) тогда приобретает вид:

или

Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол

к оглавлению ▴

Универсальная подстановка

Запомним две важные формулы:

Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной тригонометрической подстановки. 

Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.

11. а) Решите уравнение: 
б) Найдите все корни уравнения на отрезке 

Решение:

Выражаем , используя универсальную тригонометрическую подстановку:

Делаем замену  :

Получаем кубическое уравнение:

Оно имеет единственный корень .

Стало быть, , откуда .

Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало .

б) Найдем корни уравнения, принадлежащие отрезку    с помощью двойного неравенства:

Получим, что

Ответ: а)
б) 

Универсальная тригонометрическая подстановка может также пригодиться при решении задач по планиметрии из второй части ЕГЭ. Поэтому формулы лучше выучить.

к оглавлению ▴

Учет ОДЗ уравнения

12. а) Рассмотрим уравнение: 
б) Найдите все корни уравнения на отрезке 

Решение:

Перепишем уравнение в виде, пригодном для возведения в квадрат:

Тогда наше уравнение равносильно системе:

Решаем уравнение системы:

,

,

Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:

Теперь нужно произвести отбор решений в соответствии с неравенством . Серия  не удовлетворяет этому неравенству, а серия удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия .

Ответ в пункте (а):  .

б) Найдем корни уравнения, принадлежащие отрезку  с помощью двойного неравенства:

Неравенство имеет единственное целое решение 

Тогда 

Ответ: а)
б) 

Мы рассмотрели основные методы решения тригонометрических уравнений, которые применяются в задаче 12 ЕГЭ.

Где же еще нам могут встретиться тригонометрические уравнения? Конечно, в задачах с параметрами. Или на олимпиадах по математике. Сейчас мы увидим еще несколько полезных приемов решения.

к оглавлению ▴

Метод оценки

В некоторых уравнениях на помощь приходят оценки .

13. Рассмотрим уравнение: 

Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в том случае, когда они равны единице одновременно:

Таким образом, должны одновременно выполняться следующие равенства:

Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:

Умножаем обе части на 90 и сокращаем на π:

;

;

Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.

Искать k, в принципе, уже не нужно. Сразу находим x:

Ответ:

14. Рассмотрим уравнение: 

Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.

Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:

;

Тем самым мы сокращаем работу вдвое, получая лишь одну систему:

Имеем:

Ищем пересечение:

Умножаем на 21 и сокращаем на π:

Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.

Ответ: решений нет.

Это был тренировочный пример. А в задачах ЕГЭ решения есть всегда.

Посмотрите, как применяется метод оценки в задачах с параметрами.

15. Страшное с виду уравнение  также решается методом оценок.

В самом деле, из неравенства  следует, что .

Следовательно, , причём равенство возможно в том и только в том случае, когда

Остаётся решить полученную систему. Это не сложно.

Перенесем в левую часть и вынесем общий множитель за скобки ,  получим:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл.

Каждое уравнение равносильно совокупности:

Это значит, что синус угла х равен нулю, а его косинус равен 0, 1 или -1.

Или синус угла х равен 1, а косинус этого угла равен 0, 1 или -1.

Такие углы легко найти на тригонометрическом круге. Найденные серии решений запишем в ответ.

Ответ: 

к оглавлению ▴

Тригонометрические уравнения повышенной сложности.
Приемы решения

16. Рассмотрим такое уравнение: 

Сделаем замену .

Как выразить  через t? Имеем:

,

откуда . Получаем:

Начнем со второго уравнения.

Так как  и   то их сумма может быть равна 2, только оба слагаемых равны 1. Но на единичной окружности не существует точки, в которой одновременно синус и косинус равен единице. Значит, второе уравнение корней не имеет.

Решим первое уравнение методом введения дополнительного угла.

Для этого разделим обе части уравнения на  и получим:

Ответ: 

17. Помним формулы косинуса и синуса тройного угла:

,

Вот, например, уравнение:

Оно сводится к уравнению относительно :

,

,

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:

Решим второе уравнение с помощью замены sinx = t.

Получим:  или 

Обратная замена:

А решением первого уравнения sinx = 0 являются числа вида 

Ответ: 

Интересно, что формулы синуса и косинуса тройного угла также могут пригодиться вам в решении задач по планиметрии из второй части ЕГЭ.

18. Как бороться с суммой четвёртых степеней синуса и косинуса?

Рассмотрим уравнение: 

Выделяем полный квадрат!

;

;

;

;

;

;

19. А как быть с суммой шестых степеней?

Рассмотрим такое уравнение: 

Раскладываем левую часть на множители как сумму кубов: .

Получим:

;

С суммой четвёртых степеней вы уже умеете обращаться.

Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.

В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

26 мая

Как за­ра­бо­тать +20–30 бал­лов на ЕГЭ бла­го­да­ря раз­бо­рам ЕГЭ с Даль­не­го Вос­то­ка

Новости

28 мая

Что сроч­но пов­то­рить к зав­траш­не­му ЕГЭ рус­ско­му язы­ку

24 мая

Обновлённая панель инструментов

22 мая

Беседы Решу ЕГЭ по подготовке к ЕГЭ

11 мая

Решение досрочных ЕГЭ по всем предметам

5 мая

Обновленный поиск заданий по ключевым словам

1 мая

Новый сервис: можно исправить ошибки!

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение

Немного теории.

Тригонометрические уравнения

Уравнение cos(х) = а

Из определения косинуса следует, что ( -1 leqslant cos alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.

Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right] ); если a

Уравнение sin(х) = а

Из определения синуса следует, что ( -1 leqslant sin alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.

Уравнение sin х = а, где ( |a| leqslant 1 ), на отрезке ( left[ -frac<pi><2>; ; frac<pi> <2>right] ) имеет только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right] ); если а

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Уравнение tg x = а для любого a имеет на интервале ( left( -frac<pi><2>; ; frac<pi> <2>right) ) только один корень. Если ( |a| geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right) ); если а

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Уравнения, сводящиеся к квадратным

Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0

Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y₁ = -3, y₂ = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; ( x = (-1)^n text(0,5) + pi n = (-1)^n frac<pi> <6>+ pi n, ; n in mathbb )
Ответ ( x = (-1)^n frac<pi> <6>+ pi n, ; n in mathbb )

Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0

Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y₁ = 1, y₂ = 1/3

Уравнение вида a sin(x) + b cos(x) = c

Решить уравнение 2 sin(x) + cos(x) — 2 = 0

Используя формулы ( sin(x) = 2sinfrac <2>cosfrac<2>, ; cos(x) = cos^2 frac <2>-sin^2 frac <2>) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac <2>+ cos^2 frac <2>right) ) получаем

Поделив это уравнение на ( cos^2 frac <2>) получим равносильное уравнение ( 3 text^2frac <2>- 4 textfrac <2>+1 = 0 )
Обозначая ( textfrac <2>= y ) получаем уравнение 3y 2 — 4y + 1 = 0, откуда y₁=1, y₁= 1/3

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0

Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0

Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0

Решение тригонометрических уравнений онлайн

В общем виде, тригонометрическое уравнение можно записать следующим образом:

f ( trig ( x ) ) = 0

где — некоторая произвольная функция, trig ( x ) — некоторая тригонометрическая функция.

Как правило, метод решения тригонометрических уравнений заключается в преобразовании исходного уравнения к более простому, решение которого известно. Преобразования осуществляются при помощи различных тригонометрических формул.

Например, рассмотрим решение тригонометрического уравнения:

Используя формулу косинуса двойного угла, преобразуем данное уравнение:

Полученное уравнение является простейшим и легко решается. Наш онлайн калькулятор, построенный на системе Wolfram Alpha способен решить более сложные тригонометрические уравнения с описанием подробного хода решения.

Решение тригонометрических уравнений

Данный калькулятор предназначен для решения тригонометрических уравнений.
Тригонометрические уравнения – это уравнения, которые содержат в себе тригонометрические функции неизвестного аргумента. Под тригонометрическими функциями понимают математические функции от величины угла. Как правило, тригонометрические функции определяются как отношения сторон прямоугольного треугольника или длины определенных отрезков в единичной окружности.

К основным видам тригонометрических уравнений относят простейшие уравнения, содержащие модуль, с параметрами, с целой и дробной частью, со сложными аргументами, с обратными тригонометрическими функциями.

С помощью калькулятора можно вычислить корни тригонометрического уравнения.
Для получения полного хода решения нажимаем в ответе Step-by-step.