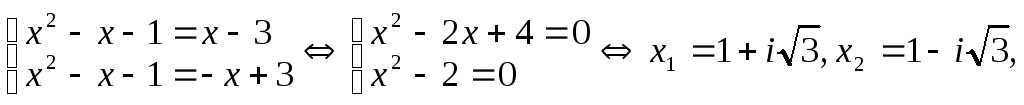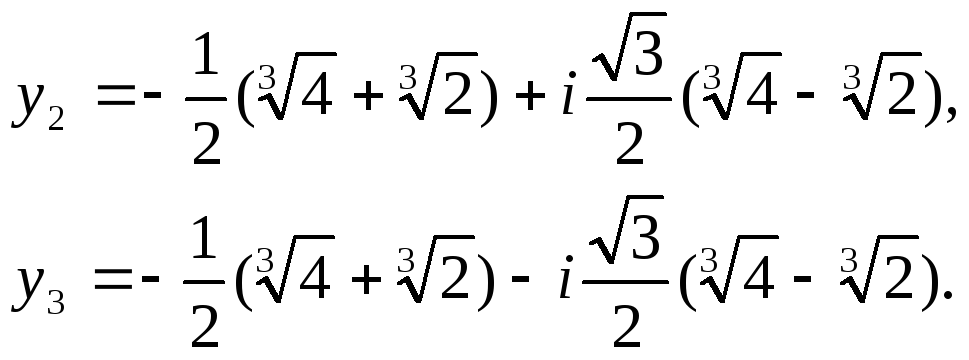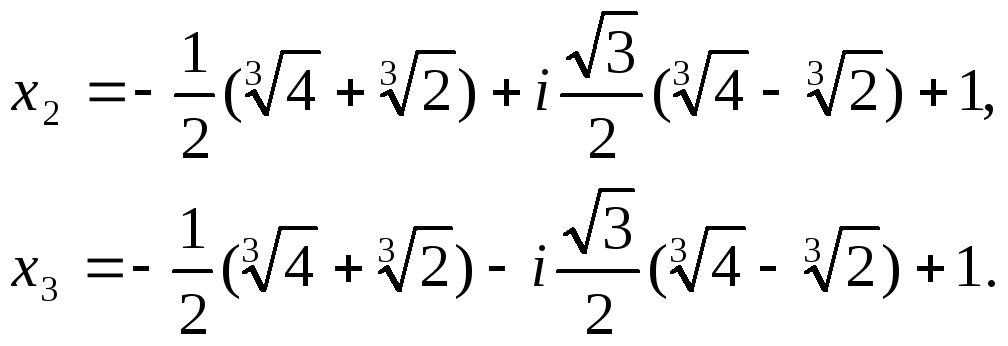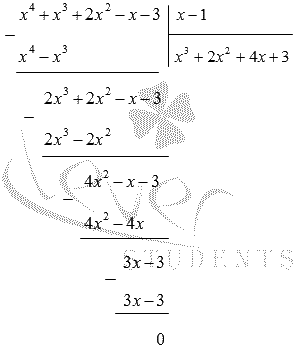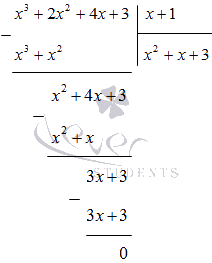Вычисление корней полинома
Вычисляет вещественные корни полинома любой степени численным методом или аналитически, если аналитическое решение существует
Калькулятор вычисляет вещественные корни полинома с целыми или рациональными коэффициентами. Для полинома степени меньше 5 используются аналитические формулы, для полиномов более высоких степеней применяется численный метод. Перед вычислением корней делается попытка разложения исходного многочлена на множители свободные от квадратов. Для иллюстрации отображается график, определяемый полиномом функции. Функция проверяется на четность и нечетность для сокращения области вычислений корней.
Вычисление корней многочлена любой степени
Коэффициенты многочлена, разделенные пробелом.
Точность вычисления
Знаков после запятой: 5
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
График
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Алгоритм вычисления вещественных корней полинома любой степени
- Выполняется проверка на четность — если f(x) = f(-x) — функция четная, если f(x)=-f(-x) — функция нечетная, для этих случаев корни можно искать только в положительной области, отрицательные корни — это положительные с обратным знаком. В противном случае — корни ищутся и в отрицательной и в положительной области
- Многочлен раскладывается на свободные от квадратов множители при помощи алгоритма Юна Разложение многочлена на свободные от квадратов множители.
- Каждый множитель, полученный на предыдущем шаге представляет собой многочлен, который решается аналитически если степень<5:
-
- Для многочлена 1-й степени — корень — это свободный член с противоположным знаком, деленный на коэффициент при x
-
- Многочлен 2-й степени решается при помощи Решение квадратного уравнения
-
- 3-й степени Кубическое уравнение
-
- 4-й степени Решение уравнения 4-й степени
- Если степень многочлена больше или равна 5, применяются численные методы
-
- Для работы численных методов необходимо уточнить области локализации корней, для этого мы используем алгоритм VAS-CF: Изоляция корней многочлена. Если многочлен четный или нечетный, то для поиска берем только положительную область.
-
- Далее для каждого интервала изоляции находится корень методом: Метод бисекции
-
- Если многочлен четный или нечетный добавляем в результат полученные ранее корни с противоположным знаком
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Изоляция корней многочлена
- • Метод выделения полного квадрата
- • Разложение многочлена на свободные от квадратов множители
- • Интерполяционный многочлен Ньютона (полином Ньютона)
- • Интерполяционный многочлен Лагранжа (полином Лагранжа)
- • Раздел: Алгебра ( 46 калькуляторов )
PLANETCALC, Вычисление корней полинома
Итак,
мы
показали в п. 4, что достаточным условием
приводимости многочлена над полями С,
R,
Q
является наличие хотя бы одного корня
многочлена f(x)
в поле С, R
или Q.
Дня отыскания этих корней приходится
решать уравнения n
— ой степени в поле С, R
или Q.
Мы уже отмечали, что если
многочлен
f(x)
имеет рациональный корень, то он приводим
и над полем R,
и над С. Поэтому, обычно, решение задачи
о приводимости многочлена начинается
с поиска его рациональных корней.
Необходимые, но не достаточные условия
существования рациональных корней
многочлена с целыми коэффициентами
даёт следующая теорема.
Теорема
1.
Если
—
рациональный корень многочленаf(x)
с целыми коэффициентами, причем (p,
q)
= l,
то числитель дроби (р) является делителем
свободного члена а0,
а знаменатель (q)
является делителем старшего коэффициента
аn.
Доказательство.
Пусть
—
корень многочленаf(x)=anxn
+
an-1xn-1
+…+
a1x
+ a0,
где все аi
Î
Z.
Подставим
,
где (p,
q)
= l,
q
¹
1 в многочлен, получим:
(1)
Умножим
обе части равенства (1) на qn,
тогда:
anpn
+
an-1qpn-1
+…+
a1
pqn-1
+
a0qn
= 0 (2)
Из равенства (2)
сначала можно выразить
anpn
= (-an-1pn-1
-…- a1pqn-2
—
a0qn-1)q
=> (аn
/q),
а
потом
-a0qn
=
p(anpn-1
+
an-1pn-2q+…
…+ а1qn-l)
=> (а0
/p) т.к.
(p, q) = 1
Замечание
1.
Так как
Z,
0 имеет лишь конечное число делителей,
то теорема позволяет, путем конечного
числа шагов, найти все рациональные
числа многочлена или проверить что их
нет.
Следствие
1.
Нормированный многочлен f
(x)
Z[x]
не имеет дробных корней;
Следствие
2.
Целый корень многочлена f(x)Z[x]
является
делителем свободного члена.
Задача
1.
Разложить многочлен
f(x)
= x6
— 2х5
+ х4
+ 6х3
— 10х2
— 4х + 8
над
полями Q,
R
и С.
Решение.
На
основании теоремы (1), рациональные корни
данного многочлена следует искать среди
делителей числа 8, т.к. аn
=
1
Делители:
+ 1, ±2,
±4,
±8.
Известно,
что число ()
является корнем многочлена f(x)
тогда и только тогда, когда f(x)
делится на (х
— )
(Смотри п. 4). Следовательно, для проверки,
какие из чисел ±1, ±2, ±4, ±8 являются
рациональными корнями, можно использовать
схему Горнера, а можно непосредственно
проверить, будет ли f(±1)
= 0, f(±2)
= 0,
f(±4)
= 0, f(±8)
= 0.
|
1 |
-2 |
1 |
6 |
-10 |
-4 |
8 |
|
|
1 |
1 |
-1 |
0 |
6 |
-4 |
-8 |
0 |
|
1 |
1 |
0 |
0 |
6 |
2 |
-6 |
|
|
-1 |
1 |
-2 |
2 |
4 |
-8 |
0 |
|
|
-1 |
1 |
-3 |
5 |
-1 |
-7 |
||
|
2 |
1 |
0 |
2 |
8 |
8 |
||
|
-2 |
1 |
-4 |
10 |
-16 |
24 |
||
|
4 |
1 |
2 |
10 |
44 |
166 |
||
|
-4 |
1 |
-6 |
26 |
… |
0 |
||
|
8 |
1 |
6 |
50 |
… |
0 |
||
|
-8 |
1 |
-10 |
42 |
… |
- |
Итак,
f(x)
= (x
— l)(x
+ l)(
x4
—
2x3
+
2x2
+
4x
— 
Чтобы
найти разложение над полями R
и С, нужно найти действительные и
комплексные корни этого многочлена,
для этого надо решить уравнение четвертой
степени х4
—
2х3
+
2х2
+
4х — 8 = 0.
Для
решения уравнений 4-ой степени разработан
частный метод
Феррари.
1-й шаг. Оставляем
в левой части равенства члены 4-ой и 3-ей
степени, остальные переносим в правую
часть, получим:
х4
—
2х3
=
-2х2
—
4х + 8
2-й
шаг. Дополняем левую часть равенства
до полного квадрата: х4
—
2х3
+
х2
=
х2
—
2х2
—
4х + 8
(х2
—
х)2
=
-х2
—
4х + 8
3-й шаг. Вводим
новую переменную (у) и дополняем левую
часть еще раз до полного квадрата,
получим:
(х2
—
х)2+2(х2—
x)у
+ у2
=
-х2
—
4х + 8 + 2(х2
—
х)у +
y2
[(x2-x)+y)]2
= (2y-1)x2+(-2y-4)x+(y2+8)
*
4-й
шаг. Потребуем, чтобы правая часть
также стала полным
квадратом,
для этого D
= В2
— 4АС = О
D=(-2y
— 4)2
—
4(2y
— l)(y2
+

у3
—
у2
+
6у – 6 = 0
Это
уравнение имеет рациональный корень
у0
=
1.
5-й
шаг. Подставим у0
в правую
и
левую части уравнения (*) вместо у.
Получим: (х2-х+1)2
= х2-6х+9
= (х-3)2
x3
=
-2,
x4
=
2
Итак,
многочлен f(x)
над полем С может быть представлен в
виде: f(х)
= (х — 1)(х + 1)(х + 2)(х
— 2)(x
— 1- i3)(x
— 1 + i3)
Для
того, чтобы найти разложение многочлена
над полем R,
нужно перемножить две последние скобки,
тогда:
f(х)
= (х — 1)(х + 1)(х + 2)(x
—
2)((х
— 1)2
+ 3).
Задача
2.
Разложить многочлен f(x)
= х4
— 2х3
— 6х2
— 4х — 1
Решение.
Так как многочлен
4-ой степени, то можно методом Феррари
сразу искать его действительные и
комплексные корни, а можно как и в первом
случае, найти сначала рациональные
корни (если они есть).
Так
как аn
= 1, то многочлен может иметь в качестве
рациональных корней целые числа, которые
являются делителями свободного члена
а0
= 1, т.е. ±1. Непосредственной подстановкой
убеждаемся, что (-1) является корнем, а
(1) нет, т.к. f(-l)
= 0, f(l)
¹
0.
Тогда,
f(x)
= (х + 1)( х3
— 3х2
— 3х — 1) над полем Q.
Теперь
найдем корни многочлена в поле С и R.
Для этого решим
уравнение:
х3
— 3х2
— 3х — 1 = 0.
Это
уравнение 3-ей степени, для таких уравнений
также существует частный метод решения
— метод
Кардано.
1-
й шаг. Приведем уравнение к виду, не
содержащему второй степени неизвестного.
Для этого введем подстановку
где (а) коэффициент при х2
.
Тогда,
(у + 1)3
— 3(у + 1)2
— 3(у + 1) – 1 = 0. Раскрыв скобки и приведя
подобные, получим: у3
— 6у — 6 = 0.
2-й
шаг. Полагаем, что у
=
+ ,
где
,
р — коэффициент при у,q
— свободный член.
В
нашем случае р = -6, q
= -6 Поэтому
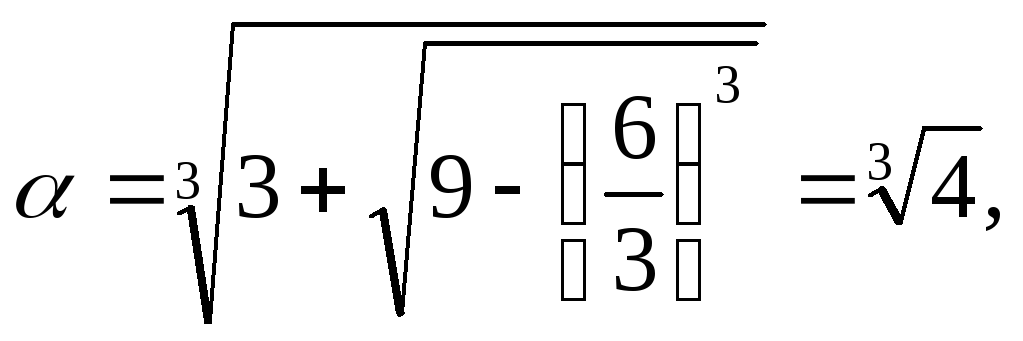
.
Тогда,
,
Наконец, находим
(х) из формулы х = у + 1
,
Тогда,
f(x)
= (x
+ l)(x
– x1)(x
— x2)(x
— x3)
— разложение многочлена над полем С.
Для
нахождения разложения многочлена f(x)
над полем действительных чисел R
достаточно в полученном выше разложении
перемножить скобки, соответствующие
сопряженным комплексным корням.
Тогда:
над полемR.
Замечание
2.
Если дан многочлен f(х),
степень которого выше четвертой, причем
он не имеет рациональных корней, то
задача разложения многочлена f(x)
на неприводимые многочлены над полем
С и R
становится трудноразрешимой, т.к. общих
методов решения уравнений n-ой
степени, где n
> 4 не существует.
Существуют
различные методы приближенного вычисления
действительных корней многочлена f(x)
(метод хорд, метод касательных и т.п.)
Замечание
3.
В том случае, когда нужно найти сумму
корней многочлена f(x),
могут быть использованы формулы Виета,
которые устанавливают зависимость
между корнями и коэффициентами многочлена.
Выведем эти формулы:
Пусть
f(z)
= zn
+
c1zn-1
+
c2zn-2
+…+ cn-1z
+ cn
и 1,
2,…,
n
корни
этого многочлена в поле С, тогда
zn
+
c1zn-1
+
c2zn-2
+… + cn-1z
+ cn
= (z
— a1)(z
— a2)…(z
— an)
= = zn
– (a1
+ a2
+…+
an)zn-1
+ (a1a2
+ a1a3
+…+
an-1an)zn-2
+…+
+(-1)n
(a1a2
…an)
Приравняв
коэффициенты при соответствующих
степенях, получим формулы Виета:
с1
=
-(a1
+ a2
+…+ an)
с2
= (a1a2
+ a1a3
+…+
an-1an)
c3
= -(a1a2a3+
a1a2a4
+…+ an-2an-1an)
сn
=
(-1)n
(a1a2
…an)
Задача
3.
Найти сумму кубов корней многочлена
f(x)
= x4
+ 2х3
+ х2
+ 5х + 3, f(x)Q[x]
Решение.
Над
полем комплексных чисел С многочлен
f(x)
имеет четыре корня: х1,
х2,
х3,
х4.
Нам нужно найти X13+
X23+
X33+
X43
не находя самих корней.
По формулам Виета
х1+x2+
х3+
х4
= -2 =1
х1х2
+
х1х3
+
х1х4
+
x2x3+
х2х4
+
х3х4
=
1 = 2
х1х2х3
+ x1x2x4
+ х1х3х4
+
х2х3х4
= -5 = s3
х1х2х3х4
= 3 = s4
Тогда
X13+
X23+
X33+
X43
= 13
—
312
+ 33
=
=(-2)3
— 3(-2)l
+ 3(-5) = -17
Ответ: -17.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Разложение многочлена на множители. Часть 3. Теорема Безу и схема Горнера
Разложение многочлена на множители. Теорема Безу и схема Горнера
При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим, каким образом это сделать проще всего.
Как обычно, обратимся за помощью к теории.
Теорема Безу утверждает, что остаток от деления многочлена на двучлен
равен
.
Но для нас важна не сама теорема, а следствие из нее:
Если число является корнем многочлена
, то многочлен
делится без остатка на двучлен
.
Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на , где
— корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.
Эта задача распадается на две: как найти корень многочлена , и как разделить многочлен на двучлен.
Остановимся подробнее на этих моментах.
1. Как найти корень многочлена.
Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.
Здесь нам помогут такие факты:
Если сумма всех коэффициентов многочлена равна нулю, то число является корнем многочлена.
Например, в многочлене сумма коэффициентов равна нулю:
. Легко проверить, что
является корнем многочлена.
Если сумма коэффициентов многочлена при четных степенях равна сумме коэффициентов при нечетных степенях, то число
является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку
, а
— четное число.
Например, в многочлене сумма коэффициентов при четных степенях
:
, и сумма коэффициентов при нечетных степенях
:
. Легко проверить, что
является корнем многочлена.
Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.
Для приведенного многочлена степени (то есть многочлена, в котором старший коэффициент — коэффициент при
— равен единице) справедлива формула Виета:
, где
— корни многочлена
.
Если многочлен не является приведенным, то его можно сделать таковым, разделив на старший коэффициент.
Есть ещё формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.
Из этой формулы Виета следует, что если корни приведенного многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.
Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.
Рассмотрим, например, многочлен .
Для этого многочлена произведение корней равно
Делители числа :
;
;
Сумма всех коэффициентов многочлена равна , следовательно, число 1 не является корнем многочлена.
Сумма коэффициентов при четных степенях :
Сумма коэффициентов при нечетных степенях :
, следовательно, число -1 также не является корнем многочлена.
Проверим, является ли число 2 корнем многочлена: , следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен
делится без остатка на двучлен
.
2. Как разделить многочлен на двучлен.
Многочлен можно разделить на двучлен столбиком.
Разделим многочлен на двучлен
столбиком:
Есть и другой способ деления многочлена на двучлен — схема Горнера.
Посмотрите это видео, чтобы понять, как делить многочлен на двучлен столбиком, и с помощью схемы Горнера.
Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на её месте пишем 0 — так же, как при составлении таблицы для схемы Горнера.
Итак, если нам нужно разделить многочлен на двучлен
и в результате деления мы получаем многочлен
, то коэффициенты многочлена
мы можем найти по схеме Горнера:
Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число является корнем многочлена
, то остаток от деления многочлена на
равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.
Используя схему Горнера, мы «убиваем двух зайцев»: одновременно проверяем, является ли число корнем многочлена
и делим этот многочлен на двучлен
.
Пример. Решить уравнение:
1. Выпишем делители свободного члена, и будем искать корни многочлена среди делителей свободного члена.
Делители числа 24:
2. Проверим, является ли число 1 корнем многочлена.
Сумма коэффициентов многочлена , следовательно, число 1 является корнем многочлена.
3. Разделим исходный многочлен на двучлен с помощью схемы Горнера.
А) Выпишем в первую строку таблицы коэффициенты исходного многочлена.
Так как член, содержащий отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при
пишем 0. Слева пишем найденный корень: число 1.
Б) Заполняем первую строку таблицы.
В последнем столбце, как и ожидалось, мы получили ноль, мы разделили исходный многочлен на двучлен без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:
Будем делить дальше. Нам нужно найти корни многочлена . Корни также ищем среди делителей свободного члена, то есть теперь уже числа -24.
Легко проверить, что числа 1 и -1 не являются корнями многочлена
В) Продолжим таблицу. Проверим, является ли число 2 корнем многочлена :
Так степень многочлена, который получается в результате деления на единицу меньше степени исходного многочлена, следовательно и количество коэффициентов и количество столбцов на единицу меньше.
В последнем столбце мы получили -40 — число, не равное нулю, следовательно, многочлен делится на двучлен
с остатком, и число 2 не является корнем многочлена.
Идем дальше.
В) Проверим, является ли число -2 корнем многочлена . Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:
Отлично! В остатке мы получили ноль, следовательно, многочлен разделился на двучлен
без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена
на двучлен
в таблице изображены зеленым цветом.
В результате деления мы получили квадратный трехчлен , корни которого легко находятся по теореме Виета:
Итак, корни исходного уравнения :
{}
Ответ: {}
И.В. Фельдман, репетитор по математике.
Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
О теореме Абеля-Руффини без групп и теории Галуа
Историческая справка
Поиск решения алгебраических уравнений оказал колоссальное влияние на развитие математики. Формула решения общего кубического уравнения впервые была получена итальянскими математиками 16-го века. Это событие ставшее первопричиной рассмотрения комплексных чисел, считается одним из поворотных моментов в истории математики. Судьбы Джероламо Кардано, Никколо Тартальи, Сципиона дель Ферро и их поисков решения кубического уравнения заслуживают отдельного романа со своими интригами, скандалами и расследованиями. Столь яркие истории достаточно редки в математике.
Начиная с 19-го века поиск формул для решения уравнений произвольных степеней положил начало теории групп и абстрактной алгебре, которые преобразили практически все разделы современной математики. Думаю, многие, кто интересовался историей и развитием алгебры, знают, что формулы для решения общего алгебраического уравнения степени выше четвертой не существует. Как сообщается, первое доказательство этого факта было дано итальянским математиком Паоло Руффини в самом конце восемнадцатого века, оно составляло около 500 страниц и все же содержало некоторые пробелы. Хотя отдельные математики, как Огюстен Коши, и признавали данное доказательство, но ввиду столь большого объема и сложности изложения, оно так и не было принято математическим сообществом. Считается, что первое полное доказательство дано норвежским математиком Нильсом Абелем и содержалось в двух работах, изданных в 1824 и 1826 годах. С тех пор оно носит название теоремы Абеля или теоремы Абеля-Руффини.
Если вы попытаетесь изучить это доказательство в его современном изложении, то окажется, что оно практически полность опирается на Теорию Галуа. Эварист Галуа был французским математиком 19-го века и современником Нильса Абеля. Помимо занятий математикой он вел активную политическую жизнь из-за чего несколько раз попадал в тюрьму. В возрасте всего двадцати лет был застрелен на дуэли, поводом для которой послужила любовная интрига, хотя есть предположения, что дуэль была подстроена его политическими противниками. Об этой истории написано достаточно много, кроме того, имеется перевод на русский язык его мемуаров и писем. Последнее письмо его другу Огюсту Шевалье было написано в ночь накануне дуэли, в нем он наспех излагает свои последние идеи. Несмотря на столь короткую жизнь, Эварист Галуа считается одним из родоначальников современной алгебры. Хотел бы заметить, что в популярном изложении создается некий романтический образ Галуа, как подростка-гения, который в одиночку, с нуля создал теорию групп и преобразил всю алгебру. Несомненно его идеи сыграли огромную роль, но если почитать его сочинения, то мы увидим, что он хорошо знал и опирался на знаменитые работы Лагранжа, Эйлера, Гаусса, Абеля, Якоби. Зачатки теории групп и перестановок появляются еще в работах Жозефа Луи Лагранжа по теории алгебраических уравнений, а также Карла Фридриха Гаусса в его знаменитых «Арифметических исследованиях». К тому же, теория Галуа в современном изложении была оформлена многими последующими математиками — Дедекиндом, Кронекером, Гильбертом, Артином и другими.
Мотивация данной статьи
Чуть менее года назад меня сильно увлекла статья об истории решения кубического уравнения и последующих безуспешных поисков формулы уравнения 5-й степени, длившихся почти триста лет. Сразу хочу отметить, что специального математического образования у меня нет и поэтому, попробовав прочесть современную версию доказательства теоремы Абеля-Руффини, я естественно ничего не понял. В моем сознании термины группа, кольцо и поле никак не ассоциировались с алгебраическими структурами. Но желание разобраться было столь велико, что я принялся за изучение курса высшей алгебры.
На первых этапах абстрактная алгебра была наверное самым сложным из того, что мне приходилось изучать ранее. Объем новых терминов и определений просто зашкаливал: группы, факторгруппы, моноиды, поля, кольца, тела, модули, идеалы, ядра, векторные пространства, биекции, сюръекции, инъекции, изоморфизмы, автоморфизмы, гомоморфизмы, эндоморфизмы и тд. Спустя несколько месяцев упорных занятий, я начал понимать формальную часть, но, к сожалению, интуитивного понимания, которое и являлось моей изначальной целью, я так и не достиг.
Дело в том, что практически все современные доказательства неразрешимости уравнений 5-й степени в радикалах сводятся к следующему. Рассматривается некоторое неприводимое уравнение, например x 5 -10x+2, после чего методами мат анализа определяется, что оно имеет три действительных и два комплексно-сопряженных корня. После чего заключается, что группой Галуа данного уравнения есть группа S5, которая не является разрешимой, и следовательно данное уравнение неразрешимо в радикалах. Доказательство теоремы Абеля-Руффини о неразрешимости общего уравнения также сводится к неразрешимости группы Sn. Для меня данные доказательства были слишком абстрактными и оторванными от конкретных уравнений. Когда я пытался представить их в терминах элементарных алгебраических операций, чтобы понять в чем заключается главная причина неразрешимости уравнений, у меня ничего не получалось. Возможно для тех, кто занимается этим достаточно долго, эти вещи могут казаться интуитивно понятными.
Немного иной подход описан в книге Алексеева «Теорема Абеля в задачах и решениях», основанной на лекциях Владимира Арнольда, но в изложенном там доказательстве помимо теории групп используются элементы комплексного анализа и Римановых поверхностей. Я также находил похожие статьи, использующие топологические аргументы в виде комбинаций петель и коммутаторов, но мне хотелось найти что-то чисто алгебраическое.
Параллельно изучая историю математики и понимая, что современная формулировка и доказательство сильно отличаются от того, как излагали свои идеи Лагранж, Руффини, Абель и Галуа, я решил прочесть первоисточники. К сожалению, на русский или английский по этой теме переведены лишь сочинения Галуа и одна из работ Абеля.
После некоторых поисков я наткнулся на статью 1845 года французского математика Пьера Лорана Ванцеля, в которой он переработал и сильно упростил доказательство Абеля-Руффини, о чем он пишет во введении. В этой работе, он так же упоминает мемуары Галуа и отмечает, что они будут опубликованы в скором времени. Для заметки — работы Галуа были опубликованы лишь в 1846 году Жозефом Лиувиллем, спустя почти 15 лет после смерти Галуа. Кстати, Пьер Лоран Ванцель, также был первым, кто доказал неразрешимость трисекции угла и удвоения куба с помощью циркуля и линейки — знаменитых задач стоявших еще со времен античности. Доказательства Ванцеля были изложены без использования абстрактной алгебры и теории Галуа, поскольку на тот момент они еще не были разработаны. Хотя работа и была доступна лишь на французском, которого я до этого практически не знал, но ввиду специфической темы, небольшого размера (всего 7 страниц) и наличия гугл переводчика, я справился достаточно быстро. По моему субъективному мнению, его доказательство теоремы Абеля-Руффини является наиболее простым для понимания.
Уже позже я нашел пример подобного доказательства основанного на работе Руффини в книге Чеботарёва “Основы Теории Галуа”. Далее я постараюсь кратко изложить принцип решения уравнений в радикалах и идею доказательства неразрешимости уравнения 5-й степени.
Решения уравнений в радикалах
Для дальнейшего понимания, потребуются минимальные пререквизиты:
Формулы Виета — напомню, что коэффициенты произвольного уравнения являются элементарными симметрическими функциями от его корней, то есть функциями, которые не меняют своего значения при любых перестановках корней. Примеры: x1 + x2 + x3, x1x2x3, x1x2 + x1x3 + x2x3.
Теорема о симметрических многочленах — каждую симметрическую функцию от корней, можно выразить с помощью элементарных симметрических функций (коэффициентов уравнения).
Первообразные корни n-й степени из единицы — комплексные величины не равные единице, но n-я степень которых, равна единице. Примеры: (-1) 2 = 1, (-1/2 + sqrt(-3)/2) 3 = 1, i 4 = 1 соответственно квадратный, кубический и биквадратный корни из единицы.
Основная теорема алгебры — гласит о том, что уравнение n-й степени с комплексными коэффициентами имеет ровно n комплексных корней с учетом кратности (корни могут быть одинаковые).
Первоначальная идея восходит к работе Жозефа Луи Лагранжа “Размышления о решении уравнений” 1770-1771 годов. Это достаточно объемное сочинение и я не нашел его перевода на русский или английский язык. Как указывается в разных источниках, в попытке найти формулу для уравнения 5-й степени, Лагранж проанализировал все имеющиеся к тому времени способы решения уравнений и выделил общий принцип, позволяющий решить уравнения 4-й и низших степеней. В этой же работе, изучая перестановки корней, он пришел к теореме, которая сейчас носит его имя. Принцип, открытый Лагранжем, заключался в том, чтобы найти выражения от корней заданного уравнения n-й степени, которые при всех возможных перестановках этих корней принимали n-1 значений, но в тоже время через них выражались первоначальные корни. На эти значения, можно составить уравнение n-1 степени и повторить операцию, тем самым сводя изначальное уравнение к цепочке уравнений меньших степеней, решив которые, можно получить корни первоначального уравнения. Рассмотрим один из примеров:
Пусть f(x) = x 4 + ax 3 + bx 2 + cx + d общее уравнение 4-й степени с произвольными коэффициентами a, b, c, d и x1, x2, x3, x4 его корни.
Напомним, что его коэффициенты — это элементарные симметрические функции от корней, в чем можно убедиться просто раскрыв скобки в выражении (x — x1)(x -x2)(x — x3)(x — x4):
Так как корни являются произвольными, то существует 4! = 24 различных вариантов их расположения, но можно составить выражение x1x2 + x3x4, которое принимает всего три разных значения при всех 24-х перестановках корней:
На эти три значения мы можем составить уже кубическое уравнение, корнями которого они и будут являться. Таким образом, мы сводим решение уравнения 4-й степени к уравнению 3-й степени. Для решения кубического уравнения мы можем воспользоваться резольвентой Лагранжа (y1 + wy2 + w 2 y3) 3 , где w — это кубический корень из единицы. Данное выражение принимает всего два разных значения при всех возможных 3! = 6 перестановках. Оно будет сохранять значение при циклических перестановках и менять знак при любой транспозиции. Получим:
Теперь составим квадратное уравнение на z1 и z2:
z1+z2 и z1z2 — будут симметрическими функциями от корней нашего изначального уравнения f(x), следовательно, по теореме о симметрических многочленах, напрямую выражаться через коэффициенты a, b, c, d. Решив квадратное уравнение мы получим значения z1, z2. После чего, извлекая кубические корни из z1, z2, и складывая с коэффициентом b, сможем выразить y1. Далее, c помощью y1 и коэффициентов a, b, d, решив два квадратных уравнения, мы доберемся до корней x1, x2, x3, x4 изначального уравнения.
Данный пример показывает, что произвольное уравнение 4-й степени решается путем составления вспомогательных кубического и квадратных уравнений. Далее я приведу рассуждение, почему подобный прием невозможен для общего уравнения 5-й степени.
Неразрешимость уравнения 5-й степени
Итак, мы хотим показать, что ни один корень общего уравнения 5-й степени не может быть выражен через его коэффициенты путем решения цепочки вспомогательных двучленных уравнений низших степеней.
Пусть f(x) = x 5 + ax 4 + bx 3 + cx 2 + xd + e общее уравнение 5-й степени с произвольными коэффициентами a, b, c, d, e и x1, x2, x3, x4, x5 его корни. Обозначим за y1 первый радикал входящий в значение x1 в порядке вычисления. Пусть y1 n = p, где p будет какой-то симметрической функцией от корней и, следовательно, напрямую выражаться через коэффициенты a, b, c, d, e. Заметим, что y1 уже не будет симметрической, а лишь рациональной функцией g от корней — g(x1, x2, x3, x4, x5). Следовательно, g должно менять значение при перестановке любых двух корней. Тогда эти значения будут являться корнями уравнения y1 n = p, которые имеют вид g, zg, z 2 g, z 3 g … z n-1 g, где z — первообразный корень n-й степени из единицы (z n =1). Рассмотрим произвольную транспозицию, например (x1, x2), тогда
если мы применим ее еще раз, то получим:
Из этого следует, что z 2 = 1, то есть z должен быть квадратным корнем из единицы (z = -1) и соответственно первый радикал y1 будет квадратным. Поясним: так как корни являются произвольными, то g должно сохранять значение при любых четных перестановках корней и менять знак при нечетных. Теперь покажем, что значение функции g не будет меняться при циклической перестановке трех корней (x1, x2, x3). Здесь стоит пояснить, что циклическая перестановка (x1, x2, x3) четная и может быть представлена, как произведение транспозиций (x1, x2)(x2, x3). То есть, функция g не поменяет своего значения при данной перестановке. Еще заметим, что функция g не изменится при циклической перестановке пяти корней, так как она так же раскладывается в произведение четного количества транспозиций. Присоединяя радикал y1 к выражениям от коэффициентов с помощью базовых арифметических операций, мы будем получать симметрические функции относительно всех циклов на трех и пяти корнях и вообще любых четных перестановок, но при перестановке содержащей нечетное количество транспозиций, y1 будет менять знак. Дальнейшее присоединение квадратных радикалов не даст нам ничего нового. Теперь предположим, что мы пришли к радикалу, который меняет свое значение лишь при тройных циклах. Обозначим его y2, тогда y2 n = q, где q — это рациональная функция от коэффициентов a, b, c, d, e и радикала y1.
В данном случае z 3 = 1, то есть z здесь будет кубическим корнем из единицы.
Теперь произведем циклическую перестановку 5-и корней
Так как z должен быть кубическим корнем из единицы, как мы выяснили ранее, то единственным вариантом будет z = 1 и g должна быть инвариантна при любой из этих циклических перестановок. Но тогда она должна быть инвариантна и при циклической перестановке x3,x2,x5,x1,x4 -> x2,x5,x1,x4,x3. Отсюда, одной транспозицией мы можем получить, что
но, выше мы уже видели, что
а из этого следует
что приводит нас к противоречию, так как мы предполагали, что g меняет значение при циклической перестановке трех корней (x1, x2, x3).
Еще одним вариантом, было бы показать что все четные перестановки на пяти корнях порождаются тройными циклами, то есть, если есть тройные циклы, то никаких выражений от корней, которые бы сохраняли набор значений при всех четных перестановках, не существует. Если теперь перевести это на теоретико-групповой язык, то получается, что группа общего уравнения пятой степени есть симметрическая группа S5, в которой существует 5! = 120 различных перестановок пяти корней. Далее, путем присоединения квадратного корня из дискриминанта, мы можем понизить ее до знакопеременной группы четных перестановок A5, которая содержит 120/2 = 60 перестановок. Но A5 является простой группой, в которой нет никаких нетривиальных нормальных подгрупп, которым бы соответствовали выражения от корней сохраняющие значения при определенных перестановках, из чего следует, что присоединение любых дополнительных радикалов не приблизит нас к решению.
Заключение
Поводом для написания данной статьи послужило желание структурировать свои мысли по этой теме и представить идеи о неразрешимости уравнений в радикалах без привлечения абстрактной алгебры и теории Галуа. По моему мнению, в подавляющем большинстве современных изложений теряется связь между областью, в которой происходит доказательство и конкретными уравнениями. Если у кого-то есть замечания, дополнения или ссылки на подобные элементарные изложения, буду рад услышать.
Формулы для корней алгебраического уравнения пятой степени ?
Формулы для корней алгебраического уравнения пятой степени ?
Формулы для корней алгебраического уравнения пятой степени ?
Комментарий теории:#1 Рутен » 02 дек 2011, 15:50
Основной теоремой алгебры является теорема о количестве корней алгебраического уравнения произвольной степени. Следовательно, основной задачей алгебры является (во всяком случае так было до конца 19 века) задача нахождения формул для корней алгебраического уравнения произвольной степени. Как известно, формулы для квадратного уравнения были известны еще с времен Вавилона. Формулы для корней кубического уравнения получил Сципион Дель Ферро в 1530 году (сейчас они известны, как формулы Кардано (по имени профессора в чьей книге впервые были опубликованы)). Формулы для корней алгебраического уравнения четвертой степени полученны Феррари в 1545 году. С тех пор (скоро уже пятьсот лет) человечество так и несмогло получить формулы для алгебраических уравнений степени выше четырех. Правда, Абель, а затем Галуа (1831-1834 гг.) доказали, что в радикалах таких формул не существует. Однако, это не означает, что их нельзя получить вообще. Формулы для алгебраических уравнений более высоких степеней можно, очевидно, получить через трансцендентные функции, или при помощи степенных рядов. Это доказал немецкий ученый Биркланд, который установил эти корни (через гипергеометрические функции) для усеченного уравнения любой степени (когда в левой части всего три члена, первый — это неизвестное в любой степени, второй — неизвестное степени единица, с произвольным коэффициентом, третий — произвольная постоянная). Все же, когда алгебраическое уравнение задано в общем виде (не знаю как его здесь выписать. не понял, извините, технологии набора формул) — его корни, если коэффициенты произвольные переменные, получить пока никто не может. Поэтому лучшие математики мира (Эйлер, Лобачевский, Ньютон) сосредоточились на нахождении корней алгебраического уравнения для более простого случая, а именно, когда коэффициенты уравнения заданые числа. Эта задача в настоящее время полностью решена. Но построение математических моделей реальных физических процессов не возможно без существования такой теории. В частности даже линейное обыкновенное дифференциальное уравнение становится неразрешимым по этой причине. Т.е. основная задача Алгебры до сих пор не решена. А, вдруг я не прав.
http://habr.com/ru/post/568552/
http://www.newtheory.ru/mathematics/formuli-dlya-korney-algebraicheskogo-uravneniya-pyatoy-stepeni-t1481.html
Алгоритм расчёта вещественных корней полиномов
Время на прочтение
8 мин
Количество просмотров 29K
Основополагающая идея этого алгоритма очень проста и может быть изложена двумя предложениями. Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома. Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.
А теперь по порядку.
Проблема нахождения корней алгебраических полиномов известна давно, по крайней мере со средневековья. В школе учат решать квадратные уравнения. В википедии можно найти формулы Кардано для решения кубических уравнений и описание метода Феррари для решения в радикалах уравнения четвёртой степени. Там же описан метод Лобачевского для решения алгебраических уравнений произвольной степени. Суть метода Лобачевского вкратце сводится к следующему.
Нетрудно, имея некоторый исходный полином, построить полином2, имеющий те же по модулю корни, что и исходный полином, но с противоположным знаком. Перемножая исходный полином и полином2, получаем полином, корни которого равны квадратам корней исходного полинома.
Это преобразование (квадрирование) полезно повторить несколько раз. В результате, если корни исходного полинома не были равны друг другу, их многократно квадрированные значения оказываются далеко разнесёнными по величине, а их приближенные значения очень просто выражаются через коэффициенты соответствующего квадрированного полинома.
В частности, если коэффициент при старшей степени аргумента полинома равен единице, то следующий по старшинству коэффициент равен (с обратным знаком) сумме корней уравнения, а поскольку значения этих корней сильно разнесены, то приближенно можно считать эту сумму равной наибольшему по модулю корню.
Для конкретности сообщим, что для полинома 4-й степени с корнями 1, 2, 3, 4 метод Лобачевского уже после четвёртого квадрирования даёт правильные до второго знака после запятой значения корней. При этом для представления коэффициентов полиномов достаточно формата long double.
Бесспорно, этот метод является ценным инструментом в руках исследователя, наделённого интеллектом. Однако, его программирование для современной вычислительной техники вызывает серьёзные затруднения при необходимости строгой гарантии достоверности результата при всевозможных особых случаях расположения корней.
Теперь я начну описывать иной метод. В общедоступной печати упоминание о нём начинается с работы [1]. Какие-либо независимые публикации о применении такого метода мне неизвестны. Этот алгоритм сводится к последовательному исследованию интервалов монотонного изменения исходного полинома. Если на границах этого интервала монотонности значения полинома имеют разные знаки, то запускается процедура деления отрезка пополам для расчёта точного значения очередного корня. Границами интервалов монотонности являются точки, в которых значение производной полинома обращается в нуль, т.е. это корни производного полинома. Производный полином имеет степень на единицу меньшую, чем исходный полином, и процесс расчёта коэффициентов производных полиномов следует продолжить до полинома первой степени, корень которого находится непосредственно, без привлечения процедуры деления отрезка пополам. В результате этого шага получим два интервала монотонного изменения для производного полинома второй степени.
Теперь можно найти два вещественных корня производного полинома второй степени (если они существуют) и далее по лестнице из производных полиномов подниматься до корней исходного полинома. Остаётся пояснить, как технически реализуются границы «плюс, минус бесконечность» интервалов монотонности исходного и производных полиномов.
Нормируем полином так, чтобы коэффициент при старшей степени аргумента стал равным единице. Пусть M — наибольшее по модулю значение среди его остальных коэффициентов. Тогда значение полинома больше единицы для всех значений аргумента, больших, чем M+1.
Для доказательства рассмотрим расчёт полинома p(x)=x^n+k[n-1]*x^(n-1)+…+k[1]*x+k[0] по схеме Горнера.
На первом шаге вычисляется p[1]=k[n-1]+x и очевидно, что p[1]>1.
На втором шаге вычисляется p[2]=k[n-2]+x*p[1] и вновь очевидно, что p[2]>1.
Аналогичное имеет место на последующих шагах.
На последнем шаге вычисляется p(x)=k[0]+x*p[n-1] и окончательно получим p(x)>1.
Таким образом, если нужно определить знак полинома при бесконечном значении аргумента, следует взять аргумент равным M+1.
Прилагаемый текст соответствующей программы вполне заменяет занудное изложение отдельных технических подробностей описанного тут алгоритма.
Прокомментирую, наконец, не вполне очевидную особенность реализации алгоритма деления отрезка пополам.
Пробная точка pt, расположенная посередине между текущими концами ng и vg отрезка, вычисляется оператором pt=0.5*(ng+vg); а цикл делений пополам прерывается оператором if(pt<=ng||pt>=vg)break;.
В силу конечной точности представления вещественных чисел в машине рано или поздно наступает состояние, при котором операция деления пополам вместо нового числа даёт значение одной из исходных границ. Именно в этом состоянии следует прекратить цикл делений пополам. Это состояние соответствует максимально достижимой точности результата.
Недавно мне удалось использовать этот алгоритм для решения задачи вычисления комплексного корня полинома, не имеющего вещественных корней. Но об этом я планирую рассказать на Хабре в следующей статье.
Ниже, как приложение, приведен полный текст файла polynomRealRoots.cpp, реализующего описанныйалгоритм.
файл polynomRealRoots.cpp
//*************************************************************************
double polinom(int n,double x,double *k)
//полином вида x^n+k[n-1]*x^(n-1)+k[n-2]*x^(n-2)+...+k[1]*x+k[0]
//со старшим коэффициентом, равным единице
{
double s=1;
for(int i=n-1;i>=0;i--)
s=s*x+k[i];
return s;
}//polinom
//расчёт корня полинома методом деления пополам отрезка, содержащего этот корень
double dihot(int degree,double edgeNegativ,double edgePositiv,double *kf)
{
for(;;)
{//цикл деления отрезка пополам
double x=0.5*(edgeNegativ+edgePositiv);
if(x==edgeNegativ||x==edgePositiv)return x;
if(polinom(degree,x,kf)<0)edgeNegativ=x;
else edgePositiv=x;
}//цикл деления отрезка пополам
}//dihot
//один шаг подъёма по лестнице из производных полиномов
void stepUp(
int level, //индекс достигаемой ступеньки лестницы
double **A, //вспомогательные массивы
double **B, //параметров производных полиномов
int *currentRootsCount //сформированные в вызывающей процедуре
)
{
//аргумент полинома, равносильный его бесконечно большому значению
double major=0;
for(int i=0;i<level;i++)
{//формирование major
double s=fabs(A[level][i]);
if(s>major)major=s;
}//формирование major
major+=1.0;
currentRootsCount[level]=0; //рабочая инициализация
//основной цикл поиска корня уравнения
//A[level][0]+A[level][1]*x+...+A[level][level-1]*x^(level-1)+x^level=0
//на очередном интервале монотонности
for(int i=0;i<=currentRootsCount[level-1];i++)
{//очередной интервал монотонности
//signLeft signRight - знаки текущего A-полинома на левой и правой границе интервала монотонности
int signLeft,signRight;
//предварительная левая и правая границы интервала поиска
double edgeLeft,edgeRight;
//границы интервала монотонности, несущие информацию о знаке полинома на них
double edgeNegativ,edgePositiv;
//формирование левой границы поиска
if(i==0)edgeLeft=-major;
else edgeLeft=B[level-1][i-1];
//значение текущего A-полинома на левой границе
double rb=polinom(level,edgeLeft,A[level]);
if(rb==0)
{//маловероятный случай попадания в корень
B[level][currentRootsCount[level]]=edgeLeft;
currentRootsCount[level]++;
continue;
}//маловероятный случай попадания в корень
//запомнить знак текущего A-полинома на левой границе
if(rb>0)signLeft=1;else signLeft=-1;
//формирование правой границы поиска
if(i==currentRootsCount[level-1])edgeRight=major;
else edgeRight=B[level-1][i];
//значение текущего A-полинома на правой границе
rb=polinom(level,edgeRight,A[level]);
if(rb==0)
{//маловероятный случай попадания в корень
B[level][currentRootsCount[level]]=edgeRight;
currentRootsCount[level]++;
continue;
}//маловероятный случай попадания в корень
//запомнить знак текущего A-полинома на правой границе
if(rb>0)signRight=1;else signRight=-1;
//если знаки полинома на границах интервала монотонности совпадают,
//то корня нет
if(signLeft==signRight)continue;
//теперь можно определить плюс границу и минус границу поиска корня
if(signLeft<0){edgeNegativ=edgeLeft;edgePositiv=edgeRight;}
else {edgeNegativ=edgeRight;edgePositiv=edgeLeft;}
//всё готово для локализации корня методом деления пополам интервала поиска
B[level][currentRootsCount[level]]=dihot(level,edgeNegativ,edgePositiv,A[level]);
currentRootsCount[level]++;
}//очередной интервал монотонности
return;
}//stepUp
//процедура находит все вещественные корни полинома любой степени
void polynomRealRoots(
int n, //степень исходного полинома
double *kf, //массив коэффициентов исходного полинома
double *rootsArray, //выходной массив вычисленных корней
int &rootsCount //количество найденных корней
)
{
//используются вспомогательные массивы A и B, имеющие следующее содержание
//A это коэффициенты а B корни производных полиномов
//все A-полиномы нормируются так,
//чтобы коэффициент при старшей степени был равен единице
//A[n] - это массив нормированных коэффициентов исходного полинома
//B[n] - это массив корней исходного полинома
//A[n-1] - это массив нормированных коэффициентов производного полинома
//B[n-1] - это массив корней производного полинома
//аналогичным образом
//A[n-2] и B[n-2] - это коэффициенты и корни дважды производного полинома
//наконец A[1] - это массив коэффициентов последнего полинома
//в цепочке производных полиномов
//это линейный полином и B[1] - это массив его корней,
//представленный единственным значимым элементом
//выделение памяти для вспомогательных массивов
double **A=new double *[n+1];
double **B=new double *[n+1];
//количество вещественных корней для каждого из A-полиномов
int *currentRootsCount=new int[n+1];
for(int i=1;i<=n;i++)
{
A[i]=new double[i];
B[i]=new double[i];
}
//нормировка исходного полинома
for(int i=0;i<n;i++)A[n][i]=kf[i]/kf[n];
//расчёт производных A-полиномов
for(int i1=n,i=n-1;i>0;i1=i,i--)
{
for(int j1=i,j=i-1;j>=0;j1=j,j--)
{
A[i][j]=A[i1][j1]*j1/i1;
}
}
//формирование исходного корня последнего производного полинома
currentRootsCount[1]=1;
B[1][0]=-A[1][0];
//подъём по лестнице производных полиномов
for(int i=2;i<=n;i++)stepUp(i,A,B,currentRootsCount);
//формирование результата
rootsCount=currentRootsCount[n];
for(int i=0;i<rootsCount;i++)rootsArray[i]=B[n][i];
//очистка памяти
for(int i=1;i<=n;i++)
{
delete[]A[i];
delete[]B[i];
}
delete[]A;
delete[]B;
delete[]currentRootsCount;
return;
}//polynomRealRoots
//*************************************************************************
Примите также текст заголовочного файла polynomRealRoots.h, позволяющего легко организовать ссылку на приведенный выше программный модуль.
//*************************************************************************
//процедура вычисления вещественных корней полинома
void polynomRealRoots(int n,double *kf,double *rootsArray,int &rootsCount);
//**
***********************************************************************
Литература
1. Костин И.К. Семейство алгоритмов расчета интервалов прохождения космического аппарата над круговым наземным объектом с учетом продольной ошибки определения параметров орбиты
Вопросы радиоэлектроники, сер. РЛТ, 2004г., вып. 1
Эту ссылку можно найти в Яндексе поиском по закавыченной фразе «семейство алгоритмов расчета», но текст этой статьи в электронном виде, кажется, недоступен. Поэтому приведу здесь цитату из двух предложений этой статьи:
Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома.
Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.