Как найти корни функции онлайн - AvtoShod.ru - решение различных проблем

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Показать Этапы

Номер Строки

Примеры

корни:-6x^{2}+36x-59
корни:x^{2}-x-6
корни:x^{2}-1
корни:x^{2}+2x+1
корни:2x^{2}+4x-6
Показать больше

Описание

Найдите корни любой функции шаг за шагом

roots-calculator

Блог-сообщения, имеющие отношение к Symbolab

High School Math Solutions – Exponential Equation Calculator

Solving exponential equations is pretty straightforward; there are basically two techniques: <ul> If the exponents…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Решение уравнений

Данный онлайн-калькулятор предназначен для нахождения корней функции.

Для решения уравнений вида ax²+bx+c=0 можно воспользоваться сервисом Дискриминант онлайн. В решении приводятся подробное нахождение дискриминанта, а также корней функции. Результаты оформляются в формате Word.
Для нахождения корней уравнения методами дихотомии, Ньютона и других используйте сервис Решение нелинейных уравнений.
Для уравнений высших степеней используйте следующий сервис. Например, x³-3x²+4=0 записываем как x^3-3x^2+4=0.

Примечание: число «пи» (π) записывается как pi; корень квадратный как sqrt, например, sqrt(3)

Более подробно о нахождении корней функции.

Для нахождения нулей функции также можно использовать графический метод, при котором строится график и уже по нему определяется примерное значение x₀. Также применим и метод подбора, когда задается определенный диапазон [a;b] поиска корней функции с некоторым шагом Δh. Например в MS Excel для функции ln(x)+x² с шагом Δh=0.2:

	A	B	C
1	x	f(x)	Условия
2	0	=ln(A2)+A2^2	=Если(B2=0;»корень найден»;»продолжить»)
3	=A2+0,2	=ln(A3)+A3^2	=Если(B3=0;»корень найден»;Если((B2<0)(B3>0)+(B2>0)(B3<0);»корень найден»;»продолжить»))

Пример №1. Красная лента в 4 раза длиннее желтой ленты, а длина желтой ленты короче длины красной на 39 см. Найдите длину каждой ленты.

Решение. Эта задача на составление системы уравнений. Длину красной ленты обозначим за x. Длину желтой ленты обозначим как y.

По условию красная лента в 4 раза длиннее желтой ленты: 4y=x, а длина желтой ленты короче длины красной на 39 см: y=x-39

Имеем систему из двух уравнений:

4y=x

y=x-39

Решаем ее.

1) выразим x=y+39 и подставим в первое уравнение

4y=y+39 или 3y=39

Откуда y=13

x=4*13=52

Ответ: x=52, y=13

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Этот онлайн калькулятор применяет метод Ньютона (также известный как метод касательных) используя калькулятор производных для получения аналитической формулы производной заданной функции (метод Ньютона требует вычисления производной). Под калькулятором можно прочитать краткое описание метода.

Метод Ньютона

Критерий останова (погрешность)

Точность вычисления

Знаков после запятой: 4

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Метод Ньютона¹

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. Далее процесс повторяется, пока не будет достигнута необходимая точность.

Уравнение касательной к графику функции выглядит следующим образом:
$y(x)=f(x_{n})+(x-x_{n})cdot mathrm {tg} ,alpha _{n}$ ,
где $mathrm {tg} ,alpha _{n}$ — тангенс угла пересечения касательной с осью абсцисс.

Тангенс угла пересечения касательной с осью абсцисс, $frac{Delta y}{Delta x}$ — не что иное, как значение производной в точке x_n .
С учетом того факта, что в точке пересечения с осью абсцисс значение y равно нулю, можно записать следующее выражение для нахождения точки пересечения (следующей точки приближения):
$x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}$

Анимация метода Ньютона (Ralf Pfeifer, https://commons.wikimedia.org/wiki/File:NewtonIteration_Ani.gif)

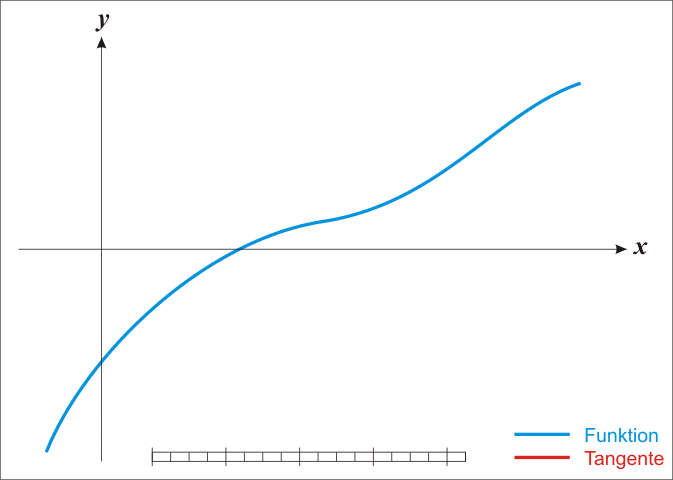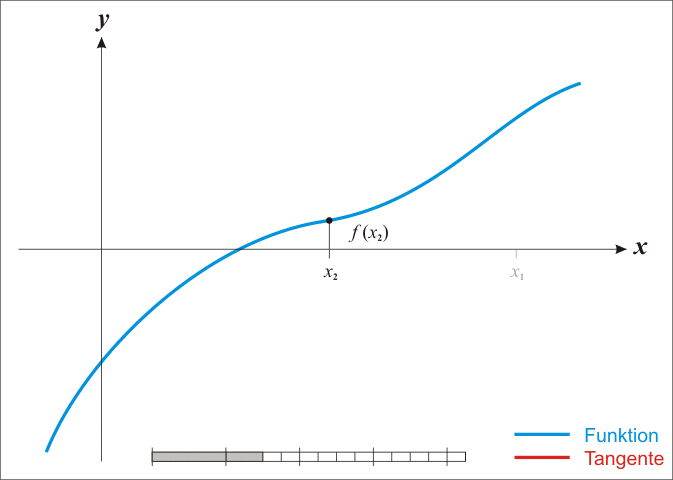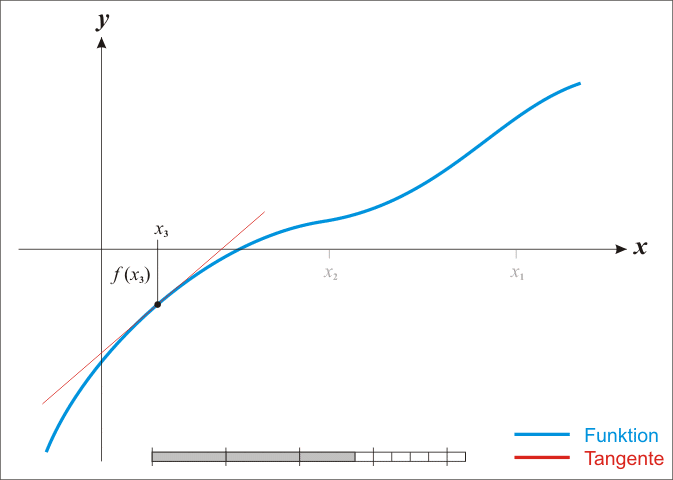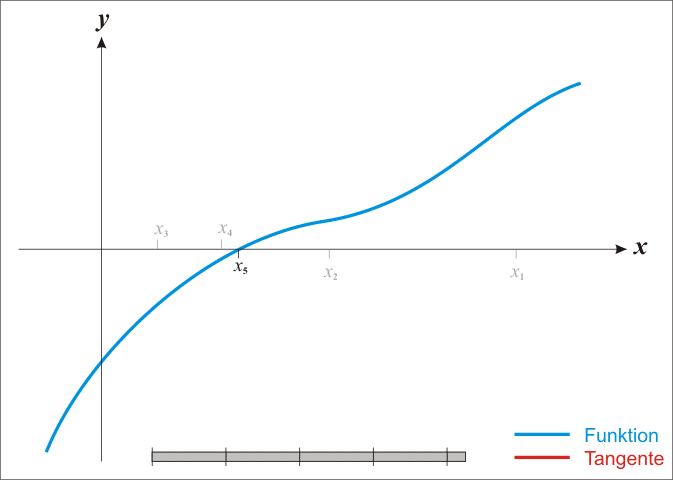
Метод Ньютона является очень мощным методом поиска корней функции, так как имеет квадратичную скорость сходимости — количество значащих цифр примерно удваивается с каждым шагом итерации, однако существуют и ограничения, затрудняющие его применение. Так, например, если начальное приближение недостаточно близко к решению, то метод может не сойтись, если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня, если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена, если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Теорема Канторовича дает следующие условия применимости метода для поиска корней функции:

функция должна быть ограничена;
функция должна быть гладкой, дважды дифференцируемой;
её первая производная f'(x) равномерно отделена от нуля;
её вторая производная f»(x) должна быть равномерно ограничена.

Источник

Решение функций представляется важным при решении множества инженерных и проектировочных задач по возведению тех или иных строительных объектов, изготовлению деталей, планированию грузоперевозок, технологических и иных процессов. К неотъемлемым основным атрибутам всякой функции относится область определения D(f).

При решении функций требуется выявить соответствие, при котором все числа «X» из массива (множества) области определения будут сопоставляться по определенному Правилу численному значению «Y», находящемуся в некоторой зависимости от числа «X».

Важно знать области определения корня, степенной, показательной, логарифмической, основных тригонометрических и обратных тригонометрических функций.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Источник

Производная по-шагам

Примеры производных

Производные от степенных функций
```
x^7/10
```
```
(x^2 - 1)/(x^a - 5)
```
Производные от сложных функций
```
sin(ln(x))
```
```
ln(sin(x))
```
Производные от показательных функций
```
e^(-x^2)
```
Производные от логарифмов
```
1-log(x-5)
```
```
ln(a*x) / ln(x^3)
```
Производные от обратных тригонометрических функций
```
arcsin(1-x)
```
```
arctan(a*x + b)
```
Производная неявной функции
```
e^y/x = x*y + 1
```
Частная производная функции
```
x^2*sin(-y) + y/x
```
```
x*y*cos(z)
```

Подробнее про Производная функции.

Указанные выше примеры содержат также:

модуль или абсолютное значение: absolute(x) или |x|
квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x)
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x)
знак числа:
sign(x)
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x)
Факториал от x:
x! или factorial(x)
Гамма-функция gamma(x)
Функция Ламберта LambertW(x)
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)

Правила ввода

Можно делать следующие операции

2*x: — умножение
3/x: — деление
x^2: — возведение в квадрат
x^3: — возведение в куб
x^5: — возведение в степень
x + 7: — сложение
x — 6: — вычитание
Действительные числа: вводить в виде 7.5, не 7,5

Постоянные

pi: — число Пи
e: — основание натурального логарифма
i: — комплексное число
oo: — символ бесконечности

Источник

Номер Строки

Решение уравнений

Метод Ньютона

Метод Ньютона1

Производная по-шагам

Примеры производных

Правила ввода

Постоянные

Не пропустите также:

Метод Ньютона¹