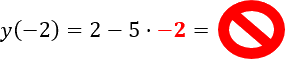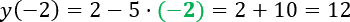Как найти корни функции математика - AvtoShod.ru

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Обратная пропорциональность

Если переменная у обратно пропорциональная переменной х, то эта зависимость выражается формулой

k — коэффициент обратной пропорциональности.

Например:

Область определения функции есть множество всех чисел, отличных от нуля.

Графиком обратной пропорциональности является гипербола. Если k>0, то ветви гиперболы расположены в I и в III координатных четвертях: если k<0, то ветви гиперболы расположены во II и в IV координатных четвертях.

График функции строится по точкам, для этого составляют таблицу значений функции:

x	-4	-3	-2	-1	1	2	3	4
y	k:(-4)	k:(-3)	k:(-2)	k:(-1)	k:1	k:2	k:3	k:4

Свойства функции

1. Область определения: D(y)=(-∞; 0) U (0; +∞).

2. Множество значений: Е(у)=(-∞; 0) U (0; +∞).

3. Функция не имеет минимального и максимального значения.

4. Нули функции: функция не имеет нулей.

5. Промежутки знакопостоянства функции:

если k>0: y<0 при х ∈(-∞; 0);

y>0 при х ∈(0; +∞);

если k<0: y<0 при х ∈(0; +∞);

y>0 при х ∈(-∞; 0).

6. Промежутки монотонности:

если k>0 функция убывает на промежутке (-∞; 0) U (0; +∞);

если k<0 функция возрастает на промежутке (-∞; 0) U (0; +∞).

Функция у=x³

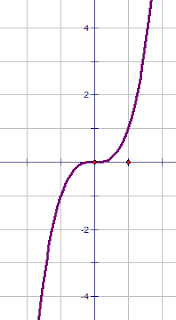
Функцию вида y= x³ называют кубической функцией. Графиком кубической функции является кубическая парабола, проходящая через начало координат. Ветви кубической параболы y=x³находятся в I и III четвертях.

График функции строится по точкам, для этого составляют таблицу значений функции:

x	-2,5	-2	-1,5	-1	1	1,5	2	2,5
y	-15,625	-8	-3,375	-1	1	3,375	8	15,625

Свойства функции

1. Область определения: D(y)=(-∞; +∞).

2. Множество значений: Е(у)=(-∞; +∞).

3. Функция не имеет минимального и максимального значения.

4. Нули функции: х=0.

5. Промежутки знакопостоянства функции:

y<0 при х ∈(-∞; 0);

y>0 при х ∈(0; +∞).

6. Промежутки монотонности:

функция возрастает на промежутке (-∞; +∞).

Функция квадратного корня

Функцией арифметического корня называют функцию, заданную формулой

Т.к. выражение имеет смысл только при неотрицательных значениях х, то функция задается на промежутке (0; +∞).

График функции строится по точкам, для этого составляют таблицу значений функции:

x	0	4	9	16
y	0	2	3	4

Свойства функции

1. Область определения: D(y)=[0; +∞).

2. Множество значений: Е(у)=[0; +∞).

3. Функция не имеет максимального значения; минимальное значение равно 0.

4. Нули функции: х=0.

5. Промежутки знакопостоянства функции:

y>0 при х ∈(0; +∞).

6. Промежутки монотонности:

функция возрастает на промежутке [0; +∞).

УПРАЖНЕНИЯ

1. Графиком каких из функций является гипербола?

Решение:

а) График функции у=k/x — гипербола, следовательно гипербола является графиком функции у=1/х.

Ответ: 3)

2. Из данных функций укажите те, график которых проходит через начало координат:

Решение:

а) Если график функции проходит через начало координат, то при х=0 у=0.

Следовательно графики функций

проходят через начало координат.

Ответ: 1), 3), 4), 5).

3. а) График обратной пропорциональности проходит через точку с координатами (2; -2). Найдите коэффициент обратной пропорциональности.

б) График обратной пропорциональности проходит через точку с координатами (4; 1,75). Найдите коэффициент обратной пропорциональности.

Решение:

а) Формула обратной пропорциональности y=k/x. Подставим вместо х и у координаты точки (2; -2) и найдем коэффициент k.

-2=k:2; k=-4.

Ответ: -4.

4. Укажите функции, областью определения которых являются все действительные числа:

Решение:

а) Область определения функции ограничена, если в формуле, которой задана функция есть квадратные корни и знаменатели, которые могут принимать значение 0 при некоторых значениях х. Область определения — все действительные числа у функций:

Ответ: 1), 4).

5. Из указанных функций

выберите обратную пропорциональность, график которой расположен:

а) в I и III координатных четвертях;

б) во II и IV координатных четвертях.

Решение:

а) в I и III координатных четвертях находятся графики обратной пропорциональности с коэффициентом k>0.

Ответ: 3), 4).

6. Переменные х и у обратно пропорциональны.

а) Известно, что при х=0,5 у=12. Найдите значение у при х=-2;

б) известно, что при х=1,5 у=-6. Найдите значение у при х=2.

Решение:

а) Составим формулу обратной пропорциональности, для этого в формулу y=k/x подставим значения х=0,5 и у=12, найдем коэффициент k.

12=k:0,5; k=12*0,5=6. Обратная пропорциональность задана формулой у=6/х. Подставим в эту формулу х=-2: у=6: (-2)=-3.

Ответ: -3.

7. Найдите область определения функции:

Решение:

а) Выражение под корнем (4х-1)(х+0,5) должно быть неотрицательным. Решим неравенство:

(4х-1)(х+0,5)≥0,

Найдем нули функции (4х-1)(х+0,5)=0:

4х-1=0 или х+0,5=0

х=0,25 х=-0,5

Решим неравенство методом интервалов:

Ответ: (-∞; -0,5]U[0,25; +∞).

8. а) Найдите значения аргумента, при которых функция принимает отрицательные значения

б) Найдите значения аргумента, при которых функция принимает положительные значения

Решение:

а) Рассмотрим неравенство

Умножив обе части неравенства на (-1) получим:

Числитель равен 3 — положительное число, знаменатель тоже является положительным числом, следовательно дробь положительна на области определения. Найдем область определения функции:

16-x²>0,

x²<16,

|x|<4.

Ответ: (-4; 4).

9. График какой из функций симметричен относительно начала координат? Постройте график выбранной функции:

Решение:

а) Симметричен относительно начала координат график функции у=0,5x³
Построим таблицу значений функции:

x	-3	-2	-1	0	1	2	3
y	-13,5	-4	-0,5	0	0,5	4	13,5

Построим график:

10.Постройте график функции:

Решение:

Построим таблицу значений функции:

x	-3	-2	0	1	2	3
y	-3	-6	6	3	2	1,5

Построим график:

11. а) Построив графики функций у=5-х и Найдите количество корней уравнения

б) Построив графики функций у=-2-х и y=x³ найдите количество корней уравнения -х-2=x³

Решение:

а) Графиком функции y=5-x является прямая, для ее построения найдем координаты двух точек:

Таблица значений функции :

Построим оба этих графика в одной системе координат и найдем их точку пересечения:

12. Найдите область определения функции:

Решение:

а) Выражения под корнем должны быть неотрицательны. Решим систему неравенств:

Ответ: [4; +∞).

13. Постройте графики функций и найдите точки пересечения графика с осями координат:

Решение:

a) Графиком данной функции является гипербола. Построить можно выполнив сдвиг графика функции у=3/х на 3 единицы вправо и на две единицы вверх.

Построим таблицу значений функции:

x	-4	-3	-2	-1	0	2	3	4
y	4,4	4,25	4	3,5	2	8	6,5	6

Построим график:

График с осями координат имеет две точки пересечения.

14. а) Докажите, что данная функция убывает на промежутке (3; +∞);

б) Докажите, что данная функция возрастает на промежутке (-2; +∞):

Решение:

а) Найдем область определения функции

D=(-∞; 3)U(3; +∞).

Рассмотрим х1 и х2, принадлежащие промежутку (3; +∞) такие, что x1>x2.

Тогда

Найдем разность у1-у2:

Т.к. x1>x2, то числитель будет отрицательным числом. (х1-3) и (х2-3) на промежутке (3; +∞) будут положительными числами, следовательно у1-у2<0.

Т.к. х1>x2 и y1-y2<0, то функция убывает на промежутке (3; +∞).

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. В каких координатных четвертях расположен график функции, заданный формулой:

а) у=-0,9/х; б) у=1,4/х?

2. Из числовых промежутков (-∞; 5], (0;+∞), (5; +∞) и [5;+∞) выберите тот, который является областью определения функции

3. Какой из графиков функций, заданных формулами не проходит через начало координат

4. Найдите область определения функции, заданной формулой:

5. Постройте график функции, заданной формулой:

6. а) График обратной пропорциональности проходит через точку А(8; 4). Найдите значение этой функции при х=-10.

б) График обратной пропорциональности проходит через точку А(-16; 2). Найдите значение этой функции при х=5.

7. Найдите точки пересечения с осью Оу графика функции, заданного формулой:

8. Постройте график функции и укажите нули функции, если они существуют:

9. Докажите, что при х≥1 функция возрастает

10. Найдите область определения функции:

Проверь себя

Источник

Что такое функция? Представим себе машину, которая двигается по дороге из одного города в другой. Мы можем в каждый момент времени определить положение машины. То есть у нас есть множество различных моментов времени и множество точек, определяющих положение машины на дороге. При этом положение машины на дороге зависит от того, в какой момент времени мы определяем это положение. То есть одно множестве переменных величин зависит от другого множества, каждая отдельная переменная из одного множества зависит от переменной из другого множества. Зависимость одной переменной от другой называется функциональной зависимостью.

Функция – это что

В этой статье мы рассмотрим что такое функция, дадим определения области определения функции и области ее значений, понятие графика функции.

Область определения и область значений функции
Как найти область определения функции
- Пример 1
- Пример 2
- Пример 3
График функции
Способы задания функции
Монотонность функции
- Пример
Четные и нечетные функции
- Пример 1
- Пример 2
- Пример 3
Периодические функции
Промежутки знакопостоянства и корни функции

Область определения и область значений функции

– значение функции в точке .

Если область определения функции и область ее значений определены в множестве рациональных чисел, то функцию называют числовой.

Элементы множества еще называют значениями аргумента, а соответствующие им элементы – значениями функции.

Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

Например, область определения функции, заданной формулой $y=frac{1}{x}$ , состоит из всех чисел, кроме нуля.

Как найти область определения функции

Для того, чтобы найти область определения функции, мы должны определить – где функция будет существовать, при каких значениях аргумента. Приведем примеры:

Пример 1

Найти область определения функции $y=frac{x}{x-5}$

Зададимся вопросом – при каких значениях функция будет существовать? Очевидно, что функция существует, если знаменатель дроби не равен нулю. То есть .

Для определения этого значения решим уравнение:

Находим, .

То есть функция не будет существовать при значении . Тогда областью определения функции (где она существует) – будут все значения кроме 5. Через интервалы можно записать так:

Пример 2

Найти область определения функции .

Здесь функция определена при любых значениях аргумента. То есть D(f) – все числа.

Пример 3

Определить область определения функции

Выражение, стоящее под знаком квадратного корня, должно быть больше или равно нулю. Таким образом, мы можем записать:

Решим данное неравенство и получим: .

Тогда область определения функции будет интервал значений аргумента .

График функции

Графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. То есть график функции – это изображение на координатной плоскости множества пар , связанных зависимостью , где .

Способы задания функции

Функция может быть задана аналитически в виде формулы , где переменная – элемент множества значений аргумента, а переменная – соответствующее значение функции.

Например, формула определяет некоторую функцию, где каждому значению переменной , взятому из области определения функции, соответствует единственное значение переменной .

Функция полностью определяется заданием множества пар , где принимает все значения из , а – соответствующие значения функции.

Однако не всякое множество точек координатной плоскости является графиком некоторой функции. Например, если мы рассмотрим следующий график, то увидим, что значению соответствуют три значения , и, следовательно, такое соответствие не является функцией.

График не является графиком функции

Для того, чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси , пересекалась с указанным графиком не более чем в одной точке.

Монотонность функции

Функция называется возрастающей на данном числовом промежутке , если большему значению аргумента соответствует большее значение функции . Это значит, что для любых и из промежутка , таких, что , выполнено неравенство .

Функция называется убывающей на данном числовом промежутке , если большему значению аргумента соответствует меньшее значение функции . Это значит, что для любых и из промежутка , таких, что , выполнено неравенство .

Функция только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.

О монотонности функции можно судить по ее графику. Например, функция, график которой изображен ниже является монотонно возрастающей на всей числовой оси.

Монотонно возрастающая функция

А вот эта функция является монотонно убывающей.

Монотонно убывающая функция – график функции.

А теперь рассмотрим вот такой график функции – на ней функция убывает на промежутке и возрастает на промежутке .

График функции которая монотонно убывает и монотонно возрастает на определенных интервалах области определения функции.

Пример

Докажите, что функция, заданная формулой , где , возрастающая.

Решение: Пусть , где и . Тогда $f(x_2)-f(x_1)=5{x_2}^2-5{x_1}^2=5({x_2}^2-{x_1}^2)=5(x_2-x_1)(x_2+x_1)>0$ .

Поскольку , то и , а, значит, . То есть большему значению аргумента соответствует большее значение функции, таким образом, функция возрастающая на промежутке .

Четные и нечетные функции

Пример 1

Доказать, что функция не является ни четной, ни нечетной.

Доказательство.

Областью определения данной функции является вся числовая прямая, то есть условие 1 выполнено. Проверяем условие 2.

Чтобы доказать, что функция не является четной, нам нужно доказать, что условие 2 для четной функции не выполняется, то есть что .

Пусть , тогда . Проверяем: , а , таким образом . Функция не является четной. Одновременно, не выполняется и второе условие для нечетной функции, мы получили, что: . То есть функция не является нечетной.

Пример 2

Определите четность или нечетность функции:

$y=x+frac{1}{x}$

Решение: область определения данной функции – вся числовая ось, кроме точки (на ноль делить нельзя). Найдем .

Получим: $y(-x)=-x+frac{1}{-x}$ . Вынесем минус за скобки:

$y(-x)=-(x+frac{1}{x})=-y(x)$ .

Отсюда выходит, что , то есть выполняется условие для нечетной функции. А, значит, функция $y=x+frac{1}{x}$ – нечетная функция.

Пример 3

Определить четность или нечетность функции:

Решение: Первое условие о симметричности области определения функции выполняется, так как область определения функции . Переменим знак аргумента функции и упростим:

Получается, что . То есть функция – четная.

Периодические функции

Если – период функции, то , где , , также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривается наименьший положительный период.

Значения периодической функции через промежуток, равный периоду, повторяются. Это обстоятельство используется при построении графиков.

Промежутки знакопостоянства и корни функции

Числовые промежутки, на которых функция сохраняет свой знак (то есть остается положительной или отрицательной), называются промежутками знакопостоянства функции.

О промежутках знакопостоянства функции можно сделать вывод, посмотрев на график функции. Например, возьмем график функции . Здесь при $x in R_{+}$ , при $x in R_{-}$ . В первом случае график расположен выше оси , во втором – ниже ее.

График линейной функции

Корни функции

Итак, мы с вами изучили что такое функция, определили когда функция является четной, а когда нечетной, способы задания функции, область определения функции и область ее значений. А также дали понятие периодической функции и корней функции. Выяснили, что называется промежутками знакопостоянства функции. Привели примеры.

Читайте еще похожие статьи:

Источник

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».

После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание.
Функция задана формулой «y = 2x − 1»

Вычислить «y» при «x = 15»
Найти значение «x», при котором
значение «y» равно «−19».

Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.

Запись решения выглядит следующим образом.

y(15) = 2 · 15 − 1 = 30 − 1 = 29

Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.

То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .

−19 = 2x − 1

Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.

Запомните!

Не забывайте про правило переноса в уравнениях.

При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.

−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.

−2x = 18 | · (−1)
2x = −18

Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .

2x = −18 | (: 2)
x = −9

Как проверить верно ли равенство для функции

Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».

Верно ли равенство
«f(−2) = −18»?

Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.

Важно!

Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.

Не забывайте использовать
правило знаков.

Неправильно

Правильно

С помощью расчетов мы получили
«f(−2) = 12».

Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию «y = x² −5x + 6»

Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).

Для этой задачи нет необходимости, строить график заданной функции.

Запомните!

Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).

Если получится верное равенство, значит, точка принадлежит функции.

Вернемся к нашему заданию. Подставим в функцию «y = x² − 5x + 6»
координаты точки (1; 2).

Вместо «x» подставим «1».
Вместо «y» подставим «2».

2 = 1² − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)

У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x² − 5x + 6»?

Вместо «x» подставим «0».
Вместо «y» подставим «1».

1 = 0² − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)

В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x² − 5x + 6»

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.

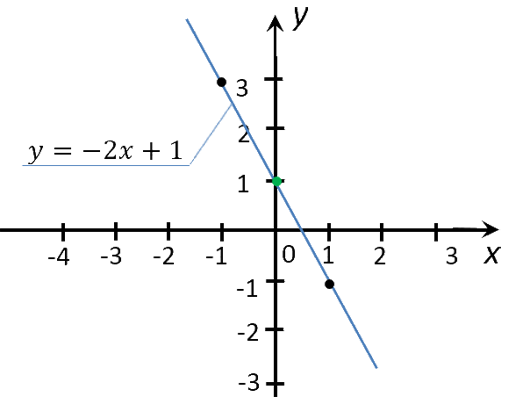
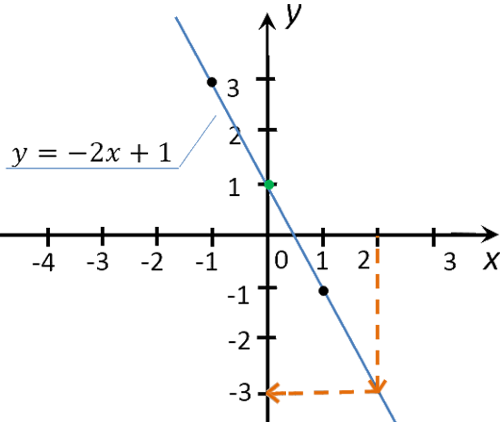
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.

Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.

Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».

Полученное значение «−3» на оси «Oy» и будет искомым значением «y».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».

Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.

y(2) = −2 · 2 + 1 = −4 + 1 = −3

При расчетах мы также получили y = −3.

Значит, мы правильно получили координаты с графика функции.

Важно!

Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.

При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Только подстановка значений в формулу функции дает точные результаты.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

11 ноября 2018 в 15:46

Веточка Сакуры
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Веточка Сакуры
Профиль
Благодарили: 0

Сообщений: 1

Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= — x² — 8x.Найдите значение фун. в т. минимума (y min).

0
Спасибо thanks
Ответить

12 ноября 2018 в 3:25
Ответ для Веточка Сакуры

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

y_min= y(4) = -16.

0
Спасибо thanks
Ответить

17 сентября 2018 в 13:28

Alesger Mammedov
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Alesger Mammedov
Профиль
Благодарили: 0

Сообщений: 1

Добрый день помогите пожалуйста с задачкой
f(x²-3x)=3x²+5x-4
f(3)=?

0
Спасибо thanks
Ответить

17 сентября 2018 в 23:01
Ответ для Alesger Mammedov

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

f(3) = 26 ± 7√21

0
Спасибо thanks
Ответить

13 ноября 2016 в 6:43

Роман Безбородов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Роман Безбородов
Профиль
Благодарили: 0

Сообщений: 1

определите вид графика

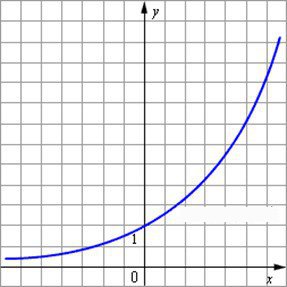
0
Спасибо thanks
Ответить

14 ноября 2016 в 17:30
Ответ для Роман Безбородов

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

y = a^x; a > 1.

0
Спасибо thanks
Ответить

7 сентября 2016 в 22:08

Иван Баранов
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Иван Баранов
Профиль
Благодарили: 0

Сообщений: 3

у=Х²+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10

0
Спасибо thanks
Ответить

8 сентября 2016 в 15:26
Ответ для Иван Баранов

Юлия Анарметова
(^-^)
Профиль
Благодарили: 0

Сообщений: 11

(^-^)
Юлия Анарметова
Профиль
Благодарили: 0

Сообщений: 11

аргумент это х значит у=(-2)²+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5

0
Спасибо thanks
Ответить

Источник

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Функция

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Парабола

Графиком функции y = a x 2 + b x + c является парабола.

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

Коэффициент a указывает на то, куда направлены ветки параболы.

Если a > 0 , ветки параболы направлены вверх.
Если a < 0 , ветки параболы направлены вниз.

Коэффициент c указывает, в какой точке парабола пересекает ось y.
Коэффициент b помогает найти x в – координату вершины параболы.

x в = − b 2 a

Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

Если D > 0 – две точки пересечения.
Если D = 0 – одна точка пересечения.
Если D < 0 – нет точек пересечения.

Гипербола

Графиком функции y = k x является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Квадратный корень

Функция y = x имеет следующий график:

Возрастающие/убывающие функции

Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

Скачать домашнее задание к уроку 5.

Источник

На этой странице вы узнаете:

За что отвечают коэффициенты в записи линейной функции?
Как пронумерованы четверти на координатной плоскости?
Чем отличается график функции квадратного корня от графика квадратичной функции и почему?

Линейная функция

Любую функцию можно изобразить на графике (рисунке) и наглядно определить многие её свойства. Этим пользуются люди, составляя графики движения транспорта, посещения соцсетей или просмотра видеороликов на канале.

Вспомним, что функция – это зависимость одной переменной от другой, а график функции – это представление данной зависимости на координатной плоскости.

С помощью графика функции можно изучать поведение функции: возрастает или убывает, имеет ли нули, на каких промежутках значения положительные, а на каких отрицательные, наибольшее и наименьшее значение, является ли симметричной относительно OY.

Теперь давайте рассмотрим основные элементарные функции.

Что же такое линейная функция?

Линейная функция – это функция вида y=kx+b, где k и b – известные числа, графиком которой является прямая.

y = kx + b, где
k – коэффициент
b – свободный член
x – переменная

С линейной функцией мы встречаемся, когда оплачиваем проезд в общественном транспорте.

Коэффициент и переменная определяют стоимость билета в зависимости от дальности поездки. Свободным членом может выступать доплата за комфортное место или за поезд-экспресс.

Пункт назначения	Станция 200 км	Станция 300 км	Станция 400 км
Цена поездки в обычном вагоне (kx)	500 руб.	750 руб.	1000 руб.
Цена за вагон “Люкс” (kx + b)	750 руб.	1000 руб.	1250 руб.

Рассмотрим пример такой функции и ее график:
y = 2x + 3

Составим таблицу значений.

Теперь отметим найденные точки на координатной плоскости и проведём через них прямую.

Полученный нами график является графиком данной линейной функции.

Также можно составить уравнение линейной функции самостоятельно при наличии графика.

За что отвечают коэффициенты в записи линейной функции?

Коэффициент b – это длина отрезка по оси OY, на который происходит сдвиг от начала координат (может быть отрицательным, если пересечение графика с осью Y в точке с отрицательным значением).

Коэффициент k – это угол наклона прямой, он равен отношению разностей координат двух произвольных точек.

На графике найдем сначала коэффициент b , после определим координаты двух произвольных точек прямой и вычислим коэффициент k.

Подставим найденные коэффициенты в формулу линейной функции и получим
(y = frac{1}{2}x + 2)

Свойства линейной функции:

Область определения: D(y) = (-∞; +∞)
Область значений функции: E(y) = (-∞; +∞)
Наименьшего и наибольшего значения не существует.
Непериодическая.
Возрастает при k > 0, убывает при k < 0.

Квадратичная функция

Квадратичная функция – это функция вида y = ax², где a – известное число и a ≠ 0, графиком которой является парабола.

y = ax², где
a – известное число
a ≠ 0
x – переменная

Для примера построим график функции y = 2x²

Параболой можно описать полет мяча в баскетбольную корзину.

Какой вид имеет парабола в зависимости от коэффициента a ?

При a > 0 – ветви параболы вверх

При a < 0 – ветви параболы вниз

Сдвиг параболы по оси Y

y = ax² + c

При c > 0 – сдвиг параболы вверх

При c < 0 – сдвиг параболы вниз

Сдвиг параболы по оси X

y = a(x — n)²

При n > 0 – сдвиг параболы вправо

При n < 0 – сдвиг параболы влево

Свойства квадратичной функции:

Область определения: D(y) = (-∞; +∞)
Область значений функции: E(y) = [0; +∞)
При a > 0 – наименьшее значение y = 0.
При a < 0 – наибольшее значение y=0.
Непериодическая.
На (-∞; 0] – убывает при a > 0 и возрастает при a < 0.
На [0; +∞) — убывает при a < 0 и возрастает при a > 0.
Нуль функции x=0.
Четная (симметричная относительно OY).

Функция обратной пропорциональности

Функция обратной пропорциональности – это функция вида y = (frac{k}{x}), где k – известное число и k ≠ 0, графиком которой является гипербола.

(y = frac{k}{x}), где
k – известное число
k ≠ 0
x – переменная

Рассмотрим пример такой функции (y = frac{2}{x})

Как коэффициент k влияет на расположение гиперболы?

Как пронумерованы четверти на координатной плоскости?

Вспомним четверти плоскостей. Они идут против часовой стрелки начиная с четверти, где и x, и y — положительные.

Гипербола при k > 0 – в первой и третьей плоскостях

Гипербола при k< 0 – во второй и четвертой плоскостях

Гипербола может также двигаться по оси X или по оси Y

Движение графика по оси Y

(y = frac{k}{x} + n) при k> 0

При n < 0, сдвиг вниз
При n > 0, сдвиг вверх

По графику выше можно сделать вывод, что n = 3.

Движение графика по оси X

(y = frac{k}{x + c}) при k> 0

При c < 0, сдвиг вправо
При c > 0, сдвиг влево

По графику выше можно сделать вывод, что c = 3.

Свойства функции обратной пропорциональности:

Область определения: D(y) = (-∞; 0) U (0; +∞)
Область значений функции: E(y) = (-∞; 0) U (0; +∞)
Наименьшего и наибольшего значений не существует.
Непериодическая.
При k > 0 убывает на (-∞;0) и (0; +∞).
При k < 0 возрастает на (-∞; 0) и (0; +∞).
Нулей нет.
Нечетная.

Где же в реальной жизни мы можем встретить эту функцию?

Самый простой пример – движение автомобиля: чем выше его скорость, тем меньше времени потребуется, чтобы преодолеть одно и то же расстояние.

Функция квадратного корня

Функция квадратного корня – это функция вида (y = sqrt{x}), где x ≥ 0 .

(y = sqrt{x}), где
x – переменная
x ≥ 0

В жизни такая функция часто используется для определения стороны квадрата при известной площади. Например: при проектировании дома или разбиения участка земли на квадраты.

Рассмотрим график такой функции.

Чем отличается график функции квадратного корня от графика квадратичной функции и почему?

По графику квадратного корня уже видно, что это половина параболы, изображенной вдоль оси х. А график квадратичной функции — это целая парабола, изображенная вдоль оси y.
Так как корень всегда положительный, у функции квадратного корня (y = sqrt{x}) , всегда y ≥ 0. А значит не будет части параболы, где y < 0.
Если возвести обе части функции квадратного корня в квадрат, то получим y² = x. Получившаяся функция будет уже квадратичной функцией относительно y, следовательно, будет строиться относительно х.

Какие бывают сдвиги функции квадратного корня?

Сдвиг по оси Y

(y = sqrt{x} + n)

При n < 0, сдвиг вниз
При n > 0, сдвиг вверх

По графику выше можно утверждать, что n = -2.

Сдвиг по оси X

(y = sqrt{x + c})

При c < 0, сдвиг вправо
При c > 0, сдвиг влево

Сделаем вывод, что для рисунка выше c = -2.

Свойства функции квадратного корня:

Область определения: D(y) = [0; +∞)
Область значений функции: E(y) = [0; +∞)
Наименьшее значение при y = 0.
Непериодическая.
Возрастает на всей области определения.
Нуль функции x = 0.

Фактчек

Линейная функции y = kx + b.
Квадратичная функции y = ax².
Функция обратной пропорциональности (y = frac{k}{x}).
Функция квадратного корня (y = sqrt{x}).

Термины

Элементарная функция – это функция вида y = f(x) , где f(x) – это формула, содержащая конечное число арифметических операций.

Парабола – это незамкнутая линия, точки на которой равноудалены от оси ординат.

Проверь себя

Задание 1.
Определите какая из функций является линейной

(y = 2x^2 + frac{1}{2})
(y = sqrt{x + 2})
(y = frac{1}{2}x + 3)
(y = frac{1}{x — 2})

Задание 2.
Определите какая из функций является квадратичной

y = 4(x — 1)²
y = 2x + 11
(y = frac{x}{2} + 1)
(y = sqrt{x} + 3)

Задание 3.
Определите какая функция является обратной пропорциональностью

(y = frac{x}{2} + 5)
(y = frac{1}{x + 2})
(y = sqrt{x + 1})
y = x²

Задание 4.
Определите какая функция является функцией квадратного корня

y = x²
(y = sqrt{x — 1} — 4)
(y = 6x + frac{1}{3})
y = 2x² + 3

Задание 5.
В какую сторону будет сдвиг у параболы y = (x + 4)²?

Вправо
Вниз
Вверх
Влево

Ответы: 1. – 3; 2. – 1; 3. – 2; 4. – 2; 5. – 4

Источник

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Обратная пропорциональность

Свойства функции

Функция у=x3

Свойства функции

Функция квадратного корня

Свойства функции

УПРАЖНЕНИЯ

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Проверь себя

Область определения и область значений функции

Как найти область определения функции

Пример 1

Пример 2

Пример 3

График функции

Способы задания функции

Монотонность функции

Пример

Четные и нечетные функции

Пример 1

Пример 2

Пример 3

Периодические функции

Промежутки знакопостоянства и корни функции

Как получить значение функции

Как проверить верно ли равенство для функции

Неправильно

Правильно

Как проверить, что точка принадлежит графику функции

Как получить координаты точки функции

Ваши комментарии

Декартова система координат

Функция

Прямая

Парабола

Гипербола

Квадратный корень

Возрастающие/убывающие функции

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

На этой странице вы узнаете:

Линейная функция

Квадратичная функция

Функция обратной пропорциональности

Функция квадратного корня

Фактчек

Термины

Проверь себя

Не пропустите также:

Функция у=x³