Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
2+1=3
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
x+2-2=7-2
x+0=7-2
x=7-2
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
x=5
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
x-4+4=12+4
x=12+4
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
x=16
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x=2x-5
4+3x-2x=-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4+3x-2x=-5
3x-2x=-5-4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅(-9)=2⋅(-9)-5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x:5=20:5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅4=20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
1x=21 или x=21
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
3x=45
Далее делим все уравнение на 3.
3x:3=45:3
(3:3)x=15
1x=15 или x=15
Сделаем проверку. Подставим в уравнение найденный корень.
5=5
Ответ: x=15
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
Математика
6 класс
Урок №50
Уравнения.Часть 2
Перечень рассматриваемых вопросов:
– уравнения;
– корни уравнений.
Тезаурус
Уравнение – равенство содержащее букву, значение которой надо найти.
Решить уравнение – значит найти все его корни.
Корнем уравнения называют такое число, при подстановке которого в уравнение вместо неизвестного, получается верное числовое равенство.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Как решаются уравнения? Чем уравнение отличается от буквенного выражения? На эти и другие вопросы, связанные с уравнениями, мы сегодня и будем отвечать.
Дадим определение уравнению. Уравнением называют равенство, содержащее букву, значение которой надо найти.
Например, 2х – 5=17.
Решить уравнение – значит найти все его корни.
В нашем случае x=11.
Корнем уравнения называют такое число, при подстановке которого в уравнение вместо неизвестного, получается верное числовое равенство.
Подставим в уравнение корень
2 ∙ 11 – 5 = 17,
17 = 17.
Получается, что левая и правая части равны семнадцати.
При решении уравнений можно использовать следующие приёмы:
– переносить числа из одной части уравнения в другую, меняя их знак на противоположный.
– делить или умножать обе части уравнения на одно и тоже число отличное от нуля.
Решим уравнение:
2х + 7 = – 3х – 8.
Равенство не изменится, если к обеим частям уравнения прибавить по числу три икс:
2х + 3х + 7 = – 8.
Перенесём число 7 из левой части в правую часть уравнения с противоположным знаком:
2х + 3х = – 8 – 7.
Применим распределительный закон для правой части:
(2 + 3)х = – 8 – 7.
Упростим левую и правую части уравнения:
5х = – 15.
Равенство не изменится, если обе части уравнения разделить на 5:
x = – 15 : 5.
Корень уравнения:
х = – 3.
Ответ: х = – 3.
Проверка:
2х + 7 = – 3х – 8,
х = – 3,
2 ∙ (– 3) + 7 = – 3 ∙ (– 3) – 8,
– 6 + 7 = 9 – 8,
1 = 1.
Значит, корень уравнения найден верно.
Решим уравнение:
1/2 x+3=-8.
Перенесём число 3 в правую часть уравнения с противоположным знаком:
Где используются уравнения?
Ответ на этот вопрос достаточно прост. Уравнения используются практически везде. В школе мы решаем с помощью уравнений текстовые задачи. В окружающем нас мире все природные и жизненные процессы протекают по определённым закономерностям, большинство из которых можно описать с помощью уравнений. Например, если нужно определить во сколько должен выехать автомобиль, чтобы прибыть вовремя из пункта А в пункт В, необходимо использовать уравнения движения. Для точного расчёта затрат и прибыли на предприятиях используют экономические уравнения. В медицине для обработки данных ультразвуковых исследований организма тоже используются уравнения.
Итак, уравнения – это универсальный инструмент для решения самых разных прикладных задач.
Разбор заданий тренировочного модуля
Тип 1.Найдите корни уравнения.
2х – х – 5= – 18
Решение.
Перенесём – 5 в правую часть уравнения с противоположным знаком:
2х – х= – 18 + 5.
Вычислим отдельно левую и правую части уравнения.
x= – 13.
Это и есть корень уравнения.
Ответ: х= – 13.
Тип 2. Будет ли являться корнем данного уравнения число 7?
x+6= 17 – 2х
Решение.
Чтобы выполнить данное задание нужно подставить число 7 вместо неизвестного х и проверить, будут лиравны правая и левая части уравнения. Если будут равны, то число является корнем уравнения, если правая и левая части уравнения не равны, то число не является корнем уравнения.
Получаем
7+6=17 – 2 • 7
13= 17 – 14
13 ≠ 3
Видно, что при подстановке в уравнение числа 7 верное равенство не получилось. Следовательно, число 7не является корнем уравнения.
Корень уравнения
4.3
Средняя оценка: 4.3
Всего получено оценок: 164.
4.3
Средняя оценка: 4.3
Всего получено оценок: 164.
Тема уравнения сопровождает учеников на протяжении всей школьной программа. Немного странно, что большая часть учащихся 6 класса математики забывают, что же такое корень и решают уравнения, не понимая своих действий. Чтобы не допускать этой ошибки поговорим обо всех особенностях корней уравнения
Неизвестное
Чтобы говорить об уравнениях, нужно вспомнить, что такое неизвестное. Под неизвестным понимается буквенное выражение, которое в общем случае может принимать абсолютно любое значение.
Неизвестные могут перемножаться с числом или друг с другом. Таким образом, получается классический одночлен. Например, выражение 3 а*в является одночленом.
Если одночлены складываются, вычитаются или делятся друг на друга, получается многочлен. Многочлен, приравненный к какому-то числу, называется тождеством.
После того, как многочлен приравняли к какому-то числу, превратив его в тождество, появляются некоторые ограничения. Этих ограничений может быть недостаточно для того, чтобы точно определить значения неизвестных, но они есть.
Функция
Именно такие ограничения и называются функцией. Функцией зовется зависимость одной неизвестной от другой или других неизвестных. Например, в выражении:
х+у=12 – от выбранного значения х зависит значение у и наоборот.
В классическом виде функция имеет вид у(х)=в . В качестве независимого параметра принимается число х, в качестве зависимого – у. Это значит, что число х принимается равным любому числу, а у высчитывается в соответствии с этим равенством. Если х уже задан, то у нельзя принимать любым числом, из-за строгого ограничения функции у числа у появляется единственно определенное значение.
Число у зовется функцией, а число х аргументом. При этом у функции может быть множество аргументов, но у аргумента может быть только одна функция. Например, в функции у=x+z+n – 3 аргумента. Такие функции не используются в школьной программе, но нельзя забывать, что они существуют.
Функции часто изображаются в виде графиков. На плоскости можно отобразить зависимость функции лишь от одного аргумента. Но в пространстве можно отобразить изменение функции в зависимости от двух аргументов.
Существую типовые функции, поведение которых на графике изучено. Каждая из таких функций имеет свое название. Например:
- Линейная функция
- Квадратичная функция
- Степенная функция
- Логарифмическая функция и так далее
Большую часть типовых функций ученики изучают в математике старших классов.
Корень уравнения
Важно понять, что любое уравнение это частный случай функции. Уравнение это точка или точки пересечения двух функций. Задачей любого уравнения является нахождение координат точки пересечения этих функций. Так как график функции может быть не только прямой линией, то количество корней уравнения может быть разным. Если количество корней определено, то их называют простыми корнями уравнения.
Корнем уравнения называют значение х, при котором тождество выполняется. То есть это значение, при котором не нарушается равенство правой и левой сторон. Приведем пример:
х+10=5 – это уравнение, как и любое другое, представляет собой равенство двух функций:
у=х+10
у=5
Точку пересечения можно найти при х = -5. Корень только один, так как оба графика будут являться прямыми линиями, а прямые пересекаются только в одной точке.
В любом степенном уравнении количество корней равняется старшей степени многочлена. Корни могут быть одинаковыми. Линейное уравнение является частным случаем степенного, со старшей степенью равной 1. По этой же причине, в линейных уравнениях всегда один корень.
Что мы узнали?
Мы подробно разобрали определение корня уравнения. Рассмотрели обозначения неизвестных и узнали, что такое функция.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 164.
А какая ваша оценка?
Вспомним немного об уравнениях, с которыми встречались в начальных классах и в (5) классе.
Известно, что
уравнение — это выражение, в котором есть знак «равно» и латинская буква, которая обозначает переменную и значение которой надо найти.
Корень уравнения — это число, которое можно подставить вместо буквы и при вычислении получить равенство.
Решить уравнение — это отыскать все такие значения, корни уравнения, или доказать, что корней у уравнения нет.
Пример:
Для определения неизвестного уменьшаемого надо к разности прибавить вычитаемое:
3x=6+12;3x=18.
Для определения неизвестного множителя надо произведение разделить на известный множитель:
(x=18:3);
Пример:
Можно рассуждать и иначе, решая уравнение.
Здесь мы имеем равенство двух выражений, значит, их разность равна нулю:
((2x-12) — (6-x)=0).
Раскроем скобки и упростим выражение в левой части уравнения:
(2x-12-6+x=0);
(3x-18=0);
(3x=18);
Можно заметить, что
для решения уравнения надо последовательно выполнить следующие действия:
1) слагаемые, содержащие переменную, перенести в левую часть уравнения,
а числа — в его правую часть, не забывая при переносе менять знаки на противоположные;
2) привести подобные слагаемые в левой и правой частях уравнения;
3) разделить число в правой части уравнения на коэффициент при переменной.
В рассмотренных примерах
уравнения приводились к виду (ax=b), где
a≠0
.
Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнением с одним неизвестным.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Уравнения
Уравнение — это равенство, содержащее букву, значение которой надо найти. Например: 
+ 5 = 10. Чтобы решить данное уравнение, требуется найти такое число, при подстановке которого в данное равенство вместо буквы (то есть найти значение переменной), числовое равенство будет верным. В нашем случае вместо необходимо подставить 5. Говорят, что число 5 — корень уравнения + 5 = 10.
Корень уравнения — это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
Корень уравнения — это решение уравнения. Уравнение может иметь один и более корней или не иметь их вообще. Тогда говорят, что решить уравнение — значит найти все его корни или показать, что их нет вообще.
Для решения уравнений используют правило нахождения неизвестного:
1) слагаемого: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Решим уравнение + 125 = 200;
= 200 — 125;
= 75.
Ответ: = 75.
2) уменьшаемого: чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Решим уравнение — 24 = 36;
= 36 + 24;
= 60.
Ответ: = 60.
3) вычитаемого: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Решим уравнение 135 — = 115;
= 135 — 115;
= 20.
Ответ: = 20.
4) множителя: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Решим уравнение 
6 = 42;
= 42 : 6;
= 7.
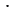
Ответ: = 7.
5) делимого: чтобы найти неизвестное делимое, надо частное умножить на делитель.
Решим уравнение : 12 = 5;
= 5 12;
= 60.
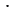
Ответ: = 60.
6) делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.
Решим уравнение 184 : = 46;
= 184 : 46;
= 4.
Ответ: = 4.
При решении уравнений проводится проверка решения, для этого найденный корень (или корни) подставляются в уравнение вместо переменной. Если числовое равенство получается верным, то решение найдено верно. При оформлении решения проверка записывается под чертой после решения, а затем пишется ответ, при этом каждое действие записывается на новой строке (т.е. одна строка один знак равенства).
Например, решим уравнение + 36 = 45 и проведем проверку:
+ 36 = 45;
= 45 — 36;
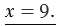
9 + 36 = 45;
45 = 45 — верно.
Ответ: = 9.
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 442,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 685,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1126,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1326,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1352,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1462,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1552,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 508,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 97,
Мерзляк, Полонский, Якир, Учебник
Номер 646,
Мерзляк, Полонский, Якир, Учебник
Номер 1154,
Мерзляк, Полонский, Якир, Учебник
Номер 1208,
Мерзляк, Полонский, Якир, Учебник
Номер 1238,
Мерзляк, Полонский, Якир, Учебник
Номер 1292,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Задание 1114,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1330,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 8,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 70,
Мерзляк, Полонский, Якир, Учебник
Номер 86,
Мерзляк, Полонский, Якир, Учебник
Номер 88,
Мерзляк, Полонский, Якир, Учебник
Номер 182,
Мерзляк, Полонский, Якир, Учебник
Номер 244,
Мерзляк, Полонский, Якир, Учебник
Номер 427,
Мерзляк, Полонский, Якир, Учебник
Номер 657,
Мерзляк, Полонский, Якир, Учебник
Номер 891,
Мерзляк, Полонский, Якир, Учебник
Номер 918,
Мерзляк, Полонский, Якир, Учебник
Номер 9,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 174,
Мерзляк, Полонский, Якир, Учебник
Номер 354,
Мерзляк, Полонский, Якир, Учебник
Номер 369,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
Номер 393,
Мерзляк, Полонский, Якир, Учебник
Номер 395,
Мерзляк, Полонский, Якир, Учебник
Номер 402,
Мерзляк, Полонский, Якир, Учебник
Номер 406,
Мерзляк, Полонский, Якир, Учебник
Номер 411,
Мерзляк, Полонский, Якир, Учебник