Equations and systems solver
Support for character vector or string inputs has been removed. Instead, use syms to declare variables and replace inputs such as solve('2*x == with
1','x')solve(2*x == 1,x).
Syntax
Description
example
S = solve(eqn,var)
solves the equation eqn for the variable var. If
you do not specify var, the symvar function determines the variable to solve for. For example,
solve(x + 1 == 2, x) solves the equation x + 1 = 2 for x.
example
S = solve(eqn,var,Name,Value)
uses additional options specified by one or more Name,Value pair
arguments.
example
Y = solve(eqns,vars)
solves the system of equations eqns for the variables
vars and returns a structure that contains the solutions. If you do
not specify vars, solve uses symvar to find the variables to solve for. In this case, the number of
variables that symvar finds is equal to the number of equations
eqns.
example
Y = solve(eqns,vars,Name,Value)
uses additional options specified by one or more Name,Value pair
arguments.
example
[y1,...,yN] = solve(eqns,vars)
solves the system of equations eqns for the variables
vars. The solutions are assigned to the variables
y1,...,yN. If you do not specify the variables,
solve uses symvar to find the variables to
solve for. In this case, the number of variables that symvar finds is
equal to the number of output arguments N.
[y1,...,yN] = solve(eqns,vars,Name,Value)
uses additional options specified by one or more Name,Value pair
arguments.
example
[y1,...,yN,parameters,conditions]
= solve(eqns,vars,'ReturnConditions',true)
returns the additional arguments parameters and
conditions that specify the parameters in the solution and the
conditions on the solution.
Examples
collapse all
Solve Quadratic Equation
Solve the quadratic equation without specifying a variable to solve for. solve chooses x to return the solution.
syms a b c x eqn = a*x^2 + b*x + c == 0
S =(-b+b2-4 a c2 a-b-b2-4 a c2 a)
Specify the variable to solve for and solve the quadratic equation for a.
Solve Polynomial and Return Real Solutions
Solve a fifth-degree polynomial. It has five solutions.
syms x
eqn = x^5 == 3125;
S = solve(eqn,x)
S =(5-σ1-54-5 2 5-5 i4-σ1-54+5 2 5-5 i4σ1-54-5 2 5+5 i4σ1-54+5 2 5+5 i4)where σ1=5 54
Return only real solutions by setting 'Real' option to true. The only real solutions of this equation is 5.
S = solve(eqn,x,'Real',true)
Numerically Solve Equations
When solve cannot symbolically solve an equation, it tries to find a numeric solution using vpasolve. The vpasolve function returns the first solution found.
Try solving the following equation. solve returns a numeric solution because it cannot find a symbolic solution.
syms x
eqn = sin(x) == x^2 - 1;
S = solve(eqn,x)
Warning: Unable to solve symbolically. Returning a numeric solution using <a href="matlab:web(fullfile(docroot, 'symbolic/vpasolve.html'))">vpasolve</a>.
S = -0.63673265080528201088799090383828
Plot the left and the right sides of the equation. Observe that the equation also has a positive solution.
fplot([lhs(eqn) rhs(eqn)], [-2 2])
Find the other solution by directly calling the numeric solver vpasolve and specifying the interval.
V = vpasolve(eqn,x,[0 2])
V = 1.4096240040025962492355939705895
Solve Multivariate Equations and Assign Outputs to Structure
When solving for multiple variables, it can be more convenient to store the outputs in a structure array than in separate variables. The solve function returns a structure when you specify a single output argument and multiple outputs exist.
Solve a system of equations to return the solutions in a structure array.
syms u v eqns = [2*u + v == 0, u - v == 1]; S = solve(eqns,[u v])
S = struct with fields:
u: 1/3
v: -2/3
Access the solutions by addressing the elements of the structure.
Using a structure array allows you to conveniently substitute solutions into other expressions.
Use the subs function to substitute the solutions S into other expressions.
expr1 = u^2; e1 = subs(expr1,S)
expr2 = 3*v + u; e2 = subs(expr2,S)
If solve returns an empty object, then no solutions exist.
eqns = [3*u+2, 3*u+1]; S = solve(eqns,u)
Solve Inequalities
The solve function can solve inequalities and return solutions that satisfy the inequalities. Solve the following inequalities.
x>0
y>0
x2+y2+xy<1
Set 'ReturnConditions' to true to return any parameters in the solution and conditions on the solution.
syms x y eqn1 = x > 0; eqn2 = y > 0; eqn3 = x^2 + y^2 + x*y < 1; eqns = [eqn1 eqn2 eqn3]; S = solve(eqns,[x y],'ReturnConditions',true); S.x
The parameters u and v do not exist in MATLAB® workspace and must be accessed using S.parameters.
Check if the values u = 7/2 and v = 1/2 satisfy the condition using subs and isAlways.
condWithValues = subs(S.conditions, S.parameters, [7/2,1/2]); isAlways(condWithValues)
isAlways returns logical 1 (true) indicating that these values satisfy the condition. Substitute these parameter values into S.x and S.y to find a solution for x and y.
xSol = subs(S.x, S.parameters, [7/2,1/2])
ySol = subs(S.y, S.parameters, [7/2,1/2])
Solve Multivariate Equations and Assign Outputs to Variables
Solve the system of equations.
2u2+v2=0
u-v=1
When solving for more than one variable, the order in which you specify the variables defines the order in which the solver returns the solutions. Assign the solutions to variables solv and solu by specifying the variables explicitly. The solver returns an array of solutions for each variable.
syms u v eqns = [2*u^2 + v^2 == 0, u - v == 1]; vars = [v u]; [solv, solu] = solve(eqns,vars)
solv =(-23-2 i3-23+2 i3)
Entries with the same index form the pair of solutions.
solutions =(-23-2 i313-2 i3-23+2 i313+2 i3)
Use Parameters and Conditions to Refine Solution
Return the complete solution of an equation with parameters and conditions of the solution by specifying 'ReturnConditions' as true.
Solve the equation sin(x)=0. Provide two additional output variables for output arguments parameters and conditions.
syms x eqn = sin(x) == 0; [solx,parameters,conditions] = solve(eqn,x,'ReturnConditions',true)
The solution πk contains the parameter k, where k must be an integer. The variable k does not exist in the MATLAB® workspace and must be accessed using parameters.
Restrict the solution to 0<x<2π. Find a valid value of k for this restriction. Assume the condition, conditions, and use solve to find k. Substitute the value of k found into the solution for x.
assume(conditions) restriction = [solx > 0, solx < 2*pi]; solk = solve(restriction,parameters)
valx = subs(solx,parameters,solk)
Alternatively, determine the solution for x by choosing a value of k. Check if the value chosen satisfies the condition on k using isAlways.
Check if k=4 satisfies the condition on k.
condk4 = subs(conditions,parameters,4); isAlways(condk4)
isAlways returns logical 1(true), meaning that 4 is a valid value for k. Substitute k with 4 to obtain a solution for x. Use vpa to obtain a numeric approximation.
valx = subs(solx,parameters,4)
ans = 12.566370614359172953850573533118
Shorten Result with Simplification Rules
Solve the equation exp(log(x)log(3x))=4.
By default, solve does not apply simplifications that are not valid for all values of x. In this case, the solver does not assume that x is a positive real number, so it does not apply the logarithmic identity log(3x)=log(3)+log(x). As a result, solve cannot solve the equation symbolically.
syms x
eqn = exp(log(x)*log(3*x)) == 4;
S = solve(eqn,x)
Warning: Unable to solve symbolically. Returning a numeric solution using <a href="matlab:web(fullfile(docroot, 'symbolic/vpasolve.html'))">vpasolve</a>.
S = -14.009379055223370038369334703094-2.9255310052111119036668717988769 i
Set 'IgnoreAnalyticConstraints' to true to apply simplification rules that might allow solve to find a solution. For details, see Algorithms.
S = solve(eqn,x,'IgnoreAnalyticConstraints',true)
S =(3 e-log(256)+log(3)2233 elog(256)+log(3)223)
solve applies simplifications that allow the solver to find a solution. The mathematical rules applied when performing simplifications are not always valid in general. In this example, the solver applies logarithmic identities with the assumption that x is a positive real number. Therefore, the solutions found in this mode should be verified.
Ignore Assumptions on Variables
The sym and syms functions let you set assumptions for symbolic variables.
Assume that the variable x is positive.
When you solve an equation for a variable under assumptions, the solver only returns solutions consistent with the assumptions. Solve this equation for x.
eqn = x^2 + 5*x - 6 == 0; S = solve(eqn,x)
Allow solutions that do not satisfy the assumptions by setting 'IgnoreProperties' to true.
S = solve(eqn,x,'IgnoreProperties',true)
For further computations, clear the assumption that you set on the variable x by recreating it using syms.
Solve Polynomial Equations of High Degree
When you solve a polynomial equation, the solver might use root to return the solutions. Solve a third-degree polynomial.
syms x a eqn = x^3 + x^2 + a == 0; solve(eqn, x)
ans =(root(z3+z2+a,z,1)root(z3+z2+a,z,2)root(z3+z2+a,z,3))
Try to get an explicit solution for such equations by calling the solver with 'MaxDegree'. The option specifies the maximum degree of polynomials for which the solver tries to return explicit solutions. The default value is 2. Increasing this value, you can get explicit solutions for higher order polynomials.
Solve the same equations for explicit solutions by increasing the value of 'MaxDegree' to 3.
S = solve(eqn, x, 'MaxDegree', 3)
S =(19 σ1+σ1-13-118 σ1-σ12-13-3 19 σ1-σ1 i2-118 σ1-σ12-13+3 19 σ1-σ1 i2)where σ1=a2+1272-1729-a2-1271/3
Return One Solution
Solve the equation sin(x)+cos(2x)=1.
Instead of returning an infinite set of periodic solutions, the solver picks three solutions that it considers to be the most practical.
syms x
eqn = sin(x) + cos(2*x) == 1;
S = solve(eqn,x)
Choose only one solution by setting 'PrincipalValue' to true.
S1 = solve(eqn,x,'PrincipalValue',true)
Input Arguments
collapse all
eqn — Equation to solve
symbolic expression | symbolic equation
Equation to solve, specified as a symbolic expression or symbolic equation. The
relation operator == defines symbolic equations. If
eqn is a symbolic expression (without the right side), the solver
assumes that the right side is 0, and solves the equation eqn ==.
0
var — Variable for which you solve equation
symbolic variable
Variable for which you solve an equation, specified as a symbolic variable. By
default, solve uses the variable determined by symvar.
eqns — System of equations
symbolic expressions | symbolic equations
System of equations, specified as symbolic expressions or symbolic equations. If any
elements of eqns are symbolic expressions (without the right side),
solve equates the element to 0.
vars — Variables for which you solve an equation or system of equations
symbolic vector | symbolic matrix
Variables for which you solve an equation or system of equations, specified as a
symbolic vector or symbolic matrix. By default, solve uses the
variables determined by symvar.
The order in which you specify these variables defines the order in which the solver
returns the solutions.
Name-Value Arguments
Example: 'Real',true specifies that the solver returns real
solutions.
Real — Flag for returning only real solutions
false (default) | true
Flag for returning only real solutions, specified as the comma-separated pair
consisting of 'Real' and one of these values.
false |
Return all solutions. |
true |
Return only those solutions for which every subexpression of the original equation represents a real number. This option also assumes that all symbolic parameters of an equation represent real numbers. |
See Solve Polynomial and Return Real Solutions.
ReturnConditions — Flag for returning parameters and conditions
false (default) | true
Flag for returning parameters in solution and conditions under which the solution
is true, specified as the comma-separated pair consisting of
'ReturnConditions' and one of these values.
false |
Do not return parameterized solutions and the conditions under which the solution holds. The solve function replaces parameterswith appropriate values. |
true |
Return the parameters in the solution and the conditions under which the solution holds. For a call with a single output variable, solve returns a structure with the fieldsparameters and conditions. Formultiple output variables, solve assigns the parametersand conditions to the last two output variables. This behavior means that the number of output variables must be equal to the number of variables to solve for plus two. |
See Solve Inequalities.
Example: [v1, v2, params, conditions] = solve(sin(x) +y == 0,y^2 == returns the parameters in
3,'ReturnConditions',true)
params and conditions in
conditions.
IgnoreAnalyticConstraints — Simplification rules applied to expressions and equations
false (default) | true
Simplification rules applied to expressions and equations, specified as the
comma-separated pair consisting of 'IgnoreAnalyticConstraints' and
one of these values.
false |
Use strict simplification rules. |
true |
Apply purely algebraic simplifications to expressions and equations. Setting IgnoreAnalyticConstraints totrue can give you simpler solutions, which could lead toresults not generally valid. In other words, this option applies mathematical identities that are convenient, but the results might not hold for all possible values of the variables. In some cases, it also enables solve to solve equations and systems that cannot besolved otherwise. For details, see Algorithms. |
See Shorten Result with Simplification Rules.
IgnoreProperties — Flag for returning solutions inconsistent with properties of variables
false (default) | true
Flag for returning solutions inconsistent with the properties of variables,
specified as the comma-separated pair consisting of
'IgnoreProperties' and one of these values.
false |
Do not include solutions inconsistent with the properties of variables. |
true |
Include solutions inconsistent with the properties of variables. |
See Ignore Assumptions on Variables.
MaxDegree — Maximum degree of polynomial equations for which solver uses explicit formulas
2 (default) | positive integer smaller than 5
Maximum degree of polynomial equations for which solver uses explicit formulas,
specified as a positive integer smaller than 5. The solver does not use explicit
formulas that involve radicals when solving polynomial equations of a degree larger
than the specified value.
See Solve Polynomial Equations of High Degree.
PrincipalValue — Flag for returning one solution
false (default) | true
Flag for returning one solution, specified as the comma-separated pair consisting
of 'PrincipalValue' and one of these values.
false |
Return all solutions. |
true |
Return only one solution. If an equation or a system of equations does not have a solution, the solver returns an empty symbolic object. |
See Return One Solution.
Output Arguments
collapse all
S — Solutions of equation
symbolic array
Solutions of an equation, returned as a symbolic array. The size of a symbolic array
corresponds to the number of the solutions.
Y — Solutions of system of equations
structure
Solutions of a system of equations, returned as a structure. The number of fields in
the structure correspond to the number of independent variables in a system. If
'ReturnConditions' is set to true, the
solve function returns two additional fields that contain the
parameters in the solution, and the conditions under which the solution is true.
y1,...,yN — Solutions of system of equations
symbolic variables
Solutions of a system of equations, returned as symbolic variables. The number of
output variables or symbolic arrays must be equal to the number of independent variables
in a system. If you explicitly specify independent variables vars,
then the solver uses the same order to return the solutions. If you do not specify
vars, the toolbox sorts independent variables alphabetically, and
then assigns the solutions for these variables to the output variables.
parameters — Parameters in solution
vector of generated parameters
Parameters in a solution, returned as a vector of generated parameters. This output
argument is only returned if ReturnConditions is
true. If a single output argument is provided,
parameters is returned as a field of a structure. If multiple
output arguments are provided, parameters is returned as the
second-to-last output argument. The generated parameters do not appear in the
MATLAB® workspace. They must be accessed using
parameters.
Example: [solx, params, conditions] = solve(sin(x) == 0, 'ReturnConditions', returns the parameter
true)k in the argument
params.
conditions — Conditions under which solutions are valid
vector of symbolic expressions
Conditions under which solutions are valid, returned as a vector of symbolic
expressions. This output argument is only returned if
ReturnConditions is true. If a single output
argument is provided, conditions is returned as a field of a
structure. If multiple output arguments are provided, conditions is
returned as the last output argument.
Example: [solx, params, conditions] = solve(sin(x) == 0, 'ReturnConditions', returns the condition
true)in(k, 'integer') in
conditions. The solution in solx is valid only
under this condition.
Tips
-
If
solvecannot find a solution and
ReturnConditionsisfalse, the
solvefunction internally calls the numeric solver
vpasolvethat tries to find a numeric solution. For polynomial
equations and systems without symbolic parameters, the numeric solver returns all
solutions. For nonpolynomial equations and systems without symbolic parameters, the
numeric solver returns only one solution (if a solution exists). -
If
solvecannot find a solution and
ReturnConditionsistrue,
solvereturns an empty solution with a warning. If no solutions
exist,solvereturns an empty solution without a warning. -
If the solution contains parameters and
ReturnConditionsis
true,solvereturns the parameters in the
solution and the conditions under which the solutions are true. If
ReturnConditionsisfalse, the
solvefunction either chooses values of the parameters and returns
the corresponding results, or returns parameterized solutions without choosing particular
values. In the latter case,solvealso issues a warning indicating
the values of parameters in the returned solutions. -
If a parameter does not appear in any condition, it means the parameter can take any
complex value. -
The output of
solvecan contain parameters from the input
equations in addition to parameters introduced bysolve. -
Parameters introduced by
solvedo not appear in the MATLAB workspace. They must be accessed using the output argument that contains
them. Alternatively, to use the parameters in the MATLAB workspace usesymsto initialize the parameter. For
example, if the parameter isk, usesyms k. -
The variable names
parametersandconditionsare
not allowed as inputs tosolve. -
To solve differential equations, use the
dsolvefunction. -
When solving a system of equations, always assign the result to output arguments.
Output arguments let you access the values of the solutions of a system. -
MaxDegreeonly accepts positive integers smaller than 5 because, in
general, there are no explicit expressions for the roots of polynomials of degrees higher
than 4. -
The output variables
y1,...,yNdo not specify the variables for
whichsolvesolves equations or systems. If
y1,...,yNare the variables that appear in
eqns, then there is no guarantee that
solve(eqns)will assign the solutions to
y1,...,yNusing the correct order. Thus, when you run
[b,a] = solve(eqns), you might get the solutions for
aassigned toband vice versa.To ensure the order of the returned solutions, specify the variables
vars. For example, the call[b,a] =assigns the solutions for
solve(eqns,b,a)ato
aand the solutions forbto
b.
Algorithms
When you use IgnoreAnalyticConstraints, the solver applies some of
these rules to the expressions on both sides of an equation.
-
log(a) +
log(b) = log(a·b) for all values of a and b. In
particular, the following equality is valid for all values of a,
b, and c:(a·b)c = ac·bc.
-
log(ab) = b·log(a) for all values of a and b. In
particular, the following equality is valid for all values of a,
b, and c:(ab)c = ab·c.
-
If f and g are standard mathematical functions
and f(g(x)) = x for all small positive numbers, f(g(x)) = x is assumed to be valid for all complex values x. In
particular:-
log(ex) = x
-
asin(sin(x)) = x, acos(cos(x)) = x, atan(tan(x)) = x
-
asinh(sinh(x)) = x, acosh(cosh(x)) = x, atanh(tanh(x)) = x
-
Wk(x·ex) = x for all branch indices k of the Lambert W function.
-
-
The solver can multiply both sides of an equation by any expression except
0. -
The solutions of polynomial equations must be complete.
Version History
Introduced before R2006a
Symbolic Math Toolbox™ offers both numeric and symbolic equation solvers. For a comparison of numeric and symbolic solvers, see Select Numeric or Symbolic Solver. An equation or a system of equations can have multiple solutions. To find these solutions numerically, use the function vpasolve. For polynomial equations, vpasolve returns all solutions. For nonpolynomial equations, vpasolve returns the first solution it finds. These examples show you how to use vpasolve to find solutions to both polynomial and nonpolynomial equations, and how to obtain these solutions to arbitrary precision.
Find All Roots of a Polynomial Function
Use vpasolve to find all the solutions to the function f(x)=6×7-2×6+3×3-8.
syms f(x)
f(x) = 6*x^7-2*x^6+3*x^3-8;
sol = vpasolve(f)
sol =(1.0240240759053702941448316563337-0.88080620051762149639205672298326+0.50434058840127584376331806592405 i-0.88080620051762149639205672298326-0.50434058840127584376331806592405 i-0.22974795226118163963098570610724+0.96774615576744031073999010695171 i-0.22974795226118163963098570610724-0.96774615576744031073999010695171 i0.7652087814927846556172932675903+0.83187331431049713218367239317121 i0.7652087814927846556172932675903-0.83187331431049713218367239317121 i)
vpasolve returns seven roots of the function, as expected, because the function is a polynomial of degree seven.
Find Zeros of a Nonpolynomial Function Using Search Ranges and Starting Points
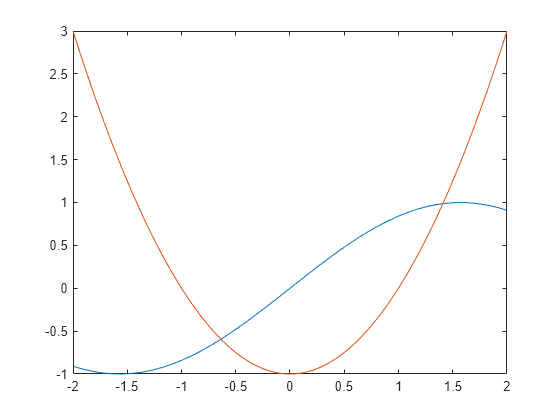
A plot of the function f(x)=e(x/7)cos(2x) reveals periodic zeros, with increasing slopes at the zero points as x increases.
syms x h = fplot(exp(x/7)*cos(2*x),[-2 25]); grid on
Use vpasolve to find a zero of the function f. Note that vpasolve returns only one solution of a nonpolynomial equation, even if multiple solutions exist. On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x); for k = 1:3 vpasolve(f,x) end
ans = -7.0685834705770347865409476123789
ans = -7.0685834705770347865409476123789
ans = -7.0685834705770347865409476123789
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly. For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true) end
ans = -226.98006922186256147892598444194
ans = 98.174770424681038701957605727484
ans = 52.621676947629036744249276669932
To find a zero close to x=10, set the starting point to 10.
ans = 10.210176124166828025003590995658
To find a zero close to x=1000, set the starting point to 1000.
ans = 999.8118620049516981407362567287
To find a zero in the range 15≤x≤25, set the search range to [15 25].
ans = 21.205750411731104359622842837137
To find multiple zeros in the range [15 25], you cannot call vpasolve repeatedly because it returns the same result on each call, as previously shown. Instead, set the search range and set 'Random' to true.
for k = 1:3 vpasolve(f,x,[15 25],'Random',true) end
ans = 21.205750411731104359622842837137
ans = 21.205750411731104359622842837137
ans = 16.493361431346414501928877762217
Because 'Random' selects starting points randomly, the same solution might be found on successive calls.
Find All Zeros in a Specified Search Range
Create a function findzeros to systematically find all zeros for f in a given search range, within a specified error tolerance. The function starts with the input search range and calls vpasolve to find a zero. Then, it splits the search range into two around the zero value and recursively calls itself with the new search ranges as inputs to find more zeros.
The function is explained section by section here.
Declare the function with the three inputs and one output. The first input is the function, the second input is the range, and the optional third input allows you to specify the error between a zero and the higher and lower bounds generated from it.
function sol = findzeros(f,range,err)
If you do not specify the optional argument for error tolerance, findzeros sets err to 0.001.
if nargin < 2 err = 1e-3; end
Find a zero in the search range using vpasolve.
If vpasolve does not find a zero, exit.
If vpasolve finds a zero, split the search range into two search ranges above and below the zero.
else
lowLimit = sol-err;
highLimit = sol+err;
Call findzeros with the lower search range. If findzeros returns zeros, copy the values into the solution array and sort them.
temp = findzeros(f,[range(1) lowLimit],1); if ~isempty(temp) sol = sort([sol temp]); end
Call findzeros with the higher search range. If findzeros returns zeros, copy the values into the solution array and sort them.
temp = findzeros(f,[highLimit range(2)],1); if ~isempty(temp) sol = sort([sol temp]); end return end end
The entire function findzeros is as follows. Save this function as findzeros.m in the current folder.
function sol = findzeros(f,range,err) if nargin < 3 err = 1e-3; end sol = vpasolve(f,range); if(isempty(sol)) return else lowLimit = sol-err; highLimit = sol+err; temp = findzeros(f,[range(1) lowLimit],1); if ~isempty(temp) sol = sort([sol temp]); end temp = findzeros(f,[highLimit range(2)],1); if ~isempty(temp) sol = sort([sol temp]); end return end end
Call findzeros with search range [15 25] to find all zeros in that range for f(x) = exp(x/7)*cos(2*x), within the default error tolerance.
syms f(x)
f(x) = exp(x/7)*cos(2*x);
sol = findzeros(f,[15 25])'
sol =(16.49336143134641450192887776221718.06415775814131112116019945385719.63495408493620774039152114549721.20575041173110435962284283713722.77654673852600097885416452877624.347343065320897598085486220416)
Obtain Solutions to Arbitrary Precision
Use digits to set the precision of the solutions returned by vpasolve. By default, vpasolve returns solutions to a precision of 32 significant figures.
f = exp(x/7)*cos(2*x); vpasolve(f)
ans = -7.0685834705770347865409476123789
Use digits to increase the precision to 64 significant figures. When modifying digits, ensure that you save its current value so that you can restore it.
digitsOld = digits; digits(64) vpasolve(f)
ans = -7.068583470577034786540947612378881489443631148593988097193625333
Next, change the precision of the solutions to 16 significant figures.
Solve Multivariate Equations Using Search Ranges
Consider the following system of equations.
z=10(cos(x)+cos(y))z=x+y2-0.1x2yx+y-2.7=0
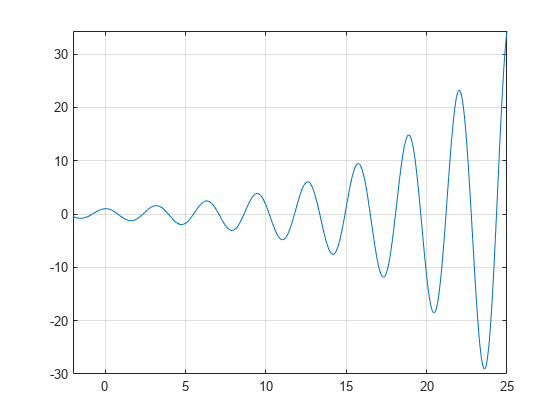
A plot of the equations for 0≤x≤2.5 and 0≤x≤2.5 shows that the three surfaces intersect in two points. To better visualize the plot, use view. To scale the colormap values, use caxis.
syms x y z eqn1 = z == 10*(cos(x) + cos(y)); eqn2 = z == x+y^2-0.1*x^2*y; eqn3 = x+y-2.7 == 0; equations = [eqn1 eqn2 eqn3]; fimplicit3(equations) axis([0 2.5 0 2.5 -20 10]) title('System of Multivariate Equations') view(69, 28) caxis([-15 10])
Use vpasolve to find a point where the surfaces intersect. The function vpasolve returns a structure. To access the x-, y-, and z-values of the solution, index into the structure.
sol = vpasolve(equations); [sol.x sol.y sol.z]
ans = (2.3697477224547980.33025227754520212.293354376823228)
To search a region of the solution space, specify search ranges for the variables. If you specify the ranges 0≤x≤1.5 and 1.5≤y≤2.5, then vpasolve function searches the bounded area shown.
Use vpasolve to find a solution for this search range. To omit a search range for z, set the third search range to [NaN NaN].
vars = [x y z]; range = [0 1.5; 1.5 2.5; NaN NaN]; sol = vpasolve(equations, vars, range); [sol.x sol.y sol.z]
ans = (0.91062661725633361.7893733827436663.964101572135625)
To find multiple solutions, set the 'Random' option to true. This makes vpasolve use random starting points on successive runs. The 'Random' option can be used in conjunction with search ranges to make vpasolve use random starting points within a search range. Because 'Random' selects starting points randomly, the same solution might be found on successive calls. Call vpasolve repeatedly to ensure you find both solutions.
clear sol range = [0 3; 0 3; NaN NaN]; for k = 1:5 temp = vpasolve(equations,vars,range,'Random',true); sol(k,1) = temp.x; sol(k,2) = temp.y; sol(k,3) = temp.z; end sol
sol =(2.3697477224547980.33025227754520212.2933543768232282.3697477224547980.33025227754520212.2933543768232282.3697477224547980.3302522775452022.2933543768232280.91062661725633361.7893733827436663.9641015721356250.91062661725633361.7893733827436663.964101572135625)
Plot the equations. Superimpose the solutions as a scatter plot of points with yellow X markers using scatter3. To better visualize the plot, make two of the surfaces transparent using alpha. Scale the colormap to the plot values using caxis, and change the perspective using view.
vpasolve finds solutions at the intersection of the surfaces formed by the equations as shown.
clf ax = axes; h = fimplicit3(equations); h(2).FaceAlpha = 0; h(3).FaceAlpha = 0; axis([0 2.5 0 2.5 -20 10]) hold on scatter3(sol(:,1),sol(:,2),sol(:,3),600,'yellow','X','LineWidth',2) title('Randomly Found Solutions in Specified Search Range') cz = ax.Children; caxis([0 20]) view(69,28) hold off
Lastly, restore the old value of digits for further calculations.
solve
Уравнения и системный решатель
Поддержка вектора символов или входных параметров строки была удалена. Вместо этого используйте syms объявить переменные и входные параметры замены, такие как solve('2*x == 1','x') с solve(2*x == 1,x).
Синтаксис
Описание
пример
S = solve(eqn,var)eqn для переменной var. Если вы не задаете var, symvar функция определяет переменную, чтобы решить для. Например, solve(x + 1 == 2, x) решает уравнение x + 1 = 2 для x.
пример
S = solve(eqn,var,Name,Value)Name,Value парные аргументы.
пример
Y = solve(eqns,vars)eqns для переменных vars и возвращает структуру, которая содержит решения. Если вы не задаете vars, solve использование symvar найти, что переменные решают для. В этом случае, количество переменных это symvar находки равны количеству уравнений eqns.
пример
Y = solve(eqns,vars,Name,Value)Name,Value парные аргументы.
пример
[ решает систему уравнений y1,...,yN] = solve(eqns,vars)eqns для переменных vars. Решения присвоены переменным y1,...,yN. Если вы не задаете переменные, solve использование symvar найти, что переменные решают для. В этом случае, количество переменных это symvar находки равны количеству выходных аргументов N.
[ дополнительные опции использования заданы одним или несколькими y1,...,yN] = solve(eqns,vars,Name,Value)Name,Value парные аргументы.
пример
[ возвращает дополнительные аргументы y1,...,yN,parameters,conditions]
= solve(eqns,vars,'ReturnConditions',true)parameters и conditions это задает параметры в решении и условиях на решении.
Примеры
свернуть все
Решите квадратное уравнение
Решите квадратное уравнение, не задавая переменную, чтобы решить для. solve выбирает x возвратить решение.
syms a b c x eqn = a*x^2 + b*x + c == 0
S =(-b+b2-4 a c2 a-b-b2-4 a c2 a)
Задайте переменную, чтобы решить для и решить квадратное уравнение для a.
Решите полином и возвратите действительные решения
Решите полином пятой степени. Это имеет пять решений.
syms x
eqn = x^5 == 3125;
S = solve(eqn,x)
S =(5-σ1-54-5 2 5-5 i4-σ1-54+5 2 5-5 i4σ1-54-5 2 5+5 i4σ1-54+5 2 5+5 i4)where σ1=5 54
Возвратите только действительные решения установкой 'Real' опция к true. Единственными действительными решениями этого уравнения является 5.
S = solve(eqn,x,'Real',true)
Численно решите уравнения
Когда solve не может символически решить уравнение, оно пытается найти числовое решение с помощью vpasolve. vpasolve функция возвращает первое найденное решение.
Попытайтесь решить следующее уравнение. solve возвращает числовое решение, потому что оно не может найти символьное решение.
syms x
eqn = sin(x) == x^2 - 1;
S = solve(eqn,x)
Warning: Unable to solve symbolically. Returning a numeric solution using <a href="matlab:web(fullfile(docroot, 'symbolic/vpasolve.html'))">vpasolve</a>.
S = -0.63673265080528201088799090383828
Постройте левые и правые стороны уравнения. Заметьте, что уравнение также имеет положительное решение.
fplot([lhs(eqn) rhs(eqn)], [-2 2])
Найдите другое решение путем прямого вызова числового решателя vpasolve и определение интервала.
V = vpasolve(eqn,x,[0 2])
V = 1.4096240040025962492355939705895
Решите многомерные уравнения и присвойте Выходные параметры структуре
При решении для нескольких переменных может быть более удобно сохранить выходные параметры в массиве структур, чем в отдельных переменных. solve функция возвращает структуру, когда вы задаете один выходной аргумент, и существуют несколько выходных параметров.
Решите систему уравнений, чтобы возвратить решения в массиве структур.
syms u v eqns = [2*u + v == 0, u - v == 1]; S = solve(eqns,[u v])
S = struct with fields:
u: 1/3
v: -2/3
Доступ к решениям путем обращения к элементам структуры.
Используя массив структур позволяет вам удобно заменять решениями в другие выражения.
Используйте subs функционируйте, чтобы заменить решениями S в другие выражения.
expr1 = u^2; e1 = subs(expr1,S)
expr2 = 3*v + u; e2 = subs(expr2,S)
Если solve возвращает пустой объект, затем никакие решения не существуют.
eqns = [3*u+2, 3*u+1]; S = solve(eqns,u)
Решите неравенства
solve функция может решить неравенства и возвратить решения, которые удовлетворяют неравенствам. Решите следующие неравенства.
x>0
y>0
x2+y2+xy<1
Установите 'ReturnConditions' к true возвратить любые параметры в решении и условиях на решении.
syms x y eqn1 = x > 0; eqn2 = y > 0; eqn3 = x^2 + y^2 + x*y < 1; eqns = [eqn1 eqn2 eqn3]; S = solve(eqns,[x y],'ReturnConditions',true); S.x
Параметры u и v не существуйте в рабочей области MATLAB®, и должен быть получен доступ с помощью S.parameters.
Проверяйте если значения u = 7/2 и v = 1/2 удовлетворите условию с помощью subs и isAlways.
condWithValues = subs(S.conditions, S.parameters, [7/2,1/2]); isAlways(condWithValues)
isAlways возвращает логическую единицу (true) указание, что эти значения удовлетворяют условию. Замените этими значениями параметров в S.x и S.y найти решение для x и y.
xSol = subs(S.x, S.parameters, [7/2,1/2])
ySol = subs(S.y, S.parameters, [7/2,1/2])
Решите многомерные уравнения и присвойте Выходные параметры переменным
Решите систему уравнений.
2u2+v2=0
u-v=1
При решении больше чем для одной переменной порядок, в котором вы задаете переменные, задает порядок, в котором решатель возвращает решения. Присвойте решения переменных solv и solu путем определения переменных явным образом. Решатель возвращает массив решений для каждой переменной.
syms u v eqns = [2*u^2 + v^2 == 0, u - v == 1]; vars = [v u]; [solv, solu] = solve(eqns,vars)
solv =(-23-2 i3-23+2 i3)
Записи с тем же индексом формируют пару решений.
solutions =(-23-2 i313-2 i3-23+2 i313+2 i3)
Используйте параметры и условия совершенствовать решение
Возвратите полное решение уравнения параметрами и условиями решения путем определения 'ReturnConditions' как true.
Решите уравнение sin(x)=0. Обеспечьте две дополнительных выходных переменные для выходных аргументов parameters и conditions.
syms x eqn = sin(x) == 0; [solx,parameters,conditions] = solve(eqn,x,'ReturnConditions',true)
Решение πk содержит параметр k, где k должно быть целое число. Переменная k не существует в рабочем пространстве MATLAB и должен быть получен доступ с помощью parameters.
Ограничьте решение 0<x<2π. Найдите допустимое значение k для этого ограничения. Примите условие, conditions, и используйте solve найти k. Замените значением k найденный в решение для x.
assume(conditions) restriction = [solx > 0, solx < 2*pi]; solk = solve(restriction,parameters)
valx = subs(solx,parameters,solk)
В качестве альтернативы определите решение для x путем выбора значения k. Проверяйте, удовлетворяет ли выбранное значение условию на k использование isAlways.
Проверяйте если k=4 удовлетворяет условию на k.
condk4 = subs(conditions,parameters,4); isAlways(condk4)
isAlways возвращает логическую единицу (true), подразумевать, что 4 допустимое значение для k. Замена k с 4, чтобы получить решение для x. Используйте vpa получить числовое приближение.
valx = subs(solx,parameters,4)
ans = 12.566370614359172953850573533118
Сократите результат с правилами упрощения
Решите уравнение exp(log(x)log(3x))=4.
По умолчанию, solve не применяет упрощения, которые не допустимы для всех значений x. В этом случае решатель не принимает это x положительное вещественное число, таким образом, оно не применяет логарифмическую идентичность log(3x)=log(3)+log(x). В результате solve не может решить уравнение символически.
syms x
eqn = exp(log(x)*log(3*x)) == 4;
S = solve(eqn,x)
Warning: Unable to solve symbolically. Returning a numeric solution using <a href="matlab:web(fullfile(docroot, 'symbolic/vpasolve.html'))">vpasolve</a>.
S = -14.009379055223370038369334703094-2.9255310052111119036668717988769 i
Установите 'IgnoreAnalyticConstraints' к true применять правила упрощения, которые могут позволить solve найти решение. Для получения дополнительной информации см. Алгоритмы.
S = solve(eqn,x,'IgnoreAnalyticConstraints',true)
S =(3 e-log(256)+log(3)2233 elog(256)+log(3)223)
solve применяет упрощения, которые позволяют решателю находить решение. Математические правила применялись, когда выполняющие упрощения не всегда допустимы в целом. В этом примере решатель применяет логарифмические тождества учитывая, что x положительное вещественное число. Поэтому решения, найденные в этом режиме, должны быть проверены.
Проигнорируйте предположения на переменных
sym и syms функции позволяют вам установить предположения для символьных переменных.
Примите что переменная x положительно.
Когда вы решаете уравнение для переменной под предположениями, решатель только возвращает решения, сопоставимые с предположениями. Решите это уравнение для x.
eqn = x^2 + 5*x - 6 == 0; S = solve(eqn,x)
Позвольте решения, которые не удовлетворяют предположениям установкой 'IgnoreProperties' к true.
S = solve(eqn,x,'IgnoreProperties',true)
Для дальнейших расчетов очистите предположение, что вы устанавливаете на переменной x путем воссоздания его с помощью syms.
Решите полиномиальные знатные уравнения
Когда вы решаете полиномиальное уравнение, решатель может использовать root возвратить решения. Решите полином третьей степени.
syms x a eqn = x^3 + x^2 + a == 0; solve(eqn, x)
ans =(root(z3+z2+a,z,1)root(z3+z2+a,z,2)root(z3+z2+a,z,3))
Попытайтесь получить явное решение для таких уравнений путем вызова решателя с 'MaxDegree'. Опция задает максимальную степень полиномов, для которых решатель пытается возвратить явные решения. Значением по умолчанию является 2. Увеличивая это значение, можно получить явные решения для полиномов высшего порядка.
Решите те же уравнения для явных решений путем увеличения значения 'MaxDegree' к 3.
S = solve(eqn, x, 'MaxDegree', 3)
S =(19 σ1+σ1-13-118 σ1-σ12-13-3 19 σ1-σ1 i2-118 σ1-σ12-13+3 19 σ1-σ1 i2)where σ1=a2+1272-1729-a2-1271/3
Возвратите одно решение
Решите уравнение sin(x)+cos(2x)=1.
Вместо того, чтобы возвратить бесконечное множество периодических решений, решатель выбирает три решения, что он считает самым практическим.
syms x
eqn = sin(x) + cos(2*x) == 1;
S = solve(eqn,x)
Выберите только одно решение установкой 'PrincipalValue' к true.
S1 = solve(eqn,x,'PrincipalValue',true)
Входные параметры
свернуть все
eqn — Уравнение, чтобы решить
символьное выражение | символьное уравнение
Уравнение, чтобы решить в виде символьного выражения или символьного уравнения. Оператор отношения == определяет символьные уравнения. Если eqn символьное выражение (без правой стороны), решатель принимает, что правая сторона 0 и решает уравнение eqn == 0.
var — Переменная, для которой вы решаете уравнение
символьная переменная
Переменная, для которой вы решаете уравнение в виде символьной переменной. По умолчанию, solve использует переменную, определенную symvar.
eqns Система уравнений
символьные выражения | символьные уравнения
Система уравнений в виде символьных выражений или символьных уравнений. Если любые элементы eqns символьные выражения (без правой стороны), solve приравнивает элемент к 0.
vars — Переменные, для которых вы решаете уравнение или систему уравнений
символьный вектор | символьная матрица
Переменные, для которых вы решаете уравнение или систему уравнений в виде символьного вектора или символьной матрицы. По умолчанию, solve использует переменные, определенные symvar.
Порядок, в котором вы задаете эти переменные, задает порядок, в котором решатель возвращает решения.
Аргументы name-value
Пример: 'Real',true указывает, что решатель возвращает действительные решения.
Real — Отметьте для возврата только действительных решений
false (значение по умолчанию) | true
Отметьте для возврата только действительных решений в виде разделенной запятой пары, состоящей из 'Real' и одно из этих значений.
false |
Возвратите все решения. |
true |
Возвратите только те решения, для которых каждое подвыражение исходного уравнения представляет вещественное число. Эта опция также принимает, что все символьные параметры уравнения представляют вещественные числа. |
Смотрите решают полином и возвращают действительные решения.
ReturnConditions — Отметьте для возврата параметров и условий
false (значение по умолчанию) | true
Отметьте для возврата параметров в решении и условиях, при которых решение верно в виде разделенной запятой пары, состоящей из 'ReturnConditions' и одно из этих значений.
false |
Не возвращайте параметрированные решения и условия, при которых решение содержит. solve функционируйте заменяет параметры на соответствующие значения. |
true |
Возвратите параметры в решении и условиях, при которых решение содержит. Для вызова с одной выходной переменной, solve возвращает структуру с полями parameters и conditions. Для нескольких выходных переменных, solve присваивает параметры и условия к последним двум выходным переменным. Это поведение означает, что количество выходных переменных должно быть равно количеству переменных, чтобы решить для плюс два. |
Смотрите решают неравенства.
Пример: [v1, v2, params, conditions] = solve(sin(x) +y == 0,y^2 == 3,'ReturnConditions',true) возвращает параметры в params и условия в conditions.
IgnoreAnalyticConstraints — Правила упрощения применились к выражениям и уравнениям
false (значение по умолчанию) | true
Правила упрощения применились к выражениям и уравнениям в виде разделенной запятой пары, состоящей из 'IgnoreAnalyticConstraints' и одно из этих значений.
false |
Используйте строгие правила упрощения. |
true |
Примените чисто алгебраические упрощения в выражениях и уравнениях. Установка IgnoreAnalyticConstraints к true может дать вам простые решения, которые могли привести к результатам, не обычно допустимым. Другими словами, эта опция применяет математические тождества, которые удобны, но результаты не могут содержать для всех возможных значений переменных. В некоторых случаях это также включает solve решить уравнения и системы, которые не могут быть решены в противном случае. |
Смотрите сокращают результат с правилами упрощения.
IgnoreProperties — Отметьте для возврата решений, противоречивых со свойствами переменных
false (значение по умолчанию) | true
Отметьте для возврата решений, противоречивых со свойствами переменных в виде разделенной запятой пары, состоящей из 'IgnoreProperties' и одно из этих значений.
false |
Не включайте решения, противоречивые со свойствами переменных. |
true |
Включайте решения, противоречивые со свойствами переменных. |
Смотрите игнорируют предположения на переменных.
MaxDegree — Максимальная степень полиномиальных уравнений, для которых решатель использует явные формулы
2
Максимальная степень полиномиальных уравнений, для которых решатель использует явные формулы в виде положительного целого числа, меньшего, чем 5. Решатель не использует явные формулы, которые вовлекают радикалов при решении полиномиальных уравнений степени, больше, чем заданное значение.
Смотрите решают полиномиальные знатные уравнения.
PrincipalValue — Отметьте для возврата одного решения
false (значение по умолчанию) | true
Отметьте для возврата одного решения в виде разделенной запятой пары, состоящей из 'PrincipalValue' и одно из этих значений.
false |
Возвратите все решения. |
true |
Возвратите только одно решение. Если уравнение или система уравнений не имеют решения, решатель возвращает пустой символьный объект. |
Смотрите возвращают одно решение.
Выходные аргументы
свернуть все
S — Решения уравнения
символьный массив
Решения уравнения, возвращенного как символьный массив. Размер символьного массива соответствует количеству решений.
Y — Решения системы уравнений
структура
Решения системы уравнений, возвращенной как структура. Количество полей в структуре соответствует количеству независимых переменных в системе. Если 'ReturnConditions' установлен в true, solve функция возвращает два дополнительных поля, которые содержат параметры в решении и условия, при которых решение верно.
y1,...,yN — Решения системы уравнений
символьные переменные
Решения системы уравнений, возвращенной как символьные переменные. Количество выходных переменных или символьных массивов должно быть равно количеству независимых переменных в системе. Если вы явным образом задаете независимые переменные vars, затем решатель использует тот же порядок возвратить решения. Если вы не задаете vars, независимые переменные видов тулбокса в алфавитном порядке, и затем присваивают решения для этих переменных к выходным переменным.
parameters — Параметры в решении
вектор из сгенерированных параметров
Параметры в решении, возвращенном как вектор из сгенерированных параметров. Этот выходной аргумент только возвращен если ReturnConditions true. Если один выходной аргумент обеспечивается, parameters возвращен как поле структуры. Если несколько выходных аргументов обеспечиваются, parameters возвращен как предпоследний выходной аргумент. Сгенерированные параметры не появляются в MATLAB® рабочая область. К ним нужно получить доступ с помощью parameters.
Пример: [solx, params, conditions] = solve(sin(x) == 0, 'ReturnConditions', true) возвращает параметр k в аргументе params.
conditions — Условия, при которых решения допустимы
вектор из символьных выражений
Условия, при которых решения допустимы, возвратились как вектор из символьных выражений. Этот выходной аргумент только возвращен если ReturnConditions true. Если один выходной аргумент обеспечивается, conditions возвращен как поле структуры. Если несколько выходных аргументов обеспечиваются, conditions возвращен как последний выходной аргумент.
Пример: [solx, params, conditions] = solve(sin(x) == 0, 'ReturnConditions', true) возвращает условие in(k, 'integer') в conditions. Решение в solx допустимо только при этом условии.
Советы
-
Если
solveне может найти решение иReturnConditionsfalse,solveфункционируйте внутренне вызывает числовой решательvpasolveэто пытается найти числовое решение. Для полиномиальных уравнений и систем без символьных параметров, числовой решатель возвращает все решения. Для неполиномиальных уравнений и систем без символьных параметров, числовой решатель возвращает только одно решение (если решение существует). -
Если
solveне может найти решение иReturnConditionstrue,solveвозвращает пустое решение с предупреждением. Если никакие решения не существуют,solveвозвращает пустое решение без предупреждения. -
Если решение содержит параметры и
ReturnConditionstrue,solveвозвращает параметры в решении и условиях, при которых решения верны. ЕслиReturnConditionsfalse,solveфункционируйте или выбирает значения параметров и возвращает соответствующие результаты или возвращает параметрированные решения, не выбирая особые значения. В последнем случае,solveтакже выдает предупреждение, указывающее на значения параметров в возвращенных решениях. -
Если параметр не появляется ни в каком условии, это означает, что параметр может взять любое комплексное число.
-
Выход
solveможет содержать параметры от исходных уравнений в дополнение к параметрам, введеннымsolve. -
Параметры, введенные
solveне появляйтесь в рабочем пространстве MATLAB. К ним нужно получить доступ с помощью выходного аргумента, который содержит их. В качестве альтернативы использовать параметры в использовании рабочего пространства MATLABsymsинициализировать параметр. Например, если параметром являетсяk, используйтеsyms k. -
Имена переменных
parametersиconditionsне позволены как входные параметрыsolve. -
Чтобы решить дифференциальные уравнения, используйте
dsolveфункция. -
При решении системы уравнений всегда присваивайте результат выходным аргументам. Выходные аргументы позволяют вам получить доступ к значениям решений системы.
-
MaxDegreeтолько принимает положительные целые числа, меньшие, чем 5 потому что, в целом, нет никаких явных выражений для корней полиномов степеней выше, чем 4. -
Выходные переменные
y1,...,yNне задавайте переменные для которыйsolveрешает уравнения или системы. Еслиy1,...,yNпеременные, которые появляются вeqns, затем нет никакой гарантии чтоsolve(eqns)присвоит решенияy1,...,yNиспользование правильного порядка. Таким образом, когда вы запускаете[b,a] = solve(eqns), вы можете получить решения дляaприсвоенныйbи наоборот.Чтобы гарантировать порядок возвращенных решений, задайте переменные
vars. Например, вызов[b,a] = solve(eqns,b,a)присваивает решения дляaкaи решения дляbкb.
Алгоритмы
Когда вы используете IgnoreAnalyticConstraints, решатель применяет эти правила к выражениям с обеих сторон уравнения.
-
регистрируйте (a) + журнал (b) = журнал (a · b) для всех значений a и b. В частности, следующее равенство допустимо для всех значений a, b и c:
A, B c = acBc.
-
журнал (ab) = b · регистрируйте (a) для всех значений a и b. В частности, следующее равенство допустимо для всех значений a, b и c:
Ab)c = ab·c.
-
Если f и g являются стандартными математическими функциями и f (g (x)) = x для всех маленьких положительных чисел, f (g (x)) = , x принят, чтобы быть допустимым для всех комплексных чисел x. В частности:
-
журнал (ex) = x
-
asin (sin (x)) = x, acos (cos (x)) = x, atan (tan (x)) = x
-
asinh (sinh (x)) = x, acosh (дубинка (x)) = x, atanh (tanh (x)) = x
-
Wk (x · ex) = x для всех индексов ветви k функции Ламберта В.
-
-
Решатель может умножить обе стороны уравнения по любому выражению кроме
0. -
Решения полиномиальных уравнений должны быть завершены.
Представлено до R2006a
Тема
5.2. Технология решения нелинейных
уравнений средствами MatLab
Для
решения систем алгебраических уравнений
и одиночных уравнений служит функция
solve:
-
solve(expr1,
expr2,…
exprN,
var1,
var2,…
varN)—
возвращает значения переменных
var1,
при которых соблюдаются равенства,
заданные выражениями
exprI.
Если в выражениях не используются знаки
равенства, то
полагается ехргI
= 0; -
solve(expr1,
expr2,
….. exprN)—аналогична
предшествующей функции,
но переменные, по которым ищется решение,
определяются функцией
findsym.
Пример
4.2-1. Решить
несколько нелинейных уравнений.
|
|
|
» » ans [ 1] [ [ » » ans [ [ »S S
x
y » ans [4] [1] [1] » ans [-1] [2] [2] » ans 0.52359877559829887307710723054658 >> |
Пример4.2-2.
Отделить корни уравнения
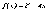
непрерывной правой частью.
Найдем отрезок, на концах которого

разные знаки. Т.е. решим уравнение

|
|
|
syms >> >> >> >> |
В математическом пакете
MatLab
имеется также ряд встроенных функций
для численного вычисления корней
уравнений.
Рассмотрим программные
средства MatLabна
примерах.
Пример
4.2-3. Локализовать
корни уравнения f(x)=x3–cos(x)+1.
|
|
|
>>f >>x |
|
>>figure(‘Name’, >>plot(x, >>figure(‘Name’, >>figure(‘Name’, >> |
Решение
алгебраических и трансцендентных
уравнений в среде MatLAB
проще реализовать с помощью встроенных
функций: solve(),
fzero(),
roors().
Для
нахождения вещественных корней уравнений
вида f(х)=0
используется функция fzero().
Алгоритм,
реализованный этой функцией, представляет
собой комбинацию
метода дихотомии (деления пополам),
метода секущих и метода обратной
квадратичной интерполяции.
В простейшем варианте обращения кроме
указателя
на функцию, корень которой ищется,
задается окрестность х0,
с которой
начинается поиск: х
= fzero(f,
x0).
Аргумент
fможет
быть задан одним из способов:
-
формойс
неизвестным х,
заключенная в апострофы; -
именем
m-файла
(в апострофах и без расширения m); -
указателем
на функцию (например, @f_name); -
указателем
на анонимную функцию (например, f_handie).
При этом формула, заключенная
в апострофы, в качестве независимой
переменной может
содержать только х.
Использование независимой переменной
с другим именем
вызовет сообщение об ошибке.
Аргумент
х0
может быть задан одним из двух способов:
-
вектором
[a;b],
представляющим интервал (а<b),на
концах которого функция
f()меняет
знак, что гарантирует нахождение, по
крайней мере, одного
корня на этом интервале; -
скалярным
значением, в окрестности которого
предполагается нахождение
корня. В этом случае функция fzero()
сама пытается найти отрезок
с центром в заданной точке х0,
на концах которого функцияf
()меняет
знак.
Чтобы
облегчить работу по выбору начального
приближения, разумнее всего построить
график функции y=f
(x).
Пример
4.2-4.
Построить график функции f(x)=x∙e—x+sin(x)
для локализации корня.
|
|
|
x y plot(x, grid title(‘y=x*exp(-x)+sin(x) |
Из
графика видно, что один из корней
находится на интервале [3;4].
Используем
полученную информациюи
обратимся к функции
fzero(
):
|
|
|
>> x= 3.2665 >> |
Вместо
явного задания формулы для функции f
мы могли бы объявить соответствующую
функцию, запомнив ее в виде автономного
m-файла
или включив
ее в качестве подфункции в файл нашей
программы.
|
|
|
function x=fzero(@f1, function
y= |
Если
мы хотим получить не только значение
корня, но и узнать значение функции в
найденной точке, то к функции fzero( ) можно
обратиться с двумя выходными параметрами.
В ряде
задач такая точность может оказаться
излишней. MatLab предоставляет пользователю
возможность формировать различные
условия прекращения итерационного
процесса — по точности вычисления
координаты х, по модулю значения функции
f(), по количеству обращений к функции
f() и т. д.
Пример
4.2-5.
Найти
решения tg(x)=0
на
интервале[1;2].
|
|
|
>> х 1.5708 f -1.2093e+015 >> |
Якобы
«корень», соответствующий приближенному
значению ?/2,
на самом деле является точкой разрыва,
при переходе через которую функция
меняет знак. Выведенное значение функции
в найденной точке убеждает нас в том,
что найден не корень.
Функция
fzero() может возвратить еще два выходных
параметра.
|
|
|
>> >> |
Положительное
значение e_fiag
(обычно, это 1) означает, что удалось
найти
интервал, на концах которого функция
f(
)
меняет знак (пример с tg(x)не
должен притупить вашу бдительность).
Если такой интервал не обнаружен,
то e_fiag=-1.
Структура inform
содержит три поля с именами iterations,
funcCountи
algorithm.
В первом из них находится количество
итераций,
выполненных при поиске корня, во втором
–
количество обращений к функции f(
),
в третьем –
наименование алгоритма, использованного
для нахождения корня.
Пример
4.2-6.
Найти
корень уравнения с помощью функции
fzero().
|
|
|
» x f= e_flag inform iterations: funcCount:
algorithm: >> |
В данном случае достижение
высокой точности потребовалось
8 итераций. Простое деление отрезка
пополам для достижения
такой же точности потребовало бы больше
итераций.
Отделение отрезка, на концах
которого функция принимает значения
разных знаков, является принципиальным
для алгоритма, использованного
в функции fzero().
Даже в таких тривиальных уравнениях,
как х2=0,
обычно
не удается найти решение.
Для символьного (аналитического)
решения уравнений в MatLab используется
функция solve(),которая
представляется в следующем
виде:solve(‘f(x)’,x),solve(‘f(x)’),где:
‘f(x)’–
решаемое уравнение, записанное в
одиночных кавычках и представленное в
произвольной форме; x–
искомая символьная неизвестная (symsx).
Рассмотрим технологию
определения корня с помощью функции
solve()
на примерах.
Пример
4.2-7.Найти
решение уравнения2x–3(a–b)=0
в символьном
виде.
|
|
|
>>syms >> y log((3*a-3*b)/log(2)) >> |
Пример
4.2-8.Решить
уравнение 2x–4∙x+3=0
аналитически.
|
|
|
>>syms >> y 1.418 3.413 >> |
Функция
в ряде случаев позволяет определить
все корни уравнения f(x)=0
без указания начальных
значений x
или областей изоляции корней.
Функция solve()
имеет следующий недостаток. Она не
требует информации о начальном значении
корня или области его изоляции. Поэтому
в случае трансцендентных уравнений и
в ряде других случаев, она не находит
всех корней уравнения.
Пример
4.2-9.Решить
уравнение 2x–3(a–b)=0,
где a
– независимая
переменная.
|
|
|
>>syms >> y 1/3*2^x+ >> |
[Введите текст] Страница
11
Соседние файлы в папке Учебное пособие
- #
- #
- #
- #
- #
- #
- #
- #
- Получите корни многочлена с помощью функции
roots()в MATLAB - Получите корни полинома с помощью функции
solve()в MATLAB
Это руководство познакомит вас с тем, как найти корни многочлена с помощью функций roots() и solve() в MATLAB.
Получите корни многочлена с помощью функции roots() в MATLAB
Если вы хотите найти корни многочлена, вы можете использовать функцию roots() в MATLAB. Этот вход этой функции — вектор, который содержит коэффициенты полинома. Если в полиноме нет степени, то в качестве его коэффициента будет использоваться 0. Результатом этой функции является вектор-столбец, содержащий действительные и мнимые корни данного многочлена. Например, давайте найдем корни квадратного полинома: 2x ^ 2 — 3x + 6 = 0. Мы должны определить коэффициенты полинома, начиная с наивысшей степени, и если степень отсутствует, мы будем использовать 0 в качестве ее коэффициента. . См. Код ниже.
poly = [2 -3 6];
p_roots = roots(poly)
Выход:
p_roots =
0.7500 + 1.5612i
0.7500 - 1.5612i
В приведенном выше коде мы использовали только коэффициенты полинома, начиная с наибольшей степени. Вы можете изменить коэффициенты многочлена в соответствии с данным многочленом. Знаем, давайте найдем корни многочлена четвертой степени: 2x ^ 4 + 1 = 0. См. Код ниже.
poly = [2 0 0 0 1];
p_roots = roots(poly)
Выход:
p_roots =
-0.5946 + 0.5946i
-0.5946 - 0.5946i
0.5946 + 0.5946i
0.5946 - 0.5946i
Мы использовали три 0 между двумя полиномами в приведенном выше коде, потому что три степени отсутствуют. Проверьте эту ссылку для получения дополнительной информации о функции root().
Получите корни полинома с помощью функции solve() в MATLAB
Если вы хотите найти корни многочлена, вы можете использовать функцию resolve() в MATLAB. Этот вход этой функции является полиномом. Результатом этой функции является вектор-столбец, содержащий действительные и мнимые корни данного многочлена. Например, давайте найдем корни квадратного многочлена: 2x ^ 2 — 3x + 6 = 0. Нам нужно определить многочлен. См. Код ниже.
syms x
poly = 2*x^2 -3*x +6 == 0;
p_roots = solve(poly,x)
p_roots = vpa(p_roots,2)
Выход:
p_roots =
0.75 - 1.6i
0.75 + 1.6i
В приведенном выше коде мы определили весь многочлен и использовали функцию vpa(), чтобы изменить точность результата. Вы можете изменить полином в соответствии с заданным полиномом и точностью в соответствии с вашими требованиями. Знаем, давайте найдем корни многочлена четвертой степени: 2x ^ 4 + 1 = 0. См. Код ниже.
syms x
poly = 2*x^4 +1 == 0;
p_roots = solve(poly,x);
p_roots = vpa(p_roots,2)
Выход:
p_roots =
- 0.59 - 0.59i
- 0.59 + 0.59i
0.59 - 0.59i
0.59 + 0.59i
В приведенном выше коде мы определили весь многочлен и использовали функцию vpa() для изменения точности результата. Вы можете изменить полином в соответствии с заданным полиномом и точностью в соответствии с вашими требованиями.




 Пример4.2-1
Пример4.2-1 Пример
Пример
 Пример
Пример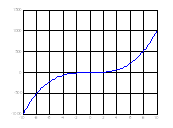



 Пример
Пример
 Пример
Пример Пример
Пример Пример
Пример Пример
Пример Пример
Пример Пример
Пример

