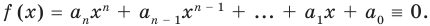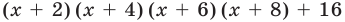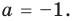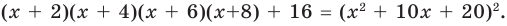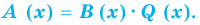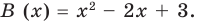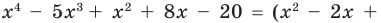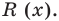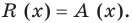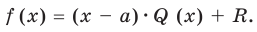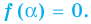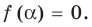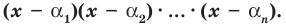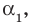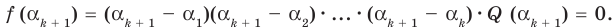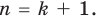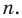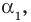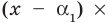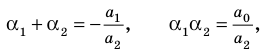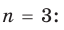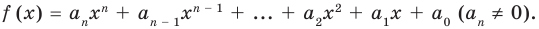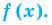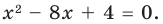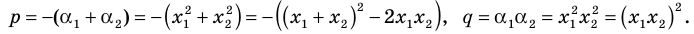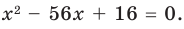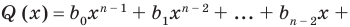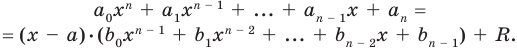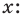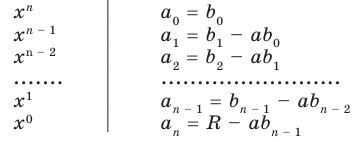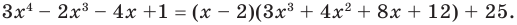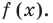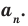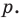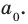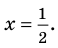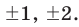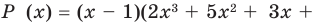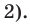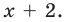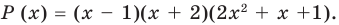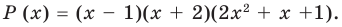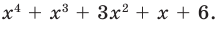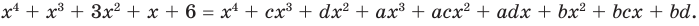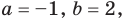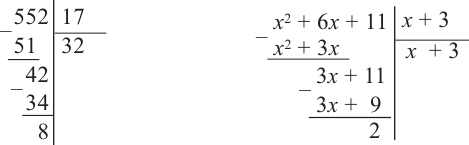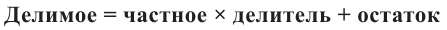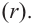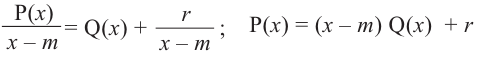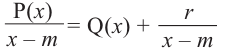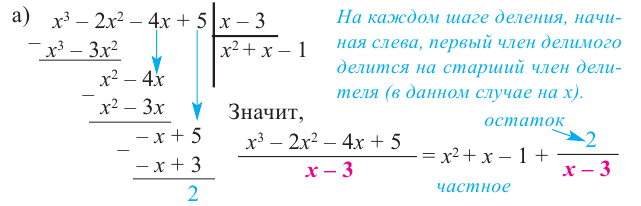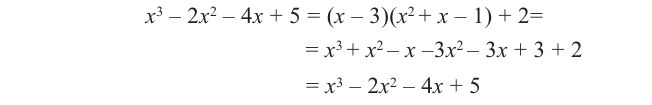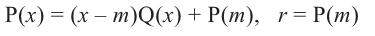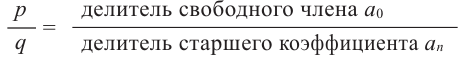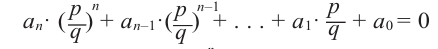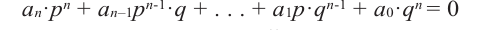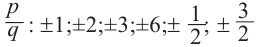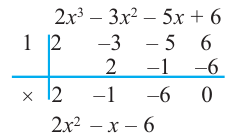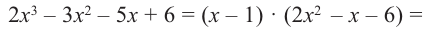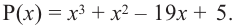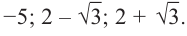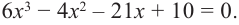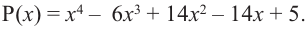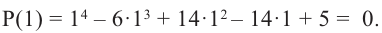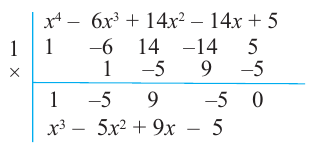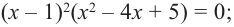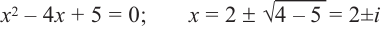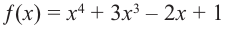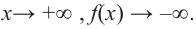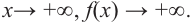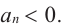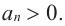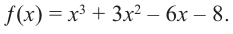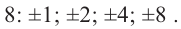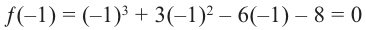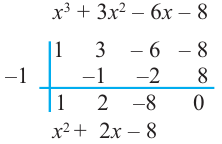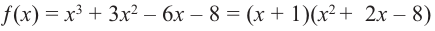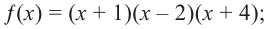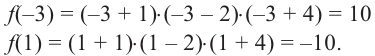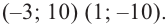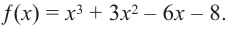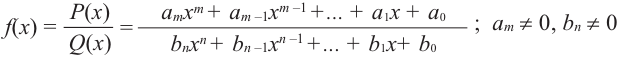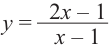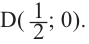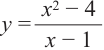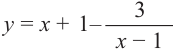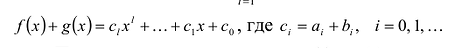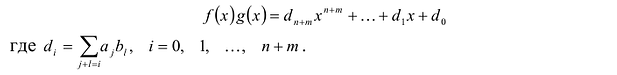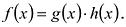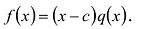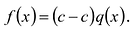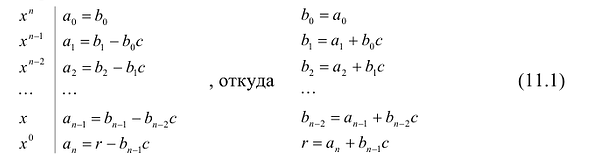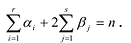Инфоурок
›
Другое
›Презентации›Способы нахождения корней многочленов
Способы нахождения корней многочленов
Скачать материал

Скачать материал




- Сейчас обучается 268 человек из 65 регионов


- Сейчас обучается 389 человек из 62 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
по математике:
Исполнитель: Лукин Николай Сергеевич
МОУ СОШ №21, г. ПодольскНаучный руководитель: Буянова Анна Матвеевна
учитель математики МОУ СОШ №21, г. Подольск
2011 год
СПОСОБЫ НАХОЖДЕНИЯ
КОРНЕЙ МНОГОЧЛЕНОВ -
2 слайд
Цели
Рассмотреть решение квадратных, кубических и биквадратных уравнений;
Делимость многочленов;
Деление многочленов с остатком;
Решение алгебраических уравнений 3-й и 4-й степени;
Симметрические и возвратные уравнения;
формулы Виета, Горнера и Безу.
Применить полученные знания при решении задач группы С, а именно С5. -
3 слайд
КВАДРАТНОЕ УРАВНЕНИЕ
ЕСЛИ:
D>0, то уравнение имеет два корня.
D=0, то уравнение имеет один корень.
D<0, то уравнение не имеет корней.
Уравнение вида ax2+bx+c=0 называется квадратным уравнением,
где x – переменная, а, b и с – некоторые числа,
причем, а≠0.
Чтобы найти корни квадратного уравнения вида: ax2+bx+c=0, нужно найти его дискриминант. Дискриминант находится по формуле: D=b2-4ac. -
4 слайд
ТЕОРЕМА ВИЕТА
Если числа m и n таковы, что сумма равна р, а произведение равно q, то эти числа являются корнями уравнения x2+px+q=0.
Частные случаи при решении
квадратного уравнения -
5 слайд
БИКВАДРАТНОЕ УРАВНЕНИЕ
Уравнения вида x4+bx2+c=0 будем называть биквадратными уравнениями.
Первый способ:
Биквадратное уравнение можно заменой y=x2 свести к квадратному уравнению у2+by+c=0.
Второй способ. -
6 слайд
СИММЕТРИЧЕСКИЕ УРАВНЕНИЯ
Уравнение вида
а0хn+ а1хn-1+…+ аkхn-k+…+ аkхk+…+ а1х+a0=0
Свойства
симметрического уравнения -
7 слайд
Пример симметрического уравнения
-
8 слайд
ВОЗВРАТНЫЕ УРАВНЕНИЯ
Уравнения вида
а0х2n+1+ а1x2n+…+ аnхn+1+ аn+1хn+…+ а2nх+a2n+1=0
называют возвратными уравнениями нечетной степени, если
где λ- некоторое действительное число.
Уравнения вида
а0х2n+ а1x2n-1+…+ аn-1хn+1+ аnхn+…+ а2n-1х+a2n=0
называют возвратными уравнениями четной степени, если
Свойства возвратного уравнения -
9 слайд
ПРИМЕР ВОЗВРАТНОГО УРАВНЕНИЯ
-
-
11 слайд
ТЕОРЕМА II
Пример -
12 слайд
ТЕОРЕМА III
Пример -
-
14 слайд
Пример
ТЕОРЕМА БЕЗУ -
-
-
17 слайд
Решение алгебраических уравнений 3-й
степени с одним неизвестным -
-
19 слайд
Решение алгебраических уравнений 4-й степени
с одним неизвестным -
-
-
-
-
24 слайд
—
—
+
yх
y
ya
xa
0
f(x)
х
y
ya
xa
0
f(x)
D<0, a>0.
D<0, a<0. -
25 слайд
х
y
xa
0
f(x)
х
y
f(x)
0
xa
xa
х
0
y
ya
f(x)
x-
x+
х
0
ya
xa
x+
-x
f(x)
y
D>0, a>0.
D>0, a<0.
D=0, a>0.
D=0, a<0. -
26 слайд
ВЫВОД:
В своей работе я рассмотрел, изучил и опробовал на примере
одиннадцать способов решения уравнений .
И я считаю, что нужно знать хотя бы самые простые способы решения уравнений высших степеней.
Упростил запись и ход решения схемы Горнера.
Применил полученные знания при решении задач группы С, а именно С5.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 264 258 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 06.11.2020
- 123
- 0
- 04.11.2020
- 181
- 0
- 27.10.2020
- 101
- 0
- 20.10.2020
- 242
- 0
- 03.10.2020
- 157
- 0
- 24.09.2020
- 91
- 0
- 24.09.2020
- 178
- 0
- 11.09.2020
- 91
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
-
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
-
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
-
Курс повышения квалификации «Экономика: инструменты контроллинга»
-
Курс профессиональной переподготовки «Организация маркетинга в туризме»
-
Курс повышения квалификации «Методы и инструменты современного моделирования»
-
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс профессиональной переподготовки «Осуществление и координация продаж»
-
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
-
Курс повышения квалификации «Информационная этика и право»
-
Настоящий материал опубликован пользователем Ашеко Кристина Александровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 2 года и 5 месяцев
- Подписчики: 0
- Всего просмотров: 71034
-
Всего материалов:
220
Урок по алгебре в 7-м классе по теме: «Решение уравнений с применением приемов разложения многочлена на множители»
Разделы: Математика
Ребята, достаточно долго овладевая приёмами разложения многочлена на множители, подошли к моменту, когда необходимо систематизировать и обобщить изученные способы, попытаться сделать новые открытия и самое главное: найти интересное применение разнообразных приёмов разложения на множители к решению порой одинаковых по смыслу уравнений.
1. Что, значит, разложить многочлен на множители?
2. В каком случае произведение множителей равно 0?
3. Степень, какого числа равна нулю? 1?
4. Какие приёмы разложения на множители вам известны? (Вынесение общего множителя за скобки, группировка слагаемых с последующем вынесением общего множителя, с помощью формул сокращенного умножения).
5. Чему равны квадрат суммы, разности двух слагаемых?
6. Чему равна разность квадратов двух слагаемых?
На доске записаны уравнения:
По какому признаку можно разбить эти уравнения в группы? (Уравнения, содержащие многочлен второй степени. Уравнения, содержащие многочлен выше второй степени. Уравнение, содержащее многочлен второй степени, коэффициенты которого периодические дроби).
Нам предстоит решить эти уравнения, подбирая непохожие способы решения, несмотря порой на похожесть уравнений.
Предлагаю учащимся решить уравнение 
Один ученик решает уравнение разбиением одночлена 6х на сумму двух одночленов
Вопрос: Какой способ оказался более рациональным? (Конечно второй). Как его можно назвать?
(Выделение полного квадрата суммы)
Обсуждаем решение уравнения 
Можно ли решить уравнение, разбивая одно из слагаемых на два?
(да,
А выделением полного квадрата суммы?
(затруднительно, так как, число 3 не является квадратом никакого рационального числа)
И всё-таки попробуем выделить полный квадрат суммы: дополните сумму первых двух слагаемых до квадрата суммы.
Как можно разложить многочлен в левой части уравнения на множители? (По формуле разности квадратов).
Сообразите, можно ли рассуждая аналогично решить уравнение 
(Неудобное в данном случае число 5).
И все-таки, попробуем строго следовать формуле квадрата суммы при выделении полного квадрата:
Обратите внимание на коэффициенты уравнения 
(Одинаково читаются слева направо)
Что происходит с показателями переменной x?
(Уменьшаются на один)
Выскажите предположение для многочлена в левой части уравнения.
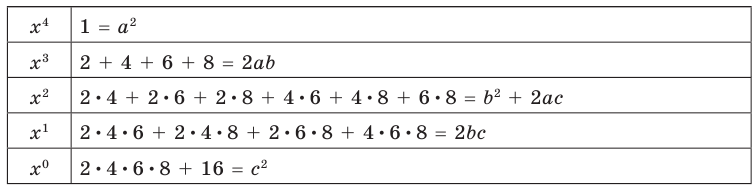
(Многочлен х 4 +4х 3 +6х 2 +4х+1 есть (х+1) 4 ). Обоснуйте это.
(Построим треугольник Паскаля
14641 4-ая строка содержит коэффициенты возведения в 4-ую степень двучлена (х+1)
Итак, какой вид примет уравнение? Решите его устно.
Решите устно уравнение
Какими числами являются коэффициенты уравнения
(Периодическими десятичными дробями)
Обратите периодические дроби в обыкновенные и решите, получившееся уравнение.
(Правило обращения периодической десятичной дроби в обыкновенную: чтобы периодическую десятичную дробь обратить в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде и после девятки дописать столько нулей, сколько цифр между запятой и первым периодом)
(Подберите рациональный способ решения и найдите корни уравнения, х=1 или 
Вновь обратимся к уравнению 
Сравните значения найденных корней со значениями переменных b и d. (Они противоположны)
Найденные корни подтверждают мысль о том, что независимо от способа решения корни не меняются.
Чем уравнение 
(Коэффициент при х 2 равен 1)
Попробуем решить это уравнение устно, не применяя ни один из рассмотренных приёмов, но
принимая во внимание некоторые рассуждения в предыдущем случае:
Запишите разложение многочлена 
Тогда, скажите чему, будут равны значения выражений 

( Легко догадаться, что или наоборот).
Сообразите, чему будут равны корни уравнения?
Устно решите уравнения:
1. С каким новым способом решения квадратных уравнений вы познакомились?
(Выделение полного квадрата суммы или разности)
2. Как вы думаете, почему этот способ не всегда удобен?
(Например, в уравнении 3х 2 -2х-1=0 3х 2 не является квадратом рационального выражения)
3. Какое открытие вы сделали, применяя метод неопределённых коэффициентов для
решения квадратных уравнений, если коэффициент при равен 1?
(Чтобы найти корни, надо сначала найти два таких числа в и с, чтобы их сумма была равна второму коэффициенту, а произведение – третьему слагаемому. А корни будут равны числам, противоположным числам .
В 8 классе вы познакомитесь с ещё одним способом решения квадратных уравнений – по формулам. Узнаете, кто такой Франсуа Виет и какое отношение он имеет к нашему открытию.
Учим алгебра 7 класс. Как решать уравнения алгебра 7 класс, примеры, дроби, функции, степени, модули
В 7 классе ученикам предстоит научиться решать уравнения, дроби, строить функции, разбираться в модулях. Для этого следует познакомиться с основными понятиями в темах, рассмотреть алгоритм решения и пошагово учиться находить ответы. Главное правило — начать с простых примеров, постепенно переходя на более сложные. Большинство задач можно решать несколькими методами (это касается и примеров), следует выбрать самый простой и удобный для себя.
Как решать уравнения алгебра 7 класс
Начнем с решения линейных уравнений (на рисунке показано, по какому принципу они устроены). Чтобы найти ответ в таких уравнениях, нужно совершать действия: раскрытие скобок, поиск подобных слагаемых, умножение/деление частей на одно и тоже число, перенос слагаемых из одной части уравнения в другую. Всё зависит от конкретного примера.
Рассмотрим несколько примеров пошагового решения линейных уравнений.
Пример 1.
6x + 24 = 0
Поскольку части уравнения (левая и правая) равны, то можно отнять из каждой одинаковое число. Равенство не изменится, а пример станет значительно проще. В представленном уравнении отняли 24 и слева, и справа. В левой части 24 сократилось, а в правой (0 — 24) получилось -24 (не забываем ставить знак минуса).
Получилось: 6x = -24. Теперь можем сократить 6 и -24 на число 6 (или рассуждаем так: чтобы найти множитель, нужно произведение разделить на другой множитель). В ответе будет -4. Не забудьте в самом конце подставить полученное число вместо х. Совпал ответ — значит, все правильно.
Можно рассуждать проще: чтобы упростить уравнение, нужно из левой части отправить в правую число 24, поменяв его знак. Равенство сохранится (на рисунке ниже).
Пример 2.
9 + 16x = 41 + 14x
Это уравнение более сложное. Здесь важно запомнить несколько моментов:
- числа без х переносятся в левую часть, а с х — в правую;
- при переносе знаки меняют.
Пример 3.
7(10 — 4x) + 5x = 12 — 3(5x + 2)
- Раскрыть скобки, выполнив умножение: 7 умножаем на каждое число в скобках (в правой части -3 на каждое). При выполнении действия не забывайте сохранять знаки.
- Записываем уравнение, получившееся после раскрытия скобок. Ещё раз сверяем знаки.
- Числа с х отправляются в левую часть, без х — в правую. Знаки чисел, которые переходят в другую часть, меняем.
- Подсчитываем результат с обеих сторон.
- Делим -64 на -8 и получаем ответ. Не забываем, что минус на минус при делении и умножении дают плюс.
В рассмотренных уравнениях корень точно определён. Так получается не всегда.
Пример 4.
Обратите внимание, в ответе получилось 0x = 0. Это значит, что x может быть любым числом, потому что при умножение хоть какого числа на 0 получится 0.
В этом примере корней нет, так как любое число, которое умножают на 0, будет равно 0 (21 никак не получится).
Как решать систему уравнений алгебра 7 класс
Системой называют несколько уравнений, в которых нужно найти такие значения неизвестных, чтобы равенство сохранилось. Разберемся на примерах, как выглядят системы и какие методы их решения существуют.
метод подстановки
Из самого названия следует, что алгоритм требует что-то подставлять. Ниже представлена система, где нужно найти значения x и y.
Суть метода подстановки: переменную в одном из уравнений выражают через другую переменную. Затем подставляют полученное выражение в другое уравнение.
Смотрим на систему. Видим, что удобнее будет выразить x во втором уравнении (так как он один). Выражаем путем переноса за знак «равно» 12y. Получилось: x = 11 — 12y (не забываем менять знак при переносе числа).
В первое уравнение вместо «x» записываем получившееся выражение. Меняем только x, остальное сохраняется в прежнем виде.
Далее преобразуем уравнение, в которое поместили выражение. Раскрываем скобки (перемножаем 5 на каждое значение). y оставляем в левой части, числа переносим в правую, знаки меняем. Таким образом нашли значение y (y = 1).
Теперь подставляем полученную единицу во второе уравнение (x = 11 — 12y).
Убедиться в правильном решение можно так: подставьте полученные значения в систему. Если равенства сохранятся, значит, решено верно.
метод сложения
Чтобы решить систему методом сложения, нужно из двух уравнений сделать одно. Просто складываем первое и второе. Здесь «y» просто сократились, и получилось простое уравнение. Как только нашли значение «х», нужно подставить его в любой пример (здесь поставили во второе уравнение). В ответе пишется так: (4; 3) — первым всегда пишется х, затем у.
графический метод
У нас есть система, где y = 5x и y = -2x + 7. Рассмотрим алгоритм решения системы уравнений:
- Подбираем 2 числа для х. Мы взяли 0 и 1, подставляем в первое уравнение: y = 5 * 0 = 0; у = 5 * 1 = 5. Значит первая прямая имеет координаты: (0; 0) и (1; 5).
- Для второго уравнения подбираем значения х. Взяли 3 и 2, подставляем и находим у: -2 * 3 + 7 = 1; -2 * 2 + 7 = 3. Значит прямая имеет координаты (3; 1) и (2; 3).
- Отмечаем на графике соответствующие прямые, подписываем их название.
- на месте пересечения получившихся прямых ставим точку — это будет решение.
- Точка имеет координаты (1; 5).
На заметку! Старайтесь подбирать такие значения х, чтобы у был небольшим. Так отмечать будет проще.
Выбирайте самый удобный способ решения. Третий метод — графический, считают самым неточным.
Как решать дроби 7 класс
Дроби можно разделить на 2 основных вида:
Они различаются в способе написания (смотрите рисунок ниже). В свою очередь и те, и другие делятся еще на несколько видов.
Для начала рассмотрим решение примеров с десятичными дробями.
Особое внимание при решении стоит уделить запятым. При сложении и вычитании запятые стоят строго друг под другом, при умножении это не имеет значения.
Примеры решения обыкновенных дробей.
- при сложении и вычитании нужно привести дроби к общему знаменателю, найти дополнительные множители. Так, для чисел 6 и 4 общим знаменателем стало число 24. Дополнительные множители считали так: 24 : 6 = 4 (для первой дроби) и 24 : 4 = 6 (для второй). Потом умножили доп. множители на числители и полученные числа сложили. Если в ответе получилась неправильная дробь, то выделяем целую часть, при необходимости сокращаем дроби.
- при умножении пишем дроби под одной чертой, сокращаем.
- при делении нужно вторую дробь перевернуть, поставить знак умножения и сократить дроби.
Если пример состоит из простой и десятичной дроби, то следует привести их к одному виду (к которому проще или удобнее считать).
Примеры 7 класс как решать
Теперь закрепим решение дробей на примерах.
Решение примера, представленного ниже:
- Видим, что присутствует как обыкновенная дробь, так и десятичные. Нужно привести к одному виду. Так как десятичных больше, и превратить 1/4 в этот вид проще, то делим 1 на 4, а целую часть сохраняем. Вышло 5,25.
- Далее умножаем — 3 на каждое число в скобках, внимательно следим за знаками.
- Остается от 10,4 отнять 9,3. В итоге вышло 1,1.
Но можно было решить проще. Первое действие всегда в скобках. Поэтому от 5,25 отнимаем 2,15. Получится 3,1. Умножаем ее на 3 — вышло 9,3. И отнимаем: 10,4 — 9,3 = 1,1. Этот способ даже проще, потому что не нужно следить за знаками при раскрытии скобок.
Чтобы верно решить следующий пример, нужно:
- точно проставить порядок действий (умножение и деление делаем в первую очередь, затем складываем);
- Умножить десятичные дроби столбиком, не забыть поставить запятую;
- деление здесь простое: переставили запятую на один знак вправо, поделили, получили -2.
- сложили числа.
Как решать задачи алгебра 7 класс
Задачи решаются путем составления уравнений.
Другие примеры задач с подробными решениями в видео-материалах.
Как решать функции алгебра 7 клас с
Функцией принято считать зависимость y от x. При этом x является переменной (или аргументом), а у — это значение функции (зависимая переменная).
- y(x) = 8x
- y(x) = −3x — 62
- y(x) = x−1 + 18
Чтобы найти значение у, которое бы соответствовало определенному значению х, нужно просто это значение х подставить в функцию.
Как решать степени алгебра 7 класс
Если требуется взять какое-либо число несколько раз, то проще записать его в степени. Например, нужно двойку взять три раза, т. е.: 2 * 2 * 2. Получается длинная запись. Поэтому придумали писать так: 2³ (читается: два в третьей степени).
Чтобы число возвести в степень (она указывается справа от числа вверху), нужно его умножать на самого себя столько раз, какая цифра указана. Рассмотрим подробнее на примерах.
Не всегда получается возвести число в степень «в уме». Иногда посчитать сложно. Например, возвести 6 в 5 степень, быстро получится не у каждого. Чтобы всякий раз не считать столбиком, лучше выучить основные степени. Они представлены в таблице.
При возведении любого числа в степень 1, получится это же число. Если возводить число в нулевую степень, в ответе будет 1.
Рассмотрим несколько примеров со степенями.
Отдельное внимание обращаем на возведение в степень отрицательного числа. Если такое число возводить в четную степень (2; 4; 6 и т.д.), то получится положительный ответ, если в нечетную, то ответ со знаком минус.
Алгебра модули как решать
Модулем числа называют это же число, только без знака минус. Например: | − 9 | = 9. При этом если число изначально неотрицательное, то оно остается прежним.
Перейдем к простым примерам.
Логично предположить, что под модулем будет число 4. Также подойдет число -4, ведь из-под модуля все равно выйдет положительное. Так, корнями уравнения будут: x = 4 и x = − 4.
Из-под модуля не может выйти отрицательное число. Поэтому, если видим что-то похожее: Ι-8 + хΙ = -8, значит, корней не будет, так как уравнение заведомо нерешаемо.
Другие примеры описаны в видео.
Об Авторе
Смотрите также
Сочинение рассуждение на тему патриотизм, патриотизм сочинение ЕГЭ: ложный и истинный патриотизм, народный патриотизм роман Война и мир, примеры сочинений
Урок патриотизма в школе. Тема урока патриотизм: урок литературы патриотизм, патриотическое воспитание на уроках истории, урок мужества патриотизм. Дети герои Великой Отечественной войны Валя Котик, Валерий Волков, Марат Казей, Надя Богданова, Люся Герасименко, Вашкевич Лида, Валя Зенкина, Костя Кравчук, Вася Коробко, Витя Хоменко, Саша Ковалёв: краткая биография
Современный сценарий выпускного в школе: сценарий выпускного современный прикольный веселый, красивые платья на выпускной 11 класс, современные песни текст на выпускной
2 комментария
Спасибо большое очень помогли.
Огромное спасибо!А то учитель неможет нормально тему объяснить
Уравнение и его корни
п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
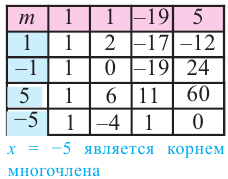
В уравнении x(x + 5)(x — 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x in Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x — (3 — 2x) = 9
x-(3-2x)=9 $iff$ x-3+2x=9 $iff$ x+2x=9+3 $iff$ 3x=12 $iff$ x=4
$4 -(3 — 2 cdot 4)=9 implies 4 — 3 + 8 = 9 implies 9 equiv 9$
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
7(x + 3)=56 |:7 $iff$ x + 3 = 8 $iff$ x = 8 — 3 $iff$ x=5
$7(5 + 3) = 56 implies 7 cdot 8 = 56 implies 56 equiv 56$
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
(3x + 4) : 2=14 |$times$2 $iff$ 3x + 4 = 28 $iff$ 3x = 28 — 4 $iff$ 3x = 24 $iff$ x=8
$(3 cdot 8 + 4) : 2 = 14 implies (24 + 4) : 2 = 14 implies 28 : 2 = 14 implies 14 equiv 14$
Пример 4. Решите уравнение $ frac<3x-7> <3>- frac <5x-11> <5>= 0$
$frac <3x-7> <3>- frac <5x-11> <5>= 0 | times 15 iff5(3x-7)-3(5x-11)=0 iff$
$ iff 15x-35-15x+33=0 iff 0x=2 iff x in varnothing $
Ответ: $x in varnothing $
Пример 5. Решите уравнение $frac <2x — 7> <2>= frac <3x+6><3>$
$frac <2x-7><2>=frac <3>| times 6 iff 3(2x-7)=2(x+6) iff 6x-21=2x+12 iff $
$iff 6x-2x=12+21 iff 4x=33 iff x= frac <33> <4>=8 frac 14$
Ответ: $8 frac 14$
Пример 6. Решите уравнение |x+1|=5
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
$$ |x + 1| = x + 3 iff left[ begin <left< begin x+1 ge 0 \ x+1=x+3 end right.>\ <left< begin x+1 Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $cdot$ (-3) + 18 = 3 $iff$ -15a = 3 — 18 $iff$ -15a = -15 $iff$ a = -15:(-15)=1
Учим алгебра 7 класс. Как решать уравнения алгебра 7 класс, примеры, дроби, функции, степени, модули
http://reshator.com/sprav/algebra/7-klass/uravnenie-i-ego-korni/
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен — это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 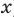
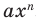
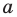
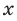
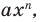
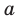
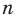
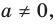
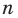
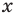
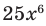
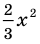
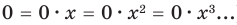
По определению многочлен от одной переменной 
многочленом от одной переменной 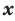
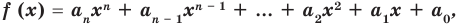
где коэффициенты 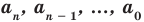
Если 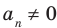
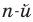
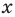
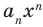
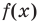
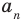
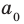
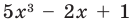
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 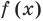
где 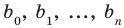
Теорема 1. Одночлены 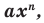
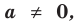
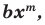
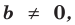
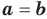
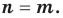
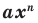
Поскольку равенство одночленов
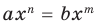
выполняется при всех значениях 
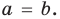
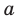
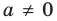
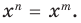
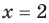
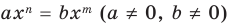
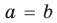
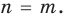
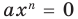
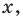
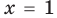
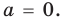
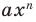
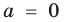
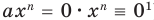
Далее любой одночлен вида 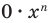
Теорема 2. Если многочлен 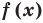
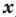
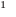
Для доказательства используем метод математической индукции. Пусть
При 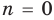
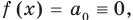
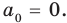
Предположим, что при 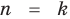
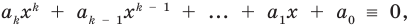
Докажем, что данное утверждение выполняется и при 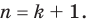
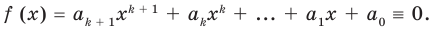
Поскольку равенство (3) выполняется при всех значениях 
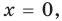
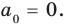
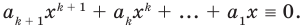

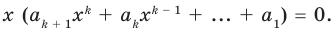
Равенство (4) должно выполняться при всех значениях 
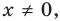
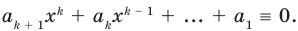
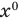
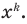
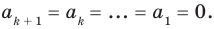
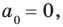
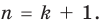
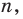
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 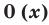
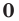
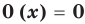
Теорема 3. Если два многочлена 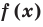
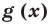
Пусть многочлен 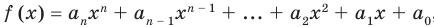
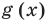
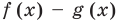
Но 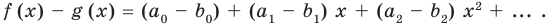
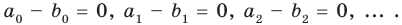
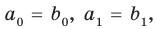
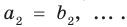
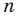
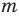
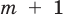
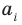
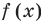
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
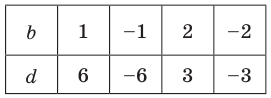
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 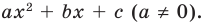
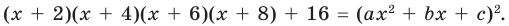
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 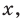
Из первого равенства получаем 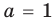
При 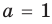
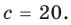
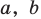
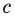
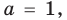
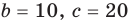
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 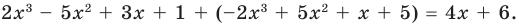
Например, 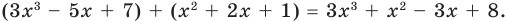
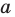
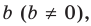
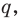
Определение: Многочлен 
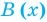
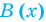

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 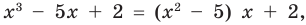
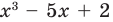
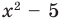
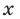
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 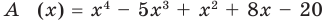
Решение:
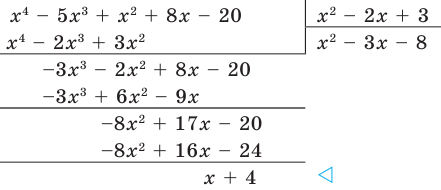
Если обозначить результат выполнения первого шага алгоритма через 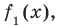
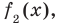
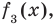
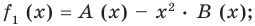
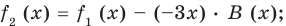
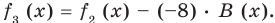
Сложим почленно равенства (1), (2), (3) и получим
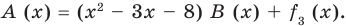
Учитывая, что степень многочлена 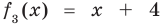
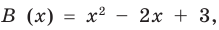
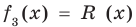
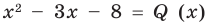
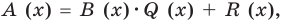
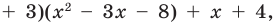
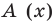
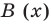
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 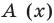
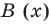
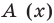
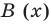
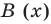
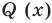
Отметим, что в случае, когда степень делимого 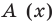
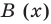
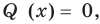
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 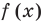
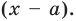
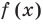
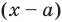
Это равенство выполняется тождественно, то есть при любом значении 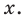
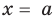
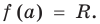
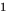
Теорема 1 (теорема Безу). Остаток от деления многочлена 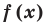
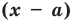
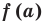
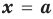
Пример №2
Докажите, что 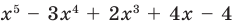
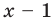
Решение:
► Подставив в 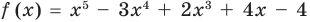
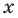
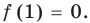


Определение: Число 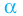
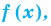
Если многочлен 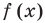

Действительно, если 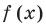
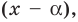

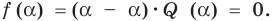
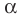
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 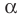
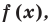
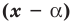
По теореме Безу остаток от деления 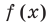

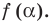
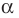
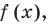
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 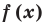
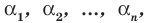
Для доказательства используем метод математической индукции.
При 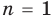
Допустим, что утверждение справедливо при 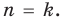
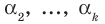
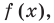
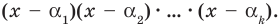
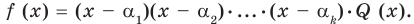
Докажем, что утверждение теоремы справедливо и при 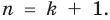
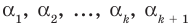
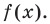
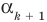
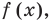
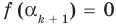
По условию все корни 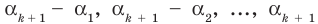
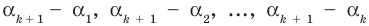
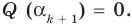
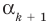
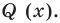
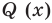
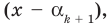
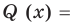
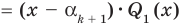
Это означает, что 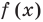
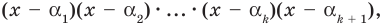
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 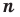
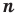
Допустим, что многочлен 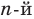
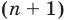
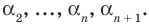
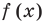
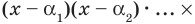
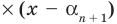
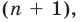
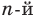
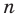
Пусть теперь многочлен 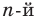
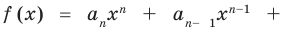
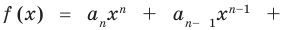
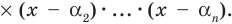
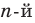
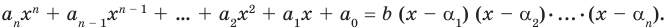
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 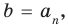
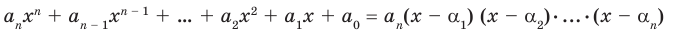
Сравнивая коэффициенты при одинаковых степенях 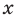
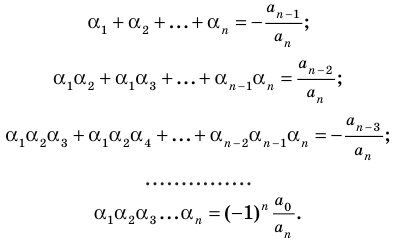
Например, при 
а при
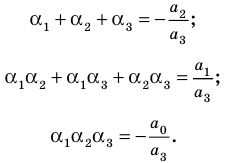
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 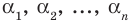
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 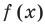
Если многочлен 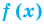
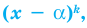
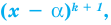


Например, если произведение 
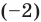
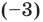
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 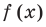
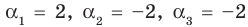
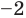
Проверим справедливость формулы (5). В нашем случае: 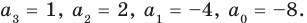
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 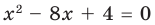
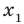
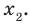
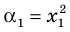
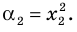
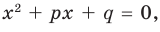
По формулам Виета имеем 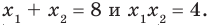
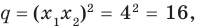
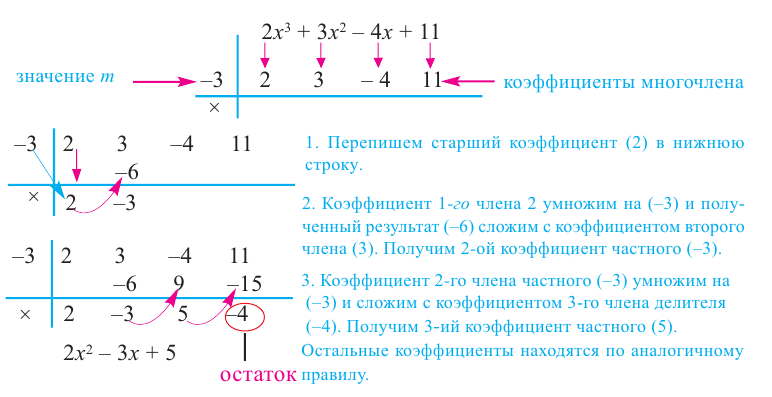
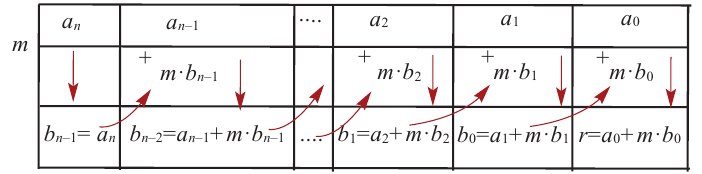
Схема Горнера
Делить многочлен 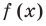
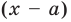
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 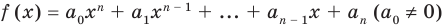
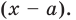
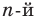
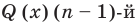
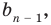
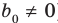
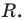
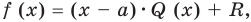
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 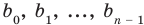
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 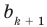
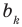
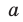
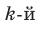
Пример №5
Разделите по схеме Горнера многочлен 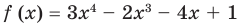
Решение:
► Запишем сначала все коэффициенты многочлена 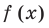
Таким образом,
Пример №6
Проверьте, является ли 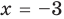
Решение:
► По теореме Безу остаток от деления многочлена 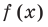
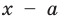
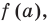
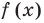
Поскольку 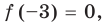
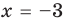
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 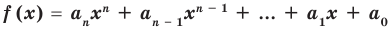
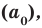
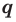
Если 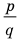
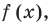
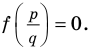
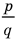
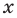
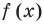
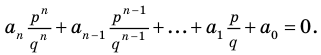
Умножим обе части равенства (1) на 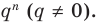
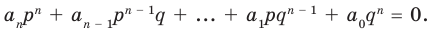
В равенстве (2) все слагаемые, кроме последнего, делятся на 
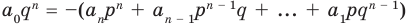
Но когда мы записываем рациональное число в виде 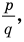
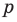
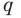
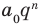
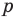
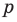
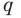
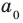
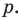
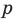
Аналогично все слагаемые равенства (2), кроме первого, делятся на 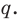
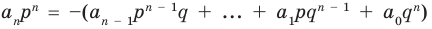
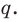
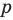
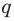
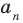
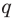
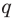
Отметим два следствия из этой теоремы. Если взять 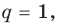
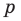
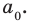
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 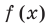
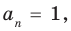
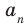
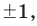
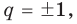
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 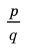
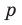
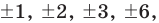
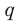
Таким образом, рациональные корни многочлена необходимо искать среди чисел 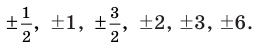
При 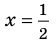
Кроме того, по схеме Горнера можно записать, что
Многочлен 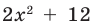
Пример №8
Разложите многочлен 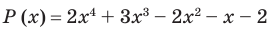
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 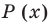

Тогда
Ищем целые корни кубического многочлена 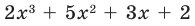
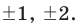
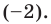
Имеем
Квадратный трехчлен 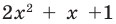
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 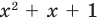
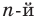
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
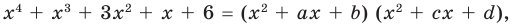
где 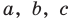
Получаем систему
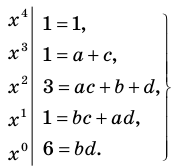
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 
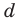
Коэффициенты 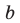
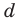
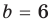
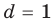
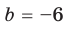
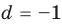
Для каждой пары значений 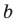
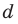
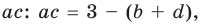
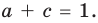
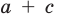
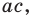
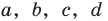
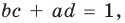
Как видим, системе (4) удовлетворяет набор целых чисел 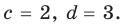
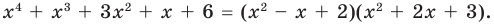
Поскольку квадратные трехчлены 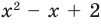
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 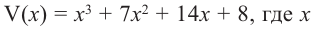
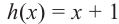
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 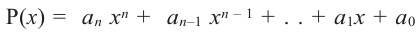
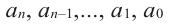
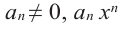
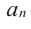
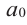
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 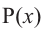
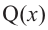
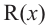
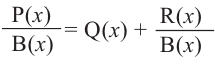
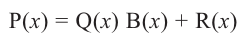
Здесь, степень многочлена 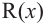
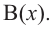
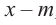
В этом случае:
Пример №10
а) Разделите многочлен 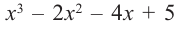
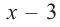
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 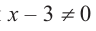
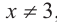
c) Должно выполняться тождество
Пример №11
Разделите 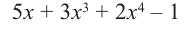
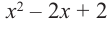
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 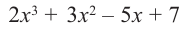
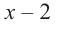
2) На каждом шаге деления делимое делится на старший член делителя, на 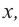
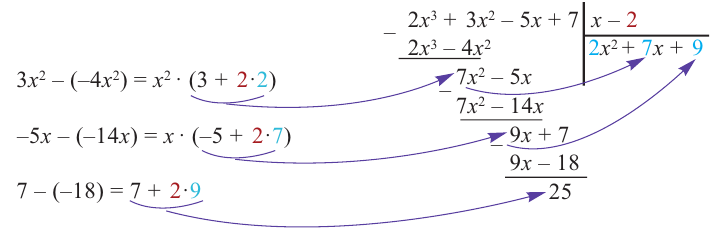
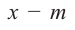
При делении многочлена на двучлен вида 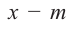
Пример №13
Разделите многочлен 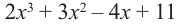
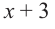
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 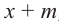
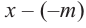
Запишем двучлен 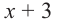
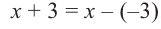
Таким образом, для делимого 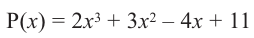
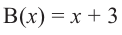
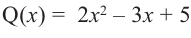
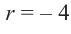
Деление можно записать в виде: 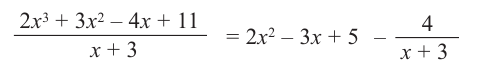
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 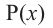
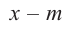
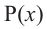
Доказательство: В равенстве 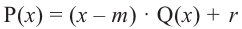
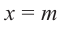
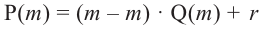
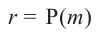
Пример №14
Найдите остаток от деления многочлена 
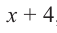
Решение: запишем делитель в виде 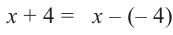
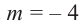
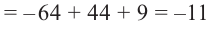
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 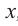
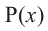
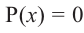
Теорема. Если число 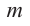
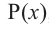
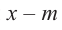
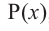
Действительно, если 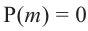
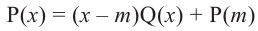
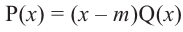
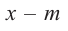
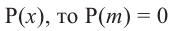
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 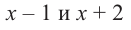
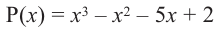
Решение: вычислим значение многочлена 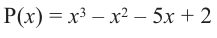
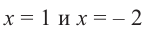
Значит, 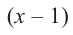
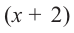
Пример №16
Зная, что 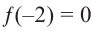
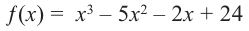
Решение: так как 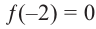
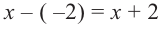
Учитывая, что 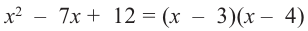
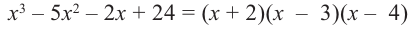
Отсюда получаем, что 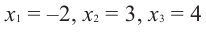
Примечание: Если многочлен задан в виде 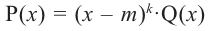
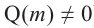
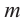
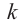
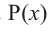
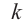
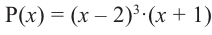
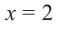
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 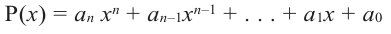
Доказательство. Пусть несократимая дробь 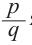
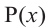
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 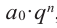
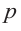
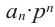
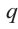
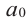
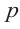
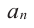
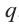
Пример №17
Найдите рациональные корни многочлена 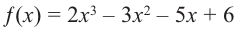
Решение: свободный член 6, старший коэффициент 2.
Для 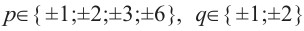
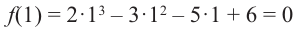
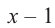
Так как, 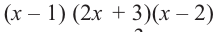
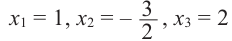
Следствие 1. Если старший коэффициент 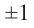
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 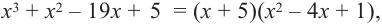
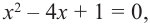
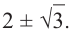
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 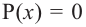
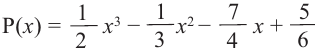
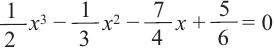
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 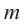
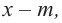
3. Для данного многочлена при помощи синтетического деления на двучлен 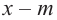
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 
Проверим: 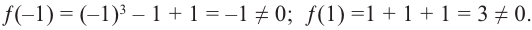
Основная теорема алгебры
Покажем на примере, что многочлен 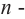
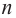
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 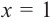
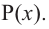
В выражении 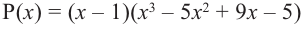
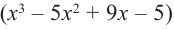
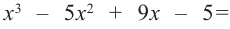
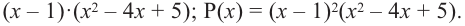
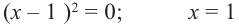
Корни:
Во всех рассмотренных нами примерах уравнение 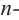
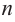
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 
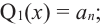
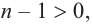
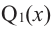
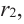
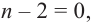
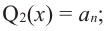
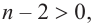
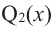
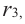
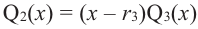
Продолжая процесс 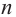
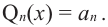
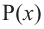
здесь числа 
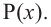
Следствие. Многочлен 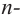
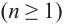
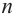
Отметим, что если комплексное число 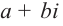
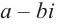
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 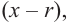
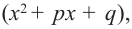
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 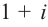
- Заказать решение задач по высшей математике
Пример №21
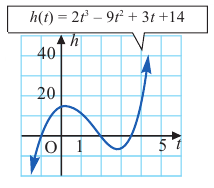
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 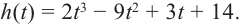
Решение: во всех случаях, кроме значений 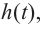
1. Проверим, является ли число 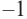
2. Число 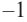
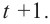
Учитывая, что 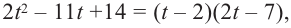
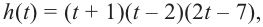
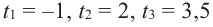
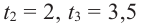
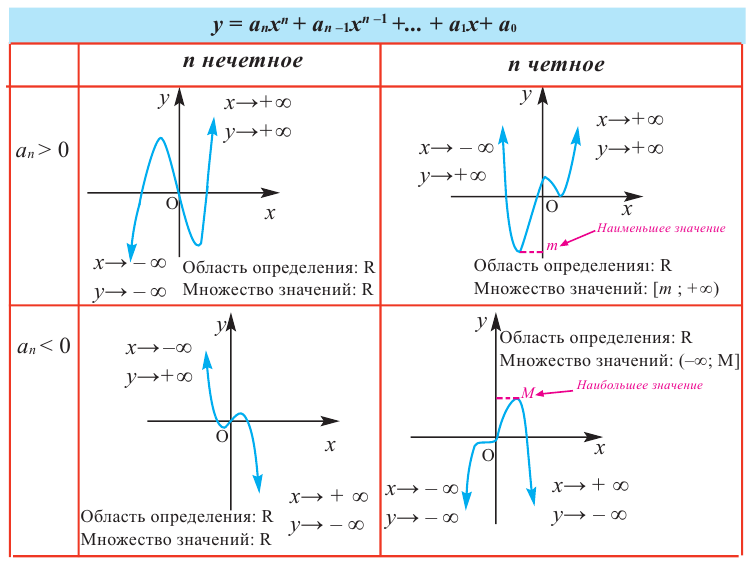
Функция-многочлен
График функции-многочлен
В стандартном виде функция — многочлен записывается как 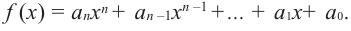
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 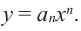
Пример №22
Определите характер поведения функции — многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 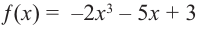
Решение: а) степень многочлена 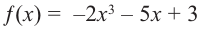
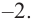
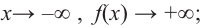
b) степень многочлена 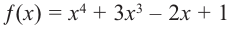
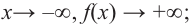
Пример №23
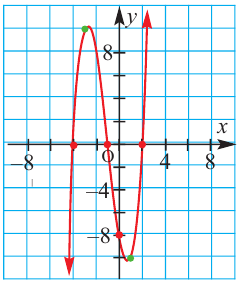
По графику определите как ведет себя функция — многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 
Алгоритм построения эскиза графика функции — многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 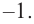
Значит, двучлен 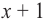
Зная, что 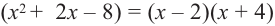
Отсюда находим нули 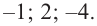
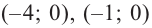
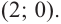
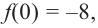
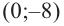
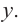
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 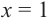
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 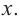
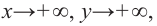
4. Соединим отмеченные точки и получим схематический график функции
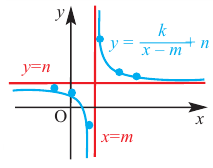
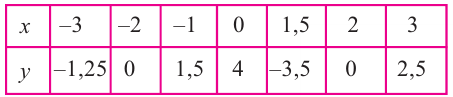
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
Самым простым примером рациональной функции является функция
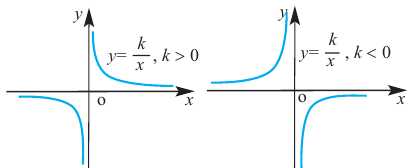
График функции 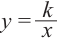
При стремлении значений 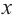
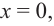
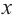
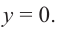
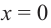
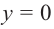
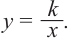
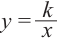
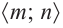
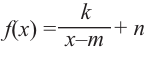
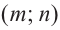
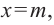
Пример №25
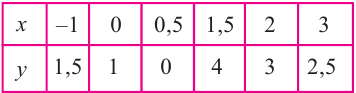
Постройте график функции
Решение: точки пересечения с осью 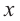
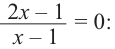
При 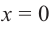
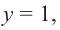
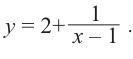
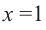
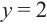
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 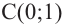
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 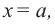
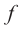
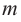
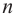
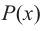
Для 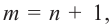
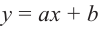
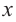
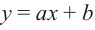
Пример №26
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 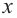
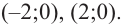
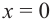
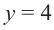
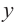
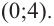
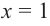
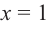
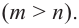
Для больших, но модулю, значений 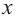
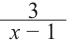
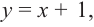
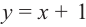
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
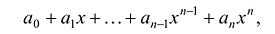
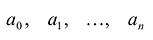
Если коэффициент 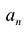
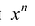
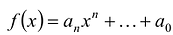
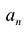
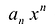
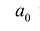
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 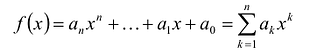
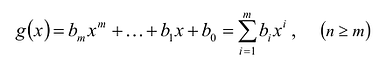
Произведением многочленов 
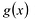
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 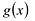
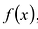
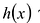
Теорема о делении с остатком
Для любых многочленов 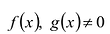
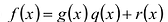
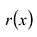
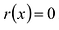
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
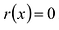
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с — корень многочлена 


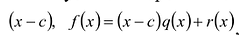
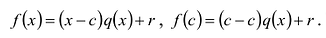

Обратно, пусть (х-с) делит 
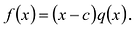
Следствие. Остаток от деления многочлена 
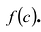
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 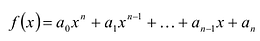
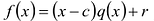
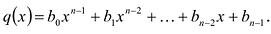
Число с-называется корнем кратности к многочлена 
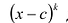

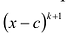

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 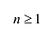
где 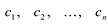

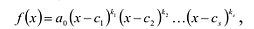
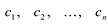

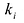
Если многочлен 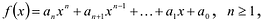
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 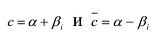


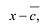
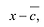

Утверждение 2. Многочлен с действительными коэффициентами степени 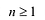
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где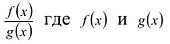

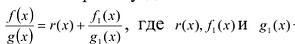
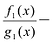
Лемма 1, Если 
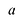
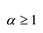
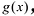
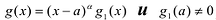
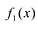
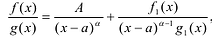
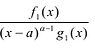
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
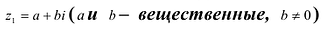
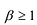
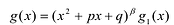
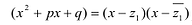
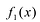
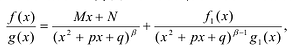
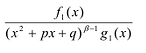
Рациональные дроби вида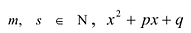
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 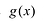
Число неизвестных 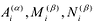
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
План урока:
Целое уравнение и его степень
Решение уравнений методом подбора корня
Решение уравнений с помощью разложения многочлена на множители
Графический метод решения уравнений
Решение дробно-рациональных уравнений
Целое уравнение и его степень
Ранее мы уже изучали понятие целого выражения. Так называют любое выражение с переменной, в котором могут использоваться любые арифметические операции, а также возведение в степень. Однако есть важное ограничение – в целом выражении переменная НЕ может находиться в знаменателе какой-нибудь дроби или быть частью делителя. Также переменная не может находиться под знаком корня. Для наглядности приведем примеры целых выражений:
х – 5;
(а3 + 6а)(а – 5а2);
(n3 + 7)/5 (в знаменателе находится только число, без переменной);
А вот примеры нецелых выражений:
Отличительной особенностью целых выражений является то, что в них переменная может принимать любое значение. В нецелых же выражениях возникают ограничения на значения переменной, ведь знаменатель дроби не должен равняться нулю, в выражение под знаком корня не должно быть отрицательным.
Введем понятие целого уравнения.
Приведем примеры целых ур-ний:
0,75х7 + 0,53х6 – 45х = 18
Напомним, что в математике существует понятие равносильных уравнений.
Когда мы решаем ур-ния, мы в каждой новой строчке записываем ур-ние, равносильное предыдущему. Для этого используются равносильные преобразования (перенос слагаемых через знак «=» с противоположным знаком, деление обоих частей равенства на одинаковые числа и т. д.).
Можно доказать (мы этого делать не будем), что любое целое ур-ние можно возможно преобразовать так, чтобы получилось иное, равносильное ему ур-ние, где в левой части будет находиться многочлен, а справа – ноль. Для этого надо лишь раскрыть скобки и умножить ур-ние на какое-нибудь число, чтобы избавиться от дробей.
Пример. Преобразуйте целое ур-ние
так, чтобы слева стоял многочлен, а справа – ноль.
Решение. В ур-нии есть дроби со знаменателями 5 и 4. Если умножить обе части на 20 (это наименьшее общее кратное чисел 5 и 4), то дроби исчезнут:
Теперь раскроем скобки:
4(5х3 – 3х4 + 45х – 27х2) – 40 = 10х2 + 5х + 35
20х3 – 12х4 + 180х – 108х2 – 40 = 10х2 + 5х + 35
Осталось перенести все слагаемые влево и привести подобные слагаемые:
20х3 – 12х4 + 180х – 108х2 – 40 – 10х2 – 5х – 35 = 0
– 12х4 + 20х3 – 118х2 + 175х – 75 = 0
Получили ур-ние в той форме, которую и надо было найти по условию.
Ответ:– 12х4 + 20х3 – 118х2 + 175х – 75 = 0
В математике любой полином можно обозначить как Р(х). Если ур-ние привели к тому виду, когда в одной части многочлен, а в другой ноль, то говорят, что получили ур-ние вида Р(х) = 0.
Получается, что решение целого уравнения всегда можно свести к решению равносильного ему ур-ния Р(х) = 0. Именно поэтому многочлены играют такую большую роль в математике
Напомним, что степенью многочлена называется максимальная степень входящего в его состав одночлена. Это же число является и степенью целого уравнения Р(х) = 0, а также степенью любого равносильного ему целого ур-ния.
Пример. Определите степень ур-ния
(х3 – 5)(2х + 7) = 2х4 + 9
Решение. Приведем ур-ние к виду Р(х) = 0. Для этого раскроем скобки:
(х3 – 5)(2х + 7) = 2х4 + 9
2х4 + 7х3 – 10х – 35 = 2х4 + 9
Перенесем все слагаемые влево и приведем подобные слагаемые:
2х4 + 7х3 – 10х – 35 – 2х4 – 9 = 0
7х3 – 10х – 44 = 0
Получили в левой части многочлен 3-ей степени. Следовательно, и исходное ур-ние имело такую же степень
Ответ: 3
Приведем примеры ур-ний первой степени:
5х + 8 = 0
9z– 6 = 0
5,4568у + 0,0002145 = 0
Все они являются линейными ур-ниями, метод их решения изучался ранее. Они имеют 1 корень.
Приведем примеры ур-ний второй степени:
6t2 + 98t – 52 = 0
54у + 23у = 0
12x2– 65 = 0
Это квадратные ур-ния. У них не более двух действительных корней. Для их нахождения в общем случае надо вычислить дискриминант и использовать формулу
Квадратные и линейные ур-ния умели решать ещё в Древнем Вавилоне 4 тысячи лет назад! А вот с ур-ния 3-ей степени (их ещё называют кубическими уравнениями) оказались значительно сложнее. Приведем их примеры:
2х3 + 4х2 – 19х + 17 = 0
у3 – 5у + 7 = 0
Лишь в 1545 году итальянец Джералимо Кардано опубликовал книгу, в которой описывался общий алгоритм решения кубических ур-ний. Он достаточно сложный и не входит в школьный курс математики. Его ученик, Лодовико Феррари, предложил метод решения ур-ний четвертой степени. В качестве примера такого ур-ния можно привести:
5х4 + 6х3 – 2х2 – 10х + 1 = 0
Лишь в XIX веке было доказано, что для ур-ний более высоких степеней (5-ой, 6-ой и т. д.) не существует универсальных формул, с помощью которых можно было бы найти их корни.
Отметим, что если степень целого ур-ния равна n, то у него не более n корней (но их число может быть и меньше). Так, количество корней кубического уравнения не превышает трех, а у ур-ния 4-ой степени их не более 4.
Чтобы доказать это утверждение, сначала покажем способ составления уравнения Р(х) = 0, имеющего заранее заданные корни. Пусть требуется составить ур-ние, имеющее корни k1, k2,k3,…kn. Приравняем к нулю следующее произведение скобок:
(х – k1)(х – k2)(х – k3)…(х – kn) = 0
Составленное ур-ние имеет все требуемые корни и никаких других корней. Действительно, произведение множителей может равняться нулю только в случае, если хотя бы один из множителей нулевой. Поэтому для решения ур-ния
(х – k1)(х – k2)(х – k3)…(х – kn) = 0
надо каждую скобку приравнять к нулю:
х – k1 = 0 или х – k2 = 0 или х – k3 = 0 или…х – kn = 0
Перенесем второе слагаемое вправо в каждом равенстве и получим:
х = k1 или х = k2 или х = k3 или…х = kn
Чтобы вместо произведения скобок слева стоял многочлен, надо просто раскрыть скобки.
Пример. Составьте уравнение в виде Р(х) = 0, имеющее корни 1, 2, 3 и 4.
Запишем целое ур-ние, имеющее требуемые корни:
(х – 1)(х – 2)(х – 3)(х – 4) = 0
Будем поочередно раскрывать скобки, умножая 1-ую скобку на 2-ую, полученный результат на 3-ю и т.д.:
(х2 – 3х + 2)(х – 3)(х – 4) = 0
(х3 – 6х2 + 11х – 6)(х – 4) = 0
х4 – 10х3 + 35х2 – 50х +24 = 0
Получили ур-ние вида Р(х) = 0. Для проверки вычислений можно подставить в него числа 1, 2, 3 и 4 и убедиться, что они обращают ур-ние в верное равенство.
Ответ: х4 – 10х3 + 35х2 – 50х +24 = 0
Заметим, что в рассмотренном примере, когда мы перемножали многочлены, мы получали новый полином, чья степень увеличивалась на единицу. Мы перемножили 4 скобки (х – k1), а потому получили полином 4 степени. Если бы мы перемножали, скажем, 10 таких скобок, то и многочлен бы получился 10-ой степени. Именно поэтому ур-ние n-ой степени не более n корней.
Действительно, предположим, что какое-то ур-ние n-ой степени имеет хотя бы (n + 1) корень. Обозначим эти корни как k1, k2,k3,…kn, kn+1 и запишем уравнение:
(х – k1)(х – k2)(х – k3)…(х – kn)(х – kn+1) = 0
Оно, по определению, равносильно исходному ур-нию, ведь оно имеет тот же набор корней. Слева записаны (n + 1) скобок, поэтому при их раскрытии мы получим полином степени (n + 1). Значит, и исходное ур-ние на самом деле имеет степень n + 1, а не n. Получили противоречие, которое означает, что на самом деле у уравнения n-ой степени не более n корней.
Особо акцентируем внимание на том факте, что если корнями уравнения являются некоторые числа k1, k2,k3,…kn, то этому ур-нию равносильна запись (х – k1)(х – k2)(х – k3)…(х – kn) = 0
Этот факт будет использован далее при решении ур-ний.
Решение уравнений методом подбора корня
Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!
Пример. Докажите, что корнями ур-ния
х3 – 2х2 – х + 2 = 0
являются только числа (– 1), 1 и 2.
Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:
(– 1)3 – 2(– 1)2 – (– 1) + 2 = 0
–1 – 2 + 1 + 2 = 0
0 = 0
При х = 1 получаем:
13 – 2•12 – 1 + 2 = 0
1 – 2 – 1 + 2 = 0
0 = 0
Наконец, рассмотрим случай, когда х = 2
23 – 2•22 – 2 + 2 = 0
8 – 8 – 2 + 2 = 0
0 = 0
Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.
Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.
Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:
а0xn + a1xn–1 + … + аn–1х + аn = 0
Числа а0, а1, а2,…аnи называют коэффициентами уравнений.
Например, для уравнения
5х4 – 7х3 + 9х2 – х + 12 = 0
коэффициенты равны
а0 = 5
а1 = – 7
а2 = 9
а3 = – 1
а4 = + 12
Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии
х3 + 2х – 15 = 0
нет слагаемого с буквенной частью х2. Можно считать, что ур-ние равносильно записи
х3 + 0х2 + 2х – 15 = 0
где слагаемое х2 есть, но перед ним стоит ноль. Тогда коэффициент а1 = 0.
Для обозначения первого коэффициента а0 может использоваться термин старший коэффициент, а для последнего коэффициента аn – термин «свободный член» или «свободный коэффициент».
Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:
Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами
а0xn + a1xn–1 + … + аn–1х + аn = 0
Тогда можно подставить туда число m и получить верное равенство:
а0mn + a1mn–1 + … + аn–1m + аn = 0
Поделим обе его части на m и получим
а0mn–1 + a1mn–2 + … + аn–1 + аn/m = 0
Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа а0mn–1, a1mn–2, аn–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число аn/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа аn.
Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.
Пример. Найдите целые корни уравнения
2х4 – х3 – 9х2 + 4х + 4 = 0
Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):
2•14 – 13 – 9•12 + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0
2•24 – 23 – 9•22 + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0
2•(– 2)4 – (– 2)3 – 9•(– 2)2 + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0
Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.
Ответ: 1; 2; (– 2).
Пример. Решите ур-ние
0,5х3 + 0,5х + 5 = 0
Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:
0,5х3 + 0,5х + 5 = 0
(0,5х3 + 0,5х + 5)•2 = 0•2
х3 + х + 10 = 0
Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:
(– 2)3 + (– 2) + 10 = – 8 – 2 + 10 = 0
Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х3 и у = х + 10. Значит, и вся левая часть х3 + х + 10 монотонно возрастает. Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.
Ответ: – 2
Ещё быстрее можно узнать, является ли единица корнем уравнения.
Докажем это. Подставим в ур-ние
а0xn + a1xn–1 + … + аn–1х + аn = 0
значение х = 1. Так как единица в любой степени равна самой единице, то получим:
а01n + a11n–1 + … + аn–11 + аn = 0
а0 + a1 + … + аn–1 + аn = 0
Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.
Пример. Укажите хотя бы 1 корень ур-ния
499х10 – 9990х7 + 501х6 – 10х5 + 10000х4 – 1000 = 0
Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:
499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0
Следовательно, единица является его корнем.
Ответ: 1.
Решение уравнений с помощью разложения многочлена на множители
Если в уравнении вида P(x) = 0в левой части удается выполнить разложение многочлена на множители, то дальше каждый из множителей можно отдельно приравнять к нулю.
Пример. Решите ур-ние
х4 – 16 = 0
Решение. Степень х4 можно представить как (х2)2, а 16 – как 42. Получается, что слева стоит разность квадратов, которую можно разложить на множители по известной формуле:
х4 – 16 = 0
(х2 – 4)(х2 + 4) = 0
Приравняем каждую скобку к нулю и получим два квадратных ур-ния:
х2 – 4 = 0 или х2 + 4 = 0
х2 = 4 или х2 = – 4
Первое ур-ние имеет два противоположных корня: 2 и (– 2). Второе ур-ние корней не имеет.
Ответ: 2 и (– 2).
Предположим, что у ур-ния 3-ей степени есть 3 корня, и подбором мы нашли один из них. Как найти оставшиеся корни? Здесь помогает процедура, известная как «деление многочленов в столбик». Продемонстрируем ее на примере. Пусть надо решить ур-ние
100х3 – 210х2 + 134х – 24 = 0
Можно заметить, сумма всех коэффициентов ур-ния равна нулю:
100 – 210 + 134 – 24 = 0
Следовательно, первый корень – это 1.
Предположим, что у исходного ур-нияР(х) = 0 есть 3 корня, k1, k2и k3. Тогда ему равносильно другое ур-ние
(х – k1)(х – k2)(х – k3) = 0
Мы нашли, что первый корень k1 = 1, то есть
(х – 1)(х – k2)(х – k3) = 0
Обозначим как P1(x) = 0 ещё одно ур-ние, корнями которого будут только числа k2 и k3. Очевидно, что корнями ур-ния
(х – 1)•P1(x) = 0
Будут числа 1, k2 и k3. Его корни совпадают с корнями исходного ур-ния, а потому запишем
(х – 1)•P1(x) = 100х3 – 210х2 + 134х – 24
Поделим обе части на (х – 1):
Итак, если «поделить» исходное ур-ние на х – 1, то получим какой-то многочлен Р1(х), причем решением уравнения P1(x) = 0 будут оставшиеся два корня, k2и k3. Деление можно выполнить в столбик. Для этого сначала запишем «делимое» и «делитель», как и при делении чисел:
Смотрим на первое слагаемое делимого. Это 100х3. На какой одночлен нужно умножить делитель (х – 1), чтобы получился полином со слагаемым 100х3? Это 100х2. Действительно, (х – 1)100х2 = 100х3 – 100х2. Запишем слагаемое 100х2 в результат деления, а результат его умножения на делитель, то есть 100х3 – 100х2, вычтем из делимого:
Теперь вычтем из делимого то выражение, которое мы записали под ним. Слагаемые 100х3, естественно, сократятся:
(100х3 – 210х2) – (100х3 – 100х2) = 100х3 – 210х2 – 100х3 + 100х2 = – 110х2
Далее снесем слагаемое 134х вниз:
На какое слагаемое нужно умножить (х – 1), что получился полином со слагаемым (– 110х2). Очевидно, на (– 110х):
(х – 1)(– 110х2) = –110х2 + 110х
Запишем в поле «ответа» слагаемое (– 110х2), а под делимый многочлен – результат его умножения на (х – 1):
При вычитании из (–110х2 + 134х) полинома (–110х2 + 110х) остается 24х. Далее сносим последнее слагаемое делимого многочлена вниз:
Выражение х – 1 нужно умножить на 24, чтобы получить 24х – 24. Запишем в поле «ответа» число 24, а в столбике произведение 24(х –1) = 24х – 24:
В результате в остатке получился ноль. Значит, всё сделано правильно. С помощью деления столбиком мы смогли разложить полином 100х3 – 210х2 + 134х – 24 на множители:
100х3 – 210х2 + 134х – 24 = (х – 1)(100х2 – 110х + 24)
Теперь перепишем исходное ур-ние с учетом этого разложения:
100х3 – 210х2 + 134х – 24 = 0
(х – 1)(100х2 – 110х + 24) = 0
Теперь каждую отдельную скобку можно приравнять нулю. Получим ур-ние х – 1 = 0, корень которого, равный единице, мы уже нашли подбором. Приравняв к нулю вторую скобку, получим квадратное ур-ние:
100х2 – 110х + 24 = 0
D =b2 – 4ас = (– 110)2 – 4•100•24 = 12100 – 9600 = 2500
Итак, мы нашли три корня ур-ния: 1; 0,3 и 0,8.
В данном случае мы воспользовались следующим правилом:
Пример. Решите уравнение
2х3 – 8х2 + 16 = 0
Решение. Все коэффициенты целые, а потому, если у уравнения есть целый корень, то он должен быть делителем 16. Перечислим эти делители: 1, – 1, 2, – 2, 4, – 4, 8, – 8, 16, – 16. Из всех них подходит только двойка:
2•23 – 8•22 + 16 = 16 – 32 + 16 = 0
Итак, первый корень равен 2. Это значит, что исходный многочлен можно разложить на множители, один из которых – это (х – 2). Второй множитель найдем делением в столбик. Так как в многочлене 2х3 – 8х2 + 16 нет слагаемого с буквенной часть х, то искусственно добавим её:
2х3 – 8х2 + 16 = 2х3 – 8х2 + 0х + 16
Теперь возможно деление:
Получили, что 2х3 – 8х2 + 16 = (х – 2)(2х – 4х – 
С учетом этого перепишем исходное ур-ние:
2х3 – 8х2 + 16 = 0
(х – 2)(2х – 4х – 
х – 2 = 0 или 2х – 4х – 8 = 0
Решим квадратное ур-ние
D =b2 – 4ас = (– 4)2 – 4•2•(– 
В 8 классе мы узнали, что если у квадратного ур-ния ах2 + bx + c = 0 есть два корня, то многочлен ах2 + bx + c можно разложить на множители по формуле
ах2 + bx + c = а(х – k1)(х – k2)
где k1 и k2– корни квадратного ур-ния. Оказывается, такое же действие можно выполнять с многочленами и более высоких степеней. В частности, если у кубического ур-ния есть 3 корня k1, k2 и k3, то его можно разложить на множители по формуле
ах3 +bx2 + cx + d = a(х – k1)(х – k2)(х – k3)
Пример. Разложите на множители многочлен 2х3 – 4х2 – 2х + 4.
Решение. Целые корни этого многочлена (если они есть), должны быть делителем четверки. Из всех таких делителей подходят три: 1, (– 1) и 2:
2•13 – 4•12 – 2•1 + 4 = 2 – 4 – 2 + 4 = 0
2•(– 1)3 – 4•(– 1)2 – 2•(– 1) + 4 = – 2 – 4 + 2 + 4 = 0
2•23 – 4•22 – 2•2 + 4 = 16 – 16 – 4 + 4 = 0
Значит, многочлен можно разложить на множители:
2х3 – 4х2 – 2х + 4 = 2(х + 1)(х – 1)(х – 2)
Возникает вопрос – почему перед скобками нужна двойка? Попробуем сначала перемножить скобки без ее использования:
(х + 1)(х – 1)(х – 2) = (х2 – 1)(х – 2) = х3 – 2х2 – х + 2
Получили не тот многочлен, который стоит в условии. Однако ур-ние
х3 – 2х2 – х + 2 = 0
имеет те же корни (1, 2 и (– 1)), что и ур-ние
2х3 – 4х2 – 2х + 4 = 0
Дело в том, что это равносильные ур-ния, причем второе получено умножением первого на два:
2•(х3 – 2х2 – х + 2) = 2х3 – 4х2 – 2х + 4
Надо понимать, что хотя ур-ния 2х3 – 4х2 – 2х + 4 = 0 и х3 – 2х2 – х + 2 = 0, по сути, одинаковы, многочлены в их левой части различны. Заметим, что при перемножении скобок (х – k1), (х – k2), (х – k3) и т.д. всегда будет получаться полином, у которого старший коэффициент равен единице. Поэтому, чтобы учесть этот самый коэффициент, надо домножить произведение скобок на него:
2х3 – 4х2 – 2х + 4= 2•(х3 – 2х2 – х + 2) = 2(х + 1)(х – 1)(х – 2)
Ответ: 2(х + 1)(х – 1)(х – 2).
Графический метод решения уравнений
Любое ур-ние с одной переменной можно представить в виде равенства
у(х) = g(x)
где у(х) и g(x) – некоторые функции от аргумента х.
Построив графики этих функций, можно примерно найти точки их пересечений. Они и будут соответствовать корням уравнения.
Пример. Решите графически уравнение
х3 – х2 – 1 = 0
Решение. Строить график уравнения х3 – х2 – 1 = 0 довольно сложно, поэтому перенесем слагаемое (– х2 – 1) вправо:
х3 – х2 – 1 = 0
х3 = х2 + 1
Построим графики у = х3 и у = х2 + 1 (второй можно получить переносом параболы у = х2 на единицу вверх):
Видно, они пересекаются в точке, примерно соответствующей значению х ≈ 1,4. Если построить графики уравнения более точно (с помощью компьютера), то можно найти, что х ≈ 1,46557.
Ответ: х ≈ 1,46557
Конечно, графический метод решения уравнений не является абсолютно точным, однако он помогает быстро найти примерное положение корня. Также с его помощью можно определить количество корней уравнения. В рассмотренном примере был только 1 корень.
Пример. Определите количество корней уравнений
а)х3 – х – 3 = 0
б) х3 – 2х + 0,5 = 0
Решение. Перенесем два последних слагаемых вправо в каждом ур-нии:
а) х3 = х + 3
б) х3 = 2х – 0,5
Построим графики функций у = х3, у = х + 3 и у = 2х – 0,5:
Видно, что прямая у = х + 3 пересекает график у = х3 в одной точке, поэтому у первого ур-ния будет 1 решение.Прямая у = 2х – 0,5 пересекает кубическую параболу в трех точках, а потому у второго ур-ния 3 корня.
Ответ: а) один корень; б) три корня.
Решение дробно-рациональных уравнений
До этого мы рассматривали только целые ур-ния, где переменная НЕ находится в знаменателе какого-нибудь выражения. Однако, если в ур-нии есть выр-ние, содержащее переменную в знаменателе, или присутствует деление на выр-ние с переменной, то его называют дробно-рациональным уравнением.
Приведем несколько примеров ур-ний, считающихся дробно-рациональными:
С помощью равносильных преобразований любое дробно-рациональное ур-ние возможно записать в виде отношения двух полиномов:
Дробь равна нулю лишь тогда, когда ее числитель равен нулю, а знаменатель – не равен. Таким образом, нужно сначала решить ур-ние Р(х) = 0 и потом проверить, что полученные корни не обращают полином Q(x) в ноль.
Обычно для решения дробно-рациональных уравнений используют такой алгоритм:
1) Приводят все дроби к единому знаменателю, умножают на него ур-ние и получают целое ур-ние.
2) Решают полученное целое ур-ние.
3) Исключают из числа корней те, которые обращают знаменатель хотя бы одной из дробей в ноль.
Пример. Решите ур-ние
Решение.
Умножим обе части равенства на знаменатель 1-ой дроби:
2х2 – 3х – 2 = х2(х – 2)
Раскроем скобки и перенесем все слагаемые в одну сторону:
2х2 – 3х – 2 = х3– 2х2
х3 – 2х2 – 2х2 + 3х + 2 = 0
х3 – 4х2 + 3х + 2 = 0
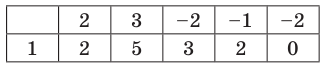
У ур-ния могут быть только те целые корни, которые являются делителями двойки. Из кандидатов 1, – 1, 2 и – 2 подходит только двойка:
23 – 4•22 + 3•2 + 2 = 8 – 16 + 6 + 2 = 0
Нашли один корень, а потому исходный многочлен можно поделить в столбик на (х – 2):
Получили, что х3 – 4х2 + 3х + 2 = (х – 2)(х2 – 2х – 1)
Тогда ур-ние примет вид:
(х – 2)(х2 – 2х – 1) = 0
х – 2 = 0 или х2 – 2х – 1 = 0
Решим квадратное ур-ние:
D =b2 – 4ас = (– 2)2 – 4•1•(– 1) = 4 + 4 = 8
Мы нашли все 3 корня кубического ур-ния. Теперь надо проверить, не обращают ли какие-нибудь из них знаменатели дроби в исходном ур-нии
в ноль. Очевидно, что при х = 2 знаменатель (х – 2) превратится в ноль:
х – 2 = 2 – 2 = 0
Это значит, что этот корень надо исключить из списка решений. Такой корень называют посторонним корнем ур-ния.
Также ясно, что два остальных корня не обращают знаменатель в ноль, а потому они НЕ должны быть исключены из ответа:
Пример. Найдите все корни ур-ния
Решение. Если сразу привести выражение слева к общему знаменателю 4(х2 + х – 2)(х2 + х – 20), то получится очень длинное и неудобное выражение. Однако знаменатели довольно схожи, поэтому можно провести замену. Обозначим х2 + х как у:
у = х2 + х
Тогда уравнение примет вид
Приведем дроби к общему знаменателю 4(у – 2)(у – 20):
Знаменатель должен равняться нулю:
4(у – 20) + 28(у – 2) + (у – 2)(у – 20) = 0
4у – 80 + 28у – 56 + у2 – 20у – 2у + 40 = 0
у2 + 10у – 96 = 0
Решаем квадратное ур-ние:
D =b2 – 4ас = (10)2 – 4•1•(– 96) = 100 + 384 = 484
Получили, что у1 = – 16, а у2 = 6. Произведем обратную замену:
у = х2 + х
х2 + х = – 16 или х2 + х = 6
х2 + х + 16 = 0 или х2 + х – 6 = 0
Дискриминант 1-ого ур-ния отрицателен:
D =b2 – 4ас = (1)2 – 4•1•(16) = 1– 64 = – 63
А потому оно не имеет решений. Решим 2-ое ур-ние:
D = b2 – 4ас = (1)2 – 4•1•(– 6) = 1+ 24 = 25
Нашли два корня: 2 и (– 3). Осталось проверить, не обращают ли они знаменатели дробей в ур-нии
в ноль. Подстановкой можно убедиться, что не обращают.
Ответ: – 3 и 2.
При решении дробно-рациональных ур-ний может использоваться и графический метод.
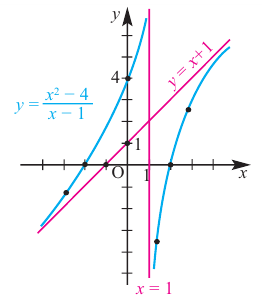
Пример. Сколько корней имеет уравнение
Решение. Построим графики функций у = х2 – 4 и у = 2/х:
Видно, что графики пересекаются в 3 точках, поэтому ур-ние имеет 3 корня.
Ответ: 3 корня.
Основные правила математики с примерами. 7 класс Алгебра.
Содержание
- Уравнения. Равносильные уравнения. Свойства
- Линейное уравнение
- Одночлены и многочлены
- Формулы сокращенного умножения
- Степень. Свойства степени с целым показателем
- Функция. Область определения и область значений функции
- Линейная функция, её график и свойства
- Системы линейных уравнений с двумя переменными
- Графический метод решения системы двух линейных уравнений с двумя переменными
- Решение системы двух линейных уравнений с двумя переменными методом подстановки
- Решение систем линейных уравнений методом сложения
Уравнения. Равносильные уравнения. Свойства
Корень уравнения
- Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
- Решить уравнение означает найти все его корни или убедиться, что их вообще нет. Также можно сказать, что решить уравнение — это значит найти множество его корней.
2 x + 6 =36x = 15 —корень уравнения, поскольку2 · 15 + 6 =3636 = 36 —верное равенство.5x — 5x = 100 —не имеет корней, посколькуx(5 — 5)∥0 = 100 0 = 100 — неверно.
Равносильные уравнения
Два уравнения называют равносильными, если они имеют одно и тоже множество корней.
2x — 5 = 5 ≡равносильно 4x — 10 =10,поскольку x = 5 корень и для 1—го, и для 2—го уравнения.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
2x — 5 = 7 +52x — 5 + 5 = 7 + 52x = 12x = 12 : 2x = 6
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
2x — 5 =+5→ 72x = 7 + 52x =12x = 12 : 2x =6
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному
12x = 24 : 1212x :12 = 24 : 12x = 2.×5 = 3 · 5×5 · 5 = 3 · 5x = 15
Линейное уравнение
Уравнение вида , где
— переменная,
и
некоторые числа, называют линейным уравнением с одной переменной.
| Значения |
|||
|---|---|---|---|
| Корни уравнения |
корней нет |
2x = 0, 5y —3 = 12 — линейные уравненияx2 —4 = 0, 5x = 8 —нелинейные уравнения
Одночлены и многочлены
Одночлены
- Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
2x, 356x2y, 0,2a20, b, 15 — одночлены.
- Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
2x, 356x2y, 0,2a20 — одночлены стандартного вида.
- Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
2x, 356x2y, 0,2a20.2, 356, 0,2 —коэффициенты.
- Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
2x2y3z , —15x2y3z, 0,5x2y3z —подобные.2x2y3z и 2x2y3 — не подобные.
- Нуль-одночлен степени не имеет.
Многочлены
- Выражение, являющееся суммой нескольких одночленов, называют многочленом.
2x + 3x2y
- Одночлены, из которых состоит многочлен, называют членами многочлена.
2x + 3x2y —многочлен;2x и 3x2y — его одночлены
- Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Формулы сокращенного умножения
Разность квадратов двух выражений
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:
Произведение разности и суммы двух выражений
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражении:
Преобразование многочлена в квадрат суммы или разности двух выражений
Формулы
позволяют «свернуть» трёхчлен в квадрат двучлена.
Трёхчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.
Сумма и разность кубов двух выражений
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:
Многочлен называют неполным квадратом суммы.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
Многочлен называют неполным квадратом разности.
Степень. Свойства степени с целым показателем
Свойства степени с целым показателем
Для любого и любых целых
выполняются равенства:
Для любых ,
и любого целого
выполняются равенства:
Функция. Область определения и область значений функции
Функция
Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной пeременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают
, функцию(правило) —
.
Независимую переменную называют аргументом функции. Значение зависимой переменной
называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Способы задания функции
Описательный, табличный, с помощью формулы, графический.
График функции
Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Линейная функция, её график и свойства
Системы линейных уравнений с двумя переменными
Уравнение с двумя переменными
Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.
Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Если некоторая фигура является графиком уравнения, то выполняются два условия:
- все решения уравнения являются координатами точек, принадлежащих графику;
- координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.
Графический метод решения системы двух линейных уравнений с двумя переменными
Графический метод решения системы уравнений заключается в следующем:
- построить в одной координатной плоскости графики уравнений, входящих в систему;
- найти координаты всех точек пересечения построенных графиков;
- полученные пары чисел и будут искомыми решениями.
Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.
- если прямые совпадают, то система имеет бесконечно много решении.
- если прямые параллельны, то система решений не имеет.
Решение системы двух линейных уравнений с двумя переменными методом подстановки
Чтобы решить систему линейных уравнений методом подстановки, следует:
- выразить из любого уравнения системы одну переменную через другую;
- подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное значение переменной в выражение, полученное на первом шаге;
- вычислить значение второй переменной;
- записать ответ.
Решение систем линейных уравнений методом сложения
Чтобы решить систему линейных уравнений методом сложения, следует:
- подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
- сложить почленно левые и правые части уравнений, полученных на первом шаге
- решить уравнение с одной переменной, полученной на втором шаге
- подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
- вычислить значение второй переменной;
- записать ответ.