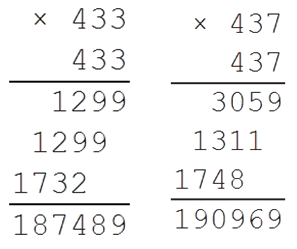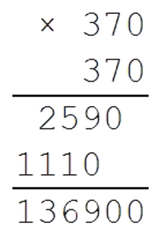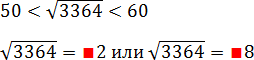06
Фев 2014
Категория: Справочные материалы
Извлечение корня из большого числа
2014-02-06
2021-06-25
А у вас есть зависимость от калькулятора? Или вы считаете, что кроме как с калькулятором или при помощи таблицы квадратов очень сложно вычислить, например, 
.
Случается, школьники привязаны к калькулятору и даже 
на 
умножают, нажимая на заветные кнопочки. Говорят, ну я все равно знаю как посчитать, а сейчас сэкономлю время… Вот будет экзамен… тогда и напрягусь…
Так дело в том, что на экзамене и так будет предостаточно «напряжных моментов»… Как говорится, вода камень точит. Вот и на экзамене мелочи, если их много, способны подкосить…
Давайте минимизируем количество возможных неприятностей.
Извлекаем квадратный корень из большого числа
Мы будем говорить сейчас только о случае, когда результат извлечения корня квадратного – целое число.
Случай 1 + показать
Случай 2 + показать
Смотрите также «Отдельные случаи вычисления дискриминанта»
Автор: egeMax |
комментария 4
[Вся длинная арифметика]
Эта задача далась мне тяжелее всех. Наверное потому, что я пытался зачесть ее на acm.sgu.ru и acmp.ru, где ограничения на количество разрядов в числе 1000 и 3000 соответственно. Для начала зачтем эту задачу на informatics.mccme.ru, где ограничение всего 100.
Здесь можно пойти двумя путями:
I) Бинарным поиском подбирать число, квадрат которого не превосходит данное число. При этом придется не полениться и реализовать компаратор, короткий плюс и минус, длинное умножение и сложение, а также деление на короткое. Многовато, не правда ли? Общую логику видно по следующему фрагменту:
BigInt sqrt()
{
BigInt l , r = *this;
BigInt res;
while (l<=r)
{
BigInt m = (l + r)/2;
if (m*m <= *this)
{
res = m;
l = m + 1;
}
else
r = m - 1;
}
return res;
}
* This source code was highlighted with Source Code Highlighter.
II) Оценить максимальное количество цифр в ответе и подбирать бинарным поиском цифры ответа, начиная со старшего разряда. При таком раскладе нам нужны только компаратор и умножение на длинное. Да и сама функция будет работать быстрее первого варианта:
BigInt sqrt()
{
BigInt cur;
// максимальное количество разрядов в ответе
int pos = (amount + 1) / 2;
cur.amount = pos;
pos--;
while (pos>=0)
{
int l = 0, r = osn;
int curDigit = 0;
while (l<=r) // подбираем текущую цифру
{
int m = (l+r)>>1;
cur.digits[pos] = m;
if (cur * cur <= *this)
{
curDigit = m;
l = m + 1;
}
else
r = m - 1;
}
cur.digits[pos] = curDigit;
pos--;
}
// избавляемся от лидирующих нулей
if (cur.amount!=1 && !cur.digits[cur.amount-1])
cur.amount--;
return cur;
}
* This source code was highlighted with Source Code Highlighter.
Справедливости ради нужно отметить, что представленные решения со всеми возможными моими ухищрениями по оптимизации получили TLE#22, TLE#23 на acmp.ru и TLE#15, TLE#29 на acm.sgu.ru соответственно. И как еще удалось выяснить на sgu имеются пробелы во входных данных 6 теста(=.
На acmp.ru имеется разбор, который идентичиен второму решению. Т.е. нужно подумать где можно соптимизировать еще. И надо считать, что именно этот подход нужно использовать в полевых условиях, т.е. на контестах).
Картина была бы неполной, если бы речь не зашла про совершенно магический способ вычисления квадратного корня “ручками”. С ним можно ознакомиться в книге
“Математика: Справочные материалы. Гусев В.А., Мордкович А.Г.[с.45]” Общий механизм представлю ниже:
1. Считываем входное число при osn = 100. В дальнейшем считаем что osn = 10.
2. Подбираем цифру, квадрат которой не превосходит старший разряд входного числа. Это есть первая цифра ответа.
3. Найдем разницу между старшим разрядом входного числа и квадратом найденной цифры. Ответ припишем слева ко второму разряду входного числа. Получим некое число A.
4. Удвоим имеющуюся часть ответа, получим число a. Подберем наибольшую цифру x, такую что произведение чисел ax(a — десятки, x — единицы) и x не превосходило А. Число x — вторая цифра ответа.
5. Число A — ax * x припишем слева к третьему разряду входного числа. Получим некое число B. Повторяем итерации 4-5 до тех пор пока не закончатся разряды во входном числе.
Более нагляднее рассмотрим пример на основе числа 138384.
1) Храним число как 84-83-13
2) 3*3 <=13. Текущий ответ: 3
3) 13-3*3 = 4. Припишем 4 к 83. Получаем А = 483.
4) a = 3*2 = 6. 6x * x <=483. x = 7. Текущий ответ: 37.
5)483-67*7 = 14. Припишем 14 к 84. Получаем B = 1484.
6). b = 37*2 = 74. 74x*x <=1484. x = 2. Текущий ответ = 372. Он же и окончательный.
III) Все вышеизложенное реализовано
здесь.
Как видно время работы пропорционально количеству разрядов в корне входного числа. С таким решением не стыдно показаться на любом сервере проверки). На acm.sgu.ru эта реализация работала 0.095 с, на acmp.ru 0.389 с.
Извлечение корня из большого числа. Дорогие друзья! В этой статье мы с вами разберём как извлекать корень из большого числа без калькулятора. Это необходимо не только для решения некоторых типов задач ЕГЭ (есть такие — на движение), но и для общего математического развития этот аналитический приём знать желательно.
Казалось бы, всё просто: разложи на множители, да извлекай. Проблемы нет. Например число 291600 при разложении даст произведение:
Вычисляем:
Есть одно НО! Способ хорош если легко определяются делители 2, 3, 4 и так далее. А что делать если число, из которого мы извлекаем корень является произведением простых чисел? Например 152881 является произведением чисел 17, 17, 23, 23. Попробуй-ка сходу найди эти делители.
Суть рассматриваемого нами метода — это чистый анализ. Корень при наработанном навыке находится быстро. Если навык не отработан, а просто понят подход, то немного медленнее, но всё же определяется.
Извлечём корень из 190969.
Сначала определим — между какими числами (кратными ста) лежит наш результат.
Очевидно, что результат корня из данного числа лежит в пределах от 400 до 500, так как
4002=160000 и 5002=250000
Действительно:
Далее смотрим, где «стоит» это число:
посредине, ближе к 160 000 или к 250 000?
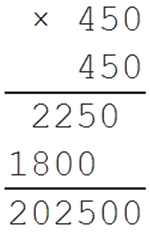
Число 190969 находится примерно посредине, но все же ближе к 160000. Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:
Действительно, он меньше 450, так как 190 969 < 202 500.
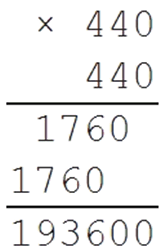
Теперь проверим число 440:
Значит наш результат меньше 440, так как 190 969 < 193 600.
Проверяем число 430:
Мы установили, что результат данного корня лежит в пределах от 430 до 440.
Далее используются свойства произведений чисел. Известно, что:
Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце. Например, 21 на 21 равно 441.
Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце. Например, 18 на 18 равно 324.
Произведение чисел имеющих на конце 5 дают число с 5 в конце. Например, 25 на 25 равно 625.
Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце. Например 26 на 26 равно 676.
Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце. Например, 17 на 17 равно 289.
Так как число 190969 заканчивается цифрой 9, то это произведение либо числа 433, либо 437.
*Только они при возведении в квадрат могут дать 9 в конце.
Проверяем:
Значит результат корня будет равен 437.
То есть, мы как бы «нащупали» верный ответ.
Как видите, максимум что потребуется это осуществить 5 действий столбиком. Возможно, вы сразу попадёте в точку, или сделаете всего три действия. Всё зависит о того, как точно вы сделаете начальную оценку числа.
Извлеките самостоятельно корень из 148996
Такой дискриминант получается в задаче:
Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.
Результат корня находится между числами 300 и 400:
3002=90000 4002=160000
Действительно, 90000<148996<160000.
Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел.
Вычислим разности 148996 — 90000=58996 и 160000 — 148996=11004.
Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360.
Далее пробуем возводить в квадрат, например число 370. Как бы «щупаем» результат:
Можем сделать вывод, что наш результат больше 370. Далее ясно: так как 148996 оканчивается цифрой 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6. *Только эти числа при возведении в квадрат дают в конце 6.
Проверяем числа 374, 376, 384, 386, 394 …
Ответ: 386
Объективно говоря, вероятность того, что вам попадёт подобная задача, очень мала. Но пусть этот приём в вашем арсенале будет. Впереди вас ждёт много полезного, не пропустите!
Есть ещё метод по извлечению корня из большого числа, называют его алгоритмом Евклида. Его достоинство состоит в том, что можно извлекать корень из любого числа с необходимой точностью до десятых, сотых и тд. То есть корни неизвлекаемые в целых числах. *В будущем статья будет обязательно дополнена.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
При решении текстовых задач на составление уравнений очень часто приходится вычислять квадратный корень из больших чисел. Если говорить про стандартные задачи из ОГЭ и ЕгЭ , то в таких случаях обычно предполагается, что корень (из дискриминанта при решении квадратного уравнения) извлечь можно.
Но как без калькулятора вычислить корни больших чисел? Предположим, вам требуется найти корень из 1369. Есть простой и логичный алгоритм. Сначала надо определить десятки. Для этого ищем целые числа, в квадраты которых заключено число. Так квадрат 30- это 900, квадрат 40- 1600. Значит искомое число от 30 до 40.
Проверим теперь какие числа точно не подойдут. Т.к. произведение чётных чисел всегда четно, то отпадают все четные — 32, 34, 36, 38. Так как исходное число оканчивается не на 5, то 35 тоже отпадает. Теперь вспоминаем таблицу умножения. Число заканчивается на 9. 3 * 3 =9 и 7 * 7 = 49. Значит это либо 33, либо 37. Путем не сложной проверки можно убедиться, что искомое число — 37.
Извлечение квадратного корня из многозначного числа
В предисловии к своему первому изданию “В царстве смекалки” (1908 год) Е. И. Игнатьев пишет: “. умственную самодеятельность, сообразительность и “смекалку” нельзя ни “вдолбить”, ни “вложить” ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний совершается в лёгкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью”.
В предисловии к изданию 1911 г “Роль памяти в математике” Е.И. Игнатьев пишет “… в математике следует помнить не формулы, а процесс мышления”.
Для извлечения квадратного корня существуют таблицы квадратов для двухзначных чисел, можно разложить число на простые множители и извлечь квадратный корень из произведения. Таблицы квадратов бывает недостаточно, извлечение корня разложением на множители — трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Попробуйте извлечь квадратный корень из числа 209764? Разложение на простые множители дает произведение 2*2*52441. Методом проб и ошибок, подбором – это, конечно, можно сделать, если быть уверенным в том, что это целое число. Способ, который я хочу предложить, позволяет извлечь квадратный корень в любом случае.
Когда-то в институте (Пермский государственный педагогический институт) нас познакомили с этим способом, о котором сейчас хочу рассказать. Никогда не задумывалась, есть ли у этого способа доказательство, поэтому сейчас пришлось некоторые доказательства выводить самой.
Основой этого способа, является состав числа =.
1. Разбиваем число (5963364) на пары справа налево (5`96`33`64)
2. Извлекаем квадратный корень из первой слева группы ( — число 2). Так мы получаем первую цифру числа &.
3. Находим квадрат первой цифры (2 2 =4).
4. Находим разность первой группы и квадрата первой цифры (5-4=1).
5.Сносим следующие две цифры (получили число 196).
6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4).
7.Теперь необходимо найти вторую цифру числа &: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 — вторая цифра числа &.
8. Находим разность (196-176=20).
9. Сносим следующую группу (получаем число 2033).
10. Удваиваем число 24, получаем 48.
11.48 десятков в числе, при умножении которого на число единиц, мы должны получить число меньшее 2033 (484*4=1936). Найденная нами цифра единиц (4) и есть третья цифра числа &.
Далее процесс повторяется.
Доказательство приведено мной для случаев:
1. Извлечение квадратного корня из трехзначного числа;
2. Извлечение квадратного корня из четырехзначного числа.
Приближенные методы извлечения квадратного корня (без использования калькулятора) [2].
1.Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а 2 +b, где а 2 ближайший к числу х точный квадрат натурального числа а (а 2 ?х), и пользовались формулой . (1)
Извлечем с помощью формулы (1) корень квадратный, например из числа 28:
Результат извлечения корня из 28 с помощью МК 5,2915026.
Как видим способ вавилонян дает хорошее приближение к точному значению корня.
2. Исаак Ньютон разработал метод извлечения квадратного корня, который восходил еще к Герону Александрийскому (около 100 г. н.э.). Метод этот (известный как метод Ньютона) заключается в следующем.
Пусть а1— первое приближение числа (в качестве а1 можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего х) .
Следующее, более точное приближение а2числа найдется по формуле .
Третье, еще более точное приближение и т.д.
(n+1)-е приближение найдется по формуле .
Нахождение приближенного значения числа методом Ньютона дает следующие результаты: а1=5; а2= 5,3; а3=5,2915.
— итерационная формула Ньютона для нахождения квадратного корня из числа х (n=2,3,4,…, аn — n-е приближение .
Указанный мною способ позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.
Как быстро извлекать квадратные корни
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень. Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней.
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.
Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
.
90 2 = 8100;
100 2 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
[Подпись к рисунку]
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа.
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
2 2 = 4;
8 2 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]
Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный 🙂
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
[Подпись к рисунку]Для начала выясним, между какими числами лежит число 576:
400 < 576 < 900
20 2 < 576 < 30 2
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
Осталось возвести каждое число в квадрат и сравнить с исходным:
24 2 = (20 + 4) 2 = 576
Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
[Подпись к рисунку]Здесь и далее я буду писать только основные шаги. Итак, ограничиваем число:
900 < 1369 < 1600;
30 2 < 1369 < 40 2;
Смотрим на последнюю цифру:
Возводим в квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]2500 < 2704 < 3600;
50 2 < 2704 < 60 2;
Смотрим на последнюю цифру:
Возводим в квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]3600 < 4225 < 4900;
60 2 < 4225 < 70 2;
Смотрим на последнюю цифру:
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Многие спрашивают: зачем вообще считать такие корни? Не лучше ли взять калькулятор и не парить себе мозг?
Извлечение корня из большого числа
А у вас есть зависимость от калькулятора? Или вы считаете, что кроме как с калькулятором или при помощи таблицы квадратов очень сложно вычислить, например, .
Случается, школьники привязаны к калькулятору и даже на умножают, нажимая на заветные кнопочки. Говорят, ну я все равно знаю как посчитать, а сейчас сэкономлю время… Вот будет экзамен… тогда и напрягусь…
Так дело в том, что на экзамене и так будет предостаточно «напряжных моментов»… Как говорится, вода камень точит. Вот и на экзамене мелочи, если их много, способны подкосить…
Давайте минимизируем количество возможных неприятностей.
Извлекаем квадратный корень из большого числа
Мы будем говорить сейчас только о случае, когда результат извлечения корня квадратного – целое число.
Случай 1 + показать
Итак, пусть нам во что-бы то ни стало (например, при вычислении дискриминанта) нужно вычислить корень квадратный из
Мы будем раскладывать число на простые множители. Делим на – получаем снова делим на – получаем На больше нацело число не делится. Но так как сумма цифр делится на то и само число делится на (вообще говоря, видно, что оно и на делится). . Еще раз делим на – получаем на нацело не делится. На пять не делится (не оканчивается цифрой или ).
Подозреваем делимость на Действительно, а ,
Итак, Полный порядок!
Случай 2 + показать
Пусть нам нужно вычислить . Действовать так же, как описано выше, неудобно. Пытаемся разложить на простые множители…
На число нацело не делится (не является четным)…
На нацело не делится (сумма цифр не кратна )…
На нацело не делится (последняя цифра – не и не )…
На нацело не делится, на не делится, на не делится… Ну и долго нам так перебирать все простые числа?
Будем рассуждать несколько иначе.
Мы понимаем, что
Мы сузили круг поиска. Теперь перебираем числа от до Причем ясно, что раз последняя цифра числа – то останавливаться стоит на вариантах или – только эти числа при возведении в квадрат дадут последнюю цифру