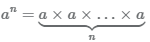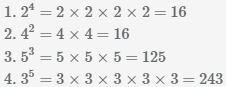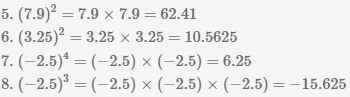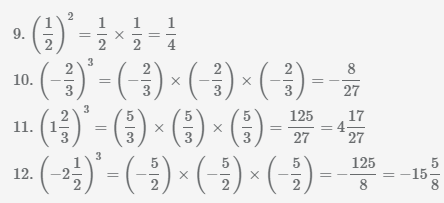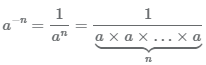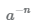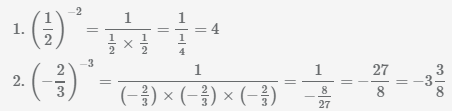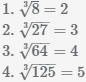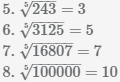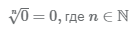Как извлечь корень 4-ой степени из числа?
Корень 4-ой степени обозначается знаком — 4√
4√y=x (корень 4-ой степени из числа y, равен х)
x4= y (в свою очередь при возведении x в 4-ую степень, получим искомое число y)
Например:
Чему равен корень 4-ой степени из 16.
Краткое решение: 4√16 =4√(24) = 24/4 = 2. Ответ: корень 4-ой степени из 16 равен 2.
Чему равен корень 4-ой степени из 243.
Краткое решение: 4√6561 =4√(38) = 38/4 = 32 = 9. Ответ: корень 4-ой степени из 6561 равен 9.
Калькулятор корней поможет извлечь любой корень из числа.
Чтобы извлечь корень введите два числа — основание (из чего извлекается корень) и степень. Калькулятор корней в режиме онлайн извлечет корень. Степень может быть как положительной, так и отрицательной. Число, из которого извлекается корень, должно быть больше нуля.
К примеру, чтобы извлечь квадратный корень из числа 289 мы вводим значения как на картинке ниже и нажимаем кнопку Посчитать. Результат увидим тут же. Помимо этого наш калькулятор может извлекать корни из дробных чисел (дробей), а также извлекать корень дробной степени.
Чтобы извлечь корень любой степень просто введите степень вместо двойки в примере. Также на сайте есть калькулятор степеней, который позволит возвести число в степень.
Ваша оценка
[Оценок: 9152 Средняя: 3.9]
Калькулятор корней Автор admin средний рейтинг 3.9/5 — 9152 рейтинги пользователей
Возведение числа в степень, извлечение корня
- Алгебра
- Возведение в степень, извлечение корня
Калькулятор степеней и извлечения корня
Для возведения числа в степень и нахождения корня, введите число и степень.
Возведение в положительную и отрицательную степень
Положительная степень
Степень числа a с натуральным показателем n (n>1) можно представить в виде произведения 
Пример Выполнить возведение в степень.
Выполним возведение в степень положительных и отрицательных чисел, десятичных дробей, правильных и смешанных дробей.
Отрицательная степень
Степень числа a с отрицательным натуральным показателем n (n<1) можно представить в виде произведения 
Числа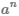 
и 
являются взаимно обратными и их произведение равно единице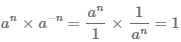 
.
Пример Вычислить значение числа в отрицательной степени.
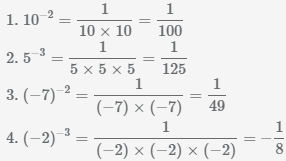
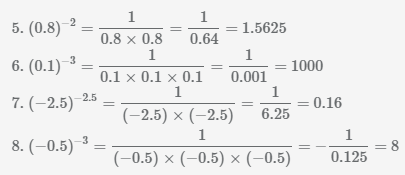
Пример Выполните возведение дроби в отрицательную степень.
Иногда значительно легче вычислить дробь в отрицательной степени, сразу поменяв числить и знаменатель местами и умножив степень на -1. Рассмотрим данное преобразования на примерах.
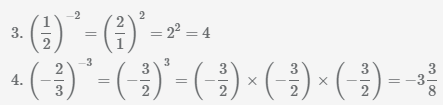
Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: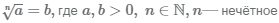 
.
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
Корни 3 степени также называют кубическими корнями.
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: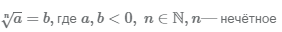 
.
Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
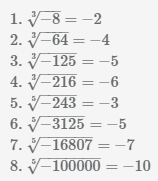
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: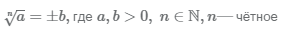 
.
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень четной степени из отрицательного числа не существует для вещественных чисел.
Корень любой степени из нуля
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби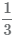 
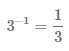
.Обратная операция также верна 
,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Число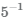 
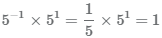
является обратным числом 5, т.е. их произведение равно единице 
, такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
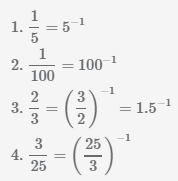
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1
Смотрите также
Другие страницы
Корень n-й степени из числа a определяется как такое число b, что bn = a.
Здесь n — натуральное число, называемое показателем корня (или степенью корня); как правило, оно больше или равно 2, потому что случай n = 1 не представляет интереса.
Обозначение: 
символ (знак корня) в правой части называется радикалом, число a (подкоренное выражение) чаще всего вещественное или комплексное.
Примеры для вещественных чисел:
Как видно из первого примера, у вещественного корня могут быть два значения (положительное и отрицательное),
и это затрудняет работу с корнями. Чтобы обеспечить однозначность, вводится понятие арифметического корня,
значение которого всегда неотрицательно, в первом примере это число 3.
Арифметический корень второй степени называется квадратным корнем, третьей степени — кубическим корнем.
Данный калькулятор позволит Вам найти корень любой степени из любого вещественного числа.
Просто введите число, из которого нужно извлечь корень, степень корня и найдите результат.
Поделиться страницей в социальных сетях: